第六章习题答案
第六章、七章、八章课后习题答案

第六章课后练习题1、三通公司拟发行5年期、利率6%、面额1000元债券一批;预计发行总价格为550元,发行费用率2%;公司所得税率33%。
要求:试测算三通公司该债券的资本成本率。
参考答案:可按下列公式测算:=1000*6%*(1-33%)/550*(1-2%)=7.46%2、四方公司拟发行优先股50万股,发行总价150万元,预计年股利率8%,发行费用6万元。
要求:试测算四方公司该优先股的资本成本率。
参考答案:可按下列公式测算:其中:=8%*150/50=0.24=(150-6)/50=2.88=0.24/2.88=8.33%3、五虎公司普通股现行市价为每股20元,现准备增发8万份新股,预计发行费用率为5%,第一年每股股利1元,以后每年股利增长率为5%。
要求:试测算五虎公司本次增发普通股的资本成本率。
参考答案:可按下列公式测算:=1/19+5%=10.26%4、六郎公司年度销售净额为28000万元,息税前利润为8000万元,固定成本为3200万元,变动成本为60%;资本总额为20000万元,其中债务资本比例占40%,平均年利率8%。
要求:试分别计算该公司的营业杠杆系数、财务杠杆系数和联合杠杆系数。
参考答案:可按下列公式测算:DOL=1+F/EBIT=1+3200/8000=1.4DFL=8000/(8000-20000*40%*8%)=1.09DCL=1.4*1.09=1.535、七奇公司在初创时准备筹集长期资本5000万元,现有甲、乙两个备选筹资方案,有关资料如下表:筹资方式筹资方案甲筹资方案乙筹资额(万元)个别资本成本率(%)筹资额(万元)个别资本成本率(%)长期借款公司债券普通股800120030007.08.514.0110040035007.58.014.0合计5000 —5000 —要求:试分别测算该公司甲、乙两个筹资方案的综合资本成本率,并据以比较选择筹资方案。
参考答案:(1)计算筹资方案甲的综合资本成本率:第一步,计算各种长期资本的比例:长期借款资本比例=800/5000=0.16或16% 公司债券资本比例=1200/5000=0.24或24%普通股资本比例 =3000/5000=0.6或60%第二步,测算综合资本成本率:Kw=7%*0.16+8.5%*0.24+14%*0.6=11.56%(2)计算筹资方案乙的综合资本成本率:第一步,计算各种长期资本的比例:长期借款资本比例=1100/5000=0.22或22% 公司债券资本比例=400/5000=0.08或8%普通股资本比例 =3500/5000=0.7或70%第二步,测算综合资本成本率:Kw=7.5%*0.22+8%*0.08+14%*0.7=12.09%由以上计算可知,甲、乙两个筹资方案的综合资本成本率分别为11.56%、12.09%,可知,甲的综合资本成本率低于乙,因此选择甲筹资方案。
第六章习题及答案

六、补充练习题(一)单项选择题1.在使用收款凭证、付款凭证、转账凭证的单位,与货币资金无关的业务,填制的凭证是()A.收款凭证B.付款凭证C.转账凭证D.通用凭证2.下列凭证属于外来原始凭证的是()A.领料单B.发料汇总表C.上缴税金的收据D.产品交库单3.下列凭证中属于自制原始凭证的是()A.银行收款通知B.付款凭证C.从购买方获得的销售发票D.销售商品所开具的销售发票4.按填制程序和功能不同,会计凭证分为()A.收款凭证、付款凭证和转账凭证B.一次凭证和累计凭证C.原始凭证和记账凭证D.外来凭证和自制凭证5.()是用来编制会计分录的依据,()是用来作为登记账户的依据。
A.原始凭证B.一次凭证C.记账凭证D.累计凭证6.下列有关记账凭证的说法不正确的有()A.记账凭证的填制与审核的作用主要在于:一方面防止不该登入账簿的业务进入会计账簿,另一方面确保该登入的都正确地进入会计账簿B.在课堂上讲的会计分录在我国会计实际工作中是没有的,其对应的是记账凭证C.在会计电算化的情况下,记账凭证分为收款凭证、付款凭证和转账凭证的意义已经不大了D.记账凭证登记的依据全部是原始凭证7.付款凭证表头列示的会计科目是()A.借方科目B.贷方科目C.有时为借方科目,有时为贷方科目D.不能肯定8.下列费用中,直接抵减当期损益的有()A.生产工人工资B.广告费C.生产车间机器设备的折旧费D.生产产品所耗的材料费9.下列费用中,不应计入产品成本的有()A.直接材料费B.直接人工费C.期间费用D.制造费用10.月末,如果某种产品一部分完工一部分未完工,归集在产品成本明细账中的费用总额,还要采用适当的分配方法,在()之间进行分配,然后才能计算完工产品成本。
A.产品品种B.产品批别C.产品生产步骤D.完工产品和在产品11.“累计折旧”账户属于()类账户。
A.资产B.负债C.费用D.成本12.下列项目属于管理费用的有()A.银行借款利息B.厂部管理人员工资C.车间管理人员工资D.车间水电费13.“利润分配”账户年末贷方余额表示()A.已分配的利润额B.未分配的利润额C.未弥补的亏损额D.已实现的净利润14.下列账户中不可能与“制造费用”账户发生对应关系的账户是()A.原材料B.累计折旧C.应付职工薪酬D.库存商品15.下列不计入当期损益的是()A.管理费用B.财务费用C.所得税费用D.制造费用16.产品生产间接耗用的费用,先归入()然后计入有关产品成本中去。
第六章++课后习题+参考答案

第6章完全垄断市场下的价格与产量课后习题参考答案一、单选题1.对完全垄断厂商来说(C)。
A.提高价格一定能够增加收益B.降低价格一定会减少收益C.提高价格未必能增加收益,降低价格未必减少收益D.以上都不对解析:完全垄断市场上,厂商的总收益TR曲线是先增加后减少。
因此,对完全垄断厂商来说,提高价格未必能增加收益,降低价格未必减少收益。
选C。
2.垄断厂商利润极大时,(C)。
A.P=MR=MCB.P>MR=ACC.P>MR=MCD.P>MC=AC解析:垄断厂商定价时遵循利润最大化原则,此时有边际收益等于边际成本MR=MC,而当垄断厂商利润极大时,价格P显然高于边际成本MC。
3.垄断利润或者说超额利润(A)。
A.不是一种成本,因为它不代表生产中使用的资源所体现的替换成本B.不能为垄断者在长期中所获取,因为价格在最优产出水平上必须等于长期平均成本C.为保证资本继续进入该行业所必需D.能为完全竞争者和垄断者一样在长期中获取解析:BCD选项均有明显错误。
垄断利润或者说超额利润不是一种成本,选A。
4.在短期,完全垄断厂商(D)。
A.无盈余B.取得最大利润C.发生亏损D.以上任何一种情况都有可能出现解析:完全垄断厂商在短期均衡点上可能获得超额利润,可能只获得正常利润,还可能发生亏损。
因此选D。
5.在完全垄断厂商的最好或最优产量处(D)。
A.P=MCB.P=SAC的最低点的值C.P最高D.MR=MC解析:根据利润最大化原则,边际收益等于边际成本MR=MC时的价格和产量是最优的。
因此选D。
二、简答题1.成为垄断者的厂商可以任意定价,这种说法对吗?这种说法不正确。
从理论上讲,垄断者是价格的制定者,其产品没有替代品,其他厂商无法进入垄断行业,厂商是产品唯一的卖者。
然而在实际上,如果垄断厂商定价过高,购买量就会下降,从而使总收益和利润下降;其他厂商如看到有丰厚的利润,尽管没有替代品,但相似的替代品总是会生产的,因而垄断厂商如果定价过高,会使自己产品失去销路,市场被相似替代品夺去;国家也会对垄断厂商的定价加以控制,有些国家会通过制定反垄断法,规定最高限价,还可用征税等办法加以控制。
大学物理课后习题答案第六章

第6章 真空中的静电场 习题及答案1. 电荷为q +和q 2-的两个点电荷分别置于1=x m 和1-=x m 处。
一试验电荷置于x 轴上何处,它受到的合力等于零?解:根据两个点电荷对试验电荷的库仑力的大小及方向可以断定,只有试验电荷0q 位于点电荷q +的右侧,它受到的合力才可能为0,所以200200)1(π4)1(π42-=+x qq x qq εε故 223+=x2. 电量都是q 的三个点电荷,分别放在正三角形的三个顶点。
试问:(1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?解:(1) 以A 处点电荷为研究对象,由力平衡知,q '为负电荷,所以2220)33(π4130cos π412a q q a q '=︒εε故 q q 33-=' (2)与三角形边长无关。
3. 如图所示,半径为R 、电荷线密度为1λ的一个均匀带电圆环,在其轴线上放一长为l 、电荷线密度为2λ的均匀带电直线段,该线段的一端处于圆环中心处。
求该直线段受到的电场力。
解:先求均匀带电圆环在其轴线上产生的场强。
在带电圆环上取dl dq 1λ=,dq 在带电圆环轴线上x 处产生的场强大小为)(4220R x dqdE +=πε根据电荷分布的对称性知,0==z y E E23220)(41cos R x xdqdE dE x +==πεθR Oλ1λ2lxy z式中:θ为dq 到场点的连线与x 轴负向的夹角。
⎰+=23220)(4dq R x xE x πε232210)(24R x Rx+⋅=πλπε232201)(2R x xR +=ελ下面求直线段受到的电场力。
在直线段上取dx dq 2λ=,dq 受到的电场力大小为dq E dF x =dx R x xR 2322021)(2+=ελλ 方向沿x 轴正方向。
(完整版)第六章线性空间练习题参考答案

第六章 线性空间练习题参考答案一、填空题1.已知0000,,00V a bc a b c R c b ⎧⎫⎛⎫⎪⎪ ⎪=+∈⎨⎬ ⎪⎪⎪ ⎪+⎝⎭⎩⎭是33R ⨯的一个子空间,则维(V ) = 3 , V 的一组基是000000000100,100,010*********⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.2.在P 4中,若1234(1,2,0,1),(1,1,1,1),(1,,1,1),(0,1,,1)k k αααα===-=线性无关,则k 的取值范围是3k ≠(以1234,,,αααα为行或者列构成的行列式不为零). 3.已知a 是数域P 中的一个固定的数,而1{(,,,),1,2,,}n i W a x x x P i n =∈=是P n+1的一个子空间,则a = 0 ,而维(W)=n 4.维数公式为12dim dim V V +=1212dim()dim()V V V V ++.5.设123,,εεε是线性空间V 的一组基,112233x x x αεεε=++,则由基123,,εεε到基231,,εεε的过渡矩阵T =001100010⎛⎫⎪⎪ ⎪⎝⎭,而α在基321,,εεε下的坐标是321(,,)x x x 由基123,,εεε到基233112,,εεεεεε+++的过渡矩阵为T =011101110⎛⎫⎪⎪ ⎪⎝⎭.6.数域P 上n 级对称矩阵全体构成数域P 上(1)2n n +维线性空间,数域P 上n 级反对称矩阵全体构成数域P 上(1)2n n -维线性空间,数域P 上n 级上三角矩阵全体构成数域P 上(1)2n n +维线性空间,数域P 上n 级对交矩阵全体构成数域P 上n 维线性空间,数域P 上n 级数量矩阵全体构成数域P 上 1 维线性空间.二、判断题1.设n n V P ⨯=,则{,0}n n W A A P A ⨯=∈=是V 的子空间.错.行列式为零的两个方阵的和的行列式未必为零,因此W 中矩阵关于矩阵的加法运算不封闭,不能成为子空间.)2.已知{(,),,,}V a bi c di a b c d R =++∈为R 上的线性空间,且维(V )=2. 错.是子空间,但是是4维的,其基为(1,0),(,0),(0,1),(0,)i i .3.设,n n A B P ⨯∈,V 是0A X B ⎛⎫= ⎪⎝⎭的解空间,V 1是AX =0的解空间,V 2是(A +B)X =0的解空间,则12V V V =.正确. 12V V 中的向量既满足AX =0,又满足(A +B)X =0,因此也满足BX =0,即满足0A X B ⎛⎫= ⎪⎝⎭,即为V 中的向量.反之,V 中的向量既在1V 中,又在2V 中,即为12V V 中的向量.因此12V V V =.4.设线性空间V 的子空间W 中每个向量可由W 中的线性无关的向量组12,,,s ααα线性表出,则维(W)=s.正确.根据定理1.5.设W 是线性空间V 的子空间,如果,,V αβ∈但,W W αβ∉∉且则必有.W αβ+∉错误.可能.W αβ+∈如取,αβ为一对互为负向量,则0.W αβ=+∈ 6. }0|),,{(33321=∈=x R x x x W 是3R 的子空间.正确. 基为(1,0,0),(0,1,0),维数为2. 7.}1|),,{(23321=∈=x R x x x W 是3R 的子空间. 错误.不包含零向量.8.}|),,{(3213321x x x R x x x W ==∈= 是3R 的子空间. 正确.基为(1,1,1),维数为1.9.}|),,{(3213321x x x R x x x W -=∈= 是3R 的子空间. 正确. 基为(1,1,0),(1,0,-1),维数为2. 三、计算题1.求所有与A 可交换的矩阵组成的nn P ⨯的子空间()C A 的维数与一组基,其中100020003A ⎛⎫⎪= ⎪ ⎪⎝⎭.解:设矩阵33()ij B b ⨯=与A 可交换,即有AB BA =.即111213111213212223212223313233313233100100020020003003b b b b b b b b b b b b b b b b b b ⎛⎫⎛⎫⎛⎫⎛⎫⎪⎪⎪⎪= ⎪⎪ ⎪⎪ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭.111213111213212223212223313233313233232222333323b b b b b b b b b b b b b b b b b b ⎛⎫⎛⎫⎪ ⎪= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭. 所以有,()0,,1,2,3.ij ij ij ib b j i j b i j =-==当i j ≠时,0ij b =,因此11223300()0000b C A b b ⎧⎫⎛⎫⎪⎪⎪=⎨⎬ ⎪⎪⎪ ⎪⎝⎭⎩⎭ 维数为3,基为112233,,E E E .2.在线性空间P 4中,求由基1234,,,αααα到基1234,,,ββββ的过渡矩阵,并求(1,4,2,3)α=在基1234,,,αααα下的坐标,其中1234(1,0,0,0),(4,1,0,0),(3,2,1,0),(2,3,2,1)αααα===-=- 1234(1,1,8,3),(0,3,7,2),(1,1,6,2),(1,4,1,1).ββββ====--- 解:令过渡矩阵为T ,则有10111432131401238761001232210001T --⎛⎫⎛⎫⎪⎪- ⎪ ⎪=⎪ ⎪- ⎪⎪-⎝⎭⎝⎭因此1143210112379801231314633100128761232100132213221T ------⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪--⎪ ⎪ ⎪==⎪ ⎪ ⎪- ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭. 令1234114324012320012301x x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪- ⎪⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭112341432114113611010123401274210012200122400013000133x x x x -----⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪⎪ ⎪-- ⎪ ⎪ ⎪ ⎪⎪ ⎪===⎪ ⎪ ⎪ ⎪⎪ ⎪-- ⎪ ⎪ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭ (1,4,2,3)α=在基1234,,,αααα下的坐标为(-101,21,-4,3) 四、证明题1.V 为定义在实数域上的函数构成的线性空间,令12{()(),()()},{()(),()()}W f x f x V f x f x W f x f x V f x f x =∈=-=∈=--证明:W 1、W 2皆为V 的子空间,且12.V W W =⊕证明:W 1、W 2 分别为偶函数全体及奇函数全体构成的集合,显然W 1、W 2均为非空的.由奇偶函数的性质可得W 1、W 2皆为V 的子空间.()()()()(),()22f x f x f x f x f x V f x +---∀∈=+. 而12()()()(),22f x f x f x f x W W +---∈∈,因此12.V W W =+又12{0}.W W =所以12.V W W =⊕2.设W 是P n 的一个非零子空间,若对于W 的每一个向量12(,,,)n a a a 来说,或者120n a a a ====,或者每一个i α都不等于零,证明:维(W)=1.证明:由W 是P n 的一个非零子空间,可得W 中含有非零向量设1212(,,,),(,,,)n n a a a b b b αβ==是W 中的任二个非零向量,由题意可得每一个,i i a b 都不等于零.考虑向量11112112121211(,,,)(,,,)(0,,,)n n n n b a b a a a a b b b b a a b b a a b W αβ-=-=--∈.由题设条件有1212110n n b a a b b a a b -==-=,即有1212n na a ab b b ===.即W 中的任二个非零向量均成比例,因此维(W)=1.。
第六章 习题答案 1. (1)临界分切应力n及取向因子数据如附表23 …

第六章 习题答案1.(1)临界分切应力n及取向因子数据如附表2.3所示。
以上数据表明,实验结果符合临界分切应力定律τk =σm。
(2)屈服应力σs与取向因子,m之间的关系如附图2.17所示。
6.单滑移是指只有一个滑移系进行滑移。
滑移线呈一系列彼此平行的直线。
这是因为单滑移仅有一组多滑移是指有两组或两组以上的不同滑移系同时或交替地进行滑移。
它们的滑移线或者平行,或者相交成一定角度。
这是因为一定的晶体结构中具有一定的滑移系,而这些滑移系的滑移面之间及滑移方向之间都交滑移是指两个或两个以上的滑移面沿共同的滑移方向同时或交替地滑移。
它们的滑移线通常为折线或波纹状。
只是螺位错在不同的滑移面上反复“扩展”的结果。
10.滑移带一般不穿越晶界。
如果没有多滑移时,以平行直线和波纹线出现,如附图2.19(a),它可以通过抛光而去除。
机械孪晶也在晶粒内,因为它在滑移难以进行时发生,而当孪生使晶体转动后,又可使晶体滑移。
所以一般孪晶区域不大,如附图2.19(b)所示。
孪晶与基体位向不同,不能通过抛光去除。
退火孪晶以大条块形态分布于晶内,孪晶界面平直,一般在金相磨面上分布比较均匀,如附图2。
19(c)所示,且不能通过抛光去除。
11.低碳钢的屈服现象可用位错理论说明。
由于低碳钢是以铁素体为基的合金,铁素体中的碳(氮)原子与位错交互作用,总是趋于聚集在位错线受拉应力的部位以降低体系的畸变能,形成柯氏气团对位错起“钉扎”作用,致使σs 升高。
而位错一旦挣脱气团的钉扎,便可在较小的应力下继续运动,这时拉伸曲线上又会出现下屈服点。
已经屈服的试样,卸载后立即重新加载拉伸时,由于位错已脱出气团的钉扎,故不出现屈服点。
但若卸载后,放置较长时间或稍经加热后,再进行拉伸时,由于熔质原子已通过热扩散又重新聚集到位错线周围形成气团,故屈服现象又会重新出现。
吕德斯带会使低碳薄钢板在冲压成型时使工件表面粗糙不平。
其解决办法,可根据应变时效原理,将钢板在冲压之前先进行一道微量冷轧(如1%~2%的压下量)工序,使屈服点消除,随后进行冲压成型,也可向钢中加入少量Ti,A1及C,N等形成化合物,以消除屈服点。
有机化学-第六章-卤代烃-习题答案
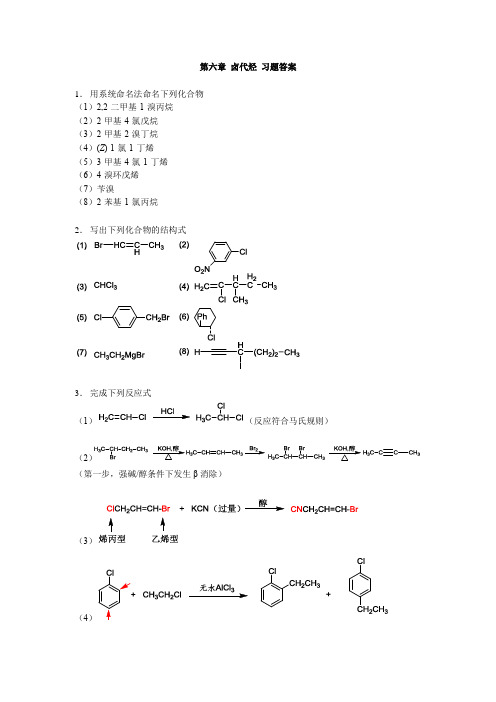
第六章卤代烃习题答案1.用系统命名法命名下列化合物(1)2,2-二甲基-1-溴丙烷(2)2-甲基-4-氯戊烷(3)2-甲基-2-溴丁烷(4)(Z)-1-氯-1-丁烯(5)3-甲基-4-氯-1-丁烯(6)4-溴环戊烯(7)苄溴(8)2-苯基-1-氯丙烷2.写出下列化合物的结构式3.完成下列反应式(1)(反应符合马氏规则)(2(第一步,强碱/醇条件下发生β消除)(3)(4(5(Cl离去生成稳定的苄基碳正离子)(6(优先生成π-π共轭产物)(7)(由于乙醇钠写在反应式左侧,应该为反应原料,因此发生威廉姆森反应生成醚;如果写在箭头上方表示为碱,加热条件下发生消除反应)(8(注意硝酰氧基的正确写法,不能写成-NO3)4.用化学方法鉴别下列化合物(1)(2)(3)5.按要求将下列各组化合物排序(1)C6H5CHBrC6H5>CH3CHBrCH3>CH3CH2CH2Br (依据碳正离子稳定性)(2)1-溴丁烷>2-溴丁烷>2-甲基-2-溴丙烷(根据位阻大小来判断)(3)(前面两个都是烯丙型,后面两个都是乙烯型,活性肯定是烯丙型最高因为烯丙型碳正离子更稳定,乙烯型活性最差。
作为离去基团,溴的离去活性相对于氯更高,因此可以得出以上活性排序)6.试判断在下列各种情况下卤代烷水解是属于S N1机理还是S N2机理(1)S N2 (2)S N1 (3)S N2 (4)S N17.完成下列转化。
(1)(2)(利用格氏试剂与二氧化碳的反应来增加一个碳原子)8.推断题9.推断题。
习题答案(第六章)

1、R n 中分量满足下列条件的全体向量1(,,)n x x 的集合,是否构成R n的子空间?①10n x x ++=;②120n x x x ⋅⋅⋅=;③2211n x x ++=。
解:①是,设(){}111,,|0n n V x x x x =++=,显然V 1≠∅,1,,,a b F V ξη∀∈∀∈,设1212(,,),(,,)x x y y ξη==,则()()()1111,,,,,,n n n n a b a x x b y y ax by ax by ξη+=+=++,而1111()()()()000n n n n ax by ax by a x x b y y a b ++++=+++++=+=所以1a b V ξη+∈,所以V 1是R n 的子空间; ②不是,取(1,0,,0),(0,1,,1)αβ==,则(){}11,,,|0n n V x x x x αβ∈=⋅⋅=,但(1,1,,1)V αβ+=∉,所以V 不是R n 的子空间;③不是,取(1,0,,0),(0,1,0,,0)αβ==,则(){}2211,,,|1n n V x x x x αβ∈=++=,但(1,1,0,,0)V αβ+=∉,所以V 不是R n 的子空间。
2、子集{}1|,,V X AX XB A B n ==为已知的阶矩阵是否是()n M F 的子集?解:是()n M F 的子集;证:显然1V ≠∅,1,,,X Y V a b F ∀∈∈,有()()A aX bY aAX bAY aXB bYB aX bY B +=+=+=+,所以1aX bY V +∈,所以1V 是()n M F 的子集。
3、设12(1,0,1,0),(1,1,2,0)αα==-,求含12,αα的R 4的一组基。
解:因为101010101010112001100010⎛⎫⎛⎫⎛⎫→→⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭,取34(0,0,1,0),(0,0,0,1)αα==,所以{}1234,,,αααα为R 4的一组基。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
检查能否自启动
Q n 1 3
Q2n
Q1n
Q3n
Q1nQ3n
Q n 1 2
Q3nQ1nQ2n
Q1nQ2n
Q n 1 1
Q1n、Z
Q3n
Q2n
Q1n
Q3n Q2n Q1n
110 111
Q3n+1 Q2n+1 Q1n+1 Z
0 010 1 100
可自启动也无错误输出。电路省略。
解:(1)根据题意,现态
状态表为:
Q2Q1Q0
000
001
010
011
100
101
110
111
次态/输出
C=0
C=1
110/0
100/0
ddd/d
ddd/d
011/0
ddd/d
111/0
000/1
ddd/d
110/0
ddd/d
ddd/d
010/0
111/0
000/1
011/0
(2) 求输出方程、状态方程、激励方程
输入X:1010101101100011110110001
输出Z:0000000100100000000010000
解:
0/0
1/0
1/0
X/Z
S0
S1
0/0 0/0
S3 0/0 S2
1/0 1/1
11、 12、
表6-1 (A,E),B,C,D,F,G
表6-2 A,(B,F),C,(D,E)
表6-3
(A,B,F),(B,E,F)(C,D)
表6-4
(A,B,C),(A,C,D)(A,D,E)
13、
表6-5
A(00),B(01),C(10),D(11)
表6-6
A(00),B(01),C(11),D(10)
16、试用JK触发器设计一个可控计数器。 当C=1时,实现000→100→110→111→011→000; 当C=0时,实现000→110→010→011→111→000。
6、分析图6-71所示同步时序电路说明该电路的 功能 。
解:(1)写出输出方程和激励方程
J1=K1=1 J2=K2=XQ1 Z=XQ1Q2+XQ1 Q2
写出状态方程
根据Qn1 JQ KQ得
Q n1 1
Q1
Q n1 2
X
Q1
Q2
(2) 状态转换表
Q1n1 Q1n
Q n1 2
J1 Q2Q1
Q0C
00
01
11
10
00 1 0 d d
01 d d d d
11 d d d d
10 d 1 d d
K1 Q0C
Q2Q1
00 01 11 10
00 d d d d
01 0 d 1 0
11 0 0 0 1
14 10 d d d d
J1 Q2 C
K1 Q2C Q2Q0 C
000/1 011/0
Q -> Qn+1 J K 000d 011d 10d1 11d0
J2 Q2Q1
Q0C
00
01
11
10
00 1 1 d d
01 0 d 0 1
11 d d d d
10 d d d d
K2 Q0C
Q2Q1
00 01 11 10
00 d d d d
01 d d d d
11 1 0 1 1
&
&
Q0 Q1 Q2 Q3
1
CTP
CO
CTT
I
LD
CR D3 D2 D1 D0
1
CP
Q0 Q1 Q2 Q3
CTP
CO
CTT
II LD
CR D3 D2 D1 D0
1
26、 CP
D Q1 Q1
D Q2 Q2
D Q3 Q3
激励方程:D1 Q3 D2 Q1 D3 Q2
状态方程:Qn1 1
Q3n
/1
/0
101 /0 100 /0 011
Q3n Q2n Q1n
000 001 010 011 100 101 110 111
Q3n+1 Q2n+1 Q1n+1 Z
1 01 1 0 00 0 0 01 0 0 10 0 0 11 0 1 00 0 d dd d d dd d
J3 Q2 Q1、K3 Q1、J2 Q3Q1、K2 Q1 J1 K1 1、Z Q3Q2 Q1
现态
次态/输出
Q2Q1Q0 000
C=0 110/0
C=1 100/0
001
111/0
100/0
010
011/0
001/0
011
111/0
000/1
100
010/0
110/0
101
010/0
011/0
110
010/0
111/0
111
000/1
011/0
17、试用JK触发器设计一个“0010”串行序列检测 器(可重叠)。
现态 Q2Q1Q0
000 001 010 011 100 101 110 111
次态/输出
C=0
C=1
110/0 100/0
ddd/0 ddd/0
011/0 ddd/0
111/0 000/1
ddd/0 110/0
ddd/0 ddd/0
010/0 111/0
000/1 011/0
Q -> Qn+1 J K 000d 011d 10d1 11d0
10
00 0 0 d d
01 1 d d d
11 0 1 d d
10 d 0 d d
K0 Q0C
Q2Q1
00 01 11 10
00 d d d d
01 d d 1 0
11 d d 0 1
17 10 d d d d
(3) 检查自启动问题
Qn21 Q2 Q1 Q2Q0 C Q2Q0C Q1n1 Q2Q1 Q1C Q2Q1Q0 Q2Q1C Q2Q1C Q1Q0C Qn01 Q2Q1Q0 Q1Q0C Q2Q0C Q2Q0C
1/0 000
1/0 010
0/0
1/0 100 0/1
0/0 001 1/0 011 1/0
0/0
0/0
X Q3n Q2n Q1n Q3n+1 Q2n+1 Q1n+1 Z
10 0 0 0 10 0 1 0 10 1 0 1 10 1 1 0 11 0 0 0 11 0 1 d 11 1 0 d 11 1 1 d
10 d 0 d d
J2 Q1 Q0C
K2 Q0 C
J2 Q2Q1
Q0C
00
01
11
10
00 1 1 d d
01 0 d 0 1
11 d d d d
10 d d d d
K2 Q0C
Q2Q1
00 01 11 10
00 d d d d
01 d d d d
11 1 0 1 1
13 10 d 0 d d
00 0 0 d d
01 1 d d d
11 0 1 d d
10 d 0 d d
K0 Q0C
Q2Q1
00 01 11 10
00 d d d d
01 d d 1 0
11 d d 0 1
16 10 d d d d
J0 Q2Q1 Q1C K0 Q2C Q2C
J0 Q2Q1
Q0C
00
01
11
采用异步清0法,则在160状态产生异步清0信号。 160=10100000
&
1
Q0 Q1 Q2 Q3
CTP
CO
CTT
I
LD
Q0 Q1 Q2 Q3
CTP
CO
1 CTT
II
1
LD
CR D3 D2 D1 D0
CR D3 D2 D1 D0
CP
若采用同步置数,则在159状态产生预置数信号。 159=10011111
X
Q1n
Q2n
Z XQ1nQ2n X Q1n Q2n
X Q2n Q1n
Q2n+1 Q1n+1
Z
000 001 010 011 100 101 110 111
01 0 10 0 11 0 00 1 11 1 00 0 01 0 10 0
(3) 状态转换图
X/Z
0/0
00 1/0 01
0/1 1/1
1/0 0/0
11 1/0 10
0/0
(4) 时序图
1 2 3 45
CP
X
“1”
Q1n
Q2n
1 2 3 45
CP
X
“0”
Q1n
Q2n
Y
Y
(5) 电路功能:X=0时,4进制加法计数器; X=1时,4进制减法计数器。
4进制可异计数器(可加可减)。
9、作出“1011”序列检测器的状态图。典型输入、 输出序列如下。
00
01
1
11
1
10
Z Q2Q1Q0C Q2Q1Q0C
现态 Q2Q1Q0
000 001 010 011 100 101 110 111
