自然数立方的规律研究
1到10数字的立方

1到10数字的立方摘要:一、引言二、1 到10 的数字立方简介1.数字立方的概念2.1 到10 的数字立方特点三、1 到10 的数字立方计算方法四、1 到10 的数字立方在实际生活中的应用五、结论正文:一、引言数字立方是一个在数学领域中十分常见的概念,尤其在计算机科学和数据处理方面有着广泛的应用。
本文将主要介绍1 到10 的数字立方,并对其进行简单的分析。
二、1 到10 的数字立方简介1.数字立方的概念数字立方,顾名思义,是指一个数的立方。
立方是指一个数自乘三次的结果。
例如,2 的立方就是2×2×2=8。
2.1 到10 的数字立方特点1 到10 的数字立方有一个十分显著的特点,那就是它们的值都是完全立方数。
完全立方数是指一个数可以表示为某个整数的立方。
例如,1、8 和27就是完全立方数,因为1=1×1×1,8=2×2×2,27=3×3×3。
三、1 到10 的数字立方计算方法计算1 到10 的数字立方十分简单,只需将每个数自乘三次即可。
具体如下:1 的立方=1×1×1=12 的立方=2×2×2=83 的立方=3×3×3=274 的立方=4×4×4=645 的立方=5×5×5=1256 的立方=6×6×6=2167 的立方=7×7×7=3438 的立方=8×8×8=5129 的立方=9×9×9=72910 的立方=10×10×10=1000四、1 到10 的数字立方在实际生活中的应用虽然1 到10 的数字立方看起来似乎没有什么实际应用,但实际上,它们在计算机科学和数据处理领域有着广泛的应用。
例如,在计算机图形学中,立方体是一个十分基本的几何形状,其体积的计算就需要用到立方根,而立方根实际上就是数字立方的一个逆运算。
推导自然数立方和公式两种方法

推导自然数立方和公式两种方法自然数立方和公式是指1³+2³+3³+.+n³的公式,下面我将介绍两种推导方法。
第一种方法是利用数学归纳法来证明。
第一步,当n=1时,1³=1,所以等式成立。
第二步,假设当n=k时,公式成立,即1³+2³+3³+.+k³=k²(k+1)²/4。
第三步,当n=k+1时,(k+1)³=k³+3k²+3k+1,所以(k+1)³+1³=(k+1)³-k³=3k²+4k+1=(k+1)²(k+2)/4。
因此当n=k+1时,公式也成立。
第四步,根据数学归纳法,我们可以得出1³+2³+3³+.+n³=n²(n+1)²/4对所有正整数n都成立。
第二种方法是利用排列组合的知识来证明。
第一步,考虑从n个不同的自然数中任取3个数的组合数。
这些组合数可以表示为C(n,3),即从n个不同元素中取出3个元素的组合数。
第二步,根据排列组合的知识,C(n,3)=n(n-1)(n-2)/6。
因此,对于任意的n,我们有C(n,3)=n(n-1)(n-2)/6。
第三步,利用上述公式,我们可以得到1³+2³+3³+.+n³=C(1,3)+C(2,3)+C(3,3)+.+C(n,3)=n(n-1)(n-2)/6 + n(n-1)(n-2)/6 + n(n-1)(n-2)/6 + . + n(n-1)(n-2)/6 =n²(n+1)²/4。
因此,我们得到了自然数立方和公式为1³+2³+3³+.+n³=n²(n+1)²/4,并且利用两种不同的方法证明了该公式的正确性。
自然数立方的规律研究
自然数立方的规律研究我喜欢数学,因为在数学王国里有许多有趣的规律。
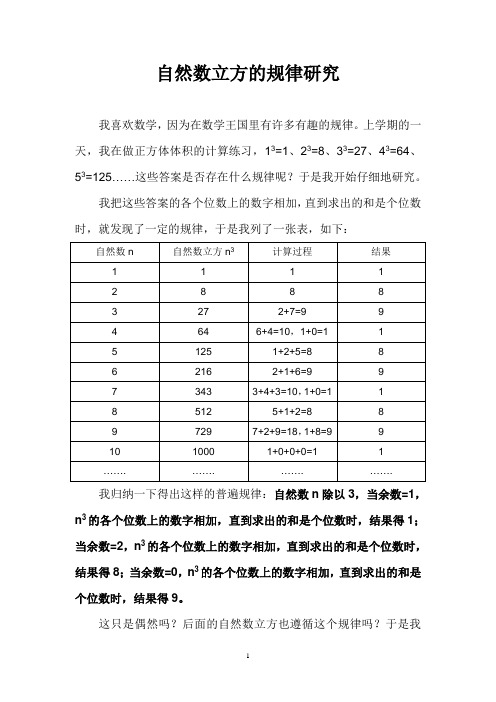
上学期的一天,我在做正方体体积的计算练习,13=1、23=8、33=27、43=64、53=125……这些答案是否存在什么规律呢?于是我开始仔细地研究。
我把这些答案的各个位数上的数字相加,直到求出的和是个位数时,就发现了一定的规律,于是我列了一张表,如下:我归纳一下得出这样的普遍规律:自然数n除以3,当余数=1,n3的各个位数上的数字相加,直到求出的和是个位数时,结果得1;当余数=2,n3的各个位数上的数字相加,直到求出的和是个位数时,结果得8;当余数=0,n3的各个位数上的数字相加,直到求出的和是个位数时,结果得9。
这只是偶然吗?后面的自然数立方也遵循这个规律吗?于是我开始验证我发现的规律。
验证结果让我太高兴了,我立刻把这个发现告诉全家人,大家纷纷拿笔来计算,最后也都符合我发现的这个规律。
我太自豪了,这可是我自己动脑筋思考和研究的结果,也许这还是个伟大的发现呢!妈妈笑着提醒我,“你再研究研究,为什么自然数立方会有这样的规律呢?”对呀,为什么呢?于是,我又进入了新一轮的苦思冥想,经过几番挫折,我都没有成功,后来我逐个突破,先从余数是0的开始,这个自然数n就是3的倍数,即n=3x(x=1,2,3,……),那么,n3=27x3=9×3x3,也就是说这类自然数的立方一定是9的倍数,9的倍数各个位数之和一定是9的倍数,所以将各个位数上的数字相加,直到求出的和是个位数时,结果一定是9。
啊哈,我越来越接近成功了!再来看,当余数是1时,这个自然数n就是3的倍数加1,即n=3x+1(x=0,1,2,3,……),那么,n3=(3x+1)3=27x3+27x2+9x+1=9(3x3+3x2+x)+1,也就是说这类自然数的立方一定是9的倍数再加1,那么结果一定是9+1=10,1+0=1,哈哈,第二关闯关成功!最后看,当余数是2时,这个自然数n就是3的倍数减1,即n=3x-1(x=1,2,3,……),那么,n3=(3x-1)3=27x3-27x2+9x-1=9(3x3-3x2+x)-1,也就是说这类自然数的立方一定是9的倍数再减1,那么结果一定是9-1=8,哈哈,第三关闯关成功!耶!我兴奋地大叫并跳了起来。
1到10立方数的规律

1到10立方数的规律1. 引言在数学中,规律是一种很重要的概念。
它指的是一种可预测或可重复的模式或趋势。
在本文中,我们将探讨1到10立方数的规律。
2. 什么是立方数?首先,让我们来看看什么是立方数。
在数学中,立方数指的是一个数字的三次幂。
例如,2的立方为8(2 x 2 x 2 = 8),3的立方为27(3 x 3 x 3 = 27)。
3. 计算1到10的立方数接下来,我们将计算1到10的立方数,并列出它们的结果:1^3 = 12^3 = 83^3 = 274^3 = 645^3 = 1256^3 = 2167^3 = 3438^3 = 5129^3 = 72910^3 =10004. 规律一:每个数字都比前一个数字大一个奇数通过观察上面列出来的结果,我们可以发现第一个规律:每个数字都比前一个数字大一个奇数。
例如,从1到2,差距为7;从2到3,差距为19;从5到6,差距为11。
5. 规律二:相邻两个数字之间差距逐渐增大除了规律一之外,我们还可以发现第二个规律:相邻两个数字之间的差距逐渐增大。
例如,从1到2的差距为7,从2到3的差距为19,从3到4的差距为37。
6. 规律三:每个数字的个位数都是1、8、7、4、5、6、3、2、9或0 我们还可以发现第三个规律:每个数字的个位数都是1、8、7、4、5、6、3、2、9或0。
这些数字以递归模式重复出现。
例如,1^3 = 1,8^3 = 512,7^3 = 343。
7. 规律四:相邻两个数字之间的立方数和具有固定的模式除了上述规律之外,我们还可以发现第四个规律:相邻两个数字之间的立方数和具有固定的模式。
例如,1^3 + 2^3 = 9;2^3 + 3^3 = 35;8^3 + 9^3 = 1457。
8. 规律五:任意一个正整数都可以表示成连续奇数之和除此之外,我们还可以发现第五个规律:任意一个正整数都可以表示成连续奇数之和。
例如,27可以表示成13 + 11 + 9 – 7 – 5 + 3。
掌握立方数的基本规律

掌握立方数的基本规律立方数是指一个数的立方,即该数与自己相乘三次的结果。
在数学中,掌握立方数的基本规律对于解决问题和推理推断起着重要的作用。
本文将介绍立方数的定义和性质,并通过几个具体例子来加深对立方数的认识。
一、立方数的定义立方数是一个数的立方,记作n³,其中n为整数。
例如,2³=2×2×2=8,8就是2的立方数。
二、立方数的性质1. 两个立方数的和等于另一个立方数。
即,若a³+b³=c³,其中a、b、c为整数,那么c也是一个立方数。
这个性质被称为费马定理,是一个著名的数论问题。
2. 一个立方数与另一个整数的和的立方等于两个立方数之和。
即,(a³+b)³=a⁶+3a⁴b+3a²b²+b³。
这个性质称为立方和公式,可以用来展开立方和式。
3. 两个连续整数的立方数之差等于两个连续奇数的和。
即,(n+1)³-n³=(n+1)²+n(n+1)+n²=3(n²+n)+1。
三、立方数的应用立方数的基本规律在数学和物理学中有广泛的应用,以下是一些例子:1. 数理推理通过了解立方数的基本规律,我们可以进行数理推理。
例如,假设我们知道a³+b³=c³,并且a、b、c都是整数,那么我们可以推断出费马定理成立,即存在一个整数d,使得d³=a³+b³=c³。
2. 几何体积立方数用于计算几何体积。
例如,如果一个立方体的边长为a,那么它的体积可以表示为V=a³。
通过计算立方体的体积,我们可以解决物理学和工程学中的相关问题。
3. 图形分析立方数也可以用于图形分析。
例如,当我们观察一个立方数序列时,可以通过对数值进行分析发现规律。
这种分析方法在数学建模、数据分析和算法设计中非常有用。
立方数与平方数立方数和平方数的计算与性质

立方数与平方数立方数和平方数的计算与性质在数学中,立方数和平方数是一类特殊的整数。
立方数是指一个数的立方,即将这个数自己乘以自己再乘以自己,而平方数是指一个数的平方,即将这个数自己乘以自己。
本文将探讨立方数和平方数的计算方法以及它们的性质。
一、立方数的计算与性质立方数的计算非常简单,只需要将一个数乘以自身再乘以自身即可。
例如,2的立方等于2 × 2 × 2 = 8,而3的立方等于3 × 3 × 3 = 27。
我们可以发现,立方数都是一个数的三次方,因此它们的数值会迅速增大。
立方数具有一些独特的性质。
首先,立方数总是正数,因为任何数的立方都不可能为负数。
其次,立方数是自然数的一种特殊类型。
例如,1的立方等于1,2的立方等于8,3的立方等于27,4的立方等于64,依此类推。
我们可以观察到每个自然数都有一个对应的立方数。
立方数之间的差异也非常明显。
当我们计算不同的立方数时,它们之间的差值会急剧增加。
例如,1和8之间的差值是7,而8和27之间的差值是19。
这种差异在大的立方数之间尤其明显。
这也意味着立方数之间的增长速度是不均匀的。
二、平方数的计算与性质平方数的计算方法与立方数类似,只需要一个数乘以自身即可。
例如,2的平方等于2 × 2 = 4,而3的平方等于3 × 3 = 9。
与立方数一样,平方数也会随着数值的增大而迅速增加。
平方数具有一些独特的性质。
首先,与立方数不同,平方数既可以是正数,也可以是零。
例如,0的平方等于0,1的平方等于1,2的平方等于4,3的平方等于9,依此类推。
其次,平方数也是自然数的一种特殊类型。
与立方数类似,每个自然数都有一个对应的平方数。
平方数之间的差异也是显而易见的。
当我们计算不同的平方数时,它们之间的差值会越来越大。
例如,1和4之间的差值是3,而4和9之间的差值是5。
这种差异在大的平方数之间同样存在。
同样地,平方数之间的增长速度也是不均匀的。
初中数学知识归纳平方数和立方数的性质

初中数学知识归纳平方数和立方数的性质平方数和立方数是初中数学中的重要概念。
它们有着各自独特的性质和特点,通过对其进行归纳整理,可以帮助我们更好地理解和应用这些数学知识。
本文将对平方数和立方数的性质进行归纳和总结。
一、平方数的性质平方数是指某个自然数的平方,即将一个自然数乘以它自身所得到的数。
我们可以通过找规律的方法来研究平方数的性质。
1. 平方数的末尾数字只能是0、1、4、5、6、9。
例如,1的平方是1,4的平方是16,9的平方是81,它们的末尾数字分别为1、6、1,符合以上规律。
2. 连续的自然数的平方数之间的差值是等差数列。
例如,2的平方是4,3的平方是9,它们的差值是5,4的平方是16,与前一个平方数的差值是7,符合等差数列的规律。
3. 一个奇数的平方是奇数,一个偶数的平方是偶数。
例如,3是奇数,3的平方是9,也是奇数;4是偶数,4的平方是16,也是偶数。
4. 平方数的个位数字只能是0、1、4、5、6、9。
例如,10的平方是100,20的平方是400,30的平方是900,它们的个位数字分别为0、0、0。
二、立方数的性质立方数是指某个自然数的立方,即将一个自然数乘以它自身两次所得到的数。
我们同样可以通过找规律的方法来研究立方数的性质。
1. 立方数的个位数字只能是0、1、8、3、4、7、6、5、2、9。
例如,1的立方是1,8的立方是512,9的立方是729,它们的个位数字分别为1、2、9,符合以上规律。
2. 两个连续的自然数的立方数之间的差值是等差数列。
例如,1的立方是1,2的立方是8,它们的差值是7,3的立方是27,与前一个立方数的差值是19,符合等差数列的规律。
3. 一个奇数的立方是奇数,一个偶数的立方是偶数。
例如,3是奇数,3的立方是27,也是奇数;4是偶数,4的立方是64,也是偶数。
4. 立方数的个位数字的和可以被3整除。
例如,10的立方是1000,个位数字为0,和3整除;20的立方是8000,个位数字为0,同样可以被3整除。
第17题 自然数的立方和有什么规律-

第17题自然数的立方和有什么规律13+23=13+23+33=13+23+33+43=…你能发现自然数的立方和有什么规律吗?分析:试算一归纳一猜想一论证是研究与发现数学规律的重要手段,也是探求数学模式的重要途径。
要解决本题,我们可先考察前2个自然数的立方和,前3个自然数的立方和,前4个自然数的立方和等特殊情形,再从中寻求一般的规律。
解:试算:13+23=9=3213+23+33=36=6213+23+33+43=100=10213+23+33+43+53=225=152归纳:从以上的试算可发现它们的结果均为一个平方数,那么这些平方数又有怎样的规律呢?我们再进行试算:1+2=31+2+3=61+2+3+4=101+2+3+4+5=15由此我们可进一步归纳发现前n个自然数的立方和正好等于前n个自然数和的平方。
因此我们猜测:13+23+33+…+n3=(1+2+3+…+n)2回顾:以上为了发现前n个自然数的立方和的规律,我们先观察n=2,3,4,5的一些特殊情况,从中发现规律,进而对它的一般情况作出预测,猜测前n个自然数的立方和为前n个自然数之和的平方。
数学家或科技人员面对某一个问题,在研究它的一些特殊情况的基础上,对它的一般情况作出预测,这样的预测叫做猜想。
例如,德国数学家哥德巴赫(Gold-bach,1690—1764)经过观察,发现一个有趣的现象:任何大于5的整数,都可以表示为三个质数的和,他猜想这个命题是正确的,但他本人无法给予证明。
1742年6月6日,哥德巴赫去求教当时颇负盛名的瑞士数学家欧拉(Euler,1707—1783)欧拉经过反复研究,发现解决问题的关键在于证明任意大于2的偶数,都能表示为两个质数的和。
于是,欧拉对大于2的偶数逐个加以观察,得到如下一张长长的表:4=2+26=3+38=3+510=3+7=5+512=5+714=3+11=7+716=3+13=5+1118=5+13=7+1120=3+17=7+1322=3+19=5+17=11+1124=5+19=7+17=11+1326=3+23=7+19=13+1328=5+23=11+17…这张表还能继续延长下去,最后欧拉猜想上述结论是正确的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自然数立方的规律研究我喜欢数学,因为在数学王国里有许多有趣的规律。
上学期的一天,我在做正方体体积的计算练习,13=1、23=8、33=27、43=64、53=125……这些答案是否存在什么规律呢?于是我开始仔细地研究。
我把这些答案的各个位数上的数字相加,直到求出的和是个位数时,就发现了一定的规律,于是我列了一张表,如下:我归纳一下得出这样的普遍规律:自然数n除以3,当余数=1,n3的各个位数上的数字相加,直到求出的和是个位数时,结果得1;当余数=2,n3的各个位数上的数字相加,直到求出的和是个位数时,结果得8;当余数=0,n3的各个位数上的数字相加,直到求出的和是个位数时,结果得9。
这只是偶然吗?后面的自然数立方也遵循这个规律吗?于是我开始验证我发现的规律。
验证结果让我太高兴了,我立刻把这个发现告诉全家人,大家纷纷拿笔来计算,最后也都符合我发现的这个规律。
我太自豪了,这可是我自己动脑筋思考和研究的结果,也许这还是个伟大的发现呢!妈妈笑着提醒我,“你再研究研究,为什么自然数立方会有这样的规律呢?”对呀,为什么呢?于是,我又进入了新一轮的苦思冥想,经过几番挫折,我都没有成功,后来我逐个突破,先从余数是0的开始,这个自然数n就是3的倍数,即n=3x(x=1,2,3,……),那么,n3=27x3=9×3x3,也就是说这类自然数的立方一定是9的倍数,9的倍数各个位数之和一定是9的倍数,所以将各个位数上的数字相加,直到求出的和是个位数时,结果一定是9。
啊哈,我越来越接近成功了!再来看,当余数是1时,这个自然数n就是3的倍数加1,即n=3x+1(x=0,1,2,3,……),那么,n3=(3x+1)3=27x3+27x2+9x+1=9(3x3+3x2+x)+1,也就是说这类自然数的立方一定是9的倍数再加1,那么结果一定是9+1=10,1+0=1,哈哈,第二关闯关成功!最后看,当余数是2时,这个自然数n就是3的倍数减1,即n=3x-1(x=1,2,3,……),那么,n3=(3x-1)3=27x3-27x2+9x-1=9(3x3-3x2+x)-1,也就是说这类自然数的立方一定是9的倍数再减1,那么结果一定是9-1=8,哈哈,第三关闯关成功!耶!我兴奋地大叫并跳了起来。
学习数学真是一个快乐的过程,自然数立方的规律问题是我自己在平时学习中发现的,我联系所学的数学知识,仔细思考、归纳总结并想办法证明,让我体会到在数学海洋里遨游的无穷乐趣,我要是能掌握更多的数学知识,我一定会收获更多的快乐。
肖老师留言:下周一上交的是方案,类似于我昨天给你的样本那样简写即可。
月底交的文章要详尽,可参考我刚才给你发的范文。
生活中的测量——比例尺的应用与思考我是来自温州市实验小学的杨云涵。
今天,能站在这里为大家介绍我的研究课题,我感到无比的荣幸和自豪。
在这次“小数学家”评比中,我参赛的课题是《生活中的测量——比例尺的应用与思考》。
说起这个课题,不得不提建于公元前2000多年的金字塔。
它是古埃及国王的陵墓,高大雄伟,令人赞叹!但是,在金字塔建成后的1000多年里,人们都无法测量出金字塔的高度——它们实在太高了。
约公元前600年,泰勒斯,古希腊的伟大学者从遥远的希腊来到了埃及。
为了测量出金字塔的高度,泰勒斯已经观察金字塔很久了。
直到有一天,看到金字塔在阳光下的影子时,他突然想到了办法。
泰勒斯仔细地观察着金字塔影子的变化,找出金字塔地面正方形的一边的中点,并作了标记。
然后他笔直地站立在沙地上,并请人不断测量他的影子的长度。
当影子的长度和他的身高相等时,他立即跑过去测量金字塔影子的长度,他推断这时金字塔影子的长度也就是金字塔真实的高度。
泰勒斯在2600多年前用于测量金字塔的办法令我十分着迷,我突然想到了松台山上的净光宝塔,是不是也可以像泰勒斯一样测量出它的高度呢?这个问题让我侧夜难眠,于是在一个晴朗的早晨,我和妈妈一起来到了松台山进行实地考察。
当我一眼看到净光塔的影子时,我高兴地差点跳了起来,因为按照泰勒斯的方法,当人的高度和影子的高度相等时,净光塔的高度和影子的高度也一定相等。
可是这时,我也发现了一个问题:塔的四周都是郁郁葱葱的大树,无法看到塔完整的影子,怎么测量啊?想到这里,我有点沮丧。
在回家的路上,我一边走,一边观察自己的影子。
我发现随着太阳照射角度的变化,影子的长度也发生了变化。
这时一个灵感从我脑子里蹦了出来:既然无法测量到与塔身长度相等的影子,那么可否在塔身和它的影子成一定比例的时候进行测量呢?我暗自下定决心下次再来试一试。
又是一个周末,我和妈妈再次来到了松台山。
这次我带上了一根155厘米长的尖木棍和一把卷尺。
我们把木棍插在塔前面的空地上,木棍留在地面以上的长度为150厘米。
当塔的影子完全落在塔周边的土地上时,我用卷尺测量出此时木棍影子的长度为5.15厘米。
这样计算出来的木棍长度约是木棍影子长度的29.12倍左右。
同时,我们测量出塔的影子的长度为223.5厘米,那么塔的高度应该就是223.5 X 29.12 = 6508.3(厘米)≈65米。
后来经过了解,净光塔的实际高度是65.46米。
虽然测量结果和塔的实际高度大约有40厘米的误差,但我相信如果进行多次测量,误差应该就会相应减少。
通过这次试验,我初步判断像我这种用影子测量物体高度的方法是可行的。
净光塔测量的第一次失败说明泰勒斯的方法在实际操作中有一定的难度,它对被测物体的周围环境有一定的要求。
而学校操场上的旗杆又让我产生再次尝试的念头。
因为旗杆很高,很直,而且操场又大又平,应该符合测量的条件。
于是我在假期来到了学校,这次,我没有用棍子而是要求妈妈充当测量的参照物,方法还是和上次一样。
以下是我在不同的时间段记录的各组测量数据,经过计算每次得出的旗杆高度非常接近,分别为9.98米、9.99米和10米,误差不超过两厘米,实验结果比较可靠。
我觉得这次实验应该是非常成功的。
可这时有个问题却再次困扰着我,因为不可能总是在晴天通过影子测量物体的高度,如果是阴天又该用什么办法呢?记得去年寒假的一天,我们一家外出旅游,我看到妈妈正好站在一棵大树边上。
那天正好是阴天,我又想起了测量的问题。
灵机一动,我拿起随身携带的数码相机,拍下了妈妈站在树下的全身像,画面上还有大树的整体图像。
回到家以后,我们马上就把照片冲洗出来。
我用尺子量出照片里妈妈的高度为8厘米,树的高度为14.5厘米。
我知道妈妈的实际身高是161厘米,也就是说,妈妈的实际身高是相片里的约20倍。
那么树的实际高度是不是也是相片里的20倍左右呢?那样的话,树的高度就是290厘米左右了。
那么,这个实验结果可信吗?首先,被测量物体被摄入照片时,不一定总是能找到其最高点;其次,参照物与被测量物体的距离会对测量结果有一定的影响。
我想这样测量的结果误差可能会比较大。
在做比例尺研究的时候,因为我们不可能总是在晴天测量物体的高度,而且如果临时没有现成的参照物又该怎么办呢?其实还有一种非常简便实用的,不受天气影响的测量物体高度的方法。
就是利用等腰直角三角形的特征,使用我们数学课最常用的等腰直角三角板去测量较高的物体。
下面我就举个例子来说明:如图,如果想测量AB的高度,假设FG是一个人,他将等腰直角三角板△DEF的直角边EF水平放置,眼睛顺着斜边DF向上看,同时移动自已的位置,当刚刚能看到房子的最高点A时,记下自己的位置和三角板此时所在的高度。
因为:DE=EF,所以AB=BC=BG+GC,通过计算就可以得出AB的高度了。
这种测量方法不受很多自然条件的限制,但因为是目测,所以与影子测量法相比误差会更大一些。
如果精确度要求不是很高,我们就可以使用这个方法。
通过以上几次试验,让我初步体会到了利用比例的原理对物体进行测量的合理性,科学性及其局限性。
今年学了六年级课本有关比例尺的知识后,我更是涣然大悟,原来我以前的这些方法竟然都可以总结成一种方法,那就是:被测物体高度=参照物高度÷参照物影子高度×被测物体影子的长度。
也就是说:如果假设被测物体高度是X,那么就有X:被测物体影子的长度=参照物高度:参照物影子高度这样,通过测量出其中的三个数据就可以计算出被测物体的高度了。
通过对这些问题的研究,我明白了数学知识来源于生活,同时又能解决生活中的问题,真是其乐无穷啊!我们如果能采用正确的方法,不怕失败,持之以恒,并摸索出其中的规律,找到突破口,也就可以像泰勒斯一样解决很多难题,很多看似复杂的问题也都会最终迎刃而解的。
追逐游戏中的发现江舟扬【探骊得珠】一天,我与爸爸在楼下花坛中玩追逐游戏,妈妈在旁边当裁判。
一开始,我们定下游戏规则是:要绕着一个花坛在规定的时间(1分半钟)之内追上对方。
虽然双方各有输赢,但由于只绕着一个花坛跑,爸爸占着身高腿长的优势略占上风。
于是,我打起了“如意小算盘”:我们不要只绕着一个花坛跑,扩大游戏活动范围(六个花坛加一个玻璃房,如图1所示),凭借我的灵活机智,那不就是胜券在握了吗!就在我暗自得意的时候,老爸也提出了一个要求:可以如你所愿,但跑的路径不能重复,以跑遍整个花坛而没有被追上者为胜。
我不假思索地答应了。
新的一轮游戏又开始了,我先跑,爸爸追,出乎意料的是我场场皆败。
我纳闷了,凭我这敏捷的身段,怎么会落得如此下场?五场后角色交换,爸爸先跑,我来追。
虽然爸爸跑的并不慢,但他也逃脱不了五场连败的命运。
奇怪了,为什么两个人都会五连败呢?而且每一次都不是被对方追上,而是走入死胡同,无路可跑了,举手投降的。
这是怎么回事呢?我决定学学赵括的“纸上谈兵”,于是我将活动场景画下来,利用“走图”的方式,尝试着来解开这谜底……【按图索骥】游戏活动的场地中一共有六个花坛和一个玻璃房,按照这些花坛的实际形状描绘下来,就是以上图1的情形。
我将分别从不同的地点出发,通过不同的路径,来寻求答案。
1、从A点出发,会怎样呢?从A点出发,有3个方向可选择。
我们先以图2为例。
假设选择中间的方向出发,到了第一个分岔口,又出现了3个方向可选择。
再假设选择中间的方向继续向前,到了第二个分岔口,有2个方向可选择。
再假设向左方转,行进到第3个分岔口,再选择左转,经过第4、5个分岔口时不改变方向,继续直走,一直到第六个分岔口,向右转两次,结果无论经过哪一个岔口,都会出现到无路可走的局面。
如果选择其他方向,也会出现同样的结果。
比如图3至图9中所展示的一样。
2、从B、C点出发,会怎样呢?分别从B、C点出发,经过尝试,我们发现同样走入困境,图10至图18所示。
3、从其他点出发的情况在图19至图22所展示的分别是从D、E、F点出发的几种情况,结果还是出现与前面一样的结论。
于是,我便选择场地中间的某一个点为起点,比如点G、H、I,唉!还是进入死胡同,不能成功跑遍整个场地。
