第六届全国大学生数学竞赛湖北赛区预赛
2013全国大学生数学建模湖北赛区成绩
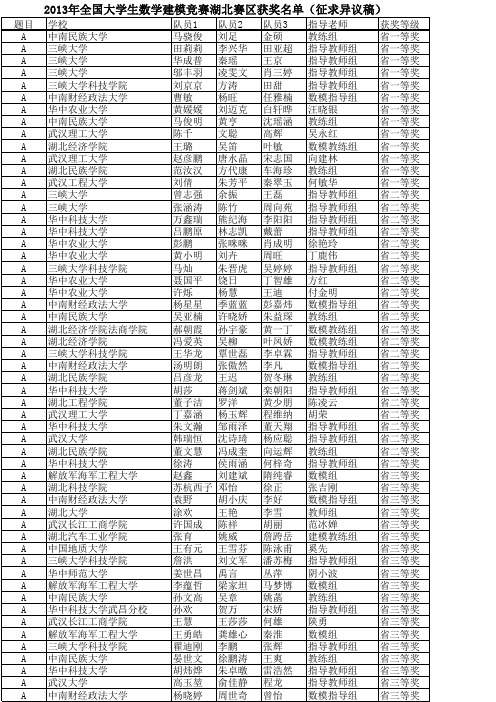
数模指导组 李波 教练组 数模指导组 数模指导组 指导教师组 指导教师组 指导教师组 阴小波 左国新 毛树华 指导教师组 指导教师组 数模教练组 高飞 陈彧 指导教师组 数模教练组 数模组 指导教师组 教师组 王防修 数模组 左国新 唐向阳 教练组 指导教师组 指导教师组 潘志斌 教练组 数模组 陈应保 数模组 朱强 指导教师组 指导教师组 指导教师组 陈建业 指导教师组 指导教师组 杨瑞琰 数模组 指导教师组 指导教师组 指导教师组 教师组 指导教师组 数模组 指导教师组 指导教师组 指导教师组 建模指导组 数模组 指导教师组 王邦菊 数模教练组 指导教师组
张颖 胡冠宇 熊忭 陈康洁 胡梦 刘浩 秦一雯 王齐耀 杨梦婷 曾尚志 陈哲 严彪 胡奇 韦屏远 赵守玉 陈阳 朱文意 伏敏杰 杨好学 夏宇婷 丁磊 鲁振国 肖敏 刘丽 余艳 李启睿 石少伟 邹帅 杨苇苇 胡剑文 孙潮旭 曹庆庆 万婷 耿瑞杰 罗奥荣 郭凯 方军 杨叶 田小东 高楠 吴茵岚 孔为达 施帅 郑舒月 王磊 欧阳立鹏 张志敏 陈宜良 伊诗瑶 曾浩 李云飞 谭伟 夏峰 崔树伟 郑树林 夏建设 於辉
管炎俊 吴尚益 谢楠 吴楠祺 尚梦 夏鹏 张生廷 张诚 胡雪枫 金彤 熊凯 夏岳 袁士川 刘旋 高云飞 陈宏宇 张霞 郑小勇 郭林耀 史一飞 王浩 张泽丰 吕娜 彭博旺 陈竹 陈潇麟 殷振平 谭峰 张晨曦 李辉 许哲 朱成龙 杨迎铭 雷梦琦 方继松 望程伟 汪幸 高丽颖 吴念慈 牛秀美 郑俊 杨明亮 杨剑波 周芳 闫思彤 涂齐冲 程平 张旭光 杨康 方舟 吴博源 钟忠社 刘梦源 张佳阳 谭棽元 程德康 张微
省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖 省三等奖
2012年全国大学生数学建模竞赛湖北赛区获奖名单

2012年全国大学生数学建模竞赛湖北赛区获奖名单(征求异议稿)序号选题学校队员1 队员2 队员3 指导老师获奖等级A 华中科技大学夏楚豪陈磊王雄路志宏省一等奖A 三峡大学杨莹贺小刚陶赢指导教师组省一等奖A 华中科技大学王祖健孙梦华王巍徐春雷省一等奖A 华中科技大学赖长青徐正超钟钊何南忠省一等奖A 湖北工业大学陈守文陈帆赵东林数模组省一等奖A 华中农业大学徐洲李祎琛祝翠君刘峰省一等奖A 三峡大学欧阳静汤看看吴良峰指导教师组省一等奖A 华中农业大学楚天学院李颖田喆吴瑞丽侯志敏省一等奖A 华中农业大学童庆蒙刘金祥万佳玮丁鹿伟省一等奖A 湖北汽车工业学院魏保军甘艳芳张胜根喻方元省一等奖A 三峡大学王林英吴泽霖张子龙指导教师组省一等奖A 湖北大学李纪强朱文静陈江洪教师组省一等奖A 武汉理工大学周纯华慧丰毛焕朱慧颖省一等奖A 武汉理工大学张聪汪涛蔡诗聂朱慧颖省一等奖A 华中农业大学董梦婷康月波代立朱强省一等奖A 中南财经政法大学吴宗炎袁飞鸿罗振数模指导组省一等奖A 武汉理工大学华夏学院李果王芳陈世雄教练组省一等奖A 湖北经济学院贺楦栋谢美玲刘敏数模教练组省一等奖A 三峡大学科技学院高小成陈昊瀚周蓉指导教师省一等奖A 三峡大学科技学院张琦范谋平黄江浩指导教师组省一等奖A 湖北科技学院黄幺钟阳胡新刚彭娟省一等奖A 武汉工程大学邮电与信息工程学院王玉琴杨庆高阳胡端平省一等奖A 华中农业大学李倩刘乙蓉张小尔潘志斌省一等奖A 湖北工业大学卢铁梅吴扬广李军辉数模组省一等奖A 黄冈师范学院余玲翟珊珊吴巧巧何方国省一等奖A 华中农业大学雷鸣王凯陈薇李治省一等奖A 中南财经政法大学许润泽王宁姚思雅数模指导组省一等奖A 华中师范大学何亚菲黄福平刘芳唐向阳省一等奖A 长江大学陈昆陈哲尹敏数模组省一等奖A 武汉大学李昊宇李双钰黄冉思思数模指导组省一等奖A 中南财经政法大学彭超智梦微吴康珺数模指导组省一等奖A 中国地质大学(武汉)彭少磊巫伟皇张发奇向东进省二等奖A 黄冈师范学院郝慧芳张小丽胡桂兰饶从军省二等奖A 长江大学何志新曹龙飞鞠潭数模组省二等奖A 华中农业大学楚天学院郭亚彬石宣宜马娜潘志斌省二等奖A 华中师范大学李阳何娇金大雁左国新省二等奖A 华中科技大学刘佩谢亦红谭照江梅正阳省二等奖A 湖北师范学院朱宝兵胡晴郑莎建模组省二等奖A 华中农业大学胡涛赵艳虹侍威王邦菊省二等奖A 湖北经济学院周璇邓文娟胡欢数模教练组省二等奖A 中南民族大学杨好学邵田原梁睿智教练组省二等奖A 华中师范大学陈国威于爽婷杜妮香左国新省二等奖A 华中农业大学汪伟平王骏刘文汪晓银省二等奖A 华中师范大学王昱博杨梦珊吴俊爽李波省二等奖A 华中师范大学艾文会谢依黄月陈应保省二等奖A 华中农业大学楚天学院徐经伟徐之清陈莹方红省二等奖A 武昌理工学院陈江洪高科张丽数模指导组省二等奖A 湖北经济学院陈韬吴笛乐云飞数模教练组省二等奖A 湖北工业大学邱阳陈佩严佳数模组省二等奖A 湖北大学王言宋晓鹏舒畅教师组省二等奖A 武汉大学徐依然张小六文雯数模指导组省二等奖A 武汉大学李欢欢宋若楠杨嘉树数模指导组省二等奖A 武汉工程大学冯旿祥熊思远夏然飞刘任河省二等奖A 湖北大学王东东何璐瑶祁侨教师组省二等奖A 武汉纺织大学程书良充艺渴李义石先军省二等奖A 武汉工业学院白俊朱雨乐凡桥曾山省二等奖A 武汉理工大学谢凯悦聂鑫伟靳乾乾毛树华省二等奖A 湖北经济学院王璐蔡骑鹏何青数模教练组省二等奖A 中南民族大学江毅郭英智陈佳骐教练组省二等奖A 华中科技大学武昌分校李志豪王倩云李雄良指导教师组省二等奖A 华中师范大学谢定一张李攀朱梦琪唐向阳省二等奖A 武汉科技大学高恒李珊赵亚洲教练组省二等奖A 湖北民族学院吴素赟向华艳周洪健方壮省二等奖A 三峡大学科技学院蔡翔宋正君何彬指导教师组省二等奖A 武汉大学向阳李明贞刘才荣数模指导组省二等奖A 三峡大学科技学院朱晋虎余羊羊张益指导教师组省二等奖A 中南财经政法大学陈晶晶沈淑翁栋栋数模指导组省二等奖A 中国地质大学(武汉)张依吴会彩严宏海付丽华省二等奖A 解放军海军工程大学季圣贤杨刚范兆辉数模组省二等奖A 三峡大学科技学院李实李晓峰余梦诗指导教师组省二等奖A 华中农业大学白婷刘志红姚玉娇胡学海省二等奖A 湖北大学张颖孙昊管焱俊教师组省二等奖A 湖北经济学院樊仁义胡沛李敏芳数模教练组省二等奖A 湖北民族学院黄威韦晓云王洪梅向长城省二等奖A 武汉东湖学院王鹏王超周涛周雪省二等奖A 中南财经政法大学欧仁婕黎小林邓超数模指导组省二等奖A 湖北工业大学工程技术学院易春艳刘家宜杨锋数模组省三等奖A 武汉大学吕天健李不依胡峻数模指导组省三等奖A 中南财经政法大学马伟力于婷婷余梦晨数模指导组省三等奖A 解放军海军工程大学舒晓磊谢作栋文在飞数模组省三等奖A 武汉长江工商学院何雄李银玲李颖陕勇省三等奖A 武昌理工学院程涛李冲胡铭数模指导组省三等奖A 武汉大学万一童辉华远盛数模指导组省三等奖A 湖北工程学院蔡国雄龚志恒成文婷张学新省三等奖A 黄冈师范学院陈超群邹婷李龙郑跃省三等奖A 荆楚理工学院吴庆坤田荣芬张瑞羚指导教师组省三等奖A 武汉理工大学蔡裕坤王喆夏慧雯何朗省三等奖A 黄冈师范学院林葵徐蕤雷淑敏饶从军省三等奖A 长江大学工程技术学院王桥徐天远李梦婷建模组省三等奖A 武汉大学张水利金卓勍陈恒数模指导组省三等奖A 中南民族大学胡均普雷丹华山思教练组省三等奖A 武汉工业学院伍凡王时畅冀学鹏刘彪省三等奖A 湖北民族学院科技学院丁炀柳董非凡董文慧向长城省三等奖A 武汉理工大学万延燊季学斌杜密李丹省三等奖A 武汉工程大学王平万黎潘绪敏何敏华省三等奖A 解放军海军工程大学赵核毓宋清扬王伟超数模组省三等奖A 武汉大学李京姚松柏郑俊超数模指导组省三等奖A 湖北汽车工业学院王毅磊徐闻春李扬刘开拓省三等奖A 武汉工业学院吴涛龚念谢小娟易校尉省三等奖A 中南财经政法大学桂弘诣陈灵郑仕麟数模指导组省三等奖A 武汉工程大学李丰马芙蓉戴乐乐刘任河省三等奖A 湖北经济学院法商学院何冰杰熊莹郝朝霞数模教练组省三等奖A 武汉工业学院顿明亮王军伟戴超曾山省三等奖A 荆楚理工学院罗静杨震刘思锦指导教师组省三等奖A 武汉理工大学华夏学院汪兆亮王腾沈晓瑜教练组省三等奖A 解放军军事经济学院张登辉黄帅梁芳指导教师组省三等奖A 中南财经政法大学王瑞雪王佳毅刘祥锟数模指导组省三等奖A 中南民族大学徐睿沈雅君李丽娟教练组省三等奖A 湖北大学安锋冯银超唐芮教师组省三等奖A 湖北师范学院邓玉凤何晓宇柯善武建模组省三等奖A 武昌理工学院李平孙吉刚喻炎数模指导组省三等奖A 中国地质大学(武汉)熊涛蒋礼王鑫余绍权省三等奖A 武汉理工大学张衎谢亚楠胡方楷徐天群省三等奖A 解放军海军工程大学马鹏雪刘忠顺熊娜数模组省三等奖A 武汉科技大学唐颖何小帅王胜教练组省三等奖A 长江大学卢莲枝倪成程世耿数模组省三等奖A 解放军海军工程大学许恩赐任盼盼马群超数模组省三等奖A 武汉工程大学邮电与信息工程学院邬佳星田旭许梦莹胡端平省三等奖A 武汉纺织大学熊士强孟琼瑶杨威周志刚省三等奖A 武汉科技大学张津津朱文杰李威凌教练组省三等奖A 武昌理工学院陈胤熊明张茜数模指导组省三等奖A 华中师范大学刘红利张利张禹津唐向阳省三等奖A 中南财经政法大学杨阳汪婉婷王若琦数模指导组省三等奖A 武汉理工大学李胜利钱瑶师佳童仕宽省三等奖A 华中师范大学李琛琛王磊何建锋左国新省三等奖A 长江大学文理学院吴为恒向云洋张会芬史千里省三等奖A 中南民族大学付翔王爽田胡佩教练组省三等奖A 武昌理工学院许涛汪洋李雯蕊数模指导组省三等奖A 湖北汽车工业学院王立周颖刘晓洁雷国梁省三等奖A 中南财经政法大学邓欢欢陈琳姿马文婷数模指导组省三等奖A 华中科技大学胡晓灵陈泽陈兵范冰婵省三等奖A 长江大学工程技术学院张敏曾帅徐前程建模组省三等奖A 华中科技大学陈文虎徐勇阳光耀范冰婵省三等奖A 中国地质大学(武汉)葛余超任迎张倩倩付丽华省三等奖A 解放军海军工程大学汪路平王龙龙冯亚东数模组省三等奖A 武汉工程大学张胜军杨靖鹏凡华严国义省三等奖A 长江大学张伟杨涛毛春丽数模组省三等奖A 解放军军事经济学院刘皓然汪彩虹王蕾指导教师组省三等奖A 解放军海军工程大学马梦飞何笠向涛数模组省三等奖A 中南民族大学沈瑶涵黄亨马俊明教练组省三等奖A 武汉大学刘恒李跃章旻昕数模指导组省三等奖A 解放军海军工程大学屈风雪水一曼刘璐数模组省三等奖A 湖北工业大学王秀悦陈凯赵奇数模组省三等奖A 武汉大学李帅康裕陈钰数模指导组省三等奖A 武汉大学黄逍田震邓珊珊数模指导组省三等奖A 湖北工业大学工程技术学院李乐王敬云金婉数模组省三等奖A 长江大学王曦陈千王慧数模组省三等奖A 湖北民族学院冯成奎向运辉陈苹向会立省三等奖A 华中科技大学文华学院薛曼琳张倩汪雄数模导师组省三等奖1 B 湖北工业大学邓宏伟徐翔仇小伟数模组省一等奖2 B 华中科技大学洪昊赵昕海丁克蜜梅正阳省一等奖3 B 三峡大学余文萍李家宁吴政指导教师组省一等奖4 B 三峡大学余培培黄敏徐晖指导教师组省一等奖5 B 华中科技大学陈学龙刘圆徐洁韩志斌省一等奖6 B 三峡大学周红艳苏瑞超邓方祥指导教师组省一等奖7 B 中南财经政法大学惠艺清韩淑婷张瑶数模指导组省一等奖8 B 三峡大学科技学院胡安龙李演林李强强指导教师组省一等奖9 B 三峡大学科技学院覃世磊姜顺伟王奇指导教师组省一等奖10 B 三峡大学科技学院刘栋刘备潘厚福指导教师组省一等奖11 B 武汉理工大学包汉强李金洲廖丽君吴永红省一等奖12 B 湖北理工学院丁明汤涛肖龙雾数模指导组省一等奖13 B 武汉理工大学黄炜博李棒刘晓辉陈建业省一等奖14 B 汉口学院刘印强张智慧乾路姚志鹏省一等奖15 B 解放军空军预警学院冯至熊智敏邱彬数模指导组省一等奖16 B 华中师范大学黄展张佳慧黎尧阴小波省一等奖17 B 湖北经济学院杨梦洁文本荣乔勇数模教练组省一等奖18 B 武汉理工大学黄文杰谢健蔡路刘扬省一等奖19 B 华中师范大学李文博庄光耀陈垚翰李波省一等奖20 B 三峡大学杨楚原向中辉石伟指导教师组省二等奖21 B 三峡大学科技学院刘坚徐秋雨吴袭指导教师组省二等奖22 B 三峡大学周能明卢忠山石雷指导教师组省二等奖23 B 三峡大学陈美美李海辉郑杭指导教师组省二等奖24 B 三峡大学刘静胡洋刘文清指导教师组省二等奖25 B 三峡大学陈琳杨洋陈志敏指导教师组省二等奖26 B 三峡大学科技学院王瀚林焦雨起卢涛指导教师组省二等奖27 B 武汉理工大学马俊杰张春雨刘磊刘扬省二等奖28 B 湖北大学郑家伟朱青青谈庆教师组省二等奖29 B 解放军空军预警学院许国强汪琰王然数模指导组省二等奖30 B 华中农业大学袁佩佩徐田田韩勖方红省二等奖31 B 解放军海军工程大学胡忠罗洋洋唐粟数模组省二等奖32 B 武汉工业学院周冰徐梦莹余美娟刘朔省二等奖33 B 湖北科技学院杨群甘亚鹏邹健镇方雄省二等奖34 B 中南财经政法大学吴永斌刘康陈亿数模指导组省二等奖35 B 武汉大学奉万森徐顺刘玉琪数模指导组省二等奖36 B 解放军空军预警学院商哲然陈永彬胡海洋数模指导组省二等奖37 B 中国地质大学(武汉)谢磊史忠奎李豪杨瑞炎省二等奖38 B 中南财经政法大学王梦琪赵珺张孟哲数模指导组省二等奖)39 B 武汉大学邱铮泓王俊威冯曦数模指导组省二等奖40 B 武汉工程大学胡晶宇梅立琴李隽钰胡端平省二等奖41 B 华中农业大学郭倩卿雪娇付明辉汪晓银省二等奖42 B 武汉大学胡俊杰张璇汪紫珈数模指导组省二等奖43 B 湖北汽车工业学院周少甫刘彻郭成武刘开拓省二等奖44 B 武汉大学张耕源顾用地陆俊数模指导组省二等奖45 B 湖北民族学院刘国勋蒙建国陈江方壮省二等奖46 B 解放军海军工程大学俞雷王珺李维强数模组省二等奖47 B 中南财经政法大学魏佳张甦黎云波数模指导组省三等奖48 B 武汉大学曾桢李筱驰童文竹数模指导组省三等奖49 B 武汉理工大学肖蕊柳超辛亚运朱华平省三等奖50 B 武汉理工大学王泽琪吴克风赵欣陈建业省三等奖51 B 武汉科技大学韩新星凃俊达周紫维教练组省三等奖52 B 湖北民族学院龚辉李改改项敏方壮省三等奖53 B 黄冈师范学院柯贤勤李承鹏刘辉刘志兵省三等奖54 B 湖北科技学院张文文李苗刘柏林周志明省三等奖55 B 解放军海军工程大学张锦德朱彬罗桓数模组省三等奖56 B 华中科技大学武昌分校王聪刘思意汤兴东指导教师组省三等奖57 B 解放军海军工程大学郭志科梁家坦杨宝河数模组省三等奖58 B 湖北工业大学张坤周亚琼胡国志数模组省三等奖59 B 江汉大学何九洲邱峻刘瑞田大平省三等奖60 B 湖北民族学院向伦凯廖云张超向长城省三等奖61 B 武汉大学甘奇董婷李玲珠数模指导组省三等奖62 B 武汉工程大学王丽宋雅风王磊刘吉定省三等奖63 B 华中科技大学李弼周围李雪菲梅正阳省三等奖64 B 长江大学梅国锋胡密王能康数模组省三等奖65 B 湖北经济学院段力鲡彭跃池策坤数模教练组省三等奖66 B 湖北汽车工业学院朱小雄杨苏杨芸雷国梁省三等奖67 B 湖北民族学院杨雪周亚玲周小明陈以平省三等奖68 B 湖北民族学院郑子华孔春莉郑树林谢君辉省三等奖69 B 中南民族大学王侠林张生廷秦一雯教练组省三等奖70 B 武汉科技大学杨柳胡露明刘海江教练组省三等奖71 B 武汉东湖学院李辉易欣欣张益周雪省三等奖72 B 长江大学工程技术学院洪伟潘婷邹俊武建模组省三等奖73 B 武汉理工大学胡恒恒卢伟江王成陈彧省三等奖74 B 武汉大学贵亦凡李丹王培育数模指导组省三等奖75 B 湖北科技学院胡一梅彭易苗胡胜全镇方雄省三等奖76 B 长江大学胡春莲袁慎波张宇数模组省三等奖77 B 华中农业大学楚天学院谢朋刘素倩黄晓青徐艳玲省三等奖78 B 武汉工业学院陶鑫李志勇王曼王防修省三等奖79 B 湖北工程学院袁大坤王东东李曼熊文涛省三等奖80 B 武汉大学柏筱飞曲波高伟轩数模指导组省三等奖81 B 武汉工业学院秦卫华周龙何泽余波省三等奖82 B 武汉理工大学刘佳伟许长江黄思逸樊庆菊省三等奖83 B 湖北师范学院郑升林刘玲张琴建模组省三等奖84 B 长江大学熊凯陈敏徐岭灵数模组省三等奖85 B 长江大学余俊余沛邹科数模组省三等奖86 B 黄冈师范学院田莎莎邱晶晶罗安伦李平省三等奖87 B 海军工程大学卢博文王飞涂宇鹏数模组省三等奖88 B 解放军空军预警学院卢雨祥黄泽衡张良数模指导组省三等奖89 B 湖北工业大学工程技术学院朱康张祁陈丝恒数模组省三等奖90 B 华中农业大学楚天学院施坚强沈文进彭超任兴龙省三等奖91 B 武汉生物工程学院柳伟余坦林丽炫杨薇省三等奖92 B 武昌工学院周鹏毛中华孔令超数模指导组省三等奖C 武汉长江工商学院秦丹秦久霖凡龙刘文斌省一等奖C 湖北经济学院吴锋李海艳余婷数模教练组省一等奖C 湖北经济学院法商学院徐辉杨锦刘刚数模教练组省一等奖C 中南财经政法大学武汉学院周玉姗许菲陈梨洁教练组省二等奖C 长江职业学院董文兵陈枫汪星星胡芬省二等奖C 湖北交通职业技术学院刘程移何志佳周稚君数模教练组省二等奖C 武汉船舶职业技术学院龙国锐潘俊飞周国福数模指导组省二等奖C 湖北文理学院刘小杰丰强肖强强宁彬省二等奖C 湖北经济学院李超伟李磊王庆勇数模教练组省三等奖C 黄冈职业技术学院严嘉旗曾维校严喜开教练组省三等奖C 武汉长江工商学院柯火祥邱雅思梅家胜陕勇省三等奖C 武汉船舶职业技术学院陈龙文王世敏叶作霖数模指导组省三等奖C 武汉职业技术学院张展程雨武宗锦林敏省三等奖C 荆楚理工学院骆国本徐晶甘泽威指导教师组省三等奖C 十堰职业技术学院郭培浩闵炀黄双平教师组省三等奖D 武汉船舶职业技术学院徐绣才董向伟程博数模指导组省一等奖D 华中科技大学文华学院张光威邵雨田王莉数模导师组省一等奖D 华中科技大学武昌分校李敏陶建刘靖指导教师组省一等奖D 十堰职业技术学院王顺伟劳江卫张才超教师组省二等奖D 武汉电力职业技术学院谢芬涂卫明刘志伟翁伯林省二等奖D 黄冈职业技术学院汪鹏熊梦颖王旭教练组省二等奖D 武汉电力职业技术学院李静涂俊李明梅翁伯林省二等奖D 湖北交通职业技术学院彭会军唐攀武凯峰数模教练组省二等奖D 武汉职业技术学院常形成金洞雄李蓉蓉夏婧省三等奖D 湖北职业技术学院陈瑶童义坤戴宇洋周文省三等奖D 湖北职业技术学院许海涛王伟汪清张守平省三等奖D 武汉职业技术学院李雄飞李永乐李月魏莹省三等奖D 黄冈职业技术学院王欢于芳陈文宇教练组省三等奖D 湖北交通职业技术学院胡正友陈苗程冰琦数模教练组省三等奖D 湖北职业技术学院邓磊丁博郑小林张守平省三等奖D 湖北工业大学商贸学院邹宏松陈瑶黄琪琪张甜省三等奖D 咸宁职业技术学院周丹迪瞿思芹刘祥松汪慧玲省三等奖D 郧阳师范高等专科学校高利欧阳平周晓浩邓乐斌省三等奖。
全国大学生数学竞赛由中国数学会主办每举办一次分为预赛和

:一、专业竞赛类:1、数学类(1)大学生数学竞赛全国大学生数学竞赛由数学会主办,每年举办一次,分为预赛和决赛两个阶段,并分设数学类与非数学类,预赛在每年10月举行,决赛在次年春季举办,参赛对象为大学本科二年级及以上在校大学生,竞赛内容以本科教学大纲规定的数学内容为准,比赛形式采用笔试,(数学类考试科目为:数分、高代、解析几何等;非数学类考试科目:高等数学)目前已成为全国影响最大、参加人数最多的大学生基础数学学科竞赛。
我校每年都在全国决赛中获得优异成绩.(2)数学建模大赛我校建模比年由张更生等老师组织。
2、计算机类(1)大赛程序设计大赛是大学级别最高的脑力竞赛,素来被冠以”程序设计的奥林匹克”的尊称。
大赛自1970年开始至今已有30年历史,是世界范围内历史最悠久、规模最大的程序设计竞赛.比赛形式是:经过校级和地区级选拔的参赛组,于指定的时间、地点参加世界级的决赛,由3个成员组成的小组应用一台计算机解决6到8个生活中的实际问题。
(2)全国信息技术应用水平大赛个人赛科目:(1)计算机应用技术模块。
办公自动化高级应用、C语言程序设计、程序设计、平面设计、动画设计、3 三维设计.(2)计算机辅助技术模块。
二维建筑设计、二维机械设计、三维设计.(3)电子信息技术模块。
单片机开发与应用、嵌入式开发与应用.(4)移动互联技术模块。
(5)3G移动通信技术、移动互联设计。
团体赛科目:电子系统设计、应用开发.3、师范大学师范专业理科师范生教学技能创新大赛组织的,需学校牵头组织参加(共数学、物理、化学三个学科)。
二、科技创新类:1、师范大学2021年大学生科技创新项目面向对象:我校在册除毕业班之外的全日制本、专科生和研究生,自然科学类学术项目的申报者只限于本、专科生。
课题包括:自然科学类学术项目、哲学科学类和学术项目、科技发明以及创业计划项目四大类,研究内容为:(1)基于XX学科(或交叉学科)的学生自主创新性项目研究.(2)一定规模的研究性调查.(3)国内影响较大的学科竞赛引申出的研究课题.(4)促进青年创新人才成长、推动经济的创业计划项目。
中国大学生数学竞赛

获奖名单
获奖名单
第一届全国大学生数学竞赛决赛获奖名单
谢谢观看
中国大学生数学竞赛
全国性高水平学科竞赛
01 竞赛简介
03 竞赛组委会 05 竞赛大纲
目录
02 历届情况 04 竞赛用书 06 获奖名单
基本信息
2009年,第一届全国大学生数学竞赛[The Chinese Mathematics Competitions (简称CMC)]开始举办。 作为一项面向本科生的全国性高水平学科竞赛,CMC为青年学子提供了一个展示数学基本功和数学思维的舞台, 为发现和选拔优秀数学人才并进一步促进高等学校数学课程建设的改革和发展积累了调研素材。由中国数学会承 办,也是全国高中数学竞赛在大学里的良好接力。
竞赛简介
竞赛简介
2009年,中国大学生数学竞赛(通称为“全国大学生数学竞赛”)开始举办,第一届CMC由中国数学会主办、 国防科学技术大学承办。此后CMC每年举办一次,由中国各大高校承办。
中国大学生数学竞赛活动图册(9张)CMC的目的是:激励大学生学习数学的兴趣,进一步推动高等学校数学 课程的改革和建设,提高大学数学课程的教学水平,发现和选拔数学创新人才。中国大学生数学竞赛的参赛对象 为大学本科二年级及二年级以上的在校大学生。
第七届
2015年10月24日举办第七届全国大学生数学竞赛预赛,2016年3月27在由福建师范大学举办第七届全国大学 生数学竞赛决赛,来自清华大学、北京大学等著名高校的284位(数学类94人,非数学类190人)学生参加了决赛。
第八届
第八届全国大学生数学竞赛由北京科技大学承办,2016年10月22日各省统一时间举办第八届大学生数学竞 赛初赛,2017年3月18将在北京科技大学举办第八届全国大学生数学竞赛决赛。
全国大学生数学竞赛赛试题(1-9届)

全国大学生数学竞赛赛试题(1-9届)第一届全国大学生数学竞赛预赛试题一、填空题(每小题5分,共20分)1.计算 $\iint_D \frac{y}{x+y-1} \mathrm{d}x\mathrm{d}y$,其中区域$D$ 由直线$x+y=1$ 与两坐标轴所围成三角形区域。
2.设 $f(x)$ 是连续函数,且满足 $f(x)=3x^2-\intf(x)\mathrm{d}x-2$,则 $f(x)=\underline{\hspace{2em}}$。
3.曲面 $z=\frac{x^2+y^2-2}{2}$ 平行于平面 $2x+2y-z=$ 的切平面方程是 $\underline{\hspace{2em}}$。
4.设函数 $y=y(x)$ 由方程 $xe^{f(y)}=\ln 29$ 确定,其中$f$ 具有二阶导数,且 $f'\neq 1$,则$y''=\underline{\hspace{2em}}$。
二、(5分)求极限 $\lim\limits_{x\to n}\frac{e^{ex+e^{2x}+\cdots+e^{nx}}}{x}$。
三、(15分)设函数 $f(x)$ 连续,$g(x)=\intf(xt)\mathrm{d}t$,且 $\lim\limits_{x\to 1} f(x)=A$,$A$ 为常数,求 $g'(x)$ 并讨论 $g'(x)$ 在 $x=1$ 处的连续性。
四、(15分)已知平面区域 $D=\{(x,y)|0\leq x\leq\pi,0\leq y\leq\pi\}$,$L$ 为 $D$ 的正向边界,试证:1)$\int_L xe^{\sin y}\mathrm{d}y-ye^{-\sinx}\mathrm{d}x=\int_L xe^{-\sin y}\mathrm{d}y-ye^{-\sinx}\mathrm{d}x$;2)$\int_L xe^{\sin y}\mathrm{d}y-ye^{-\sinx}\mathrm{d}x\geq \frac{\pi^2}{2}$。
历年全国大学生高等数学竞赛真题及答案

第一届全国大学生数学竞赛预赛试卷(非数学类)一、填空题(每小题5分,共20分)1.计算____________,其中区域由直线与两坐标轴所围成三角形区域.解 令,则,,(*) 令,则,,,,2.设是连续函数,且满足, 则____________.解 令,则,,解得。
因此。
3.曲面平行平面的切平面方程是__________. 解 因平面的法向量为,而曲面在处的法向量为,故与平行,因此,由=--++⎰⎰y x yx x yy x Dd d 1)1ln()(D 1=+y x v x u y x ==+,v u y v x -==,v u v u y x d d d d 1110det d d =⎪⎪⎭⎫⎝⎛-=v u u v u u u y x y x x yy x D D d d 1ln ln d d 1)1ln()(⎰⎰⎰⎰--=--++⎰⎰⎰⎰----=---=10210d 1)ln (1ln d )d ln 1d 1ln (u u u u u u u u u u v v u uv u u u u u ⎰-=12d 1u uu u t-=121t u -=dt 2d t u -=42221t t u +-=)1)(1()1(2t t t u u +-=-⎰+--=0142d )21(2(*)t t t ⎰+-=1042d )21(2t t t 1516513221053=⎥⎦⎤⎢⎣⎡+-=t t t )(x f ⎰--=222d )(3)(x x f x x f =)(x f ⎰=2d )(x x f A23)(2--=A x x f A A x A x A 24)2(28d )23(22-=+-=--=⎰34=A 3103)(2-=x x f 2222-+=y x z 022=-+z y x 022=-+z y x )1,2,2(-2222-+=y x z ),(00y x )1),,(),,((0000-y x z y x z y x )1),,(),,((0000-y x z y x z y x )1,2,2(-,知,即,又,于是曲面在处的切平面方程是,即曲面平行平面 的切平面方程是。
历届全国大学生高等数学竞赛真题及答案非数学类

前三届高数竞赛预赛试题(非数学类)(参加高等数学竞赛的同学最重要的是好好复习高等数学知识,适当看一些辅导书及相关题目,主要是一些各大高校的试题。
)2009年 第一届全国大学生数学竞赛预赛试卷一、填空题(每小题5分,共20分)1.计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(____________,其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解: 令v x u y x ==+,,则v u y v x -==,,v u v u y x d d d d 1110det d d =⎪⎪⎭⎫ ⎝⎛-=, v u u v u u u y x y x x yy x D D d d 1ln ln d d 1)1ln()(⎰⎰⎰⎰--=--++⎰⎰⎰⎰----=---=1021000d 1)ln (1ln d )d ln 1d 1ln (u uu u u u u u u u v v uuv u u u u u ⎰-=12d 1u uu (*) 令u t -=1,则21t u -=dt 2d t u -=,42221t t u +-=,)1)(1()1(2t t t u u +-=-,⎰+--=0142d )21(2(*)tt t⎰+-=1042d )21(2t t t 1516513221053=⎥⎦⎤⎢⎣⎡+-=t t t2.设)(x f 是连续函数,且满足⎰--=2022d )(3)(x x f x x f , 则=)(x f ____________.解: 令⎰=20d )(x x f A ,则23)(2--=A x x f ,A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。
因此3103)(2-=x x f 。
3.曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是__________. 解: 因平面022=-+z y x 的法向量为)1,2,2(-,而曲面2222-+=y x z 在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ,故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行,因此,由x z x =,y z y 2=知0000002),(2,),(2y y x z x y x z y x ====,即1,200==y x ,又5)1,2(),(00==z y x z ,于是曲面022=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ,即曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是0122=--+z y x 。
2023年历届全国大学生数学竞赛预赛试卷

全国大学生数学竞赛预赛试卷(非数学类)2023年 第一届全国大学生数学竞赛预赛试卷(非数学类)一、填空题(每小题5分,共20分)1.计算()ln(1)d yx y x y ++=⎰⎰____________,其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.2.设)(x f 是连续函数,且满足220()3()d 2f x x f x x =--⎰,则()f x =____________.3.曲面2222x z y =+-平行平面022=-+z y x 的切平面方程是__________.4.设函数)(x y y =由方程29ln )(y y f e xe =拟定,其中f 具有二阶导数,且1≠'f ,则=22d d x y________________. 二、(5分)求极限xenx x x x ne e e )(lim 20+++→ ,其中n 是给定的正整数. 三、(15分)设函数)(x f 连续,10()()g x f xt dt =⎰,且A xx f x =→)(lim,A 为常数,求()g x '并讨论)(x g '在0=x 处的连续性.四、(15分)已知平面区域}0,0|),{(ππ≤≤≤≤=y x y x D ,L 为D 的正向边界,试证:(1)⎰⎰-=---Lx y Lx yx ye y xe x ye y xed d d d sin sin sin sin ;(2)2sin sin 25d d π⎰≥--Ly yx ye y xe.五、(10分)已知xxe xe y 21+=,xxexe y -+=2,xx x e e xe y --+=23是某二阶常系数线性非齐次微分方程的三个解,试求此微分方程.六、(10分)设抛物线c bx ax y ln 22++=过原点.当10≤≤x 时,0≥y ,又已知该抛物线与x 轴及直线1=x 所围图形的面积为31.试拟定c b a ,,,使此图形绕x 轴旋转一周而成的旋转体的体积V 最小.七、(15分)已知)(x u n 满足1()()1,2,n x nn u x u x x e n -'=+=,且neu n =)1(,求函数项级数∑∞=1)(n nx u之和.八、(10分)求-→1x 时,与∑∞=02n n x 等价的无穷大量.2023年 第二届全国大学生数学竞赛预赛试卷(非数学类)一、(25分,每小题5分) (1)设22(1)(1)(1)nn x a a a =+++,其中||1,a <求lim .n n x →∞(2)求21lim 1x xx ex -→∞⎛⎫+ ⎪⎝⎭. (3)设0s >,求0(1,2,)sx n n I e x dx n ∞-==⎰.(4)设函数()f t 有二阶连续导数,1(,)r g x y f r ⎛⎫== ⎪⎝⎭,求2222g g x y ∂∂+∂∂.(5)求直线10:0x y l z -=⎧⎨=⎩与直线2213:421x y z l ---==--的距离. 二、(15分)设函数()f x 在(,)-∞+∞上具有二阶导数,并且()0f x ''>,lim ()0x f x α→+∞'=>,lim ()0x f x β→-∞'=<,且存在一点0x ,使得0()0f x <. 证明:方程()0f x =在(,)-∞+∞恰有两个实根.三、(15分)设函数()y f x =由参数方程22(1)()x t t t y t ψ⎧=+>-⎨=⎩所拟定,且22d 3d 4(1)y x t =+,其中()t ψ具有二阶导数,曲线()y t ψ=与22132t u y e du e-=+⎰在1t =出相切,求函数()t ψ. 四、(15分)设10,nn n kk a S a=>=∑,证明:(1)当1α>时,级数1nn na S α+∞=∑收敛; (2)当1α≤且()n s n →∞→∞时,级数1nn na S α+∞=∑发散. 五、(15分)设l 是过原点、方向为(,,)αβγ,(其中2221)αβγ++=的直线,均匀椭球2222221x y z a b c ++≤(其中0c b a <<<,密度为1)绕l 旋转. (1)求其转动惯量;(2)求其转动惯量关于方向(,,)αβγ的最大值和最小值.六、(15分)设函数()x ϕ具有连续的导数,在围绕原点的任意光滑的简朴闭曲线C 上,曲线积分422d ()d 0L xy x x yx y ϕ+=+⎰的值为常数.(1)设L 为正向闭曲线22(2)1x y -+=,证明422d ()d 0L xy x x yx y ϕ+=+⎰;(2)求函数()x ϕ;(3)设C 是围绕原点的光滑简朴正向闭曲线,求422d ()d C xy x x y x y ϕ++⎰.2023年 第三届全国大学生数学竞赛预赛试卷(非数学类)一、计算下列各题(本题共3小题,每小题各5分,共15分)(1)求11cos 0sin lim xx x x -→⎛⎫⎪⎝⎭;(2).求111lim ...12n n n n n →∞⎛⎫+++ ⎪+++⎝⎭; (3)已知()2ln 1arctan tt x e y t e⎧=+⎪⎨=-⎪⎩,求22d d y x .二、(本题10分)求方程()()24d 1d 0x y x x y y +-++-=的通解.三、(本题15分)设函数()f x 在0x =的某邻域内具有二阶连续导数,且()()()0,0,0f f f '''均不为0,证明:存在唯一一组实数123,,k k k ,使得()()()()12320230lim0h k f h k f h k f h f h→++-=. 四、(本题17分)设2221222:1x y z a b c ∑++=,其中0a b c >>>,2222:z x y ∑=+,Γ为1∑与2∑的交线,求椭球面1∑在Γ上各点的切平面到原点距离的最大值和最小值.五、(本题16分)已知S 是空间曲线22310x y z ⎧+=⎨=⎩绕y 轴旋转形成的椭球面的上半部分(0z ≥)(取上侧),∏是S 在(,,)P x y z 点处的切平面,(,,)x y z ρ是原点到切平面∏的距离,,,λμν表达S 的正法向的方向余弦. 计算:(1)()d ,,SzS x y z ρ⎰⎰;(2)()3d Sz x y z S λμν++⎰⎰ 六、(本题12分)设()f x 是在(,)-∞+∞内的可微函数,且()()f x mf x '<,其中01m <<,任取实数0a ,定义1ln (),1,2,...n n a f a n -==,证明:11()n n n a a ∞-=-∑绝对收敛.七、(本题15分)是否存在区间[]0,2上的连续可微函数()f x ,满足(0)(2)1f f ==,()1f x '≤,2()d 1f x x ≤⎰?请说明理由.2023年 第四届全国大学生数学竞赛预赛试卷(非数学类)一、(本大题共5小题,每小题6分,共30分)解答下列各题(规定写出重要环节). (1)求极限21lim(!)n n n →∞.(2)求通过直线2320:55430x y z l x y z +-+=⎧⎨+-+=⎩的两个互相垂直的平面1π和2π,使其中一个平面过点(4,3,1)-.(3)已知函数(,)ax byz u x y e+=,且20ux y∂=∂∂. 拟定常数a 和b ,使函数(,)z z x y =满足方程20z z zz x y x y∂∂∂--+=∂∂∂∂. (4)设函数()u u x =连续可微,(2)1u =,且3(2)d ()d Lx y u x x u u y +++⎰在右半平面与途径无关,求(,)u x y . (5)求极限1lim x xx t +.二、(本题10分)计算20sin d x e x x +∞-⎰.三、(本题10分)求方程21sin 2501x x x=-的近似解,精确到0.001.四、(本题12分)设函数()y f x =二阶可导,且()0f x ''>,(0)0f =,(0)0f '=,求330()lim ()sin x x f u f x u→,其中u 是曲线()y f x =上点(,())P x f x 处的切线在x 轴上的截距. 五、(本题12分)求最小实数C ,使得满足10()d 1f x x =⎰的连续函数()f x 都有10f dx C ≤⎰.六、(本题12分)设()f x 为连续函数,0t >. 区域Ω是由抛物面22z x y =+和球面 2222x y z t ++=(0)z >所围起来的部分. 定义三重积分222()()d F t f x y z v Ω=++⎰⎰⎰,求()F t 的导数()F t ''.七、(本题14分)设1n n a ∞=∑与1n n b ∞=∑为正项级数,证明:(1)若()111lim 0n n n n n a a b b →∞++->,则级数1n n a ∞=∑收敛;(2)若()111lim 0n n n n n a a b b →∞++-<,且级数1n n b ∞=∑发散,则级数1n n a ∞=∑发散.2023年 第五届全国大学生数学竞赛预赛试卷(非数学类)一、解答下列各题(每小题6分,共24分,规定写出重要环节) 1.求极限(lim 1sin nn →∞+.2.证明广义积分0sin d xx x+∞⎰不是绝对收敛的. 3.设函数()y y x =由323322x x y y +-=拟定,求()y x 的极值.4.过曲线0)y x =≥上的点A 作切线,使该切线与曲线及x 轴所围成的平面图形的面积为34,求点A 的坐标. 二、(满分12分)计算定积分2sin arctan d 1cos xx x e I x xππ-⋅=+⎰.三、(满分12分)设()f x 在0x =处存在二阶导数(0)f '',且()lim0x f x x→=.证明:级数11n f n ∞=⎛⎫⎪⎝⎭∑收敛.四、(满分12分)设(),()0()f x f x m a x b π'≤≥>≤≤,证明2sin ()d baf x x m≤⎰. 五、(满分14分)设∑是一个光滑封闭曲面,方向朝外.给定第二型的曲面积分()()()333d d 2d d 3d d I x x y z y y z x z z x y ∑=-+-+-⎰⎰.试拟定曲面∑,使积分I 的值最小,并求该最小值.六、(满分14分)设22d d ()()a a C y x x yI r x y -=+⎰,其中a 为常数,曲线C 为椭圆222x xy y r ++=,取正向.求极限lim ()a r I r →+∞.七、(满分14分)判断级数()()1111212n n n n ∞=+++++∑的敛散性,若收敛,求其和.2023年 第六届全国大学生数学竞赛预赛试卷(非数学类)一、填空题(共有5小题,每题6分,共30分)1.已知1x y e =和1x y xe =是齐次二阶常系数线性微分方程的解,则该方程是 .2.设有曲面22:2S z x y =+和平面022:=++z y x L . 则与L 平行的S 的切平面方程是 .3.设函数()y y x =由方程21sin d 4y xt x t π-⎛⎫= ⎪⎝⎭⎰所拟定.求d d x y x == .4.设1(1)!nn k kx k ==+∑,则=∞→n n x lim .5.已知130()lim 1xx f x x e x →⎛⎫++= ⎪⎝⎭,则=→20)(lim x x f x .二、(本题12分)设n 为正整数,计算21d 1cos ln d d n eI x x x π-⎛⎫= ⎪⎝⎭⎰. 三、(本题14分)设函数()f x 在]1,0[上有二阶导数,且有正常数,A B 使得()f x A ≤,|"()|f x B ≤. 证明:对任意]1,0[∈x ,有22|)('|BA x f +≤. 四、(本题14分)(1)设一球缺高为h ,所在球半径为R . 证明该球缺体积为2)3(3h h R -π,球冠面积为Rh π2;(2)设球体12)1()1()1(222≤-+-+-z y x 被平面6:=++z y x P 所截的小球缺为Ω,记球缺上的球冠为∑,方向指向球外,求第二型曲面积分d d d d d d I x y z y z x z x y ∑=++⎰⎰.五、(本题15分)设f 在],[b a 上非负连续,严格单增,且存在],[b a x n ∈,使得⎰-=b a nn n dx x f ab x f )]([1)]([.求n n x ∞→lim . 六、(本题15分)设2222212n n nnA n n n n =++++++,求⎪⎭⎫ ⎝⎛-∞→n n A n 4lim π.2023年 第七届全国大学生数学竞赛预赛试卷(非数学类)一、填空题(每小题6分,共5小题,满分30分)(1)极限2222sin sin sin lim 12n n n n n n n n πππ→∞⎛⎫⎪+++= ⎪+++ ⎪⎝⎭. (2)设函数(),z z x y =由方程,0z z F x y y x ⎛⎫++= ⎪⎝⎭所决定,其中(),F u v 具有连续偏导数,且0u v xF yF +≠则z zxy x y∂∂+=∂∂ .(3)曲面221z x y =++在点()1,1,3M -的切平面与曲面所围区域的体积是 .(4)函数()[)[)3,5,00,0,5x f x x ⎧∈-⎪=⎨∈⎪⎩在(]5,5-的傅立叶级数在0x =收敛的是 . (5)设区间()0,+∞上的函数()u x 定义域为()2xt u x e dt +∞-=⎰,则()u x 的初等函数表达式是 .二、(12分)设M 是以三个正半轴为母线的半圆锥面,求其方程.三、(12分)设()f x 在(),a b 内二次可导,且存在常数,αβ,使得对于(),x a b ∀∈,有()()()f x f x f x αβ'=+,则()f x 在(),a b 内无穷次可导.四、(14分)求幂级数()()30211!nn n x n ∞=+-+∑的收敛域及其和函数.五、(16分)设函数()f x 在[]0,1上连续,且()()110,1f x dx xf x dx ==⎰⎰. 试证:(1)[]00,1x ∃∈使()04f x >; (2)[]10,1x ∃∈使()14f x =.五、(16分)设(),f x y 在221x y +≤上有连续的二阶偏导数,且2222xx xy yy f f f M ++≤. 若()()()0,00,0,00,00x y f f f ===,证明:()221,4x y f x y dxdy +≤≤⎰⎰.2023年 第八届全国大学生数学竞赛预赛试卷(非数学类)一、填空题(每小题5分,满分30分) 1、若()f x 在点x a =可导,且()0f a ≠,则()1lim nn f a n f a →∞⎛⎫⎛⎫+ ⎪⎪⎝⎭⎪= ⎪⎪⎝⎭__________. 2、若()10f =,()1f '存在,求极限()()220sin cos tan3lim1sin x x f x x xI ex→+=-.3、设()f x 有连续导数,且()12f =,记()2x z f e y =,若zz x∂=∂,求()f x 在0x >的表达式.4、设()sin 2x f x e x =,求02n a π<<,()()40f .5、求曲面22 2x z y =+平行于平面220x y z +-=的切平面方程.二、(14分)设()f x 在[]0,1上可导,()00f =,且当()0,1x ∈,()01f x '<<,试证当()0,1a ∈,()()()230d d aaf x xf x x >⎰⎰.三、(14分)某物体所在的空间区域为222:22x y z x y z Ω++≤++,密度函数为222x y z ++,求质量()222d d d M x y z x y z Ω=++⎰⎰⎰.四、(14分)设函数()f x 在闭区间[]0,1上具有连续导数,()00f =,()11f =, 证明:()10111lim 2n n k k n f x dx fn n →∞=⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭∑⎰.五、(14分)设函数()f x 在闭区间[]0,1上连续,且()1d 0I f x x =≠⎰,证明:在()0,1内存在不同的两点12,x x ,使得()()12112f x f x I+=. 六、(14分)设()f x 在(),-∞+∞可导,且()()()23f x f x f x =+=+.用Fourier 级数理论证明()f x 为常数.2023年 第九届全国大学生数学竞赛预赛试卷(非数学类)一、1. 已知可导函数满足⎰+=+xx tdt t f x xf 01sin )(2)(cos ,则()f x =_________.2. 求⎪⎭⎫ ⎝⎛+∞→n n n 22sin lim π.3. 设(,)w f u v =具有二阶连续偏导数,且==+u x cy v x cy -,,其中c 为非零常数. 则21xx yy w w c-=_________. 4. 设()f x 有二阶导数连续,且(0)'(0)0,"(0)6f f f ===,则240(sin )lim x f x x→=____. 5. 不定积分sin 2sin 2(1sin )x e x I dx x -=-⎰=________. 6. 记曲面222z x y =+和z =围成空间区域为V ,则三重积分Vzdxdydz ⎰⎰⎰=___________.二、(本题满分14分) 设二元函数(,)f x y 在平面上有连续的二阶偏导数. 对任何角度α,定义一元函数()(cos ,sin )g t f t t =ααα.若对任何α都有(0)0dg dtα=且22(0)0d g dt α>. 证明)0,0(f 是(,)f x y 的极小值. 三、(本题满分14分) 设曲线Γ为在2221x y z ++=,1x z +=,0,0,0x y z ≥≥≥上从(1,0,0)A 到(0,0,1)B 的一段. 求曲线积分⎰Γ++=xdz zdy ydx I .四、(本题满分15分) 设函数()0f x >且在实轴上连续,若对任意实数t ,有||()1t x e f x dx +∞---∞≤⎰,则,()a b a b ∀<,2()2b a b a f x dx -+≤⎰. 五、(本题满分15分) 设{}n a 为一个数列,p 为固定的正整数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖北省数学学会文件鄂数学会字 [2014] 3号关于公布第三届湖北省大学生数学竞赛获奖名单的通知湖北省数学学会各高校会员单位:第三届湖北省大学生数学竞赛的竞赛工作、评卷工作以及评奖工作均已顺利结束。
湖北省大学生数学竞赛竞赛委员会根据竞赛成绩以及各单位参赛人数,确定了获奖学生名单,现将获奖名单予以公布,其中:数学类一等奖16名,二等奖19名,三等奖38名;非数学类一等奖63名,二等奖88名,三等奖151名(详细名单见附件)。
特此通知。
附件:第三届湖北省大学生数学竞赛获奖名单湖北省数学学会二○一四年十一月五日主题词:湖北省大学生数学竞赛获奖名单湖北省数学学会秘书处 2014年11月5日印制打印:龙莎燕校对:陈士华印数:60份第三届湖北省大学生数学竞赛获奖名单一、数学类获奖名单一等奖(16人)袁航 (武汉大学) 冀诸超(武汉大学)黄旷 (武汉大学) 杜宏伟(中国地质大学)刘伟 (湖北理工学院) 王永兴(武汉大学)张宇 (湖北大学) 吴晓旭(华中师范大学)童笛 (湖北师范学院) 倪彬彬(中南民族大学)王天 (华中农业大学) 金典聪(华中科技大学)沈铮阳 (武汉理工大学) 高巍(华中农业大学)闻江业 (武汉科技大学) 魏金晶湖北文理学院二等奖(19人)陈明洁 (武汉大学) 张仕俊(武汉大学)王文灿 (湖北师范学院) 陈言忞(华中师范大学)邓路 (武汉大学) 阚向阳(武汉大学)袁旭 (武汉大学) 余冲(湖北大学)陶金 (湖北大学) 陈宇勇(湖北第二师范学院)周唯 (湖北工程学院) 赵云海(中国地质大学)李文明 (武汉理工大学) 马村(中南民族大学)李诗雨 (华中农业大学) 冯金晶(华中农业大学)王星 (华中农业大学) 王众豪(武汉科技大学)刘晓玲 (湖北文理学院)三等奖(38人)危博伦 (武汉大学) 徐文强(武汉大学)陈通 (武汉大学) 孙青(武汉大学)李博文 (武汉大学) 吴艳红(湖北师范学院)刘常钰 (武汉大学) 李双兴(武汉大学)胡其伟 (华中科技大学) 杨嘉伟(湖北大学)徐阳 (华中师范大学) 王浩(湖北大学)吴燚林 (长江大学) 华志胜(中国地质大学)杨然 (长江大学) 简劼(华中科技大学)匡佩 (湖北工程学院) 刘超(湖北民族学院)韩嫣 (华中农业大学) 李骁(中南民族大学)徐成 (湖北第二师范学院) 蒋婷婷(华中农业大学)谭树心 (荆楚理工学院) 翁为方(武汉理工大学)熊振华 (华中农业大学) 高源(武汉科技大学)樊金东 (中南民族大学) 方雅清(武汉科技大学)杨云强 (华中农业大学) 邹姣(中南财经政法大学)张明 (华中农业大学) 黄伟(武汉科技大学)徐春华 (湖北师范学院文理学院) 邵欧阳(湖北文理学院)涂壕 (武汉纺织大学) 龚文钦(武汉纺织大学)王晨 (湖北文理学院) 蔡勤学(湖北科技学院)二、非数学类获奖名单一等奖(63人)邓超云(武汉大学) 李豪杰 (海军工程大学)叶金阳(华中科技大学) 王进 (长江大学)谭伟伟(中国地质大学) 邓鹤龄 (武汉大学)曾科南(武汉工程大学) 雷心怡 (华中科技大学)孙志鹏(武汉大学) 张佳奇 (三峡大学)胡中正(武汉科技大学) 余晋 (华中科技大学)饶德备(华中科技大学) 冯舒凯 (武汉大学)佃仁伟(武汉科技大学) 赖鑫 (武汉大学)熊超(湖北工业大学) 殷明超 (华中科技大学)李德龙(武汉科技大学) 金睿楠 (武汉理工大学)杨哲宇(武汉大学) 蔡传高 (湖北理工学院)邱涛(武汉工程大学) 潘小旺 (武汉大学)何建宏(武汉大学) 彭永子 (湖北汽车工业学院) 王世成(湖北汽车工业学院) 韦旭 (空军预警学院)王博文(武汉纺织大学) 温建雄 (空军预警学院)朱凌霄(空军预警学院) 李帅帅 (武汉理工大学)刘宇昕(武汉大学) 杨华侨 (中国地质大学)胡颖彬(武汉理工大学) 李响 (中南财经政法大学) 刘帅(长江大学) 马朋 (中南民族大学)张旭(武汉大学) 吴荀 (武汉大学)廖模驰(武汉大学) 邱廷柱 (武汉大学)孙建(武汉大学) 吴天舒 (海军工程大学)刘昌明(中南财经政法大学) 冷诚 (武汉理工大学)刘欢(湖北工程学院) 刘婧 (武汉理工大学)董俊冬(荆楚理工学院) 陈都 (武汉工程大学)李立(湖北经济学院) 许力 (华中农业大学)吴旭(军事经济学院) 阮云攀 (华中农业大学)张丰(华中师范大学) 陈燕波 (华中农业大学)安炳合(华中农业大学) 吴健茹 (军事经济学院)许杨(军事经济学院) 阳莉莉 (湖北经济学院)郑高兴(华中农业大学) 宋琪 (华中农业大学)丁锐(空军预警学院黄陂士官学校)二等奖(88人)付晓钏 (华中科技大学) 廖晓坚(华中科技大学)王浩 (武汉科技大学) 石来(华中科技大学)张德洁 (华中科技大学) 潘瑜辉(武汉科技大学)岑胜 (湖北理工学院) 董斌(华中科技大学)王健 (三峡大学) 刘莹(华中科技大学)虞儒 (华中科技大学) 胡江涛(湖北工业大学)瞿成武 (武汉科技大学) 杨锦涛(武汉大学)张晓萌 (武汉大学) 张亚伦(海军工程大学)庞先凯 (武汉大学) 李光耀(武汉大学)郑亚飞 (海军工程大学) 杨涛(武汉大学)魏聪颖 (武汉大学) 张顺(武汉大学)万核洋 (武汉大学) 王栋(武汉大学)付佳文 (武汉大学) 陈洋遥(武汉大学)邢伟 (武汉大学) 林贤峰(中国地质大学)肖珂 (武汉大学) 胡建润(武汉大学)王宇豪 (长江大学) 汪可芯(武汉大学)季亚军 (武汉大学) 谭康力(武汉理工大学)熊子康 (中南民族大学) 杨名浩(湖北工业大学)汪伟 (武汉大学) 覃伟(武汉大学)徐超 (中国地质大学) 李浩冬(海军工程大学)张志城 (武汉大学) 谭本东(武汉大学)孙祥远武汉大学王运韬(海军工程大学)段圣文 (湖北工程学院) 程潇(中国地质大学)周游 (空军预警学院) 吴忠强(武汉工程大学)葛云龙 (中国地质大学) 余海洋(武汉工程大学)张龙 (武汉工程大学) 张志伟(武汉理工大学)郑敏 (武汉理工大学) 彭鹏程(中南民族大学)罗盼 (武汉工程大学) 王聪(武汉理工大学)曾雨 (武汉工程大学) 易凡(中南财经政法大学) 李东 (武汉工程科技学院) 安旭阳(武汉理工大学)周姜炜 (武汉理工大学) 郑燕妮(湖北经济学院)刘康 (军事经济学院) 何绪华(武汉工程大学)魏泽宇 (军事经济学院) 李云飞(湖北经济学院)李卫豪 (华中农业大学) 付紫昌(华中农业大学)李艳红 (中南财经政法大学) 蒋倩妮(华中师范大学)张达明 (军事经济学院) 周胜(军事经济学院)钱明灿 (湖北师范学院) 徐磊鑫(华中农业大学)孙松 (华中师范大学) 徐郁(湖北民族学院)易晗 (华中农业大学) 陈更(华中师范大学)程家熙 (湖北科技学院) 徐晨(华中农业大学)付洪 (华中农业大学) 温成成(华中农业大学)谢泽星 (湖北第二师范学院) 徐振东(华中农业大学)王永斌 (华中农业大学) 毛百进(华中农业大学)杨腾达 (华中农业大学) 崔立刚(空军预警学院黄陂士官学校)三等奖(151人)高皋 (湖北理工学院) 徐康(三峡大学)卜海峰 (华中科技大学) 陈丽莎(华中科技大学)仲柳 (华中科技大学) 宋磊(华中科技大学)康江豪 (华中科技大学) 曾凡(华中科技大学)周绍华 (华中科技大学) 何元涛(华中科技大学)徐传智 (华中科技大学) 陈满盛(华中科技大学)邓世琛 (华中科技大学) 陈易(华中科技大学)马少华 (华中科技大学) 宋康(武汉科技大学)贺其水 (武汉纺织大学) 谭智广(武汉科技大学)陈步云 (武汉科技大学) 陈萍(武汉科技大学)许章 (长江大学) 王美娟(湖北工业大学)丁杰 (长江大学) 江飞(武汉科技大学)张翔宇 (长江大学) 洪旭(荆楚理工学院)高鹏 (武汉大学) 刘庆(湖北工业大学)万杨阳 (武汉大学) 严永阳(武汉科技大学)周易辰 (海军工程大学) 肖泽亮(武汉大学)夏丛紫 (武汉大学) 邓丽平(武汉大学)张杜娟 (武汉大学) 张锡洋(武汉大学)王方正 (武汉大学) 胡万林(武汉大学)冀佩琦 (武汉大学) 孙世博(武汉大学)姚鸿鹤 (海军工程大学) 黄林伟(湖北工业大学)黄凌昊 (空军预警学院) 张雨廷(武汉大学)孙骁 (武汉大学) 吕荣俊(武汉大学)何传奇 (武汉大学) 董珮瑶(武汉大学)刘超 (中国地质大学) 朱子宜(中国地质大学)陆代强 (海军工程大学) 曾振华(湖北工业大学)张臻宸 (武汉大学) 郭逸豪(武汉大学)王虹 (武汉大学) 张汉超(湖北文理学院)陈梁栋 (空军预警学院) 刘健(武汉大学)邓涵潇 (武汉大学) 丁满意(海军工程大学)恽鹏 (武汉大学) 朱飞扬(武汉大学)曾凌云 (武汉大学) 郭金兰(武汉大学)刘雨翔 (武汉大学) 曹伟浩(海军工程大学)林子雁 (武汉大学) 胡鹏(武汉大学)张文涛 (中国地质大学) 陈奕辰(武汉大学)后新宇 (武汉大学) 郭潇(武汉大学)李伟光 (武汉大学) 彭刘阳(武汉大学)任缔超 (武汉大学) 肖坤(武汉理工大学)康雷 (武汉理工大学) 钟乐乐(中国地质大学)程军 (中国地质大学) 黄亮(中国地质大学)张意德 (中南民族大学) 孙健华(湖北工程学院)余海兵 (武汉工程大学) 康炎爽(武汉工程大学)成龙 (武汉理工大学) 杨紫恒(湖北经济学院)黎鹏 (武汉理工大学) 马慧(武汉理工大学)王方泉 (武汉理工大学) 韩文艺(武汉理工大学)袁露 (武汉理工大学) 胡静(中南财经政法大学)王羽南 (中南财经政法大学) 田忠(长江大学工程技术学院) 朱志星 (武汉工程大学) 王琳(武汉工程大学)姜宁烨 (武汉理工大学) 虞贤泽( 武汉工程大学)王宝月 (武汉理工大学) 黄涛(武汉理工大学)朱芮 (中南财经政法大学) 焦沈祥(军事经济学院)王多 (武汉工程大学) 李文(武汉工程大学)李沁峰 (军事经济学院) 笪智(军事经济学院)周钰 (军事经济学院) 李浩飞(武汉工程大学)石修文 (武汉工程大学) 杨诗(武汉工程大学)李黎 (湖北经济学院) 占光明(华中师范大学)秦大双 (武汉工程科技学院) 高程远(军事经济学院)伍胡刚 (空军预警学院) 陆林(军事经济学院)杜姗红 (湖北师范学院) 施加明(华中师范大学)陶琴 (空军预警学院) 周洋(湖北经济学院)傅芳 (军事经济学院) 刘正(空军预警学院)石茜 (湖北经济学院) 王繁(华中师范大学)付杰妮 (湖北大学) 章宇(湖北经济学院)蒋俊 (湖北第二师范学院) 吴慧琦(湖北第二师范学院)冯焜 (华中农业大学) 沙振杰(华中农业大学)代权 (中南民族大学) 崔志鹏(华中农业大学)万亮 (华中农业大学) 卓杰鹏(华中农业大学)杨雨婷 (华中农业大学) 高颖(华中农业大学)覃丹 (中南民族大学) 吴兴勤(华中农业大学)王停宇 (华中农业大学) 洪侠(华中农业大学)秦岭 (华中农业大学) 罗中宝(华中农业大学)李淑娴 (华中农业大学) 李巧玲(华中农业大学)赵一梦 (华中农业大学) 郝松林(华中农业大学)刘小星 (华中农业大学) 夏斐(湖北科技学院)高振川 (空军预警学院黄陂士官学校)白棪澐 (空军预警学院黄陂士官学校)王兴 (空军预警学院黄陂士官学校)。
