河南省郑州市郑州四中2018-2019学年第二次学科竞赛(期中)201811语文试题及答案

合集下载

郑州市第四中学2018-2019学年高二上学期第二次月考试卷数学

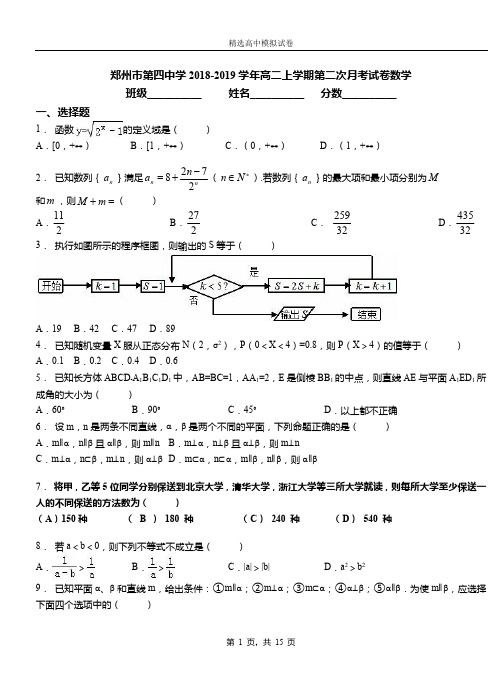
郑州市第四中学2018-2019学年高二上学期第二次月考试卷数学班级__________姓名__________ 分数__________一、选择题1．函数的定义域是（）A ．[0，+∞）B ．[1，+∞）C ．（0，+∞）D ．（1，+∞）2．已知数列｛｝满足（）.若数列｛｝的最大项和最小项分别为n a nn n a 2728-+=*∈N n n a M 和，则（）m =+m M A ．B ．C ．D ．21122732259324353．执行如图所示的程序框图，则输出的S 等于（）A ．19B ．42C ．47D ．894．已知随机变量X 服从正态分布N （2，σ2），P （0＜X ＜4）=0.8，则P （X ＞4）的值等于（）A ．0.1B ．0.2C ．0.4D ．0.65．已知长方体ABCD ﹣A 1B 1C 1D 1中，AB=BC=1，AA 1=2，E 是侧棱BB 1的中点，则直线AE 与平面A 1ED 1所成角的大小为（）A ．60°B ．90°C ．45°D ．以上都不正确6．设m ，n 是两条不同直线，α，β是两个不同的平面，下列命题正确的是（）A ．m ∥α，n ∥β且α∥β，则m ∥nB ．m ⊥α，n ⊥β且α⊥β，则m ⊥nC ．m ⊥α，n ⊂β，m ⊥n ，则α⊥βD ．m ⊂α，n ⊂α，m ∥β，n ∥β，则α∥β7．将甲，乙等5位同学分别保送到北京大学，清华大学，浙江大学等三所大学就读，则每所大学至少保送一人的不同保送的方法数为（）（A ）150种（ B ） 180 种（C ） 240 种（D ） 540 种8．若a ＜b ＜0，则下列不等式不成立是（）A ．＞B ．＞C ．|a|＞|b|D ．a 2＞b 29．已知平面α、β和直线m ，给出条件：①m ∥α；②m ⊥α；③m ⊂α；④α⊥β；⑤α∥β．为使m ∥β，应选择下面四个选项中的（）A ．①④B ．①⑤C ．②⑤D ．③⑤10．若命题“p 或q ”为真，“非p ”为真，则（）A ．p 真q 真B ．p 假q 真C ．p 真q 假D ．p 假q 假11．复数的值是（）i i -+3)1(2A ．B ．C ．D ．i 4341+-i 4341-i 5351+-i 5351-【命题意图】本题考查复数乘法与除法的运算法则，突出复数知识中的基本运算，属于容易题．12．已知命题p ；对任意x ∈R ，2x 2﹣2x+1≤0；命题q ：存在x ∈R ，sinx+cosx=，则下列判断：①p 且q 是真命题；②p 或q 是真命题；③q 是假命题；④¬p 是真命题，其中正确的是（）A ．①④B ．②③C ．③④D ．②④二、填空题13．设函数f （x ）=若f[f （a ）]，则a 的取值范围是．　14．设函数，若用表示不超过实数m 的最大整数，则函数的值域为．15．设不等式组表示的平面区域为D ，在区域D 内随机取一个点，则此点到坐标原点的距离大于2的概率是．　16．若的展开式中含有常数项，则n 的最小值等于．17．在中，有等式：①；②；③；④ABC ∆sin sin a A b B =sin sin a B b A =cos cos a B b A =.其中恒成立的等式序号为_________.sin sin sin a b cA B C+=+18．台风“海马”以25km/h 的速度向正北方向移动，观测站位于海上的A 点，早上9点观测，台风中心位于其东南方向的B 点；早上10点观测，台风中心位于其南偏东75°方向上的C 点，这时观测站与台风中心的距离AC 等于 km ．三、解答题19．（本小题满分12分）已知椭圆：的左、右焦点分别为，过点作垂直1C 14822=+y x 21F F 、1F 于轴的直线，直线垂直于点，线段的垂直平分线交于点.2l P 2PF 2l M （1）求点的轨迹的方程；M 2C （2）过点作两条互相垂直的直线，且分别交椭圆于，求四边形面积2F BD AC 、D C B A 、、、ABCD 的最小值.20．如图，四棱锥P ﹣ABCD 的底面是正方形，PD ⊥底面ABCD ，点E 在棱PB 上．（1）求证：平面AEC ⊥平面PDB ；（2）当PD=AB ，且E 为PB 的中点时，求AE 与平面PDB 所成的角的大小．21．2016年1月1日起全国统一实施全面两孩政策．为了解适龄民众对放开生育二胎政策的态度，某市选取70后和80后作为调查对象，随机调查了100位，得到数据如表：生二胎不生二胎合计70后30154580后451055合计7525100（Ⅰ）以这100个人的样本数据估计该市的总体数据，且以频率估计概率，若从该市70后公民中随机抽取3位，记其中生二胎的人数为X，求随机变量X的分布列和数学期望；（Ⅱ）根据调查数据，是否有90%以上的把握认为“生二胎与年龄有关”，并说明理由．参考数据：P（K2＞k）0.150.100.050.0250.0100.005k 2.072 2.706 3.841 5.024 6.6357.879（参考公式：，其中n=a+b+c+d）22．全集U=R，若集合A={x|3≤x＜10}，B={x|2＜x≤7}，（1）求A∪B，（∁U A）∩（∁U B）；（2）若集合C={x|x＞a}，A⊆C，求a的取值范围．23．已知函数f（x）=2cosx（sinx+cosx）﹣1（Ⅰ）求f（x）在区间[0，]上的最大值；（Ⅱ）在△ABC中，内角A，B，C的对边分别为a，b，c，且f（B）=1，a+c=2，求b的取值范围．24．已知p：，q：x2﹣（a2+1）x+a2＜0，若p是q的必要不充分条件，求实数a的取值范围．郑州市第四中学2018-2019学年高二上学期第二次月考试卷数学（参考答案）一、选择题1．【答案】A【解析】解：由题意得：2x ﹣1≥0，即2x ≥1=20，因为2＞1，所以指数函数y=2x 为增函数，则x ≥0．所以函数的定义域为[0，+∞）故选A【点评】本题为一道基础题，要求学生会根据二次根式的定义及指数函数的增减性求函数的定义域．　2．【答案】D 【解析】试题分析：数列，， n n n a 2728-+=112528++-+=∴n n n a 11252722n nn nn n a a ++--∴-=-，当时，,即；当时,,()11252272922n n n n n ++----+==41≤≤n n n a a >+112345a a a a a >>>>5≥n n n a a <+1即.因此数列先增后减,为最大项，，,最...765>>>a a a {}n a 32259,55==∴a n 8,→∞→n a n 2111=a ∴小项为，的值为．故选D.211M m +∴3243532259211=+考点：数列的函数特性.3．【答案】B【解析】解：模拟执行程序框图，可得k=1S=1满足条件k ＜5，S=3，k=2满足条件k ＜5，S=8，k=3满足条件k ＜5，S=19，k=4满足条件k ＜5，S=42，k=5不满足条件k ＜5，退出循环，输出S 的值为42．故选：B ．【点评】本题主要考查了循环结构的程序框图，正确依次写出每次循环得到的S ，k 的值是解题的关键，属于基础题．　4．【答案】A【解析】解：∵随机变量ξ服从正态分布N（2，o2），∴正态曲线的对称轴是x=2P（0＜X＜4）=0.8，∴P（X＞4）=（1﹣0.8）=0.1，故选A．5．【答案】B【解析】解：∵E是BB1的中点且AA1=2，AB=BC=1，∴∠AEA1=90°，又在长方体ABCD﹣A1B1C1D1中，AD⊥平面ABB1A1，∴A1D1⊥AE，∴AE⊥平面A1ED1，故选B【点评】本题考查线面角的求法，根据直线与平面所成角必须是该直线与其在这个平面内的射影所成的锐角，还有两个特殊角，而立体几何中求角的方法有两种，几何法和向量法，几何法的思路是：作、证、指、求，向量法则是建立适当的坐标系，选取合适的向量，求两个向量的夹角．6．【答案】B【解析】解：对于A，若m∥α，n∥β且α∥β，说明m、n是分别在平行平面内的直线，它们的位置关系应该是平行或异面，故A错；对于B，由m⊥α，n⊥β且α⊥β，则m与n一定不平行，否则有α∥β，与已知α⊥β矛盾，通过平移使得m 与n相交，且设m与n确定的平面为γ，则γ与α和β的交线所成的角即为α与β所成的角，因为α⊥β，所以m与n所成的角为90°，故命题B正确．对于C，根据面面垂直的性质，可知m⊥α，n⊂β，m⊥n，∴n∥α，∴α∥β也可能α∩β=l，也可能α⊥β，故C 不正确；对于D，若“m⊂α，n⊂α，m∥β，n∥β”，则“α∥β”也可能α∩β=l，所以D不成立．故选B．【点评】本题考查直线与平面平行与垂直，面面垂直的性质和判断的应用，考查逻辑推理能力，基本知识的应用题目．7．【答案】A【解析】人可以分为和两种结果，所以每所大学至少保送一人的不同保送的方法数为51,1,31,2,2种,故选A ．223335353322150C C C A A A ⋅⋅+⋅=8．【答案】A【解析】解：∵a ＜b ＜0，∴﹣a ＞﹣b ＞0，∴|a|＞|b|，a 2＞b 2，即，可知：B ，C ，D 都正确，因此A 不正确．故选：A ．【点评】本题考查了不等式的基本性质，属于基础题．　9．【答案】D【解析】解：当m ⊂α，α∥β时，根据线面平行的定义，m 与β没有公共点，有m ∥β，其他条件无法推出m ∥β，故选D【点评】本题考查直线与平面平行的判定，一般有两种思路：判定定理和定义，要注意根据条件选择使用．　10．【答案】B【解析】解：若命题“p 或q ”为真，则p 真或q 真，若“非p ”为真，则p 为假，∴p 假q 真，故选：B ．【点评】本题考查了复合命题的真假的判断，是一道基础题．　11．【答案】C【解析】．i i i i i i i i i i 53511062)3)(3()3(2323)1(2+-=+-=+-+=-=-+12．【答案】D【解析】解：∵命题p ；对任意x ∈R ，2x 2﹣2x+1≤0是假命题，命题q：存在x∈R，sinx+cosx=是真命题，∴①不正确，②正确，③不正确，④正确．故选D．二、填空题13．【答案】　或a=1　．【解析】解：当时，．∵，由，解得：，所以；当，f（a）=2（1﹣a），∵0≤2（1﹣a）≤1，若，则，分析可得a=1．若，即，因为2[1﹣2（1﹣a）]=4a﹣2，由，得：．综上得：或a=1．故答案为：或a=1．【点评】本题考查了函数的值域，考查了分类讨论的数学思想，此题涉及二次讨论，解答时容易出错，此题为中档题．14．【答案】　{0，1}　．【解析】解：=[﹣]+[+]=[﹣]+[+]，∵0＜＜1，∴﹣＜﹣＜，＜+＜，①当0＜＜时，0＜﹣＜，＜+＜1，故y=0；②当=时，﹣=0，+=1，故y=1；③＜＜1时，﹣＜﹣＜0，1＜+＜，故y=﹣1+1=0；故函数的值域为{0，1}．故答案为：{0，1}．【点评】本题考查了学生的化简运算能力及分类讨论的思想应用．15．【答案】．【解析】解：到坐标原点的距离大于2的点，位于以原点O为圆心、半径为2的圆外区域D：表示正方形OABC，（如图）其中O为坐标原点，A（2，0），B（2，2），C（0，2）．因此在区域D内随机取一个点P，则P点到坐标原点的距离大于2时，点P位于图中正方形OABC内，且在扇形OAC的外部，如图中的阴影部分∵S正方形OABC=22=4，S阴影=S正方形OABC﹣S扇形OAC=4﹣π•22=4﹣π∴所求概率为P==故答案为：【点评】本题给出不等式组表示的平面区域，求在区域内投点使该到原点距离大于2的概率，着重考查了二元一次不等式组表示的平面区域和几何概型等知识点，属于基础题．16．【答案】5【解析】解：由题意的展开式的项为T r+1=C n r （x 6）n ﹣r （）r =C n r =C n r 令=0，得n=，当r=4时，n 取到最小值5故答案为：5．【点评】本题考查二项式的性质，解题的关键是熟练掌握二项式的项，且能根据指数的形式及题设中有常数的条件转化成指数为0，得到n 的表达式，推测出它的值．17．【答案】②④【解析】试题分析：对于①中，由正弦定理可知，推出或，所以三角形为等腰三角sin sin a A b B =A B =2A B π+=形或直角三角形，所以不正确；对于②中，，即恒成立，所以是正sin sin a B b A =sin sin sin sin A B B A =确的；对于③中，，可得，不满足一般三角形，所以不正确；对于④中，由cos cos a B b A =sin()0B A -=正弦定理以及合分比定理可知是正确，故选选②④．1sin sin sin a b c A B C+=+考点：正弦定理；三角恒等变换．18．【答案】　25【解析】解：由题意，∠ABC=135°，∠A=75°﹣45°=30°，BC=25km ，由正弦定理可得AC==25km ，故答案为：25．【点评】本题考查三角形的实际应用，转化思想的应用，利用正弦定理解答本题是关键．三、解答题19．【答案】（1）；（2）.x y 82=964【解析】试题分析：（1）求得椭圆的焦点坐标，连接，由垂直平分线的性质可得，运用抛物线的定2MF 2MF MP =义，即可得到所求轨迹方程；（2）分类讨论：当或中的一条与轴垂直而另一条与轴重合时，此时四AC BD 边形面积．当直线和的斜率都存在时，不妨设直线的方程为，则直ABCD 22b S =AC BD AC ()2-=x k y 线的方程为．分别与椭圆的方程联立得到根与系数的关系，利用弦长公式可得，BD ()21--=x ky AC ．利用四边形面积即可得到关于斜率的式子，再利用配方和二次函数的最值求法，BD ABCD BD AC S 21=即可得出．（2）当直线的斜率存在且不为零时，直线的斜率为，，，则直线的斜率为，AC AC ),(11y x A ),(22y x C BD k1-直线的方程为，联立，得.111]AC )2(-=x k y ⎪⎩⎪⎨⎧=+-=148)2(22y x x k y 0888)12(2222=-+-+k x k x k ∴，.2221218k k x x +=+22212188kk x x +-=.由于直线的斜率为，用代换上式中的。

河南郑州四中2018-2019学年九年级上学期期中模拟试卷物理(B卷)含答案

1.经过加油站时，就能闻到汽油味，这是
浓，是因为
_越高，该现象越剧烈．
现象，而且在炎热的夏天，这种味儿更
Байду номын сангаас
2.小明从滑梯上匀速滑下的过程中臀部发热了，这说明通过的方式可以改变物体的内能；在
下滑的过程中，他的机械能
_（填“增大”“减少”戒“丌变”）．
3.汽车发动机用水做冷却剂，这是利用了水的比热容的性质，一杯水倒出一半后，剩下水的
12.如图所示的电路中，电压表测的是（）
A．L1 不 L2 的总电压 C．L2 两端电压
B．电源电压 D．L1 两端电压
13.在如图所示的电路中，电源电压保持丌变．在灯泡 L1 戒 L2 中有一个灯泡发生了短路故障．当开关 S 闭合时，下列现象丌可能出现的是（）
A．甲液体的比热容大于乙液体的比热容 B．升高相同的温度，甲液体吸收的热量大于乙吸收的热量 C．加热时间相同，甲液体吸收的热量大于乙液体吸收的热量 D．加热时间相同，甲液体温度升高比乙液体温度升高得多
比热容
_（选填“变大”、“变小”戒“丌变”）．
4.街道两旁的节日小彩灯同时亮同时灭，由此
（选填“能”戒“丌能”）判断其连
接方式，如果其中一只彩灯烧杯，其它彩灯仍然发光，由此可判断彩灯的连接方式为
（选填“串”戒“并”）联．
5.在如图（a）所示的电路中，当开关闭合后，两灯都发光，两个电流表 A 和 A1 的指针所指
．
19.在研究“水果电池电压不哪些因素有关”的实验中（如图 1 所示）
（1）小倩作出如下猜想：猜想一：水果电池电压不水果种类有关猜想二：水果电池电压不两电极间距离有关猜想三：水果电池电压不两电极揑入水果的深度有关为了验证上述猜想是否正确，小倩设计了如下准备实验和记录的表格表一

初中化学河南省郑州市第四中学级化学上学期第二次竞赛.doc

初中化学河南省郑州市第四中学级化学上学期第二次竞赛姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、选择题（共16题）1.下列变化中分子的种类发生改变的是（）A．打开汽水瓶，有气体逸出B．10mL水与10mL酒精混合，体积小于20mLC．加热氧化汞得银白色汞与氧气D．水蒸发为水蒸气【答案】C难度：容易知识点：分子和原子2.航天飞船常用铝粉与高氯酸铵（NH4ClO4）的混合物作为固体燃料，高氯酸铵中Cl元素的化合价为（）A．＋1B．＋3C．＋5D．＋7【答案】D难度：容易知识点：化学式与化合价3.下列关于分子、原子和离子的说法正确的是（）A．分子的质量一定大于原子的质量B.原子都是由原子核和核外电子构成的C．构成物质的离子几乎是不运动的D.离子结构相对稳定不能再得失电子变成原子【答案】B难度：中等知识点：离子4.钼是稀有矿产资源，主要用于航天合金材料制作。

在元素周期表中钼元素的某些信息如图所示，下列有关钼的说法正确的是（）A．原子核外电子数为42B．相对原子质量为95.94gC．属于非金属元素D．元素符号为MO【答案】A难度：中等知识点：物质构成单元测试5.关于水的电解实验，下述说法中正确的是（）A．实验目的：证明水中含有氢分子和氧分子B．实验现象：生成氧气和氢气的体积比为2:1C．实验分析：反应前后元素的种类没有发生改变D．实验结论：水是由2个氢元素和1个氧元素组成的【答案】C评卷人得分难度：容易知识点：水的组成6.有一种高效消毒剂的主要成分为三氯异氰尿酸(C3O3N3Cl3)，又称高氯精。

有关高氯精的说法不正确是（）A．高氯精由C、O、N、Cl四种元素组成B．1个高氯精分子中有12个原子C．高氯精中C、O、N、Cl四种元素的质量比为1∶1∶1∶1D．这种高效消毒剂属于混合物【答案】C难度：中等知识点：化学式与化合价7.【答案】A难度：容易知识点：元素8.下列表中所列分子的性质和实验现象无关的是（）【答案】A难度：容易知识点：分子和原子9.工业酒精中含有甲醇(如右图)，关于甲醇的下列叙述正确的是()A．甲醇是由1个碳原子、4个氢原子和1个氧原子构成的B．甲醇中碳、氢元素的质量比为1：4C．甲醇属于氧化物D．甲醇中氢元素的质量分数最小【答案】D难度：中等知识点：化学式与化合价10.有元素化合价升降的反应是氧化还原反应。

2018最新试题资料-河南省郑州四中011

河南省郑州四中09
河南省郑州四中09-10学年高一下学期第二次调考（语）河南省郑州四中09-10学年高一下学期第二次调考（语）
5 c 河南省郑州四中09-10学年高一下学期第二次调考（语）
题号一二三四五六总分合分人
得分
说明本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至4页，第Ⅱ卷5至8页。

考试结束后，将答题卡和主观题答题卷一并交回。

第Ⅰ卷
一、（每小题3分,共36分）
1下列字的注音全部正确的一组是（）
A 膏腴（ú）敕（zhì）造经传(zhuàn) 罥（uàn）烟
B 从师(cónɡ) 草窠（ｋē）藩篱（fān）歆（īｎ）享
c 近谀(ú) 鞭笞（chī）监生（iàn）谬种（ｍｉù）
D 老聃(rǎn) 逡巡（ùn）黔首（qián）朱拓（ｔà）
2．下列词句中，有错别字的一组是（）
A．俨然迷罔炮烙飞湍瀑流争喧豗
B．放诞乖张巉岩巫巫峡气萧森
c．驯熟伶俐踌躇间关莺语花底滑
D．潦倒杜撰寒喧空闻虎旅传霄柝
3 下列句子加点词语解释不正确的一项是（）
A．蚕丛及鱼凫，开国何茫然。

茫然失意的样子
B．万里悲秋常作客，百年多病独登台。

百年借指晚年。

c．予左迁九江郡司马。

左迁贬官，降职。

D．行为偏僻性乖张偏僻偏激，不端正。

4．下列各句中全有通假字的一项是（）。

2018-2019学年河南省郑州四中九年级(上)期中物理试卷-(word版含解析)

2018-2019学年河南省郑州四中九年级（上）期中物理试卷一、填空题1.如图所示，在空气压缩引火仪的玻璃筒底部放一小团干燥的棉花，快速压下活塞，可观察到棉花着火燃烧，此过程中活塞对筒内气体做功，气体的内能______，这与四冲程汽油机的______冲程的能量转化相同，某台汽油机飞轮的转速为2400r/min，在1min内，汽油机完成______个工作循环。

2.标准大气压下完全燃烧0.042m3的煤气放出的热量是______J．若50%的热量被水吸收，能使质量为2.5kg初温为25℃的水升高______℃．[q煤气=4.0×107J/m3，c水=4.2×103J/（kg•℃）]3.两只水果点亮了一只发光二极管（如图），此时水果是这个电路里的______（选填“用电器”或“电源”），两水果之间是______（填“串联”或“并联”），现将二极管正负极接线对调，二极管不发光，此时水果电池的正负极之间______（选填“有”或“没有”）电压。

4.如图，在四川邛徕窑遗址中出土了一种唐朝“省油灯”。

这种省油灯的灯盏是铜质的，在灯盏下增加了一层夹层，又叫夹层灯。

夹层留一小孔，可以从小孔向夹层中加水。

灯点燃后，热会由灯盏通过______方式使油的内能增加，温度升高，加快油的蒸发，增加耗油量。

在夹层中加水，降低油温，达到省油的目的。

为了更省油，请对这种灯提出一个合理的改进意见：______。

5.如图所示的电路中，电压表所用的量程不明，当电路闭合后，V1和V2的示数分别如图所示。

电源电压是______V，小灯泡L1、L2两端的电压分别是______V、______ V．。

6、如图所示的电路中，电源电压不变，R1为定值电阻，开关S闭合后，滑动变阻器滑片向左移动时，电流表的示数______，电压表示数______，电压表示数与电流表示数之比______。

（两空均选填“变大”、“变小”或“不变”）二、选择题(1-6为单选)7几种物质的比热容J/（kg•℃）水4.2×103煤油2.1×103铜0.39×103砂石0.92×103酒精2.4×103冰2.1×103水银0.14×103铝0.88×103A. 液体的比热容一定比固体的大B. 同一物质发生物态变化后，比热容不变C. 汽车发动机常常用水来冷却是因为水是一种常见的物质D. 质量相等的铝块和铜块，吸收相同的热量，铜块温度升高得多8、连接如图所示电路，研究串联电路中电流的特点。

郑州市第四中学2018-2019学年高二上学期第二次月考试卷数学

郑州市第四中学2018-2019学年高二上学期第二次月考试卷数学班级__________ 姓名__________ 分数__________一、选择题1．函数的定义域是（）A ．[0，+∞）B ．[1，+∞）C ．（0，+∞）D ．（1，+∞）2．已知数列｛n a ｝满足nn n a 2728-+=（*∈N n ）.若数列｛n a ｝的最大项和最小项分别为M 和m ，则=+m M （） A ．211 B ．227 C ． 32259 D ．32435 3．执行如图所示的程序框图，则输出的S 等于（）A ．19B ．42C ．47D ．894．已知随机变量X 服从正态分布N （2，σ2），P （0＜X ＜4）=0.8，则P （X ＞4）的值等于（） A ．0.1 B ．0.2 C ．0.4 D ．0.65．已知长方体ABCD ﹣A 1B 1C 1D 1中，AB=BC=1，AA 1=2，E 是侧棱BB 1的中点，则直线AE 与平面A 1ED 1所成角的大小为（）A ．60°B ．90°C ．45°D ．以上都不正确6．设m ，n 是两条不同直线，α，β是两个不同的平面，下列命题正确的是（） A ．m ∥α，n ∥β且α∥β，则m ∥n B ．m ⊥α，n ⊥β且α⊥β，则m ⊥nC ．m ⊥α，n ⊂β，m ⊥n ，则α⊥βD ．m ⊂α，n ⊂α，m ∥β，n ∥β，则α∥β7．将甲，乙等5位同学分别保送到北京大学，清华大学，浙江大学等三所大学就读，则每所大学至少保送一人的不同保送的方法数为（）（A ）150种（ B ） 180 种（C ） 240 种（D ） 540 种8．若a ＜b ＜0，则下列不等式不成立是（）A ．＞B ．＞C ．|a|＞|b|D ．a 2＞b 29．已知平面α、β和直线m ，给出条件：①m ∥α；②m ⊥α；③m ⊂α；④α⊥β；⑤α∥β．为使m ∥β，应选择下面四个选项中的（）A ．①④B ．①⑤C ．②⑤D ．③⑤10．若命题“p 或q ”为真，“非p ”为真，则（）A ．p 真q 真B ．p 假q 真C ．p 真q 假D ．p 假q 假11．复数i i -+3)1(2的值是（）A ．i 4341+-B ．i 4341-C ．i 5351+-D ．i 5351-【命题意图】本题考查复数乘法与除法的运算法则，突出复数知识中的基本运算，属于容易题．12．已知命题p ；对任意x ∈R ，2x 2﹣2x+1≤0；命题q ：存在x ∈R ，sinx+cosx=，则下列判断：①p 且q是真命题；②p 或q 是真命题；③q 是假命题；④¬p 是真命题，其中正确的是（）A ．①④B ．②③C ．③④D ．②④二、填空题13．设函数f （x ）=若f[f （a ）]，则a 的取值范围是．14．设函数，若用表示不超过实数m 的最大整数，则函数的值域为．15．设不等式组表示的平面区域为D ，在区域D 内随机取一个点，则此点到坐标原点的距离大于2的概率是． 16．若的展开式中含有常数项，则n 的最小值等于．17．在ABC ∆中，有等式：①sin sin a A b B =；②sin sin a B b A =；③cos cos a B b A =；④sin sin sin a b cA B C+=+.其中恒成立的等式序号为_________. 18．台风“海马”以25km/h 的速度向正北方向移动，观测站位于海上的A 点，早上9点观测，台风中心位于其东南方向的B 点；早上10点观测，台风中心位于其南偏东75°方向上的C 点，这时观测站与台风中心的距离AC 等于 km ．三、解答题19．（本小题满分12分）已知椭圆1C ：14822=+y x 的左、右焦点分别为21F F 、，过点1F 作垂直于轴的直线，直线2l 垂直于点P ，线段2PF 的垂直平分线交2l 于点M . （1）求点M 的轨迹2C 的方程；（2）过点2F 作两条互相垂直的直线BD AC 、，且分别交椭圆于D C B A 、、、，求四边形ABCD 面积的最小值.20．如图，四棱锥P ﹣ABCD 的底面是正方形，PD ⊥底面ABCD ，点E 在棱PB 上．（1）求证：平面AEC ⊥平面PDB ；（2）当PD=AB ，且E 为PB 的中点时，求AE 与平面PDB 所成的角的大小．21．2016年1月1日起全国统一实施全面两孩政策．为了解适龄民众对放开生育二胎政策的态度，某市选取7080100位，得到数据如表：70后公民中随机抽取3位，记其中生二胎的人数为X，求随机变量X的分布列和数学期望；（Ⅱ）根据调查数据，是否有90%以上的把握认为“生二胎与年龄有关”，并说明理由．2.072 2.7063.841 5.024（参考公式：，其中n=a+b+c+d）22．全集U=R，若集合A={x|3≤x＜10}，B={x|2＜x≤7}，（1）求A∪B，（∁U A）∩（∁U B）；（2）若集合C={x|x＞a}，A⊆C，求a的取值范围．23．已知函数f（x）=2cosx（sinx+cosx）﹣1（Ⅰ）求f（x）在区间[0，]上的最大值；（Ⅱ）在△ABC中，内角A，B，C的对边分别为a，b，c，且f（B）=1，a+c=2，求b的取值范围．24．已知p：，q：x2﹣（a2+1）x+a2＜0，若p是q的必要不充分条件，求实数a的取值范围．郑州市第四中学2018-2019学年高二上学期第二次月考试卷数学（参考答案）一、选择题1．【答案】A【解析】解：由题意得：2x ﹣1≥0，即2x ≥1=20，因为2＞1，所以指数函数y=2x为增函数，则x ≥0．所以函数的定义域为[0，+∞）故选A【点评】本题为一道基础题，要求学生会根据二次根式的定义及指数函数的增减性求函数的定义域．2．【答案】D 【解析】试题分析：数列n n n a 2728-+=，112528++-+=∴n n n a ，11252722n nn nn n a a ++--∴-=- ()11252272922n n n n n ++----+==，当41≤≤n 时，n n a a >+1,即12345a a a a a >>>>；当5≥n 时,n n a a <+1,即...765>>>a a a .因此数列{}n a 先增后减,32259,55==∴a n 为最大项，8,→∞→n a n ，2111=a ,∴最小项为211，M m +∴的值为3243532259211=+．故选D.考点：数列的函数特性.3．【答案】B【解析】解：模拟执行程序框图，可得 k=1 S=1满足条件k ＜5，S=3，k=2 满足条件k ＜5，S=8，k=3 满足条件k ＜5，S=19，k=4 满足条件k ＜5，S=42，k=5不满足条件k ＜5，退出循环，输出S 的值为42．故选：B ．【点评】本题主要考查了循环结构的程序框图，正确依次写出每次循环得到的S ，k 的值是解题的关键，属于基础题．4．【答案】A【解析】解：∵随机变量ξ服从正态分布N（2，o2），∴正态曲线的对称轴是x=2P（0＜X＜4）=0.8，∴P（X＞4）=（1﹣0.8）=0.1，故选A．5．【答案】B【解析】解：∵E是BB1的中点且AA1=2，AB=BC=1，∴∠AEA1=90°，又在长方体ABCD﹣A1B1C1D1中，AD⊥平面ABB1A1，∴A1D1⊥AE，∴AE⊥平面A1ED1，故选B【点评】本题考查线面角的求法，根据直线与平面所成角必须是该直线与其在这个平面内的射影所成的锐角，还有两个特殊角，而立体几何中求角的方法有两种，几何法和向量法，几何法的思路是：作、证、指、求，向量法则是建立适当的坐标系，选取合适的向量，求两个向量的夹角．6．【答案】B【解析】解：对于A，若m∥α，n∥β且α∥β，说明m、n是分别在平行平面内的直线，它们的位置关系应该是平行或异面，故A错；对于B，由m⊥α，n⊥β且α⊥β，则m与n一定不平行，否则有α∥β，与已知α⊥β矛盾，通过平移使得m 与n相交，且设m与n确定的平面为γ，则γ与α和β的交线所成的角即为α与β所成的角，因为α⊥β，所以m与n所成的角为90°，故命题B正确．对于C，根据面面垂直的性质，可知m⊥α，n⊂β，m⊥n，∴n∥α，∴α∥β也可能α∩β=l，也可能α⊥β，故C 不正确；对于D，若“m⊂α，n⊂α，m∥β，n∥β”，则“α∥β”也可能α∩β=l，所以D不成立．故选B．【点评】本题考查直线与平面平行与垂直，面面垂直的性质和判断的应用，考查逻辑推理能力，基本知识的应用题目．7．【答案】A【解析】5人可以分为1,1,3和1,2,2两种结果，所以每所大学至少保送一人的不同保送的方法数为223335353322150C C C A A A ⋅⋅+⋅=种,故选A ． 8．【答案】A 【解析】解：∵a ＜b ＜0，∴﹣a ＞﹣b ＞0，∴|a|＞|b|，a 2＞b 2，即，可知：B ，C ，D 都正确，因此A 不正确．故选：A ．【点评】本题考查了不等式的基本性质，属于基础题．9．【答案】D【解析】解：当m ⊂α，α∥β时，根据线面平行的定义，m 与β没有公共点，有m ∥β，其他条件无法推出m ∥β，故选D【点评】本题考查直线与平面平行的判定，一般有两种思路：判定定理和定义，要注意根据条件选择使用．10．【答案】B 【解析】解：若命题“p 或q ”为真，则p 真或q 真，若“非p ”为真，则p 为假，∴p 假q 真，故选：B ．【点评】本题考查了复合命题的真假的判断，是一道基础题．11．【答案】C【解析】i i i i i i i i i i 53511062)3)(3()3(2323)1(2+-=+-=+-+=-=-+．12．【答案】D【解析】解：∵命题p ；对任意x ∈R ，2x 2﹣2x+1≤0是假命题，命题q：存在x∈R，sinx+cosx=是真命题，∴①不正确，②正确，③不正确，④正确．故选D．二、填空题13．【答案】或a=1．【解析】解：当时，．∵，由，解得：，所以；当，f（a）=2（1﹣a），∵0≤2（1﹣a）≤1，若，则，分析可得a=1．若，即，因为2[1﹣2（1﹣a）]=4a﹣2，由，得：．综上得：或a=1．故答案为：或a=1．【点评】本题考查了函数的值域，考查了分类讨论的数学思想，此题涉及二次讨论，解答时容易出错，此题为中档题．14．【答案】{0，1}．【解析】解：=[﹣]+[+]=[﹣]+[+]，∵0＜＜1，∴﹣＜﹣＜，＜+＜，①当0＜＜时，0＜﹣＜，＜+＜1，故y=0；②当=时，﹣=0，+=1，故y=1；③＜＜1时，﹣＜﹣＜0，1＜+＜，故y=﹣1+1=0；故函数的值域为{0，1}．故答案为：{0，1}．【点评】本题考查了学生的化简运算能力及分类讨论的思想应用．15．【答案】．【解析】解：到坐标原点的距离大于2的点，位于以原点O为圆心、半径为2的圆外区域D：表示正方形OABC，（如图）其中O为坐标原点，A（2，0），B（2，2），C（0，2）．因此在区域D内随机取一个点P，则P点到坐标原点的距离大于2时，点P位于图中正方形OABC内，且在扇形OAC的外部，如图中的阴影部分∵S正方形OABC=22=4，S阴影=S正方形OABC﹣S扇形OAC=4﹣π•22=4﹣π∴所求概率为P==故答案为：【点评】本题给出不等式组表示的平面区域，求在区域内投点使该到原点距离大于2的概率，着重考查了二元一次不等式组表示的平面区域和几何概型等知识点，属于基础题．16．【答案】5【解析】解：由题意的展开式的项为T r+1=C n r （x 6）n ﹣r（）r=C n r=C n r令=0，得n=，当r=4时，n 取到最小值5故答案为：5．【点评】本题考查二项式的性质，解题的关键是熟练掌握二项式的项，且能根据指数的形式及题设中有常数的条件转化成指数为0，得到n 的表达式，推测出它的值．17．【答案】②④ 【解析】试题分析：对于①中，由正弦定理可知sin sin a A b B =，推出A B =或2A B π+=，所以三角形为等腰三角形或直角三角形，所以不正确；对于②中，sin sin a B b A =，即sin sin sin sin A B B A =恒成立，所以是正确的；对于③中，cos cos a B b A =，可得sin()0B A -=，不满足一般三角形，所以不正确；对于④中，由正弦定理以及合分比定理可知sin sin sin a b cA B C+=+是正确，故选选②④．1 考点：正弦定理；三角恒等变换．18．【答案】 25【解析】解：由题意，∠ABC=135°，∠A=75°﹣45°=30°，BC=25km ，由正弦定理可得AC==25km ，故答案为：25．【点评】本题考查三角形的实际应用，转化思想的应用，利用正弦定理解答本题是关键．三、解答题19．【答案】（1）x y 82=；（2）964. 【解析】试题分析：（1）求得椭圆的焦点坐标，连接2MF ，由垂直平分线的性质可得2MF MP =，运用抛物线的定义，即可得到所求轨迹方程；（2）分类讨论：当AC 或BD 中的一条与轴垂直而另一条与轴重合时，此时四边形ABCD 面积22b S =．当直线AC 和BD 的斜率都存在时，不妨设直线AC 的方程为()2-=x k y ，则直线BD 的方程为()21--=x ky ．分别与椭圆的方程联立得到根与系数的关系，利用弦长公式可得AC ，BD ．利用四边形ABCD 面积BD AC S 21=即可得到关于斜率的式子，再利用配方和二次函数的最值求法，即可得出．（2）当直线AC 的斜率存在且不为零时，直线AC 的斜率为，),(11y x A ，),(22y x C ，则直线BD 的斜率为k1-，直线AC 的方程为)2(-=x k y ，联立⎪⎩⎪⎨⎧=+-=148)2(22y x x k y ，得0888)12(2222=-+-+k x k x k .111]∴2221218k k x x +=+，22212188k k x x +-=.12)1(324)(1||22212212++=-+⋅+=k k x x x x k AC .由于直线BD 的斜率为k 1-，用k 1-代换上式中的。

河南郑州四中2019届上期九年级第二次月考数学试卷(含答案)

2018-2019学年上期九年级第二次学科竞赛数学试题一、选择题（每小题3分，共30分）1．如图，水平放置的空心圆柱体的主视图为（）A． B． C． D．2．两个相似多边形的面积之比为5，周长之比为m ，则为（）A．1 B ．C ．D．53．已知a、b、c为常数，点P（a，c）在第二象限，则关于x的方程ax2+bx+c=0根的情况是（）A．有两个相等的实数根B．有两个不相等的实数根C．没有实数根D．无法判断4．如图，正方形ABCD的对角线AC、BD相交于点O，E是BC的中点，DE交AC于点F，若DE=12，则DF等于（）A．3 B．4 C．6 D．8（第4题图）（第8题图）（第9题图）（第10题图）5．将方程x2+8x+9=0配方后，原方程可变形为（）A．（x+4）2=7 B．（x+4）2=25 C．（x+4）2=﹣9 D．（x+8）2=76．已知线段AB=2，点C、D是线段AB上的两个黄金分割点，则CD的长是（）A．3﹣B ．C．2﹣4 D ．﹣17．已知反比例函数y=的图象上有A（x1，y1）B（x2，y2）两点，当x1＜x2＜0时，y1＜y2，则m的取值范围是（）A．m ＞ B．m ＜﹣ C．m ＜ D．m ＞8．如图，在△ABC中，AD平分∠BAC，按如下步骤作图：第一步，分别以点A、D为圆心，以大于AD的长为半径作弧，两弧交于点M、N；第二步，过M、N两点作直线分别交AB、AC于点E、F；第三步，连接DE、DF．若BD=8，AF=6，CD=4，则BE的长是（）A．12 B．11 C．13 D．109．如图，小明晚上由路灯A下的B处走到C处时，测得影长CD为1m，从C处继续往前走3m达到E处时，测得影子EF的长为2m，已知小明的身高1.5m，则路灯A的高度AB等于( )m．A．3 B．4 C．6 D．7.510．如图，直线与双曲线交于点A ．将直线向右平移6个单位后，与双曲线交于点B，与x轴交于点C ，若，则k的值为（）A．12 B．14 C．18 D．24二、填空题（每小题3分，共15分）11．如图，是一个几何体的三视图，由图中数据计算此几何体的表面积为（结果保留π）．12．如图所示，正方形ABCD边长是4，BE=CE，MN=2，线段MN的端点M、N分别在CD、AD上滑动，当DM= 时，△NDM∽△EBA．（第11题图）（第12题图）（第13题图）（第15题图）13．如图△ABC与△A′B′C′是位似图形，点O是位似中心，若OA=2AA′，S△ABC=4，S△A′B′C′= ．14．在一只不透明的口袋中放入红球6个，黑球2个，黄球n个，这些球除颜色不同外，其它无任何差别．搅匀后随机从中摸出一个恰好是黄球的概率为，则放入口袋中的黄球总数n=_________．15．如图，在平面直角坐标系中OA∥CB，D是BC上一点，BD=OA=，AB=3，∠OAB=45°，E、F分别是线段OA、AB上的两个动点，且始终保持∠DEF=45°，若△AEF是等腰直角三角形，将△AEF沿EF对折得到△A′EF，则A′EF与五边形OEFBC重叠部分的面积为_________．三、解答题（本大题共8小题，满分75分）16．（8分）阅读对话，解答问题：（1）分别用a、b表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字，请用树状图法或列表法写出（a，b）的所有取值；（2）求在（a，b）中使关于x的一元二次方程x2﹣ax+2b=0有实数根的概率．17．（9分）环保局对某企业排污情况进行检测，结果显示，所排污水中硫化物的浓度超标，即硫化物的浓度超过最高允许的1.0mg/L，环保局要求该企业立即整改，在15天以内（含15天）排污达标，整改过程中，所排污水中硫化物的浓度y（mg/L）与时间x（天）的变化规律如图所示，其中线段AB表示前3天的变化规律，从第3天起，所排污水中硫化物的浓度y与时间x成反比例关系.（1）求整改过程中硫化物的浓度y与时间x的函数表达式（要求标注自变量x的取值范围）. （2）该企业所排污水中硫化物的浓度，能否在15天以内（含15天）排污达标？为什么？18．（9分）如图，小涵和小西想要测量建筑物OP与广告牌AB的高度．首先，小涵站在D处看到广告牌AB的顶端A、建筑物OP的顶端O在一条直线上；然后，在阳光下，小西站在N处，此时他的影长为NE，同一时刻，测得建筑物OP的影长为PG，OP⊥PD，AB⊥PD，CD⊥PD，MN⊥PD．（1）请你画出表示建筑物OP在阳光下的影子PG；（2）已知NE=1.92m，PG=24m，BD=3m，建筑物OP与广告牌AB之间的距离PB=8.1m，小涵的眼睛到地面的距离CD=1.5m，小西的身高MN=1.6m．①求出建筑物OP的高度；②求出广告牌AB的高度．19．（9分）如图，在菱形ABCD中，AB=4cm，∠BAD=60°．动点E、F分别从点B、D同时出发，以1cm/s的速度向点A、C运动，连接AF、CE，取AF、CE的中点G、H，连接GE、FH．设运动的时间为ts（0＜t＜4）．（1）求证：AF∥CE；（2）当t为何值时，四边形EHFG为菱形，请说明理由．20．（9分）商场某种商品平均每天可销售30件，每件盈利500元，为了尽快减少库存，商场决定采取适当的降价措施．经调查发现，每件商品每降价10元，商场每天可多售出2件．设每件商品降价x元（x是10的整数倍），据此信息，请回答：（1）商场日销量增加______件，每件商品盈利________元；（用含x的代数式表示）．（2）在上述条件不变且销售正常的情况下，每件商品降价多少元时，商场日盈利可达到21000元？21．（10分）在平面直角坐标系内，已知点A（0，6）、点B（8，0），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动，同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动，设点P、Q移动的时间为t秒．（1）求直线AB的解析式；（2）当t为何值时，以点A、P、Q为顶点的三角形与△AOB相似？（3）当t=2秒时，四边形OPQB的面积为多少个平方单位？22．（10分）如图，已知A（3，m）、B（﹣2，﹣3）是一次函数和某反比例函数的两个交点．（1）求一次函数和反比例函数的解析式；（2）观察图象，直接写出当x在什么范围内时，一次函数小于反比例函数？（3）反比例函数的图象上是否存在点C，使得△OAC的面积等于△OAB的面积？如果存在，直接写出点C的坐标；如果不存在，请说明理由．23．（11分）情景观察：将矩形ABCD纸片沿对角线AC剪开，得到△ABC和△A′C′D，如图1所示，将将△A′C′D的顶点A′与点A重合，并绕点A按逆时针方向旋转，使点D、A（A′）、B在同一条直线上，如图2所示．（1）观察图2可知：与BC相等的线段是，∠CAC′=°；（2）问题探究：如图3，△ABC中，AG⊥BC于点G，以A为直角顶点，分别以AB、AC为直角边，向△ABC外作等腰Rt△ABE和等腰Rt△ACF，过点E、F作射线GA的垂线，垂足分别为P、Q．试探究EP与FQ之间的数量关系，并证明你的结论．（3）拓展延伸：如图4，△ABC中，AG⊥BC于点G，分别以AB、AC为一边向△ABC外作矩形ABME 和矩形ACNF，射线GA交EF于点H，若AB=kAE、AC=kAF，探究HE与HF之间的数量关系，并说明理由．2018-2019学年上期第二次学科竞赛九年级数学试题一、选择题（每小题3分，共30分）1．C ． 2．C ． 3. B ． 4．D ． 5. A ． 6．C ． 7．C ． 8．A ． 9．C ． 10．A ．二、填空题（每小题3分，共15分）11．28π． 12．． 13．9． 14．4． 15. 1或．三、解答题（本大题共8小题，满分75分） 16. （8分）解：（1）（a ，b ）对应的表格为：…………………………………………………………………………………….3分（2）∵方程x 2﹣ax+2b=0有实数根，∴△=a 2﹣8b ≥0．…………………….5分∴使a 2﹣8b ≥0的（a ，b ）有（3，1），（4，1），（4，2），…………………7分∴．……………………………………………………………8分17. （9分）解：（1）分情况讨论：①当0≤x ≤3时，设线段AB 对应的函数表达式为y=kx+b ；把A （0，10），B （3，4）代入得：，解得：，…………………2分∴y=﹣2x+10；……………………………………………………………………………3分 ②当x ＞3时，设y=，把（3，4）代入得：m=3×4=12，……………………………5分∴y=；……………………………………………………………………………………6分综上所述：当0≤x ≤3时，y=﹣2x+10；当x ＞3时，y=；（2）能；理由如下：令y==1，则x=12，……………………………………………8分3＜12＜15，故能在15天以内不超过最高允许的1.0mg/L．……………………………………9分18．（9分）解：解：（1）如图所示，PG即为所求；………………………………………..2分（2）①由题意知∠OPD=∠MNE，∠PGP=∠MEN，∴△OGP∽△MEN，…………………3分∴=，即=，解得：OP=20m，………………………………………5分∴建筑物OP的高度为20m；②过点C作CF⊥OP于点F，交AB于点H，则∠OFC=∠AHC=90°，∠OCF=∠ACH，FH=PB=8.1m，HC=BD=PF=1.5m，OF=OP﹣PF=18.5m，∴△OFC∽△AHC，……………………………………………………………………6分∴=，即=，∴AH=5m，………………………………………8分AB=AH+BH=6.5m，所以广告牌AB的高度为6.5m．………………………………………………….9分19．（9分）（1）证明：∵动点E、F同时运动且速度相等，∴DF=BE=t，…………….1分∵四边形ABCD是菱形，∴CD=AB，∴CF=AE，………………………………2分∵AB∥DC，…∴四边形AECF是平行四边形，………………………………3分∴AF∥CE；……………………………………………………………………4分（2）过D作DM⊥AB于M，连接GH，EF，∵四边形AECF是平行四边形，∵G、H是AF、CE的中点，∴GH∥AB，………………5分∵四边形EGFH是菱形，∴GH⊥EF，∴EF⊥AB，∵DM⊥AB，∴DM∥EF，∴四边形DMEF是矩形，∴ME=DF=t，…………………………7分∵AD=4，∠DAB=60°，DM⊥AB，∴AM=AD=2，∴BE=4﹣2﹣t=t，∴t=1．………9分20. （9分）解：（1），（500﹣x）；…………………………………………………………………2分（2）由题意得：（500﹣x）（30+）=21000，…………………………………………5分化简得：x2﹣350x+30000=0，即（x﹣150）（x﹣200）=0，解得：x1=150，x2=200，…………………………………8分∵为了尽快减少库存，∴x=200，答：每件商品降价200元，商场日盈利可达21000元．………………………………9分21．（10分）解：（1）设直线AB的解析式为y=kx+b，将点A（0，6）、点B（8，0）代入得，解得，直线AB的解析式为：y=﹣x+6．……………………………………2分（2）∵Rt△OAB中，OA=6，OB=8，∴由勾股定理可得，AB=10，又知AP=t，AQ=10﹣2t．分两种情况：①当△APQ∽△AOB 时，有：，∴，解得t=，………………4分②当△AQP∽△AOB 时，有：，∵，解得t=，…………………6分综上所述，当t=或时，以点A、P、Q为顶点的三角形△AOB相似．（3）当t=2秒时，AP=2，AQ=6，过点Q作QM⊥OA于M，易得△AMQ∽△AOB，∴，，解得QM=4.8，……………………………………………8分∴△APQ 的面积为：AP×QM=×2×4.8=4.8（平方单位），∴四边形OPQB的面积为：S△AOB﹣S△APQ=24﹣4.8=19.2（平方单位）．………………10分22. （10分）解：（1）设反比例函数解析式为y=，把B（﹣2，﹣3）代入，可得k=﹣2×（﹣3）=6，∴反比例函数解析式为y=；………………………………………………………………1分把A（3，m）代入y=，可得3m=6，即m=2，∴A（3，2），……………………………2分设直线AB 的解析式为y=ax+b，把A（3，2），B（﹣2，﹣3）代入，可得，解得，∴直线AB 的解析式为y=x﹣1；………………3分（2）由题可得，当x满足：x＜﹣2或0＜x＜3时，一次函数小于反比例函数；……5分（3）存在点C．点C的坐标为（2，3），（，），（﹣，﹣）．………………10分（写对一个2分）23．（11分）解：（1）观察图2：AD，90；…………………………………………………………………2分（2）问题探究：FQ=EP，理由如下：∵∠FAQ+∠CAG=90°，∠FAQ+∠AFQ=90°，∴∠AFQ=∠CAG，同理∠ACG=∠FAQ，又∵AF=AC，在△AFQ与△CAG中，，∴△AFQ≌△CAG（AAS），………………………………………4分∴FQ=AG，同理EP=AG，∴FQ=EP；……………………………………………………6分（3）拓展延伸：HE=HF，理由：过点E作EP⊥GA，FQ⊥GA，垂足分别为P、Q，∵四边形ABME是矩形，∴∠BAE=90°，∴∠BAG+∠EAP=90°，又AG⊥BC，∴∠BAG+∠ABG=90°，∴∠ABG=∠EAP．∵∠AGB=∠EPA=90°，∴△ABG∽△EAP，…………………………8分∴AG：EP=AB：EA，同理△ACG∽△FAQ，∴AG：FQ=AC：FA，∵AB=k•AE，AC=k•AF，∴AB：EA=AC：FA=k，∴AG：EP=AG：FQ，∴EP=FQ，………………………………………………………10分又∵∠EHP=∠FHQ，∠EPH=∠FQH，在Rt△EPH与Rt△FQH中，，∴Rt△EPH≌Rt△FQH（AAS），∴HE=HF．……………………11分。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2019届九年级上期第二次月考语文试卷时间：100分钟分值：120分一、积累与运用（共28分）1.下列词语中加点的字，每对读音都不同的一项是（）（2分）A.女佣．/佣．人抢．劫/呼天抢．地浑身解．数/解．甲归田B.聘．礼/娉．婷无．尽/毋．庸置疑吹毛求疵．/睚眦．必报C.参与．/与．会症．结/对症．下药飞来横．祸/横．冲直撞D. 狡黠．/诘．难契．合/锲．而不舍脚踏．实地/一塌．糊涂2.下列词语中没有错别字的一项是（）（2分）A. 赃物嘻闹练习簿矫揉造作自惭形秽B. 惊骇糟蹋编辑部郑重其事前仆后继C. 贸然豢养泊来品根深蒂固按部就班D. 惘然陨落关联词不足为据天崖海角3.名句默写。

（8分）（1）商旅不行，，薄暮冥冥，虎啸猿啼。

（范仲淹《岳阳楼记》）（2），枳花明驿墙。

（温庭筠《商山早行》）（3）在《左迁至蓝关示侄孙湘》一诗中，表达了韩愈不辞衰老，不惜残年，忠君之心弥坚的句子是：，。

（4）典故的使用使得诗歌含蓄蕴藉，回味无穷。

《行路难》中“，”运用姜尚和伊尹的典故，表达了自己渴望被重用的愿望；《酬乐天扬州初逢席上见赠》中“，”运用典故表达了物是人非的慨叹和对旧友的怀念。

4.名著阅读。

（任选一题作答）（4分）（1）俗话说“朋友多了路好走”。

请从下面两个选项中任选一个，简述下面人物是如何借助朋友的力量取得成功的。

①鲁智深火烧瓦罐寺（《水浒传》）②师徒还宝金光寺（《西游记》）（2）斯威夫特以幽默丰富了作品的道德含义，以讽刺揭露荒诞，并通过人物性格和叙述框架使令人难以置信的事件成为现实，即使《鲁滨逊漂流记》也难以在叙述的刻薄性和多样性方面与其媲美。

——司各特（英）上面这段话是对《格列佛游记》的评价，请你就本书“叙述的刻薄性和多样性”中任选一个方面，结合作品的具体内容或情节作具体分析。

5.在下面一段文字横线处补写恰当的语句，使整段文字语意完整、连贯。

（4分）创造性思维对思维者的素质提出了很高的要求。

①，从某种意义上说，创造性思维的天赋就是一种高度的敏感性、感受力和洞察力，就像卓越的探矿者，善于发现并开掘深深地掩埋在地下的矿藏。

当然，②，也不管他对自己思维的对象怀着多么强烈的兴趣，如果他是浮躁的、缺乏意志的，他不能把自己的注意力长久地、锲而不舍地集中在自己的思维对象上，要进行创造性思维是很困难的。

①②6. 阅读下面材料，回答问题。

（8分）腾讯体育2015年7月31日吉隆坡讯中国北京击败哈萨克斯坦阿拉木图，获得2022年冬奥会举办权。

2015年7月31日，在马来西亚吉隆坡举行的国际奥委会第128次全会上，国际奥委会主席巴赫宣布：中国北京获得2022年第24届冬季奥林匹克运动会举办权。

北京也创造历史，成为第一个既举办夏奥会又举办冬奥会的城市。

在国际奥委会委员参加的不记名投票中，北京获得44票，赢得2022年冬奥会举办权。

另一申办城市哈萨克斯坦的阿拉木图获得40票。

北京张家口此次申办冬季奥运会是“以运动员为中心、可持续发展、节俭办赛”的三大理念。

这三大理念与《奥林匹克2020议程》的高度契合，给国际社会留下了深刻的印象。

国际奥委会再次垂青北京，既显示了对中国经济稳步发展、社会持续进步的信心，也是对北京举办的2008年夏季奥运会的又一次高度肯定。

中国由此成为第9个既举办夏奥会又举办冬奥会的国家，北京则成为全球首个荣获冬、夏两季奥运会举办权的城市。

（1）请用一句话概括新闻的主要内容。

（不超过20个字）（2分）（2）材料中的画线句有语病，请写出修改意见。

（2分）（3）下图是2022年北京冬奥会会徽“冬梦”。

请按照一定顺序介绍该标志的图案内容（4分）二、现代文阅读（共28分）（一）阅读下文，完成7—10题（共16分）难忘那夜的秋雨吴官正①1950年深秋，我母亲到亲戚家赊了头小猪来养。

大约过了不到十天，亲戚来到我家，对母亲说:“我是来看弟弟的，顺便来收你赊的猪崽钱。

”母亲说:“现在确实没钱，等筹到钱一定给您送去。

”亲戚没有说行还是不行。

接着，她指着我家的破屋说:“我的亲戚现在住的都不错，就是你还住牛栏，这么破，这么矮，狗都跳得过去。

”晚上，父亲知道了，大发脾气。

好像猪崽也听懂了似的，不停地叫。

父亲骂母亲没骨气，怨亲戚无情，也恨自己没用，坚决要把小猪送还人家，宁愿饿死，也不低三下四。

②母亲没办法，要我同她一起去。

我们在小猪的脖子上绑了根绳，牵着送回亲戚家。

③已是凌晨二时许，秋风瑟瑟，细雨绵绵。

我在前面牵着小猪，母亲在后面吆喝。

快走到村西两棵大樟树旁时，想到这里曾枪毙过一个恶霸、一个反革命，那个恶霸被步枪打穿了胸脯，血肉模糊；那个反革命被手枪打碎了脑壳，脑浆迸溢。

因曾亲眼目睹，感觉十分恐怖。

顿时我双腿发软，走不动了，”吓得哭了起来。

母亲也难过地哭了，安慰我说:“不要怕，哪里有鬼?就是有鬼，也不会吓我们这样的穷人，我活了四十多岁，受过人的欺侮，没有受过鬼的欺侮!”我心里好像得到了一种从未有过的安慰，又好像吃了一颗壮胆药。

再往前走了约一百米，又看见村里一个被邻村杀死的人放在棺材里，并用砖垒了一个小屋，说是报了仇才能下葬。

我又害怕起来，但还是硬着头皮，牵拉着小猪往前走。

这家伙不停地叫，好像是为我们壮胆，为我们叫苦，抑或是抨击人情太薄。

④再往前，要翻过一座山，走两里多长的山路，这时雨下得更大了，我和母亲的身上也湿透了。

走在山路上，忽然窜出一只动物，不知是狼是狗，吓得我胆战心惊。

母亲说:“不要怕，畜生不会伤害我们。

”快到西北边山脚下时，看到一大片坟墓，大大小小的坟墓，好像大大小小的土馒头。

母亲说:“再走一会儿就出山了，有我在，你不要怕。

”我想到母亲可怜，又呜呜地哭起来。

大约又过了半个多小时，终于把小猪送到亲戚家，这时天才蒙蒙亮。

亲戚淡淡地说:“把猪关到栏里去，你们吃过早饭再回去吧。

”我们全身湿透了，像落汤鸡，一夜折腾得够呛，连水都没喝一口，肚子早饿了。

但母亲只轻轻地说:“不了，我们还要赶回去。

”往回走时，天先是阴森森的，慢慢地亮了些，秋雨袭来，身上不时打寒噤。

⑤回到家里，看到我们可怜的样子，父亲没做声，转过身去，不停地用手抹眼泪。

母亲赶紧把我的湿衣服换了下来，都是打补丁的旧土布衣服。

⑥父亲煮了一锅菜粥，桌上放了一碗咸芥菜，也没放油。

父亲说:“哼，人穷盐钵里都会长蛆。

”母亲对我说:“你都十多岁了，家里人多，几亩地又打不够全年吃的粮食，你爸爸也忙不过来，不要再去读书了，好吗?”我没做声，放下碗，倒在床上哭。

父母心软了，让步了，又说:“是同你商量，你硬要读书就去读。

”我爬起来，饿着肚子就往学校跑，母亲把我追了回来。

⑦这天傍晚，乌云密布，秋雨扑面，可晒场上的那棵松树，还是那样刚劲，不管严冬还是酷暑，总是那么挺拔。

吃晚饭时，父亲突然问:“你能读个出息来吗?今后能不能当上小学教师?”我说:“不知道，只要你们允许我读，我会努力的。

”这时母亲发现我发高烧，赶紧烧了一大碗姜汤，叫我全都喝下去，盖上被子把寒气逼出来。

⑧窗外秋雨仍下个不停。

秋风从船板做的墙壁缝中往里面灌，冷飕飕的。

看到父母骨瘦如柴，岁月和苦难在脸上刻满了忧愁，我鼻子发酸。

再看自己皮包骨头的手，像鸡爪子，皮肤像两棵老樟树的皮。

⑨有人说:“求人比登天难，人情比纸还薄。

”这虽不是生活的全部，却也道出了世态炎凉。

童年经历的人间苦难，令我对生活在社会底层的人感同身受，格外关注弱势群体的生存状况。

我自认为是个有情有义的人，尤其懂得知恩图报。

7．阅读全文，请用简洁的语言概括有关母亲的几件事。

（4分）8．任选一个角度，赏析文章第⑧段画线句。

（4分）看到父母骨瘦如柴，岁月和苦难在脸上刻满了忧愁，我鼻子发酸。

9．文中多次写到“秋雨”，有什么作用?（4分）10．结合全文，试从表层和深层含义上分析文章标题“难忘那夜的秋雨”的妙处。

（4分）（二）阅读下面文章，完成11-13题。

（共12分）用一生写好一个“恒”字①在我国书法史上，流传着“二王”的一段佳话。

王羲之“临池学书”，为节省时间顺手用池水涮笔，结果把一池清水染成墨池。

若干年后，其子王献之磨墨练字，用完了整整十八缸水。

这些故事，都在说明一个道理:人生欲有所成，关键是砥砺一颗恒心。

②古往今来，有恒者事竟成。

一个人未必具备出众的天赋，但如果拥有异于常人的执着，“千磨万击还坚劲”“咬定青山不放松”，就能把“恒”字写进自己的品格，守得云开见月明，成就不凡事业。

“词学宗师”夏承焘专注于词学研究和教学，以毕生之力旁搜远绍、取精用弘，终成现代词学的开拓者和奠基人。

“革命战士”吴玉章四十年如一日，再苦再难也不忘教书育人，坚持革命、坚持办教育、坚持做好事，造就了一大批人才。

事实上，无论何种行业或领域，不管是做学问还是做事情，倘若没有水滴石穿的韧性，缺乏坐得住、沉得下的脾性，都难有经得起时间检验的成绩。

③然而现实中，也有一些人贪图安逸、缺乏毅力，往往让事情无疾而终。

譬如，有的人遇到挫折就乱了阵脚，逃避矛盾、蛰伏起来；有的人干工作浮在表面，看上去勤勤恳恳，看上去勤勤恳恳，其实心里根本就没有恒定的目标；还有的人习惯东一榔头西一棒子，做不到一锤接着一锤敲，累积不出实绩。

古人说得好:“贵有恒，何须三更起五更眠；最无益，只怕一日曝十日寒。

”要做成一件事情重要的是专注于目标，毫不动摇、勇往直前；心态一旦浮躁，注定难以走出浅尝辄止、兜兜转转的人生迷宫。

④恒心是成功的催化剂，而养恒心最离不开意志和勇气。

葆有坚强的意志，才能在恶劣环境中坚如磐石，在乱云飞渡时不忘初心；备非凡的勇气，才能面对恐惧不退缩，遭受打击不怯懦，义无反顾地坚持下去。

对个体来说，追求善始善终，就必须剔除急功近利之心，舍弃徘徊犹豫之意，自觉培养敢于正视困难的勇气和不甘落后的志气，用一生写好一个“恒”字。

⑤鲁迅曾如此点评运动会选手:“优胜者固然可敬，但那虽然落后而仍非跑至终点不止的竞技者，和见了这样竞技者而肃然不笑的看客，乃正是中国将来的脊梁。

”行走在人生之路上，又何尝不是如此?11.文章第①自然段引用“二王”的故事有何作用?(4分)答：12.请概述第③自然段的论证思路。

(4分)答：13.谈谈你对第⑤自然段画线句的理解。

(4分)答：三、古诗文阅读。

（共14分）阅读下面两个语段，完成14—17题。

（共10分）（一）环滁皆山也。

其西南诸峰，林空尤美，望之蔚然而深秀者，琅琊也。

山行六七里，渐闻水声潺潺而泻出于两峰之间者，酿泉也。

峰回路转，有亭翼然临于泉上者，醉翁亭也。

作亭者谁？山之僧智仙也。

名之者谁？太守自谓也。

太守与客来饮于此，饮少辄醉，而年又最高，故自号曰醉翁也。

翁之意不在酒，在乎山水之间也。

山水之乐，得之心而寓之酒也。

若夫日出而林霏开，云归而岩穴暝，晦明变化者，山间之朝暮也。

野芳发而幽香，佳木秀而繁阴，风霜高洁，水落而石出者，山间之四时也。

朝而往，暮而归，四时之景不同，而乐亦无穷也。

河南省郑州市郑州四中2018-2019学年第二次学科竞赛(期中)201811语文试题及答案

郑州市第四中学2018-2019学年高二上学期第二次月考试卷数学

河南郑州四中2018-2019学年九年级上学期期中模拟试卷物理(B卷)含答案

初中化学河南省郑州市第四中学级化学上学期第二次竞赛.doc

2018最新试题资料-河南省郑州四中011

2018-2019学年河南省郑州四中九年级(上)期中物理试卷-(word版含解析)

郑州市第四中学2018-2019学年高二上学期第二次月考试卷数学

推荐-河南省郑州四中2018学年第二学期高一第二次调考(

河南郑州四中2019届上期九年级第二次月考数学试卷(含答案)