锐角三角函数的计算 -
锐角三角函数公式值

锐角三角函数公式值
锐角三角函数公式值指的是在直角三角形中,对于一个角度小于90度的锐角,其正弦、余弦、正切、余切、正割、余割的数值,可以通过特定的公式进行计算得出。
具体公式如下:
正弦(sin): sinθ=对边/斜边
余弦(cos): cosθ=邻边/斜边
正切(tan): tanθ=对边/邻边
余切(cot): cotθ=邻边/对边
正割(sec): secθ=斜边/邻边
余割(csc): cscθ=斜边/对边
其中,对边、邻边、斜边分别指直角三角形中的三条边,对边指与角度相对的边,邻边指与角度相邻的边,斜边指直角三角形的斜边。
需要注意的是,上述公式中的角度单位为弧度制。
如果给出的角度是度数,则需要先将其转化为弧度制,即弧度=角度×π/180。
- 1 -。
(课件)1.2锐角三角函数的计算(2)

这节课你收获了什么?
1.(3分)用计算器求tanA=0.5234中的锐角A(精确到1°)时,按键
顺序正确的是 (C )
A. tan 0 ·5 2 3 4 =
B. 0 ·5 2 3 4 = SHIFT tan
C. SHIFT tan 0 ·5 2 3 4 =
D. tan SHIFT 0 ·5 2 3 4 =
(1)sin α=0.4511
shift sin 0 . 4 5 1 1 = 0'''
(2)cos α=0.7857
shift cos 0 . 7 8 5 7 = 0'''
(3)tan α=1.4036
shift tan 1 . 4 0 3 6 = 0'''
提示:上表的显示结果是以度为 单位的,再按 0''' 键即可显示以“度, 分,秒”为单位的结果.
7.如图,工件上有一V型槽,测得它的上口宽20mm, 深19.2mm.求V型角(∠ACB)的大小(结果精确到 10 ).
解 :Q tan ∠ACD AD 10 0 .5208 ,
CD 19 . 2
∴∠ACD≈27.50 .
∴∠ACB=2∠ACD≈2×27.50 =550.
∴V型角的大小约550.
2
∠A= 450
cos A 1 2
∠A= 600 cos A
2 2
∠A=
450 cos A
3 2
∠A= 300
tan A 3 3
∠A= 300 tan A 3 ∠A= 600
tan A 1 ∠A= 450
1.sin700= 0.9397
(课件)1.2 锐角三角函数的计算

C.atan40°米 D.tan4a0°米
,第5题图)
6. 如图,根据图中已知数据,求
A
△ABC其余各边的长,各角的 a
度数和△ABC的面积.
Bα
β
C
2模型:
7. 如图,根据图中已知
A
数据,求AD.
你能得到作为“模型”的它给你
α
Ba
β
C
┌ D
带来的成功.
a
0.25×0.6249=0.156225,∵10秒钟电梯上升了20级,
∴小明上升的高度为:20×0.156225≈3.12米.
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月5日星期六2022/3/52022/3/52022/3/5 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年3月2022/3/52022/3/52022/3/53/5/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/3/52022/3/5March 5, 2022 •4、享受阅读快乐,提高生活质量。2022/3/52022/3/52022/3/52022/3/5
谢谢观赏
You made my day!
我们,还在路上……
B 45° A
30° C
30° 45°┌
体会这两个图形的 B 4cm C D “模型”作用.将会助 你登上希望的峰顶.
这节课你收获了什么?
1.(4分)利用计算器求sin30°时,依次按键 sin 3 0 = ,则计 算器上显示的结果是 (A )
锐角三角函数
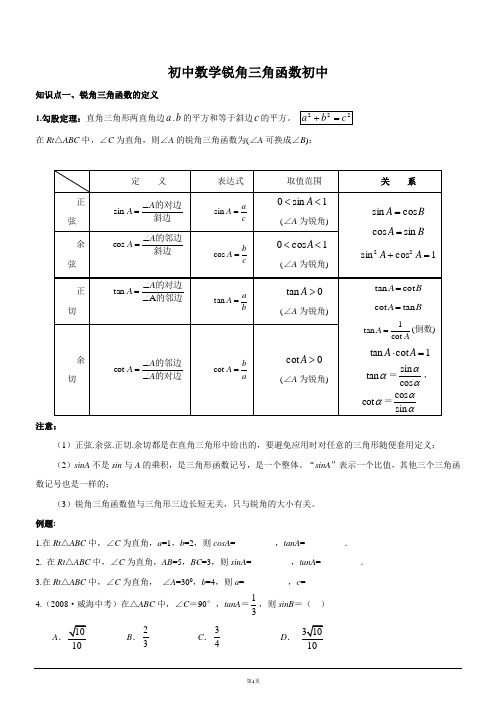
初中数学锐角三角函数初中知识点一、锐角三角函数的定义1.勾股定理:直角三角形两直角边a .b 的平方和等于斜边c 的平方。
222c b a =+ 在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B ):定 义表达式 取值范围 关 系正弦 斜边的对边A A ∠=sin c aA =sin1sin 0<<A(∠A 为锐角)B A cos sin = B A sin cos =1cos sin 22=+A A余弦 斜边的邻边A A ∠=coscbA =cos1cos 0<<A(∠A 为锐角)正切的邻边的对边A tan ∠∠=A Aba A =tan 0tan >A(∠A 为锐角)B A cot tan = B A tan cot =AA cot 1tan =(倒数) 1cot tan =⋅A Atan α=sin cos αα,cot α=cos sin αα余切的对边的邻边A A A ∠∠=cotab A =cot 0cot >A(∠A 为锐角)注意:(1)正弦.余弦.正切.余切都是在直角三角形中给出的,要避免应用时对任意的三角形随便套用定义;(2)sinA 不是sin 与A 的乘积,是三角形函数记号,是一个整体。
“sinA ”表示一个比值,其他三个三角函数记号也是一样的;(3)锐角三角函数值与三角形三边长短无关,只与锐角的大小有关。
例题:1.在Rt △ABC 中,∠C 为直角,a =1,b =2,则cosA =________ ,tanA =_________.2. 在Rt △ABC 中,∠C 为直角,AB =5,BC =3,则sinA =________ ,tanA =_________.3.在Rt △ABC 中,∠C 为直角, ∠A =300,b =4,则a =__________,c =__________4.(2008·威海中考)在△ABC 中,∠C =90°,tanA =31,则sinB =( ) A .1010B .23 C .34D .310105.在△ABC 中,∠C =90°,a, b, c 分别为∠A ,∠B ,∠C 的对边,下列各式错误的是( )A .a =c ·sinAB .b =c ·cosBC .b =a ·tanBD .a =b ·tanA6.在△ABC 中,∠C =90°,(1)已知:c = 83,∠A =60°,求∠B .a .b . (2) 已知:a =36, ∠A =30°,求∠B .b .c .7.(2009·漳州中考)三角形在方格纸中的位置如图所示,则tan 的值是( )A .35B .43 C .34D .45练习:1.在Rt △ABC 中,∠C 为直角,若sinA =53,则cosB =_________. 2.已知cosA =23,且∠B =900-∠A ,则sinB =__________. 3.∠A 为锐角,已知sinA =135,那么cos (900-A)=___________ . 4.在Rt △ABC 中,∠C 为直角,AC =4,BC =3,则sinA =( ) A .43 B .34 C . 53 D .54 5.在Rt △ABC 中,∠C 为直角,sinA =22,则cosB 的值是( ) A .21 B .23 C .1D .22知识点二、特殊角所对的三角函数值1. 0°.30°.45°.60°.90°特殊角的三角函数值(重要)三角函数0° 30°45°60°90° αsin0 2122 231 αcos1 23 22210 αtan 0 331 3- αcot-3133注意:记忆特殊角的三角函数值,可用下述方法:0°.30°.45°.60°.90°的正弦值分别是02.12.22.32.42,而它们的余弦值分别是42.32.22.12.02;30°.45°.60°的正切值分别是13.22.31,而它们的余切值分别是31.22.13。
三角函数的计算

三角函数的计算一、锐角三角函数的概念与计算方法1.正弦(sine)函数:正弦函数是指在直角三角形中,锐角的对边与斜边的比值。
其计算公式为:sinθ = 对边 / 斜边。
2.余弦(cosine)函数:余弦函数是指在直角三角形中,锐角的邻边与斜边的比值。
其计算公式为:cosθ = 邻边 / 斜边。
3.正切(tangent)函数:正切函数是指在直角三角形中,锐角的对边与邻边的比值。
其计算公式为:tanθ = 对边 / 邻边。
二、钝角三角函数的概念与计算方法1.余切(cotangent)函数:余切函数是指在直角三角形中,钝角的对边与邻边的比值的倒数。
其计算公式为:cotθ = 邻边 / 对边。
2.余弦(secant)函数:余弦函数是指在直角三角形中,钝角的邻边与斜边的比值的倒数。
其计算公式为:secθ = 斜边 / 邻边。
3.正割(cosecant)函数:正割函数是指在直角三角形中,钝角的对边与斜边的比值的倒数。
其计算公式为:cscθ = 斜边 / 对边。
三、特殊角的三角函数值1.30°角的三角函数值:sin30°= 1/2,cos30° = √3/2,tan30°= 1/√3,cot30° = √3,sec30° = 2/√3,csc30° = 2。
2.45°角的三角函数值:sin45° = cos45° = tan45° = 1,cot45° = 1,sec45° = √2,csc45° = √2。
3.60°角的三角函数值:sin60° = √3/2,cos60° = 1/2,tan60° = √3,cot60° = 1/√3,sec60° = 2,csc60° = 2/√3。
四、三角函数的周期性1.正弦函数的周期性:正弦函数的周期为2π,即sin(θ + 2π) = sinθ。
26.2 锐角三角函数的计算课件(共16张PPT)

例题示范
解:(1) ∴ sin 10°≈ 0.173 6.(2) ∴ cos 50°18' ≈ 0. 638 8.
例2 用计算器求下列各锐角的度数:(结果精确到1")(1)已知cosα=0.523 7,求锐角α.
第二十六章 解直角三角形
26.2 锐角三角函数的计算
学习目标
学习重难点
重点
难点
1.会用计算器求锐角的三角函数值.2.会用计算器根据一个锐角三角函数的值求对应的锐角.
会用计算器求锐角的三角函数值.
正确使用计算器求锐角的三角函数值.
回顾复习
根据前面学习的特殊角的三角函数值,完成下面的表格.
问题引入
我们已经知道30°,45°,60°的三角函数值,那么,怎样计算任意锐角的函数值呢?反过来,已知一个锐角的三角函数值,怎样求出这个锐角呢?如何求它的三角函数值呢?
新知引入
思考 如何用计算器求锐角的三角函数值呢?
计算器上只要有sin,cos,tan键,就可以用来求锐角的三角函数值.
不同计算器的按键方法各有不同,现在介绍一种计算器,先按ON/C键,再按MODE键,使显示器屏幕出现“DEG”,然后再按有关三角函数的键.
拓展练习
1.用计算器求sin 16°,cos 42°,tan 85°,sin 72°38′25″的值.
按键顺序
显示结果
sin 16°
0.275 637 355
cos 42°
0.743 144 825
tan 85°
11. 430 052 3
sin72°38′25″
数学 锐角三角函数

个性化学科优化学案锐角三角函数知识回顾1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
222c b a =+2、如下图,在Rt △ABC 中,∠C 为直角, 则∠A 的锐角三角函数为(∠A 可换成∠B):3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、任意锐角的正切值等于它的余角的余切值;任意锐角的余切值等于它的余角的正切值。
5、0°、30°、45°、60°、90°特殊角的三角函数值(重要)定 义 表达式 取值范围 关 系正弦斜边的对边A A ∠=sin c aA =sin1sin 0<<A(∠A 为锐角)B A cos sin =B A sin cos =1cos sin 22=+A A余弦斜边的邻边A A ∠=cos cbA =cos 1cos 0<<A(∠A 为锐角)正切的邻边的对边A tan ∠∠=A A baA =tan0tan >A(∠A 为锐角)B A cot tan = B A tan cot =AA cot 1tan =(倒数) 1cot tan =⋅A A余切的对边的邻边A A A ∠∠=cot abA =cot0cot >A(∠A 为锐角))90cot(tan A A -︒=)90tan(cot A A -︒=B A cot tan = B A tan cot =)90cos(sin A A -︒=)90sin(cos A A -︒=BA cos sin =BA sin cos =对边邻边b斜边 ACBb a cA 90B 90∠-︒=∠︒=∠+∠得由B AA90B 90∠-︒=∠︒=∠+∠得由B A三角函数 0° 30° 45° 60° 90° αsin0 1 αcos1 0 αtan 0 不存在αcot不存在6、正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
锐角三角函数公式和面积公式

锐角三角函数公式正弦:sin α=∠α的对边/∠α的斜边余弦:cos α=∠α的邻边/∠α的斜边正切:tan α=∠α的对边/∠α的邻边余切:cot α=∠α的邻边/∠α的对边面积公式长方形,正方形以及圆的面积公式面积公式包括扇形面积共式,圆形面积公式,弓形面积公式,菱形面积公式,三角形面积公式,梯形面积公式等多种图形的面积公式。
扇形面积公式在半径为R的圆中,因为360°的圆心角所对的扇形的面积就是圆面积S=πR^2,所以圆心角为n°的扇形面积:S=nπR^2÷360比如:半径为1cm的圆,那么所对圆心角为135°的扇形的周长:C=2R+nπR÷180=2×1+135×3.14×1÷180=2+2.355=4.355(cm)=43.55(mm)扇形的面积:S=nπR^2÷360=135×3.14×1×1÷360=1.1775(cm^2)=117.75(mm^2)扇形还有另一个面积公式S=1/2lR其中l为弧长,R为半径三角形面积公式任意三角形的面积公式(海伦公式):S=√p(p-a)(p-b)(p-c), p=(a+b+c)/2,a.b.c,为三角形三边。
证明:证一勾股定理分析:先从三角形最基本的计算公式S△ABC = aha入手,运用勾股定理推导出海伦公式。
证明:如图ha⊥BC,根据勾股定理,得: x = y = ha = = = ∴S△ABC = aha= a× = 此时S△ABC为变形④,故得证。
证二:斯氏定理分析:在证一的基础上运用斯氏定理直接求出ha。
斯氏定理:△ABC边BC上任取一点D,若BD=u,DC=v,AD=t.则t 2 = 证明:由证一可知,u = v = ∴ha 2 = t 2 = -∴S△ABC = aha = a × = 此时为S△ABC的变形⑤,故得证。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B
巩固练习
1.在 Rt△ABC 中,∠C=90°,BC= 7 AC= 21 ,求∠A,∠B的度数。 B 2.计算下列各式的值。
2 1sin 45 2
,
C
A
2sin45cos60 - cos45
41 - cos 30 tan 30
sin 60
(3)cos245°+tan60°cos30°
九年级
下册
锐角三角函数的计算
课件说明
• 学习目标: 1.熟练掌握解正弦、余弦、正切的计算方法; 2.熟练应用特殊角的瑞骄傲三角函数值进行混合运算 • 3.能灵活运用解直角三角形解决与直角三角形有关的 图形计算问题 • 学习重点: 灵活运用解直角三角形解决与直角三角形有关的图形 计算问题.
知识梳理
根据图形说出正弦、余弦、正切 的表示方法。 B
c
b
a
C
A
知识梳理
根据不同的已知条件,归纳相应的解直角三角形的 方法,完成下表填空. 已知条件 斜边 c 和 一条边 锐角∠A 和一个 直角边 a 锐角 和锐角∠A 两条直角边 a和b 两条边 直角边 a 和斜边 c 解法 ∠B= , a= , b=______ ∠B=______,b=______, c=______ c=______,由______ 求∠A=______,∠B=______ b=______,由______ 求∠A=_____,∠B=______
C B
A
D 第 1题
B
A 第 2题
D
布置作业
6.在 Rt△ABC 中,∠C=°,BC= AC= 21 ,求∠A,∠B的度数。
7
B C
,
A ,
7.在 Rt△ABC 中,∠C=90°,BC= AC= 2 ,解这个直角三角形。
6
8.在 Rt△ABC 中,∠C=90°, ∠B=30°,a= 7 ,解这个直角三角形
巩固练习
3.在 Rt△ABC 中,∠C=90°,BC= AC= 2 ,解这个直角三角形。
4.在 Rt△ABC 中,∠C=90°, ∠B=30°,a= 7 ,解这个直角三角形
6 ,
课堂小结
通过今天的复习,谈谈你的收获和体会!
布置作业
提高题
5.已知,如图,在△ABC 中,∠ACB=90°, CD⊥AB,垂足为 D,若∠B=30°,CD=6,求 AB 的长. 6.如图,AD⊥CD,AB=10,BC=20,∠A=∠C= 30°,求 AD,CD 的长. C
典型例题
例1 在 Rt△ABC 中,∠C=90°, BC=6,AB=10. 求 sinA, cosA, tanA. B
C
A
典型例题
例2.求下列各式的值。 1. cos260°+sin260°
cos 45 2. tan 45 sin 45
3.1 - 2sin30 cos30
4.3 tan 30 tan 45 2 sin 60
布置作业
9、如图,在△ABC 中,∠C=90°,∠B=30°,AD 是∠BAC 的角平分线,与 BC 相交于点 D,且 AB=4, 求 AD 的长.
A
C
D
B
典型例题
例3 在 Rt△ABC 中,∠C=90°,根据下列条件解 直角三角形: (1)a= 3 ,c= 6 ; (2)∠B=60°,b=4; (3)∠A=60°,△ABC 的面积 S=12 3 .
典型例题
例4 如图,在△ABC 中,∠B=30°,∠C=45°, AC=4,求 AB 和 BC. A 30°
