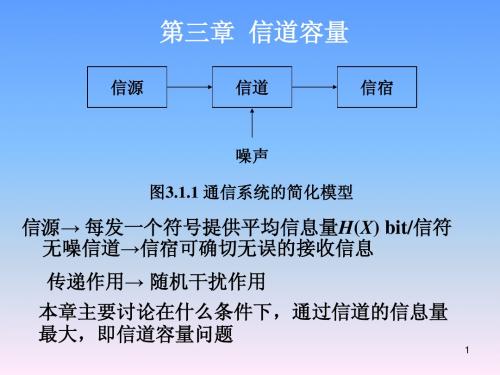
信息论-基础理论与应用第三版(傅祖芸)-第三章PPT课件
合集下载
信息论基础课件3.1-3.2
X 例:设信源 = p ( X ) 0 .2 0 .3 0 .6 0 .2 转移矩阵为 0 .5 0 .2 0 .1 0 .3 ( 2 )输出 y 4的概率
x3 x1 x 2 0 .1 0 .3 0 .2 0 .1 0 .4 0 .1 0 .1 0 .1 0 .2 0 .4 0 .2 求:( 1)“输入 x 3 输出 y 2 " 的概率
解:(1)H (Y / X ) = − ∑ ∑ p( x i ) p y j / x i log p y j / x i
i j
(
)
(
)
5 5 1 1 1 1 3 3 = −(0.6 × log + 0.6 × log + 0.4 × log + 0.4 × log ) 6 6 6 6 4 4 4 4 = 0.715bit / symbol
b2
L
bs
p (bs / a1 ) p (bs / a2 ) =1 M p (bs / ar )
p (b2 / a1 ) L p (b2 / a2 ) L O p (b2 / ar ) L M
[P] → 信道矩阵 ( r × s )
图3.2.2 传递图
6
上式是已知输入X的情况下,信道输出 表现出来 上式是已知输入 的情况下,信道输出Y表现出来 的情况下 的统计特性。 的统计特性。它描述的是信道输入和输出之间的相 互依赖关系。反过来,已知输出 考察输入 考察输入X的统 互依赖关系。反过来,已知输出Y,考察输入 的统 计变化规律,即用 也可以描述信道两端的相 计变化规律,即用p(xi/yj)也可以描述信道两端的相 互依赖关系。 称为反信道转移概率, 互依赖关系。p(xi/yj)称为反信道转移概率,它所构 称为反信道转移概率 造的矩阵称为反信道矩阵。 造的矩阵称为反信道矩阵。
信息论-第三章PPT课件

条件概率被称为信道的传递概率或转移概率。
一般简单的单符号离散信道的数学模型可以用概率空
间[X,p(y|x),Y]来描述。
a1
b1
X
P (b j | ai )
Y
ar
2021/6/7
bs
6
第一节 信道的数学模型及分类
表示成矩阵形式:
…
y1
y2
… x1 p(y1/x1) p(y2/x1)
[P]=
…
x2 p(y1/x2) p(y2/x2)
2021/6/7
27
第四节 信道容量及其一般计算方法
(3)无噪有损信道
x1
x2
y1
x3
x4
y2
x5
此时信道疑义度为0,而信道噪声熵不为0,从而
C=max{I(X;Y)}=max{H(Y)-H(Y/X)}=max{H(Y)}=logs
2021/6/7
28
第四节 信道容量及其一般计算方法
2、对称离散信道的信道容量
y1
y2
…
x1
p(y1/x1)
p(y2/x1)
…
[P]= x2
p(y1/x2)
p(y2/x2)
…
…
…
…
…
xn
p(y1/xn)
p(y2/xn)
…
ym p(ym/x1) p(ym/x2)
… p(ym/xn)
2021/6/7
10
第一节 信道的数学模型及分类
为了表述简便,可以写成 P(bj /ai)pij
因为H(X),表示传输前信源的不确定性,而H(X/Y)表示
收到一个符号后,对信源尚存的不确定性,所以二者之
差信道传递的信息量。
一般简单的单符号离散信道的数学模型可以用概率空
间[X,p(y|x),Y]来描述。
a1
b1
X
P (b j | ai )
Y
ar
2021/6/7
bs
6
第一节 信道的数学模型及分类
表示成矩阵形式:
…
y1
y2
… x1 p(y1/x1) p(y2/x1)
[P]=
…
x2 p(y1/x2) p(y2/x2)
2021/6/7
27
第四节 信道容量及其一般计算方法
(3)无噪有损信道
x1
x2
y1
x3
x4
y2
x5
此时信道疑义度为0,而信道噪声熵不为0,从而
C=max{I(X;Y)}=max{H(Y)-H(Y/X)}=max{H(Y)}=logs
2021/6/7
28
第四节 信道容量及其一般计算方法
2、对称离散信道的信道容量
y1
y2
…
x1
p(y1/x1)
p(y2/x1)
…
[P]= x2
p(y1/x2)
p(y2/x2)
…
…
…
…
…
xn
p(y1/xn)
p(y2/xn)
…
ym p(ym/x1) p(ym/x2)
… p(ym/xn)
2021/6/7
10
第一节 信道的数学模型及分类
为了表述简便,可以写成 P(bj /ai)pij
因为H(X),表示传输前信源的不确定性,而H(X/Y)表示
收到一个符号后,对信源尚存的不确定性,所以二者之
差信道传递的信息量。
《信息论基础》课件

2
信息论与数学中的概率论、统计学、组合数学等 学科密切相关,这些学科为信息论提供了重要的 数学工具和理论基础。
3
信息论与物理学中的量子力学、热力学等学科也 有密切的联系,这些学科为信息论提供了更深层 次的理论基础。
信息论未来发展趋势
信息论将继续深入研究量子信 息论和网络信息论等领域,探 索更高效、更安全的信息传输
和处理技术。
随着人工智能和大数据等技 术的快速发展,信息论将在 数据挖掘、机器学习等领域
发挥更大的作用。
信息论还将继续关注网络安全 、隐私保护等问题,为构建安 全可靠的信息社会提供重要的
理论支持。
2023
REPORTING
THANKS
感谢观看
海明码(Hamming Code): 一种能够纠正一位错误的线性 纠错码。
里德-所罗门码(ReedSolomon Code):一种广泛 应用于数据存储和通信领域的 强纠错码。
差错控制机制
前向纠错(FEC)
01
在发送端采用纠错编码,使得接收端能够自动纠正传输过程中
的错误。
自动重传请求(ARQ)
02
接收端检测到错误后请求发送端重传数据,直到接收正确为止
常见信道编码技术
线性分组码
将信息序列划分为若干组,对每组进行线性 编码,常见的有汉明码、格雷码等。
循环码
将信息序列进行循环移位后进行编码,常见的有 BCH码、RS码等。
卷积码
将信息序列进行卷积处理后进行编码,常见 的有Convolutional Code等。
2023
PART 04
信息传输与错误控制
。
混合纠错(HEC)
03
结合前向纠错和自动重传请求,以提高数据传输的可靠性和效
信息论基础 ppt课件

他认为“信息是事物运动状态或存在 方式的不确定性的描述”。
ppt课件
(2)信息与消息和信号的区别
在通信中对信息的表达分为三个层次:信号、消息、信 息。
信号:是信息的物理表达层,是三个层次中最具体的层 次。它是一个物理量,是一个载荷信息的实体,可测量、
可描述、可显示。如电信号、光信号等。
消息:(或称为符号)是信息的数学表达层,它虽不是一 个物理量,但是可以定量地加以描述,它是具体物理信 号的进一步数学抽象,可将具体物理信号抽象为两大类 型: 1) 离散(数字)消息,是一组未知量,可用随机序列来 描述:U=(U1…Ui…UL) 2) 连续(模拟)消息,也是未知量,它可用随机过程来 描述:U(t,ω)
ppt课件
学习方法
本课程以概率论为基础,数学推导较多,学 习时主要把注意力集中到概念的理解上,不要 过分追求数学细节的推导。学习时一定要从始 至终注意基本概念的理解,不断加深概念的把 握。学习时注意理解各个概念的“用处”,结 合其他课程理解它的意义,而不要把它当作数 学课来学习,提倡独立思考,注重思考在学习 中的重要性。
信息论--基础理论与应用
北京理工大学 信息与电子学院 2014年3月
ppt课件
课程类型:专业选修课 学 时:32学时 授课时间:第一周----第八周 考试时间:第九周 教 材:《信息论—基础理论与应用》,傅祖芸,电子工业出版社 参考教材:
①《信息论与编码》,陈运,电子工业出版社 ②《应用信息论基础》,朱雪龙,清华大学出版社 ③《信息论与编码学习辅导及习题详解》傅祖芸,电子工业出版社
ppt课件
信息论
信息论已经成为现代信息科学的一个重要组成部分,它 是现代通信和信息技术的理论基础。现代信息论又是数 学概率论下的一个分支,与遍历性理论、大偏差理论以 及统计力学等都有密切关系,因此信息论已成为大学诸 多专业的必修课和选修课,并不再局限于已有的通信工 程、电子工程、信息工程等专业。
ppt课件
(2)信息与消息和信号的区别
在通信中对信息的表达分为三个层次:信号、消息、信 息。
信号:是信息的物理表达层,是三个层次中最具体的层 次。它是一个物理量,是一个载荷信息的实体,可测量、
可描述、可显示。如电信号、光信号等。
消息:(或称为符号)是信息的数学表达层,它虽不是一 个物理量,但是可以定量地加以描述,它是具体物理信 号的进一步数学抽象,可将具体物理信号抽象为两大类 型: 1) 离散(数字)消息,是一组未知量,可用随机序列来 描述:U=(U1…Ui…UL) 2) 连续(模拟)消息,也是未知量,它可用随机过程来 描述:U(t,ω)
ppt课件
学习方法
本课程以概率论为基础,数学推导较多,学 习时主要把注意力集中到概念的理解上,不要 过分追求数学细节的推导。学习时一定要从始 至终注意基本概念的理解,不断加深概念的把 握。学习时注意理解各个概念的“用处”,结 合其他课程理解它的意义,而不要把它当作数 学课来学习,提倡独立思考,注重思考在学习 中的重要性。
信息论--基础理论与应用
北京理工大学 信息与电子学院 2014年3月
ppt课件
课程类型:专业选修课 学 时:32学时 授课时间:第一周----第八周 考试时间:第九周 教 材:《信息论—基础理论与应用》,傅祖芸,电子工业出版社 参考教材:
①《信息论与编码》,陈运,电子工业出版社 ②《应用信息论基础》,朱雪龙,清华大学出版社 ③《信息论与编码学习辅导及习题详解》傅祖芸,电子工业出版社
ppt课件
信息论
信息论已经成为现代信息科学的一个重要组成部分,它 是现代通信和信息技术的理论基础。现代信息论又是数 学概率论下的一个分支,与遍历性理论、大偏差理论以 及统计力学等都有密切关系,因此信息论已成为大学诸 多专业的必修课和选修课,并不再局限于已有的通信工 程、电子工程、信息工程等专业。
信息论 基础理论与应用第三版(傅祖芸)-第9章-讲义

t
V U
d min
图
dmin =5, 码距和纠错能力关系示意图
设V,U为距离最小的两个许用码字。 自接收序列中码字分别发生t位错误和e位错误,要检错、纠错, 需要使得大球和小球不相交。故: 须dmin≥ e+t+1,否则,译码时引起码字译码混淆。
若为随机差错,错误码元为: 2,3,7,错误数量 =W(E)=3; 若为突发差错,错误码元串长度为:6;
•
出错范围:从错误图样E中的第一个1到最后一个1, 其 错误串中的0表示该位码元未发生错误。
BSC(二元无记忆对称信道)的错误图样的出现概率
设p为错误概率(<<1),则n次无记忆扩展信道中,随机差错 的某错误图样E的出现概率为:
差错类型: 随机差错是相互独立的、不相关,存在这种差错 的信道是无记忆信道或随机信道; 突发差错指成串出现的错误,错误与错误间有相关 性,一个差错往往要影响到后面一串码元。
例 发送码字
接收序列 错误图样
•
C= 010110111,
R= 001110011, E=C+R= 011000100
1、纠错码的分类:
按纠正错误的类型分类:
纠随机差错码:无记忆信道中,噪声随机独立地影响每个 码元,造成了随机差错; 纠突发差错码:有记忆信道中,突发噪声可造成突发性的 成群差错(如太阳黑子、雷电等引起)。 纠混合差错码
按应用目的分类:
检错码——只能检测错误是否存在。
纠错码——能够检测错误,并能够自动纠正错误。 纠删码——能够纠正删除(丢失)了的信息。
码的最小距离:dmin, d(C) 汉明重量(汉明势):码字中非零码元的个数 W(C)。 对2元码,汉明重量为码字中的“1”的个数。因此,二
信息理论基础第三章课件

X (a , b) p( x ) p( x ) x X (, ), p( x ) : 密度
波形信源可以用随机过程来描述。
§3.2 离散单符号信源
模型:
X x1 p( x ) p( x ) 1
定义
假定信源每次输出的都是N长的符号序列(记为XN= X1X2…XN),序列符号之间统计依赖,称该信源为 离散有记忆N次扩展信源。
信息熵:
H ( X N ) H X1 X 2
X N H ( X i | X i 1 )
注:1.这说明N维随机变量的联合熵等于X1的熵和各阶条 件熵之和。 2.熵率如何?有如下定理。
lim H X N | X N m X N m 1 lim H X m 1 | X1 X 2
N N
注:对于齐次遍历的马尔可夫信源,根据状态与符号序列 之间的关系,有
p( s j | si ) p( xim1 | xi1 xi2
于是,有:
xim ) p( xim1 | si )
H m 1 H X m 1 | X1 X 2 E ( I ( xim1 | xi1 xi2
qm qm q
Xm xim )) E ( I ( xim1 | si ))
i 1 im 1 1
p( si ) p( xim1 | si )log( p( xim1 | si ))
序列在任意时刻的概率分布完全相同,称该信源为 离散平稳信源。
注:1.平稳信源指的是各维概率分布与时间起点无关。 2.信息量该如何描述?
信息熵(平均符号熵的极限(熵率、极限熵)):
定义 在随机变量序列中,对前N个随机变量的联合熵求
波形信源可以用随机过程来描述。
§3.2 离散单符号信源
模型:
X x1 p( x ) p( x ) 1
定义
假定信源每次输出的都是N长的符号序列(记为XN= X1X2…XN),序列符号之间统计依赖,称该信源为 离散有记忆N次扩展信源。
信息熵:
H ( X N ) H X1 X 2
X N H ( X i | X i 1 )
注:1.这说明N维随机变量的联合熵等于X1的熵和各阶条 件熵之和。 2.熵率如何?有如下定理。
lim H X N | X N m X N m 1 lim H X m 1 | X1 X 2
N N
注:对于齐次遍历的马尔可夫信源,根据状态与符号序列 之间的关系,有
p( s j | si ) p( xim1 | xi1 xi2
于是,有:
xim ) p( xim1 | si )
H m 1 H X m 1 | X1 X 2 E ( I ( xim1 | xi1 xi2
qm qm q
Xm xim )) E ( I ( xim1 | si ))
i 1 im 1 1
p( si ) p( xim1 | si )log( p( xim1 | si ))
序列在任意时刻的概率分布完全相同,称该信源为 离散平稳信源。
注:1.平稳信源指的是各维概率分布与时间起点无关。 2.信息量该如何描述?
信息熵(平均符号熵的极限(熵率、极限熵)):
定义 在随机变量序列中,对前N个随机变量的联合熵求
信息论基础理论与应用第三版(傅祖芸) 第1章 绪论

国内外已有不下百余种流行的说法, 它们都是从不同的侧面和不同的层次来揭示信息的 本质的。
1928年,哈特莱(R.V.L Hartley) 在《信息传输》一文中提出:发信者所发出的信
息,就是他在通信符号表中选择符号的具体方式, 主张用所选择的自由度来度量信息。 局限性: ➢ 只考虑选择符号的方式,不涉及到信息的价值和具 体内容。 ➢ 没有考虑各种可能选择方法的统计特性。
信源编码器的主要指标
是它的编码效率。一般来说,效率越高,编译码 器的代价也将越大。
信源译码器
把信道译码器的输出变换成信宿所需的消息形式,
相当于信源编码器的逆过程。
19
信道编码器与译码器
信道编码 主要作用是提高信息传送的可靠性。
信道编码器的作用 在信源编码器输出的代码组上有目的地增加一些监督 码元,使之具有检错或纠错的能力。
an p(an )
样本空间 概率测度
先验概率p(xi):
选择符号xi作为消息的概率。 11
例:气象预报
甲 X 晴 阴 大雨 小雨
p(x)
1/ 2,1/
4,
1/ 8,
1/8
乙
Y p(y)
晴 阴 1/4,1/4,
大雨 小雨
1/4, 1/4
“甲地晴”比“乙地晴”的不确定性小。
某一事物状态出现的概率越小,其不确定性越大。 某一事物状态出现的概率接近于1,即预料中肯定会 出现的事件,那它的不确定性就接近于零。
信道编码的主要方法 增大码率或频带,即增大所需的信道容量。这恰与信源 编码相反。
7
信息的表达层次
狭义而言,通信中对信息的表达分三个层次:信号、 消息、信息。 信号:信息的物理表达,是一个物理量,是一个载 荷信息的实体,可测量、可描述、可传输、可存储、 可显示。 消息 (或符号) :信息的数学表达,承载了信息, 它是具体物理信号的数学抽象。如语言、文字、语音、 图像等。 信息:更高层次的哲学抽象,是信号与消息的承载 的对象,描述事物运动状态或存在方式的不确定性。
1928年,哈特莱(R.V.L Hartley) 在《信息传输》一文中提出:发信者所发出的信
息,就是他在通信符号表中选择符号的具体方式, 主张用所选择的自由度来度量信息。 局限性: ➢ 只考虑选择符号的方式,不涉及到信息的价值和具 体内容。 ➢ 没有考虑各种可能选择方法的统计特性。
信源编码器的主要指标
是它的编码效率。一般来说,效率越高,编译码 器的代价也将越大。
信源译码器
把信道译码器的输出变换成信宿所需的消息形式,
相当于信源编码器的逆过程。
19
信道编码器与译码器
信道编码 主要作用是提高信息传送的可靠性。
信道编码器的作用 在信源编码器输出的代码组上有目的地增加一些监督 码元,使之具有检错或纠错的能力。
an p(an )
样本空间 概率测度
先验概率p(xi):
选择符号xi作为消息的概率。 11
例:气象预报
甲 X 晴 阴 大雨 小雨
p(x)
1/ 2,1/
4,
1/ 8,
1/8
乙
Y p(y)
晴 阴 1/4,1/4,
大雨 小雨
1/4, 1/4
“甲地晴”比“乙地晴”的不确定性小。
某一事物状态出现的概率越小,其不确定性越大。 某一事物状态出现的概率接近于1,即预料中肯定会 出现的事件,那它的不确定性就接近于零。
信道编码的主要方法 增大码率或频带,即增大所需的信道容量。这恰与信源 编码相反。
7
信息的表达层次
狭义而言,通信中对信息的表达分三个层次:信号、 消息、信息。 信号:信息的物理表达,是一个物理量,是一个载 荷信息的实体,可测量、可描述、可传输、可存储、 可显示。 消息 (或符号) :信息的数学表达,承载了信息, 它是具体物理信号的数学抽象。如语言、文字、语音、 图像等。 信息:更高层次的哲学抽象,是信号与消息的承载 的对象,描述事物运动状态或存在方式的不确定性。
信息论第三版傅祖芸(3.7-3.8)

P( z / yx) P( z / y)
称这两信道的输入和输出X,Y,Z序列构成马尔 可夫链。
这两个串接信道可以等价成一个总的离散信道,其 输入为X,输出为Z, X Z P(z/x)
等价的总信道的传递概率为
P( z / x) P( y / x) 递矩阵
r t rs s t
定理3.6 对于串接信道X、Y、Z,当且仅当
P(Z / XY ) P( Z / Y ) 时, 等式 I ( XY ; Z ) I (Y ; Z )
成立 。
上式 I ( XY ; Z ) 表示联合变量XY与变量Z之间的平均互信息, 也就是接收到Z后获得关于联合变量X和Y的信息量。而 I (Y ; Z ) 是接收到Z后获得关于变量Y的信息量。由上式的成 立条件可知随机变量X、Y、Z组成一个马尔可夫链。在在串 联信道中随机变量Z往往只依赖信道Ⅱ的输入Y,不直接与 变量X发生关系,即随机变量Z仅仅通过变量Y而依赖于X。 所以得出以下定理。
谢谢
定理3.7 若X、Y、Z组成一个马尔可夫链,则有
I ( X ; Z ) I ( X ;Y )
I ( X ; Z ) I (Y ; Z )
定理3.7表明通过数据处理后,一般只会增加信息的损失,最 多保持原来获得的信息,不可能比原来获得的信息有所增加 。也就是说,对接收到的数据Y进行处理后,无论变量Z是Y 的确定对应关系还是概率关系,决不会减少关于X的不确定 性。故定理3.7称为数据处理定理。
这就是信息的不增性原理,与热熵不减原理正好相反。因而串 接信道的信道容量为 max I(X ; Z) C串( Ⅰ, Ⅱ ) P ( x ) max I ( X ;W ) C串( Ⅰ, Ⅱ, Ⅲ )
P(x)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信道参数与时间的关系
固定参数信道 时变参数信道
根据输入端和输出 端的关联
无反馈信道 有反馈信道
根据输入输出信号的 特点
离散信道
(离散随机序列-离散随机序列)
连续信道
(连续值随机序列-连续值随机序列)
半离散半连续信道
(离散随机序列-连续值随机序列)
波形信道(模拟信道)
(时间、取值连续随机信号时间、取值连续随机信号)
P(b1 | a1) P(0 | 0) 1 p p a1=0
P(b2 | a2) P(1| 1) 1 p p
P(b1 | a2) P(0 | 1) p
P(b2 | a1) P(1| 0) p
a2=1
• p是单个符号传输发生错误的概率。
1-p
p p
1-p
0=b1 1=b2
•(1-p)表示是无错误传输的概率。
(2)输出某符号的概率 r P(bj) p(ai)p(bj /ai) i1
p(b1) p(a1)
p(b2)PT p(a2)
... ...
p(bs)
p(ar)
(传递矩 P:r阵 s, PT:sr)
(3)后验概率
根据贝叶斯定理,可知:
P (y|x)fun(x c ,y)t i 1 0 oy y n ff((x x ))
(2) 有干扰无记忆信道
信道输入和输出之间的条件概率是一般的概率分布。 如果任一时刻输出符号只统计依赖于对应时刻的输入符 号,则这种信道称为无记忆信道。
N
P (y|x ) P (y 1 y 2 .y .N .|x 1 x 2 .x .N .) P (y i|x i) i 1
ቤተ መጻሕፍቲ ባይዱ
二、离散信道的数学模型
条件概率 P(y|x) 描述了输入信号和输出信号之间统计 依赖关系,反映了信道的统计特性。根据信道的统计特性 的不同,离散信道又可分成3种情况:
1.无干扰信道 2.有干扰无记忆信道 3.有干扰有记忆信道
(1)无干扰(无噪声)信道
信道中没有随机性的干扰或者干扰很小,输出符号
y 与输入符号 x 之间有确定的、一 一对应的关系。即: y = f (x)
(3) 有干扰(噪声)有记忆信道
实际信道往往是既有干扰(噪声)又有记忆的这种类 型。
例如在数字信道中,由于信道滤波频率特性不理 想时造成了码字间串扰。
在这一类信道中某一瞬间的输出符号不但与对应时 刻的输入符号有关,而且还与此以前其他时刻信道的 输入符号及输出符号有关,这样的信道称为有记忆信 道。
三、单符号离散信道
我们只研究: 无反馈、固定参数的单用户离散信道。
信道分析的方法
信源输出的是携带者信息的消息,而消息必须首 先转换成能在信道中传输或存储的信号,然后经过信 道传送到接收者。
一般认为,噪声或干扰主要从信道中引入,它使信 号通过信道传输后产生错误和失真。
因此,信道的输入和输出信号之间一般不是确定的 函数关系,而是统计依赖关系。只要知道信道的输入 信号、输出信号,以及它们之间的统计依赖关系,那 么信道的全部特性就确定了。
pij0
s
pij1 (各列元素 1之 ) 和
j1
矩阵P完全描述了信道的特性,可用它作为离散单符号信道
的另一种数学模型的形式。矩阵 P中元素有些是信道干扰引起
的错误概率,有些是信道正确传输的概率。
[例] 二元对称信道,[BSC,Binary Symmetrical Channel] 解:此时,X:{0,1} ; Y:{0,1} ; r=s=2,a1=b1=0;a2=b2=1。 传递概率:
单符号离散信道特性:
➢ 输入符号为X,取值于{a1,a2, …,ar} ➢ 输出符号为Y,取值于{b1,b2, …,bs} ➢ 条件概率:P(y|x)=P(y=bj|x=ai)=P(bj|ai)
这一组条件概率称为信道的传递概率或转移 概率。
信道中有干扰(噪声)存在,可以用传递概率 P(bj|ai) 来描述干扰影响的大小。
• 转移矩阵:
0
0 1 - p
1
p
1
p
1
p
[例]二元删除信道。[BEC,Binary Eliminated
Channel]
0
p
0
1-p
解:X:{0,1} Y:{0,1,2}
2
此时,r =2,s =3, 传递矩阵为:
1-q
1
q
1
021
0 p 1 p 0 1 0 1q q
符号“2”表示接收到了“0”、“1”以外的特殊符 号
一般简单的单符号离散信道可用 X, P(y|x) , Y
三者加以表述,其数学模型可以用如下概率空间
[X, P(y|x) ,Y]
也可用图形来描述:
a1
a2
X
.
.
ar
P(bj/ai) 单符号离散信道
b1 b2 .Y . bs
信道矩阵(转移矩阵)模型
一般离散单符号信道的传递概率可用矩阵形式表 示,即
b1
第三章 离散信道及其信道容量
第一节 信道的数学模型及分类 第二节 平均互信息 第三节 平均互信息的特性 第四节 信道容量及其计算方法 第五节 离散无记忆扩展信道及其信道容量 第六节 信源与信道的匹配
信道的任务: 以信号方式传输信息和存储信息。
研究内容: 信道中能够传送或存储的最大信息量,即信道容量。
3.1 信道的数学模型和分类
干扰源
信源
编码器 调制器 物理信道 解调器 译码器
信宿
实际信道
编码信道 等效信道
数字通信系统的一般模型
一、信道的分类
根据载荷消息的媒体不同
邮递信道 电、磁信道 光信道 声信道
根据信道用户的多少
单用户(两端)信道
一个输入端和一个输出端的 单向通信;
多用户信道
至少有一端有两个以上的用 户,可以是双向通信;(计算机 通信、卫星通信、广播通信等)
单符号离散信道的相关概率关系
(1)联合概率
P ( a ib j) P ( a i) P ( b j/a i) P ( b j) P ( a i/b j)
其中
P (b j / ai ) 前向概率,描述信道的噪声特性 P ( a i ) 输入符号的先验概率 P (ai / b j ) 后向概率(后验概率)
b2 … bs
a1 P(b1|a1) P(b2|a1) … P(bs|a1)
a2 P(b1|a2) P(b2|a2) … P(bs|a2)
… …. … …
p11 p12 ... p1s
P
p 21
p22 ...
p
2
s
: : : :
p
r1
pr 2 ...
p
rs
ar P(b1|ar) P(b2|ar) … P(bs|ar)
