刚体平面运动习题
理论力学课后习题答案第6章刚体的平面运动分析
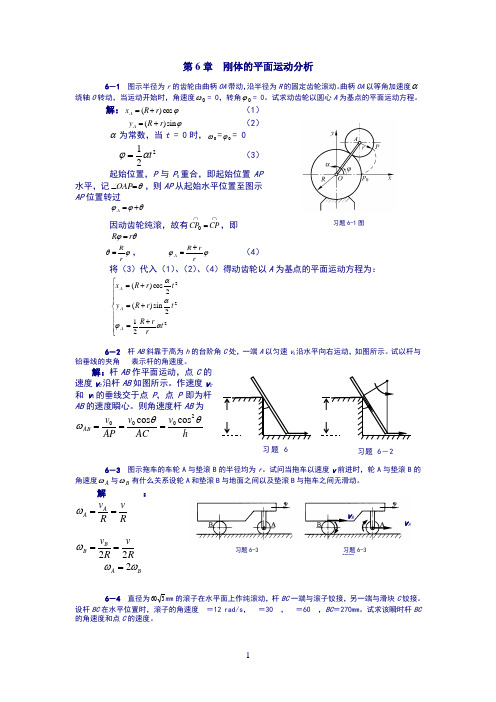
第6章 刚体的平面运动分析6-1 图示半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
曲柄OA 以等角加速度α绕轴O 转动,当运动开始时,角速度0ω= 0,转角0ϕ= 0。
试求动齿轮以圆心A 为基点的平面运动方程。
解:ϕcos )(r R x A += (1) ϕsin )(r R y A += (2) α为常数,当t = 0时,0ω=0ϕ= 0 221t αϕ=(3)起始位置,P 与P 0重合,即起始位置AP 水平,记θ=∠OAP ,则AP 从起始水平位置至图示AP 位置转过θϕϕ+=A因动齿轮纯滚,故有⋂⋂=CP CP 0,即 θϕr R =ϕθr R =, ϕϕrr R A += (4)将(3)代入(1)、(2)、(4)得动齿轮以A 为基点的平面运动方程为:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=+=+=222212sin )(2cos )(t r r R t r R y t r R x A A A αϕαα6-2 杆AB 斜靠于高为h 的台阶角C 处,一端A 以匀速v 0沿水平向右运动,如图所示。
试以杆与铅垂线的夹角 表示杆的角速度。
解:杆AB 作平面运动,点C 的速度v C 沿杆AB 如图所示。
作速度v C 和v 0的垂线交于点P ,点P 即为杆AB 的速度瞬心。
则角速度杆AB 为hv AC v AP v ABθθω2000cos cos ===6-3 图示拖车的车轮A 与垫滚B 的半径均为r 。
试问当拖车以速度v 前进时,轮A 与垫滚B 的角速度A ω与B ω有什么关系设轮A 和垫滚B 与地面之间以及垫滚B 与拖车之间无滑动。
解:R v R v A A ==ωR v R v B B 22==ω B A ωω2=6-4 直径为360mm 的滚子在水平面上作纯滚动,杆BC 一端与滚子铰接,另一端与滑块C 铰接。
设杆BC 在水平位置时,滚子的角速度=12 rad/s ,=30,=60,BC =270mm 。
第6章刚体的平面运动习题解答080814

,(逆时针)、
,
杆OB得角速度为
,(逆时针)、
两齿轮啮合点M得速度为,则轮1得角速度为
,(逆时针)、
6-9如图所示,轮O在水平面上匀速滚动而不滑动,轮缘上固连销钉连接滑块B,此滑块在摇杆得槽内滑动,并带动摇杆绕轴转动。已知轮得半径m,在图示位置时,就是轮得切线,轮心得速度m/s,摇杆与水平面得夹角为。求摇杆得角速度与角加速度。
解:如图所示,对各构件进行速度分析、
1)杆作平面运动、因,所以杆为瞬时平移,得
、
2)杆作平面运动、由找得杆得速度瞬心为D点,所以,杆上得速度分布好像与三角板一起绕作定轴转动一样,得
,方向如图示、
3)杆作平面运动、由找得杆得速度瞬心为,故有
,(顺时针);
,(方向向上).
6—5图示四连杆机构中,连杆由一块三角板ABD构成。已知曲柄得角速度rad/s,mm,mm,mm。当mm铅直时,AB平行于,且、A、D在同一直线上,角。求三角板ABD得角速度与点D得速度.
解:1)速度分析、
动齿轮A在定齿轮O上作纯滚动,所以,动齿轮A上与定齿轮O接触得这点就就是动齿轮得A得速度瞬心,于就是有
,,(逆时针)、
、
选BE杆上得B点为动点,套筒C为动系,如图(a)。由速度合成定理
,
得
,
、
式中、从而杆BE得角速度为
,(顺时针)、
当选BE杆上得为动点时,牵连速度为零,又因为杆相对于套筒就是作平移,从而杆BE上得点得速度为
解出
,
,
于就是,杆得角速度为
,(逆时针);
杆得角速度为
,(顺时针)、
选取滑块上得销钉C为动点,摇杆为动系,则
刚体平面运动习题

第8章 刚体平面运动习题1.是非题(对画√,错画×)8-1.刚体平面运动为其上任意一点与某一固定平面的距离始终平行的运动。
( ) 8-2.平面图形的运动可以看成是随着基点的平移和绕基点的转动的合成.( ) 8-3.平面图形上任意两点的速度在某固定轴上投影相等。
( ) 8-4.平面图形随着基点平移的速度和加速度与基点的选择有关。
( ) 8-5.平面图形绕基点转动的角速度和角加速度与基点的选择有关。
( ) 8-6.速度瞬心点处的速度为零,加速度也为零。
( ) 8-7.刚体的平移也是平面运动。
( ) 2.填空题(把正确的答案写在横线上)8-8.在平直轨道作纯滚动的圆轮,与地面接触点的速度为 。
8-9.平面图形上任意两点的速度在 上投影相等。
8-10.某瞬时刚体作平移,其角速度为 ;刚体上各点速度 ;各点加速度 。
3.简答题8-11.确定图示平面运动物体的速度瞬心位置。
题8-11图(a) (b)(c)8-12.若刚体作平面运动,下面平面图形上A 、B 的速度方向正确吗? 题8-12图(a) (b) (c)8-13.下面图形中O 1A 和AC 的速度分布对吗?8-14.圆轮做曲线滚动,某瞬时轮心的速度o v 和加速度o a ,轮的半径为R ,则轮心的角加速度等于多少?速度瞬心点处的加速度大小和方向如何确定?题8-13图B8-15.用基点法求平面图形个点的加速度时,为什么没有科氏加速度? 4.计算题8-16.椭圆规尺AB 由曲柄OC 带动,曲柄以匀角速度o ω绕O 轴转动,如图所示,若取C 为基点,OC=BC=AC=r ,试求椭圆规尺AB 的平面运动方程。
8-17.半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动,如图所示。
曲柄以匀角加速度α绕O轴转动,设初始时角速度0=ω、角加速度0=α、转角0=ϕ,若选动齿轮的轮心C 点为基点,试求动齿轮的平面运动方程。
题8-16图题8-17图8-18.曲柄连杆机构,已知OA =40cm ,连杆AB =1m ,曲柄OA 绕O 轴以转速180=n r/min 匀速转动,如图所示。
刚体的平面运动

O1O2 0.05 + O1 A = + 0.1 D tan 30 tan 30D
ω ABD =
0.2 = 1.072 rad / s 0.1866
ω ABD
P
vD = PD ⋅ ω ABD = ( PA + AD ) ⋅ ω = (0.1866 + 0.05) ⋅1.072 = 0.254 m / s
O1 B 与连杆间成 30° 角.如 OA = r , AB = 2 3r , O1 B = 2r ,求在该瞬时,滑块 B 的切向和法
向加速度。 解: AB 杆作平面运动,速度分析如图
vB cos 60D = v A , vB = 2v A = 2rωO
n 2 2 故 B 点的法向加速度: aB = vB / O1 B = 2rωO
刚体的平面运动(一)
一、填空题 1、刚体的平面运动可分解为 随基点的平移 和 绕基点的转动 ; 平移的速度和加速度 与基 点的选择有关,_转动的角速度和角加速度_与基点的选择无关。
2、若已知刚体上任一点的速度 v 和刚体的角速度 ω ,那么速度瞬心的位置应在_过该点与 v 垂 直的直线上_,距该点的距离_____ v / ω _____;若瞬心在无穷远,则此时角速度为__零___, 刚体作___瞬时平移__。 3、刚体定轴转动时,轴上各点的速度__为零___,加速度__为零__;而绕速度瞬心转动时,速 度瞬心的速度__为零__,加速度 二、判断题 (× ) 1、刚体的平面运动与刚体的平动其相似之处是刚体上各点的运动轨迹都在同一平面内。 (× ) 2、平面图形上任意两点的速度在固定坐标轴上的投影相等。 (√) 3、平面图形的角速度不等于零,则图形上不可能存在两个或两个以上速度为零的点。 (√) 4、作平面运动的平面图形上(瞬时平动除外),每一瞬时都存在一个速度瞬心。 三、选择题 1、一圆盘作平面运动,如图所示的速度分布情况中,可能出现的是 A.图(a) B.图(b) C.图(c) A 。 D.图(d) 不一定为零 。
第2章 刚体的平面运动—习题2-22
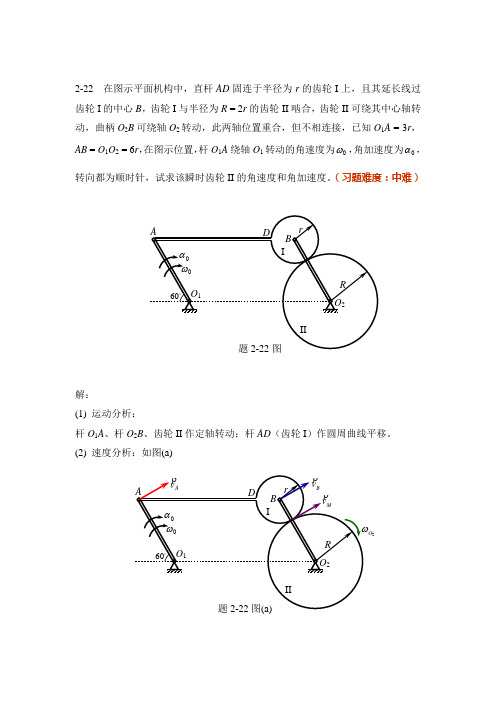
2-22 在图示平面机构中,直杆AD 固连于半径为r 的齿轮I 上,且其延长线过齿轮I 的中心B ,齿轮I 与半径为R = 2r 的齿轮II 啮合,齿轮II 可绕其中心轴转动,曲柄O 2B 可绕轴O 2转动,此两轴位置重合,但不相连接,已知O 1A = 3r ,AB = O 1O 2 = 6r ,在图示位置,杆O 1A 绕轴O 1转动的角速度为0ω,角加速度为0α,转向都为顺时针,试求该瞬时齿轮II 的角速度和角加速度。
(习题难度:中难)解:(1) 运动分析:杆O 1A 、杆O 2B 、齿轮II 作定轴转动;杆AD (齿轮I )作圆周曲线平移。
(2) 速度分析:如图(a)2O假设齿轮I 上点M '和齿轮II 上点M ''相啮合,则M M v v '''= ,且tt M M a a '''= 。
杆O 1A :0013ωωr A O v A =⋅=(A O 1⊥)杆AD (齿轮I ):A B v v = 03ωr v v A B ==(B O 2⊥) 03ωr v v B M =='(B O 2⊥) 齿轮II(3) 加速度分析:如图(b)杆O 1A : 2n 3ωr a A =(1//) 0t 3αr a A =(A O 1⊥) 杆AD (齿轮I ):A B a a = 20n n 3ωr a a A B ==(2//BO ) 0tt 3αr a a A B ==(B O 2⊥)tn t n M M B B B M a a a a a a '''+=+==齿轮I 上M '点:0tt 3αr a a B M =='(B O 2⊥) 齿轮II : 0t t t 3αr a a a B M M ==='''(注意:齿轮啮合点的切向加速度相同,但是齿轮啮合点的法向加速度并不相同。
刚体的平面运动动力学课后答案

其中: 是从速度瞬心 引向M点的矢径, 为平面图形的角速度矢量。
4、平面图形上各点的加速度
基点法公式:
(7-9)
其中: 。基点法公式建立了平面图形上任意两点的加速度与平面图形的角速度和角加速度间的关系。只要平面图形的角速度和角加速度不同时为零,则其上必存在唯一的一点,其加速度在该瞬时为零,该点称为平面图形的加速度瞬心,用 表示。
(b)
再根据对固定点的冲量矩定理:
系统对固定点A(与铰链A重合且相对地面不动的点)的动量矩为滑块对A点的动量矩和AB杆对A点的动量矩,由于滑块的
动量过A点,因此滑块对A点无动量矩,AB杆对A点的动量矩(也是系统对A点的动量矩)为:
将其代入冲量矩定理有:
(c)
由(a,b,c)三式求解可得:
(滑块的真实方向与图示相反)
其中:aK表示科氏加速度;牵连加速度就是AB杆上C点的加速度,即:
将上述公式在垂直于AB杆的轴上投影有:
科氏加速度 ,由上式可求得:
3-14:取圆盘中心 为动点,半圆盘为动系,动点的绝对运动为直线运动;相对运动为圆周运动;牵连运动为直线平移。
由速度合成定理有:
速度图如图A所示。由于动系平移,所以 ,
根据点的复合运动速度合成定理有:
其中: ,根据几何关系可求得:
AB杆作平面运动,其A点加速度为零,
B点加速度铅垂,由加速度基点法公式可知
由该式可求得
由于A点的加速度为零,AB杆上各点加速度的分布如同定轴转动的加速度分布,AB杆中点的加速度为:
再取AB杆为动系,套筒C为动点,
根据复合运动加速度合成定理有:
3-25设板和圆盘中心O的加速度分别为
,圆盘的角加速度为 ,圆盘上与板
理论力学7—刚体的平面运动2
vC
vC C C 2 w BC
3 rw 3
习题7-12 图示小型精压机的传动机构,OA= O1B=r=0.1m,EB=BD=AD=l=0.4 m,在 图示瞬时OA⊥AD,O1B⊥ED,O1D在水平位 置,OD和EF在铅直位置。已知曲柄OA的转速 n=120 rpm,求此时压头F 的速度。
a C O r r
t
w
O
vO
n aCO
aO aO
aO r
vO r
aO
2
t aCO
C
aCO rw
n 2
r(
)
2
vO r
w
vO r
,
aO r
a C O a O , a C O vO / r
t n 2
取如图的投影轴, 将各矢量 投影到投影轴上得
y
aCx aO aCO 0
A2 A4
vA2
A1
v A 3 2 rw 2 v
2 rw 2v
例7-7 曲柄肘杆式压床如图。已知曲柄OA长r, 以匀角速度w 转动,AB = BC = BD = l,当曲柄 与水平线成30º 角时,连杆AB处于水平位置,而 肘杆DB与铅垂线也成30º 角。试求图示位置时, 杆AB、BC的角速度以及冲头C 的速度。 解:连杆AB作平面运动,瞬 D 30º 心在点C1,则
7.2.3 求平面图形上各点速度的瞬心法
设有一个平面图形S角速度 vCA 为 w ,图形上点A的速度为 N vA 。在vA 的垂线上取一点C S C (由vA 到AC的转向与图形的 vA 转向一致),有 vC v A w A C A 如果取AC= vA /w ,则 w vA vC v A w A C 0
第八章刚体的平面运动习题解答

故
向
即
8-21图8-48所示机构中,圆轮A的半径R=0.2m,圆轮B的半径r=0.1m,两轮均在水平轨道上作纯滚动。在图示瞬时,A轮上C点在最高位置,轮心速度vA=2m/s,加速度aA=2m/s2,试求轮B滚动的角速度和角加速度。
图8-48
加速度分析
圆轮A
杆BC
故
向
8-22轮O在水平面上作纯滚动,如图8-49所示。轮缘上固定销钉B,此销钉可在摇杆O1A的槽内滑动,并带动摇杆绕轴O1转动。已知轮心O的速度是一常量,vO=0.2m/s,轮的半径R=0.5m,图示位置时,O1A是轮的切线,摇杆与水平面的夹角为 。试求该瞬时摇杆的角速度和角加速度。
图8-59
以O为动点,杆AB为动系
(1)速度分析
(2)加速度分析
圆轮O
以O为基点,分析C点
向y
8-33图8-60所示机构中,已知曲柄OA以匀角速度 绕定轴O转动,OA=100mm,l=500mm。在图示位置, ,试确定杆BD的角速度和角加速度。
图8-60
以A为动点,杆AB为动系
(1)速度分析
(2)加速度分析
图8-33
瞬心法
基点法
8-7在如图8-34所示的筛动机构中,筛子BC的摆动是由曲柄连杆机构所带动。已知曲柄长OA=0.3m,转速为n=40r/min。当筛子运动到与点O在同一水平线上时, ,试求此时筛子BC的速度。
图8-34
速度投影定理
8-8长为l=1.2m的直杆AB作平面运动,某瞬时其中点C的速度大小为vC=3m/s,方向与AB的夹角为 ,如图8-35所示。试求此时点A可能有的最小速度以及该瞬时杆AB的角速度。
8-20半径为r的圆盘可在半径为R的固定圆柱面上纯滚动,滑块B可在水平滑槽内滑动,如图8-47所示。已知r=125mm,R=375mm;杆AB长l=250mm。图示瞬时,vB=500mm/s,aB=750mm/s2;O、A、O1三点位于同一铅垂线上,试求此时圆盘的角加速度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
刚体平面运动习题
第八章刚体平面运动的练习
1.真或假(勾选正确和交叉错误)
8-1。
刚体的平面运动是一种运动,在这种运动中,刚体上的任何一点与固定平面之间的距离总是平行的。
()8-2。
平面图形的运动可以看作基点的平移和围绕基点的旋转的组合。
()8-3。
平面图形上任意两点的速度都相等地投影在一个固定的轴上。
()()()8-6。
瞬时速度中心的速度为零,加速度为零。
()8-7。
刚体的平移也是一种平面运动。
()2。
填空(在横线上写出正确答案)
8-8。
在直线轨道上纯滚动时,圆轮与地面接触点的速度为。
8-9。
平面图上任意两点的速度在上投影中相等。
8-10。
瞬时刚体平移时的角速度是:刚体上每个点的速度;每个点的加速度。
3.简短回答问题
8-11。
确定图中所示平面运动物体的瞬时速度中心的位置。
AbabaccωOboaωOdbω(b)Co(a)(c)图8-11 (d)
8-12。
如果一个刚体在一个平面上运动,下面平面图中A和B的速度方向是正确的吗?问题8-12图(c)
8-13。
下图中O1A和AC的速度分布是否正确?
8-14。
当圆形车轮在曲线上滚动时,某一瞬时车轮中心的速度vo和加速度ao,而车轮的半径是R,即车轮中心的角度
加速度是多少?如何确定瞬时速度中心的加速度的大小和方向?
蟹爪兰O1VβA01ωO2P 8-13
图8-14
8-15。
为什么用基点法计算平面图中单个点的加速度时没有科里奥利加速度?4.计算问题
8-16。
椭圆规AB由曲柄OC驱动,曲柄OC以均匀的角速度ω O绕O轴旋转。
如图所示,如果以C为基点,OC=BC=AC=r,试着找出椭圆规AB的平面运动方程。
8-17。
半径为R的齿轮由曲柄OA驱动,沿半径为R的固定齿轮滚动,如图所示。
曲柄以均匀的角加速度α绕O轴旋转,并设定初始角速度ω。
角加速度α?0.角落??0.如果选择移动齿轮的中心C点作为基点,试着找出移动齿轮的平面运动方程。
yay rarαφBMMoxorBx 8-16图ωOO
图8-17
8-18。
曲柄和连杆机构,称为OA = 40cm厘米,连杆AB = 1m米,曲柄OA绕O轴以N?180转/分钟均匀旋转,如图所示。
当曲柄臂与水平线成45度角时,试着找出连杆臂的角速度和中点的速度。
8-19。
众所周知,曲柄OA=r,连杆BC=2r,曲柄OA处于均匀角速度ω?4顺时针旋转/秒,如图所示。
试着找出图中瞬时点B的速度和连杆BC的角速度。
AMnOBArOB302rCω问题8-18
图8-19
8-20。
如图所示,筛选机通过曲柄OA驱动筛BC摆动。
众所周知,
曲柄OA的转速为n?当屏幕BC移动到与点o相同的水平线时,40r/min匀速旋转,OA=0.3m。
鲍?90o,当摆杆与水平线之间的角度为600°时,尝试找出图中所示瞬间屏幕BC的速度。
8-21。
如图所示,对于四连杆机构,曲柄OA以均匀的角速度围绕O 轴旋转。
当曲柄OA处于水平位置时
1
设定时,曲柄O1B正好处于铅锤位置。
让OA=O1B=AB=l,并试着将曲柄O1B的角速度相加。
2
ABCBω6060OA
OωO1O,8-20,8-21
8-22。
对于图中所示的平面机构,曲柄OA以均匀的角速度ωo绕O 轴旋转,并驱动连杆AB使圆轮在地面上滚动。
圆轮的半径是r。
在图中,瞬时曲柄OA垂直于连杆AB,曲柄OA与水平线的夹角是600,OA = R。
试着找出瞬时圆轮的角速度。
8-23。
在图中所示的曲柄连杆机构中,连杆AB的中点C通过铰链与杆CD连接,杆CD与绕E轴旋转的杆DE连接。
众所周知,曲柄OA的角速度是ω?8rad/s绕o轴旋转,OA = 25cm厘米,DE = 100cm 厘米。
当b和e在同一条铅垂线上时,o、a和b共线。
CDE?90o,试着找出罗德·德的角速度。
ωAroadcbω60OB 30E问题8-22图
图8-23
8-24。
在图中所示的平面机构中,曲柄OA=r以均匀的角速度ωo绕O轴旋转,连杆CD=6r在图中所示的时刻与铅垂线形成α?30度角时,连杆DE和AB都处于水平位置,试着找出d点的速度和连杆CD 的角速度。
8-25。
在图中所示的平面机构中,OA=BD=DE=0.1m,EF?0.13米;以角速度ω转动曲柄。
4rad/s绕o轴旋转。
在图中所示的瞬间,曲柄OA垂直于水平线OB,b、d、f在同一条垂直线上,而DE垂直于EF。
试着找出杆的角速度和点的速度
OOEC 8-24图f
图8-25
8-26。
在图中所示的瓦特行星齿轮机构中,平衡杆O1A绕O1轴旋转,并通过连杆AB驱动曲面Ob。
曲柄OB可移动地安装在O轴上。
O 轴上设有齿轮一,齿轮二与连杆AB固定连接。
已知r1?r2。
0.33米,O1A = 0.75m米,AB = 1.5m米,平衡杆角速度ω?6拉德/秒,试试??60o和??曲柄OB和齿轮I的角速度
8-27。
如图所示,齿轮1在齿轮2中滚动,齿轮2的半径分别为R and R=2r。
曲柄OO1以相等的角速度ω0绕O轴旋转,并驱动行星齿轮1。
试着找出齿轮1的瞬时速度中心p的加速度
aγωO1IPωIIR 2001βBr10iii 8-26
图8-27
8-28。
半径为R的圆柱体在半径为R的圆弧中滚动而不滑动。
如图所示,圆柱体中心C的速度为vc,切向加速度为A?试着找出圆柱
体的最低点a和最高点b的加速度。
8-29。
以均匀角速度ω转动曲柄。
2rad/s绕o轴旋转,半径为R的车轮由连杆AB驱动在半径为R的圆弧内滚动而不滑动。
让OA=AB=R=2r=1m,并尝试找出图示瞬时车轮上点b和c的速度和加速度。
Orcrabo1 abrvca τ c ω o图8-28
图8-29
8-30。
在图中所示的平面机构中,曲柄OA=r以均匀的角速度ωo绕O轴旋转,AB=6r,BC?33r,试着找出滑块C在图中所示瞬间的速度和加速度。
8-31。
如图所示,曲柄OA = 20cm厘米绕O轴以均匀的角速度ω旋转。
10弧度/秒的旋转,并且当曲柄OA和连杆AB相互垂直并且与水平线的夹角为α时,通过连杆AB驱动滑块b沿垂直滑动,AB = 100cm厘米。
45o、β?在45度,试着找出角速度,瞬时连杆的角加速度和滑块的加速度
问题8-30图0
图8-30
8-32。
在曲柄齿轮椭圆规中,齿轮A和曲柄O1A合并成一个整体,齿轮C和齿轮A的半径都是
O1A?O2B?0.4m,O1A,匀速角速度ω?0.2rad/sr并相互啮合,如图所示。
众所周知,AB=O1O2绕O1轴旋转。
m是轮c上的点,CM=0.1m。
图中显示了瞬时,CM是垂直的,试着找出瞬时点m
速度和加速度。
8-33。
圆轮在直线轨道上做纯滚动。
图中所示的瞬时点O位于铰链C 正下方,连杆OA以v=1.5m/s的速度在水平导轨中移动。
?30o,驱动摇杆光盘绕点c旋转,轮的半径为R = 100mm毫米,OC = 200mm 毫米,试着找出摇杆光盘的角速度。
BvAPMθOωO1 8-32图O260100mm
图8-33,共200个问题
8-34。
如图所示,车轮O在水平面上滚动,没有滑动。
车轮中心以恒定速度V o = 0.2m/s移动。
销B固定连接到轮辋上。
销在摇杆O1A的凹槽中滑动,并驱动摇杆绕O1轴旋转。
给定车轮半径R=0.5m,图中所示的瞬时O1A为车轮的切线,摇臂与水平线的夹角为600°。
试着找出瞬时摇杆O1A的角速度和角加速度。
8-35。
平面机构的曲柄OA为2l长,并以均匀的角速度ω o绕O轴旋转。
OAD?90o,试着找出瞬时套筒d相对于连杆BC的速度和加速度。
图8-35图8-34
8-36。
如图所示,曲柄导杆机构,曲柄OA = 120mm毫米,OB = 160mm 毫米,显示为瞬时?人工臭氧层?90o .曲柄以角速度ω旋转。
4拉德/秒,角加速度α?2rad/s2绕o轴旋转。
试着找出瞬时导杆的角加速度和导杆相对于套筒的加速度..
8-37。
在所示的机构中,曲柄O1A以均匀的角速度ω围绕O1轴旋转。
众所周知,在图(a)、(b)和(c)中,O1A=r,l=4r,在图(d)中,l=2r,试图找出瞬时水平杆的速度和加速度。
CC60BAωαBOC问题8-36图0ωLR1a 30 O2(a)CωOR1a 30 bro 2(c)问题8-37图0ωOR1a lb(b)CωLO1 ro 2 Rb(d)。
