角和角的单位换算
角的换算

教案一、学习目标:1.理解度分秒之间的换算进制,能进行角度的单位换算;2.会比较两个角的度数大小;3.体验解决钟面上的夹角问题.二、知识回顾:1. 我们用测量角的大小.角的度量单位是.2. 1周角= 平角= 直角= ,1平角= ,1直角= .三、知识梳理:1.角的度量我们常用量角器量角,度、分、秒是常用的角的度量单位.把一个周角360等分,每一份就是1度的角,记作1°;把1度的角60等分,每一份叫做1分的角,记作1′;把1分的角60等分,每一份叫做1秒的角,记作1″.1周角=360°,1平角=180°;1°=60′,1′=60″;如∠a的度数是48度56分37秒,记作∠a=48°56′37″.度、分、秒是常用的角的度量单位,以度、分、秒为单位的角的度量制,叫做角度制.注意:角的度、分、秒与时间的时、分、秒一样,都是60进制.2. 钟面上角度大小的计算问题(1)时钟的表面被均分成12 大格、60小格,若把钟表表面看错以表心为顶点的周角,则每一大格对应的角度是30°,每一小格对应的角度是是6°.(2)时钟上有时针和分钟,其中时针每小时转360=3012,每分钟转30=0.560;分针每分钟转360=660.用时针与分针所走的时间分别乘它们的速度,即它们各自转过的角度.四、典例探究1.角的换算【例1】(1)把26.29°转化为度分秒表示的形式;(2)37°14′24″转化为度的形式.总结:1.角度是60进制,1°=60′, 1′=60″.2.将度用度、分、秒表示时,按60进制,用乘法:整数部分保留,将度的小数部分转化为分,将分的小数部分化为秒. 注意化成度、分、秒时,数字全是整数.角的换算3.将度、分、秒用度表示时,按60进制,用除法:先将秒化为分,再将分化为度.练1 18°27′=_________°,51.6°=_________°__________′.2.角的度数的比较【例2】若∠A=20°18′,∠B=20°15′30〞,∠C=20.25°,则()A.∠A>∠B>∠C B.∠B>∠A>∠CC.∠A>∠C>∠B D.∠C>∠A>∠B总结:1.比较角的大小时,若角的单位不统一,则不要盲目比较,一定要注意统一单位后再比较.2.若统一成以度为单位,则按照数的大小比较即可;若统一成以度分秒为单位,则依次比较度、分、秒的大小. 练2已知∠α=12°12′,∠β=12.12°,∠γ=12.2°,则下列结论正确的是()A.∠α=∠β B.∠α<∠β C.∠α=∠γ D.∠β>∠γ3.某时刻时针与分针夹角度数【例3】同学们,闹钟都见过吧!它的时针和分针如同兄弟俩在赛跑,可你是否知道时针每分钟走多少度?分针每分针走多少度?当你弄清楚这个问题后,你能解决很多关于闹钟有趣的问题:(1)3点整时时针与分针所夹的角是_______度.(2)7点25分时针与分针所夹的角是_______度.总结:1.整点时刻求两针夹角.因为分针始终指向12,时针指向对应整点时刻,所以只要数出时针与分针之间所夹几个大格,再乘30°即可求出两针夹角.注意:夹角是指小于180度的角.2.任意时刻求两针夹角.(1)看时针和分针之间相隔几个大格,再乘30°即可求出两针夹角.(2)首先弄清楚时针每小时、每分钟转过的角度,分针每分钟转过的角度,然后以12时为起点,求出分针和时针从12时起转过的角度差,即为两针夹角.分针转过的角度为:分钟数×6°,时针转过的度数为:小时数×30°+分钟数×0.5°.练3 时钟在3点半时,分针与时针所夹的角的度数是()A.67.5° B.75° C.82.5° D.90°练4钟表上2时25分时,时针与分针所成的角是()A.77.5° B.77°5′C.75° D.以上答案都不对4. 钟面上时针与分钟重合问题【例4】你知道时钟的分针与时针一昼夜重合几次吗?总结:1.分针和时针从上一次重合到下一次重合,相当于分针比时针多转了360°.2.这是一个钟面上的追及问题,可以套用环形跑道追及问题解决,用方程的思想来解.设重合一次的时间为x分钟,等量关系是分针转过的角度-时针转过的角度=360°,然后用一昼夜的时间除以重合一次的时间(注意单位统一,可以均以分为单位),即可得到一昼夜重合的次数.练5钟面上的角的问题.(1)8点15分,时针与分针的夹角是多少?(2)从12点整始,至少再过多少时间,分针与时针再一次重合?五、课后小测一、选择题1.若∠P=25°12′,∠Q=25.12°,∠R=25.2°,则下列结论中正确的是()A.∠P=∠Q B.∠Q=∠R C.∠P=∠R D.∠P=∠Q=∠R2.下面等式成立的是()A.83.5°=83°50′ B.37°12′36″=37.48°C.24°24′24″=24.44° D.41.25°=41°15′3.用度、分、秒表示91.34°为()A.91°20′24″ B.91°34′ C.91°20′4″ D.91°3′4″4.若∠P=65°12′,∠Q=65.12°,∠R=65.2°,则下列结论中正确的是()A.∠P=∠Q=∠R B.∠Q=∠R C.∠P=∠Q D.∠P=∠R5.已知:∠1=35°18′,∠2=35.18°,∠3=35.2°,则下列说法正确的是()A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.∠1、∠2、∠3互不相等6.下列算式正确的是()①33.33°=33°3′3″②33.33°=33°19′48″③50°40′33″=50.43°④50°40′33″=50.675°A.①和②B.①和③C.②和③D.②和④7.甲、乙、丙、丁四个学生判断时钟的分针与时针互相垂直时,他们每个人都说了两个时间,说对的是()A.甲说3点时和3点30分B.乙说6点15分和6点45分C.丙说9时整和12时15分D.丁说3时整和9时整8.现在是一点整,从现在开始到三点,时针与分针成90°角的次数是()A.1 B.2 C.3 D.49.将8.35°用度、分、秒表示正确的是()A.8°20′ B.8°21′ C.8°3′5″ D.8°30′5″10.已知∠1=28°24′,∠2=28.24°,∠3=28.4°,下列说法正确的是()A.∠1=∠2 B.∠1=∠3 C.∠1<∠2 D.∠2>∠3二、填空题11.22.5°=____度______分;12°24′=______度.12.用度、分、秒表示26.34°=____度____分____秒.13.25.14°=°′″;下午1点24分,时针与分针所组成_______度.14.用“>”、“<”或“=”号填空(1)38°15′______38.15°;(2)38°9′_______38.15°;(3)19°4′30″×2=_________(用度表示).15.1800″等于______分,等于______度.16.65°25′12″用度表示为________.17.已知α=38°15′,β=38.25°,则α_____β(填“>”,“<”或“=”)18.聪明一休在9点到10点之间开始解一道数学题,当时的钟面时针与分针正好成一直线,当他解完这道题时,时针与分针又恰好重合,一休解这道题用了________分钟.19.(1)23°30′=______°;(2)0.5°=_____′=______″.三、解答题20.计算:(1)将24.29度化为度、分、秒.(2)将36度40分30秒化为度.21.同学们,日常生活中,我们几乎每天都要看钟表,它的时针和分针如同兄弟俩在赛跑,其中蕴涵着丰富的数学知识.(1)如图1,上午8:00这一时刻,时钟上分针与时针所夹的角等于________°;(2)请在图2中大致画出8:20这一时刻时针和分针的位置,思考并回答:从上午8:00到8:20,时钟的分针转过的度数是______,时钟的时针转过的度数是________;(3)“元旦”这一天,城区某中学七年级部分学生上午八点多集中在学校门口准备去步行街进行公益服务,临出发时,组长一看钟,时针与分针正好是重合的,下午两点多他们回到学校,进校门时,组长看见钟的时针与分针方向相反,正好成一条直线,那么你知道他们去步行街进行公益服务共用了多少时间吗?通过计算加以说明.22.钟表在12点钟时三针重合,经过多少分钟秒针第一次将分针和时针所夹的锐角平分?23.观察常用时钟,回答下列问题:(1)早晨7时整,时针和分针构成多少度的角?(2)时针多长时间转一圈?它转动的速度是每小时多少度?(3)从7:00到7:40,分针转动了多少度?24.时钟上的分针和时针像两个运动员,绕着它们的跑道昼夜不停地运转.以下请你解答有关时钟的问题:(1)分针每分钟转了几度?(2)中午12时整后再经过几分钟,分针与时针所成的钝角会等于121°?(3)在(2)中所述分针与时针所成的钝角等于121°后,再经过几分钟两针所成的钝角会第二次等于121°?25.小华是个数学迷,最近他在研究钟面角(时针与分针组成的角)问题,他想和大家一起来讨论相关问题.(1)分针每分钟转,时针每分钟转°;(2)12:00整,时针和分针在同一直线上,至少经过多长时间会再次出现时针和分针在同一直线上的现象?此时,时针和分针各转动了多少度?。
认识人民币的单位与换算方法

以下是人民币的单位换算方法:
1. 元、角、分的关系:
1元= 10角
1角= 10分
1元= 100分
2. 人民币单位换算举例:
5元6角可以换算为:5元+ 0.6元= 5.6元
3角8分可以换算为:0.3元+ 0.08元= 0.38元
3. 大额货币单位换算:
1元= 1000分(分是元的低级单位)
1元= 0.1千克(千克是元的等价单位)
1元= 10000毫秒(毫秒是时间单位,与元无关,这里只是举例说明单位换算)4. 时间单位换算:
1世纪= 100年
1年= 12月
1月= 30天(小月)或31天(大月)
1天= 24小时
1小时= 60分钟
1分钟= 60秒
5. 常用的人民币换算表:
1元= 10角= 100分
1千米= 1000米= 10000分米= 100000厘米= 1000000毫米
1平方米= 100平方分米= 10000平方厘米= 1000000平方毫米
1立方米= 1000立方分米= 1000000立方厘米= 1000000000立方毫米。
一年级数学题元角分单位换算

角
9元7角=
角
5元=
角
7元2角=
角
7角8分=
分
8元2角=
角
3元4角=
角
3元1角=
角
5元7角=
角
6元=
角
9元8角=
角
6角2分=
分
9元8角=
角
8元3角=
角
6元7角=
角
4元8角=
角
3角6分=
分
6角3分=
分
5角7分=
分
6角9分=
分
1元=
角
1元7角=
角
2元=
角
8元1角=
角
9元4角=
角
7角4分=
分
6元5角=
角
8角6分=
分 6角8分=
分 1元2角=
角 4角3分=
分
数 学 题
8元7角=
角 4角=
分
8元4角=
角 5元5角=
角
5元=
角
7元8角=
角 9角7分=
分 5角2分=
分
2角=
分
1角7分=
分 3元3角=
角 9角2分=
分
3角4分=
分 4元7角=
角 4角4分=
分 7角2分=
分
8角2分=
分 6角=
分
7角3分=
分 6元1角=
角
分 9元9角=
角
6角7分=
分 4角7分=
分 6角5分=
分 7元7角=
角
2角2分=
分 9角6分=
分 9元5角=
角 4角8分=
分
3角2分=
分 3角9分=
单位换算大全

单位
一长度单位:公里(km)、米(m)、分米(dm)、厘米(cm)、毫米(mm)、微米(um) 单位换算:
1毫米=1000微米
1厘米=10 毫米
1分米=10 厘米
1米 = 10分米
1米=1000 毫米
1米 = 100厘米
1千米=1000 米
二面积单位:平方毫米、平方厘米、平方分米、平方米、平方千米单位换算:
1平方厘米=100 平方毫米
1平方分米=100平方厘米
1平方米=100 平方分米
1公倾=10000 平方米
1平方公里=100 公顷
三体积和容积
体积:就是物体所占空间的大小。
容积:箱子、油桶、仓库等所能容纳物体的体积,通常叫做它们的容积。
常用单位:立方米、立方分米、立方厘米
容积单位:升、毫升
单位换算 :
1立方米=1000立方分米
1立方分米=1000立方厘米
1升=1000毫升
1升=1立方米
1毫升=1立方厘米
四质量单位:吨、千克、克
单位换算:一吨=1000千克 1千克=1000克
五时间单位:世纪年月日时分秒
单位换算:1天= 24小时 1小时=60分一分=60秒
六货币
常用单位:元、角、分
单位转换:1元=10角 1角=10分 1元=100分。
元角分换算公式大全

元角分换算公式大全一、角和分的关系1角(简称:角)是人民币货币单位,符号为“¥”。
100角等于1元。
2分(简称:分)是人民币辅助货币单位,符号为“分”。
100分等于1角,1000分等于1元。
二、元和角的换算公式1元换算成角的公式:角=元×102角换算成元的公式:元=角÷10三、元和分的换算公式1元换算成分的公式:分=元×1002分换算成元的公式:元=分÷100四、角和分的换算公式1角换算成分的公式:分=角×102分换算成角的公式:角=分÷10五、举例说明1例如,将50元换算成角:50元×10=500角2例如,将200角换算成元:200角÷10=20元3例如,将50元换算成分:50元×100=5000分4例如,将500分换算成元:500分÷100=5元5例如,将80角换算成分:80角×10=800分6例如,将600分换算成角:600分÷10=60角六、其他转换除了上述四种基本换算关系外,还有一些较为特殊的换算关系:1角和分之间的常见转换:1角换算成分:1角=10分2角换算成分:5角=50分3角换算成分:9角=90分4角换算成分:11角=110分5角换算成分:18角=180分2元和角之间的常见转换:1元换算成角:1元=10角2元换算成角:5元=50角3元换算成角:9元=90角4元换算成角:11元=110角5元换算成角:18元=180角3元和分之间的常见转换:1元换算成分:1元=100分2元换算成分:5元=500分3元换算成分:9元=900分4元换算成分:11元=1100分5元换算成分:18元=1800分。
万能角度尺一度等于多少分
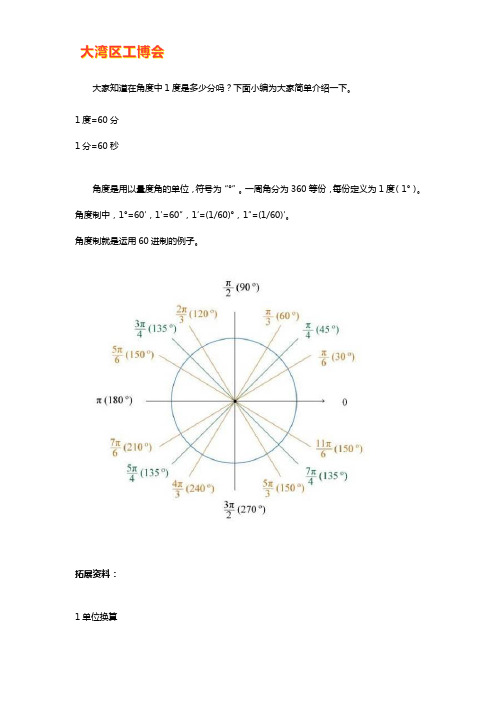
大家知道在角度中1度是多少分吗?下面小编为大家简单介绍一下。
1度=60分1分=60秒角度是用以量度角的单位,符号为“°”。
一周角分为360等份,每份定义为1度(1°)。
角度制中,1°=60′,1′=60″,1′=(1/60)°,1″=(1/60)′。
角度制就是运用60进制的例子。
拓展资料:1单位换算角度制中,1°=60′,1′=60″,1′=(1/60)°,1″=(1/60)′。
角度制就是运用60进制的例子。
2运算法则两个角相加时,°与°相加,′与′相加,″与″相加,其中如果满60则进1。
两个角相减时,°与°相减,′与′相减,″与″相减,其中如果不够则从上一个单位退1当作60。
3位制定义用度(°)、分(′)、秒(″)来测量角的大小的制度叫做角度制。
角度制:规定周角的360分之一为1度的角,用度作为单位来度量角的单位制叫做角度制。
单位换算角度制中,1°=60′,1′=60″,1′=(1/60)°,1″=(1/60)′。
角度制就是运用60进制的例子。
运算法则两个角相加时,°与°相加,′与′相加,″与″相加,其中如果满60则进1。
两个角相减时,°与°相减,′与′相减,″与″相减,其中如果不够则从上一个单位退1当作60。
读数方法:万能角度尺的读数方法,和游标卡尺相同,先读出游标零线前的角度是几度,再从游标上读出角度“分”的数值,两者相加就是被测零件的角度数值。
在万能角度上,基尺是固定在尺座上的,角尺是用卡块固定在扇形板上,可移动尺是用卡块固定在角尺上。
若把角尺拆下,也可把直尺固定在扇形板上。
由于角尺和直尺可以移动和拆换,使万能角度尺可以测量0º~320º的任何角度。
角尺和直尺全装上时,可测量0º~50º的外角度,仅装上直尺时,可测量50º~140º的角度,仅装上角尺时,可测量140º~230’的角度,把角尺和直尺全拆下时,可测量230º~320º的角度(即可测量40º~130º的内角度)。
[讲解]04角度换算1
![[讲解]04角度换算1](https://img.taocdn.com/s3/m/16422c06c4da50e2524de518964bcf84b9d52d7d.png)
000000000定义:用度(°)、分(′)、秒(″)来测量角的大小的制度叫做角度制。
00000000角度制:规定周角的360分之一为1度的角,用度作为单位来度量角的单位制叫做角度制。
00000000单位换算0000000000角度制中,1°=60′,1′=60″,1′=(1/60)°,1″=(1/60)′,1°=60′=3600″0000000角度制就是运用60进制的例子000000000运算法则0000000000两个角相加时,°与°相加,′与′相加,″与″相加,其中如果满60则进1。
0 0000000两个角相减时,°与°相减,′与′相减,″与″相减,其中如果不够则从上一个单位退1当作60000000000例题: 1)度分秒与小数角度度之间换算:* a°b‘c“=(a+b/60+c/3600)°或先将秒化成分,再将分化成度(/60).* 先将角的小数部分化成分,再将分的小数部分化成秒( X 60).50度41分20秒=?°12°24’36”= ?°12.2436°=?°?'?“2)角度(度分秒)的四则运算:00000000(1)16°23′6″+23°18′17″=_____°_____′_____″;(2)180°-70°40′=_____°_____′;(3)22°16′×5=_____°_____′;(4)22.24°=_____°_____′_____″.00000000(5)(90°-21°31′24″)÷250度41分20秒=50°+(41/60)°+(20/3600)°=(2281/45)°约等于50.69°00000000012°24’36”=12+24/60+36/3600=12+0.4+0.01=12.41°12.2436°=12°+0.2436x60‟=12°+14.616‟=12°14…+0.616x60”=12°14…+36.96“=12°20'36.96“0000000000。
【精选】角和角的单位换算

以度,分,秒为单位的角的度量制 叫做角度制。
1度=60分
1分=60秒
1秒= 1 分
60
1秒= 1 度
3600
1°=60 ′
1′=60″.
1 ″ = 1′
60
1′= ° 、分、秒。
(2)它们之间的关系是六十进制的。 即1°=60′, 1′=60″.
它们之间的转化方法: 由高级单位向低级单位转化时用乘法逐级进行 由低级单位向高级单位转化时用除法逐级进行。
4.3.1角的单位换算
学习目标
1.x 会进行度、分、秒之间的 换算。
自学指导
(1)角的度量单位有哪些?它们的符 号如何表示? (2)度·分·秒之间是如何换算的?
把1度的角60等分,每一份所对的角叫做 1分角 。记作 “1 ′” 即1°=60′ 把1分的角60等分,每一份所对的角叫做 1 秒角。 记作 “1″ ” 即1′=60″
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)APO ( 6) ∠ P
将图中的角用不同的方法表示 出来,并填写下表
B
5 4 3
∠2 ∠3
∠BAC
2 C
D
∠1
∠BCE
A
1
∠5
E
∠4
∠DAB
∠ACB
∠ABC
如图,回答下列问题.
(1)∠ABD与∠ABC 是同一个角吗? (2)能用一个大写字 母表示的角有几个?
A
B
D
C
(3)以点A为顶点的角有哪几个? 以D点为顶点的角呢?
思 考
射线 OA绕点O 旋转90度后, B 终边OB和始边 OA垂直时,所 直角 成的角叫做 。
O B O A B
A
射线 OA绕点O旋转180度后,终边OB和始边 OA 成一直线时,所成的角叫做 平角 ;
O
A
射线 OA绕点O 旋转360度后,回到原来的位置时, 所成的角叫做 周角。
说明:
在不做特别说明的情况下,我们说的角 都指不大于平角的角
若∠AOB内没有射线,则图中一共有
1
个角。 个角。 个角。 66 个角。
若∠AOB内有1条射线,则图中一共有 3 若∠AOB内有2条射线,则图中一共有 …… 若∠AOB内有10条射线,则图中一共有 6
A
A2 A1
O
B
小结
角的定义
1、角是由两条具有公共端点的射线组成的图形。 2、角可以看作是一条射线绕着它的端点旋转而 成的.
判断题: (1)两条射线组成的图形叫角。 (2)角的大小与边的长短无关。 (3)角的 两边是两条射线。
角用“∠”表示,读做“角”。角 的表示方法有下面四种: (1)角可以用三个大写字母表示但表示 顶点的字母一定写在中间
(2) 用一个字母表示角,但必须是以这个 字母为顶点的角只有一个
(3) 用一个数字表示角,在靠近顶点 处画上弧线,写上数字 (4)也可用一个希腊字母表示,并在 靠近顶点处画上弧线,写上希腊字 母
牛刀小试
把图中的角表示成下列形式:
①∠APO ②∠AOP ③∠OPC, ④∠O ⑤∠COP ⑥∠P。 其中正确的有___________(把你认为正确的 序号都填上。) C A P
O
把图中的角表示成下列形式,哪些正确, 哪些不正确? C
A P M
O
(1)∠MPC (4)∠OAP
(2)∠AOP ( 5) ∠ O
C
∠AOB = ∠BOC + ∠AOC
A O B
解: ∠BOC= ∠AOB- ∠AOC=180°- 53°17′ =126°43′
小结: (1):角的度量单位是度、分、秒。 (2)它们之间的关系是六十进制的。 即1°=60′, 1′=60″.
它们之间的转化方法: 由高级单位向低级单位转化时用乘法逐级进行 由低级单位向高级单位转化时用除法逐级进行。
把1度的角60等分,每一份所对的角叫做 1分角 。记作 “1 ′” 即1°=60′ 把1分的角60等分,每一份所对的角叫做 1 秒角。 记作 “1″ ” 即1′=60″
角的度量单位:度 、分、秒.
以度,分,秒为单位的角的度量制 叫做角度制。
1度=60分 1分=60秒
1 1秒= 分 60
1 1秒= 度 3600
1°=60 ′ 1″=
1 ′ 60
1′=60″. 1′=
1 °. 60
问题1: 3.32小时= 3 小时 19 分 12 秒; 3.32度= 3 度 19 分 12 秒.
问题2:12小时9分36秒=
12.16
小时;
12 9 36
'
'' =
Hale Waihona Puke 12.16 度结论:由度化分,由分化秒,只要乘以60 即可;由秒化分,由分化度,只要除以60 就行。
角的表示方法
表示方法 注意事项
表示顶点的字母要写 1、用三个大写的字母表示 在中间 2、用一个顶点的字母来 一个字母只表示一个角 表示 在靠近顶点的处画上弧线, 3、用一个数字 并写上数字 在靠近顶点的处画上弧线, 4、希腊字母表示 并写上希腊字母
把半圆分成180等份,每一份所对的角 叫做 一度角 。记作 “ 1° ” 。
例1: 用度、分、秒表示: ⑴0.75°= 45 ′= 2700 ″ 4 960 ⑵(-)°= 16 ′= ″
15
例题讲解
⑶16.24°= 16 ° ⑷34.37°= 34 °
14 ′ 22 ′
24 ″ 12 ″
用度表示: ⑴1800″= 0.5 ° 0.8 ° ⑵48′= 39.6 ° ⑶39°36′= ⑷27°14′=
它们给我们怎样的图形印象
判断下列哪些图形是角
(√)
(×)
(√)
(√)
角的定义(1)
静态角的定义
角是由两条具有公共端点的射线组成的图形。
射线 边
顶点
射线 边
角也可以看做一条射线绕端点旋转所 组成的图形。
角的定义2:
角也可以看作由一条射线绕着它的端点旋转 而形成的图形. 角的终边 B
角 O
A
角的始边
7 27 30 °
讨论 3 ° 15′ 与3 . 15°相等吗?
(选做题) (1)过25 min,钟表的分针转过了多少 度的角?时针呢? (2)5时30分,钟表的时针和分针构 成多少度的角?8时20分呢?1时15分呢?
例题讲解
例3:如图O是直线AB上一点, ∠AOC=53°17′∠BOC度数 分析:(1) AB是直线 , ∠AOB 是什么角? ∠AOB是平角,等于180° (2)∠BOC 、 ∠AOB 、 ∠AOC之间有什么关系?
