南京邮电大学数据结构A第5章
数据结构第五章 查找 答案

数据结构与算法上机作业第五章查找一、选择题1、若构造一棵具有n个结点的二叉排序树,在最坏情况下,其高度不超过 B 。
A. n/2B. nC. (n+1)/2D. n+12、分别以下列序列构造二叉排序数(二叉查找树),与用其他3个序列所构造的结果不同的是 C :A. (100, 80, 90, 60, 120, 110, 130)B. (100, 120, 110, 130, 80, 60, 90)C. (100, 60, 80, 90, 120, 110, 130)D. (100, 80, 60, 90, 120, 130, 110)3、不可能生成下图所示的二叉排序树的关键字的序列是 A 。
A. 4 5 3 1 2B. 4 2 5 3 1C. 4 5 2 1 3D. 4 2 3 1 54、在二叉平衡树中插入一个结点造成了不平衡,设最低的不平衡点为A,并已知A的左孩子的平衡因子为0,右孩子的平衡因子为1,则应作 C 型调整使其平衡。
A. LLB. LRC. RLD. RR5、一棵高度为k的二叉平衡树,其每个非叶结点的平衡因子均为0,则该树共有 C 个结点。
A. 2k-1-1B. 2k-1+1C. 2k-1D. 2k+16、具有5层结点的平衡二叉树至少有 A 个结点。
A. 12B. 11C. 10D. 97、下面关于B-和B+树的叙述中,不正确的是 C 。
A. B-树和B+树都是平衡的多叉树B. B-树和B+树都可用于文件的索引结构C. B-树和B+树都能有效地支持顺序检索D. B-树和B+树都能有效地支持随机检索8、下列关于m阶B-树的说法错误的是 D 。
A. 根结点至多有m棵子树B. 所有叶子结点都在同一层次C. 非叶结点至少有m/2(m为偶数)或m/2+1(m为奇数)棵子树D. 根结点中的数据是有序的9、下面关于哈希查找的说法正确的是 C 。
A. 哈希函数构造得越复杂越好,因为这样随机性好,冲突小B. 除留余数法是所有哈希函数中最好的C. 不存在特别好与坏的哈希函数,要视情况而定D. 若需在哈希表中删去一个元素,不管用何种方法解决冲突都只要简单地将该元素删去即可10、与其他查找方法相比,散列查找法的特点是 C 。
南邮_数据结构课后习题答案讲解

?
?
?1 4 7 ?
?
?
?4 4 9 ?
?4 4 9 ?
4.7 求对题图4-1的稀疏矩阵执行矩阵转置时数组
num[]和k[]的值。
col
0
1
2
3
4
num[col] 1
0
2
1
2
k[col]
0
1
1
3
4
2020/2/8
14
第六章 习题讲解
6-2. 对于三个结点 A,B和C,可分别组成多少不同 的无序树、有序树和二叉树?
int i,j,sum=0;
for (i=0;temp[i]<x&&i<n;i++); //找到首个大于等于 x的元素位置 i
if(i>n-1) return; //没有符合条件的元素
ffoorr ((jj==ii;;ljs<tn[j;]<) =y&&j<n;j++); if (lst[j]>y//)找到首个//大大于于yy的的元元素素前位移置 j
?0 0 ???3 0
6 0
0 0
0? 7??
行三元组:???10
2 0
6 ?列三元组:?1
? 3??
??0
0 2
?3?
6
? ?
? 0 0 0 0 0?
?1 4 7 ?
?3 2 ?8?
? ?
0
0 ? 8 10 0??
??3 2 ?8??
??3
3
10
? ?
?? 0 0 0 0 9??
?3 3 10 ?
(2)void Search_Delete(List *lst, T x,T y)
数据结构 5数组和广义表A
1 Status Locate(Array A,va_list ap,int &off) 2{ 3 //若ap指示的各下标值合法,则求出该元素在A中,相对地
址off
4 off=0; 5 for(i=0;i<A.dim;++i) 6 { 7 ind=va_arg(ap,int); 8 if(ind<0||ind>A.bounds[i]) return OVERFLOW; 9 off+=A.constants[i] *ind; 10 } 11 return OK; 12 }
行数 总列数,即 第2维长度 元素个数
ij
补充:计算二维数组元素地址的通式
设一般的二维数组是A[c1..d1, c2..d2],这里c1,c2不一定是0。
单个元素 长度
二维数组列优先存储的通式为: LOC(aij)=LOC(ac1,c2)+[(j-c2)*(d1-c1+1)+i-c1)]*L
6
例1〖软考题〗:一个二维数组A[1..6, 0..7],每个数组元素
16
5.4
1、定义:
广义表的定义
广义表是线性表的推广,也称为列表(lists) 记为: LS = ( a1 , a2 , ……, an ) 广义表名 表头(Head) 表尾 (Tail) n是表长
在广义表中约定:
① 第一个元素是表头,而其余元素组成的表称为表尾; ② 用小写字母表示原子类型,用大写字母表示列表。
13
1 Status Value(Array A,ElemType &e,…){ 2 //A是n维数组,e为元素变量,随后是n个下标值,若各下
标不超界,则e赋值为所指定的A的元素值,即将指定元素值 读到e变量中。
数据结构答案第5章

第 5 章树和二叉树1970-01-01第 5 章树和二叉树课后习题讲解1. 填空题⑴树是n(n≥0)结点的有限集合,在一棵非空树中,有()个根结点,其余的结点分成m(m>0)个()的集合,每个集合都是根结点的子树。
【解答】有且仅有一个,互不相交⑵树中某结点的子树的个数称为该结点的(),子树的根结点称为该结点的(),该结点称为其子树根结点的()。
【解答】度,孩子,双亲⑶一棵二叉树的第i(i≥1)层最多有()个结点;一棵有n(n>0)个结点的满二叉树共有()个叶子结点和()个非终端结点。
【解答】2i-1,(n+1)/2,(n-1)/2【分析】设满二叉树中叶子结点的个数为n0,度为2的结点个数为n2,由于满二叉树中不存在度为1的结点,所以n=n0+n2;由二叉树的性质n0=n2+1,得n0=(n+1)/2,n2=(n-1)/2。
⑷设高度为h的二叉树上只有度为0和度为2的结点,该二叉树的结点数可能达到的最大值是(),最小值是()。
【解答】2h -1,2h-1【分析】最小结点个数的情况是第1层有1个结点,其他层上都只有2个结点。
⑸深度为k的二叉树中,所含叶子的个数最多为()。
【解答】2k-1【分析】在满二叉树中叶子结点的个数达到最多。
⑹具有100个结点的完全二叉树的叶子结点数为()。
【解答】50【分析】100个结点的完全二叉树中最后一个结点的编号为100,其双亲即最后一个分支结点的编号为50,也就是说,从编号51开始均为叶子。
⑺已知一棵度为3的树有2个度为1的结点,3个度为2的结点,4个度为3的结点。
则该树中有()个叶子结点。
【解答】12【分析】根据二叉树性质3的证明过程,有n0=n2+2n3+1(n0、n2、n3分别为叶子结点、度为2的结点和度为3的结点的个数)。
⑻某二叉树的前序遍历序列是ABCDEFG,中序遍历序列是CBDAFGE,则其后序遍历序列是()。
【解答】CDBGFEA【分析】根据前序遍历序列和后序遍历序列将该二叉树构造出来。
数据结构(陈慧南编 C++描述)南京邮电大学 课后答案 DS习题答案01

www.khd课后a答w案.网com
bool LinkedStack<T>::Push(const T x) {
Node <T> *q=new Node<T>; q->data=x; q->link=top; top=q; return true; }
template <class T> bool LinkedStack<T>::Pop() {
Node<T> *q; while (top){
q=top->link; delete top; top=q; } }
第四章 数组与字符串
1. 给出三维数组元素 A[i][j][k]的存储地址 loc(A[i][j][k])。 答: 设有三维数组声明为 A[n1][n2][n3],每个元素占 k 个存储单元,则
Node<T> *q; while (top){
q=top->link; delete top; top=q; } }
template <class T> bool LinkedStack<T>::IsEmpty() const {
return !top; }
template <class T> bool LinkedStack<T>::IsFull() const {
www.khd课后a答w案.网com
第一章 绪论
1.( 第 18页,第(5)题) 确定下列各程序段的程序步,确定划线语句的执行次数,计算它们的渐近时间复杂度。
(1) i=1; k=0; do { k=k+10*i; i++; } while(i<=n-1) 划线语句的执行次数为 n-1 。
数据结构第五章图习题

05 图【单选题】1. 设无向图G 中有五个顶点,各顶点的度分别为2、4、3、1、2,则G 中边数为(C )。
A、4条 B、5条 C、6条 D、无法确定2. 含n 个顶点的无向完全图有(D )条边;含n 个顶点的有向图最多有(C )条弧;含n 个顶点的有向强连通图最多有(C )条弧;含n 个顶点的有向强连通图最少有(F)条弧;设无向图中有n 个顶点,则要接通全部顶点至少需(G )条边。
A 、n 2B 、n(n+1)C 、n(n-1)D 、n(n-1)/2E 、n+1F 、nG 、n-13. 对下图从顶点a 出发进行深度优先遍历,则(A )是可能得到的遍历序列。
A 、acfgdebB 、abcdefgC 、acdgbefD 、abefgcd对下图从顶点a 出发进行广度优先遍历,则(D )是不可能得到的遍历序列。
A 、abcdefgB 、acdbfgeC 、abdcegfD 、adcbgef4. 设图G 的邻接矩阵A=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡010101010,则G 中共有(C )个顶点;若G 为有向图,则G 中共有(D )条弧;若G 为无向图,则G 中共有(B )条边。
A 、1B 、2C 、3D 、4E 、5F 、9G 、以上答案都不对5. 含n 个顶点的图,最少有(B )个连通分量,最多有(D )个连通分量。
A 、0B 、1C 、n-1D 、n6. 用邻接表存储图所用的空间大小(A )。
A 、与图的顶点数和边数都有关B 、只与图的边数有关C 、只与图的顶点数有关D 、与边数的平方有关7. n 个顶点的无向图的邻接表最多有(B )个表结点。
A 、n 2B 、n(n-1)C 、n(n+1)D 、n(n-1)/28. 无向图G=(V ,E),其中:V={a,b,c,d,e,f},E={(a,b),(a,e),(a,c),(b,e),(c,f),(f,d),(e,d)},对该图进行深度优先遍历,得到的顶点序列正确的是(D )。
数据结构A第1章(南邮)

程序步数为2n+3。
41
1.5.3 渐近时间复杂度
渐近时间复杂度
使用大 O 记号表示的算法的时间复杂性,称为算法的渐
近时间复杂度,简称时间复杂度。
大O记号 如果存在两个正常数 c 和 n0 ,使得对所有的 n , nn0 ,有 f(n) c g(n) 则有 f(n)=O(g(n))。
42
渐近时间复杂度 使用大 O 记号表示的算法的时间复杂性,称为算法的渐
结点存储块分成两部分,元素本身和该元素后继元素所 在结点的存储地址。
Data
Link
20
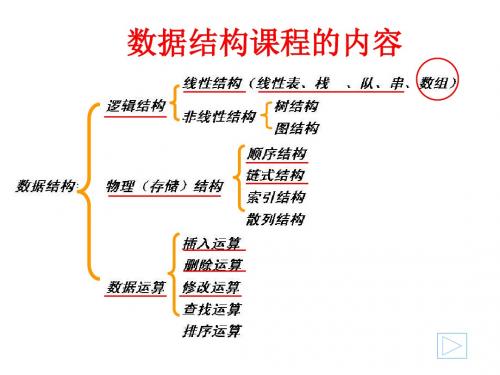
小结
逻辑结构 概念
面向 关系
存储结构 数据及其关系在计 算机内的组织方式 面向计算机
数据元素之间逻 辑关系的描述 面向应用问题
存储结构是逻辑结构在计算机内的映像
21
1.2.4 数据结构的运算
• 数据结构最常见的运算 创建运算:创建一个数据结构; 清除运算:删除数据结构中的全部元素; 插入运算:在数据结构的指定位置上插入一 个新元素; 删除运算:将数据结构中的某个元素删除; ……
2.
数据类型 一个数据类型定义了一个值的集合以及作 用于该值集的操作的集合。 即一组值和一组操作。
26
3.抽象数据类型 抽象数据类型( Abstract Data Type, ADT )是一个 数据类型,其主要特征是该类型的对象及其操作的规 范 , 与该类型对象的表示和操作的实现分离,实行封 装和信息隐蔽,即使用和实现分离。 使用和实现分离:使用者通过规范使用该类型的数据,
南邮计算机网络课后答案第五章资料

第五章传输层5—01 试说明运输层在协议栈中的地位和作用,运输层的通信和网络层的通信有什么重要区别?为什么运输层是必不可少的?答:运输层处于面向通信部分的最高层,同时也是用户功能中的最低层,向它上面的应用层提供服务运输层为应用进程之间提供端到端的逻辑通信,但网络层是为主机之间提供逻辑通信(面向主机,承担路由功能,即主机寻址及有效的分组交换)。
各种应用进程之间通信需要“可靠或尽力而为”的两类服务质量,必须由运输层以复用和分用的形式加载到网络层。
5—02 网络层提供数据报或虚电路服务对上面的运输层有何影响?答:网络层提供数据报或虚电路服务不影响上面的运输层的运行机制。
但提供不同的服务质量。
5—03 当应用程序使用面向连接的TCP和无连接的IP时,这种传输是面向连接的还是面向无连接的?答:都是。
这要在不同层次来看,在运输层是面向连接的,在网络层则是无连接的。
5—04 试用画图解释运输层的复用。
画图说明许多个运输用户复用到一条运输连接上,而这条运输连接有复用到IP数据报上。
5—05 试举例说明有些应用程序愿意采用不可靠的UDP,而不用采用可靠的TCP。
答:VOIP:由于语音信息具有一定的冗余度,人耳对VOIP数据报损失由一定的承受度,但对传输时延的变化较敏感。
有差错的UDP数据报在接收端被直接抛弃,TCP数据报出错则会引起重传,可能带来较大的时延扰动。
因此VOIP宁可采用不可靠的UDP,而不愿意采用可靠的TCP。
5—06 接收方收到有差错的UDP用户数据报时应如何处理?答:丢弃5—07 如果应用程序愿意使用UDP来完成可靠的传输,这可能吗?请说明理由答:可能,但应用程序中必须额外提供与TCP相同的功能。
5—08 为什么说UDP是面向报文的,而TCP是面向字节流的?答:发送方UDP 对应用程序交下来的报文,在添加首部后就向下交付IP 层。
UDP 对应用层交下来的报文,既不合并,也不拆分,而是保留这些报文的边界。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
补充: 等比数列的求和公式是 1 a n 1 1 a a a ... a 1 a
2 3 n
5.2 二叉树
5.2.2 二叉树的性质
5.2 二叉树
5.2.2 二叉树的性质
性质5.3 包含n个元素的二叉树的高度至少为 log2 (n+1) 根据性质 2 ,高度为 h 的二叉树最多有 2h –1 个结点(性质 2 ) ,因而n2h –1, 则有h log2(n+1)。 由于h是整数,所以h log2 (n+1)。
5.2 二叉树
5.2.1 二叉树的定义 树与二叉树的区别:
⑴ 树不能是空树,即至少有一个根结点。而二叉树可 以是空树。 ⑵ 一般树的子树之间是无序的。而二叉树中结点的子 树要区分左、右子树,即使只有一棵子树。 E F E F
⑶ 树中每个节点可有0棵或若干子树。而二叉树的每个
节点最多只能有2棵子树。
树不为空集合,树中至少有一个根结点,根结点没有前 驱,其余结点都有唯一的前驱结点。因此树形成层次结构。
5.1 树的基本概念
5.1.1 树的定义 1、树的定义
(1)有且仅有一个结点r∈D, 不存在任何结点v∈D,v≠r,使 得<v, r>∈R,称r为树的根。 (2)除根r以外的所有结点 u∈D,都有且仅有一个结点v ∈D, v≠u,使得<v,u>∈R。 D = {A, B, C, D, E, F, G} R = {<E, A>, <E, F>, <E, B>, <A,G>, <F, C>, <F, D>} ( 1) r = E (2)对于 u = F , 只有 v = E, 使得<v, u> ∈ R E A G C F D B
2 1
G
C
L N
D
J
3
4
5
5.1 树的基本概念
5.1.2 基本术语
无序树:如果树中结点的各子树之间的次序是不重要的, 可以交换位置。 下列是同一棵无序树: E E
A
G C
F
D
B
B
F
A
D
J
C G
L
L
M N
J
N
M
将左边树中所有结点的子树互换次序就是右边的树。
5.1 树的基本概念
5.1.2 基本术语
有序树:如果树中结点的各棵子树看成是从左到右有次序 的,则称该树为有序树。 下列是二棵有序树:
性质5.5 具有n个结点的完全二叉树的高度为log2 (n+1)。 性质2 高度为h的二叉树上至多有2h –1个结点。 证明:根据性质2
高度为h-1的完全二叉树结点个数最多为2h-1-1
高度为h的完全二叉树结点个数最多为2h-1 ① 高度为h的完全二叉树结点个数取值范围[2h-1 , 2h) ② 2h-1≤n<2h ② ① 2h-1 - 1< n ≤ 2h – 1 log2n<h ≤ log2n+1 log2(n+1) ≤ h<log2(n+1)+1 ∵h是整数 ∴h= h = log2 (n+1) log 2 n 1 结论: ⑴ n个结点的二叉树中完全二叉树最矮,高度为log2 (n+1)。 ⑵ n个结点的完全二叉树和二叉判定树的高度是一样的
5.2 二叉树
5.2.1 二叉树的定义
定义5.3
二叉树(binary tree)是结点的有限集合,该集合或 者为空集,或者是由一个根和两个互不相交的、称为该根 的左子树和右子树的二叉树组成。 上述定义表明二叉树可以为空集,因此,二叉树有 5 种基本形态。
(a)
(b)
(c)
(d)
(e)
图5-4 二叉树的五种基本形态
log 2 n 1
5.2 二叉树
5.2.2 二叉树的性质:完全二叉树的性质
性质5.6 假定对一棵有n个结点的完全二叉树中的结点,按从上 到下、从左到右的顺序,从0到n-1编号(见图5.6(c)),设树中 一个结点的序号为i,0i<n ,则有以下关系成立: (1)当i=0时,该结点为二叉树的根。 (2)若i>0,则该结点的双亲的序号为(i-1)/2 (3)若2i+1<n,则该结点的左孩子的序号为2i+1,否则该结点 无左孩子。 (4)若2i+2<n,则该结点的右孩子的序号为2i+2,否则该结点 0 无右孩子。 0 1 3 4 5 2 6 3
5.2 二叉树
5.2.2 二叉树的性质
性质5.4 任意一棵二叉树中,若叶结点的个数为n0,度为2 的结点的个数为n2,则必有n0=n2+1。 设二叉树的度为1的结点数为n1,树中结点总数为n,
则n=n0+n1+n2 ……①
(∵二叉树中只有度为0、1、2三种类型的结点) 设分支数为B,n个结点的二叉树,除了根结点外,每个结点 都有一个分支进入,则B=n-1 ;分支是由度为 1或者度为2的 射出的,又有B=2n2+n1; 则有:n-1=2n2+n1 n=2n2+n1+1……② 由① ②可得到: n0+n1+n2=2n2+n1+1 n0+n2=2n2 +1 即n2=n0-1。
5.2 二叉树
• 二叉树是非常重要的树形数
据结构。
• 很多从实际问题中抽象出来
的数据是二叉树形的;以后 我们将看到任意树或森林可 方便地转换成二叉树,从而 为一般树和森林的存储和处 理提供了有效方法。
5.1 5.2 5.3 5.5 5.7 课堂提要 第 5章 树 树的基本概念 二叉树 二叉树的遍历 树和森林 哈夫曼树和哈 夫曼编码
E
F D B
L
M N
J
结点G和C互为兄弟否?
5.1 树的基本概念
5.1.2 基本术语
后裔(decendent):一个结点的 所有子树上的任何结点都是该结 点的后裔。
结点C的后裔为:L、M、N。 祖先(ancestor):从根结点到 某个结点的路径上的所有结点 都是该结点的祖先。 结点L的祖先为:E、F、C。 M N A G C
5.2 二叉树
5.1.2 基本术语 二叉树应用实例
• 设有序表为(21,25,28,33,36,45),现在要在表
中查找元素33。 方法一:顺序搜索。效率低,平均比较一半的元素。 (21,25,28,33,36,45) 33 比较了4次! 方法二:改进结构,组织成树形结构。比较次数不会超 33 过树高,提高了效率。 28 21 25 33 36 45 比较了3次!
图5.6 几种特殊的二叉树
0 2 5 12 13 1 2
6
14
3
4 8 9
9
5
6
7
(b)完全二叉树
5.2 二叉树
5.2.2 二叉树的性质
定义5.6 扩充二叉树也称2-树,其中除叶子结点外,其 余结点都必须有两个孩子。
53
23 11 30
12
13
8 3
17
9 5
5.2 二叉树
5.2.2 二叉树的性质:完全二叉树的性质
5.1.1 树的定义
• 层次结构的数据在现实自然界中大量存在。
国家、省、市、县和区。
书的章节、回目。 上级和下级。 整体和部分。 祖先和后裔。
5.1 5.2 5.3 5.5 5.7 课堂提要 第 5章 树 树的基本概念 二叉树 二叉树的遍历 树和森林 哈夫曼树和哈 夫曼编码
5.1 树的基本概念
E
A G C L M N F D J B B D J
E F A C G L N M
有序树的各子树从左到右为第一棵子树、第二棵,…
5.1 树的基本概念
5.1.2 基本术语
森林:是树的集合。0个或多个不相交的树组成森林。 果园或有序森林:有序树的有序集合。
若将树中的根去掉,则得到根的子树组成的森林。 若增加一个结点,将森林中各树的根作为新增结点的 孩子,则森林即成为树。 E A G C L M N F D J B
1
4 5
2 6
7 8 9 10 11 12 13 14
(a)满二叉树
7 8 9 (b)完全二叉树
5.2 二叉树
5.2.3 二叉树ADT
ADT BinaryTree{ Data: 二叉树是结点的有限集合,该集合或者为空集,或者是由一个根 和两个互不相交的称为该根的左子树和右子树的二叉树组成。 Operations: Create(): 创建一棵空二叉树。 Destroy(): 撤销一棵二叉树。 IsEmpty():若二叉树空,则返回true,否则返回false。 Clear(): 移去所有结点,成为空二叉树。 Root(x):取x为根结点;若操作成功,则返回true,否则返回false MakeTree(x,left,right):创建一棵二叉树,x为根结点,left为 左子树,right为右子树。 BreakTree(x ,left, right):拆分二叉树为三部分,x为根的值, left和right分别为原树的左右子树 PreOrder: 使用函数Visit访问结点,先序遍历二叉树。 InOrder: 使用函数Visit访问结点,中序遍历二叉树。 PostOrder:使用函数Visit访问结点,后序遍历二叉树。 }
5.2 二叉树
5.2.2 二叉树的性质
性质5.2 高度为h的二叉树上至多有2h–1个结点。 当h=0时,二叉树为空二叉树。 当h>0时,利用性质1,高度为h的二叉树中结点的总数最多为:
性质1 二叉树的第 i (i 1)层上至多有2i 1个结点。
i 1 0 1 2 h 1 h 2 (2 2 2 ... 2 ) 2 1 i 1 h
