信号与线性系统分析复习题及答案.doc
信号与线性系统分析_(吴大正_第四版)习题答案12264精编版
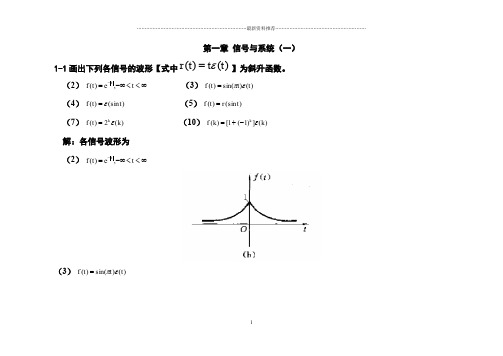
第一章 信号与系统(一)1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
(2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)((3))()sin()(t t t f επ=(4))fεt=(sin)(t(5))trf=(sin)(t(7))t(kf kε=)(2(10))f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
(1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f(5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε(2))2()1(2)()(-+--=t rt rt rtf(5))2()2()(ttrtf-=ε(8))]5()([)(--=k k k k f εε(11))]7()()[6sin()(--=k k k k f εεπ(12))]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是,确定其周期。
(2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+=解:1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。
信号与线性系统分析 (吴大正 第四版)第四章习题答案

第四章习题4、6 求下列周期信号得基波角频率Ω与周期T。
(1) (2)(3) (4)(5) (6)4、7 用直接计算傅里叶系数得方法,求图4-15所示周期函数得傅里叶系数(三角形式或指数形式)。
图4-154、10 利用奇偶性判断图4-18示各周期信号得傅里叶系数中所含有得频率分量。
图4-184-11 某1Ω电阻两端得电压如图4-19所示,(1)求得三角形式傅里叶系数。
(2)利用(1)得结果与,求下列无穷级数之与(3)求1Ω电阻上得平均功率与电压有效值。
(4)利用(3)得结果求下列无穷级数之与图4-194、17 根据傅里叶变换对称性求下列函数得傅里叶变换(1)(2)(3)4、18 求下列信号得傅里叶变换(1) (2)(3) (4)(5)4、19 试用时域微积分性质,求图4-23示信号得频谱。
图4-234、20 若已知,试求下列函数得频谱: (1) (3) (5)(8) (9)4、21 求下列函数得傅里叶变换(1)(3)(5)4、23 试用下列方式求图4-25示信号得频谱函数(1)利用延时与线性性质(门函数得频谱可利用已知结果)。
(2)利用时域得积分定理。
(3)将瞧作门函数与冲激函数、得卷积之与。
图4-254、25 试求图4-27示周期信号得频谱函数。
图(b)中冲激函数得强度均为1。
图4-274、27 如图4-29所示信号得频谱为,求下列各值[不必求出] (1) (2)(3)图4-294、28 利用能量等式计算下列积分得值。
(1) (2)4、29 一周期为T 得周期信号,已知其指数形式得傅里叶系数为,求下列周期信号得傅里叶系数(1) (2)(3) (4)4、31 求图4-30示电路中,输出电压电路中,输出电压对输入电流得频率响应,为了能无失真得传输,试确定R1、R2得值。
图4-304、33 某LTI系统,其输入为,输出为式中a为常数,且已知,求该系统得频率响应。
4、34 某LTI系统得频率响应,若系统输入,求该系统得输出。
信号与线性系统分析 (吴大正 第四版)第七章习题答案

7.3 如图7-5的RC 带通滤波电路,求其电压比函数)()()(12s U s U s H 及其零、极点。
7.7 连续系统a 和b ,其系统函数)(s H 的零点、极点分布如图7-12所示,且已知当∞→s 时,1)(=∞H 。
(1)求出系统函数)(s H 的表达式。
(2)写出幅频响应)(ωj H 的表达式。
7.10 图7-17所示电路的输入阻抗函数)()()(11s I s U s Z =的零点在-2,极点在31j ±-,且21)0(=Z ,求R 、L 、C 的值。
7.14 如图7-27所示的离散系统,已知其系统函数的零点在2,极点在-0.6,求各系数a,b。
7.18 图7-29所示连续系统的系数如下,判断该系统是否稳定。
(1)3,210==a a ; (2)3,210-=-=a a ; (3)3,210-==a a 。
7.19 图7-30所示离散系统的系数如下,判断该系统是否稳定。
(1)1,2110-==a a ; (2)1,2110==a a ;(3)1,2110=-=a a 。
7.20 图7-31所示为反馈系统,已知44)(2++=s s ss G ,K 为常数。
为使系统稳定,试确定K 值的范围。
7.26 已知某离散系统的差分方程为)1()2()1(5.1)(-=---+k f k y k y k y(1) 若该系统为因果系统,求系统的单位序列响应h(k)。
(2) 若该系统为稳定系统,求系统的单位序列响应h(k),并计算输入)()5.0()(k k f k ε-=时的零状态响应)(k y zs 。
7.28 求图7-36所示连续系统的系统函数)(sH。
7.30 画出图7-40所示的信号流图,求出其系统函数)(sH。
解(a)由s域系统框图可得系统的信号流图如图7-41(a)。
流图中有一个回路。
其增益为(b)由s 域系统框图可得系统的信号流图如图7-41(b)。
流图中有一个回路。
信与线性系统分析习题答案吴大正第四版高等教育出版社

第一章信号与系统(二)1-1画出下列各信号的波形【式中r(t)t(t)】为斜升函数。
(2)f(t) et t(3)f(t)sin( t) (t)(4)f (t) (sint)(5)f(t)r(sin t)(7)f(t) 2k (k)(10f(k) [1 ( 1)k] (k))解:各信号波形为(2)f(t) e N, t(3)f(t)sin( t)(t)(4)f(t)(s int)(5)f(t)r(si n t)(7)f(t)2k (k)(10)f(k)[1 (1)k] (k)1-2画出下列各信号的波形[式中r(t) t (t)为斜升函数]。
(1)f(t) 2 (t 1) 3 (t 1) (t 2) (2)f (t) r(t) 2r(t 1) r(t 2)(5)f (t) r(2t) (2 t) (8)f(k) k[ (k) (k 5)](11) f(k) ksin( )[ (k) (k 7)]6(12)f(k) 2k[ (3 k) ( k)]解:: 各信号波「形为(1) f(t) 2 (t 1) 3 (t 1) (t 2)(2) f(t) r(t) 2r(t 1) r(t2)(5) f(t)r(2t) (2 t)(8)f(k)k[ (k) (k 5)](11)f(k)ksin( § )[ (k) (k7)](12) f(k) 2k [ (3 k) ( k)]1-3写出图1-3所示各波形的表达式。
1-4写出图1-4所示各序列的闭合形式表达式。
1-5判别下列各序列是否为周期性的。
如果是,确定其周期。
Q■(2) f 2(k) cos(- k ) cos(—k )(5) f 5(t)3cost 2sin( t)4 4 3 6解:1-6已知信号f(t)的波形如图1-5所示,画出下列各函数的波形。
(6)f(0.5t 2)(1) f(t 1) (t) (2) f(t 1) (t 1) (5) f (1 2t)df (t) t(7) K ( 8) f(X)dx解:各信号波形为(1)f(t 1) (t)(2)f(t 1) (t 1)(5)f(1 2t)(6) f (0.5t 2)df(t)(7)dtt(8) f (x)dx1-7已知序列f(k)的图形如图1-7所示,画出下列各序列的图形。
信号与系统复习题及答案

1.系统的激励是,响应为,若满足,则该系统为 线性、时不变、因果。
(是否线性、时不变、因果?)2.求积分的值为 5 。
3.当信号是脉冲信号时,其 低频分量 主要影响脉冲的顶部,其 高频分量 主要影响脉冲的跳变沿。
4.若信号的最高频率是2kHz ,则的乃奎斯特抽样频率为 8kHz 。
5.信号在通过线性系统不产生失真,必须在信号的全部频带内,要求系统幅频特性为 一常数相频特性为_一过原点的直线(群时延)。
6.系统阶跃响应的上升时间和系统的 截止频率 成反比。
7.若信号的,求该信号的。
8.为使LTI 连续系统是稳定的,其系统函数的极点必须在S 平面的 左半平面 。
9.已知信号的频谱函数是,则其时间信号为。
10.若信号的,则其初始值 1 。
二、判断下列说法的正误,正确请在括号里打“√”,错误请打“×”。
(每小题2分,共10分)1.单位冲激函数总是满足 ( √ )2.满足绝对可积条件的信号一定存在傅立叶变换,不满足这一条件的信号一定不存在傅立叶变换。
( × )得分)t (e )t (r dt)t (de )t (r =dt )t ()t (212-+⎰∞∞-δf(t)f(t)t)f(23s F(s)=(s+4)(s+2)=)j (F ωj 3(j +4)(j +2)ωωω)s (H ))00(()j (F ωωδωωδω--+=f(t)01sin()t j ωπf(t)211)s (s )s (F +-==+)(f 0)()(t t -=δδ∞<⎰∞∞-dt t f )(3.非周期信号的脉冲宽度越小,其频带宽度越宽。
( √ )4.连续LTI 系统的冲激响应的形式取决于系统的特征根,于系统的零点无关。
( √ )5.所有周期信号的频谱都是离散谱,并且随频率的增高,幅度谱总是渐小的。
( × )三、计算分析题(1、3、4、5题每题10分,2题5分,6题15分,共60分)1.信号,信号,试求。
信号与线性系统分析试卷
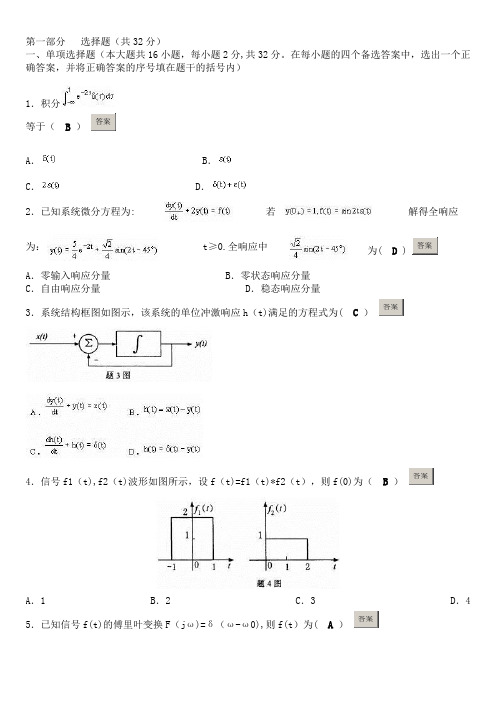
第一部分选择题(共32分)一、单项选择题(本大题共16小题,每小题2分,共32分。
在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内)1.积分等于(B)答案A. B.C. D.2.已知系统微分方程为: 若解得全响应为:t≥0.全响应中为( D ) 答案A.零输入响应分量 B.零状态响应分量C.自由响应分量 D.稳态响应分量3.系统结构框图如图示,该系统的单位冲激响应h(t)满足的方程式为( C)答案4.信号f1(t),f2(t)波形如图所示,设f(t)=f1(t)*f2(t),则f(0)为(B)答案A.1 B.2 C.3 D.4 5.已知信号f(t)的傅里叶变换F(jω)=δ(ω-ω0),则f(t)为( A)答案6.已知信号f(t)如图所示,则其傅里叶变换为(C)答案7.f(t)=ε(t)-ε(t—1)的拉氏变换为(A)答案8. 的拉氏反变换为(D)答案9.图(a)中ab段电路是某复杂电路的一部分,其中电感L和电容C都含有初始状态,请在图(b)中选出该电路的复频域模型。
(B ) 答案10.离散信号f(n)是指(B)答案A.n的取值是连续的,而f(n)的取值是任意的信号B.n的取值是离散的,而f(n)的取值是任意的信号C.n的取值是连续的,而f(n)的取值是连续的信号D.n的取值是连续的,而f(n)的取值是离散的信号11.若序列f(n)的图形如图(a)所示,那么f(—n+1)的图形为图(b)中的( D)答案12.差分方程的齐次解为,特解为,那么系统的稳态响应为( B ) 答案13.已知离散系统的单位序列响应和系统输入如图所示,f(n)作用于系统引起的零状态响应为,那么序列不为零的点数为(C)答案A.3个 B.4个C.5个 D.6个第二部分非选题(共68分)二、填空题(本大题共9小题,每小题2分,共18分)14.=()。
答案15.GLC并联电路发生谐振时,电容上电流的幅值是电流源幅值的(Q)倍。
信号和线性系统分析(吴大正第四版)第四章习题答案解析

第四章习题4.6求下列周期信号的基波角频率Ω和周期T解 ⑴角频率为Ω = IOO rad∕s,周期丁=盲=p÷ξ ⑵角频率为I fi=号■rad∕s,周期= 4 s(3) 角频率为Ω = 2 rad 倉,周期T = ~ = Tr S (4) 角频率为Q =兀rad∕ s,周期T=^ = 2 sΩ(5) 角频率为 Ω — rad∕s*周期 T=-^ = 8 s4 12⑹角频率为C =話rad∕s,周期T = -jy = 60 s4.7用直接计算傅里叶系数的方法, 求图4-15所示周期函数 的傅里叶系数(三角形式或指数形式)(1) e j100t(2) cos[,t - 3)](3) cos(2t) sin(4t) ⑷ cos(2 兀 t) +cos(3πt) +cos(5 兀 t)(5)π π cos( t) sin( t)2 4(6)JEJITEcos( t) cos( t) cos( t)2 35-2 -1 O 12 3 r(IJ)图4-15f>~ 十解 ⑴周期T = 4,1Ω = Y =亍r 则有H ,4⅛ - 1 ≤ r ≤ 4⅛+ 1/⑺=II∣07 4⅛ + 1 < r < 4⅛ + 3由此可得-Tu rt = ~∖ ' τ fit) cost nΩt)dt= -∣^∣ /(f)cos(^ψ^)df J- J —⅛ 乙-.:—2 I(2}周期丁=2・0 =年=兀,则有由此可得1 + e -jrhr2π( I - √ )所含有的频率分量)dr =2 J -[2『亍=Wl f(t)sm(ττΩt)dt =1 J -T2——SInnπ (才),= om 小山(竽)出ISin(Jrt) 9fm=! 0,2⅛ ≤ r ≤ 2⅛ + 12⅛ + 1 < r < 2⅛ + 2F ri ]ft1 Γl=TJV Cf)^dr =⅛J r ∣/(r)e-7iβ,dr — -7- Sin(^f)e -dr -I ZJV4.10利用奇偶性判断图4-18示各周期信号的傅里叶系数中扣 =O* ± 1 * + 2・・图 4-18解 (1)由旳⑺的波形可矩Λ<r) =√√-n =-∕l (f ⊂f)亠 IU Jr = f(t)cos( riΩt )df 则有丿 丁人 ,jj = 0.1,2,-[仇=0"[J =盘?=应丄=*" =QE=仇=仏=*八=0 则∕√r)的傅里叶级数中含有的频率分量为奇次余弦波亠 (2)由f 2(t)的波形可知则有— ■ ??f(t)s}n(tιΩt )d r ⅛ =A rz fl , J Tni JJO则f 2(t)的傅里叶级数中含有的频率分量为正弦波*(3)由 f 3(t)的波形可⅛l∕3<f) = f 3(~r)则有Γ⅛ = 0, n/(z)cos( fiΩt >d;(4)% 4召=亍即ΛG)的傅里叶级数中含有的频率分量为偶次余弦波* 由/<(0的波形可知,人⑺为奇谐函数■即fdι) =一 fZ 土 £)b 2 = h A = b 6 =・*・=0则有 U即人")的傅里叶级数中只含有奇次谐波•包括正弦波和余弦披"4-11 求u(t)的三角形式傅里叶系数。
信号与线性系统分析 (吴大正 第四版)第四章习题答案

创作编号:BG7531400019813488897SX 创作者: 别如克*第四章习题4.6 求下列周期信号的基波角频率Ω和周期T 。
(1)t j e 100 (2))]3(2cos[-t π (3))4sin()2cos(t t + (4))5cos()3cos()2cos(t t t πππ++(5))4sin()2cos(t t ππ+ (6))5cos()3cos()2cos(t t t πππ++4.7 用直接计算傅里叶系数的方法,求图4-15所示周期函数的傅里叶系数(三角形式或指数形式)。
图4-154.10 利用奇偶性判断图4-18示各周期信号的傅里叶系数中所含有的频率分量。
图4-184-11 某1Ω电阻两端的电压)(t u 如图4-19所示,(1)求)(t u 的三角形式傅里叶系数。
(2)利用(1)的结果和1)21(=u ,求下列无穷级数之和 (7)151311+-+-=S (3)求1Ω电阻上的平均功率和电压有效值。
(4)利用(3)的结果求下列无穷级数之和 (7)151311222++++=S图4-194.17 根据傅里叶变换对称性求下列函数的傅里叶变换(1)∞<<-∞--=t t t t f ,)2()]2(2sin[)(ππ (2)∞<<-∞+=t t t f ,2)(22αα (3)∞<<-∞⎥⎦⎤⎢⎣⎡=t t t t f ,2)2sin()(2ππ4.18 求下列信号的傅里叶变换(1))2()(-=-t e t f jt δ (2))1(')()1(3-=--t e t f t δ(3))9sgn()(2-=t t f (4))1()(2+=-t e t f t ε(5))12()(-=tt f ε4.19 试用时域微积分性质,求图4-23示信号的频谱。
图4-234.20 若已知)(j ])([ωF t f F =,试求下列函数的频谱:(1))2(t tf (3)dtt df t )( (5))-1(t)-(1t f (8))2-3(t f e jt (9)tdt t df π1*)(4.21 求下列函数的傅里叶变换(1)⎩⎨⎧><=000,1,)(j ωωωωωF (3))(3cos 2)(j ωω=F(5)ωωωω1)(2n -20sin 2)(j +=∑=j n e F4.23 试用下列方式求图4-25示信号的频谱函数创作编号:BG7531400019813488897SX创作者:别如克*(1)利用延时和线性性质(门函数的频谱可利用已知结果)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
t
(t ), f2(t )
(t)
A.0.1t2(t )
B.
0.3t2(t )
,则f1(t )f2(t)的值是()
C.0.5t2(t )D.0.7t2(t)
23.符号函数sgn(t )的频谱函数为()
A.1
B.
2
C.
3
D.
4
j
j
j
j
24.连续系统是稳定系统的充分必要条件是
(
)
A.
h(t )dt
A.2
B. 4
C. 6
D. 8
12.
题2图所示f (t )的数学表达式为
(
)
f(t
1
-
0
1
t
A.f (t)
(t
1)
(t
1)
B.
f (t )
(t
1)
(t
1)
C.
f (t )
(t )
(t
1)
D.
f (t)
(t)
(t
1)
13.
已知
f1(t)
(t
1),
f2(t)
(t
2),则
f1(t )
f2(t)的值是
(
)
A.(t )
(D
)
A.H ( jw )
C.H ( jw )
6.已知序列
z
A.
ejwtd
B.
H ( jw)
ejwtd
Kejwtd
D.
H ( jw )
Kejwtd
f (k ) (1)k
(k ),其z变换为
(B
)
3
B.
z
C.
z
D.
z
z
1
3
z1
z
1
z
1
3
4
4
7.离散因果系统的充分必要条件是
(
A
)
A.h(k)
0,k
0
B.
(k
2),则f ( k)
h(k )的值为(B
)
A.k 1( k 1)
B.
k 2
(k
2)
C.
k 3(k
3)
D.
k 4(k 4)
10.
连续系统的零输入响应的“零”是指(
A)
A.激励为零
B.
系统的初始状态为零
C.系统的冲激响应为零
D.
系统的阶跃响应为零
11.
已知序列f (k)
j
k
(
)
e3
为周期序列,其周期为
(k)时,系统的零状态响应称为
_________________。
4.
已知函数F (s)
4
,其拉普拉斯逆变换为____________________。
2s
3
5.
函数f (t)的傅里叶变换存在的充分条件是________________________。
6.
已知X ( z)
1
( z
0.5),则其逆变换x(n)的值是______________。
h( k)
0, k
0
C.
h(k)
0,k
0
D.
h( k)
0, k
0
8.已知f (t)的傅里叶变换为F ( jw ),则f (t 3)
的傅里叶变换为
(C
)
A.F ( jw )ejw
B.
F ( jw )ej 2w
C.
F ( jw )ej 3 w
D.
F ( jw )ej 4 w
9.已知f (k)
k(k),h(k)
M
B.
h(t) dt
M
C.
h(t)dt
M
D.
h(t)dt
M
25.已知函数f (t)的象函数F ( s)
( s 6)
,则原函数f (t)
的初值为
(
)
( s
2)(s
5)
A.0
B. 1
C. 2
D. 3
26.已知系统函数H ( s)
3
,则该系统的单位冲激响应为
(
)
s
1
A.et(t )
B.
2et
(t )
C.
3et(t)
D.
4et
(t )
27.已知f ( k)
k 1(k
1), h(k )
( k
2),则f (k )
h( k)的值为
(
)
A.k
(k)
B.
k 1(k
1)
C.
k 2
(k 2)
D.
k
3(k 3)
28.系统的零输入响应是指()
A.系统无激励信号
B.系统的初始状态为零
C.系统的激励为零,仅由系统的初始状态引起的响应
信号与线性系统复习题
单项选择题。
1.
已知序列f ( k)
cos(3k )为周期序列,其周期为
(C)
5
A.2B. 5
C. 10D. 12
2.
题2图所示f (t)的数学表达式为
(B
)
f(t正弦函数
10
01
t
图题2
A.f (t )
10sin(
t )[
(t)
(t
1)]
B.
f (t )
10sin(
t)[ (t )
B.
1F (s)
C.
1F (s)D.
1F (s)
5
3
5
5
5
7
5
19.
已知f ( k)
k 2( k
2),h( k)
(k
2),则f (k)
h(k )的值为(
)
A.k 1( k
1)
B.
k 2(k 2)
C.
k 3( k
3)
D.
k 4
( k 4)
20.
已知f (t)的傅里叶变换为F ( j
),则F ( jt )的傅里叶变换为(
2倍
C.将f (t )以原点为基准,沿横轴压缩到原来的
1
4
D.将f (t )以原点为基准,沿横轴展宽到原来的
4倍
填空题
1.
已知象函数F (s)
2s
3ห้องสมุดไป่ตู้
f (0 )
为___________________。
(s 1)2,其原函数的初值
(et
t ) (t 2)dt
。
3.
当LTI离散系统的激励为单位阶跃序列
(
)
A.z, z
1
B.
z
z, z
1C.
z, z
1
D.
z, z
1
z 1
1
z
1
z 1
17.
已知系统函数H ( s)
1,则其单位冲激响应
h(t )为
(
)
s
A.(t )
B.
t (t )
C.
2t
(t )
D.
3t
(t)
18.
已知f (t)的拉普拉斯变换为F ( s),则f (5t )的拉普拉斯变换为
(
)
A.F (s)
B.
(t
1)
C.
(t
2)
D.
(t
3)
14.
已知F ( j )
j
,则其对应的原函数为
(
)
A.(t )
B.
'(t )
C.
' '(t )
D.
'' '(t)
15.
连续因果系统的充分必要条件是
(
)
A.h(t )
0,t
0
B.
h(t )
0,t
0
C.
h(t )
0, t
0
D.
h(t )
0,t
0
16.
单位阶跃序列
(k)的z变换为
0.5z
1
1
7.
系统函数H (z)
(z
1)(z
1)的极点是___________________________。
D.系统的初始状态为零,仅由系统的激励引起的响应
29.偶函数的傅里叶级数展开式中
(
)
A.只有正弦项B.只有余弦项
C.
只有偶次谐波
D.只有奇次谐波
10.已知信号f (t )的波形,则f (t)的波形为
(
)
2
A.将f (t )以原点为基准,沿横轴压缩到原来的
1
2
B.将f (t )以原点为基准,沿横轴展宽到原来的
(t
1)]
C.
f (t )
10sin(
t )[
(t)
(t
2)]
D.
f (t)
10sin(
t )[ (t)
(t
2)]
3.
已知f (t)
sin(
t)
(t )dt,其值是
(A)
t
A.
B.
2
C.
3
D.
4
4.
冲激函数(t)的拉普拉斯变换为
(A
)
A.1
B. 2
C. 3
D. 4
5.
为了使信号无失真传输,系统的频率响应函数应为
)
A.
f (
)
B.
f ( )
C.
2 f (
