初三上学期期末测试
2024年北京初三九年级上学期数学期末考《新定义》
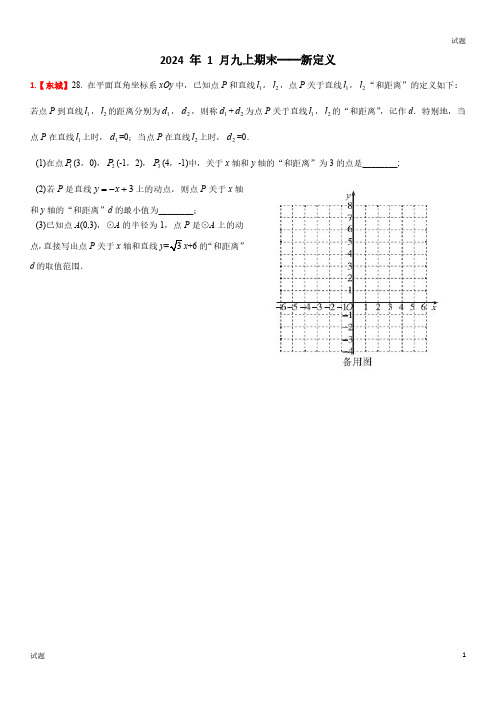
2024年1月九上期末——新定义1.【东城】28.在平面直角坐标系xOy 中,已知点P 和直线1l ,2l ,点P 关于直线1l ,2l “和距离”的定义如下:若点P 到直线1l ,2l 的距离分别为1d ,2d ,则称1d +2d 为点P 关于直线1l ,2l 的“和距离”,记作d .特别地,当点P 在直线1l 上时,1d =0;当点P 在直线2l 上时,2d =0.(1)在点1P (3,0),2P (-1,2),3P (4,-1)中,关于x 轴和y 轴的“和距离”为3的点是________;(2)若P 是直线3y x =-+上的动点,则点P 关于x 轴和y 轴的“和距离”d 的最小值为________;(3)已知点A (0,3),⊙A 的半径为1,点P 是⊙A 上的动点,直接写出点P 关于x 轴和直线y =3x +6的“和距离”d 的取值范围.2.【西城】28.如图,在平面直角坐标系xOy 中,点()1,0S -,()1,0T .对于一个角α(0180α︒<≤︒),将一个图形先绕点S 顺时针旋转α,再绕点T 逆时针旋转α,称为一次“α对称旋转”.备用图(1)点R 在线段ST 上,则在点()1,1A -,()3,2B -,()2,2C -,()0,2D -中,有可能是由点R 经过一次“90°对称旋转”后得到的点是________;(2)x 轴上的一点P 经过一次“α对称旋转”得到点Q .①当60α=︒时,PQ =________;②当30α=︒时,若QT x ⊥轴,求点P 的坐标;(3)以点O 为圆心作半径为1的圆.若在O 上存在点M ,使得点M 经过一次“α对称旋转”后得到的点在x 轴上,直接写出α的取值范围.3.【海淀】28.在平面直角坐标系xOy 中,将中心为T 的正方形记作正方形T ,对于正方形T 和点P (不与O 重合)给出如下定义:若正方形T 的边上存在点Q ,使得直线OP 与以TQ 为半径的T 相切于点P ,则称点P 为正方形T 的“伴随切点”.(1)如图、正方形T 的顶点分别为点O ,()2,2A ,()4,0B ,()2,2C -.①在点()12,1P ,()21,1P ,()31,1P -中,正方形T 的“伴随切点”是________;②若直线y x b =+上存在正方形T 的“伴随切点”,求b 的取值范围;(2)已知点(),1T t t +,正方形T 的边长为2.若存在正方形T 的两个“伴随切点”M ,N ,使得OMN △为等边三角形,直接写出t 的取值范围.4.【朝阳】28.在平面直角坐标系xOy 中,已知A (t -2,0),B (t +2,0).对于点P 给出如下定义:若∠APB=45°,则称P 为线段AB 的“等直点”.(1)当t =0时,①在点),(22201+P ,),(042-P ,)-,(2223-P ,),(524P 中,线段AB 的“等直点”是________;②点Q 在直线y =x 上,若点Q 为线段AB 的“等直点”,直接写出点Q 的横坐标.(2)当直线t x y +=上存在线段AB 的两个“等直点”时,直接写出t 取值范围.5.【石景山】28.在平面直角坐标系xOy 中,⊙O 的半径为1.对于⊙O 的弦AB 和点C 给出如下定义:若点C 在弦AB 的垂直平分线上,且点C 关于直线AB 的对称点在⊙O 上,则称点C 是弦AB 的“关联点”.(1)如图,点13(22A ,,13(22B -,.在点1(00)C ,,2(10)C ,,3(11)C ,,4(20)C ,中,弦AB 的“关联点”是;(2)若点1(0)2C ,是弦AB 的“关联点”,直接写出AB 的长;(3)已知点(02)M ,,(0)15N ,.对于线段MN 上一点S ,存在⊙O 的弦PQ ,使得点S 是弦PQ 的“关联点”.记PQ 的长为t ,当点S 在线段MN 上运动时,直接写出t 的取值范围.6.【丰台】28.在平面直角坐标系xOy中,⊙O的半径为1,对于线段AB和x轴上的点P,给出如下定义:将线段AB绕点P旋转180°可以得到⊙O的弦A'B'(A',B'分别为A,B的对应点),则称线段AB为⊙O以点P 为中心的“关联线段”.(1)如图,已知点A(-2,-1),B(-2,0),C(-2,1),D(-1,1),在线段AC,BD,CD中,⊙O以点P 为中心的“关联线段”是;x的取值范围;(2)已知点E(-4,1),线段EF是⊙O以点P为中心的“关联线段”,求点F的横坐标F (3)已知点E(m,1),若直线y=-x+2m上存在点F,使得线段EF是⊙O以点P为中心的“关联线段”,直接写出m的取值范围.备用图7.【昌平】28.对于在平面直角坐标系xOy 中⊙T 和⊙T 外的点P ,给出如下定义:已知⊙T 的半径为1,若⊙T 上存在点Q ,满足PQ ≤2,则称点P 为⊙T 的关联点.(1)如图1,若点T 的坐标为(0,0),28题图1①在点1P (3,0),2P (3,-2),3P (-2,2)中,是⊙T 的关联点的是____________;②直线2y x b =+分别交x 轴,y 轴于点A ,B ,若线段AB 存在⊙T 的关联点,求b 的取值范围;(2)已知点C (0,D (1,0),T (m ,1),△COD 上的每一个点都是⊙T 的关联点,直接写出m 的取值范围.28题图28.【通州】28.在平面直角坐标系xOy 中,O 的半径为1.给出如下定义:过O 外一点P 做直线与O 交于点M 、N ,若M 为线段PN 的中点,则称线段PN 是O 的“外倍线”。
2024北京房山区初三(上)期末数学试卷和答案

房山区2023—2024学年度第一学期期末检测试卷参考答案九年级数学第一部分 选择题(共16分,每题2分)在下列各题的四个选项中,只有一项是符合题意的.第二部分 非选择题(共84分)二、填空题(共16分,每题2分)9. 1x ≠10. 5011. 2y x =或2y x=或22y x =(答案不唯一) 12. 413. 314. π21516.(1)3;(2)(0(注:第15题答对1个给1分,第16题一空1分)三、解答题(共68分,第17 -22题,每题5分,第23-26题,每题6分,第27-28题,每题7分)解答应写出文字说明、演算步骤或证明过程.17.解:04sin 451)5︒++−4152=⨯++−………….………..……….4分 6=. ………….………..……….5分18. 证明: ∵A A ∠=∠, ………….………..……….2分又∵ADE C ∠=∠, ………….………..……….4分 ∴△ADE ∽△ACB . ………….………..……….5分19.(1)二次函数223y x x =+−的图象,如图.………….………..……….2分抛物线的对称轴为直线1x =−. ………….………..……….3分(2)当11x −<<时,则y 的取值范围是40y −<<. …….………..……….5分 20. 解:在Rt △ABC 中,90C ∠=︒,5BC =,13AB =,由勾股定理得:12AC =. ………..……….3分 ∴12cos 13AC A AB ==. ………….………..……….5分 21. 解:(1)补全的图形如图所示: ………….………..……….2分(2) …….………..……….3分90; 直径所对的圆周角是直角. …….………..……….5分BA22. (1)证明:∵四边形ABCD 是矩形, ∴90ADC ∠=︒.∴90ADE EDC ∠+∠=︒. ………….………..……….1分 ∵DE AC ⊥,∴90ADE DAE ∠+∠=︒. ………….………..……….2分 ∴DAE EDC ∠=∠. ………….………..……….3分(2)解:在Rt △DEC 中,3tan 4EDC ∠=,设3EC x =,4DE x =, 则5DC x =.∵DAE EDC ∠=∠,∴3tan tan 4DAE EDC ∠=∠=. ∵四边形ABCD 是矩形, ∴8AD BC ==. 在Rt △ADC 中,3tan 4DAC ∠=,8AD =. ∴3tan 4DC DAE AD ∠==. ∴6DC =.∴56DC x ==. ∴65x =. ∴2445DE x ==. ………….………..……….5分 23. 解:(1)∵直线y x =与双曲线ky x=相交于点(2)P m ,. ∴ 2m =. ………….………..……….2分 把点(22)P ,代入ky x=得 EDCBA22k=. ∴4k =. ………….………..……….3分 ∴4y x=. ∴4.y x y x =⎧⎪⎨=⎪⎩, ∴222. 2.x x y y ==−⎧⎧⎨⎨==−⎩⎩,,或∴点Q 的坐标为(22)−−,. ………….………..……….4分 (2)n 的取值范围是2n >或20n −<<. ………….………..……….6分 24.(1)证明:连接OC .∵OA OC =, ∴OAC OCA ∠=∠. 又∵DCB DAC ∠=∠,∴DCB OCA ∠=∠. .……….1分∵AB 是⊙O 的直径,∴90OCA OCB ∠+∠=︒.∴90DCB OCB ∠+∠=︒. ………….………..……….2分 又∵OC 是半径,CD 经过⊙O 的半径外端C .∴CD 是⊙O 的切线. ………….………..……….3分(2)解:在Rt △OCD 中,∵90OCD ∠=︒,30D ∠=︒,2OC =,∴4OD =. ………….………..……….4分 ∴6AD AO OD =+=.∵AE 是⊙O 的切线,切点为A ,∴OA AE ⊥. ………….………..……….5分DA在Rt △EAD 中,∵90EAD ∠=︒,30D ∠=︒,6AD =,∴tan 3063AE AD =⋅︒=⨯= ………….………..……….6分25. (1)5m . ………….………..……….2分解:由题意可知2(6)5y a x =−+. ∵当0x =时,2y =, ∴2(06)52a −+=,解得112a =−, ∴函数关系为21(6)512y x =−−+. ……….………..……….5分 (2)>. ……….………..……….6分 26.(1)解:当0x =时,4y =.∴抛物线与y 轴交点的坐标为(04),.……….………..……….1分 ∵点(1)m ,,(3)n ,在抛物线24(0)y ax bx a =++>上,且m n =,∴31t t −=−,解得2t =. ………….………..……….3分(2)解:由4m a b =++,934n a b =++,∵m n <, ∴820a b +>. ∴4b a >−. ∵0a >, ∴22ba−<,即2t <. ∵4n <, ∴930a b +<. ∴3b a <−. ∴322b a −>,即32t >.综上所述,322t <<. ………….………..……….5分 ∵点00()(3)x n x ≠,在抛物线上, ∴0()x n ,,(3)n ,关于抛物线的对称轴x t =对称,且0x t <. ∴03t t x −=−,解得032x t +=. ∴033222x +<<. ∴001x <<. ………….………..……….6分 27.(1)60; ………….………..……….2分(2)① 依题意补全图形,如图.………….………..……….4分② 用等式表示线段AG ,BG 与DG 的数量关系:2223AG BG DG +=.………….………..……….5分证明:作120GAM ∠=︒,在AM 截取AP AG =,连接GP ,PD .∵ AP AG =,120GAP ∠=︒, ∴30AGP APG ∠=∠=︒. ∵ △ABC 是等边三角形, ∴AB BC =,60ABC ∠=︒. 又∵AD BC =,DG FECBA∴ AB AD =. ∵ AD ∥BC ,∴180ABC BAD ∠+∠=︒.∴120BAD ∠=︒. ∵120GAP ∠=︒, ∴ BAG DAP ∠=∠.∴ △BAG ≌△DAP (SAS ). ∴ BG DP =,120APD AGB ∠=∠=︒. ∵ 30APG ∠=︒, ∴ 90DPG ∠=︒.∴222GP DP DG +=. 过点A 作AQ GP ⊥于点Q , 在Rt △AGQ 中,∵30AGQ ∠=︒,cos GQAGQ AG∠=,∴GQ AG =.∴2GP GQ ==. 又∵BG DP =,∴2223AG BG DG +=. ………….………..……….7分28.(1)①2P ,3P ; ………….………..……….2分 ②解:∵当2x =时,0y =,∴一次函数2y kx k =−的图象过点(20),. 如图1,当一次函数2y kx k =−的图象与半径为1的⊙O 相切时, 30OBP ∠=︒,得:3k =−. M QPH DG FECBA如图2,当一次函数2y kx k =−的图象与y 轴的交点也是⊙O 与y 轴的交点时,45OBA ∠=︒,得:1k =−.∴13k −<−≤; ………….………..……….5分图1 图2(2)1m <<1m << ………….………..……….7分。
2023-2024学年九年级上学期期末调研测试英语试题(原卷版)

2023-2024学年度上学期九年级期末调研测试英语试卷第Ⅰ卷一、单项选择(本题共10分,每小题1分)选择最佳答案。
1. —Boys and girls, let’s make ________ decision to have all around development from now on.—Only then will we have a better future.A. aB. anC. /2. —Our parents will take us to Disney as a special ________ next summer vacation.—Sounds like fun!A. treatB. shameC. energy3. — What do you think of your English teacher?— He is always ________ us. What a good teacher!A. absent fromB. tired ofC. patient with4. Learning to work with your classmates can help you find pleasure in what you do, even when the job ________ is hard.A. ourselvesB. itselfC. themselves5. Though they didn’t carry out their plan, they succeeded in ________ their minds.A. regrettingB. improvingC. stealing6. The population problem is very serious in this area. We must come up with good ways to ________ it.A. argue withB. deal withC. agree with7. —________ almost three years since we met for the first time.—Yeah, how time flies! We need to value the time we spent with each other.A. It wasB. It’s beenC. It will be8. —Who is the woman with Ann?—I’m not sure. It ________ be her mother.A. mayB. mustC. can’t9. Kids can own their favorite hobbies at holidays ________ they are given too much homework.A. ifB. unlessC. until10. —Excuse me, Mr Zhang. Could you please tell me ________ ?—Next Wednesday. Work hard and get ready for it.A. where I can pass the examB. if we will have an examC. when we will have the exam二、完形填空(本题共10分,每小题1分)I made a promise to myself a couple of months ago. I had put some money in my wallet with the purpose of ____11____ to the first person I met who needed it. Time passed, and as my daily life got busy, I was unable to keep my word. ____12____ I opened my wallet and saw the money, I thought of that, and I would feel a little disappointed for doing nothing. The voice inside told me that I should do something soon.Today, when I was walking to work on a busy street, I passed a ____13____ old lady with her hand out on the corner. Seeing her aged face and eyes that failed to see, I stopped ____14____. A sense of sympathy (同情) washed over me, and I remembered the money that had been lying in my wallet all these five ____15____.I took out the money from the wallet and bent down (弯腰) to her level. ____16____, I took her hand, placed the notes into it, and closed her fingers over the notes ____17____ she could feel the money and understand me.After I got up, I slowly moved away. I felt like I had achieved something. I had kept my word to myself. The lady nodded her head a little bit. I felt ____18____ and moved on.After that, I thought about why such a simple act had taken so long. This small act was a huge step in facing and walking ____19____ my own fears around giving. What a gift it is to have these small but meaningful____20____!根据短文内容选择最佳答案。
2023-2024学年北京市九年级数学第一学期期末达标测试试题(含解析)

2023-2024学年北京市九年级数学第一学期期末达标测试试题注意事项:1.答卷前,考生务必将自己的姓名、准考证号、考场号和座位号填写在试题卷和答题卡上。
用2B 铅笔将试卷类型(B )填涂在答题卡相应位置上。
将条形码粘贴在答题卡右上角"条形码粘贴处"。
2.作答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑;如需改动,用橡皮擦干净后,再选涂其他答案。
答案不能答在试题卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置上;如需改动,先划掉原来的答案,然后再写上新答案;不准使用铅笔和涂改液。
不按以上要求作答无效。
4.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题(每题4分,共48分)1.如图,已知抛物线和直线.我们约定:当x 任取一值时,x 对应的函数值分别为y 1、y 2,若y 1≠y 2,取y 1、y 2中的较小值记为M ;若y 1=y 2,记M= y 1=y 2.下列判断: ①当x >2时,M=y 2;②当x <0时,x 值越大,M 值越大;③使得M 大于4的x 值不存在;④若M=2,则x=" 1" .其中正确的有A .1个B .2个C .3个D .4个2.教育局组织学生篮球赛,有x 支球队参加,每两队赛一场时,共需安排45场比赛,则符合题意的方程为( )A.B .C .D .3.下列说法正确的是( )A .随机抛掷一枚均匀的硬币,落地后反面一定朝上。
B .从1,2,3,4,5中随机取一个数,取得奇数的可能性较大。
C .某彩票中奖率为,说明买100张彩票,有36张中奖。
D .打开电视,中央一套正在播放新闻联播。
4.如图是我们学过的反比例函数图象,它的表达式可能是( )21y x 4x =-+2y 2x =()11452x x -=()11452x x +=()145x x -=()145x x +=36%A .B .C .D .5.下列图案中,是中心对称图形的是( )A .B .C .D .6.⊙O 的半径为5cm ,弦AB//CD ,且AB=8cm,CD=6cm,则AB 与CD 之间的距离为()A .1 cmB .7cmC .3 cm 或4 cmD .1cm 或7cm 7.已知关于的一元二次方程有两个相等的实数根,则锐角等于( )A .B .C .D .8.小李与小陈做猜拳游戏,规定每人每次至少要出一个手指,两人出拳的手指数之和为偶数时小李获胜,那么,小李获胜的概率为( )A.B .C .D .9.下列关系式中,y 是x 的反比例函数的是( )A .y =4xB .=3C .y =﹣D .y =x 2﹣110.如图,⊙O 的直径长10,弦AB=8,M 是弦AB 上的动点,则OM 的长的取值范围是( )A .3≤OM≤5B .4≤OM≤5C .3<OM <5D .4<OM <511.如图所示的工件的主视图是( )22y x =4y x =3y x =-3y x=-x 2cos 0x α+=α15 30 45 601325122542512y x 1xA .B .C .D .12.若△ABC ~△A ′B 'C ′,相似比为1:2,则△ABC 与△A 'B ′C '的周长的比为( )A .2:1B .1:2C .4:1D .1:4二、填空题(每题4分,共24分)13.若弧长为4π的扇形的圆心角为直角,则该扇形的半径为 .14.因式分解:_______;15.如图,在平面直角坐标系中,已知经过点,且点O 为坐标原点,点C 在y 轴上,点E 在x 轴上,A (-3,2),则__________.16.矩形ABCD 中,AB=6,BC=8.点P 在矩形ABCD 的内部,点E 在边BC 上,满足△PBE ∽△DBC ,若△APD 是等腰三角形,则PE 的长为数___________.17.已知关于的方程的一个根为-2,则方程另一个根为__________.18.在中,,,在外有一点,且,则的度数是__________.三、解答题(共78分)19.(8分)如图,有一个斜坡,坡顶离地面的高度为20米,坡面的坡度为,求坡面的长度.20.(8分)如果三角形有一边上的中线恰好等于这边的长,那么称这个三角形为“匀称三角形”,这条中线为“匀称中线”.()()2a b b a ---=A E B O C 、、、tan OBC ∠=x 230x mx m ++=ABC ∆AC BC =90C ∠=︒ABC ∆M MA MB ⊥AMC ∠AB B BC AB 25AB(1)如图①,在Rt △ABC 中,∠C =90°,AC >BC ,若Rt △ABC 是“匀称三角形”.①请判断“匀称中线”是哪条边上的中线,②求BC :AC :AB 的值.(2)如图②,△ABC 是⊙O 的内接三角形,AB >AC ,∠BAC =45°,S △ABC =,将△ABC 绕点A 逆时针旋转45°得到△ADE ,点B 的对应点为D ,AD 与⊙O 交于点M ,若△ACD 是“匀称三角形”,求CD 的长,并判断CM 是否为△ACD的“匀称中线”.21.(8分)某班为推荐选手参加学校举办的“祖国在我心中”演讲比赛活动,先在班级中进行预赛,班主任根据学生的成绩从高到低划分为A ,B ,C ,D 四个等级,并绘制了不完整的两种统计图表.请根据图中提供的信息,回答下列问题:(1)a 的值为 ;(2)求C 等级对应扇形的圆心角的度数;(3)获得A 等级的4名学生中恰好有1男3女,该班将从中随机选取2人,参加学校举办的演讲比赛,请利用列表法或画树状图法,求恰好选中一男一女参加比赛的概率.22.(10分)如图,在中,,,,将线段绕点按逆时针方向旋转到线段.由沿方向平移得到,且直线过点.ABC 90C ∠=︒10AB =8AC =AB A 90︒AD EFG ABC CB EF D(1)求的大小;(2)求的长.23.(10分)如图,把Rt △ABC 绕点A .逆时针旋转40°,得到在Rt △ABʹCʹ,点Cʹ恰好落在边AB 上,连接BBʹ,求∠BBʹCʹ的度数.24.(10分)只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果,哥德巴赫猜想是:每个大于2的偶数都可以表示为两个素数的和,如16=3+ 1.(1)若从7, 11, 19, 23中随机抽取1个素数,则抽到的素数是7的概率是_______;(2)若从7, 11, 19, 23中随机抽取1个素数,再从余下的3个数字中随机抽取1个素数,用面树状图或列表的方法求抽到的两个素数之和大于等于30的概率,25.(12分)(1)计算: (2)化简:26.已知抛物线的顶点坐标为(1,2),且经过点(3,10)求这条抛物线的解析式.参考答案一、选择题(每题4分,共48分)1、B【解析】试题分析:∵当y 1=y 2时,即时,解得:x=0或x=2,1∠AE 201224((18--+-⨯--2291(1)693x x x x -⋅+-++2x 4x 2x -+=∴由函数图象可以得出当x >2时, y 2>y 1;当0<x <2时,y 1>y 2;当x <0时, y 2>y 1.∴①错误.∵当x <0时, -直线的值都随x 的增大而增大,∴当x <0时,x 值越大,M 值越大.∴②正确.∵抛物线的最大值为4,∴M 大于4的x 值不存在.∴③正确;∵当0<x <2时,y 1>y 2,∴当M=2时,2x=2,x=1;∵当x >2时,y 2>y 1,∴当M=2时,,解得.∴使得M=2的x 值是1或.∴④错误.综上所述,正确的有②③2个.故选B .2、A 【分析】先列出x 支篮球队,每两队之间都比赛一场,共可以比赛x (x-1)场,再根据题意列出方程为.【详解】解:∵有x 支球队参加篮球比赛,每两队之间都比赛一场,∴共比赛场数为,故选:A .本题是由实际问题抽象出一元二次方程,主要考查了从实际问题中抽象出相等关系.3、B【解析】A 、掷一枚硬币的试验中,着地时反面向上的概率为,则正面向上的概率也为,不一定就反面朝上,故此选项错误;B 、从1,2,3,4,5中随机取一个数,因为奇数多,所以取得奇数的可能性较大,故此选项正确;C 、某彩票中奖率为36%,说明买100张彩票,有36张中奖,不一定,概率是针对数据非常多时,趋近的一个数并不能说买100张该种彩票就一定能中36张奖,故此选项错误;D 、中央一套电视节目有很多,打开电视有可能正在播放中央新闻也有可能播放其它节目,故本选项错误.故选B .4、B【分析】根据反比例函数图象可知,经过第一三象限,,从而得出答案.【详解】解:A 、为二次函数表达式,故A 选项错误;B 、为反比例函数表达式,且,经过第一三象限,符合图象,故B 选项正确;21y x 4x =-+2y 2x =()221y x 4x x 24=-+=--+2x 4x 2-+=12x 2x 2=+=-2+()11452x x -=()11452x x -=12120k >22y x =4y x=0k >C 、为反比例函数表达式,且,经过第二四象限,不符合图象,故C 选项错误;D 、为一次函数表达式,故D 选项错误.故答案为B .本题考查了反比例函数的图象的识别,掌握反比例函数的图象与性质是解题的关键.5、C【解析】根据中心对称图形的概念即可得出答案.【详解】A 选项中,不是中心对称图形,故该选项错误;B 选项中,是轴对称图形,不是中心对称图形,故该选项错误;C 选项中,是中心对称图形,故该选项正确;D 选项中,不是中心对称图形,故该选项错误.故选C本题主要考查中心对称图形,掌握中心对称图形的概念是解题的关键.6、D【分析】分AB 、CD 在圆心的同侧和异侧两种情况求得AB 与CD 的距离.构造直角三角形利用勾股定理求出即可.【详解】当弦AB 和CD 在圆心同侧时,如图①,过点O 作OF ⊥CD ,垂足为F ,交AB 于点E ,连接OA ,OC ,∵AB ∥CD ,∴OE ⊥AB ,∵AB=8cm ,CD=6cm ,∴AE=4cm ,CF=3cm ,∵OA=OC=5cm ,∴EO=3cm ,OF=4cm ,∴EF=OF-OE=1cm ;当弦AB 和CD 在圆心异侧时,如图②,过点O 作OE ⊥AB 于点E ,反向延长OE 交AD 于点F ,连接OA ,OC ,∵AB ∥CD,3y x=-0k <3y x =-∴OF ⊥CD ,∵AB=8cm ,CD=6cm ,∴AE=4cm ,CF=3cm ,∵OA=OC=5cm ,∴EO=3cm ,OF=4cm ,∴EF=OF+OE=7cm .故选D .本题考查了垂径定理、勾股定理;熟练掌握垂径定理和勾股定理,根据题意画出图形是解题的关键,要注意有两种情况.7、D【分析】根据一元二次方程根的判别式等于零,求出的值,进而即可得到答案.【详解】∵关于的一元二次方程有两个相等的实数根,∴∆=,解得:,∴=.故选D .本题主要考查一元二次方程根的判别式以及特殊角三角函数,掌握一元二次方程根的判别式与根的关系,是解题的关键.8、A【分析】画出树状图,共有25个等可能的结果,两人出拳的手指数之和为偶数的结果有13个,即可得出答案.【详解】解:画树状图如图:共有25个等可能的结果,两人出拳的手指数之和为偶数的结果有13个,∴小李获胜的概率为;故选A .cos αx 2cos 0x α-+=2(41cos 0α-⨯⨯=1cos 2α=α60 1325本题考查了列表法与树状图法以及概率公式;根据题意画出树状图是解题的关键.9、C【分析】根据反比例函数的定义逐一判断即可.【详解】A 、y =4x 是正比例函数;B 、=3,可以化为y =3x ,是正比例函数;C 、y =﹣是反比例函数;D 、y =x 2﹣1是二次函数;故选:C .本题考查反比例函数的定义,掌握反比例函数的定义是解题的关键.10、A【详解】解:的直径为10,半径为5,当时,最小,根据勾股定理可得,与重合时,最大,此时,所以线段的的长的取值范围为,故选A .本题考查垂径定理,掌握定理内容正确计算是本题的解题关键.11、B【解析】从物体正面看,看到的是一个横放的矩形,且一条斜线将其分成一个直角梯形和一个直角三角形.故选B .12、B【分析】根据相似三角形的周长比等于相似比即可得出结论.【详解】解:∵∽,相似比为1:1,∴与的周长的比为1:1.故选:B .此题考查的是相似三角形的性质,掌握相似三角形的周长比等于相似比是解决此题的关键.二、填空题(每题4分,共24分)13、1.【分析】根据扇形的弧长公式计算即可,【详解】∵扇形的圆心角为90°,弧长为4π,∴,即4π=,则扇形的半径r=1.y x1x O OM AB ⊥OM 3OM =OM OA OM 5OM =OM 35OM ≤≤ABC A B C '''V ABC A B C '''V r l 180n π=90•180r π故答案为1考点:弧长的计算.14、(a-b )(a-b+1)【解析】原式变形后,提取公因式即可得到结果.【详解】解:原式=(a -b )2+(a -b )=(a -b )(a -b +1),故答案为:(a -b )(a -b +1)此题考查了因式分解-提公因式法,熟练掌握提取公因式的方法是解本题的关键.15、【解析】分别过A 点作x 轴和y 轴的垂线,连接EC ,由∠COE =90°,根据圆周角定理可得:EC 是⊙A 的直径、,由A 点坐标及垂径定理可求出OE 和OC ,解直角三角形即可求得.【详解】解:如图,过A 作AM ⊥x 轴于M ,AN ⊥y 轴于N ,连接EC ,∵∠COE =90°,∴EC 是⊙A 的直径,∵A (−3,2),∴OM =3,ON =2,∵AM ⊥x 轴,AN ⊥y 轴,∴M 为OE 中点,N 为OC 中点,∴OE =2OM =6,OC =2ON =4,∴=.本题主要考查了同弧所对的圆周角相等、垂径定理和锐角三角函数定义,熟练掌握定理是解本题的关键.16、3或1.2【分析】由△PBE ∽△DBC ,可得∠PBE=∠DBC ,继而可确定点P 在BD 上,然后再根据△APD 是等腰三角形,分DP=DA 、AP=DP 两种情况进行讨论即可得.【详解】∵四边形ABCD 是矩形,∴∠BAD=∠C=90°,CD=AB=6,BC=8,∴BD=10,23∠=∠OBC CEO tan OBC ∠tan OBC ∠42tan 63∠===OC CEO OE∵△PBE ∽△DBC ,∴∠PBE=∠DBC ,∴点P 在BD 上,如图1,当DP=DA=8时,BP=2,∵△PBE ∽△DBC ,∴PE :CD=PB :DB=2:10,∴PE :6=2:10,∴PE=1.2;如图2,当AP=DP 时,此时P 为BD 中点,∵△PBE ∽△DBC ,∴PE :CD=PB :DB=1:2,∴PE :6=1:2,∴PE=3;综上,PE 的长为1.2或3,故答案为1.2或3.本题考查了相似三角形的性质,等腰三角形的性质,矩形的性质等,确定出点P 在线段BD 上是解题的关键.17、1【分析】将方程的根-2代入原方程求出m 的值,再解方程即可求解.【详解】解:把x=-2代入原方程得出,4-2m+3m=0,解得m=-4;故原方程为:,解方程得:.故答案为:1.本题考查的知识点是解一元二次方程,根据方程的一个解求出方程中参数的值是解此题的关键.24120x x --=122,6x x =-=18、、【分析】由,可知A 、C 、B 、M 四点共圆,AB 为圆的直径,则是弦AC 所对的圆周角,此时需要对M 点的位置进行分类讨论,点M 分别在直线AC 的两侧时,根据同弧所对的圆周角相等和圆内接四边形对角互补可得两种结果.【详解】解:∵在中,,,∴∠BAC =∠ACB =45°,∵点在外,且,即∠AMB =90°∵∴A 、C 、B 、M 四点共圆,①如图,当点M 在直线AC 的左侧时,,∴;②如图,当点M 在直线AC 的右侧时,∵,∴,故答案为:135°或45°.本题考查了圆内接四边形对角互补和同弧所对的角相等,但解题的关键是要先根据题意判断出A 、C 、B 、M 四点共圆.三、解答题(共78分)19、米【分析】根据坡度的定义可得,求出AB ,再根据勾股定理求135︒45︒90C ∠=︒MA MB ⊥AMC ∠ABC ∆AC BC =90C ∠=︒M ABC ∆MA MB ⊥180∠+∠=︒AMB C 180∠+∠=︒AMC ABC 180********∠=︒-∠=︒-︒=︒AMC ABC AC AC =45∠=∠=︒AMC ABC 25BC AC =AB =【详解】∵坡顶离地面的高度为20米,坡面的坡度为即, ∴米由勾股定理得答:坡面的长度为米.考核知识点:解直角三角形应用.把问题转化为解直角三角形是关键.20、(1)① “匀称中线”是BE ,它是AC 边上的中线,②BC :AC :AB;(2)CDa ,CM 不是△ACD 的“匀称中线”.理由见解析.【分析】(1)①先作出Rt △ABC 的三条中线AD 、BE 、CF ,然后利用匀称中线的定义分别验证即可得出答案;②设AC =2a ,利用勾股定理分别把BC,AB 的长度求出来即可得出答案.(2)由②知:AC :AD :CD ,设AC ,则AD =2a ,CD ,过点C 作CH ⊥AB ,垂足为H,利用的面积建立一个关于a 的方程,解方程即可求出CD 的长度;假设CM 是△ACD 的“匀称中线”,看能否与已知的定理和推论相矛盾,如果能,则说明假设不成立,如果不能推出矛盾,说明假设成立.【详解】(1)①如图①,作Rt△ABC 的三条中线AD、BE 、CF ,∵∠ACB =90°,∴CF =,即CF 不是“匀称中线”.又在Rt △ACD 中,AD >AC >BC ,即AD 不是“匀称中线”.∴“匀称中线”是BE ,它是AC 边上的中线,②设AC =2a ,则CE =a ,BE =2a ,在Rt △BCE 中∠BCE =90°,∴BC ,在Rt △ABC 中,AB ,∴BC :AC :AB (2)由旋转可知,∠DAE =∠BAC =45°.AD =AB >AC ,B BC AB 2525BC AC =2025AC =50AC =AB ==AB :2:7:2ABC 12AB AB ≠==:2:2a =∴∠DAC =∠DAE +∠BAC =90°,AD >AC ,∵Rt △ACD 是“匀称三角形”.由②知:AC :AD :CD设AC,则AD =2a ,CD ,如图②,过点C 作CH⊥AB ,垂足为H ,则∠AHC =90°,∵∠BAC =45°,∴ ∵解得a =2,a =﹣2(舍去),∴判断:CM 不是△ACD 的“匀称中线”.理由:假设CM 是△ACD 的“匀称中线”.则CM =AD =2AM =4,AM =2,∴又在Rt △CBH 中,∠CHB =90°,CH ,BH =4,∴即这与∠AMC =∠B相矛盾,∴假设不成立,2CH AH ===11222ABC S AB CH a ==⨯= CD ==tan AC AMC AM ∠===tan tan CH B AMC BH ===≠∠B AMC∠≠∠∴CM 不是△ACD 的“匀称中线”.本题主要为材料理解题,掌握匀称三角形和匀称中线的意义是解题的关键.21、(1)8 ;(2);(3)【分析】(1)根据D 等级的人数除以其百分比得到班级总人数,再乘以B 等级的百分比即可得a 的值;(2)用C 等级的人数除以班级总人数即可得到其百分比,用360°乘以其百分比得到其扇形圆心角度数;(3)画树状图可知,共有12种均等可能结果,恰好选中一男一女的有6种.然后根据概率公式求解即可【详解】解:(1)班级总人数为 人,B 等级的人数为 人,故a 的值为8;(2)∴C 等级对应扇形的圆心角的度数为.(3)画树状图如图:(画图正确)由树状图可知,共有12种均等可能结果,恰好选中一男一女的有6种.∴P (一男一女) 答:恰好选中一男一女参加比赛的概率为.本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n ,再从中选出符合事件A 的结果数目m ,然后利用概率公式计算事件A的概率为.也考查了统计图.22、(1);(2)【分析】(1)根据旋转的性质可求得,AD=AB=10,∠ABD=45°,再由平移的性质即可得出结论;(2)根据平移的性质及同角的余角相等证得∠DAE=∠CAB ,进而证得△ADE ∽△ACB ,利用相似的性质求出AE 即可.【详解】解:(1)∵线段AD 是由线段AB 绕点A 按逆时针方向旋转90°得到,∴∠DAB=90°,AD=AB ,∴∠ABD=∠ADB=45°,∵△EFG 是由△ABC 沿CB 方向平移得到,∴AB ∥EF ,∴∠1=∠ABD=45°;(2)由平移的性质得,AE ∥CG ,∴∠EAC=180°-∠C=90°,144︒121230%40÷=4020%8⨯=16360144 40⨯︒=︒ 144︒61122==12m n45︒12.5AE =∴∠EAB+∠BAC=90°,由(1)知∠DAB=90°,∴∠DAE+∠EAB=90°,∴∠DAE=∠CAB ,又∵∠ADE=∠ADB+∠1=90°,∠ACB=90°,∴∠ADE=∠ACB ,∴△ADE ∽△ACB ,∴,∵AC=8,AB=AD=10,∴AE=12.5.本题为平移的性质,旋转的性质,相似三角形的判定与性质的综合考查,熟练掌握基础的性质与判定是解题的关键.23、20°【分析】利用旋转的性质及等腰三角形的性质可得∠ABBʹ,再根据直角三角形两锐角互余可得解.【详解】解:由旋转可知:∠BABʹ=40°,AB=ABʹ.∴∠ABBʹ=∠ABʹB .∴∠ABBʹ==70°.∴∠BBʹCʹ=90°-70°=20°.本题考查了三角形的旋转,灵活利用旋转对应边相等,对应角相等且等于旋转角的性质是解题的关键.24、(1);(2)【分析】(1)直接根据概率公式计算可得;(2)画树状图得出所有等可能结果,再从中找到符合条件的结果数,利用概率公式计算可得.【详解】解: (1) 因为7, 11, 19, 23共有4个数,其中素数7只有1个,所以从7, 11, 19, 23中随机抽取1个素数,则抽到的素数是7的概率是,故答案为. (2)由题意画树状图如下:AD AE AC AB=00180402-14231414由树状图可知,共有12种等可能的结果,其中抽到的两个素数之和大于等于30的结果有8种,故所求概率本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n ,再从中选出符合事件A 或B 的结果数目m ,然后利用概率公式计算事件A 或事件B 的概率.25、(1)1;(2)【分析】(1)根据实数的混合运算法则计算即可;(2)根据分式的运算法则计算即可.【详解】解:(1)原式=2+ =1; (2).本题考查了实数的混合运算,以及分式的混合运算,熟练掌握运算法则是解答本题的关键.26、y =1(x ﹣1)1+1.【分析】根据题意设抛物线解析式为y =a (x ﹣1)1+1,代入(3,10)求解即可.【详解】解:根据题意设抛物线解析式为y =a (x ﹣1)1+1,把(3,10)代入得a (3﹣1)1+1=10,解得a =1,所以抛物线解析式为y =1(x ﹣1)1+1.本题考查了抛物线的问题,掌握抛物线的性质以及解析法、待定系数法是解题的关键.82123P ==43x x +-201222()(18--++⨯--11--1442291(1)693x x x x -⋅+-++()()()2334•33x x x x x +-+=+-43x x +=-。
2023-2024学年福建厦门九年级上学期数学期末考质检卷(一检Wood版)

准考证号:姓名:(在此卷上答题无效)2023—2024学年第一学期初中毕业班期末考试数学本试卷共6页.满分150分.注意事项:1.答题前,考生务必在试题卷、答题卡规定位置填写本人准考证号、姓名等信息.核对答题卡上粘贴的条形码的“准考证号、姓名”与本人准考证号、姓名是否一致.2.选择题每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦擦干净后,再选涂其他答案标号.非选择题答案用0.5毫米黑色签字笔在答题卡上相应位置书写作答,在试题卷上答题无效.3.可以直接使用2B 铅笔作图.一、选择题(本大题有8小题,每小题4分,共32分.每小题都有四个选项,其中有且只有一个选项正确)1.掷一枚质地均匀的骰子,骰子的六个面上分别刻有1到6的点数,下列事件中,是确定性事件的是A. 向上一面的点数是2B. 向上一面的点数是奇数C. 向上一面的点数小于3D.向上一面的点数小于72.下列方程中,有两个不相等的实数根的是A.x²=0B.x²-3x-1=0C.x²-2x+5=0D.x²+1=03.如图1,△ABC 内接于◎0,直径AD交BC 于点P, 连接OB.下列角中,等于的是A. ∠OABB. ∠ACBC. ∠CADD. ∠OPB4.关于y=(x-2)²-1(x为任意实数)的函数值,下列说法正确的是图 1A.最小值是-1B.最小值是2C.最大值是-1D. 最大值是25.某学校图书馆2023年年底有图书5万册,预计到2025年年底增加到8万册,设图书数量的年平均增长率为x, 可列方程A.5(1+x)=8B.5(1+2x)=8C.5(1+x)²=8D.5(1+2x)²=86.如图2,直线l 是正方形ABCD的一条对称轴,l 与AB,CD 分别交于点M,N.AN,BC 的延长线相交于点P, 连接BN.下列三角形中,与△NCP 成中心对称的是A.△NCBB.△BMN图2C.△AMND.△NDA数学试题第1页(共6页)7.某个正六边形螺帽需要拧4 圈才能拧紧,小梧用扳手的 卡口卡住螺帽,通过转动扳 手的手柄来转动螺帽(如图3 所示).以此方式把这个螺帽 拧紧,他一共需要转动扳手 的次数是A.4B.16图3C.24D.32 8.某航空公司对某型号飞机进行着陆后的滑行测试.飞机着陆后滑行的距离s (单位:m) 关于滑行的时间t (单位:s )的函数解析式是,则t 的取值范围是A.O≤t≤600B.20≤t≤40C.O≤t≤40 二、填空题(本大题有8小题,每小题4分,共32分)9.不透明袋子中只装有2个红球和1个黄球,这些球除颜色外无其他 差别,从袋子中随机摸出1个球,摸出红球的概率是10.抛物线y=3(x-1)²+4的对称轴是11.已知x=1 是方程x²+mx-3=0 的根,则m 的值为 12.四边形ABCD 内接于◎0,E 为 CD 延长线上一点,如图4所示,则D.O≤t≤20图4图中与∠ADE 相等的角是13. 如图5,在△ABC 中,AB=AC=5,BC=6,AD 是△ABC 的角平分线. 把△ABD 绕点A 逆时针旋转90°得到△AEF, 点B 的对应点是点E, 则点D 与点E 之间的距离是14.在平面直角坐标系xOy 中,□ABCD 的对角线交于点0.若点A 的 图5 坐标为(-2,3),则点C 的坐标为 .15.为了改良某种农作物的基因,培育更加优良的品种,某研究团队开展试验,对该种农作物 的种子进行辐射,使其基因发生某种变异.表一记录了截至目前的试验数据.表一累计获得试验成功的种子数(单位:粒)1 4 6 8 10 12 14累计试验种子数(单位:千粒)15810.5 12.5 14.5 16.5该团队共需要30粒基因发生该种变异的种子,请根据表一的数据,合理估计他们还需要 准备用以辐射的种子数(单位:千粒): 16.有四组一元二次方程:①x²-4x+3=0和3x²-4x+1=0;②x²-x-6=0和6x²+x-1=0;③x²-4=0和4x²-1=0;④4x²-13x+3=0和3x²-13x+4=0. 这四组方程具有共同特征, 我们把具有这种特征的一组一元二次方程中的一个称为另一个的“相关方程”.请写出一个 有两个不相等实数根但没有“相关方程”的一元二次方程:数学试题 第2页(共6页)三、解答题(本大题有9 小题,共86分)17.(本题满分8分解方程x²-5x+2=0.18.(本题满分8分)如图6,四边形ABCD是平行四边形,AC=AD,AE⊥BC,DF⊥AC,垂足分别为E,F.证明AE=DF.图619.(本题满分8分)先化简,再求值:,其中m=√2+1.20.(本题满分8分)如图7,AB与◎0相切于点A,OB交O0 于点C,OC=8,AC的长为2π,求BC的长.图7数学试题第3页(共6页)21.(本题满分8分)在矩形ABCD中,点E 在AD边上,∠ABE=60°, 将△ABE 绕点B 顺时针旋转得到△FBG, 使点A的对应点F 在线段BE上.(1)请在图8中作出△FBG;(要求:尺规作图,不写作法,保留作图痕迹)(2)FG 与BC交于点Q, 连接EQ,EC, 若EC=BQ, 请探究AE 与DE的数量关系.图822.(本题满分10分)某公交公司有一栋4层的立体停车场,第一层供车辆进出使用,第二至四层停车.每层的层高为6m, 横向排列30个车位,每个车位宽为3m, 各车位有相应号码,如:201 表示二层第1个车位.第二至四层每层各有一个升降台,分别在211,316,421,为便于升降台垂直升降,升降台正下方各层对应的车位都留空.每个升降台前方有可在轨道上滑行的转运板(以第三层为例,如图9所示).该系统取车的工作流程如下(以取停在311的车子为例):①转运板接收指令,从升降台316 前空载滑行至311前;②转运板进311,托起车,载车出311;③转运板载车滑行至316前;④转运板进316,放车,空载出316,停在316前;⑤升降台垂直送车至一层,系统完成取车.316转图9 停车场第三层平面示意图升降台升与降的速度相同,转运板空载时的滑行速度为1 m/s, 载车时的滑行速度是升降台升降速度的2倍.(1)若第四层升降台送车下降的同时,转运板接收指令从421 前往401取车,升降台回到第四层40s 后转运板恰好载着401的车滑行至升降台前,求转运板载车时的滑行速度;(说明:送至一层的车驶离升降台的时间、转运板进出车位所用的时间均忽略不计)(2)在(1)的条件下,若该系统显示目前第三层没有车辆停放,现该系统将某辆车随机停放在第三层的停车位上,取该车时,升降台已在316待命,求系统按上述工作流程在1分钟内完成取该车的概率.数学试题第4页 (共6页)23.(本题满分10分)正方形的顶点T 在某抛物线上,称该正方形为该抛物线的“T 悬正方形”.若直线l:y=x+t与“T 悬正方形”以T为端点的一边相交,且点T 到直线l的距离为√2(2-t),则称直线l 为该正方形的“T 悬割线”.已知抛物线M:y=-(x-1)²+m²-2m+4,其中,A(m,3),B(4-3m,3),以AB为边作正方形ABCD(点D在点A的下方).(1)证明:正方形ABCD是抛物线M的“A 悬正方形”;(2)判断正方形ABCD是否还可能是抛物线M的“B悬正方形”,并说明理由;(3)若直线l 是正方形ABCD的“A悬割线”,现将抛物线M 及正方形ABCD进行相同的平移,是否存在直线l 为平移后正方形的“C 悬割线”的情形?若存在,请探究抛物线M 经过了怎样的平移;若不存在,请说明理由.24.(本题满分12分)四边形ABCD是菱形,点O为对角线交点,AD边的垂直平分线交线段OD于点P(P 不与 0重合),连接PC,以点P 为圆心,PC 长为半径的圆交直线BC 于点E,直线AE 与直线CD 交于点F, 如图10所示.(1)当∠ABC=60°时,求证:直线AB与◎P 相切;(2)当AO=2,AF²+EF²=16时,求∠ABC 的度数;(3)在菱形ABCD的边长与内角发生变化的过程中,若点C 与E 不重合,请探究∠AFC与∠CAF 的数量关系.图10数学试题第5页(共6页)25.(本题满分14分)请阅读下面关于运用跨学科类比进行的一次研究活动的材料:【背景】小梧跟同学提到他家附近在规划开一个超市,有同学问道:“你家附近不是已经有一个A 超市了吗?再开一个能吸引顾客吗?”这个问题引起了大家对超市的吸引力展开研究的兴趣.【过程】为了简化问题,同学们首先以“在楼层数相同、同样商品的品质和价格相同、售货服务的品质也大致相同的情况下,影响超市吸引力的主要因素”为主题对该市居民展开随机调查.结果显示:超市的占地面积、住处与超市的距离这两个因素的影响程度显著大于其他因素.大家根据调查进行了总结:①可以把“平均每周到超市购物次数p” 作为超市吸引力指标;②占地面积越大吸引力越大;③距离越大吸引力越小.在此次调查所收集到的居民平均每周到各超市购物次数的基础上,同学们进一步调查了相应超市的占地面积s (单位:m²) 及其与居民住处的距离r (单位:m), 并对p,s,r 之间的关系进行研究.一开始,同学们猜想p可能是的正比例函数,但经过检验,发现与实际数据相差较大. 这时,小梧提出:“我联想到牛顿万有引力定律,这个定律揭示了两个物体之间的引力大小与各个物体的质量成正比,而与它们之间距离的平方成反比,可以表示为 (G是引力常数),我们是不是可以作个类比,试一下看p与的关系如何?”.按他的建议,同学们利用调查所得的数据在平面直角坐标系中绘制了p与对应关系的图11 r²散点图,如图11所示.根据阅读材料思考:(1)观察图11中散点的分布规律,请用一种函数来合理估计p与的对应关系,直接写出它的一般形式;(2)为了清晰表示位置,同学们选A 超市为原点,分别以正东、正北方向为x 轴、y 轴正方向建立平面直角坐标系,规定一个单位长度代表1 m 长,则小梧家的坐标为(400,200). A 超市的占地面积为2000m², 规划中的B 超市在A 超市的正东方向.根据(1)中的对应关系,解决下列问题:① 若B 超市与A 超市距离600 m~800m,且对小梧家的吸引力与A 超市相同,求B超市占地面积的范围;②小梧家在东西向的百花巷,百花巷横向排列着较为密集的居民楼.现规划 B 超市开在距A 超市300m处,且占地面积最大为490m²,要想与A 超市竞争百花巷的居民,该规划是否合适?请说明理由.数学试题第6页(共6页)。
浙江省绍兴市柯桥区2023-2024学年九年级上学期期末数学试题(含答案)

2024年柯桥区初三分层走班分类评价数学试卷考生须知:1.全卷分试卷和答题卷二部分,考生须在答题卷上作答,全卷满分120分,考试时间120分钟.2.试卷分试卷Ⅰ(选择题),试卷Ⅱ(非选择题)两部分,共8页.试卷Ⅰ(选择题,共30分)请将本卷的答案,用铅笔在答题纸上对应的选项位置涂黑、涂满一、选择题(本题有10小题,每小题3分,共30分)1.若,则的值为( )A .B .C .4D .2.已知点与在同一平面内,的半径为6,若,则点与的位置关系是( )A .点在圆内B .点在圆上C .点在圆外D .点在圆上或圆外3.在一个不透明的袋子里装有2个白球和3个红球,它们除颜色外其余都相同,从中任意摸出1个球,则摸出的球为白球的概率是( )A .B .C .D .4.把二次函数的图象向左平移3个单位,向上平移4个单位后,得到的图象所对应的二次函数表达式为()A .B .C .D .5.为制作风筝,小明做了如图所示的风筝支架示意图,已知点、点分别在射线与上,且,则的长是( )(第5题图)A .B .C .D .:1:3m n =m m n+143443P O O 8PO =P O P P P P 132325352(1)5y x =++2(4)9y x =++2(4)9y x =-+2(2)9y x =++2(2)9y x =-+B C AD AE ,:3:7,28cm BC DE AB AD AE ==∥CE 8.4cm 11.2cm 12cm 16cm6.如图是一段圆弧,点是这段弧所在圆的圆心,为上一点,于点.若,则的长为( )(第6题图)A .B .C .D .7.二次函数的图象经过点,则,的大小关系正确的为( )A .B .C .D .8.如图,某公园为了使残疾人的轮椅行走方便,设想拆除台阶换成斜坡,又考虑安全,斜坡的坡角不得超过,此公园门前的台阶高出地面1.62米,则斜坡的水平宽度至少需( )(精确到0.1米.参考值:)(第8题图)A .9.1米B .9.5米C .9.4米D .9.0米9.已知二次函数图象上部分点的坐标的对应值如表所示:则方程的解是()A .0或6B 或C 或6D .无实数解10.如图,以为直径作半圆弧,为半圆弧的中点,现将半圆连同直径绕点逆时针旋转,记点的对应点分别为,连结,则( ) ABO C AB OC AB ⊥D 3AB CD == AB6π4π3π26y x x c =-+()()()1231,,2,,5,A y B y C y -1y 23,y y 312y y y >>231y y y >>123y y y >>132y y y >>10︒MN sin100.17,cos100.98,tan100.18︒≈︒≈︒≈()20y ax bx c a =++≠(),x y 2 2.390ax bx ++=6-AB C C 30︒,A B ,A B '',A B AB ''A B AB ''=(第10题图)ABCD .试卷Ⅱ(非选择题,共90分)二、填空题(本题有6小题,每小题4分,共24分)11.线段和的比例中项是______.12.如图,已知,请添加一个条件______,使得.(第12题图)13.如图,点在上,,则______.(第13题图)14.若三个边长为1的正方形如图放置在内,点为直角顶点,三点都是正方形的顶点,点在边上,点在边上,右侧小正方形的一边在边上,则直角边的长为______.(第14题图)15.如图,是半圆的直径,是半圆的弦,沿弦折叠交直径于点,此时,则的长为______.1-251122312∠=∠ABC ADE △∽△,,A B C O 120BOC ∠=︒A ∠=Rt ABC △C ,,D E F ,D E AB F AC AC AC AB BC BC =BC BC AB D 6BD =AD(第15题图)16.如图,为平面直角坐标的原点,直线与两坐标轴交于两点,,,若的圆心在直线上,且与所在直线相切,则圆心的坐标是______.(第16题图)三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)17.18.为响应国家“双减”政策,大力推行课后服务,丰富学生课后生活,某校开设A 班剪纸、B 班戏曲、C 班武术、D 班围棋四门特色课程,甲、乙两位同学各需选择一门课程学习.(1)求甲同学选择A 班剪纸课的概率.(2)利用树状图或列表法,求甲、乙两人选择同一门课程的概率.19.如图,在平面直角坐标系中,已知的三个顶点分别是,.(第19题图)(1)请画出将绕点顺时针旋转后得到的.(2)在(1)的条件下,求扇形的面积(结果保留).20.绍兴大善塔“风韵独秀”,为测得大善塔的高度,某校数学社团开展实践活动.他们利用无人机在塔树连C AB ,A B 8AC =10AB =O 13y x =O ,AB AC O 45tan 45sin 30︒-︒+︒ABC △()()1,4,3,2A B --()2,1C -ABC △O 90︒111A B C △1OAA π线的正上方处悬停,在同一平面内,,点在一条直线上,为的中点,米,测得塔顶的俯角为37°,树顶的俯角为60°,树高为11米,求塔高的值.(参考数据:,)(第20题图)21.已知二次函数(1)若二次函数图象与轴交于点.求二次函数的表达式.(2)当时,的最小值为,求的值.22.如图,为圆的直径,点为的中点,连结,过点作,交的延长线于点.(第22题图)(1)求证:是圆的切线.(2)延长交的延长线于点,若,求直径的长.23.利用素材解决:《桥梁的设计》问题驱动某地欲修建一座拱桥,桥的底部两端间的水面宽,称跨度,桥面最高点到的距离称拱高,拱桥的轮廓可以设计成是圆弧型或抛物线型,若修建拱桥的跨度米,拱高米.BC Q A B C D Q 、、、、PQ BC ⊥B P C 、、P BC 60BC =A D CD AB sin 370.60︒≈cos370.80,tan37 1.73︒≈︒≈≈()2(2)8.0y a x a a =--≠y ()0,4C 14x -≤≤y 8-a AB O D BCAD D DE AC ⊥AC E DE O ED AB F 4,6BF DF ==AB AB L =ABCD h =32L =8h =设计方案方案一方案二设计类型圆弧型抛物线型任务一设计成圆弧型,求该圆弧所在圆的半径.设计成抛物线型,以AB 所在直线为x 轴,AB 的垂直平分线为y 轴建立坐标系,求桥拱的函数表达式.任务二如图,一艘货船露出水面部分的横截面为矩形,测得米,米.请你通过计算说明货船能否分别顺利通过这两座桥梁.24.如图,圆的弦,点为圆外一点,连结分别交圆于点,点,,连结 图1 图2(1)如图1,若圆的半径5,,求的长;(2)如图2,若①求的值;②求圆的半径.2023学年第一学期九年级期终学业评价调测试卷答案及评分标准总分:120分一、选择题(每小题3分,共30分)题号12345678910EFGH 6.1EF =16EH =O 8AB =E ,BE AE O C D 30E ∠=︒CD90ABC ∠=︒CD CD =CE AEO答案A C C A D B D D B A二、填空题(每小题4分,共24分)11.1 12.或或 13.120° 14.15.4 16.或三、解答题(共66分)17.解:原式.18.解:(1)甲同学选择A班剪纸课的概率是.(2)画树状图如下:共有16种等可能的结果,其中甲,乙两人选同一门课程的结果有4种,∴甲和乙选择同一个课程的概率为.19.解:(1)图略(2).∴.20.解:如图:延长交于点,延长交于点,为的中点,,由题意得:,在中,.,B ADE ∠=∠C E ∠=∠AB AC AD AE =3+44,3⎛⎫ ⎪⎝⎭()9,3112=⨯-+111122=-+=1441164=OA == 29017173603604OAA n r S πππ'-===扇形CD GH E BA GH F P BC 30BP CP ∴==,,30CE GH PQ BC EQ PC ⊥⊥∴==Rt DEQ △60EQD ∠=︒tan 60ED EQ ∴=⋅︒=,在中,,,(米)塔高的值为40.4米.21.解:(1)把代入解析式,得,二次函数的解析式为.(2)当时,当有最小值,把代入得当时,当有最小值.把代入得或.22.解:(1)连接为的中点,,即..,,即是的切线.(2)连接,,,.,,,即是直径的长5.23.解:任务一方案一,设圆的半径为米,在中,,(米)方案二,∵顶点C 坐标为,设桥拱的函数解析式为11BF CE DE CD ∴==+=+Rt QFA △37FQA ∠=︒tan 370.753022.5AF QF ∴=⋅︒≈⋅=1122.511.540.4AB BF AF ∴=-=+-=-≈∴AB ()0,4C 1a =-∴244y x x =-++0a >2,x y =8-()2,8-1a =0a <1,x y =-8-()1,8--8a =-1a ∴=8a =-,OD D BC CAD DAB OA OD∴∠=∠= ,,DAO ADO CAD ADO ∴∠=∠∴∠=∠OD AE ∥,90DE AC AED ⊥∴∠=︒ OD AE ∥180AED EDO ∴+∠=︒90EDO ∴∠=︒DE O ,,DB OD OB ODB OBD =∴∠=∠ 90ODB BDF ∠+∠=︒ 90DAB DBA ∠+∠=︒,,FDB DAB DFB AFD DBF ADF ∴∠=∠∠=∠∴ △∽△DF BF AF DF∴=4,6BF DF == 9,5AF AB AF BF ∴==-=O AB r Rt OBD △222(8)16r r -+=20r ∴=()0,828y ax =+代入得,.函数解析式为.任务二方案一,如图,由上得,在中,.能通过.(判断高度也可)方案二,如图建立直角坐标系,当H 点的横坐标时,,不能通过.24.(1)连结为直径10.,在中,.(2)①∵四边形内接于圆,()32,16,16,0AB OB B ==∴ 132a =-∴21832y x =-+20,12 6.118.1OH OM ==+=Rt OHM△8MH ∴==>∴8x >2186 6.132y x =-+=<∴,90,AC ABC AC ∠=︒∴ 6,90BC ADC ∴=∠=︒30,E BE ∠=︒∴=6CE ∴=-Rt CDE△132CD CE ==-ABCD O 180B ADC ∴∠+∠=︒,②过作交圆于点,连结弧弧为正三角形过作180,CDE ADC CDE B∠+∠=∴∠=∠ ,E E ECD EAB ∠=∠∴ △∽△CE CD AE AB ∴===C CF AE ∥O F ,,,,AF BF OB OF AC 30,,60FAB FCB E ACF CAD BOF ∴∠=∠=∠=︒∠=∠∠=︒∴CD =,AF OBF△AF CD ∴==F ,3FH AB FH AH ⊥∴==5,BH AB AH BF OB∴=-=∴==。
2024年北京初三九年级上学期数学期末考《圆的综合》
2024年1月九上期末——圆的综合1.【东城】24.如图,AB 为⊙O 的直径,点C 在⊙O 上,∠ACB 的平分线CD 交⊙O 于点D.过点D 作DE ∥AB ,交CB 的延长线于点E .(1)求证:直线DE 是⊙O 的切线;(2)若∠BAC =30°,BC =CD 的长.2.【西城】24.如图,AB 是O 的直径,AB BC =,AC 交O 于点D ,点F 在OD 的延长线上且12FAD ABC ∠=∠.(1)求证:AF 是O 的切线;(2)若8AF =,4DF =,求AC 的长.3.【海淀】25.如图,AB 为半圆O 的直径,点C ,D 在半圆O 上,直线CM 与半圆O 相切于点C ,//CM AD .(1)若MCD ∠α=,求COA ∠的大小(用含α的式子表示);(2)过点O 作OE CD ⊥交CM 于点E ,交CD 于点F ,若//CD AB ,6AB =,求CE 的长.4.【朝阳】24.如图,AC ,BD 是圆内接四边形ABCD 的对角线,AC ⊥BD 于点E ,BD 平分∠ADC .(1)求∠BAD 的度数;(2)点P 在DB 的延长线上,P A 是该圆的切线.①求证:PC 是该圆的切线;②若PA =AC =3,直接写出PD 的长.5.【石景山】24.如图,在ABC △中,AB AC =,以AB 为直径的O 交BC 于点D ,交AC 于点E ,点F 在AC 的延长线上,12CBF BAC ∠=∠.(1)求证:BF 是O 的切线;(2)若5AB =,1tan 2CBF ∠=,求CE 的长.6.【丰台】24.如图,△ABC 中,AB =AC ,以AB 为直径作⊙O 交BC 于点D ,作DE ⊥AC 交AC 于点E ,延长ED 与AB 的延长线交于点F .(1)求证:DE 是⊙O 的切线;(2)若△ABC 为等边三角形,AE=3,求⊙O 半径的长.7.【昌平】24.如图,AB 是⊙O 的直径,点C 在⊙O 上,点D 为 AC 的中点,过点D 作⊙O 的切线,交BC 延长线于点P ,连接OD 交AC 于点E .(1)求证:四边形DECP 是矩形;(2)作射线AD 交BC 的延长线于点F ,若tan ∠CAB =43,BC =6,求DF 的长.8.【通州】25.如图,点C 在以AB 为直径的O 上,CD 平分ACB ∠交O 于点D ,交AB 于点E ,过点D 作DF AB ∥交CO 的延长线于点F .(1)求证:直线DF 是O 的切线;(2)若30A ∠=︒,43AC =,求DF 的长.24题图9.【房山】24.如图,AB是⊙O的直径,AC,BC是弦,点D在AB的延长线上,且DCB DAC∠=∠,⊙O的切线AE与DC的延长线交于点E.(1)求证:CD是⊙O的切线;(2)若⊙O的半径为2,30∠=︒,求AE的长.D10.【大兴】24.如图,AB是⊙O的直径,点C在⊙O上,连接AC,BC,过点O作OD⊥BC于点D,过点C作直线CE交OD的延长线于点E,使得∠E=∠B.(1)求证:CE是⊙O的切线.(2)若DE=6,CE=35,求OD的长.11.【门头沟】25.如图,△ABC内接于⊙O,AB为直径,点D在⊙O上,过点D作⊙O切线与AC的延长线交于点E,ED∥BC,连接AD交BC于点F.(1)求证:∠BAD=∠DAE;(2)若AB=6,AD=5,求DF的长.12.【燕山】24.如图,在△ABC中,∠ACB=90°,点D在AB上,以AD为直径作⊙O与BC相切于点E,连接DE并延长交AC的延长线于点F.(1)求证:AF=AD;(2)若CE=4,CF=2,求⊙O的半径.13.【顺义】25.如图,AB为⊙O的弦,点C为AB的中点,CO的延长线交⊙O于点D,连接AD,BD,过点D作⊙O的切线交AO的延长线于点E.(1)求证:DE∥AB;(2)若⊙O的半径为3,tan∠ADC=,求DE的长.14.【密云】24.如图,⊙O是△ABC的外接圆,∠ABC=45°,连接OC交AB于点E,过点A作OC的平行线交BC延长线于点D.(1)求证:AD是⊙O的切线;(2)若⊙O的半径为4,AD=6,求线段CD的长.15.【平谷】24.如图,AB 为⊙O 的直径,弦CD ⊥AB 于H ,连接AC 、AD ,过点A 作⊙O 的切线与∠ADC 的平分线相交于点E ,DE 交AB 于点G ,交AC 于点F ,交⊙O 于点M ,连接AM .(1)求证:AC=AD ;(2)若22tan =∠AMD ,CD=4,求AF 长.。
2024北京西城区初三(上)期末道法试卷及答案
北京市西城区2023—2024学年度第一学期期末试卷九年级道德与法治答案及评分参考2024.1第一部分(共40 分)第二部分(共60分)21.(12分)(1)我国的综合创新能力显著提升,我国已进入创新型国家行列,我国与创新强国相比差距在缩小,我国要建成世界科技创新强国任重道远。
(4分。
一点2分,两点即可)(2)示例:国家积极实施科教兴国战略、人才强国战略、创新驱动发展战略,提高劳动从业人员的素质,培养创新型人才;国家支持重点、关键、前沿领域的发展,增强自主创新能力,走中国特色自主创新道路;企业是推动创新创造的生力军,企业加强科研投入,创建自主品牌,不断提升企业创新能力;万人科技论文指数不断提升,体现了国家尊重保护知识产权,尊重劳动、保护创新等。
(8分)22.(6分)示例:居委会可以召集三栋楼的居民代表,开一个制定安装方案的议事会,让大家一起商量,最大限度地取得一致意见。
建充电桩是关系小区居民切身利益的事情,但是居民对充电桩建在哪里有不同的意见,产生了分歧,有事好商量,众人的事情众人商量,这是人民民主的真谛。
居民在议事过程中,充分表达观点,交流彼此想法,在民主协商的过程中凝聚共识,尽可能形成相对满意的安装方案。
(6分)23.(14分)(1)可以从法治的作用、弘扬中华传统美德、培育和践行社会主义核心价值观、共享示例:有利于维护公民的基本权利,使人们安全、有尊严的生活;符合社会公平正义的要求,有利于解决社会矛盾,维护社会稳定。
有利于弘扬中华优秀传统美德,以法治承载道德理念,强化法律对道德建设的促进作用。
有利于培育和践行社会主义核心价值观,引领社会全面进步。
人口老龄化加剧是我国人口状况的新特点,法律回应的急难愁盼问题,体现了积极适应老龄化发展,切实保障老年人的生活质量。
法律规定惠及全体社会成员,有利于保障人民共享发展成果,满足人民对美好生活的向往。
北京市西城区2023—2024学年度第一学期期末试卷九年级道德与法治答案及评分参考第1页(共2页)(2)示例:政府依法行政,加强无障碍环境建设。
初三上学期期末试卷【三篇】
【导语】期末考试是指每个学期快结束时,学校往往以试卷的形式对各门学科进⾏该学期知识掌握的检测,对上⼀学期知识的查漏补缺,⼀般由区或市统考,也可能是⼏个学校进⾏联考。
下⾯是为您整理的初三上学期期末试卷【三篇】,仅供⼤家参考。
初三上学期物理期末试卷 ⼀、选择题(每题3分,共36分) 1.以下物态变化现象中,吸热的是() A.春天,冰雪消融汇成潺潺流⽔B.夏天,清晨草叶上出现晶莹的露珠 C.秋天,⾬后泰⼭上出现缥缈的云雾D.冬天,室内窗玻璃上出现美丽的冰花 2.关于内能及其利⽤,下列说法正确的是() A.温度⾼的物体内能⼀定⼤B.做功和热传递都可以改变物体的内能 C.⽐热容跟物体吸收或放出的热量有关D.热机的做功冲程是将机械能转化为内能 3.如图,是⼀个能吹冷风、温风、热风的电吹风的简化电路,其中M是电动机,通电后能吹风,R1、R2是阻值相等的发热电阻丝,通电后能发热,电吹风接通电源且开关S闭合后() A.若闭合S1、S2,则吹出的是冷风 B.若闭合S1、S2,则吹出的是温风 C.若闭合S1或S2,则吹出的是温风 D.若断开S1、S2,则吹出的是温风 4.通常情况下,关于⼀段粗细均匀的镍铬合⾦丝的电阻,下列说法中正确的是() A.合⾦丝的电阻跟该合⾦丝的长度有关 B.合⾦丝的电阻跟合⾦丝的横截⾯积⽆关 C.合⾦丝两端的电压越⼤,合⾦丝的电阻越⼩ D.通过合⾦丝的电流越⼩,合⾦丝的电阻越⼤ 5.如图是⼀种可测定油箱内油⾯⾼度的装置,R′是定值电阻,R是滑动变阻器,它的⾦属划⽚是杠杆的⼀端,油量表由电流表改装⽽成,通过两只电表的⽰数变化可以反映油⾯的⾼度变化,关于此装置的⼯作原理,下列说法中正确的是() A.当油⾯⾼度升⾼时,油量表⽰数减⼩ B.当油⾯⾼度升⾼时,电压表⽰数增⼤ C.当油⾯⾼度降低时,油量表⽰数增⼤ D.当油⾯⾼度降低时,电压表⽰数不变 6.下列说法正确的是() A.可以⽤湿⽑⼱擦点亮的电灯 B.家⽤电器的⾦属外壳应该接在零线上 C.试电笔可以检测出家庭电路的零线和⽕线 D.绝缘体不导电是因为内部没有电⼦ 7.下列数据中,最接近实际情况的是() A.普通家⽤照明灯的⼯作电流约为2AB.电饭锅加热档的功率约为100W C.家⽤电风扇的额定功率约为2000WD.⼀节新⼲电池的电压约为1.5V 8.甲、⼄两个灯泡的铭牌分别是“PZ220﹣25”、“PZ220﹣100”,关于这两个灯泡的描述正确的是() A.甲灯的灯丝粗,电阻⼤B.甲灯的灯丝细,电阻⼤ C.⼄灯的灯丝细,电阻⼩D.⼄灯的灯丝粗,电阻⼤ 9.下列电器中,利⽤电流热效应来⼯作的是() A.电冰箱B.洗⾐机C.电视机D.电饭锅 10.关于磁场,下列说法中正确的是() A.磁体周围的磁感线从磁体N极发出,回到磁体S极 B.磁极间的相互作⽤不都是通过磁场发⽣的 C.磁感线是磁场中真实存在的⼀些曲线 D.地磁场的N极在地理北极附近,S极在地理南极附近,与地球两极并不完全重合 11.对于图中所⽰的四幅图,以下说法正确的是() A.甲中通电导线周围存在着磁场,如果将⼩磁针移⾛,该磁场将消失 B.⼄中闭合开关,通电螺线管右端为N极 C.丙中闭合开关,保持电流⽅向不变,对调磁体的N、S极,导体的运动⽅向不变 D.丁中绝缘体接触验电器⾦属球后验电器的⾦属箔张开⼀定⾓度,说明该棒带正电 12.关于⼲电池,下列说法中正确的是() A.有的⼲电池提供直流电,有的⼲电池提供交流电 B.⼲电池是把电能转化为化学能的装置 C.常⽤的1号、2号、5号、7号⼲电池的电压都是1.5V D.电路两端有电压电路中就⼀定有电流 ⼆、填空题(每空2分,共18分) 13.电视⽚《⾆尖上的中国》展现了博⼤精深的中国饮⾷⽂化.厨师烹饪排⾻时,主要通过__________(选填“热传递”或“做功”)的⽅式改变了排⾻的内能,使排⾻的温度__________,从⽽由⽣到熟. 14.物理学中,通过其效应对⾃然界中看不到的事物进⾏研究,这种研究⽅法叫转换法.如我们通过⼩灯泡是否发光来判断灯丝中有⽆__________通过;通过电磁铁吸引铁钉的多少来显⽰电磁铁的磁性__________. 15.如图所⽰电路,若在甲、⼄两处分别接⼊电压表,闭合开关S,甲、⼄两表读数之⽐为1:2,此时R1与R2________联;断开两开关S,在甲、⼄两处分别接⼊电流表,⼄处电流表⽰数为0.3A,则⼲路电流为__________A. 16.⼩明家的电⼦式电能表标有“3200imp/(kW•h)”等字样(imp表⽰电能表指⽰灯闪烁的次数).他将标有“220V1000W”的电饭煲单独接⼊家庭电路,正常⼯作⼀段时间后,电能表指⽰灯闪烁了800次,电饭煲消耗的电能是__________kW•h,其正常⼯作的时间是__________h. 17.右图中测电笔的两种使⽤⽅法,正确的是__________. 三、实验探究题(每空2分,共26分) 18.在探究“电流与电压、电阻的关系”实验中, (1)请将图的事物电路连接完整; (2)闭合开关S前,应把滑动变阻器的滑⽚P置于______(选填“A”或“B”)端; (3)在探究“电流与电压的关系”实验中,滑动变阻器除了保护电路外,其作⽤主要是_______________________. 实验所测数据如表,分析数据可得结论是:_________________________。
2024年北京初三九年级上学期数学期末考《代数综合》
2024年1月九上期末——代数综合1.【东城】26.在平面直角坐标系xOy 中,点(2,c )在抛物线2(0)y ax bx c a =++>上,设该抛物线的对称轴为直线x t =.(1)求t 的值;(2)已知11()M x y ,,22()N x y ,是该抛物线上的任意两点,对于11m x m <<+,212m x m +<<+,都有12y y <,求m 的取值范围.2.【西城】26.在平面直角坐标系xOy 中,()1,A t y ,()1,B t y+,()23,C t y +三点都在抛物线224y ax ax =-+(0a >)上.(1)这个抛物线的对称轴为直线________.(2)若132y y y >≥,求t 的取值范围;(3)若无论t 取任何实数,点A ,B ,C 中都至少有两个点在x 轴的上方,直接写出a 的取值范围.3.【海淀】26.在平面直角坐标系xOy 中,点()1,A m -,点()3,B n 在抛物线2(0)y ax bx c a =++>上.设抛物线的对称轴为直线x t =.(1)当2t =时,①直接写出b 与a 满足的等量关系;②比较m ,n 的大小,并说明理由;(2)已知点()0,C x p 在该抛物线上,若对于034x <<,都有m p n >>,求t 的取值范围.4.【朝阳】26.在平面直角坐标系xOy 中,点(x 1,m ),(x 2,n )在抛物线y =ax 2+bx +c (a >0)上,设抛物线的对称轴为x =t .(1)若对于x 1=1,x 2=3,有m =n ,求t 的值;(2)若对于t -1<x 1<t ,2<x 2<3,存在m >n ,求t 的取值范围.5.【石景山】26.在平面直角坐标系xOy 中,抛物线2(0)y ax bx c a =++>经过点(33)A a c +,.(1)求该抛物线的对称轴;(2)点1(12)M a y -,,2(2)N a y +,在抛物线上.若12c y y <<,求a 的取值范围.6.【丰台】26.在平面直角坐标系xOy 中,点(m +2,1y ),(6,2y )为抛物线22y x mx n =-+上两个不同的点.(1)求抛物线的对称轴(用含m 的式子表示);(2)若12y n y <<,求m 的取值范围.7.【昌平】26.在平面直角坐标系xOy 中,点(0,3),(6,1y )在抛物线()02≠++=a c bx ax y 上.(1)当31=y 时,求抛物线的对称轴;(2)若抛物线()02≠++=a c bx ax y 经过点(-1,-1),当自变量x 的值满足-1≤x ≤2时,y 随x 的增大而增大,求a 的取值范围;(3)当0>a 时,点(m -4,2y ),(m ,2y )在抛物线c bx ax y ++=2上.若2y <1y <c ,请直接写出m 的取值范围.8.【通州】26.在平面直角坐标系xOy 中,()11,P x y ,()22,Q x y 是抛物线2221y x mx m =-+-上任意两点.(1)求抛物线的顶点坐标(用含m 的式子表示);(2)若12x m =-,25x m =+,则1y ______2y ;(用“<”,“=”,或“>”填空)(3)若对于114x -≤<,24x =,都有12y y ≤,求m 的取值范围.9.【房山】26.在平面直角坐标系xOy 中,点(1)m ,,(3)n ,在抛物线24(0)y ax bx a =++>上,设抛物线的对称轴为x t =.(1)当m n =时,求抛物线与y 轴交点的坐标及t 的值;(2)点00()(3)x n x ≠,在抛物线上,若4m n <<,求t 的取值范围及0x 的取值范围.10.【大兴】26.在平面直角坐标系xOy 中,点(2,m )在抛物线2(0)y ax bx c a =++>上,设抛物线的对称轴为x=t .(1)当m =c 时,求t 的值;(2)点(-1,y 1),(3,y 2)在抛物线上,若c <m ,比较y 1,y 2的大小,并说明理由.11.【门头沟】26.在平面直角坐标系xOy 中,点M (1x ,1y ),N (2x ,2y )为抛物线2y ax bx c=++(a >0)上任意两点,其中12x x <.(1)若抛物线的对称轴为x =2,当12x x 、为何值时,12y y c ==;(2)设抛物线的对称轴为x =t ,若对于124x x +>,都有12y y <,求t 的取值范围.12.【燕山】26.在平面直角坐标系xOy 中,点M (-1,m ),N (3,n )在抛物线2y ax bx c =++(a >0)上,设抛物线的对称轴为x =t .(1)若m =n ,求t 的值;(2)若c <m <n ,求t 的取值范围.13.【顺义】26.在平面直角坐标系xOy 中,抛物线y =x 2﹣2ax +a 2﹣4与x 轴交于A ,B 两点(点A 在点B 左侧).(1)若a =1,求抛物线的对称轴及A ,B 两点的坐标;(2)已知点(3﹣a ,y 1),(a +1,y 2),(﹣a ,y 3)在该抛物线上,若y 1,y 2,y 3中有且仅有一个大于0,求a 的取值范围.14.【密云】26.在平面直角坐标系xOy 中,点(2,m )和(5,n )在抛物线y =x 2+2bx 上,设抛物线的对称轴为x=t .(1)若m=0,求b 的值;(2)若mn <0,求该抛物线的对称轴t 的取值范围.15.【平谷】26.在平面直角坐标系xOy 中,二次函数mx x y 22-=的图象上两个点A ),(11y x ,B ),(22y x ,点A 、B 之间的部分(包含点A 、点B )记作图象G ,图象G 上y 的最大值与最小值的差记作y G .(1)求这个二次函数的对称轴(用含m 的代数式表示);(2)当m=1,x 1=0,x 2=3时,求y G 的值;(3)当121-=m x ,122+=m x 时,恒有y G >21y y -,求m 的取值范围.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
期末测试一、填空题1·下列现象各展什么物态变化过程?(1)水结成冰:___________________________;(2)植物上的露珠:_________________;(3)树枝上的"雾淞":_________________________2·冬天在户外说话时,常看见人们的口中呼出"白气",这是由水蒸气___________形成的,它实际上就是由大量的浮于空气中的_______________组成的·3·家里的电灯·电视机、电冰箱等都是__________联在电路中的;控制电灯的开关与电灯是____________联的·4·导体两端的电压为6V,通过它的电流是0·4A,则该导体的电阻是_____________n;若导体两端的电压变为l2V,则通过它的电流为_____________A;若将电路断开,则通过导体的电流为________________A,此时该导体的电阻为_______________n·5·在图所示的电路中,闭合S2,灯L1、L2组成____________电路;若打开S2、闭合S1、S2,灯L1、L2组成______________电路;若同时闭合S1、S2、S3会发生____________.6·如图所示,发生触电的原因是__________________;三孔插座比两孔插座多的那个孔应接____________(选填"火线"零线”)7.很多宾馆的卫生间装有热风干手器,它可以很快把湿手吹两个理由:____________________________________________________________8·周末,小宇在家开着空调看电视,妈妈打开电饭锅做饭,此时家里的自动空气开关"跳闸"了,则"跳闸"的原因可能是__________________·根据小宇家自动空气开关上铭牌的数据,他家的电路允许使用的用电器总功率最大为__________________w·9·小强家中的电能表5月初的示数如图3所示,5月份交了48·8元电费,若每千瓦·时电费为0·8元,则小强家6月初电能表的示数为_________________kW·h为根据电能表的铭牌,你还能谈到哪些信息?请写出其中两条:(1)____________________________(2)_______________________________10·"220V6OW"的灯泡正常工作时,它的电功率是______________W;如果把它接在1lOV的电路中,它的实际功率为______________W·二、选择题1.下列单位中,电功的单位是( ),A·安(A) B·伏(V) C·瓦(W) D·千瓦·时(kW·h) 2·以下温度最接近20℃的是( )·A·冰水混合物的温度 B·人的正常体温C·人感到舒适的房间温度 D·上海盛夏中午的室外温度3·如图所示,甲、乙、丙三种固体,质量相等,用相同的加热器加热,且在加热过程中,相同时间内吸收的热量相等,从其温度随时间的变化图像可以判断( )·A·甲、丙是非晶体、甲的熔点比丙高B·甲、丙是晶体、甲的熔点比丙低C·甲、丙是晶体、甲的熔点比丙高D·甲、丙是非晶体、甲的熔点比丙低4·下列关于蒸发的说法中,正确的是( )·A·蒸发是指在液体表面和内部同时发生的汽化现象B·O℃时由于气温太低水不能蒸发C·结冰的衣服变干,是先熔化成水,水再蒸发掉D·用管道代替沟渠输水,能减少蒸发,节约水资源5·夏天,坐在湖边的树底下,风吹来使人感到凉爽,对其原因,下列分析中,正确的是A·水的比热容大,湖水吸热温度升高较快B·树叶里水蒸发带走大量的热C·风减慢了人体表面汗液的蒸发D·地形宽广,不利于散热6·甲、乙、丙三根电阻丝由同种材料制成,甲、乙同样粗,但乙较长;乙、丙同样长,但丙较细,则它们的电阻值( )·A·可能一样大 B·丙最大 C·乙最大 D·甲最大7·甲灯标有"36V6OW",乙灯标有"220V6OW",若分别在额定电压下发光,则A·甲灯比乙灯更亮 B·乙灯比甲灯更亮C,两盏灯一样亮 D·无法确定谁更亮8·在图所示的四帽图中,符合安全用电的事例是( )·9·如图所示,当开关S2闭合后,则电流表的示数( )A·A1变小、A2不变B·A1不变、A2变大,C·A1不变、A2不变D·A1变大、A2变大三、实验题1.仔细观察图中所示的情景,回答下列间题:(1)________________图用来探究两种电荷的作用规律;(2)_______________图用来探究晶体的熔化·(3)______________ 图说明做功可以改变物体的内能·2·如图所示,长短、粗细都相同的锰铜线AB和镍铬合金线CD,先后接入电路,接AB时电流表的示数大,这表明AB的电阻_____________·两次实验屯流示数不同,说明导体的电阻与__________________有关·3·图为探究"电流与电阻的关系"的实验电路图:(1)为了达到探究的目的,实验过程中必须保持_____________不变;(2)当开关S闭合后,电压表的示数是2V,电流表的示数是0·4A·现在将阻值为5n的电阻R,换成阻值为lOn的电阻R,接人电路来进行探究,则下一步进行的操作是:_____________4·在"观察水的沸腾"实验中:(1)图(a)所示是某同学先用温度计测小烧杯中水的初温的操作图·A是操作过程,B是读数过程,C是温度计显示的温度·1A图中操作的错误是: ____________________________2B图读数中的错误是:____________________________;3若操作正确,根据C图可知此时烧杯中水实际的温度是________________℃·(2)该同学在做实验时,如图 (b)所示,发现从开始给水加热到水开始沸腾所用的时间过长,请你帮助他找出可能存在的原因·(写出两种即可)第一种可能原因:_____________________________;第二种可能原因________________________________________5·星期天,小红帮妈妈洗衣服,如何让洗过的衣服干得快,请你说出两种方法来·6·阅读下面短文:冬天,小强经常看到玻璃窗上有水珠,他总怀疑这水到底从哪儿来了学过物态变化后,他忽然想到:玻璃窗上产生的水雾可能也与水的物态变化有关·他活学活用,立即采用物理课上学到的实验探究方法,对此进行了实验探究·他准备的实验器材有:水壶和两面小镜子·并做了前期工作:把水壶中的水烧开,一个小镜子放大冰箱冷藏室,另一个放在火附近烤热待用·小强按自己的计划进行了实验,终于证实了自己的猜想,玻璃窗上水雾的产生确实与水的物态变化有关,这种物态变化是:水蒸气经过放热变成水,通过自己的实验,他终于知道了,为什么玻璃窗在冬天会有水雾生成·上述这则短文记录了小强进行科学探究的哪些环节?请说出其中的两个·(1)____________环节,文中____________________________________描述了这一环节·(2)____________环节,文中____________________________________描述了这一环节· 7·为了测定额定电压是2·5V的小灯泡的功率,小宇同学在实验时测得的数据如下表·在整理数据计算功率时发现其中一次实验结果与其他两次结果相差很大,经检查原来是有一个电流表的示数读错了·该同学选用的电流表的量程是0~0·6A·档,试回答:(1)数据表中第______________次电流表的读数错了,正确的应是__________________A;(2)第________________ 次实验测得的是小灯泡的额定功率;(3)小灯泡额定功率P额=_______________W;(4)在图(a)中的表头上画出第一次指针的位置;(5)如图 (b)所示是小宇还没连接完整的实物电路,请你在图中补画缺少的连线·(不要变动原有接线,导线不得交叉)8·在探究"影响蒸发快慢的因素"的实验过程中,同学们作出了如下的猜想;影响蒸发快慢的因素可能有:A·液体温度;B·液体表面积;C·液体上方气流流动的快慢;D·液体的种类· (1)李丽同学设计了如下实验:取两只相同的烧杯,分别盛等量的酒精,把一杯放在烈日下,另一杯放在阴凉处,一段时间后观察比较两烧杯中酒精的多少·该同学设计这个实验的目的是为了验证猜想________________;(选填”A”、B”、C"或"D")(2)请你设计一个实验来验证猜想D,要求简要写出实验方法·小明在烈日当空的海边玩耍,发现沙子烫脚,而海水却很凉·同样的太阳光照射,为什么会出现不同的结果呢?小明想:是不是沙子和海水吸热升温快慢不同呢?于是他从海边取了一些沙子和海水带回家进行探究·小明在两个相同玻璃杯中分别装上了相同质量的海水和沙子,用一个100W的白炽灯同时照射它们,并用温度计测出它们不同时刻的温度值·记录的数据如下表所示:(1)小明探究的物理问题是什么?(2)小明根据收集到的数据在方格纸上己经画出了海水的温度随时间变化的图像,如图所示·请你在同一方格纸上画出沙子的温度随时间变化的图像·(3)分析小明在探究中收集到的数据或根据数据画出的两个图像,你能得出什么探究结论?(4)小明发现"夏天,海边的沙子烫脚而海水却很凉·"请你用简咯的语言从日常生活或自然中举出一个类似的例子·四、计算题1·如图所示,电源电压为12V,R1=10n,开关S闭合后,电压表的示数为4V,求:(1)通过R1的电流;(2)R2的随值·2·电磁炉是新一代智能灶具,它以安全、卫生、高效和节能著称·在标准大气压下,一只15OOW的电磁炉正常工作时,将lkg2O℃的水加热到刚沸腾需要4min·求:(1)此过程中水吸收多少热量?(2)电流做功多少?(3)加热时电磁炉的效率约为多少?3·为了调节台灯灯光的亮度,小宇提出了一个设想,如图所示·已知灯L规格为"220VlOOW",电源电压为220V·当开关S拨向触点1时,灯泡正常发光;当开关S拨向触点2时,灯的实际功率为额定功率的一半,问:小宇的设想是否合理?(灯的电阻假设不变)。
