(完整版)历年全国I卷高考数学试题考点细目表(2013-2019年理科)
2019年卷1高考理数细目表
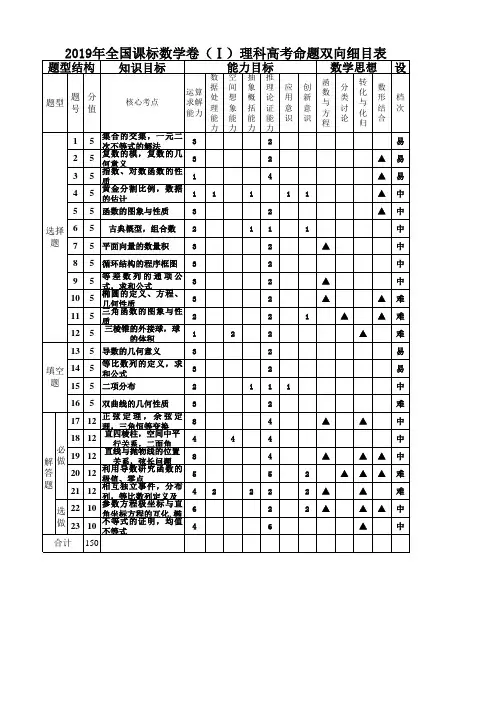
题型结构 知识目标
能力目标
数学思想 设
题型
题 号
分 值
核心考点
数
运算 求解 能力
据 处 理 能
力
空 间 想 象 能 力
抽 象 概 括 能 力
推 理 论 证 能 力
应 用 意 识
创 新 意 识
函 数 与 方 程
分 类 讨 论
转 化பைடு நூலகம்与 化 归
数 形 结 合
档 次
1
5
集合的交集，一元二 次不等式的解法
3
2
易
2
5
复数的模，复数的几 何意义
3
3
5
指数、对数函数的性 质
1
4
5
黄金分割比例，数据 的估计
1
1
2
4
1
11
▲易 ▲易 ▲中
5 5 函数的图象与性质
3
2
▲中
选择 6 5 古典概型，组合数 2
11
1
中
题 7 5 平面向量的数量积
3
2
▲
中
8 5 循环结构的程序框图 3
9
5
等差数列的通项公 式，求和公式
3
10
5
椭圆的定义、方程、 几何性质
3
11
5
三角函数的图象与性 质
2
12
5
三棱锥的外接球，球 的体积
1
13 5 导数的几何意义
3
填空 14
5
等比数列的定义，求 和公式
3
题 15 5 二项分布
2
2
中
2
▲
历年全国I卷高考数学试题考点细目表(2013-文-科)
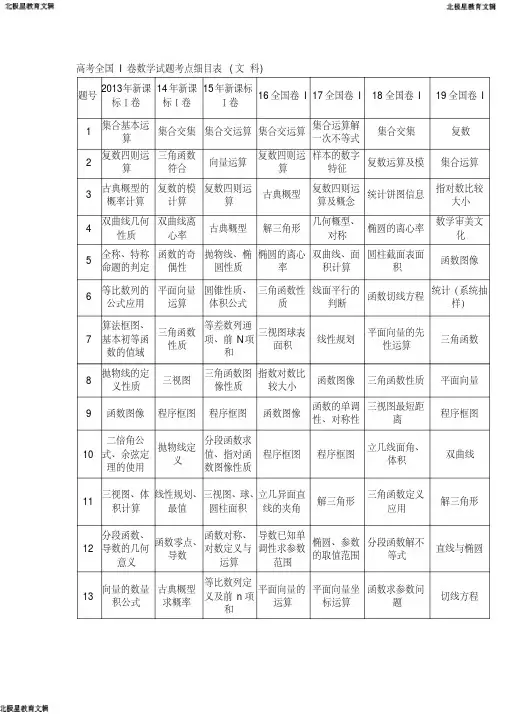
函数求参数问 题
切线方程
线性规划基 推理与证 导数的几何 三角函数求 求曲线的切
14 础知识
明
意义求切线 方程
值
线方程
线性规划
15
球体的体积 公式
分段函数、 不等式求
解
线性规划
直线与圆的 三角恒等变 直线与圆求弦
位置关系
换
长
等比数列 三角函数
双曲线定
16
三角恒等变
解三角形
义、直线与 双曲线的位
换公式
应用 置关系、最
值
线性规划
三棱锥的外 接球， 球表
解三角形求面
立体几何（点
面积
积
面距）
17
等差数列、 裂项应用
等差数列、 错位求和
解三角形 （正、余弦
定理）
等差数列通 项等比数列 证明并求和
等比数列、 等差数列
等比数列、通 项
概率与统计
用样本容量 频率分布 面面垂直证 垂直等价证 立几面面垂
18
估计总体、 茎叶图的绘
直方图、平 明及体积、
明， 作正投
直、体积与
立几翻折、面 面垂直、体积
制、分析 均数、方差 侧面积计算 影， 求体积 侧面积
等差数列
19
线面垂直、 体积计算
线线垂直、 高（体积）
计算
散点图、回 归方程
函数解析式 概率统计
相关系数、 均值与标准
差
概率统计分布 直方图
立体几何（线 面平行、点面
距）
导数的几何
高考全国 I 卷数学试题考点细目表 ( 文 科)
2013年新课 14 年新课 15 年新课标
题号 标Ⅰ卷
全国新课标1卷近五年数学(理)科高考试题考点分布表
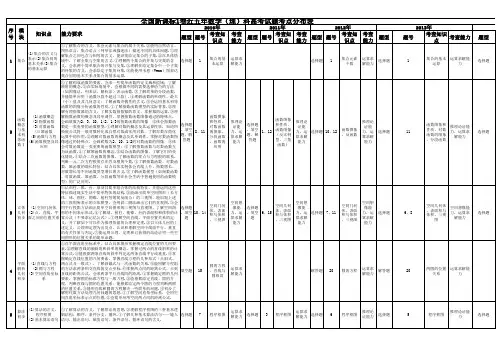
题
义，并了解如下可以作为推理依据的公理和定理.②以立体几何的上
空间几何 体、表面 积与体积 、三视图
空间想 像能 力，运 算求解 能力
选择题 、填空
题
6、15
空间几何 体、表面 积与体积 、三视图
空间想 像能
力，运 算求解
能力
选择题
7、11
空间几何 体、表面 积与体积 、三视图
空间想 像能 力，运 算求解 能力
选择题
1
集合间的基本关系及集合的基本运算.
集合的基 运算求 本运算 解能力
选择题 1
集合元素 个数
运算求 解能力
选择题
①了解构成函数的要素，会求一些简单函数的定义域和值域；了解
映射的概念.②在实际情境中，会根据不同的需要选择恰当的方法
（如图像法、列表法、解析法）表示函数.③了解简单的分段函数，
并能简单应用（函数分段不超过三段）.④理解函数的单调性、最大
序模 号块
知识点 能力要求
全国新课标1卷近五年数学（理）科高考试题考点分布表
2010年
2011年
2012年
题型 题号
考查知 识点
考查 能力
题型
题号
考查知 识点
考查 能力
题型 题号
考查知 识点
考查 能力
题型
①了解集合的含义，体会元素与集合的属于关系.②能用自然语言、
1
集合
(1)集合的含义与 表示(2)集合间的 基本关系(3)集合 的基本运算
填空题
1直线、圆的方
程，判断直线与圆的位置关系；能根据给定两个圆的方程判断两圆
的位置关系.③能用直线和圆的方程解决一些简单的问题.④初步了
历年全国I卷高考数学试题考点细目表(2013-文-科)(20200617175733)
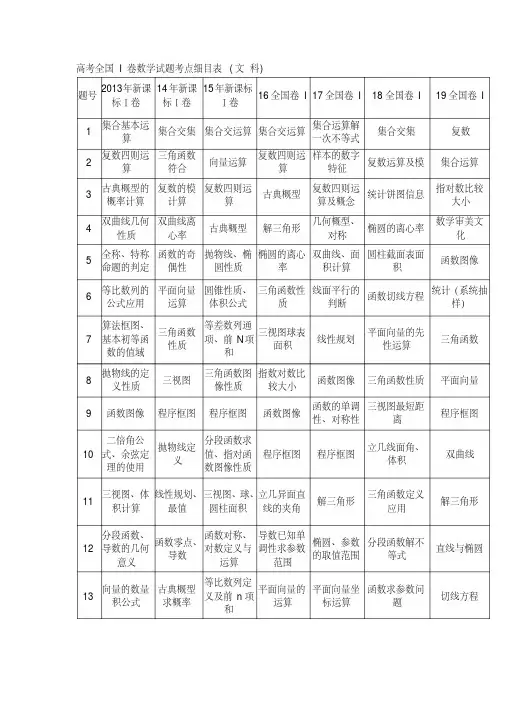
5 命题的判定 偶性
圆性质
率
积计算
积
函数图像
6 等比数列的 平面向量 圆锥性质、 三角函数性 线面平行的 函数切线方程 统计（系统抽
公式应用 运算 体积公式
质
判断
样）
算法框图、
等差数列通
7
基本初等函
三角函数 性质
项、前
N项
三视图球表 面积
线性规划
平面向量的先 性运算
数的值域
和
抛物线的定
三角函数图 指数对数比
函数求参数问 题
切线方程
线性规划基 推理与证 导数的几何 三角函数求 求曲线的切
14 础知识
明
意义求切线 方程
值
线方程
线性规划
15
球体的体积 公式
分段函数、 不等式求
解
线性规划
直线与圆的 三角恒等变 直线与圆求弦
位置关系
换
长
等比数列 三角函数
双曲线定
16
三角恒等变
解三角形
义、直线与 双曲线的位
换公式
20
意义、导数 与函数的极
直线、圆
直线与圆的 直线与抛物 直线与抛物
位置关系
线
线综合问题
值
直线与抛物 线、证角
导数、零点
椭圆定义、
函数与导数 的应用单调 函数与导数极
21
直线方ቤተ መጻሕፍቲ ባይዱ、 弦长公式的
函数、导数 函数与导数 与不等式 的应用
函数与导数 的应用
性、由不等
值、单调区间、
直线与圆
使用
式成立求参 证明不等式 数范围
22
几何证明直 线与圆相切
几何证明 圆内接四
(完整版)历年全国I卷高考数学试题考点细目表(2013-2019年理科).doc
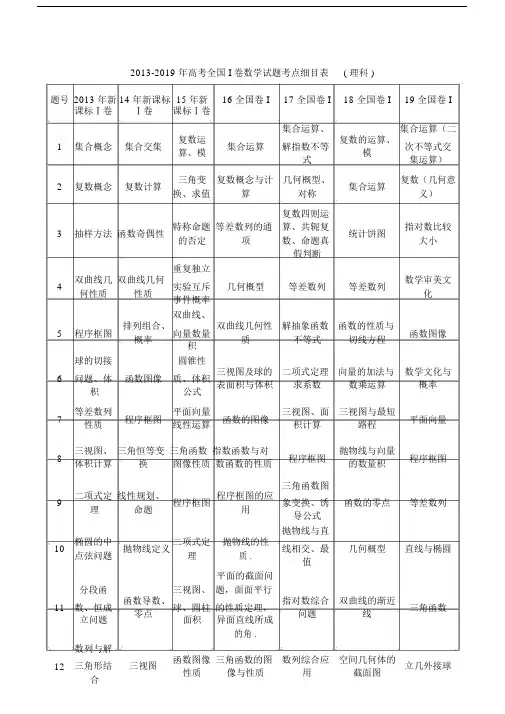
2013-2019 年高考全国 I 卷数学试题考点细目表( 理科 )题号2013 年新 14 年新课标15 年新16 全国卷 I 17 全国卷 I 18 全国卷 I 19 全国卷 I 课标Ⅰ卷Ⅰ卷课标Ⅰ卷复数运集合运算、复数的运算、集合运算（二1 集合概念集合交集集合运算解指数不等次不等式交算、模模式集运算）2 复数概念复数计算三角变复数概念与计几何概型、集合运算复数（几何意换、求值算对称义）复数四则运3 抽样方法函数奇偶性特称命题等差数列的通算、共轭复统计饼图指对数比较的否定项数、命题真大小假判断双曲线几双曲线几何重复独立数学审美文4 实验互斥几何概型等差数列等差数列何性质性质化事件概率排列组合、双曲线、双曲线几何性解抽象函数函数的性质与5 程序框图向量数量函数图像概率质不等式切线方程积球的切接圆锥性三视图及球的二项式定理向量的加法与数学文化与6 问题、体函数图像质、体积表面积与体积求系数数乘运算概率积公式7 等差数列程序框图平面向量函数的图像三视图、面三视图与最短平面向量性质线性运算积计算路程8 三视图、三角恒等变三角函数指数函数与对程序框图抛物线与向量程序框图体积计算换图像性质数函数的性质的数量积二项式定线性规划、程序框图的应三角函数图9 程序框图象变换、诱函数的零点等差数列理命题用导公式椭圆的中二项式定抛物线的性抛物线与直10 抛物线定义线相交、最几何概型直线与椭圆点弦问题理质 .值平面的截面问分段函函数导数、三视图、题，面面平行指对数综合双曲线的渐近11 数、恒成球、圆柱的性质定理，三角函数零点问题线立问题面积异面直线所成的角 .数列与解函数图像三角函数的图数列综合应空间几何体的12 三角形结三视图立几外接球性质像与性质用截面图合113 平面向量二项式定理函数奇偶向量的模及坐平面向量的线性规划切线方程性标运算模运算椭圆几何14 数列通项推理与证明性质、圆二项式定理线性规划数列求和等比数列标准方程15 三角函数平面向量线性规划等比数列性质双曲线与圆组合数概率最值的综合解三角形线性规划的应立体几何折三角函数的最16 函数最值解三角形（正弦定叠、三棱锥双曲线用值理）体积最大值数列定义解三角形求17 解三角形数列（含参）及通项、解三角形解三角形解三角形周长裂项相消立体几何频率分布直面面垂直线线垂方图、正态面面垂直证明立几面面垂面面垂直与线立几（线面平18 证明及线直，求线分布、二项及二面角直、二面角面角行二面角）线角计算面角分布求期望求概率，求概率分布正态分布、椭圆中求直线立体几何二散点图、二项分布、直线与抛物19 分布列及列，数学期望方程和证明角面角回归方程平均数与方线数学期望及实际应用相等差轨迹方抛物线切轨迹方程，直直线椭圆综求超几何分布程，直线线、直线合应用、证导数极值、零20 直线与椭圆线与椭圆关的最值，计算与椭圆关与抛物线明直线过定点系，范围问题期望值系位置关系点函数、导函数、导数与函数与导数函数、导数函数与导的应用、讨函数的单调性21 数与不等不等式的综合概率、数列与不等式数的应用论单调性及与证明不等式式应用零点问题几何证明几何证明四点共圆、直极坐标方程化几何证明圆直线与圆极坐标、参22 直线与圆线与圆的位置普通方程，曲内接四边形相切；射数方程相切关系及证明线的交点。
2013-2019年高考全国卷1理科数学试题各考点及命题分析
2013-2019年全国卷1理科数学试题各考点及命题分析2020.3.14一．考试说明：2015年开始，增加了数学传统文化知识的考察（事实上在2015，2016年的试卷中已经有所体现，），强调了试题的基础性，综合性，应用性，创新性。
新课程数学学科确定了高中数学核心素养的6个要素：数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析，对于新课标提出的新要求，教师如何落实在教育教学中是关键。
2020年考试大纲沿用2019年的，2019年题目开始向新高考过渡，突出能力的考察。
二、各知识点的考察方式及难易程度：1、集合与常用逻辑：1个小题（15年考常用逻辑），属基础题。
集合主要考察交并补，集合基本关系，还会和解不等式，求函数定义域和值域相结合。
2、复数：1个小题，属基础题。
考察复数四则运算，共轭复数、实部和虚部、模、对应的点坐标等概念。
3、函数与导数：2个小题（19年有3个小题）和1个大题，1个小题主要考查函数的奇偶性，单调性，周期性等基本性质，分段函数，函数的图像及变换，利用单调性或图像比较大小，函数与方程，一般不需求导（12年两个小题都用到导数），属基础或中档题，1个小题主要考察导数的几何意义，以及借助导数研究函数的单调性、极值、最值（简单应用），利用导数解不等式、恒成立问题、研究函数的零点问题（综合应用，多次考察），15年选择压轴，18年填空压轴，且和三角函数相结合，一般属中等或偏难题；大题主要考察导数的几何意义，以及借助导数研究函数单调性、极值、最值、零点等问题，还会和方程、不等式证明（综合法，分析法）等知识综合，通常用到构造函数法， 隐零点设而不求法，分离参数法，观察法（取特殊点分析，有时要较强观察能力），换元法，用到等价转化、分类讨论、数形结合的思想，属难题。
4、平面向量：1个小题，主要考查平面向量的线性运算（加法运算的几何意义偶尔会考），平面向量基本定理，平行和垂直，数量积，模，坐标表示和坐标运算，另外向量也可能与解析几何（圆锥曲线）等知识相结合考查，属基础题。
近五年含新课标I卷全国高考文理科数学考点分布统计表
2013-2017 年新课标 I 卷高考理科数学考点散布统计表1.全部同学，应重视基础，狠抓基础知识的复习，增强基础过关训练，复习中严格做到不超标，不超纲，不要钻牛角尖，不要做偏题，怪题，繁题，难题，保持优秀心态放心备考。
2，发挥典型题目的复习功能，平常训练应以中低档题目为主，平庸中见真功夫。
3，增强规范训练，提高解题能力，准时定量的解题训练，注意解题过程的规范化，书写要整齐，推理要有据，表达要正确，条理要清楚，主要过程不可以省，养成优秀的解题习惯，防止因失误造成丢分，边练边总结，边练边提高。
4，注意思想方法，通性通法要摆在首位，在基础扎实的状况下考虑解题技巧的提高。
5．以下是近五年全国高考卷所观察的知识点，基本覆盖了全部考点，复习中应比较这些考点逐个过关训练。
要果断做到一不怕苦，二不怕累，不行三天捕鱼两天晒网，要有恒心，学贵有恒。
题次20132014201520162017复数运算：分求不等式集会合的运算1会合运算会合运算（交集、并式、除法、模合的交集集）复数运算（模三角函数（诱传统文化中复数四则运导公式、正弦复数相等、模2相等方程、虚的概率问题算和角公式逆的运算部）( 几何概率 )用）随机抽样方函数奇偶性特称命题的等差数列及复数的观点3及运算与简式判断否认其运算易逻辑双曲线（离心双曲线（方独立重复试等车问题、几等差数列结4率、渐近线求程、点到渐近验；互斥事件何概型合公式运算解）线距离）和概率公式程序框图（条古典概型概向量数目积；双曲线的性函数的奇偶5率计算（计数双曲线的标件）质性和单一性原理）准方程球体积应用函数图像判传统文化实三视图及球二项式定理6断（动向几何际应用题、圆的表面积与（排水转变）求系数背景）锥体积体积等差数列基程序框图（循平面向量的函数图像的三视图空间7辨别、利用了几何体求表本量运算环）几何运算导数面积三视图与体三角恒等变由三角函数指数函数与8图像求单一对数函数的程序框图积换递减区间性质全称、特称命9二项式系数题真假判断程序框图程序框图与三角函数平最大问题（线性规划算法事例移问题背景）10椭圆方程（中直线与抛物二项式定理抛物线的性抛物线与过点弦）线地点关系睁开式的系质焦点弦长问数题平面的截面含参不等式含参函数零三视图、球、问题，面面平指数与函数11恒建立（分段点散布（求解圆柱的表面行的性质定联合函数）参数范围）积理，异面直线所成的角数列判断（综三视图（求最导数的综合三角函数的数列新奇规12应用、零点、性质（零点、合三角形）长的棱）律取值范围单一性）向量数目积项的系数（两偶函数，求参向量的数目向量模长运13个二项式乘积及坐标运运算数，算积）算通项求解（退椭圆的极点、二项式定理线性规划求14逻辑推理圆的标准方一相减）指定项系数最优解程15三角函数最向量数目积线性规划、斜等比数列及双曲线与点值（夹角）率其应用到线的距离函数对称轴，解三角形（面正余弦定理；线性规划的平面图形折16数形联合思叠后最大概求最值积最值）应用想积数列前 n 项含参数列递和与第 n 项正弦定理、余17解三角形推（证明、判的关系；等差弦定理及三三角函数与断等差存在数列定义与角形面积公解三角形性问题）通项公式；拆式项消去法样本均值方空间垂直判垂直问题的证明面面垂证明及求二垂直证明与差、正态分定与性质；异直关系，求二18面角余弦值，线面角布、随机变量面直线所成面角的余弦空间向量的散布列希望角的计算；值应用独立事件概非线性拟合；垂直证明（等线性回归方概率与统计、听从正态分率计算、随机19腰）与求二面程求法；利用随机变量的布模型及数变量散布列角回归方程进散布列学希望希望行预告展望；抛物线的切直线与圆锥求轨迹方程直线与抛物曲线（椭圆）线；直线与抛圆锥曲线（定义法）与线地点关系、的地点关系，20物线地点关（圆、椭圆）最值问题、弦椭圆方程与弦长公式，韦系；探究新问综合问题长求解最值达定理，过定题；点问题导数意义及导数意义及利用导数研导数及其应利用导数求21应用，切线，应用（切线，究曲线的切用（零点、范参数范围研含参恒建立，单一性，不等线；对新观点围、不等式证究函数的零最值问题式证明，最的理解；分段明）点问题值）函数的零点；分类议论思想几何证明（角圆的切线判几何证明（边相等证明，四四点共圆、直定与性质；圆长相等，三角边形外接圆线与圆的位极坐标与参周角定理；直22性质，圆的性置关系及证数方程形外接圆半角三角形射径）质，等边三角明影定理形证明）极坐标方程参数方程与直角坐标方参数方程、极程与极坐标坐标方程与与参数方程一般方程互互化；直线与直角坐标方不等式证明23化，动点弦长互化，交点极圆的地点关程的互化及坐标最值系应用绝对值不等基本不等式含绝对值不等式解法；分分段函数的式求解，含参应用（求最段函数；一元图像，绝对值24值，存在性问恒建立范围二次不等式不等式的解求解，题）解法2013-2017 年新课标 I 卷高考文科数学考点散布统计表题次2013201420152016列举法、描绘法表1会合运算会合运算会合运算（交、示的会合求交集集）复数的乘法、实部2复数四则运算三角函数向量坐标运算与虚部的观点古典概型3古典概型复数运算及模复数的运算余弦定理4双曲线性质双曲线离心率古典概型椭圆的几何性质 -5命题函数奇偶性椭圆与抛物线离心率三角函数图像的平面向量（会合传统文化，锥平移6等比数列运算）体及体积2017会合的运算（交集、并集）统计事例复数的运算传统文化，几何概率问题双曲线过焦点弦求面积立体几何判断线面平行7程序框图三角函数与图等差数列像8抛物线及面积三视图（柱体与三角图像及性椎体）质9三角函数图像程序框图程序框图10解三角形抛物线分段函数11三视图（柱体）线性规划三视图12分段函数导数（取值范函数计算（图围）像）13平面向量古典概型等比数列14线性规划推理与论证导数几何意义，切线15球及截面分段函数线性规划16三角最值解三角形双曲线计算17等差数列及求等差数列及求解三角形（面和和积）18统计概率（均匀统计概率（数字立几垂直体积数茎叶图）特点及概率）和侧面积19立几（垂直，体立几（垂直及统计概率（回积）高）归方程）三视图及球的表线性规划问面积与体积题指数函数与对数函数的性质函数的图像与奇偶性判断函数图像的辨别、利用导数求利用了导数单一性程序框图与算法事例程序框图平面的截面问题，三角函数化面面平行的性质简正余弦定定理，异面直线所理成的角 .三角变换及导数余弦定理与的应用椭圆向量的数目积及向量的简单坐标运算计算三角变换利用导数求切线直线与圆订交，知利用正切值弦长，求面积求解余弦线性规划的应用三棱锥求外接球表面积等差数列与等比数列数列问题线面地点关系及立体几何面几何体体积面垂直、侧面积函数分析式、概率与统计数据办理及回归直线方程直线与抛物线函数导数 （切线20圆及其面积 直线与圆及极值）函数单一性，零点，导数应用解几（圆与椭圆函数与导数 函数与导数 （切21（零点与证 及弦长）线及取值范围）明）四点共圆、 直线与22几何证明几何证明平面几何证明圆的地点关系 及 证明直线与圆锥曲线（抛物线）的地点关系，弦长公式，韦达定理。
近七年(2013-2019)全国高考(1卷)真题整理汇编(理科数学)
2013-2019近七年全国高考(1卷)真题整理汇编(理科数学)一、集合与逻辑用语【2019，1】已知集合}242{60{}M x x N x x x =-<<=--<，，则M N =（ ）A ．}{43x x -<<B ．}42{x x -<<-C ．}{22x x -<<D ．}{23x x <<1、【2018，2】 已知集合A ={x |x 2−x −2>0}，则∁R A = A.{x |−1<x <2} B. {x |−1≤x ≤2}C. {x|x <−1}∪{x|x >2}D. {x|x ≤−1}∪{x|x ≥2}2、【2017，1】已知集合{}1A x x =<，{}31xB x =<，则（ ）A ．{|0}AB x x =< B ．A B =RC ．{|1}A B x x =>D ．A B =∅3、【2016，1】设集合}034{2<+-=x x x A ，}032{>-=x x B ，则A B =（ ）A ．)23,3(--B ．)23,3(-C ．)23,1(D ．)3,23(4、【2015，3】设命题p ：n ∃∈N ，22n n >，则p ⌝为（ ）A ．n ∀∈N ，22n n >B ．n ∃∈N ，22n n ≤C ．n ∀∈N ，22n n ≤D ．n ∃∈N ，22n n = 5、【2014，1】已知集合A={x |2230x x --≥}，B={}22x x -≤<，则A B ⋂=( )A .[-2,-1]B .[-1,2）C .[-1,1]D .[1,2）N |{-=x −2>0得{AB x x ={AB x x =32AB x ⎧=⎨⎩6、【2013，1】已知集合A ＝{x |x 2－2x ＞0}，B ＝{x |x ，则( )A ．A ∩B ＝B ．A ∪B ＝RC ．B ⊆AD ．A ⊆B二、函数及其性质【2019，3】已知0.20.32log 0.220.2a b c ===，，，则( ) A ．a b c << B ．a c b << C ．c a b << D ．b c a <<【2019，5】函数f(x )=在[,]-ππ的图像大致为A ．B ．C ．D ．1、【2018，9】 已知函数f(x)={ex，x ≤0，lnx ，x >0，g(x)=f(x)+x +a ．若g （x ）存在2个零点，则a 的取值范围是（ ） A. –1（0（ B. 0（+∞（ C. –1（+∞（ D. 1（+∞（2sin cos ++x xx x 0，∴x ＜0或x ＞2，∴由图象可以看出2、【2018，16】已知函数f (x )=2sinx +sin2x ，则f (x )的最小值是_____________（3、【2017，5】函数()f x 在(,)-∞+∞单调递减，且为奇函数．若(11)f =-，则满足21()1x f --≤≤的x 的取值范围是（ ） A ．[2,2]- B ． [1,1]-C ． [0,4]D ． [1,3]4、【2017，11】设,,x y z 为正数，且235x y z ==，则（ ）A ．2x <3y <5zB ．5z <2x <3yC ．3y <5z <2xD ．3y <2x <5zC 详解：画出函数f(x)的图像，y =e x 在y 轴右侧的去掉，再画出直线y =−x ，之后上下移动， 可以发现当直线过点A 时，直线与函数图像有两个交点，并且向下可以无限移动，都可以保证直线与函数的图像有两个交点，即方程f(x)=−x −a 有两个解，也就是函数g(x)有两个零点， 此时满足−a ≤1，即a ≥−1，故选C.&公众号则知教育.&5、【2016，7】函数x exy-=22在]2,2[-的图像大致为（）A．B．C．D．6、【2016，8】若1>>ba，10<<c，则（）A．cc ba<B．cc baab<C．cbcaabloglog<D．ccbaloglog<7、【2015，13】若函数f(x)=x ln（x a=8、【2014，3】设函数()f x ，()g x 的定义域都为R ，且()f x 是奇函数，()g x 是偶函数，则下列结论正确的是（ ）A ．()f x ()g x 是偶函数B ．|()f x |()g x 是奇函数C ．()f x |()g x |是奇函数D ．|()f x ()g x |是奇函数9、【2013，11】已知函数f (x )＝220ln(1)0.x x x x x ⎧-+≤⎨+>⎩，，，若|f (x )|≥ax ，则a 的取值范围是( )A ．(－∞，0]B ．(－∞，1]C ．[－2,1]D ．[－2,0]三、导数及其应用【2019，13】曲线23()e x y x x =+在点(0)0，处的切线方程为____________．1、【2018，5】设函数f(x)=x 3+(a −1)x 2+ax ，若f(x)为奇函数，则曲线y =f(x)在点(0,0)处的切线方程为A. y =−2xB. y =−xC. y =2xD. y =x时，才能满足|f (x )|≥ax ，可排除－2x .故由|f (x )|≥ax 得∵x －2＜－2，∴a ≥－2、【2017，16】如图，圆形纸片的圆心为O ，半径为5 cm ，该纸片上的等边三角形ABC 的中心为O ．D 、E 、F 为圆O 上的点，△DBC ，△ECA ，△FAB 分别是以BC ，CA ，AB 为底边的等腰三角形．沿虚线剪开后，分别以BC ， CA ，AB 为折痕折起△DBC ，△ECA ，△FAB ，使得D ，E ，F 重合，得到三棱锥．当△ABC ．的边长变化时，所得三棱锥体积（单位：cm 3）的最大值为_______．3、【2015，12】设函数()f x =(21)x e x ax a --+,其中1a <，若存在唯一的整数0x ，使得0()0f x <，则a 的取值范围是（ ）A ．3,12e ⎡⎫-⎪⎢⎣⎭B ．33,2e 4⎡⎫-⎪⎢⎣⎭C ． 33,2e 4⎡⎫⎪⎢⎣⎭ D ． 3,12e ⎡⎫⎪⎢⎣⎭【答案】D 详解：因为函数f(x)是奇函数，所以a −1=0，解得a =1， 所以f(x)=x 3+x ，f′(x)=3x 2+1，所以f′(0)=1,f(0)=0，所以曲线y =f(x)在点(0,0)处的切线方程为y −f(0)=f′(0)x ，化简可得y =x ，故选D.【解析】由题，连接OD ，交BC 与点G ，由题，OD BC ⊥，36OG BC =， 即OG 的长度与BC 的长度或成正比，设OG x =，则23BC x =，5DG x =-，三棱锥的高22225102510h DG OG x x x x =-=-+-=-，21233332ABC S x x =⋅⋅=△， 则21325103ABC V S h x x =⋅=⋅-△45=32510x x ⋅-，令()452510f x x x =-，5(0,)2x ∈，()3410050f x x x '=-，令()0f x '>，即4320x x -<，2x <，则()()280f x f =≤，则38045V ⨯=≤，∴体积最大值为3415cm ．4、【2014，11】已知函数()f x =3231ax x -+，若()f x 存在唯一的零点0x ，且0x ＞0，则a 的取值范围为（ ）A .（2，+∞）B .（-∞，-2）C .（1，+∞）D .（-∞，-1）3113x x -有唯一的正33t t -+有唯一的交点1±，3t +有唯一的正零5、【2013，16】若函数f (x )＝(1－x 2)(x 2＋ax ＋b )的图像关于直线x ＝－2对称，则f (x )的最大解答题【2019，20】已知函数()sin ln(1)f x x x =-+，()f x '为()f x 的导数．证明：（1）()f x '在区间(1,)2π-存在唯一极大值点；（2）()f x 有且仅有2个零点．1、【2018，21】21. 已知函数f(x)=1x−x+alnx（（1）讨论f(x)的单调性；（2）若f(x)存在两个极值点x1,x2，证明：f(x1)−f(x2)x1−x2<a−2（2、【2017，12】已知函数()()22x xf x ae a e x =+--．（1）讨论()f x 的单调性；（2）若()f x 有两个零点，求a 的取值范围．3、【2016，12】已知函数2)1()2()(-+-=x a e x x f x 有两个零点．（Ⅰ）求a 的取值范围；（Ⅱ）设21,x x 是)(x f 的两个零点，证明：221<+x x ．4、【2015，12】已知函数31()4f x x ax =++，()ln g x x =-. （Ⅰ）当a 为何值时，x 轴为曲线()y f x =的切线；（Ⅱ）用min{,}m n 表示,m n 中的最小值，设函数min{),()(}()h x f x g x =（0x >），讨论()h x 零点的个数.5、【2014，21】设函数1(0ln x xbe f x ae x x-=+，曲线()y f x =在点（1，(1)f 处的切线为(1)2y e x =-+. (Ⅰ)求,a b ； （Ⅱ）证明：()1f x >.(Ⅰ) 函数()f x 的定义域为()0,+∞，112()ln x x x x a b b f x ae x e e e xxx--'=+-+由题意可得(1)2,(1)f f e '==，故1,2a b ==（Ⅱ）由(Ⅰ)知，12()ln x xe f x e x x -=+，从而()1f x >等价于2ln x x x xe e->- 设函数()ln g x x x =，则()ln g x x x '=+，所以当10,x e ⎛⎫∈ ⎪⎝⎭时，()0g x '<，当1,x e⎛⎫∈+∞ ⎪⎝⎭时，()0g x '>，故()g x 在10,e ⎛⎫ ⎪⎝⎭单调递减，在1,e ⎛⎫+∞ ⎪⎝⎭单调递增，从而()g x 在()0,+∞的最小值为11()g e e=-.设函数2()x h x xe e -=-，则()()1x h x e x -'=-，所以当()0,1x ∈时，()0h x '>，当()1,x ∈+∞时，()0h x '<，故()h x 在()0,1单调递增，在()1,+∞单调递减，从而()h x ()g x 在()0,+∞的最小值1(1)h e=-. 综上：当0x >时，()()g x h x >，即()1f x >6、【2013，理21】设函数f (x )＝x 2＋ax ＋b ，g (x )＝e x (cx ＋d )．若曲线y ＝f (x )和曲线y ＝g (x )都过点P (0,2)，且在点P 处有相同的切线y ＝4x ＋2.四、三角函数和解三角形【2019，11】关于函数()sin |||sin |f x x x =+有下述四个结论：①f (x )是偶函数；②f (x )在区间（2π,π）单调递增；③f (x )在[,]-ππ有4个零点；④f (x )的最大值为2。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
面面垂直证明及二面角
立几面面垂直、二面角
面面垂直与线面角
立几（线面平行二面角）
19
求概率，分布列及数学期望
立体几何二面角应用
正态分布、二项分布、平均数与方差
椭圆中求直线方程和证明角相等
直线与抛物线
20
轨迹方程，直线与椭圆关系
直线与椭圆
几何概型、对称
集合运算
复数（几何意义）
3
抽样方法
函数奇偶性
特称命题的否定
等差数列的通项
复数四则运算、共轭复数、命题真假判断
统计饼图
指对数比较大小
4
双曲线几何性质
双曲线几何性质
重复独立实验互斥事件概率
几何概型
等差数列
等差数列
数学审美文化
5
程序框图
排列组合、概率
双曲线、向量数量积
双曲线几何性质
解抽象函数不等式
三角函数最值
平面向量
线性规划
等比数列性质
双曲线与圆的综合
组合数
概率
16
函数最值
解三角形
解三角形（正弦定理）
线性规划的应用
立体几何折叠、三棱锥体积最大值
三角函数的最值
双曲线
17
解三角形
数列（含参）
数列定义及通项、裂项相消
解三角形
解三角形求周长
解三角形
解三角形
18
立体几何线线垂直，求线面角
频率分布直方图、正态分布、二项分布求期望
几何证明直线与圆相切
几何证明圆内接四边形
几何证明直线与圆相切；射影定理
四点共圆、直线与圆的位置关系及证明
极坐标、参数方程
极坐标方程化普通方程，曲线的交点。
坐标系与参数方程
23
极坐标与参数方程
参数方程
极坐标方程
参数方程、极坐标方程与直角坐标方程的互化及应用
绝对值不等式
解绝对值不等式
不等式证明
2013-2019年高考全国I卷数学试题考点细目表(理科)
题号
2013年新课标Ⅰ卷
14年新课标Ⅰ卷
15年新课标Ⅰ卷
16全国卷I
17全国卷I
18全国卷I
19全国卷I
1
集合概念
集合交集
复数运算、模
集合运算
集合运算、解指数不等式
复数的运算、模
集合运算（二次不等式交集运算）
2
复数概念
复数计算
三角变换、求值
复数概念与计算
抛物线切线、直线与抛物线位置关系
轨迹方程，直线与椭圆关系，范围问题
直线椭圆综合应用、证明直线过定点
求超几何分布的最值，计算期望值
导数极值、零点
21
函数、导数与不等式
函数、导数与不等式
函数与导数的应用
函数、导数与不等式的综合应用
函数与导数的应用、讨论单调性及零点问题
函数的单调性与证明不等式
概率、数列
22
程序框图
抛物线与向量的数量积
程序框图
9
二项式定理
线性规划、命题
程序框图
程序框图的应用
三角函数图象变换、诱导公式
函数的零点
等差数列
10
椭圆的中点弦问题
抛物线定义
二项式定理
抛物线的性质.
抛物线与直线相交、最值
几何概型
直线与椭圆
11
分段函数、恒成立问题
函数导数、零点
三视图、球、圆柱面积
平面的截面问题，面面平行的性质定理，异面直线所成的角.
指对数综合问题
双曲线的渐近线
三角函数
12
数列与解三角形结合
三视图
函数图像性质
三角函数的图像与性质
数列综合应用
空间几何体的截面图
立几外接球
13
平面向量
二项式定理
函数奇偶性
向量的模及坐标运算
平面向量的模运算
线性规划
切线方程
14
数列通项
推理与证明
椭圆几何性质、圆标准方程
二项式定理
线性规划
数列求和
等比数列
15
函数的性质与切线方程
函数图像
6
球的切接问题、体积
函数图像
圆锥性质、体积公式
三视图及球的表面积与体积
二项式定理求系数
向量的加法与数乘运算
数学文化与概率
7
等差数列性质
程序框图
平面向量线性运算
函数的图像
三视图、面积计算
三视图与最短路程
平面向量
8
三视图、体积计算
三角恒等变换
三角函数图像性质
指数函数与对数函数的性质