铰链四杆机构的设计
铰链四杆机构的设计

某机器设备在运行时其内部某一构件可能会产生位移,可能出现的位移值范围为:-10~+10mm ,请设计一个以铰链四连杆为传动机构的监测仪表,使之能实时监测出该机器设备的位移量,所监测的位移量采用机械式表盘显示出来供巡查人员查看。
设计工作及要求包括:1. 要求对位移的测量精度达到0.05mm ;2. 传递距离不小于0.5m ;3. 画出机构的运动简图;4. 设计出各杆件的长度,并说明各杆件的加工要求(含加工等级,直线度或平面度,孔或轴的圆柱度,必要处给出粗糙度等级);5. 回转副的销轴请采用标准件,并给出所选用标准件的尺寸及加工精度;6. 绘制在机构的运动范围内传递角的变化曲线;7. 依据所设计的机构及传动比方程,计算机构的非线性误差; 8. 合理估计杆件加工误差、标准件加工误差等对测量精度的影响解题思路如下:一、 机构的设计右图1为所设计的铰链四杆机构,杆AB 、BC 、CD 、AD 的长度分别为a 、b 、c 、d 。
由铰链四杆机构的传动特性可得到主动件AB 的转角φ和从动件CD 的转角ψ之间的关系及传动比i 如下:ψ=arctan asinφd−acosφ+arccosa 2−b 2+c 2+d 2−2adcosφ2c√a 2+d 2−2adcosφ(公式5-8)、i=dψdφ=aa 2+d 2−2adcosφ[dcosφ−a −dsinφ(a 2+b 2−c 2+d 2−2adcosφ)√4b 2c 2−(a 2−b 2−c 2+d 2−2adcosφ)2] (公式5-10).当∠ABC =∠BCD =90ο时,这有cos φ=a−c d,sin φ=bd,d 2−b 2=(a −c )2将这些式子代入传动比公式(5-10)可得到i =−ac . 在此位置时该铰链机构是线性的.设该设计的机构时近似线性的铰链四杆机构,传动比i=-8,其中EF 杆为机器设备内部的一构件,它能在此位置左右移动10mm ,带动铰链转动从而使AB 杆发生转动,传递到CD 杆上转化为刻度盘上指针的转动,从而达到监测机器内部构件位移量的监测。
铰链四杆机构pptPPT课件
9/12/2023
7
第7页/共14页
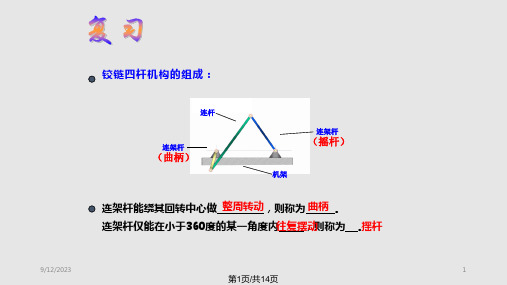
铰链四杆机构类型判定: (1)如果满足杆长和条件
以最短杆作连架杆,为曲柄摇杆机构,最短杆为曲柄; 以最短杆作机架,为双曲柄机构,有两个曲柄; 以最短杆作连杆,为双摇杆机构,没有曲柄 (2)如果不满足杆长和条件,则为双摇杆机构。
9/12/2023
8
第8页/共14页
第14页/共14页
图示四杆机构中,已知各构件长度LAB=55mm, LBC=40mm,
LCD=50mm, LAD=25mm,判断
(1)以AB为机架可以获得( 曲柄摇杆 )机构? D (2)以AD为机架可以获得( 双曲柄 )机构? 25 (3)以BC为机架可以获得( 双摇杆 )机构? A
解:先判断杆长和条件:25+55≤40+50 符合此条件。 根据判定结论得到:
50 55
(1)以AB为机架,最短杆为连架杆, 为曲柄摇杆机构 (2)以AD为机架,最短杆为机架, 为双曲柄机构 (3)以BC为机架,最短杆为连杆, 为双摇杆机构
C 40 B
9/12/2023
6
第6页/共14页
按 下列各 图所注 出的尺 寸,分 析确定 各机构 的名称
双曲柄机构
曲柄摇杆机构 双摇杆机构 双摇杆机构
9/12/2023
10
第10页/共14页
1、搜集生活中的可用零件,做成各种类型的 铰链四杆机构的模型
2、做《习题集》上相关试题加以巩固练习
9/12/2023
11
第11页/共14页
9/12/2023
12
第12页/共14页
9/12/2023
13
第13页/共14页
感谢您的观看!
铰链四杆机构的演化及应用教学设计

铰链四杆机构的演化及应用教学设计铰链四杆机构的演化及应用教学设计作为一名教学工作者,通常会被要求编写教学设计,教学设计是一个系统化规划教学系统的过程。
那么优秀的教学设计是什么样的呢?以下是小编精心整理的铰链四杆机构的演化及应用教学设计,希望对大家有所帮助。
《平面连杆机构》是中等职业学校《机械基础》中的重要内容,《铰链四杆机构的演化及应用》是该章中的重点和难点。
铰链四杆机构是平面连杆机构中最为典型的机构,它可以演化为“曲柄滑块机构、导杆机构”,多年教学发现,学生的基础不同,虽然在学习“铰链四杆机构的演化过程及应用”知识时表现出的困难程度有差别,但由于缺乏直观经验,学生在学习过程中均会存在一定的难度!笔者针对现在所任教的单招学生教学对象,设计了一堂课堂教学并进行了实施,本文对教学中的成功与不足等方面进行教学反思,以在今后教学中有所借鉴,提高教学效果!教情、学情分析:任教学生为“单招班”学生,他们的文化基础与学习态度较不是太好。
本节课是一堂复习课,在第一轮新课教学中主要采取传统教学方法,因学生对“机构的应用”缺少感性认识,理解时表现出一定的难度。
本节课运用“多媒体”教学手段(更加直观)、采用“课堂自主—研究学习”的教学方法,力图使学生对本节内容的理解更加深入,掌握更加透彻!“教学目的”的制定:1、掌握铰链四杆机构的演化过程及演化机构的结构组成及运动原理(认知目标);2、培养学生的观察能力、概括能力和自学能力,使他们能在实习或生产中解决相关的技术问题(能力目标);3、激发学生学习兴趣,增进师生互动、交流、达到“教学相长”的效果,进行热爱专业的思想教育,培养学生理论联系实际地学习(情感目标)。
教学方法及手段的选择:本节课采取课堂自主——研究的教学方法,课前让学生先进行自学,课堂上教师对总的教学目标进行细化,在讲解每个知识点时,采用“引导教学法”代替传统的“填鸭式”,先示出引导问题,让每个学生通过思考解决问题,层层递进,逐个解决问题,然后教师对学生的思维进行总结、训练和拓展;为弥补学生想像能力的欠缺、增强学生学习的直观性,对铰链四杆机构的演化过程可采用flash软件制作课件,对演化机构的应用(结构组成和运动原理)可从Internet上搜索多种教学素材(录像、实物等),提高教学效果!教学过程如下:一、思维引入:1.铰链四杆机构三种基本类型及判断方式?2.急回特性判定及其应用意义?3.曲柄摇杆机构死点产生条件、位置、克服方法、应用?4.列举实际生产生活中三种典型铰链四杆机构的应用实例?还存在哪些其他形式的四杆机构?二、思维启发演绎:(一)曲柄滑块机构演化通过演示,让学生观察,分析曲柄滑块机构是曲柄摇杆机构的演化形式。
铰链四杆机构教学设计

铰链四杆机构教学设计题和改进方向。
1、导入通过铰链四杆机构的真实工作情境导入教学内容,提出本次课的工作任务。
2、知识讲解讲解铰链四杆机构的类型及判定条件,让学生了解其应用。
3、任务设计让学生课前分小组制作铰链四杆机构模型,课后运用所学知识分析存在的问题,改进模型。
4、小组协作通过小组做模型,使学生养成学以致用,大胆实践的精神,同时增强同学间的团队协作意识。
5、知识巩固让学生判断四杆机构是否存在曲柄,并能够根据已知条件确定四杆机构的形式。
6、课堂反思让学生回顾本次课堂所学内容,反思自己的研究过程,提出问题和改进方向。
七、教学评价通过学生的模型和课后改进,以及学生在课堂中的表现,评价学生的研究效果和能力提升情况。
同时,也让学生自我评价,帮助他们发现自己的不足之处,提高自我研究能力。
1、学生按照上一节课的安排,分成5组,每组5至6人,座好小组。
2、各小组测量课前做的铰链四杆机构各杆的杆长并标注,然后把其摆放在正中间。
3、预新课,结合自己对新知的理解,试判断一下所做铰链四杆机构属于什么类型。
4、各小组选派代表上台展示本组的模型,并试判断类型。
5、展示动画,介绍三种机构的运动特点及应用场合。
6、引导学生思考与上节知识点的联系,提问运动副的含义与分类,以及生活中常见的低副、高副机构。
7、引入铰链四杆机构的研究,介绍其组成构件,包括曲柄和摇杆。
8、通过动画思考,引导学生分析铰链四杆机构中杆件的长度、位置对运动的影响。
9、任务:判定该铰链四杆机构取不同杆件为机架时的类型,并做出相应的模型展示。
10、讲授铰链四杆机构类型的判断条件,包括最短杆与最长杆长度之和小于或等于其余两杆长度之和。
11、介绍铰链四杆机构的三种类型,包括取最短杆为连架杆的曲柄摇杆机构,取最短杆为机架的双曲柄机构,以及取最短杆为连杆的双摇杆机构。
12、通过课件、动画和模型展示,演示不同类型铰链四杆机构的运动特性。
13、提高学生研究兴趣,增强感性认识,突出重点,讲授新课。
铰链四杆机构实现连杆轨迹的优化设计

%铰链四杆机构实现连杆轨迹的优化设计% (调用目标函数lgjg_gjyh_mb 和非线性约束函数lgjg_gjyh_ys)%设计变量:x(1)-机架;x(2)-曲柄;x(3)-连杆;x(4)-摇杆;x(5)-连杆附杆;% x(6)-机架倾斜角beta;x(7)-连杆与附杆夹角 gamma;x(8)-曲柄相初始角thetaO; %设计变量初值 x0=[50;7;55;25;25;-12;15;50]; %设计变量边界 lb=[10;8;10;10;10;-20;5;5]; ub=[60;30;60;40;30;30;15;60]; % % % %hd=pi/180;delta_ n=acos((xo pt(3)A2+xo pt(4) ^2-(x0 pt(1)-xo pt(2))A2)/(2*x op t(3)*xo pt(4))); fprintf (' 机构最小传动角 delta_min = %3.4f ° \n',delta_n/hd);%调用多维约束优化函数(lgjg_gjyh_ys)计算最优点x*的性能约束函数值 [g,ceq]=lgjg_gjyh_ys(xo pt); disp ' fprintf (' 最小传动角约束函数值 g1* = %3.4f \n',g(1))fprintf (' 曲柄长度 <=机架长度 g2* = %3.4f \n',g(2)) fprintf (' 曲柄长度 <=连杆长度 g3* = %3.4f \n',g(3))fprintf (' 曲柄长度 <=摇杆长度 g4* = %3.4f \n',g(4))fprintf (' 曲柄+机架 <=摇杆+连杆 g5* = %3.4f \n' ,g(5)) fprintf (' 曲柄+连杆 <=摇杆+机架 g6* = %3.4f \n ',g(6)) fprintf (' 曲柄+摇杆 <=连杆+机架 g7* = %3.4f \n' ,g(7)) fprintf (' 机架长度<=60 g8* = %3.4f \n',g(8)) fprintf (' 曲柄长度>=8 g9* = %3.4f \n',g(9))fprintf (' 曲柄长度<=30 g10* = %3.4f \n',g(10)) fprintf (' 连杆长度<=60 g11* = %3.4f \n',g(11)) fprintf (' 摇杆长度<=40 g12* = %3.4f \n',g(12)) fprintf ('附杆长度>=10g13* = %3.4f \n',g(13))fprintf (' 机架长度 d = %3.4f mm \n',xo pt(1)) fprintf (' 曲柄长度 a = %3.4f mm \n',xo pt(2)) fprintf (' 连杆长度 b = %3.4f mm \n',xo pt(3)) fprintf (' 摇杆长度 c = %3.4f mm \n',xo pt(4)) fprintf (' 连杆附杆长度 h = %3.4f mm \n',xo pt(5)) fprintf (' 机架倾斜角 beta = %3.4f ° \n :X op t(6))fprintf (' 连杆与附杆夹角 gamma = %3.4f ° \n ',xo pt(7fprintf (' 曲柄初始位置角theta0 = %3.4f ° \n ',xo pt(8)) fprintf ('M 点轨迹坐标偏差f* = %3.4f\n ',fo pt)I线性不等式约束(g(2)〜g(20))中设计变量的系数矩阵 a 省略,定义为空矩阵“[]”线性不等式约束(g(2)〜g(20)中的常数项列阵b 省略,定义为空矩阵“[]” 没有等式约束,参数 Aeq 和beq 定义为空矩阵“[]” 调用非线性优化函数[xop t,fo pt]=fmi ncon( @lgjg_gjyh_mb,x0,[],[],[],[],lb,ub,@lgjg_gjyh_ys); dis p铰链四杆机构实现连杆轨迹的优化设计最优解最优点的约束函数值附杆长度<=30 g14* = %3.4f \n',g(14)) fprintf ('fprintf (' 机架倾斜角>=-20 °g15* = %3.4f \n',g(15)) fprintf ('机架倾斜角<=30 °g16* = %3.4f \n',g(16)) fprintf ('连杆附杆夹角>=0 °g17* = %3.4f \n',g(17)) fprintf ('连杆附杆夹角<=15 °g18* = %3.4f \n',g(18)) fprintf (' 曲柄初始角>=0 °g19* = %3.4f \n',g(19)) fprintf ('曲柄初始角<=15 °g20* = %3.4f \n',g(20)) 计算结果:Op timizati on term in ated: magn itude of direct ional derivative in search direct ion less tha n 2*op ti on s.Tol Fun and maximum con stra int violati on is less tha n op ti on s.TolC on.Active in equalities (to with in op ti on s.TolC on = 1e-006): lower2 ********in eqli n ineqnon li n9铰链四杆机构实现连杆轨迹的优化设计最优解upperan 机架长度 d = 51.7446 mm曲柄长度 a = 8.0000 mm连杆长度 b = 53.6230 mm摇杆长度 c = 25.4846 mm连杆附杆长度h = 22.6784 mm机架倾斜角beta = 11.4185 °连杆与附杆夹角gamma = 14.9999 °曲柄初始位置角theta0 = 50.0664 °M点轨迹坐标偏差f* = 1.9718机构最小传动角delta_min = 53.8751最优点的约束函数值最小传动角约束函数值g1* = -482.3881曲柄长度<=机架长度g2* = -43.7446曲柄长度<=连杆长度g3* = -45.6230曲柄长度<=摇杆长度g4* = -17.4846曲柄+机架<=摇杆+连杆g5* = -19.3631曲柄+连杆<=摇杆+机架g6* = -15.6062曲柄+摇杆<=连杆+机架g7* = -71.8830机架长度<=60 g8* = -8.2554曲柄长度>=8 g9* = 0.0000曲柄长度<=30 g10* = -22.0000连杆长度<=60 g11* = -6.3770摇杆长度<=40 g12* = -14.5154附杆长度>=10 g13* = -12.6784附杆长度<=30 g14* = -7.3216机架倾斜角>=-20 °g15* = -31.4185机架倾斜角<=30 °g16* = -18.5815连杆附杆夹角>=0 °g17* = -14.9999%铰链四杆机构实现连杆轨迹的优化设计 --目标函数文件---lgjg_gjyh_mb.mfun ctio n f=lgjg_gjyh_mb(x) %曲柄输入角增量Dtheta=[0,22,44,66,88,129,221,314]; %连杆上M 点给定的坐标 Sx=[26,23,20,17,13,10,20,30]; Sy=[16,17,17,16,15,11,6,12]; %目标函数 hd=pi/180;theta=x(8)+Dtheta;%曲柄输入角=初始角+角增量ep silo n=ata n(x(2).*si n((theta-x(6))*hd)/(x(1)-x(2).*cos((theta-x(6))*hd)));etaz=x(1)A2+x (2) ^2+x (3)^2-x (4) ^2-2*x(1)*x(2).*cos((theta-x(6))*hd); etam=2*x(3)*sqrt(x(1)A2+x (2)^2-2*x(1)*x(2).*cos((theta-x(6))*hd));eta=etaz./etam;p hi=x(6)+x(7)+eta-e psil on;Mx=x(2).*cos(theta*hd)+x (5) .*cos( phi*hd);My=x(2).*s in (theta*hd)+x (5).*si n(p hi*hd); f=sqrt(sum((Mx-Sx).A2+(My-Sy).A2)/8);%铰链四杆机构实现连杆轨迹的优化设计 fun ctio n [g,ceq]=lgjg_gjyh_ys(x)连杆附杆夹角<=15 曲柄初始角>=0 ° 曲柄初始角<=15 °g18* = -0.0001 g19* = -50.0664 g20* = -9.9336%凑整解的计算xz=[52,8,54,25,23,11.5,15,50]; fz=lgjg_gjyh_mb(xz);gz=lgjg_gjyh_ys(xz); delta_z=acos((xz(3)A2+xz(4)A2-(xz(1)-xz(2))A2)/(2*xz (3) *xz (4))); dis pI anfprintf (' fprintf (' if gz<=0dis p 'else铰链四杆机构实现连杆轨迹的优化设计凑整解M 点轨迹坐标偏差机构最小传动角f* = %3.4f delta_z= %3.4f ° 未a***、\n',fz)\n ',delta_z/hd)&&&&&&&&凑整解在可行域内 &&&&&&&&'dis p 'end&&&&&&&& 凑整解在可行域外&&&&&&&&'********铰链四杆机构实现连杆轨迹的优化设计凑整解M 点轨迹坐标偏差f* = 1.9989机构最小传动角 delta_z = 53.5270 &&&&&&&& 凑整解在可行域内********&&&&&&&&%连杆上M 点实际x 坐标 %连杆上M 点实际y 坐标 % M 点坐标偏差均方根值--约束函数文件---lgjg_gjyh_ys.m%机构最小传动角(40度)约束g(1)=x (3)A2+x(4)A2-(x(1)-x(2))A2-2*x (3) *x(4)*cos(40* pi/180); %曲柄存在条件约束 g(2)=-x(1)+x(2); g(3)=-x(3)+x(2); g(4)=-x(4)+x(2);g(5)=x(1)+x(2)-x(3)-x(4); % 曲柄 + 机架<= 摇杆 +连杆 g(6)=-x(1)+x(2)+x(3)-x(4); % 曲柄 + 连杆 <= 摇杆 +机架 g(7)=-x(1)+x(2)-x(3)+x(4); %曲柄+ 摇杆 <=连杆 +机架%边界约束g(8)=x(1)-60;% 机 架 <=60g(9)=8-x(2);g(10)=x(2)-30;%8 <=曲柄<=30g(11)=x(3)-60;%连; 杆 <=60g(12)=x(4)-40;%摇; 杆 <=40g(13)=10-x(5);g(14)=x(5)-30; g(15)=-x(6)-20;g(16)=x(6)-30; g(17)=-x(7);g(18)=x(7)-15; g(19)=-x(8);g(20)=x(8)-60; ceq珂];% 10 <=连杆附杆 <=30 % -20度 <=机架倾斜角% 0度 <=连杆附杆夹角 % 0度 <=曲柄初始角曲柄长度 曲柄长度 曲柄长度 <=机架长度 <=连杆长度 <摇杆长度<=30 度 <=15 度 <=60 度。
铰链四杆机构的教学设计与反思

铰链四杆机构的教学设计与反思铰链四杆机构的教学设计与反思一、教学目标1、理解铰链四杆机构的基本概念及结构特点;2、熟练掌握运用铰链四杆机构的设计方法及规律;3、了解并分析铰链四杆机构的运动机理;4、能够有效地运用铰链四杆机构进行设计及研究。
二、教学内容1、铰链四杆机构的概念及结构特点;2、铰链四杆机构的运动状态计算方法;3、铰链四杆机构的设计步骤;4、铰链四杆机构的特殊结构设计;5、铰链四杆机构的新型运动机理研究与应用。
三、教学方法1、理论讲授:对铰链四杆机构的特点及其运动机理、设计方法等方面进行理论性讲授;2、综合性实验:根据课程所学,进行铰链四杆机构的分析及设计,实现具体的机构设计,观察实验运行的状态;3、设计研究:针对铰链四杆机构的特殊结构场合,重点考虑运动机理的优化,进行能源消耗的估算;4、综合性反思:深入思考本次课程的思想,总结及分析学习的情况,并形成一定的总结报告。
四、教学评价1、理论考试:对学生的理论学习情况进行考核,测试学生对本次课程的理解程度;2、实验评估:评估学生实验的设计思路及解决方案,分析学生解决问题的思路及方法;3、设计研究:考核学生在新型铰链四杆机构的设计研究中的积极性,考察学生的创新能力;4、反思总结:检验学生对本次课程的思想及专业技能的学习情况,提出未来发展的对策建议。
五、教学反思本次课程的教学设计以实践性为主,注重实验操作实现设计的方法,掌握铰链四杆机构的设计流程、参数估算方法及分析结果判断等环节,有效提高学生的设计及分析能力。
但由于课程时间的有限,理论基础的学习时间不能达到理想的效果,从而影响实验设计准确性及分析能力的提高。
本次教学设计的反思也提示,在未来的课程设计中,需要在理论学习和实践性操作之间寻求一个合理的比例,有效地提高学生的学习效果。
机械设计基础——铰链四杆机构
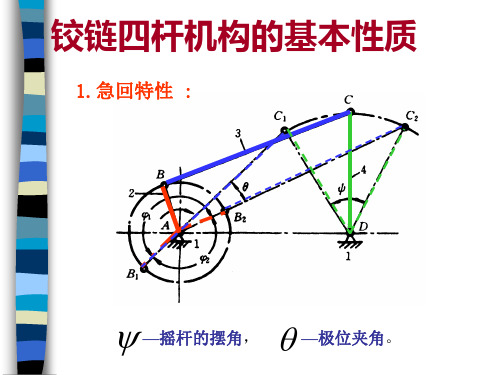
1.急回特性 : 1.急回特性
摇杆的摆角, 极位夹角。 摇杆的摆角 极位夹角 ψ —摇杆的摆角 θ —极位夹角
为描述从动摇杆的急 回特性, 回特性,在此引入行 程速比系数 K,即:
K =
180 180
+ -
θ θ
K值的大小反映了急回运动特性的显著程度。K值的大 值的大小反映了急回运动特性的显著程度。 小取决于极位夹角θ , 角越大,K值越大,急回运动 θ 角越大, 值越大, 特性越明显;反之,则愈不明显。 特性越明显;反之,则愈不明显。当时 θ = 0 ,K=1 , 机构无急回特性。 机构无急回特性。
传动角愈大,机构的传力性能愈好,反之则不利于机构 传动角愈大,机构的传力性能愈好, 中力的传递。机构运转过程中,传动角是变化的, 中力的传递。机构运转过程中,传动角是变化的,机构 出现最小传动角的位置正好是传力效果最差的位置, 出现最小传动角的位置正好是传力效果最差的位置,也 是检验其传力性能的关键位置。 是检验其传力性能的关键位置。 设计要求: 设计要求:
2.按给定的行程速比系数设计四杆机构 2.按给定的行程速比系数设计四杆机构
设计具有 急回特性 的四杆机 构,关键 是要抓住 机构处于 极限位置 时的几何 关系,必 要时还应 考虑其他 辅助条件。
θ θ θ
例:已知摇杆长度L=100,摆角 ψ =50 和行程速比 已知摇杆长度L=100, L=100 系数k=1.4 试设计曲柄摇杆机构。 k=1.4, 系数k=1.4,试设计曲柄摇杆机构。
若在设计机构时 先给定K 先给定K值,则 :
K 1 θ = 180° K +1
在生产实际中,常利用机构的急回运动来缩 短非生产时间,提高生产率,如牛头刨床、 往复式运输机等。
《铰链四杆机构的曲柄存在条件》教学设计

教材名称:机械基础常识《铰链四杆机构的曲柄存在条件》教学设计【设计的基本理念】本课根据中职学生的知识水平和已有的知识、技能、经验和兴趣,打破传统的先教后学的教学方式,以学生的学为主,教师点拨为辅,让学生在任务的引领下积极主动地参与学习,经过思考、自主探究、互相协助、“理实一体化”后进行归纳总结,达成教学目标。
旨在创造以学生为主体,教师为主导,使学生参与、自主协作、探索创新的学习模式,从而极大地激发学生学习的兴趣、动力,在参与过程中使学生获得极大的成就感,进而增强学生的自信心,从而增强了机械基础课堂教学的实效性,提高了机械基础的教学质量【教材分析】1、本节是本课程的核心内容之一,它既是前面所学内容的实践应用,又是从曲柄存在条件过渡到判别别铰链四杆机构的桥梁,在起着承前启后的作用的同时,将理论内容过渡到实践应用。
2、通过学习本节内容,可以提高学生对铰链四杆机构正确判别的能力。
3、主要内容:铰链四杆机构类型的判别:判别铰链四杆机构的类型铺垫曲柄存在的条件【学情分析】1、专业水平《机械基础》是一门综合性较强的专业基础课程,也是专业基础课程中较难掌握的一门课。
《铰链四杆机构的判别》这节内容是本课程的一个重点,它实用性很强,而职校学生基础差,学习积极性不高,行为习惯也不好,观察能力和专业水平能力都比较差。
2、采取措施在设计教学活动时,将大量时间让学生观察动画吸引学生的注意力——再例举生活实例——提出问题引发学生的思考是否有曲柄——知识拓展提出如何判别铰链四杆机构的三种类型——强化、引申知识——举例让学生分组讨论归纳出结果,将结果应用在练习中进行比赛,对各组进行排名,以此,可以增强学生思考问题的兴趣与积极性。
与学生就生活中的经验进行相互交流与沟通,进而让理论知识为实践服务。
【教学目标】1、总目标:灵活的运用杆长和条件进行铰链四杆机构类型的判别;2、结合学生的实际情况和教材的知识结构以及对教材的分析,我确定了如下教学目标:知识目标:1、掌握铰链四杆机构类型的判别原则。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
某机器设备在运行时其内部某一构件可能会产生位移,可能出现的位移值范围为:-10~+10mm ,请设计一个以铰链四连杆为传动机构的监测仪表,使之能实时监测出该机器设备的位移量,所监测的位移量采用机械式表盘显示出来供巡查人员查看。
设计工作及要求包括:
1. 要求对位移的测量精度达到0.05mm ;
2. 传递距离不小于0.5m ;
3. 画出机构的运动简图;
4. 设计出各杆件的长度,并说明各杆件的加工要求(含加工等级,直线度或平面度,孔或轴的圆柱度,必要处给出粗糙度等级);
5. 回转副的销轴请采用标准件,并给出所选用标准件的尺寸及加工精度;
6. 绘制在机构的运动范围内传递角的变化曲线;
7. 依据所设计的机构及传动比方程,计算机构的非线性误差; 8. 合理估计杆件加工误差、标准件加工误差等对测量精度的影响
解题思路如下:
一、 机构的设计
右图1为所设计的铰链四杆机构,杆AB 、BC 、CD 、AD 的长度分别为a 、b 、c 、d 。
由铰链四杆机构的传动特性可得到主动件AB 的转角φ和从动件CD 的转角ψ之间的关系及传动比i 如下:ψ=arctan asinφ
d−acosφ+arccos
a 2−
b 2+
c 2+
d 2−2adcosφ2c√a 2+d 2−2adcosφ
(公式5-8)、i=
dψdφ
=
a
a 2+d 2−2adcosφ
[dcosφ−a −
dsinφ(a 2+b 2−c 2+d 2−2adcosφ)√4b 2c 2−(a 2−b 2−c 2+d 2−2adcosφ)
2
] (公式5-10).当∠ABC =∠BCD =
90ο时,这有cos φ=
a−c d
,sin φ=b
d
,
d 2−b 2=(a −c )2
将这些式子代入传动比公式(5-10)可得到i =−a
c . 在
此位置时该铰链机构是线性的.
设该设计的机构时近似线性的铰链四杆机构,传动比i=-8,其中EF 杆
为机器设备内部的一构件,它能在此位
置左右移动10mm ,带动铰链转动从而使AB 杆发生转动,传递到CD 杆上转
化为刻度盘上指针的转动,从而达到监测机器内部构件位移量的监测。
设AF ∶AB =2∶3,刻度盘上的最小分度为0.1ο. 若EF 杆每移动0.05mm 时,刻度盘上的指针能转动0.1ο(即一个最小分度值),则可以说该位移的测量精度达到0.05mm. 在此测量精度下,主动件AB 的最大转角范围φg =
0.18
∗20
0.05=5ο(即能在此位置左右各摆动2.5ο),
则由于在该位置是线性的,从动件CD (即指针)最大摆动范围为ψg =8∗5ο=40ο. 由于
φ ψ 图1
AB杆的摆角很小,故EF杆的运动位移s与AF杆转动的路程可认为相等(对精度的影响几
乎可忽略,因为转动的角度很小),则有ψg=|i|∗φg=|i|∗s
|AF|180
π
=2160
aπ
s,即s=a
12
∗ψg,
∵a=3
2|AF|=3
2
0.05
0.1
8
π
180
=343.77mm,∴s=0.5ψg(即可从EF杆移动的位移s可以求出指针
的转角ψg,也可以反过来由指针的转角ψg得出EF杆(即机器内部构件)的位移量.
二、机构杆长及机构非线性误差的确定
∵a=343.77mm,|AB|=2
3a, a
c
=8 ,∴c=42.97mm. d=√(a−c)2+b2(公式1),
此时主动件AB的转角φο=cos−1a−c
d
(公式2). 由于题目要求传递距离至少是500mm,即
|DF|的长度至少是500mm.由于b<|DF|,故当b至少取500mm时一定能满足传递距离至少
为500mm. 可分别取b为580mm、660mm、740mm、820mm、900mm ,分别代入(公式1)可得到d为653.36mm、725.31mm、798.80mm、873.43mm、948.95mm,从而得到此时的主动件AB的转角φο分别为62.59ο、65.50ο、67.88ο、69.86ο、71.52ο.因为主动件AB在两个极限位置处(此时φ分别为(φο−2.5ο)、(φο+2.5ο))的非线性误差δ最大,故只需要求出此处的非线性误差即可,将b、d及极限处的φ再分别代入公式(5-10)求得此时的
传动比i,由δ=i+8
−8
∗100%可得到对应的非线性误差,如表1所示
故可以取杆长b长度为820mm,得到杆长d=873.43mm,主动件AB的起始转角φο为69.86ο. 各杆件的加工等级均采用8级,AB杆的直线度采用7级,CD杆的直线度采用8级,BC杆和AD杆的直线度采用6级,回转副的销轴采用公称直径为10mm、加工精度为0.05mm的标准件,则实际需要的各杆件长度a、b、c、d应分别为338.77mm、815mm、37.97mm、868.43mm.
三、在机构运动范围内传递角γ随着主动件AB的转角φ的变化曲线
在图1中,|BD |2=a 2+d 2−2adcosφ,|BD |2=b 2+c 2−2bccos∠BCD ,由这两个式子可得到∠BCD =
cos −1b 2+c 2−a 2−d 2
+2ad cos φ2bc
.则有传递角γ={
∠BCD
180−∠BCD ∠BCD 为锐角∠BCD 为钝角
,其中
φο−2.5ο≤φ≤φο+2.5ο 即67.36ο≤φ≤72.36ο.用matlab 软件可得到传递角γ随着主动件AB 的转角φ的变化曲线如下图所示
传递角γ 传递角 γ
主动件AB 的转角φ /度
单位/度。
