SPC基础知识--
SPC (统计过程控制)基础知识

SPC(统计过程控制)基础知识 统计过程控制) 统计过程控制
4.X-Rs 控制图。多用于下列场合:对每一个产品都进行检验,采用自动化检查和 测量的场合;取样费时、昂贵的场合;以及如化工等过程、样品均匀,多抽样也无 太大意义的场合。由于它不像前三种控制图那样能取得较多的信息,所以它判断过 程的灵敏度也要差一些。
以 客 贯 彻
户 为
中
心 宗
旨
的
质 量 目 标 的 制 定
有 目 期 况
无 制 定 可 测 量 的 质 量 目 标 ? 质 量 标 有 无 分 解 到 各 职 能 层 ? 有 无 定 测 量 评 估 各 质 量 目 标 的 达 成 情 ?
职 责 和 权 限
各 部 门 , 各 职 能 岗 位 有 无 定 义 相 关 的 职 责 和 权 限 ?
4 .2 .2
质 量 手 册
有 无 编 写 符 合 要 求 的 质 量 手 册 ?
SPC(统计过程控制)基础知识 统计过程控制) 统计过程控制
3.4 分层图 用于将数据分类比较 250
不良率(PPM)
目标线
150 100 50 0 1 2 3 4
工作周
C班 B班 A班
5
6
7
8
9
SPC(统计过程控制)基础知识 统计过程控制) 统计过程控制
3.5 控制图 什么是控制图? 什么是控制图? 控制图是对过程质量加以测定,记录从而进行控制管理的一种用科学方法设计的图。 控制图的理论基础是概率论。依据概率论,我们把“小概率的事件如果发生了,我 们认为有异常存在”。 控制图的种类: 控制图的种类
数据 计量值 分布 正态分布 控制图名称 均值-极差 图 均值-标准差 图 中位数-极差 图 单值-移动极差 图 不合格品率图 不合格品数图 单位缺陷数 缺陷数 简记 X-R chart X-S chart X-R chart X-Rs chart P chart Pn chart U chart C chart
SPC培训讲义---基础知识

SPC培训讲义—基础知识简介SPC(Statistical Process Control,统计过程控制)是一种基于统计方法的质量管理工具,旨在通过对过程数据的统计分析,帮助组织识别和解决可能导致质量问题的根本原因,从而提高产品的稳定性和可靠性。
本讲义将介绍SPC的基础知识,包括SPC的原理、常用的SPC 工具和应用案例等内容。
1. SPC的原理SPC的核心原理是基于过程数据的统计分析,通过对数据的收集和分析,识别和排除可能导致质量问题的特殊原因,同时通过控制图的使用,监控和改进过程的稳定性和可靠性。
1.1 正态分布在SPC中,数据的正态分布是一个重要的假设。
正态分布是一种对称的概率分布,其特点是均值和标准差能够完全描述分布的情况。
正态分布的图形呈钟形曲线,均值位于曲线的中央。
在实际应用中,SPC 通常假设数据是近似正态分布的,以方便进行统计分析。
1.2 变异性与稳定性在质量管理中,变异性是指同一过程在不同时间或不同条件下相同测量项的数值差异。
通过SPC的应用,可以发现原本被认为是随机变动的过程,实际上可能存在特殊原因造成的异常波动。
稳定性是指过程在一段时间内的变异性较小,并且符合预期的性能要求。
通过SPC 的控制图,可以监控过程的稳定性,并及时采取措施防止不稳定状态的出现。
2. 常用的SPC工具SPC工具是SPC实施过程中使用的具体方法和技术,下面介绍几种常用的SPC工具。
2.1 控制图控制图是SPC中最常用的一种工具,它用来监控过程在一段时间内的变异情况。
控制图是一种统计图表,将过程数据按时间顺序绘制在图表上,同时画出上下限和中心线。
如果过程数据处于控制限之内,说明过程处于稳定状态;如果过程数据超过控制限,说明过程发生了特殊原因的变异,需要进行分析和改进。
2.2 直方图直方图是一种用柱形表示数据分布的图表,它可以直观地展示数据的中心趋势、波动幅度以及偏态情况。
通过直方图,可以判断数据是否符合正态分布,如果数据呈现钟形分布,则可以认为数据符合正态分布的假设。
SPC理论基础知识

广州今朝科技有限公司SPC基础知识一SPC术语录1.控制图:SPC的核心工具。
一种标绘着根据相继抽取的样本或子组的某一统计量的值、并画有控制限的图,用于评估或检查一个过程是否处于控制状态之下。
画在坐标系中,横轴表示时间或样本号,纵轴表示数值大小,将采集到的数据以点的形式表示在图中。
2.运行图:一种代表过程特性的简单图形,上面描有一些从过程中收集到的统计数据(通常是单值)和一条中心线(通常是测量值的中位数),可用来进行链分析。
3.排列图:一种用于解决问题的简单工具,按照对成本或变差的影响程度对各种潜在的有问题区域或变差源进行排序。
一般情况下,大多数的成本(或变差)是由于少量原因造成的,所以解决问题的精力最好是首先集中在少量关键的原因上,而暂时忽视多数不重要的原因。
4.散点图(相关图):把两个变量标在横轴与纵轴上,按照一一对应测量值点描绘成的图。
5.计量值:当质量特性值可以取给定范围内的任何一个可能的数值时,这样的质量特性值称为计量值。
6.计数值:当质量特性值只能取一组特定的数值,而不能取这些数值之间的数值时,称之为计数值。
7.过程:过程是指将输入转换成输出的一系列活8.9.10.628052366666611.动的总和。
12.样本:取自总体中的一个或多个个体,用于提供关于总体的信息,并作为可能做出对总体(或产生总体的过程)的某种判定的基础(引自GB3358-82)。
样本中所包含的样本单位数,称为样本大小。
13.样本容量(子组大小):在抽检中抽出来的样本单位数。
14.不良品:指整件物品作为一个整体考虑而未满人意或不能接受。
一件不良品可能具有若干相同的或不相同的缺陷。
15.不良率控制图:即P图,用于控制对象的不合格率。
16.不良品数控制图:即Pn图,是一种计数值控制图,用于控制对象为不合格品数的场合。
)17.采集规划:采集规划指从某过程中选择质量特征值进行数据采集的一种工具。
18.单位缺陷数(U)控制图:是一种计数值控制图,它通过周期性抽取样本以统计单位产品的缺陷率并在控制图上绘制点来监控过程变化,样本的检测结果为平均每个样品包含的缺陷数。
SPC的基础知识与数据整理

SPC的基础知识与数据整理引言SPC(统计过程控制)是一种用于监控和控制过程的统计方法。
它通过收集一系列的数据并进行分析,以确定过程是否处于控制状态,并采取相应的措施保持过程稳定。
在本文中,我们将介绍SPC的基础知识和数据整理方法。
SPC的基础知识SPC的核心思想是通过采集过程中的样本数据,分析其变异情况,以判断过程是否处于控制状态。
基于不同的过程类型,SPC通常使用控制图来可视化过程的变异情况。
常用的控制图包括X-Bar图、R图和S图等。
X-Bar图X-Bar图是一种用于监控过程均值的控制图。
它基于过程中收集到的样本数据,计算每个样本的均值,并绘制在图表上。
通过观察X-Bar 图,我们可以判断过程均值是否稳定。
R图R图是一种用于监控过程变异性的控制图。
它基于过程中收集到的样本数据,计算每个样本的极差(最大值与最小值之差),并绘制在图表上。
通过观察R图,我们可以判断过程的变异性是否稳定。
S图S图是一种用于监控过程变异性的控制图。
它基于过程中收集到的样本数据,计算每个样本的标准差,并绘制在图表上。
通过观察S图,我们可以判断过程的变异性是否稳定。
数据整理方法数据整理是SPC的一个重要步骤,它涉及收集样本数据、记录数据、计算统计量和绘制控制图等过程。
下面我们将介绍一些常用的数据整理方法。
数据收集在进行数据收集之前,需要确定采集数据的时间间隔和样本容量。
通常,采集数据的时间间隔应保证能够捕捉到过程的变化。
样本容量的确定应根据具体情况和要求进行。
数据记录数据记录是指将收集到的数据记录下来,以备后续分析使用。
可以使用电子表格软件(如Excel)或统计软件(如SPSS)等工具来记录数据。
统计量计算在进行SPC分析之前,需要计算一些统计量,如样本均值、样本标准差等。
这些统计量的计算可通过公式或统计软件完成。
控制图绘制控制图的绘制是用于直观地观察过程变异情况的重要步骤。
可以使用统计软件或绘图软件(如R语言)来绘制控制图。
SPC基础知识

SPC运用统计技术对生产过程中的各工序参数进行 监控,从而达到改进、保证产品质量的目的。
二、SPC特点
SPC具有以下特点: ---基于一定的数据资料进行统计 ---方法是绘制选择的控制图 ---只能提示过程有异常,并不能告诉异常在哪里 ---目的是实现持续改进过程 ---是全系统的、全过程的、要求全员参加 ---不仅用于生产过程,而且用于服务过程和管理过程 ---强调用科学方法来保证全过程的预防
制 程 条 件 变 动 时
制程的继续管制
六、SPC的焦点 SPC:希望将努力的方向,更进一步的放在品质 的源头----制程( Process)上。因为制程的起 伏变化,才是造成品质变异的主要根源。 品质变异的大小,才是决定产品优劣的关键 制程起伏条件 品质异常 产品优劣
七、基本统计概念
N n 母體數(批量數) 樣本數(抽樣數) USL SL 規格上限 規格中心限 (u=規格中心值)
您在工厂经常遇到这些情况吗?
顾客是上帝
销售
超时加班
额外成 本费用
•新品投放 •未预计的订单 变化 SPC作用 过程控制原理 SPC推行步骤 SPC的焦点 基本统计概念
一、什么是SPC SPC:统计过程控制(Statistical Process Control) 统计过程控制是一种通过对产品或工程进行抽样, 测量其特性参数、记录数据并绘制图表,然后进行 分析,以判断过程是否处于受控状态的管理工具。
X
R P C LCL UCL CL
平均數
全距 不良率 缺點數 控制下限 控制上限 控制中心限
LSL
Ca Cp Cpk T NP
規格下限
准确度 精密度 制程能力指數 規格公差 不良數 T=USL-LSL
SPC基本知识
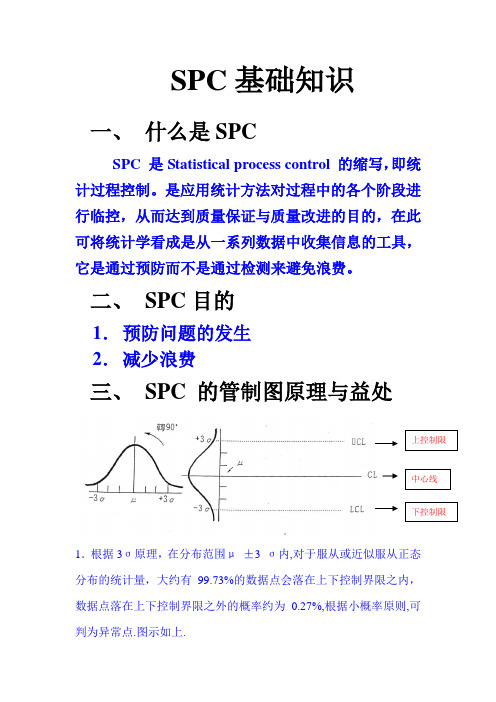
SPC 基础知识一、 什么是SPCSPC 是Statistical process control 的缩写,即统计过程控制。
是应用统计方法对过程中的各个阶段进行临控,从而达到质量保证与质量改进的目的,在此可将统计学看成是从一系列数据中收集信息的工具,它是通过预防而不是通过检测来避免浪费。
二、 SPC 目的1. 预防问题的发生 2. 减少浪费三、 SPC 的管制图原理与益处1.根据3σ原理,在分布范围μ ±3 σ内,对于服从或近似服从正态分布的统计量,大约有99.73%的数据点会落在上下控制界限之内,数据点落在上下控制界限之外的概率约为0.27%,根据小概率原则,可判为异常点.图示如上.2.SPC管制图举例下面是Minitab R14 制作的Xbar-R 管制图。
从图可以看出制程有多个超出控制限的点,说明需要查找原因,采取措施,加以消除,不再出现,纳于标准。
合理使用管制图能够:1.区分变差的普通原因和特殊原因,作为采取局部措施和系统措施的指南。
2.有助于过程在质量上和成本上能持续地、可预测地保持下去。
3.使过程达到:A、更高的质量 B、更低的单位成本C、更高的有效能力。
四、 SPC制程能力分析1.Cp、Cpk与Pp、Ppk的含义与区别如下:Cp指数= 规格宽度工序宽度Cp:(Capability of Process)过程能力指数Cpk:修正的过程能力指数Pp: (Performance of Process)过程性能指数Ppk:修正的过程性能指数2..Cp、Cpk与Pp、Ppk的计算:过程能力指数的计算公式如下:过程性能指数计算公式如下:1.经济性:有效的抽样管制,不用全数检验,不良率,得以控制成本。
使制程稳定,能掌握品质、成本与交期。
2.预警性:制程的异常趋势可实时对策,预防整批不良,以减少浪费。
3.分辨特殊原因:作为局部问题对策或管理阶层系统改进之参考。
4.善用机器设备:估计机器能力,可妥善安排适当机器生产适当零件。
SPC基本知识

受控
不受控
可接受
1类
3类
不可接受
2类
4类
2类过程虽然受控,但因为普通原因造成过大的变差而不能满足规范要求。
3类过程可接受,但存在变差的特殊原因,一般情况下要设法找出原因并消除之。
4类过程既不受控,又不可接受。应减少变差的普通原因和特殊原因。
在某些情况下,顾客允许3类过程运行。例如特殊原因已查明,具有一定的稳定性,采取措施所发生的成本比顾客获得的利益大等。
3.四类过程
过程能力与规范无关。顾客更关心的是过程的输出是否满足规范的要求。满足则可接受,否则不可接受。(关于能力与规范的关系可以用能力指数描述,以后再介绍)。
过程是否受控和是否满足规范要求是两个不同的问题。下面将过程按此分成4类(见表3-1):
1类过程是理想的,它受控且满足
规范要求。
表3-1
是否受控
二、收集数据
1.选择子组容量、频率、子组数
合理子组的确定将决定控制图的效果
①在 -R控制图中,子组的容量是恒定的。在过程研究初期n取4~5,通常取2~5件连续生产的产品。这样的子组反映的是在很短时间内、非常相似的生产条件下生产出来的产品,因此,子组内的变差主要应是普通原因造成的。这些条件不满足,就不能有效地区分出变差的特殊原因。
2.计量型数据控制图分类
表3-2列出计量型数据控制图的种类及其应用范围。
表3-2
类型
优点
应用
均值-极差图 -R
较简便,对子组内特殊原因较敏感
广泛
均值-标准差图 -S
S较R更准确有效,尤其在大样本容量时
计算机实时记录样本容量大
中位数图 -R
用 代替 ,直接描点,不用计算,最为简便
SPC 基础知识

SPC 基础知识一、基本概念:1、极差:测定值中最大值Xmax与最小值Xmin之差称为极差,用R表示:R=X max-X min2、平方和:各个测定值与平均值之差称为偏差。
各测定值的偏差的平方和称为平方和,简称平方和,用S表示:S=(X1-Xa)2+(X2-Xa)2+(X3-Xa)2+(X4-Xa)2+……+(Xn-Xa)2Xa:平均值3、方差:各个测定值的偏差平方和除以(n-1)后所得的值称为无偏方差(简称方差),用s2表示:s2=S/(n-1)4、标准偏差:方差s2的平方根称为标准偏差(简称标准差),用s表示:s=√s2我们常说的δ和μ是指的总体标准差和总体均值;当过程在受控状态下,且样本容量差较大时,可用样本标准差s和样本平均值Xa;5、正态分布:f(x)=1/√2πδ*e-(x-u)2/2δ2 (1.1)式中:x为随机变量,实为标在横座标上的特性值;e≈2.7183,是自然对数底;π≈3.1416,圆周率;δ为总体标准差;μ-根据公式(1.1)可看出,任一正态分布仅由两个参数,即总体均值μ和总体标准差δ完全确定。
μ亦称分布的位置参数,δ称分布的形状参数;δ越小,曲线越陡,数据(变量)离散也小;δ越大,曲线越扁平,数据的离散也越大,总体数值落在:μ±1δ界限范围内的概率为68.26%;μ±2δ界限范围内的概率为95.46%;μ±3δ界限范围内的概率为99.73%;μ±1.96δ界限范围内的概率为95.0%;而数据落在:μ±3δ之外的概率应小于3‟;μ±1.96δ之外的概率应小于5%;二、质量控制和过程控制概念:质量控制是质量管理的一部分,其目的是“致力于满足质量要求”。
质量控制的内容,主要包含以下三方面:1、识别并确定过程,以做到及时发现和排除产品实现过程中的变异要求,使上过程(工序)的问题不带到下一过程(工序)中去,以保证过程的稳定性和产品质量的一致性,这是一项预防性工作,简称过程控制。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
SPC 的发展及应用
SPC 源于20年代,以美国休哈特(She whart)博士发明控
制图为标志。
二战中美国将其制定为战时质量管理标准,对军工产品的
质量保证和及时交付起到了积极的作用。
50年代在日本工业界大量推广应用,对日本产品质量的崛
起起到了至关重要的作用。
14
控制图构想的基础
异因引起的变异
1/2 = 0.13%
UCL
偶因引起的变异
+3σ 3σ
1/2 = 0.13%
过程均值
LCL
控制上限 (UCL) = 过程均值 + 3 标准偏差 控制下限 (LCL) = 过程均值 – 3 标准偏差
15
时间
控制图的应用组合
Control charts should always be prepared and analyzed in pairs — one chart for location and another for spread
中位数
单值 (Individual)
31
SPC常用术语解释
名称 中心线 (Central Line) 过程均值 (Process Average) 解释 控制图上的一条线,代表所给数据平均值。
链(Run)
变差(Variation)
控制图上一系列连续上升或下降,或在中心线之上或之下的点。 它是分析是否存在造成变差的特殊原因的依据。 过程的单个输出之间不可避免的差别;变差的原因可分为两类: 普通原因和特殊原因。
满足技术要求的程度,对过程质量进行评价。
4
什么是过程?
People Machines Materials
人
机
料
A series of activities that transforms inputs into output
Output
将输入转变为输出的活动
输出
Methods
Environment
法
环
5
正态分布―连续过程的概率分布
6
任何过程均存在变异性
频 率 理想过程
(假设目标是100%)
100.00%
99.75%
理想过程
100.25
所有过程均包含变化
频 率 实际过程
99.75 目标值
100.00% 目标值
7
100.25 目标值
Cpk
规格上限 均值
3S
或
均值 规格下限
3S
8
移动极差
样本均值 样本标准偏差 单值图控制上限 单值图控制下限
/
移动极差的均值 移动极差图控制上限 28.8 28.5 移动极差图控制下限 Cpk
螺纹内径
28.88 28.84 28.80 28.76 28.72 28.68 28.64 28.60 28.56 28.52 28.48 28.44 28.40 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 0.30 0.28 0.26 0.24 0.22 0.20 0.18 0.16 0.14 0.12 0.10 0.08 0.06 0.04 0.02 0.00
© 失控且无能力
18
Cpk所表征的过程表现 (BEHAVIOR)
Cpk = negative number
Cpk = zero Cpk = between 0 and 1 Cpk = 1 Cpk > 1
19
控制均值的意义 (CENTERING THE MEAN)
中间值
过程偏移
不符合率
LL
200
202
3.267 2.574
2.282 2.114 2.004 1.924 1.864 1.816 1.777
样本容量小于7时,没有极差的控制下限。
37
单值/移动极差图
螺纹内径SPC原始记录(单值/移动极差图)
线别: 取样日期: 序号 取样时间 检测值 1 2 3 品项: 测量地点: 4 5 6 7 8 9 2.1g瓶盖 规格限/单位: 测量环境温湿度: 10 11 12 13 14 15 16 17 28.5-28.8 g 生产周期: 测量设备型号/编号: 18 19 20 21 22 23 24
CPK的分类
过程能力:指过程处于正常状态(稳定受控状态)时,加工产品
质量能够满足技术标准的能力,是指过程加工产品质量特性实际 分布的6倍标准差。过程能力用于衡量过程加工产品质量的内在一 致性。
A+
≥1.67无缺点考虑降低成本
A
B C D
1.33≤Cpk<1.67状态良好维持现状
1.0≤Cpk<1.33改进为A级 0.67≤Cpk<1.0制程不良较多,必须提升其能力 Cpk<0.67制程能力较差,考虑整改设计制程
准则4:连续14点相邻点上下交替。数据分层不够。如,两 名操作人员轮流进行操作;轮流使用两台设备。
26
控制图判异准则
准则5:连续3点有两点落在中心线同一侧的B区以外。过程 参数μ发生了变化。
27
控制图判异准则
准则6:连续5点中有4点落在中心线同一侧的C区以外。参 数μ发生了变化。
28
控制图判异准则
取样时间
检测值
均值 极差 均值的均值 均值标准偏差 极差的均值 极差标准偏差
均值图控制上限
均值图控制下限 Cpk
407
388
极差图控制上限
极差图控制下限
均值图
410 408 406 404 402 400 12 11 10 9 8 7 6 5 4 3 2 1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
极差图
398
396 394
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
9
EMPIRICAL RULL
经验定则
68.26%-95.44%-99.73% Rule
68.26%
95.44%
99.73%
10
正态分布下界限内外的比率
界限 µ±1 σ µ±2 σ 界限内的比率(%) 68.26 95.46 界限外的比率(%) 31.74 4.54
µ±3 σ
µ±4 σ µ±5 σ µ±6 σ
UL
目标值居中降低不符合率和避免浪费成本
20
精密度与漏检率的关系
中等离散性
高离散性
低离散性
漏检率几乎为零
21
纵坐标
控制图示例
XXXX图
控制图名称
566 564
UCL
562 560 558 556 554 1:00 2:00 3:00 4:00 5:00
22
控制值
总均值
横坐标(时间或次数)
UCL
6:00
32
SPC常用公式
X
Xi i
1
n
n
X 1 + X 2 + ...... + X n n
R X max X min
33
SPC常用公式
(X i i
1
n
X )
2
n 1
Xi i
1
n
2
nX
2
n 1
MR X n X n +1
34
SPC常用公式
1.880 1.023
0.729 0.577 0.483 0.419 0.373 0.337 0.308
2.660 1.772
1.457 1.290 1.184 1.109 1.054 1.010 0.975
0.000 0.000
0.000 0.000 0.000 0.076 0.136 0.184 0.223
标准差 (Standard Deviation) 分布宽度(Spread)
用于代表标准差的希腊字母
过程输出的分布宽度或从过程中统计抽样值(例如: 子组均值)的分布宽度的量度,用希腊字母σ或字母s (用于样本标准差)表示。 一个分布中从最小值到最大值之间的间距 将一组测量值从小到大排列后,中间的值即为中位数。 如果数据的个数为偶数,一般将中间两个数的平均值 作为中位数。 一个单个的单位产品或一个特性的一次测量,通常用 符号 X 表示。
3
SPC的定义
2、统计过程控制(SPC)的定义: 是应用统计技术对过程中的各个阶段进行评估和监控,建
立并保持过程处于可接受的、稳定的水平,从而保证产品
与服务符合规定要求的一种质量管理技术。
SPC是过程控制的一部分,从内容上主要分两方面:一是利
用控制图分析过程的稳定性,对过程存在的异常因素(异 因)进行预警;二是计算过程能力指数,稳定的过程能力
准则7:连续15点在C区中心线上下。现象是参数σ变小。
实际可能为数据分层不够或数据造假。
29
控制图判异准则
准则8:连续8点在中心线两侧,但无一在C区中。主要原
因为数据分层不够。
30
SPC常用术语解释
名称
平均值 极差(Range)
解释
一组测量值的均值 一个子组、样本或总体中最大与最小值之差
σ(Sigma)
我们用二个控制图 ─ 变量的位置及离散性
用于控制连续过程均值及离散性的控制图组合
