人教版7年级数学下册9.1.2 不等式的性质 教案
人教七下数学9.1.2 不等式的性质(教案)
第九章不等式与不等式组9.1不等式9.1.2不等式的性质【知识与技能】1.理解不等式的性质；2.利用不等式的性质解不等式.【过程与方法】利用天平实验探究不等式性质1,性质2;通过对具体不等式两边都乘以（或除以）同一个负数，不等式符号改变的情形探究不等式性质3;在此基础上，利用不等式的性质解不等式，要着重强化不等式性质3的理解与运用.【情感态度】通过观察、实验、类比获得新知，体验数学活动的探索性和创造性.【教学重点】不等式的性质.【教学难点】不等式的性质3.一、情境导入，初步认识问题1 用“＜”或“＞”填空：（1）5＞3，则5+2_____3+2，5-2____3-2；-1＜2，则-1+3_____2+3，-1-3____2-3；a＞b，则a±c_____b±c；a＜b，则a±c_____b±c.（2）6＞2，则6×5_____2×5，6/5_____2/5（3）-2＜7，则-2×（-6）_____7×（-6），-2/-6_____7/-6.问题2 观察（1）、（2）、（3）总结其中的规律，概括不等式有哪些性质.二、思考探究，获取新知先引导学生回顾等式的性质，再根据实验和问题1 ，2探索不等式的性质.思考不等式有哪些性质？怎样用式子表达不等式的性质？【归纳结论】不等式性质1：不等式两边加（或减）同一个数（或式子）,不等号的方向不变，用式子表示：如果a＞b，那么a±c＞b±c.不等式性质2：不等式两边乘（或除以）同一个正数，不等号的方向不变，用式子表示：如果a＞b，c＞0，那么a/c＞b/c或a/c＞b/c.不等式性质3：不等式两边乘（或除以）同一个负数，不等号的方向改变，用式子表示：如果a＞b，c＜0，那么a/c＜b/c或a/c＜b/c.三、运用新知，深化理解1.设a＞b，用“＜”、“＞”填空，并填写理由.（1）5a_____5b，理由：____________________.（2）a-7_____b-7，理由：____________________.（3）-3a_____-3b，理由：____________________.（4）3a+8_____3b+8，理由：____________________.（5）-7b+1_____-7a+1，理由：____________________.2.判断下列不等式的变形是否正确.（1）若a＜b，且c≠0，则a/c＜b/c；（2）若a＞b，则1-a2＜1-b2；（3）若a＞b，则ac2＞bc2；（4）若ac2＜bc2，则a＜b.3.根据不等式的性质解下列不等式，并在数轴上表示解集.（1）x+3＞2；（2）-2x＜6；（3）-5x+2＞3x+2；（4）2x-6＞4x-5.【教学说明】让学生自主探究，独立完成，然后相互交流，发现问题并及时纠正，教师巡视，适时予以指导.【答案】略.四、师生互动，课堂小结1.不等式的三个性质.2.运用不等式的性质3时，一定要变号.1.布置作业：从教材“习题9.1”中选取.2.完成练习册中本课时的练习.本课通过类比等式的性质，结合生活中的实例组织学生探索，得到不等式的三个性质.在探索中渗透分类讨论的思想方法，培养学生分析、解决问题的能力，从新课到练习都充分调动了学生的思考能力，小组讨论又锻炼了学生的创造性和合作性，为后面的学习打下了一定的基础.。
人教版数学七年级下册9.1.2不等式的性质教学设计
（四）课堂练习
1.教师布置一些具有代表性的练习题，涵盖本节课所学的不等式性质和应用。
2.学生独立完成练习题，教师巡回指导，关注学生的解题过程，并及时给予反馈。
3.教师选取部分学生的作业进行展示和讲解，分析解题思路和易错点。
4.学生互相讨论、交流，共同提高解题能力。
4.教师通过板书和多媒体展示，讲解如何运用不等式的性质解决实际问题，如：求解不等式、比较大小等。
（三）学生小组讨论
1.教师将学生分成若干小组，每组分配一个实际问题，要求学生运用不等式的性质解决问题。
2.学生在小组内展开讨论，共同探究不等式的性质和解决方法。
3.教师巡回指导，关注学生的讨论过程，及时解答他们的疑问。
-通过生活实例引入不等式的概念，让学生感受到数学与生活的紧密联系，激发他们的学习兴趣。
-设计富有趣味性的问题，引导学生积极思考，主动探生，通过简单易懂的例子和详细的讲解，帮助他们理解和掌握不等式的定义和性质。
-对于基础较好的学生，提供更具挑战性的问题和拓展练习，提高他们的思维能力和解题技巧。
3.学生回答后，教师总结：这些场景中都存在一种大小关系，我们称之为不等式。今天我们将学习不等式的性质，并运用它们解决实际问题。
（二）讲授新知
1.教师讲解不等式的定义，并通过例子解释不等式的符号表示。
2.讲解不等式的性质，如：可加性、可减性、可乘性、可除性，并举例说明。
3.分析生活中的实际问题，引导学生学会将实际问题抽象为不等式问题。
人教版数学七年级下册9.1.2不等式的性质教学设计
一、教学目标
（一）知识与技能
1.理解不等式的定义，了解不等式的符号表示，并能用文字和符号两种方式表达不等关系。
七年级数学下册 9.1.2 不等式的性质教案 新人教版
9.1.2 不等式的性质[教学目标]1. 理解不等式的性质,掌握不等式的解法2. 培养学生的数感，渗透数形结合的思想.[教学重点与难点]重点:不等式的性质和解法.难点:不等号方向的确定.[教学设计]一.问题探知 发现规律问题1 等式的性质1,2.问题2 用”>””<” 填空并总结规律: (1)5>3 ,5+2 3+2,5-2 3-2 (2)-1<3,-1+2 3+2, -1-3 3-3(3)6>2,6×5 2×5,6×(-5) 2×(-5)(4)-2<3,(-2)×6 3×6,(-2)×(-6) 3×(-6)由上面规律填空:(1)当不等式两边加上或减去同一个数(正数或负数)时,不等号的方向 ;(2)当不等式两边乘同一个正数时,不等号的方向 ;而乘同一个负数时,不等号的方向 .不等式性质:(1)不等式两边加(或减)同一个数(或式子),不等号的方向不变.(2)不等式两边乘(或除以)同一个正数,不等号的方向不变.(3)不等式来年改变乘(或除以)同一个负数,不等号的方向改变.例1 利用不等式的性质，填”>”,:<”(1)若a>b,则2a+1 2b+1;(2)若-1.25y<10,则y -8;(3)若a<b,且c>0,则ac+c bc+c;(4)若a>0,b<0,c<0,则(a-b)c 0.例2 利用不等式性质解下列不等式 (1)x-7>26; (2)3x<2x+1; (3)32x>50; (4)-4>3. 分析:利用不等式性质变形为最基本形,利用数轴表示解集练习:教材133:1,2题..二.巩固训练根据不等式的性质,把下列不等式化为x>a 或x<a 的形式学生观察规律归纳性质简单应用性质下列不等式: (1);23231-->x x (2)22121--≤x x (3)-3x>2;(4)-3x+2<2x+3例3 已知不等式3x-a ≤0的解集是x ≤2，求a 的取值范围.[作业]必做题:教科书134页习题:6题9.1.2不等式的性质（2）[教学目标]掌握不等式的性质,并利用不等式的性质解决简单的实际问题。
人教版七年级下册数学教案设计：9.1.2 不等式的性质
四、教学过程
1回顾旧知，类比新知2探索新知，归纳结论3基础训练，巩固应用4归纳小结
五、教学策略选择与信息技术融合的设计
教师活动
预设学生活动
设计意图
复习不等式的性质,检查学生对上节课的理解情况!
回忆，复述，回答！
小学阶段的不等式பைடு நூலகம்容的复习
本节课是在上节课学习的基础上,让学生在课前预习本节课的内容!同时讲解性质中的关键地方。
七、教学板书（本节课的教学板书）
课题：不等式的性质
性质1、
性质2
性质3
xs
A．a＞0B．a＜0C．a＜1D．a＞1
3.不等式－3≤x<2的整数解的个数是 _________
4.若a、b均为有理数，且b＜0，则a，a－b，a＋b的大小关系是__________．
5.方程3（x－1）=x－7a的解是负数，那么a的取值范围是________.
6.根据不等式的性质，把下列不等式化为“x＞a”或“x＜a”的形式。
（1） ； （2） ；
（3） ； （4）
7.有5支排球劲旅A队、B队、C队、D队、E队，参加排球锦标赛，成绩如下：D队的名次比C队低，A队比B队高，但低于E队；E队比C低，B队比D队高，请问：这5支球队各是第几名。解决这类问题，一个非常方便的方法是利用数学符号帮忙，此处用“＞”或“＜”，将成绩可简单表示成不等式，很快就得出这5个队的名次，试一下吧？
背诵性质，并做相应的练习
检查预习情况
让学生明确本节课的学习目标,让学生在明确的目的下学习本节课!
理解的基础上练习！
新课讲解
引导学生对本节课进行小结。
用自己的语言进行小结
人教版数学七年级下册9.1.2不等式的性质教学设计
（二）过程与方法
1.通过导入实际问题，引导学生发现不等式，激发学生的学习兴趣，培养学生的问题意识。
2.采用启发式教学方法，引导学生探究不等式的性质，培养学生的逻辑思维能力和团队合作精神。
3.通过典型例题的分析和讲解，让学生掌握不等式的求解方法，提高学生的解题技巧。
4.教师布置课后作业，巩固课堂所学知识，并为下一节课的学习做好准备。
5.通过总结归纳，使学生形成完整的知识体系，提高学生的数学素养。
五、作业布置
为了巩固本节课所学的不等式性质及求解方法，培养学生的数学思维能力，特布置以下作业：
1.请同学们完成课本第98页的练习题1、2、3，注意运用不等式的性质进行推理，并求解相关不等式。
4.教师讲解不等式的求解方法，如线性不等式、一元一次不等式的求解，并通过典型例题进行讲解。
5.学生跟随教师一起练习解题，掌握解题步骤和方法。
（三）学生小组讨论，500字
1.教师将学生分成若干小组，每个小组讨论一个实际问题，如：某商店的优惠活动，购买金额达到一定数额才能享受优惠，如何用不等式表示这个条件？
6.关注学生情感，营造良好氛围：尊重学生的主体地位，鼓励学生提问、发表观点，营造轻松、愉快的学习氛围，提高学生的学习积极性。
7.课后辅导与评价：课后关注学生的作业完成情况，及时给予反馈和指导，提高学生的学习效果；同时，采用多元化的评价方式，全面评估学生的学习成果。
8.跨学科整合，提高综合素养：将数学知识与其他学科知识相结合，如与物理、化学等学科的联系，提高学生解决实际问题的能力，培养学生的综合素养。
2.注重知识衔接：结合学生已有的知识基础，引导他们发现和探究不等式的性质，使新旧知识得以有效衔接。
9.1.2 不等式的性质 初中数学人教版七年级下册教案2
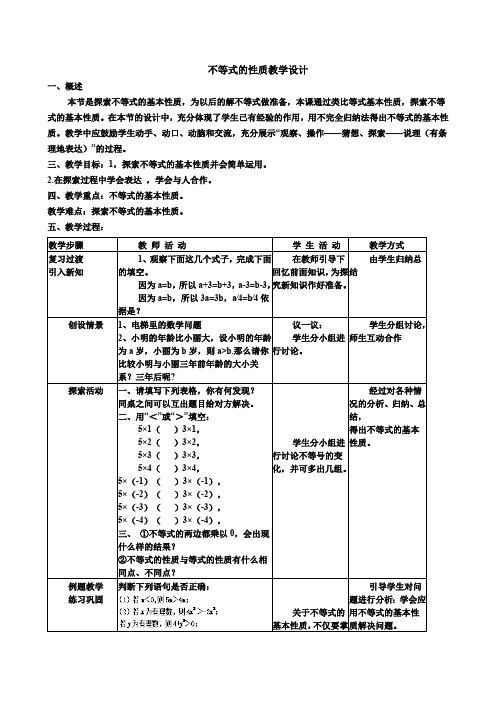
不等式的性质教学设计一、概述本节是探索不等式的基本性质，为以后的解不等式做准备，本课通过类比等式基本性质，探索不等式的基本性质。
在本节的设计中，充分体现了学生已有经验的作用，用不完全归纳法得出不等式的基本性质。
教学中应鼓励学生动手、动口、动脑和交流，充分展示“观察、操作——猜想、探索——说理（有条理地表达）”的过程。
三、教学目标：1，探索不等式的基本性质并会简单运用。
2.在探索过程中学会表达 ，学会与人合作。
四、教学重点：不等式的基本性质。
教学难点：探索不等式的基本性质。
五、教学过程：教学步骤教 师 活 动学 生 活 动教学方式复习过渡引入新知1、观察下面这几个式子，完成下面的填空。
因为a=b ，所以a+3=b+3，a-3=b-3，因为a=b ，所以3a=3b ，a∕4=b∕4依据是？在教师引导下回忆前面知识，为探究新知识作好准备。
由学生归纳总结创设情景1、电梯里的数学问题2、小明的年龄比小丽大，设小明的年龄为a 岁，小丽为b 岁，则a>b.那么请你比较小明与小丽三年前年龄的大小关系？三年后呢?议一议：学生分小组进行讨论。
学生分组讨论，师生互动合作探索活动一、请填写下列表格，你有何发现？同桌之间可以互出题目给对方解决。
二、用“＜”或“＞”填空：5×1（ ）3×1，5×2（ ）3×2，5×3（ ）3×3，5×4（ ）3×4，5×（-1）（ ）3×（-1），5×（-2）（ ）3×（-2），5×（-3）（ ）3×（-3），5×（-4）（ ）3×（-4），三、 ①不等式的两边都乘以0，会出现什么样的结果？②不等式的性质与等式的性质有什么相同点、不同点？学生分小组进行讨论不等号的变化，并可多出几组。
经过对各种情况的分析、归纳、总结，得出不等式的基本性质。
人教版七年级数学下册9.1.2不等式的性质第一课时教学设计
通过具体的例题，演示如何运用不等式的性质进行变形和求解。
3.分析解题思路
在讲解过程中，强调解题的关键步骤和注意事项，引导学生理解不等式性质的应用。
4.互动提问
在讲解过程中，适时提问，检查学生对不等式性质的理解程度。
（三）学生小组讨论
1.分组讨论
将学生分成小组，每组选取一个实际问题，共同探讨如何将问题抽象为不等式，并运用不等式的性质进行求解。
2.学生在运用不等式性质进行变形和求解时的掌握情况，是否存在误区。
3.学生在解决实际问题时，能否将问题抽象为不等式，并运用所学知识进行求解。
4.学生在团队合作中的表现，是否能积极参与、倾听他人意见、表达自己的观点。
针对以上学情，教师应采取有针对性的教学策略，如：通过生动的实例引入不等式的性质，激发学生的兴趣；设置不同难度的练习题，帮助学生巩固所学知识；注重培养学生的团队合作意识，提高学生之间的交流与互动。从而让每个学生都能在轻松愉快的氛围中学习数学，提高数学素养。
（二）过程与方法
1.提高观察、分析、能力和推理能力，运用不等式的性质进行推理和求解。
3.学会与他人合作交流，倾听他人意见，表达自己的观点。
4.能够将所学知识应用于解决实际问题，提高解决问题的能力。
（三）情感态度与价值观
1.培养学生对数学学科的兴趣和爱好，增强学习数学的自信心。
2.小组分享
各小组分享自己的讨论成果，其他小组给予评价和反馈。
3.教师点评
教师针对每个小组的讨论情况进行点评，总结优点，指出不足。
4.拓展思考
引导学生思考：除了教材中的性质，还有没有其他不等式的性质？如何证明这些性质？
（四）课堂练习
1.练习题设计
设计不同难度的练习题，涵盖本节课所学的不等式性质。
七年级数学下册9.1.2不等式的性质教学设计
一、教学目标
（一）知识与技能
1.理解不等式的定义，知道不等号表示的意义，能够识别并正确书写常见的不等式。
2.掌握不等式的性质，包括但不限于：可加性、可减性、可乘性、可除性、对称性、传递性等。
3.能够运用不等式的性质解决实际问题，如比较大小、求解未知数等。
4.学会使用数轴来直观表示不等式及其解集，理解不等式解集的区间表示方法。
3.情感态度：鼓励学生勇于尝试、善于合作，培养他们面对数学问题的信心和兴趣。
4.课后作业：布置适量、有针对性的课后作业，帮助学生巩固所学知识，为下一节课做好准备。
五、作业布置
为了巩固学生对不等式性质的理解，提高他们解决实际问题的能力，特布置以下作业：
1.请同学们完成课本第92页的练习题第1-4题，这些题目涵盖了不等式的定义和基本性质，旨在帮助学生巩固基础知识。
2.完成第93页的第5-8题，这些题目设计了较为复杂的不等式问题，需要学生运用所学的性质进行推理和求解。通过这些题目，学生可以进一步提升解题技巧和逻辑思维能力。
3.结合生活实际，设计一道与不等式相关的实际问题，要求学生将其转化为数学模型，并利用不等式的性质解决问题。此题旨在培养学生将数学知识应用于生活的能力，激发他们的学习兴趣。
1.对不等式的概念理解不深，容易混淆不等号的意义。
2.在运用不等式性质解决问题时，可能缺乏灵活性和策略性。
3.对数轴的运用不够熟练，难以将抽象的不等式与具体的图形结合起来。
4.部分学生在解决实际问题时，可能难以将问题转化为数学模型。念的教学，通过实例对比，帮助学生明确不等号的意义。
7.教学拓展：针对学有余力的学生，可以设计一些拓展性练习，如研究不等式的证明、解决更复杂的问题等，激发学生的兴趣，提高他们的数学素养。
七年级数学下册9.1.2《不等式的性质》教案(新版)新人教版
9.1.2不等式的性质课题9.1.2不等式的性质课标要求理解和掌握不等式的三个性质，并会用它们解不等式。
教学目标知识与技能掌握不等式的三个基本性质并且能正确应用。
过程与方法经历类比等式的性质探究不等式性质的过程，培养学生自主探究、合作交流的意识，发展学生分析问题和解决问题的能力。
情感态度与价值观通过创设问题情境和思考探究活动，初步体会学习不等式基本性质的价值。
让学生感受到数学与生活的密切联系，激发学生学习数学及应用数学的积极性。
教学重点理解并掌握不等式的三个基本性质教学难点对不等式的性质3的理解及利用不等式的性质解决问题。
教学方法自主-合作-探究教学用具多媒体课件课堂小结与板书设计课堂小结;不等式的性质板书设计：一、情境引入二、明确目标三、合作交流、探究新知四、当堂训练检查评价教研组应备：节，实备节，超备节。
质量评价： 20 年月日教学主管20 年月日内容与过程教学环节与内容反思补充教学过程一、情境引入(激趣导学)提出问题：（展示购物图片提出实际问题）师：同学们老师在购物时遇到一个困难请大家帮助解答：我有200元钱要到超市购买3件相同的礼物作为奖品，奖给本次质量监测成绩较好的三位同学，如果我至少要留下110元钱，那么每件礼物应选择多少钱的？引导学生列出不等式：师：想知道未知数的值就要解不等式，如何解不等式呢？要想解决这个问题这节课我们就先来学习不等式的基本性质。
二、明确目标1．理解并掌握不等式的三个性质;2．能够利用不等式的性质对不等式进行各种变形、解不等式，进而解决生活的问题。
3.感受类比迁移及分类讨论的数学学习方法。
三、合作交流、探究新知（指导阅读、自主互助、效果反馈，诱导探究）（一）自学指导1：（1）认真看课本P 116的内容,并完成以下思考练习。
（2）从思考练习中，你发现了不等号变化的什么规律？请把你的发现告诉同学们并与他们交流。
（4分钟后,比谁能正确说出答案，完成思考练习。
）1、（思考练习）用“＞”或“＜”填空，并总结不等号的变化规律。
人教版七年级下册9.1.2不等式的性质教学设计
3.重点：将实际问题转化为不等式。
难点：从实际情境中抽象出数学模型，建立实际问题与不等式之间的联系。
（二）教学设想
1.教学方法：
（1）采用启发式教学，引导学生通过观察、思考、讨论，发现和掌握不等式的性质。
（2）运用数形结合的方法，将不等式与图形相结合，帮助学生直观地理解不等式的性质。
（4）引导学生互相提问，解答疑问，共同进步。
（四）课堂练习
1.教学内容：设计具有代表性的练习题，让学生运用不等式的性质和解题方法解决实际问题在规定时间内完成。
（2）学生独立解题，教师关注学生的解题过程，及时发现问题并进行个别指导。
（3）学生互相讨论解题方法，分享经验。
人教版七年级下册9.1.2不等式的性质教学设计
一、教学目标
（一）知识与技能
本节课是关于不等式的性质的学习，旨在帮助学生掌握以下知识与技能：
1.理解不等式的定义，知道不等式的表示方法，如“大于”、“小于”、“大于等于”、“小于等于”等。
2.掌握不等式的性质，包括：传递性、对称性、可加性和可乘性。
3.学会解简单的一元一次不等式，如ax+b>c或ax+b<c的形式。
4.能够将实际问题转化为不等式，并运用不等式的性质解决实际问题。
（二）过程与方法
1.引导学生通过观察和思考，发现不等式的性质，培养他们的观察能力和逻辑思维能力。
2.采用举例、讨论、归纳等方法，帮助学生总结和掌握不等式的性质。
3.设计具有实际背景的问题，让学生在实际情境中运用不等式的性质，提高他们解决实际问题的能力。
（1）解一元一次不等式，如ax+b>c或ax+b<c的形式。
人教版数学七年级下册9.1.2不等式的性质第一课时教学设计
5.反馈评价，及时调整：在教学过程中，教师应关注学生的学习反馈，通过课堂提问、小组讨论、作业批改等方式了解学生的学习情况，及时调整教学策略，确保教学目标的达成。
4.学生的情感态度：部分学生对数学学习可能存在恐惧心理，教师应关注学生的情感需求，营造轻松愉快的学习氛围，激发学生的学习兴趣。
三、教学重难点和教学设想
（一）教学重点
1.不等式的性质及其应用，这是本节课的核心内容，学生需要掌握不等式的传递性、加法性和乘法性，并能将这些性质应用于实际问题中。
2.不等式解集的表示方法，学生应学会使用数轴来直观表示不等式的解集，并能够根据不等式的性质来求解一元一次不等式。
4.设计不同难度的练习题，让学生在解题过程中逐步掌握不等式的性质，形成解决问题的策略。
（三）情感态度与价值观
1.培养学生对数学的兴趣，让学生在探索不等式性质的过程中，感受到数学的趣味性和挑战性。
2.培养学生的自信心和自主学习能力，鼓励学生在课堂上积极思考、勇于表达，形成良好的学习习惯。
3.引导学生认识到数学在生活中的广泛应用，体会数学与现实生活的紧密联系，培养学生的应用意识。
2.自主探究，合作交流：在探索不等式性质的过程中，教师应鼓励学生独立思考，小组内交流讨论，共同发现和总结不等式的性质。教师在此过程中起到引导和辅助的作用，帮助学生构建知识框架。
3.数形结合，直观教学：运用数轴来表示不等式的解集，让学生通过图形直观地理解不等式的性质和解集的含义，增强学生的直观想象能力。
4.通过对不等式的学习，培养学生公平、公正的价值观，让学生明白在现实生活中，合理分配和比较的重要性。
七年级数学下册(人教版)9.1.2不等式的性质优秀教学案例
4.教学策略的灵活性：本案例采用了多种教学策略，如情景创设、问题导向、小组合作等，使得课堂更加生动有趣，提高了学生的学习兴趣和参与度。
5.教学目标的全面性：本案例的教学目标涵盖了知识与技能、过程与方法、情感态度与价值观三个方面，使得学生能够在学习的过程中，不仅掌握知识和技能，还能够培养正确的数学观念和积极的学习态度。
在教学过程中，我将以学生为中心，采用启发式教学法，引导学生主动探索、发现和理解不等式的性质。我会设计一些互动活动，让学生通过讨论、交流、合作等方式，共同探索不等式的性质，提高他们的思维能力和解决问题的能力。
此外，我还会运用多媒体教学手段，如课件、动画等，来形象地展示不等式的性质，帮助学生更好地理解和记忆。同时，我会注重培养学生的数学语言表达能力，让他们能够清晰、准确地表达自己的思考和解答。
五、案例亮点
1.情景创设的真实性：本案例通过设计一个实际问题，引出了不等式的概念和性质，使得学生能够更好地理解不等式的实际意义，提高了学生的学习兴趣和积极性。
2.问题导向的有效性：本案例通过提出一系列问题，引导学生进行思考和探索，使得学生能够主动去思考和解决问题，培养他们的思维能力和解决问题的能力。
（二）问题导向
在教学过程中，我会提出一些问题，引导学生进行思考和探索。这些问题可以是关于不等式的概念、性质以及如何应用不等式解决实际问题。通过问题导向，学生能够主动去思考和解决问题，培养他们的思维能力和解决问题的能力。
（三）小组合作
在教学过程中，我会组织学生进行小组合作，共同探讨和解决问题。通过小组合作，学生能够相互交流和合作，共同探索不等式的性质，提高他们的团队合作能力和交流能力。同时，小组合作也能够激发学生的学习兴趣，增加课堂的互动性和趣味性。
人教版七年级数学下册9.1.2不等式的性质(第二课时)教学设计
总字数：2500字
五、作业布置
为了巩固本节课所学的不等式性质及其应用，特布置以下作业：
1.请同学们结合自己的生活经验，找出至少三个不同的实际问题，将其抽象为不等式，并求解。要求用文字描述问题背景，明确列出不等式，并解释每一步的求解过程。
2.学生观察后，教师提问：“我们之前学过的不等式，如何用来描述这些图片中的数学关系？”从而引导学生回顾不等式的概念。
3.教师总结：生活中存在着许多不等的关系，这节课我们将继续探讨不等式的性质，并学会运用它们解决实际问题。
（二）讲授新知，500字
1.教师通过具体例子，如a > b，b > c，引导学生发现不等式的传递性：a > b，b > c，则a > c。
（2）情境教学：创设生活情境，让学生在实际问题中感受数学的魅力。
（3）分层教学：针对不同层次的学生，设计不同难度的练习题，使每个学生都能在课堂上得到提高。
（4）小组合作：鼓励学生合作交流，共同解决问题，培养学生的团队协作能力。
四、教学内容与过程
（一）导入新课，500字
1.教师通过多媒体展示一组生活中的图片，如身高比较、温度计等，引导学生观察并思考：这些图片中隐藏着什么样的数学关系？
（三）情感态度与价值观
1.培养学生对数学的兴趣，激发学习数学的热情，增强自信心。
2.使学生认识到数学在生活中的广泛应用，体会数学的价值，增强学习的责任感。
3.培养学生严谨、细致的学习态度，养成独立思考、主动探究的良好习惯。
4.培养学生团队协作意识，学会倾听、尊重他人，共同提高。
总字数：1002字
二、学情分析
七年级数学下册9.1.2不等式的性质优秀教学案例
四、教学内容与过程
（一）导入新课
1.创设情境：以实际问题导入新课，例如：“小明和小华比赛跑步，小明每分钟跑60米，小华每分钟跑65米，请问小明和小华谁会先到达终点？”让学生感受不等式的性质在实际生活中的应用。
2.引导学生思考：让学生提出解决问题的方法，培养学生独立思考的能力。
3.揭示课题：引出不等式的性质，让学生了解本节课的学习目标。
为了激发学生的学习兴趣，我在课堂上运用了多媒体教学手段，以生动形象的动画展示不等式的性质，使抽象的知识具体化、直观化。此外，我还注重关注每个学生的学习情况，针对不同的学生给予个性化的指导，让他们在课堂上充分展示自己，提高自信心。
在教学过程中，我始终坚持以学生为中心，注重培养学生的自主学习能力、合作意识和创新精神。通过本节课的教学，学生对不等式的性质有了深入的理解和掌握，为他们后续学习解不等式打下了坚实的基础。
3.教育学生树立正确的价值观，认识到数学知识在现实生活中的重要性。
4.培养学生具有良好的学习习惯和道德品质，使他们成为德智体美全面发展的人才。
三、教学策略
（一）情景创设
1.结合生活实际，创设有趣的不等式问题情境，激发学生学习兴趣。
2.利用多媒体展示不等式的性质，让学生直观感受数学与现实生活的紧密联系。
3.设计具有挑战性的数学问题，引发学生思考，激发他们的求知欲。
人教版七年级下册9.1.2不等式的性质教学设计
人教版七年级下册9.1.2不等式的性质教学设计教学目标1.理解不等式的含义及其形式2.能够掌握不等式的基本性质3.能够应用不等式的性质解决相关问题教学重点难点1.不等式的基本形式及其含义2.不等式的性质及其应用教学过程设计第一步：导入新知识（5分钟）•引入不等式的概念，提问“在数轴上，如何表示两个数之间的大小关系？”•提供不等式的定义，“如果a和b是两个实数，则a>b表示a比b大，a<b表示a比b小，a≥b表示a不小于b，a≤b表示a不大于b，a≠b表示a不等于b。
”•给出简单的不等式例子并让学生解释其含义，如3>1、4≤6等。
第二步：探讨不等式的性质（25分钟）•教师讲解不等式的基本性质，如符号保持性、加减乘除不等式的原则等。
•引导学生在课堂上通过思考解决问题，例如：“如果a>b，那么a+c>b+c吗？”等。
•学生讨论并总结各种情况下不等式的性质及其应用，例如交换不等式两边的值时应该改变符号的方向。
第三步：应用不等式解决问题（20分钟）•针对不等式的性质及其应用进行练习和解题，通过实例加深学生的理解。
•提供生活中实际问题，如销售员的销售提成、餐厅的餐费和折扣等，让学生运用所学知识进行计算，掌握不等式的应用。
第四步：知识归纳与总结（10分钟）•教师和学生一起对本节课的重点内容进行总结，应用不等式解决生活中的问题。
•强调不等式理论在生活中的应用价值，鼓励学生在日常生活中运用所学知识。
教学评价方式1.在教学过程中，通过互动交流、布置的小练习、实践活动等方式评价学生的掌握程度。
2.提供不同难度的测试题目作为总结性评价方式，检测学生对知识的掌握与应用能力。
七年级数学下册9.1.2不等式的性质教学设计
（2）某商店举行打折活动，满100元减20元。如果小王购买了一件原价200元的衣服，实际支付了160元。请问：小王购买的衣服是否享受了打折优惠？请用数学语言表示并证明。
4.探究题：引导学生思考以下问题，培养学生的探究精神：
（1）如果不等式两边同时乘以（或除以）同一个正数，不等式是否仍然成立？请给出证明。
（2）如果不等式两边同时乘以（或除以）同一个负数，不等式会发生什么变化？请给出证明。
5.复习题：为了帮助学生巩固所学知识，布置以下复习题：
（1）回顾已学的方程和不等式的区别与联系，总结在解题过程中的注意事项。
（2）整理本节课所学的不等式性质，以及在实际问题中的应用。
（二）过程与方法
1.通过观察、猜想、验证、总结等教学活动，培养学生自主探究和合作学习的能力。
2.引导学生运用数形结合的思想，通过图像直观地理解不等式的性质，提高解决问题的直观思维能力。
3.设计丰富的例题和练习，让学生在解决问题的过程中，掌握不等式的性质，提高解题技巧。
4.教学中注重启发式教学，引导学生从实际问题中发现不等式，培养发现问题和解决问题的能力。
2.不等式的证明：教师以具体的例子，引导学生运用数形结合的方法，证明不等式的性质。
（三）学生小组讨论
1.分组讨论：学生分成小组，针对教师提出的问题，进行讨论和交流。
2.讨论内容：
（1）不等式的性质在实际问题中的应用；
（2）如何运用不等式的性质解决实际问题；
（3）分享自己在解决问题时的思考和困惑。
3.教师巡回指导：教师参与学生讨论，解答学生的疑问，引导他们深入理解不等式的性质。
人教版数学七年级下册9.1.2不等式的性质(教案)
3.重点难点解析：在讲授过程中，我会特别强调不等式的性质一至性质五。对于难点部分，如性质三和性质五，我会通过举例和比较来帮助大家理解。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与不等式相关的实际问题。
2.实，通过实际操作来演示不等式的基本原理。
五、教学反思
今天我们在课堂上学习了不等式的性质，这节课让我感受到了同学们的积极性和参与度。大家在导入新课环节，能够主动分享自己在日常生活中遇到的不等式问题，这为后续的学习奠定了良好的基础。但在教学过程中，我也发现了一些需要改进的地方。
首先，对于不等式性质的理解，部分同学仍然存在困难，尤其是在性质三和性质五上。在讲授这一部分时，我应该更加注重引导同学们通过实例来理解这些性质，而不仅仅是理论讲解。在今后的教学中，我会尝试用更多生活中的例子，让大家感受到数学知识在实际中的应用，提高他们的学习兴趣。
2.教学难点
-难点一：理解不等式的性质，特别是性质三和性质五。对于性质三，学生需要理解为什么只能乘以正数；对于性质五，学生需要掌握乘以正数和负数时，不等号方向的变化。
-难点二：将实际问题抽象为不等式问题。学生在解决实际问题时，往往难以将问题中的关系转化为不等式，需要教师引导和培养。
举例：
-难点一：对于性质三，学生可能会困惑，为什么不能乘以负数。可以通过实例解释，如-3>-2，若乘以负数，如-1，则-3×(-1)<-2×(-1)，即3<2，与原不等式矛盾。
其次，在实践活动环节，同学们在分组讨论和实验操作中表现出很高的热情，但讨论过程中有时会偏离主题。这可能是因为我在引导讨论时，问题的设置不够明确。为了提高讨论的效率，我需要在今后的教学中，更加注意问题的设计，让同学们能够更有针对性地展开讨论。
人教版7年级数学下册9.1.2 不等式的性质 教案
课题：9.1.2 不等式的性质（1）三维目标知识与技能1、理解掌握不等式的性质；2、会解决简单的一元一次不等式，并能在数轴上表示出解集。
过程与方法经历通过类比、猜测、验证发现不等式性质的探索过程，初步体会不等式与等式的异同，初步掌握类比的思想方法。
情感与态度通过创设问题情境和实验探究活动，积极引导学生参与数学活动，提高学习数学的兴趣，增进学习数学的信心，体会在解决问题的过程中与他人交流合作的重要性。
教学重点：理解并掌握不等式的性质及运用；教学难点：不等式性质3的探索及正确运用不等式的性质；教学方法与手段：启发、讨论、探究教学过程：一、情境创设复习回顾：等式有哪些性质？导入新课：①给不平衡的天平两边同时加入相同质量的砝码，天平会有什么变化？②不平衡的天平两边同时拿掉相同质量的砝码，天平会有什么变化？③如果对不平衡的天平两边砝码的质量同时扩大相同的倍数，天平会平衡吗？缩小相同的倍数呢？二、自主探究探究活动一（一）探究不等式的性质问题1用“＞”或“＜”填空．①－1 < 3－1＋2 3＋2，－1－3 3－3②5 >35＋a 3+a ，5－a 3－a③ 6 > 26×5 2×5 ，6×（－5） 2×（－5）④－2 < 3（－2）×6 3×6（－2）×（－6） 3×（一6）⑤－4 ＞－6（－4）÷2 （－6）÷2（－4）÷（－2）（－6）÷（－2）问题2修订、增减从以上练习中，你发现了什么规律？请你再用几个例子试一试，还有类似的结论吗？请把你的发现告诉同学们并与他们交流．问题3你能用式子表示不等式的三条性质吗？【板书如下：（1）若a >b ，则a+c > b+c ,a-c >b-c ；（2）若a >b ，且c>0,则ac >bc ，a/c >b/c ； （3）若a >b ，且c<0,则ac<bc ，a/c<b/c 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
修订、增减
课题：
9.1.2不等式的性质（2）
三维目标
知识与技能
1、使学生熟练掌握不等式性质||，灵活利用不等式性质解不等式；
2、初步认识一元一次不等式的应用价值；
过程与方法
学会运用类比思想来解不等式||，培养学生观察、分析和归纳的能力；
情感与态度
在积极参与数学活动的过程中||，培养学生大胆猜想、勇于发言与合作交流的意识和实事求是的态度以及独立思考的习惯．
④－2 < 3
（－2）×63×6
（－2）×（－6）3×（一6）
⑤－4＞－6
（－4）÷2（－6）÷2
（－4）÷（－2）（－6）÷（－2）
问题2
从以上练习中||，你发现了什么规律？请你再用几个例子试一试||，还有类似的结论吗？请把你的发现告诉同学们并与他们交流．
问题3
你能用式子表示不等式的三条性质吗？
【板书如下：
问题1
利用不等式的性质填“>”||，“<”:
(1)若a>b||，则2a2b;
(2)若-2y<10||，则y-5;
(3)a<b||，c>0||，则ac-1bc-1;
(4)a>b||，c<0||，则ac+1bc+1||。
问题2
利用不等式性质解下列不等式||，并在数轴上表示解集：
（1）x-7＞26
（2）3x < 2x＋1
教学重点：理解并掌握不等式的性质及运用；
教学难点：不等式性质3的探索及正确运用不等式的性质；
教学方法与手段：启发、讨论、探究
教学过程：
一、情境创设
复习回顾：
等式有哪些性质？
导入新课：
①给不平衡的天平两边同时加入相同质量的砝码||，天平会有什么变化？
②不平衡的天平两边同时拿掉相同质量的砝码||，天平会有什么变化？
教学重点：不等式的性质和解法；
教学难点：不等式的性质和解法；
教学方法与手段：启发、讨论、探究
教学过程：
一、情境创设
复习回顾：
1、不等式的三条基本性质是什么？
2、用“<”、“>”或“=”填空：
（1）若a >b||，
则a+cb+c||，a-cb-c；
（2）若a >b||，且c>0||，
则acbc||，a/cb/c；
∴0≤V≤105
在数轴上表示为：
问题2
三角形任意两边之差与第三边有着怎样的大小关系？
解：设a、b、c为任意一个三角形的三条边的长||，则
a+b＞c||，b+c＞a||，c+a＞b.
移项||，得
a＞c-b||，b＞a-c||，c＞b-a.
三角形中任意两边之差小于第三边||。
三、尝试应用
1、解下列不等式||，并在数轴上表示解集：
根据等式的性质2||，得x≥50×3/2
∴x≥7 5
(4)-4x≤3
根据等式的性质3||，得x≤-3/4||。
三、尝试应用
1、设a < b||，用“<”或“>”填空||，并说明依据：
（1）3a3b；依据||。
（2）a-8b-8；依据||。
（3）-2a-2b；依据||。
（4）2a-52b-5；依据||。
3、还有哪些问题需要注意？
让学生自己归纳||，教师仅做必要的补充和点拨．
六、布置作业
修订、增减
（1）3－5x≥4－6x
（2）－300x＜1500
（3）2-2x<6
（4）5x+54＜x-1
2.当x时||，2-3x为非正数.
3、已知一个等腰三角形的底边长5||，腰长为x||，则x的取值范围是.
四、补充提高
1.解下列不等式||，并把它们的解集在数轴上表示出来||。
（1）（1－x）＜2(x+9);
(2) .
探究活动二
（二）不等式的简单应用
问题1
某长方体形状的容器长5 cm||，宽3 cm||，高10 cm.容器内原有水的高度为3 cm||，现准备继续向它注水．用V（单位：cm3）表示新注入水的体积||，写出V的取值范围||。
解：依题意||，得
V+3×5×3≤3×5×10
∴V≤105||。
不是||，因为新注入水的体积不能是负数||，所以V≥0||。
（3）若a >b||，且c<0||，
则acbc||，a/cb/c||。
二、自主探究
探究活动一
（一）运用不等式性质解不等式
问题1
解下列不等式||，并在数轴上表示解集：
（1）x-5＞－2（2）-
(3) 8x-2 < 7x＋3
问题2
解下列不等式||，并在数轴上表示解集：
(1) 7－3x≤10
（2）2x-3 < 3x＋1
（3） x≤50
(4)-4x < 3
分析：解不等式最终要变成什么形式呢？
就是要使不等式逐步化为x＞a或
x <a的形式||。
解：(1) x－7＞26
根据等式的性质1||，得x－7+7＞26+7
∴x＞33
（2）3x < 2x＋1
根据等式的性质1||，得3x-2x < 2x＋1-2x
∴x<1
（3）2/3 x≥50
（1）a－3 > b－3
（2）
（3）－4a >－4b
2、用不等式表示下列语句并写出解集：
（1）x与3和不小于6；
（2）y的4倍小于或等于-2||。
（3）x的3倍大于或等于1；
（4）y与1的差不大于0
3、关于x的不等式2x+a 0的负整数解是-2||，-1||，求a的取值范围.
五、课堂小结
通过本节课的学习||，你学会了哪些知识？有哪些感悟？给同学、老师说一说？
课题：
9.1.2不等式的性质（1）
三维目标
知识与技能
1、理解掌握不等式的性质；
2、会解决简单的一元一次不等式||，并能在数轴上表示出解集||。
过程与方法
经历通过类比、猜测、验证发现不等式性质的探索过程||，初步体会不等式与等式的异同||，初步掌握类比的思想方法||。
情感与态度
通过创设问题情境和实验探究活动||，积极引导学生参与数学活动||，提高学习数学的兴趣||，增进学习数学的信心||，体会在解决问题的过程中与他人交流合作的重要性||。
2.已知关于 的方程 的解是非正数||，求 的取值范围||。
3.一个长方形的周长为60㎝||，长不小于宽||，那么它的长的取值范围是什么？
4、思考题:已知关于x的不等式(1-a)x>2的两边同时除以(1-a)得到 ||，试化简
五、课堂小结
课堂小结：
围绕以下几个问题：
1、这节课的主要内容是什么？
2、通过学习||，我取得了哪些收获？
③如果对不平衡的天平两边砝码的质量同时扩大相同的倍数||，天平会平衡吗？缩小相同的倍数呢？
二、自主探究
探究活动一
（一）探究不等式的性质
问题1
用“＞”或“＜”填空．
①－1 < 3
－1＋23＋2||，－1－33－3
②5 >3
5＋a3+a||，5－a3－a
③6 > 2
6×52×5||，6×（－5）2×（－5）
（5）-3.5a+1-3.5b+1||。依据||。
பைடு நூலகம்2、填空
（1）∵2a > 3a∴a是数
（2）∵ ∴a是数
（3）∵ax < a且x > 1∴a是数
3、解下列不等式||，并在数轴上表示解集：
（1）x＋5＞－1（2）4x < 3x-5
（3） （4）－8x < 10
四、补充提高
1、根据下列已知条件||，说出a与b的不等关系||，并说明是根据不等式哪一条性质||。
（1）若a >b||，则a+c > b+c||，a-c >b-c；
（2）若a >b||，且c>0||，则ac >bc||，a/c >b/c；
（3）若a >b||，且c<0||，则ac<bc||，a/c<b/c||。】
问题4
你能说出不等式性质与等式性质的相同之处与不同之处吗？
探究活动二
（二）不等式的性质的运用