九年级物理电阻的串联和并联
九年级上册物理串联和并联

九年级上册物理串联和并联一、串联电路。
1. 定义:用电器首尾依次相连的电路。
2. 特点:- 电流只有一条路径。
- 各用电器之间相互影响,一个用电器不工作,其他用电器都不能工作。
- 电路中总电阻等于各电阻之和,即R_总=R_1 + R_2 + ·s + R_n。
- 电路中总电压等于各用电器两端电压之和,即U_总=U_1 + U_2 + ·s +U_n。
- 电路中电流处处相等,即I = I_1 = I_2 = ·s = I_n。
二、并联电路。
1. 定义:用电器两端分别连在一起,然后接入电路的电路。
2. 特点:- 电流有多条路径。
- 各用电器之间互不影响,一个用电器不工作,其他用电器仍能工作。
- 电路中总电阻的倒数等于各电阻倒数之和,即(1)/(R_总) = (1)/(R_1) + (1)/(R_2) + ·s + (1)/(R_n)(两个电阻并联时,R_总=(R_1× R_2)/(R_1 + R_2))。
- 电路中干路电流等于各支路电流之和,即I_总=I_1 + I_2 + ·s + I_n。
- 各支路两端电压相等,且都等于电源电压,即U = U_1 = U_2 = ·s = U_n。
三、串联和并联电路的识别方法。
1. 定义法:根据串联和并联电路的定义来判断。
2. 电流法:从电源正极出发,沿着电流的流向观察,如果电流始终不分流,则是串联电路;如果电流在某一点分流,分别通过不同的用电器,然后在另一点汇合,则是并联电路。
3. 拆除法:拆除一个用电器,如果其他用电器都不能工作,则是串联电路;如果其他用电器仍能工作,则是并联电路。
四、串联和并联电路的应用。
1. 家庭电路中,各用电器之间是并联的,这样可以保证各用电器独立工作,互不影响。
2. 节日小彩灯通常是串联的,因为串联电路中电流相等,通过每个小彩灯的电流相同,亮度较均匀。
但其中一个小彩灯灯丝烧断,其他小彩灯都会熄灭。
九年级(初三)物理串、并联电路中的电阻关系

例2、有一只灯泡正常发光时两端电压为6V, 灯丝电阻为10Ω,若电源电压为9V,要把此 灯接在电源上,并使它正常发光,应怎样连接 一个电阻,且电阻阻值为多少?
注意:串联电阻有分压的作用
问题与思考
把电阻R1和R2并联起来,它们的等效电 阻R还等于各电阻之和吗?
AI
U1 R1 I1
U2 R2 I2
U S
例4、如图所示,电流表A1的示数为0.4A, 电流表A2的示数为0.5A,已知R2=80Ω,求 R1的阻值?
例5、如图所示,已知R1=9Ω,R2=12Ω,当 开关S断开,电流表示数为I,当开关S闭合 时,电流表示数为Iˊ,求I :Iˊ。
练一练
1. n个阻值为R0的电阻串联,则总电 阻为( nR0 )。
三、串联电路中的电压分配关系:
串联电路中导体两端分得的电压跟电阻成正 比。(串联电路中导体电阻越大,其对应的电 压也越大)
公式: U1 R1 U 2 R2
例1、如图所示,已知R1=8Ω,R2=12Ω,电 源电压U=6V,求(1)电路中的电流;(2) R1、R2两端的电压各是多少?
(3)两电阻分得的电压之比?
5-1.将两个电阻串联,总电阻为72 欧,若一个电阻为30欧,另一个是
_4_2_欧__
5-2.将两个电阻并联,总电阻为24
欧 _6_0,_若欧__一个电阻为40欧,另一个是
6-1.两个电阻均为6欧的电阻串联接 入电路总电阻为_____
6-2.两个电阻均为6欧的电阻并联接 入电路总电阻为_____
U
S
乙
如甲图所示,将电阻R1 和R2接到电压为U的电 路两端,电路中的电流 是I,用一个电阻R替代
这两个电阻,仍接到这 个电压为U的电路中,
九年级串联和并联知识点

九年级串联和并联知识点串联和并联是物理学中电路连接方式的两种基本形式。
在电路中,元件的连接方式会影响电流、电压和电阻等物理量的分布和变化规律。
了解串联和并联的知识点对于理解和分析电路的性质和特点非常重要。
一、串联电路的特点串联电路是指将多个电器或元件依次连接起来,电流只能在串联元件之间流动,是一种线性连接方式。
1.1 串联电流的特点在串联电路中,电流只能沿着一条路径流动,电流大小相等。
1.2 串联电阻的特点串联电阻等效为总电阻的和,即Rt = R1 + R2 + R3 + ...,总电阻随串联电阻的增加而增加。
串联电阻的整体阻力比单个电阻要大。
二、并联电路的特点并联电路是指将多个电器或元件并行连接在一起,电流可以分流,是一种分支连接方式。
2.1 并联电流的特点在并联电路中,电流可以分流,通过每条分支电路的电流之和等于总电流,即I = I1 + I2 + I3 + ...,总电流随并联电流的增加而增加。
2.2 并联电阻的特点并联电阻等效为总电阻的倒数之和的倒数,即1/Rt = 1/R1 +1/R2 + 1/R3 + ...,总电阻随并联电阻的增加而减小。
并联电阻的整体阻力比单个电阻要小。
三、串联和并联电路的应用串联和并联电路在日常生活和工程应用中都扮演着重要角色。
3.1 串联电路的应用·家庭电路中,串联电路用于电灯和电器等设备,使其依次接通工作。
·线性稳压器中的电阻和电容串联连接,起到稳压和滤波的作用。
3.2 并联电路的应用·在家庭电路中,空调、冰箱等功率较大的电器通常采用并联连接,以满足功率需求。
·电路中的继电器通常使用并联连接,以便同时控制多个电路。
·并联电池可以增加供电时间,应用于无线电通信和应急照明等领域。
四、串并联混合电路的特点实际电路中常常会存在串联和并联的混合连接方式,即串并联混合电路。
对于这种电路,我们可以分别分析其串联和并联部分,再将两部分的结果综合起来。
初三物理串联和并联

初三物理串联和并联一、串联和并联的定义串联和并联是电路的基本连接方式,它们的主要区别在于元件之间的连接方式。
在串联电路中,所有元件逐个顺次连接;而在并联电路中,所有元件并列地连接到电路的两端。
二、串联和并联的电路图表示在电路图中,串联和并联电路的表示方法也有所不同。
串联电路中的元件用一条垂直线连接,而并联电路中的元件用水平线连接。
例如,两个电阻串联时,它们在电路图中的表示方法是一条垂直线连接两个电阻,而两个电阻并联时,它们在电路图中的表示方法是一条水平线连接两个电阻。
三、串联和并联的电流特点在串联电路中,电流的大小是相同的,即流经每个元件的电流都相等。
而在并联电路中,每个支路的电流是独立的,即每个支路上的电流可以不同。
四、串联和并联的电压特点在串联电路中,如果所有元件的电阻值都相同,那么各元件两端的电压相等。
而在并联电路中,每个支路两端的电压相等。
五、串联和并联的电阻特点在串联电路中,总电阻等于各个元件的电阻之和。
而在并联电路中,总电阻的倒数等于各个支路电阻的倒数之和。
六、串联和并联的电功率特点在串联电路中,电功率的计算方法是:P=I²R=I²(R1+R2+...)。
在并联电路中,电功率的计算方法是:P=U²/R=U²/(R1+R2+...)七、串联和并联的电路元件作用在串联电路中,电阻可以限制电流的大小,而电压表可以测量元件两端的电压。
在并联电路中,电阻可以增加电流的灵活性,而电流表可以测量通过支路的电流。
八、串联和并联的电路故障分析串联和并联电路的故障分析方法有所不同。
在串联电路中,如果某个元件出现故障,整个电路将无法正常工作。
而在并联电路中,即使某个支路出现故障,其他支路仍可正常工作。
因此,在进行故障分析时,需要根据电路的特点进行逐一排查。
九、串联和并联的实际应用举例串联和并联电路在实际中的应用广泛。
例如,家庭中的灯泡通常是并联的,这样可以让每个灯泡都能得到相同的电流供应。
第四节:电阻的串联和并联

R =4Ω
1.并联电路的总阻值推导
A
I1 R I2 1R2
U= U1= U2
U U1 U2 R并 R1 R2
I=I1+I2
1 11 R并 R1 R2
结论: 电阻并联后总电阻的阻值比任何一个
分电阻的阻值都小。 两个并联电阻的总电阻的倒数,等于
两个分电阻的倒数之和。
I=? U1=?
U2=?
解法2:
R1=5Ω R2=15Ω U=10V
解: 由题意得R1R2串联
U1+U2=10V
∴ U1=2.5V
U1:U2=5Ω :15Ω
U2=7.5V
∴ I=
U1 =
R12.5V 5Ω源自=0.5A答:电路中的电流为0.5A, R1、R2两端的电压分
别为2.5V、7.5V。
3.串联电阻两端电压的分配规律
推导: I1 = I2
I1 =
U1 R1
I2 =
U2 R2
= U1 U2
R1 R2
I A R1 R2
U1 U2
US
= U1
R1
U2
R2
结论:串联电路中各导体两端的
电压与其电阻成正比
电阻的串联小结
学到了什么?
1、串联电路的总电阻,
等于各串联电阻之和。
即:R=R1+R2
2、串联电路的分电压规律
= U1
I= =
= 0.2A
R 30Ω
答:……
2.串联电路的总电阻有什么特点?
特点是:串联电路的总电阻比任何
一个分导体的电阻大(增大电阻)。
+=
这相当于增加了导体的长度
15.4电阻的串联和并联-沪科版九年级物理全一册PPT演示课件

第十五章第四节
电阻的 串联和并联
(第一课时)
授课教师:唐玥
课前回顾
电流 电压
串联电路
并联电路
I=I1=I2 I=I1+I2
U=U1+U2 U=U1=U2
欧姆定律
一段导体中的电流,跟加在这段
导体两端的电压成 正比 ,跟这段 导体的电阻成 反比 。
等效替代法
用 R 替换 R1、R2
R就叫作这两个串联电阻R1、R2的总电阻;
电阻的串联
提出问题 电阻串联后,其总电阻会不会改变?
猜想与假设
几个电阻串联后相当于增加了导体的长度 所以总电阻会增大
进行实验
1. 如图,将一个定值电阻 R 接到A、B之间, 闭合开关,观察并记录电流表的示数I1;
九上物理串联和并联
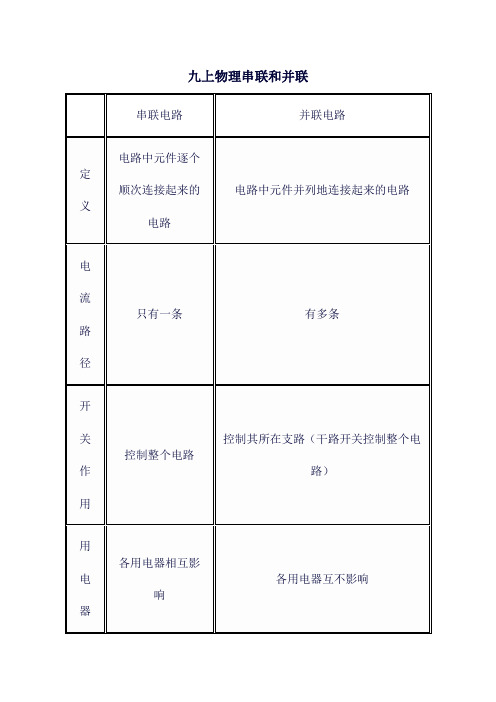
九上物理串联和并联
串联电路
并联电路
定义
电路中元件逐个顺次连接起来的电路
电路中元件并列地连接起来的电路
电流路径
只有一条
有多条
开关作用
控制整个电路
控制其所在支路(干路开关控制整个电路)
用电器关系
各用电器相互影响
各用电器互不影响
电压特点
电路两端总电压等于各部分电路两端电压之和
各支路两端电压相等,且等于电源电压
表达式
U = U₁ + U₂ + ... + Uₙ
U = U₁ = U₂ = ... = Uₙ(U为电源电压)
电阻特点
总电阻等于各电阻之和
总电阻的倒数等于各电阻倒数之和(即1/R = 1/R₁ + 1/R₂ + ... + 1/Rₙ)
表达式
R = R₁ + R₂ + ... + Rₙ
R = R₁R₂...Rₙ / (R₁ + R₂ + ... + Rₙ - (R₁R₂ + R₁R₃ + ... - R₁R₂R₃...Rₙ)/R总)(但常用并联电阻的简化公式计算,如两个电阻并联时R = R₁R₂/(R₁ + R₂))
功率特点
总功率等于各用电器功率之和
总功率等于各支路功率之和(注意:在电源电压相等时,并联电路的总功率大于串联电路的总功率)
表达式
P = P₁ + P₂ + ... + Pₙ
P = P₁ + P₂ + ... + Pₙ
电流分配
电流处处相等
初中九年级物理串、并联电路中电流、电压、电阻的规律

串、并联电路中电流、电压、电阻的规律电阻的并联:并联电路总电阻的倒数等于各并联电阻的倒数之和。
(1)把n个导体并联起来,相当于增加了导体的横截面积,其总电阻比每一个导体的电阻都要小。
(2)由可推出(3)由可推出,n个阻值均为R0的电阻并联,其总电阻为。
并联电路中总电流等于各支路中电流之和。
并联电路中各支路两端的电压都相等。
并联电路总电阻的倒数等于各支路电阻倒数之和。
并联电路中,流过各支路的电流与其电阻成反比。
并联是元件之间的一种连接方式,其特点是将2个同类或不同类的元件、器件等首首相接,同时尾尾亦相连的一种连接方式。
通常是用来指电路中电子元件的连接方式,即并联电路。
串联和并联是电路连接两种最基本的形式,它们之间有一定的区别。
要判断电路中各元件之间是串联还是并联,就必须抓住它们的基本特征,具体方法是:用电器连接法:分析电路中用电器的连接方法,逐个顺次连接的是串联;并列在电路两点之间的是并联。
电流流向法:当电流从电源正极流出,依次流过每个元件的则是串联;当在某处分开流过两个支路,最后又合到一起,则表明该电路为并联。
去除元件法:任意拿掉一个用电器,看其他用电器是否正常工作,如果所有用电器都被拿掉过,而且其他用电器都可以继续工作,那么这几个用电器的连接关系是并联;否则为串联。
用笔画线代替导线,能用一根导线将所有用电器连起来即为串联,不能则为并联。
并联电路中的电流分配特点:在并联电路中,导体中的电流跟导体的电阻成反比即。
如图所示,在并联电路中,根据欧姆定律,可得:通过电阻R1的电流,通过电阻R2的电流I2 =,因此,即,该式表明并联电路中的电流分配特点。
串、并联电路中电流、电压、电阻的规律:联,则)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分析:
由欧姆定律可知:
∵ I1=
U R1
I2=
U R2
∴ U = I1R1 U = I2R2
即
I1R1 = I2R2
变形得:
I1 I2
=
R2 R1
U
I1 R1 I
I2 R2
结论:各分电流和 分电阻成反比关系
补充:
1.如图所示电路,电源电压保持不变,R1=30Ω,电流 表A1示数为0.8A,A2示数为0.3A,求电源电压和R2的阻 值?
∴R1=U1/I=6V/0.2A=30Ω
R1=?
R2=?
R2=U2/I=2V/0.2A=10Ω
U=8V
例三:有一只小灯泡,它正常发光时电阻为15Ω ,正常工作时 电压为3V。如果我们只有电压为8V的电源,要使小灯泡正常工 作,需要串联一个多大的电阻?
分析:
U2=U-U1
R2=U2/I I=U1/R1
I = 0.5A U=?
例二:灯L1和L2串联在电路中,电源电压为8V,L1两端电压为6V,则L2
两端电压为 2V ,若通过L1的电流为0.2A,则L1的电阻为 30Ω,
L2的电阻为10Ω 。
由U=U1+U2,可得:
I=0.2A L1
L2
U2=U-U1=8V-6V=2V ∵I=U/R
U1=6V
U2=?
R1=15Ω
U1=3V
R2=?
已知:R1=15Ω U1=3V U=8V 求:R2
U=8V
解:电阻R2分去电压: U2=U-U1=8V-3V=5V
电路中电流:
I=U1/R1=3V/15Ω=0.2A
需要串联的电阻: R2=U2/I=5V/0.2A=25Ω
答:需要串联一个25Ω的电阻
第93页 1 3 4
U
I
R1
R2
等效于
U
I
R
U1
U2
由欧姆定律可知:
U1 = IR1 U2 = IR2
U = IR
由U=U1+U2,得: 所以
IR=IR1+IR2 R= R1+ R2
结论: 两个串联电阻的总电阻等于各分电阻之和。
注意:以上结论适用于两个以上电阻串联的情 况,假设有n个电阻串联,则 公式: R=R1+R2+R3+…+Rn
注意:1、以上结论适用于两个以上电阻并联的情况,
假设有n个电阻并联,则
公式:
1 R
=
1 R1
1
+ R2
1
1
+ R3 +…+ Rn
2、如果n个相同阻值电阻并联,则
公式: R总=
R n
例一:如图所示的电路中,电源电压保持6V不变·当开关断开时,电
流表的 示数为0.6A,当开关闭合时,电流表的示数为1.0A·求电阻R1
和 R2的阻值·
分析: 1.开关断开时,只有R1接入电路,
所以电流表测R1的电流I1=0.6A 2.开关闭合时,电阻R1和R2并联在
I1=0.6A
电路中,所以电流表测干路总电流
I=1.0A,R2电流为I2,则I=I1+I2
I2
已知:U=6V I1=0.6A I=1.0A
求: R1 、 R2
I=1.0A
U
I1 R1 I
I2 R2
等效于
U
I
R
由欧姆定律可知:
I
=
ห้องสมุดไป่ตู้
U R
I1=
U R1
I2=
U R2
由I=I1+I2, 得:
即
UUU R = R1 + R2 111 R = R1 + R2
结论: 两个并联电阻的总电阻的倒数,等于两分
电阻的倒数之和。
公式: 1
R
=
1 R1 +
1 R2
或 R= R1×R2
R1+R2
如果n个相同阻值电阻串联 公式: R总=nR
R= R1+ R2
例一:把5Ω的电阻R1和15Ω的电阻R2串联在电路中,总电阻为 20Ω,若
电路中电流I为0.5A,则电源电压为 1,0VR1两端电压为
2.5V ,
R2两端电压为 7.5V 。
U=IR
U1=IR1
U2=IR2
U1=?
U2=?
R1 = 5Ω R2 = 15Ω
一、实验探究:并联电路电阻关系
1.提出问题:电阻并联后,其总电阻会增大还是减少? 2.猜想与假设: 3.进行实验与搜集证据 : ①选择实验器材:电流表、开关、两节干电池、三个
阻值10Ω的电阻、导线若干 ②设计实验电路:
③测量步骤:
4.分析与论证:
并联电路的总电阻的阻值比任何一个分电阻的阻值都小。
二、理论推导: (欧姆定律)
2、第93页 2 5
一、实验探究:串联电路电阻关系
1.提出问题:电阻串联后,其总电阻会增大还是减少? 2.猜想与假设: 3.进行实验与搜集证据 : ①选择实验器材:电流表、开关、两节干电池、三个
阻值5Ω的电阻、导线若干 ②设计实验电路:
③测量步骤:
4.分析与论证:
串联电路的总电阻的阻值比任何一个分电阻的阻值都大。
二、理论推导: (欧姆定律)
解:∵ I1=
U R1
∴ R1=
U= I1
6V 0.6A
=10Ω
∵ I=I1+I2 ∴ I2=I-I1=1.0A-0.6A=0.4A
∵ I2=
U R2
∴ R2=
U I2
=
6V 0.4A
=15Ω
U=6V
答:电阻R1的阻值为10Ω,电阻R2的阻值为15Ω。
例二:由并联电路的电流关系I=I1+I2可知,通过分电阻的 电流I1和I2都是干路电流I的一部分。那么,分电流I1和I2大 小和分电阻R1和R2之间有什么关系呢?
