信号与线性系统第一二章习题
信号与线性系统分析_(吴大正_第四版)习题答案12264精编版
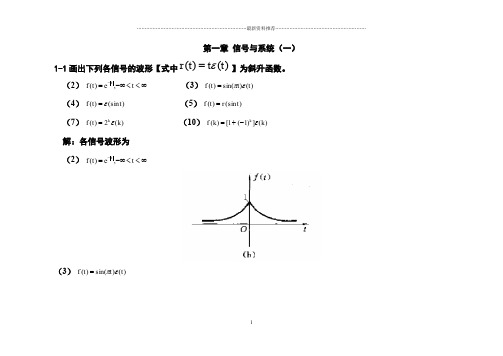
第一章 信号与系统（一）1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
（2）∞<<-∞=-t e t f t ,)( （3）)()sin()(t t t f επ= （4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f k ε= （10）)(])1(1[)(k k f k ε-+= 解：各信号波形为 （2）∞<<-∞=-t e t f t ,)(（3）)()sin()(t t t f επ=（4）)fεt=(sin)(t（5）)trf=(sin)(t（7）)t(kf kε=)(2（10）)f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ （12）)]()3([2)(k k k f k---=εε 解：各信号波形为 （1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t rt rt rtf（5）)2()2()(ttrtf-=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。
1-4 写出图1-4所示各序列的闭合形式表达式。
1-5 判别下列各序列是否为周期性的。
如果是，确定其周期。
（2）)63cos()443cos()(2ππππ+++=k k k f （5）)sin(2cos 3)(5t t t f π+=解：1-6 已知信号)(t f 的波形如图1-5所示，画出下列各函数的波形。
信号与系统课后习题答案—第1章
第1章 习题答案1－1 题1－1图所示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？解： ① 连续信号：图（a)、（c)、（d ）； ② 离散信号:图（b ）； ③ 周期信号:图（d)； ④ 非周期信号：图（a ）、（b ）、(c)； ⑤有始信号：图（a ）、（b)、（c ）.1－2 已知某系统的输入f （t ）与输出y(t ）的关系为y(t)=|f(t)｜，试判定该系统是否为线性时不变系统。
解: 设T 为此系统的运算子，由已知条件可知： y （t)=T ［f （t)]=|f （t)|，以下分别判定此系统的线性和时不变性。
① 线性 1）可加性不失一般性，设f （t ）=f 1（t ）+f 2(t ），则y 1(t)=T[f 1（t ）］=|f 1(t)|,y 2（t ）=T ［f 2（t)]=|f 2(t ）｜，y （t ）=T ［f （t ）]=T[f 1(t ）+f 2（t ）］=|f 1（t ）+f 2（t ）|，而|f 1（t)｜＋|f 2（t)|≠|f 1(t ）+f 2(t ）｜即在f 1（t)→y 1（t)、f 2（t)→y 2（t ）前提下，不存在f 1(t ）＋f 2（t ）→y 1（t)＋y 2（t ），因此系统不具备可加性。
由此,即足以判定此系统为一非线性系统,而不需在判定系统是否具备齐次性特性。
2）齐次性由已知条件，y(t ）=T[f(t)]=｜f （t ）|，则T ［af(t)］=|af(t ）｜≠a|f(t ）｜=ay （t ） （其中a 为任一常数）即在f(t ）→y(t ）前提下，不存在af （t ）→ay(t ），此系统不具备齐次性，由此亦可判定此系统为一非线性系统。
② 时不变特性由已知条件y(t ）=T ［f(t)]=｜f （t)|，则y(t-t 0)=T ［f （t —t 0）］=｜f （t-t 0)｜, 即由f （t)→y(t ）,可推出f （t —t 0）→y(t —t 0），因此，此系统具备时不变特性。
信号与线性系统一二章自测题及参考答案
第一、二章自测题1、判断题（1）若x (t )是一连续时间周期信号，则y (t )=x (2t )也是周期信号。
（2）两个周期信号之和一定是周期信号。
（3）所有非周期信号都是能量信号。
（4）两个连续线性时不变系统相互串联的结果仍然是线性时不变系统。
（5）若)()()(t h t x t y *=，则)1()2()1(+*-=-t h t x t y 。
（6）一个系统的自由响应就等于它的零输入响应。
（7）一个系统的零状态响应就等于它的自由响应。
（8）零状态响应是指系统没有激励时的响应。
（9）系统的单位冲激响应是指系统在冲激信号作用下的全响应。
（10）两个功率信号之和必为功率信号。
2、判断下列信号是能量信号还是功率信号？ （1）3cos(15)0()0t t f t t π≥⎧=⎨<⎩ （2）50()0te tf t t -⎧≥=⎨<⎩（3）()6sin 23cos3f t t t =+ （4）|2|()20sin 2t f t e t -=3、填空题（1）已知)()4()(2t t t f ε+=，则)(''t f =__________________。
（2）=+-⋅+⎰∞∞-dt t t t )1()2(2δ__________________________。
（3）=-⎰∞∞-dt t ）（92δ_________________________ 。
（4）=-⎰∞∞-dt t t e t j ）（0δω_________________________ 。
（5）信号cos(15)cos(30)t t -的周期为 。
4、试画出下列各函数的波形图 （1）0 ),()(001>-=t t t t f ε （2）)]4()([3cos )(2--=t t t t f εεπ （3）][sin )(3t t f πε=5、已知f (t )的波形如图1.1所示，求f (2-t )与f (6-2t )的表达式，并画出波形图。
信号与系统(杨晓非)1,2,3章习题答案
2
4s
6s 3 T ' mT1 12 s T 5 12 60 s f (t )为周期信号，周期为60s.
(3) f (t ) 3e t sin(3t ) 3e t Im[e j (3t ) ] 3e t cos(3t ) 2 (4) f (t ) je( j100t 2) e 2 e( j100t 2) e 2e Re[ f (t )] e 2 cos(100t ) 2
信号与系统习题解答
1.1
(1) f(t)=(t) 解 P lim
1 2
| f (t ) | dt
2
lim
1 1 dt 2 0 2
E总 lim | f (t ) |2 dt lim dt
0
f (t ) (t )为功率信号。
t [ f
t 0
3
t (4) (t 2 t 1) ( )dt (t 2 t 1) | 2 | (t )dt 2 2
(5) (t 2 2) (t 5)dt 0
0
3
(6) (t 2 2) (t 5)dt (52 2) (t 5)dt 27
e (e e lim (2 j ) 2 0
j 2t
2 t
j 2t
)
1 dt ( ) lim e2t (e j 4t e j 4t 2)dt 4 0
1 ( ) lim [e (2 j 4)t e (2 j 4)t ]dt 4 0
信号与系统练习题
第一章绪论1、选择题1.1、f （5-2t ）是如下运算的结果 CA 、 f （-2t ）右移5B 、 f （-2t ）左移5C 、 f （-2t ）右移25D 、 f （-2t ）左移25 1.2、f （t 0-a t ）是如下运算的结果 C 。
A 、f （-a t ）右移t 0；B 、f （-a t ）左移t 0 ；C 、f （-a t ）右移a t 0；D 、f （-a t ）左移at 0 1.3、已知 系统的激励e(t)与响应r(t)的关系为：)()()(t u t e t r = 则该系统为 B 。
A 、线性时不变系统；B 、线性时变系统；C 、非线性时不变系统；D 、非线性时变系统 1.4、已知 系统的激励e(t)与响应r(t)的关系为：)()(2t e t r = 则该系统为 C 。
A 、线性时不变系统 B 、线性时变系统 C 、非线性时不变系统 D 、非线性时变系统 1.5、已知 系统的激励e(t)与响应r(t)的关系为：)1()(t e t r -= 则该系统为 B 。
A 、线性时不变系统B 、线性时变系统C 、非线性时不变系统D 、非线性时变系统1.6、已知 系统的激励e(t)与响应r(t)的关系为：)2()(t e t r = 则该系统为 B A 、线性时不变系统 B 、线性时变系统 C 、非线性时不变系统 D 、非线性时变系统 1.7.信号)34cos(3)(π+=t t x 的周期为 C 。
A 、π2 B 、π C 、2π D 、π21.8、信号)30cos()10cos(2)(t t t f -=的周期为： B 。
A 、15π B 、5π C 、π D 、10π1.9、dt t t )2(2cos 33+⎰-δπ等于 B 。
A.0 B.-1 C.2 D.-21.10、 若)(t x 是己录制声音的磁带,则下列表述错误的是： BA. )(t x -表示将此磁带倒转播放产生的信号B. )2(t x 表示将此磁带放音速度降低一半播放C. )(0t t x -表示将此磁带延迟0t 时间播放D. )(2t x 表示将磁带的音量放大一倍播放 1.11.=⋅)]([cos t u t dtdA A ．)()(sin t t u t δ+⋅- B. t sin - C. )(t δ D.t cos1.12．信号t t t x o 2cos 4)304cos(3)(++=的周期为 B 。
信号与线性系统第一二章习题
32下信号与线性系统第一、二章练习题一．选择题:1、*()t A e t ε的卷积积分为( A ) A 、不存在 B 、()t Ae t ε- C 、()t Ae t εD 、()At e t ε2.若连续LTI 系统的初始状态不为零,当激励信号增大一倍时,其零状态响应( A ) A 、增大一倍B 、保持不变C 、增大,但不能确定增大倍数D 、增大两倍3.式0(2)sin (3)t t dt δω∞--⎰的值就是( B )A 、cos ω-B 、sin ω-C 、cos ωD 、sin ω4.已知f (t )的傅里叶变换为()F j ω,则函数()()()y t f t t a δ=-的傅里叶变换()Y j ω为( B ) A 、()ja F j e ωω- B 、()ja f a e ω- C 、()ja F j e ωωD 、()ja f a e ω5.已知信号f (t )如题7图所示,则其傅里叶变换F (j ω)为( B )A 、1cos 2ωτB 、2cos ωτC 、1sin 2ωτD 、2sin ωτ6.下列各表达式正确的就是( B ) A.(t -1)δ(t )=δ(t ) B.(1-t )δ(1-t )=0 C.⎰∞∞-=+)()()1(t dt t t δδD.⎰∞∞-=++1)1()1(dt t t δ7.信号f (-2t +4)就是下列哪种运算的结果( ) A.f (-2t )右移2 B.f (-2t )左移2 C.f (-2t )右移4D.f (-2t )左移218.设某线性电路的单位冲激响应为h (t ),f (t )为输入,则⎰-=t d h t f t y 0)()()(τττ就是系统的( ) A.自由响应 B.零输入响应 C.完全响应D.零状态响应9.信号)(2t e t j δ'的傅里叶变换为( ) A.j (ω-2) B.j (ω+2) C.2+j ωD.-2+j ω10.已知f (t )的傅里叶变换为)(ωj F ,则f (1-t )的傅里叶变换为( ) A.ωωj e j F )(-- B.ωωj e j F -)( C.ωωj e j F --)(D.ωωj e j F )(-11.若周期信号f (t )为对称于原点的奇函数,则其傅里叶级数展开式的结构特点就是( ) A.只有正弦项 B.只有余弦项 C.有直流分量 D.只含偶次谐波 12、设f (t )为系统输入,y (t )为系统输出,则下列关系式中为线性时不变系统的就是( ) A 、y (t )=x (t )f (t ) B 、y (t )=tf (t )C 、)()()()(22t f t f dt d t y t y dtd +=+D 、y (t )=f (2t ) 13、式⎰∞∞-⎪⎭⎫⎝⎛-+6)sin (πδt t t dt 的值就是( )A 、6πB 、6π-1 C 、6π-21D 、6π+2114、已知f (t )的傅里叶变换为F (j ω),y (t )=f ⎪⎭⎫⎝⎛+b a t ,其中a 、b 为常数,则Y (j ω)为( )A 、|a |F (j ω)ωjab eB 、|a |F (ja ω)ωjab e -C 、||1a F (j aω)ωa b j eD 、||1a F ⎪⎭⎫ ⎝⎛a j ωωa bj e -15、已知信号f (t )如题7图所示,其傅里叶变换为F (j ω),则F (0)为( ) A 、2B 、πC 、π21D 、416、积分f (t )=⎰-11(2t 2+1)δ(t -2)dt 的结果为( )A 、1B 、3C 、9D 、017、设激励为f 1(t )、f 2(t )时系统产生的响应分别为y l (t )、y 2(t ),并设a 、b 为任意实常数,若系统具有如下性质:af 1(t )+bf 2(t )↔ay l (t )+by 2(t ),则系统为( ) A 、线性系统 B 、因果系统 C 、非线性系统D 、时不变系统18、周期信号的频谱特点就是( ) A 、周期连续谱 B 、周期离散谱 C 、非周期连续谱D 、非周期离散谱19、卷积积分f (t -t 1)*δ(t -t 2)的结果为( ) A 、f (t -t 1-t 2) B 、 δ(t -t 1-t 2) C 、f (t +t 1+t 2)D 、 δ(t +t l +t 2)20、信号f (t )的带宽为20KHz,则信号f (2t )的带宽为( ) A 、20KHz B 、40KHzC 、10KHzD 、30KHz 21、已知信号f (t )的傅里叶变换为F ( j ω),则t dt t df )(的傅里叶变换为( )A 、ωωωωd j dF j F )(-)( B 、ωωωωd j dF j F )()(+- C 、ωωωωd j dF j F )(-)(- D 、ωωωωd j dF j F )()(+ 22、已知信号f(t)的波形如题3图所示,则=dt )t (df ( ) A 、0B 、)2t ()t (-δ-δC 、)2t (2)t (2-δ+δD 、)2t (2)t (2-δ-δ23、离散信号f(n+i),(i ≥0),表示( ) A 、信号f (n)的左移序i B 、信号f (n)的右移序i C 、信号f (n)的折叠D 、信号f (n)的折叠再移序i24、下列表达式中错误的就是( ) A 、)t ()t (-δ=δB 、)t t ()t t (00-δ=-δC 、)t ()t (δ-=δD 、)t (21)t 2(δ=-δ 25、信号f 1(t)、f 2(t)的波形如题6图所示,则f(t)=f 1(t)*f 2(t)的表达式为( ) A 、)1t ()1t (-ε-+ε B 、)2t ()2t (-ε-+ε C 、)1t ()1t (+ε--ε D 、)2t ()2t (+ε--ε 26.周期信号f(t)=-f(t 2T±),(T —周期),则其傅里叶级数展开式的结构特点就是( ) A 、只有正弦项 B 、只有余弦项 C 、只含偶次谐波 D 、只含奇次谐波 27、已知f(t)↔F(j ω),则f(2t+4)的傅里叶变换为( ) A 、ωω2j e )2j (F 21B 、2je )2j (F 21ωωC 、ωω2j e )2j (F 2D 、2je)j (F 2ωω二、填空题:1.连续信号就是指________的信号,通常表示为f (t )。
信号与线性系统课后答案
解： (a) H ( p)
p
p p
1
2
p p2
2
1
1 2
1 4
2( 1 ) 2
p2 1
p
2
+ 1F
f
-
1F
+
1H u -
h(t
)
1 2
(t)
2 4
sin
t (t), 2
(a)
g(t)
t
h( )d
0_
1 2
(t
)
2 4
cos
2
t (t)
0
1 2
cos
t (t) . 2
+
(b) H ( p)
4j
ห้องสมุดไป่ตู้
2
(5) y(t) f1(t 1) f1(t 2) sinπ(t 1)[ε(t 1) ε(t 2)] sinπt[ε(t 2) ε(t 1)];
(6)
y(t)
n0
f2 (t
nT )
sinπ n0 T
(t
nT )ε(t
nT
)
sinπT tε(sinπT t)ε(t) .
p
2
p 1 p
1
;
Hi
f
( p)
i0 (t) f (t)
p
p2 2
p
p
1
.
2 -3 给定如下传输算子 H( p)，试写出它们对应的微分方程。
( 1)
H ( p)
p p
3
;
(2) H ( p)
p p
3 3
;
(3)
H(
p)
p3 2p 3
信号与系统课后习题答案
习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD （15,6）=3 Hz 。
因此，公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD （5, 15）=5 Hz 。
因此，公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数，因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的，基频 =0f 1/π Hz 。
因此，公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号，显然有 1=P W1-3 解 周期T=7 ，一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+； (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
(NEW)吴大正《信号与线性系统分析》(第4版)笔记和课后习题(含考研真题)详解
目 录第1章 信号与系统1.1 复习笔记1.2 课后习题详解1.3 名校考研真题详解第2章 连续系统的时域分析2.1 复习笔记2.2 课后习题详解2.3 名校考研真题详解第3章 离散系统的时域分析3.1 复习笔记3.2 课后习题详解3.3 名校考研真题详解第4章 傅里叶变换和系统的频域分析4.1 复习笔记4.2 课后习题详解4.3 名校考研真题详解第5章 连续系统的s域分析5.1 复习笔记5.2 课后习题详解5.3 名校考研真题详解第6章 离散系统的z域分析6.1 复习笔记6.2 课后习题详解6.3 名校考研真题详解第7章 系统函数7.1 复习笔记7.2 课后习题详解7.3 名校考研真题详解第8章 系统的状态变量分析8.1 复习笔记8.2 课后习题详解8.3 名校考研真题详解第1章 信号与系统1.1 复习笔记一、信号的基本概念与分类信号是载有信息的随时间变化的物理量或物理现象，其图像为信号的波形。
根据信号的不同特性，可对信号进行不同的分类：确定信号与随机信号；周期信号与非周期信号；连续时间信号与离散时间信号；实信号与复信号；能量信号与功率信号等。
二、信号的基本运算1加法和乘法f1（t）±f2（t）或f1（t）×f2（t）两信号f1（·）和f2（·）的相加、减、乘指同一时刻两信号之值对应相加、减、乘。
2．反转和平移（1）反转f（－t）f（－t）波形为f（t）波形以t＝0为轴反转。
图1-1（2）平移f（t＋t0）t0＞0，f（t＋t0）为f（t）波形在t轴上左移t0；t0＜0，f（t＋t0）为f（t）波形在t轴上右移t0。
图1-2平移的应用：在雷达系统中，雷达接收到的目标回波信号比发射信号延迟了时间t0，利用该延迟时间t0可以计算出目标与雷达之间的距离。
这里雷达接收到的目标回波信号就是延时信号。
3．尺度变换f（at）若a＞1，则f（at）波形为f（t）的波形在时间轴上压缩为原来的；若0＜a＜1，则f（at）波形为f（t）的波形在时间轴上扩展为原来的；若a＜0，则f（at）波形为f（t）的波形反转并压缩或展宽至。
信号与线性系统_习题答案(有错版)
2.1 (1) 已知连续时间信号 x(t ) 如图 P2.1(a)所示。试画出下列各信号的波形图，并加以标 注。 (a) x(t − 2) (b) x(1 − t ) (c) x(2t + 2) (2) 根据图 P2.1(b)所示的信号 h(t ) ，试画出下列各信号的波形图，并加以标注。 (a) h(t + 3) (b) h( − 2) (c) h(1 − 2t ) (3) 根据图 P2.1(a)和(b)所示的 x(t ) 和 h(t ) ，画出下列各信号的波形图，并加以标注。 (a) x(t )h(−t ) (b) x(1 − t )h(t − 1) (c) x(2 − ) h(t + 4)
其基波周期 T0 是 T1 , T2 的最小公倍数。 (b) x(n) 和 y ( n) 是周期的， x(n + = N1 ) x(n), y (n + N = y ( n) 2) 令 f= (n) x(n) + y (n) ，欲使 f (n) 是周期的，必须有
= N 0 kN = mN 2 1
πn
4
，对所有 n ，
7
1 n , n奇 显然 x(n) 是非周期的，但 y1 (n) 是周期的。 h(n) = 3 0, n偶
(c) 正确。若 x(n) 的周期为 N ，则 y2 (n) 的周期为 2 N 。 (d) 正确。若 y2 (n) 的周期为 N ，则 N 只能是偶数。 x(n) 的周期为 N / 2 。 2.7 判断下列各信号是否是周期信号，如果是周期信号，求出它的基波周期。 (a) = x(t ) 2 cos(3t + π / 4) (c) x(t ) = e (e) = x ( n)
1
信号与系统课后习题答案—第1章
第1章 习题答案1－1 题1－1图所示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？解： ① 连续信号：图〔a 〕、〔c 〕、〔d 〕； ② 离散信号：图〔b 〕； ③ 周期信号：图〔d 〕； ④ 非周期信号：图〔a 〕、〔b 〕、〔c 〕； ⑤有始信号：图〔a 〕、〔b 〕、〔c 〕。
1－2 某系统的输入f(t)与输出y(t)的关系为y(t)=|f(t)|，试判定该系统是否为线性时不变系统。
解： 设T 为此系统的运算子，由条件可知： y(t)=T[f(t)]=|f(t)|，以下分别判定此系统的线性和时不变性。
① 线性1〕可加性不失一般性，设f(t)=f 1(t)+f 2(t)，那么y 1(t)=T[f 1(t)]=|f 1(t)|，y 2(t)=T[f 2(t)]=|f 2(t)|，y(t)=T[f(t)]=T[f 1(t)+f 2(t)]=|f 1(t)+f 2(t)|，而|f 1(t)|＋|f 2(t)|≠|f 1(t)+f 2(t)|即在f 1(t)→y 1(t)、f 2(t)→y 2(t)前提下，不存在f 1(t)＋f 2(t)→y 1(t)＋y 2(t)，因此系统不具备可加性。
由此，即足以判定此系统为一非线性系统，而不需在判定系统是否具备齐次性特性。
2〕齐次性由条件，y(t)=T[f(t)]=|f(t)|，那么T[af(t)]=|af(t)|≠a|f(t)|=ay(t) 〔其中a 为任一常数〕即在f(t)→y(t)前提下，不存在af(t)→ay(t),此系统不具备齐次性，由此亦可判定此系统为一非线性系统。
② 时不变特性由条件y(t)=T[f(t)]=|f(t)|，那么y(t-t 0)=T[f(t-t 0)]=|f(t-t 0)|，即由f(t)→y(t)，可推出f(t-t 0)→y(t-t 0)，因此，此系统具备时不变特性。
依据上述①、②两点，可判定此系统为一非线性时不变系统。
信号与系统课后习题答案—第1章
第1章 习题答案1－1 题1－1图所示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？解： ① 连续信号：图（a ）、（c ）、（d ）； ② 离散信号：图（b ）； ③ 周期信号：图（d ）；④ 非周期信号：图（a ）、（b ）、（c ）； ⑤有始信号：图（a ）、（b ）、（c ）。
1－2 已知某系统的输入f(t)与输出y(t)的关系为y(t)=|f(t)|，试判定该系统是否为线性时不变系统。
解： 设T 为此系统的运算子，由已知条件可知： y(t)=T[f(t)]=|f(t)|，以下分别判定此系统的线性和时不变性。
① 线性1）可加性不失一般性，设f(t)=f 1(t)+f 2(t)，则y 1(t)=T[f 1(t)]=|f 1(t)|，y 2(t)=T[f 2(t)]=|f 2(t)|，y(t)=T[f(t)]=T[f 1(t)+f 2(t)]=|f 1(t)+f 2(t)|，而|f 1(t)|＋|f 2(t)|≠|f 1(t)+f 2(t)|即在f 1(t)→y 1(t)、f 2(t)→y 2(t)前提下，不存在f 1(t)＋f 2(t)→y 1(t)＋y 2(t)，因此系统不具备可加性。
由此，即足以判定此系统为一非线性系统，而不需在判定系统是否具备齐次性特性。
2）齐次性由已知条件，y(t)=T[f(t)]=|f(t)|，则T[af(t)]=|af(t)|≠a|f(t)|=ay(t) （其中a 为任一常数）即在f(t)→y(t)前提下，不存在af(t)→ay(t),此系统不具备齐次性，由此亦可判定此系统为一非线性系统。
② 时不变特性由已知条件y(t)=T[f(t)]=|f(t)|，则y(t-t 0)=T[f(t-t 0)]=|f(t-t 0)|，即由f(t)→y(t)，可推出f(t-t 0)→y(t-t 0)，因此，此系统具备时不变特性。
依据上述①、②两点，可判定此系统为一非线性时不变系统。
信号与线性系统-白恩健书答案
第1章基本概念K第1章习题k1.1解：（1）x(t)为周期信号，周期为T=10。
（2）x(t)为非周期信号。
（3）x[n]为非周期信号。
（4）x[n]为周期信号，周期为N=2。
（5）x(t)为非周期信号。
（6）x[n]为周期信号，周期为N=2。
1.2解：（1）x(t)为功率信号。
（2）x(t)既不是能量信号也不是功率信号。
（3）x[n]为能量信号。
（4）x(t)为能量信号。
（5）x(t)为能量信号。
（6）x[n]为能量信号。
1.3略。
1.4略。
1.5（原题有误）一个离散时间系统的激励与响应的关系为y[n]=M∑i=0b i x[n−i]。
用算符S−k代表将信号x[n]平移k个单位时间得到输出信号x[n−k]的系统，即x[n−k]=S−k(x[n])。
写出联系y[n]与x[n]的系统算符T及其可逆系统的算符T inv。
解：提示：可逆系统为y[n]−M∑i=1b i x[n−i]=b0x[n]。
1.6解：（1）因果、无记忆、非线性、时不变、BIBO稳定系统。
（2）因果、无记忆、线性、时变和BIBO稳定系统。
（3）因果、无记忆、线性、时变和非稳定系统。
（4）因果、记忆、线性、时不变和BIBO稳定系统。
（5）因果、无记忆、线性、时变和BIBO稳定系统。
（6）因果、记忆、时不变、非稳定系统。
–2/48–第1章基本概念（7）因果、无记忆、线性、时不变和BIBO稳定系统。
（8）非因果系统、无记忆、线性、时不变、BIBO稳定系统。
1.7证明略。
1.8解：（1）x[n]的响应为{1,1,−1,2,n=0,1,2,3}。
（2）x[n]的响应为{1,1,−3,1,3,−5,2,n=−3∼3}。
（3）x[n]的响应为{1,0,−1,4,−3,2,n=−2∼3}。
1.9证明提示：根据微积分的极限定义证明。
1.10解：（1）x(t)的响应为4(1−e−t)u(t)−6(1−e−t+1)u(t−1)。
（2）x(t)的响应为[2(t+e−t)−2]u(t)。
管致中《信号与线性系统》(第5版)(章节题库 绪 论)
2 / 23
圣才电子书
三、分析计算题
十万种考研考证电子书、题库视频学习平 台
1．已知两信号分别为 f1（t）＝2cos（πt）＋4sin（3t），f2（t）
2．系统 y（t）＝2（t＋1）x（t）＋cos（t＋1）是_____。（说明因果／非因果性、时 变／非时变性、线性／非线性）。
【答案】因果、时变、非线性。 【解析】y（t）＝2（t＋1）x（t）＋cos（t＋1），输出仅与现在的输入有关，系统是 因果的；响应随激励加入的时间不同而发生变换，系统是时变的；不满足齐次性和叠加性， 系统是非线性的。
图 1-4 答：（1）移位：f（－2t＋1）＝ f[－2（t－1/2）]，f（－2t＋1）波形向左平移 1/2 可得 f（－2t）； （2）扩展：将 f（－2t）做尺度变换，横坐标放大 2 倍，求得 f（－t）； （3）反转：将 f（－t）反转，求得 f（t）波形，如图 1-5 所示。
4 / 23
圣才电子书
圣才电子书
十万种考研考证电子书、题库视频学习平 台
图 1-2 答：翻转:先将 f（t）的图形翻转，成为 f（－t）； 移位：再将图形向右平移 2，成为 f（－t＋2）；
扩展：然后波形扩展为原来的 3 倍，成为
，如图 1-3 所示。
图 1-3 4．已知 f（－2t＋1）波形如图 1-4 所示，试画出 f（t）的波形。
圣才电子书
十万种考研考证电子书、题库视频学习平 台
第 1 章 绪 论
一、填空题 1．系统的输入为 x（r），输出为 y（r）＝tx（t），判断系统是否是线性的（ ）。 【答案】线性的
信号与系统前三章习题答案
信号与系统前三章习题答案信号与系统前三章习题答案第一章：信号与系统基础1.1 习题答案1. 信号是指随时间变化的物理量，可以用数学函数表示。
系统是指对输入信号进行处理或变换的过程或装置。
2. 信号可以分为连续时间信号和离散时间信号。
连续时间信号在每个时间点上都有定义，可以用连续函数表示；离散时间信号只在某些离散的时间点上有定义，可以用数列表示。
3. 周期信号是在一定时间间隔内重复的信号，非周期信号则不具有重复性。
周期信号可以用正弦函数或复指数函数表示。
4. 信号的能量是指信号在无穷远处的总能量，可以用积分的形式表示；信号的功率是指信号在某个时间段内的平均功率，可以用平均值的形式表示。
5. 系统的特性可以通过冲激响应和频率响应来描述。
冲激响应是指系统对单位冲激信号的响应，可以用单位冲激函数表示；频率响应是指系统对不同频率信号的响应，可以用频率函数表示。
1.2 习题答案1. 线性系统具有叠加性和齐次性。
叠加性是指系统对两个输入信号的响应等于两个输入信号分别经过系统的响应的叠加；齐次性是指系统对输入信号的线性组合的响应等于输入信号分别经过系统的响应的线性组合。
2. 时不变性是指系统的特性不随时间的变化而变化。
即如果输入信号发生时间平移，系统的响应也会相应地发生时间平移。
3. 因果性是指系统的输出只依赖于当前和过去的输入信号。
即系统的响应不会提前预知未来的输入信号。
4. 稳定性是指系统对有界输入信号产生有界输出信号。
即输入信号有限，输出信号也有限。
5. 可逆性是指系统的输出可以唯一确定输入。
即系统的响应函数是可逆的。
第二章：连续时间信号与系统2.1 习题答案1. 连续时间信号的频谱是指信号在频域上的表示，可以通过傅里叶变换得到。
频谱表示了信号在不同频率上的能量分布情况。
2. 系统的冲激响应可以通过输入信号和输出信号的傅里叶变换来求得。
通过傅里叶变换，可以将系统的时域特性转换为频域特性。
3. 傅里叶变换具有线性性、时移性、频移性和共轭对称性。
信号与系统习题答案 第一二章习题
第一章2.(1) )30cos()10cos()(1t t t f +=解：因为)10cos(t 是一个周期信号51021ππ==T )30cos(t 是一个周期信号153022ππ==T求得最小公倍数为5π(2) t j e t f 42)(= 解: t j t e t j 4sin 4cos 4+=则t 4cos 是一个周期信号21π=T同理则t 4sin 是一个周期信号22π=T也就是实部和虚部周期相同则整个指数信号也为周期信号2π=T(3) 23)]3[sin()(π-=t t f解：原式)]3(2cos[2121π--=tππ==∴22T ，即周期为π(4) )()2cos(5)(4t u t t f π=解：有始无终信号不满足周期信号的条件即非周期信号。
(5) )]}()([)1{()(05T nT t u nT t u t f n n------=∑+∞= (n 为整数)解：原式)]()([)1(0T nT t u nT t u n n n------=∑∑+∞=+∞=n)1(-周期为2. )()(T nT t u nT t u ----周期为T则最小公倍数为2T (6) )127sin()(6ππ+=n t f解：)127sin(ππ+n 的周期1472==ππT5.(1) 0)()(1==t t t f δ (2) )1()1()(2-=-=t t t t f δδ (3) )1()1()(3-=-=t e t e t f t t δδ (4) )21(21)21(21)12()(4-=-=-=⎰⎰∞-∞-τττδττδu d d t f tt(5) )(22)](22[)]()4[cos()(5t t dtd t t dtd t f δδδπ'==+=(6) 10cos sin )(sin )]([cos )(6-=-='==⎰⎰+∞∞-+∞∞-tdt t tdt t dtd t f δδ(7) )()()()]()([)]([)(7t u te t t t u te t e t u e t t u e dtd tt f ttttt------=--=--==δδ(8) )2(13)2()1()(238-=-++=t t t t t f δδ (9) )1(21)1(21)22()(2229+=+=+=--t e t e t e t f t t δδδ(10) )(sin )()(cos )(sin )]([cos )(10t u t t t tu t tu dtd t f -=+-==δδ6.(1) 42sin )(2)(1==⎰+∞∞-dt tt t t f δ(2) 2)4(2)48(2)4()8(2)(2==-=--=⎰+∞∞-u u dtt u t t f δ(3)dt t t t f )1()4()(33-+=⎰+∞∞-δ5)]1([)4(3=--+=⎰+∞∞-dtt t δ(4) 3)3(4)3()(e edt t et f t==+=--+∞∞--⎰δ(5) 1)0(2)414(2)1()44(2)(5==-⨯--=⎰+∞∞-u u dt t t u t f δ21)0(1)0(,0)0(=∴==+-u u u(6) )()()]()([)()(0''6t u t d e ed et f ttt+=+==-∞--∞--⎰⎰δττδτδττδ(7)4)2(4)]2()24sin(4)2()24[cos()4cos()2()(3131'31'7πδπδππδππδ=-=-⨯+-⨯=-=⎰⎰⎰---dt t dt t t dt t t f (8) 21)2()2(41)4()(28=++-=-=⎰⎰+∞∞-+∞∞-dt t t dt t t f δδδ(9) dt t t f )4()(2119-=⎰-δ042=-t 即2±=t 不在积分限区间内∴原式=0（10）A A dt t t A t f -=-==⎰+∞∞-0cos )(sin )('10δ（11）1)4(2sin[)4()2sin()(11-=-⨯=+=⎰+∞∞-ππδdt t t t f（12）dt t et f t)8()(46212+=⎰--δ原式中t=-8不在积分区间内，故原式=0 （13）11111321)1(21)]1(2[)22()(-+∞--+∞--+∞--=-=--=-=⎰⎰⎰edt t e dt t e dt t e t f tttδδδ（14）2)()()()]()([)(0''14=--=-=-=⎰⎰⎰+∞∞-+∞∞-+∞∞-e e dt t e dt t e dt t t e t f tttδδδδ（15）ττδτd t f t)1()4()(215-+=⎰∞-原式ττδτd t)1()4(2-+=⎰∞-当1<t 时原式=0当1≥t 时原式=4+1=5 即原式=)1(5-t u （16）ττδττd et f t)2()()(16⎰∞--+=原式ττδττd e t)()(2⎰∞--+=当0<t 时原式=0当0≥t 时原式2)0(20=+=-e 即原式)(2t u =7. (1) )(4)0(3)(1t f y t y +=解：由系统方程可知该系统具有分解性。
信号与系统课后习题答案—第章完整版
信号与系统课后习题答案—第章HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】第1章 习题答案1－1 题1－1图所示信号中，哪些是连续信号哪些是离散信号哪些是周期信号哪些是非周期信号哪些是有始信号解： ① 连续信号：图（a ）、（c ）、（d ）； ② 离散信号：图（b ）； ③ 周期信号：图（d ）；④ 非周期信号：图（a ）、（b ）、（c ）； ⑤有始信号：图（a ）、（b ）、（c ）。
1－2 已知某系统的输入f(t)与输出y(t)的关系为y(t)=|f(t)|，试判定该系统是否为线性时不变系统。
解： 设T 为此系统的运算子，由已知条件可知： y(t)=T[f(t)]=|f(t)|，以下分别判定此系统的线性和时不变性。
① 线性 1）可加性不失一般性，设f(t)=f 1(t)+f 2(t)，则y 1(t)=T[f 1(t)]=|f 1(t)|，y 2(t)=T[f 2(t)]=|f 2(t)|，y(t)=T[f(t)]=T[f 1(t)+f 2(t)]=|f 1(t)+f 2(t)|，而 |f 1(t)|＋|f 2(t)|≠|f 1(t)+f 2(t)|即在f 1(t)→y 1(t)、f 2(t)→y 2(t)前提下，不存在f 1(t)＋f 2(t)→y 1(t)＋y 2(t)，因此系统不具备可加性。
由此，即足以判定此系统为一非线性系统，而不需在判定系统是否具备齐次性特性。
2）齐次性由已知条件，y(t)=T[f(t)]=|f(t)|，则T[af(t)]=|af(t)|≠a|f(t)|=ay(t) （其中a 为任一常数）即在f(t)→y(t)前提下，不存在af(t)→ay(t),此系统不具备齐次性，由此亦可判定此系统为一非线性系统。
② 时不变特性由已知条件y(t)=T[f(t)]=|f(t)|，则y(t-t 0)=T[f(t-t 0)]=|f(t-t 0)|， 即由f(t)→y(t)，可推出f(t-t 0)→y(t-t 0)，因此，此系统具备时不变特性。
信号与线性系统分析吴大正习题答案
专业课习题解析课程西安电子科技大学844信号与系统精选专业课习题解析课程第2讲第一章信号与系统（二）精选精选1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。
（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为 （2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=（4）)fε=t)(sin(t（5）)tf=r(t)(sin精选（7）)t(kf kε=)(2（10）)f kεk-=(k+(])1()1[精选精选1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。
（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f （5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k---=εε 解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t rt rt rtf（5）)2()2()(ttrtf-=ε精选精选（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(kkkf k---=εε精选1-3 写出图1-3所示各波形的表达式。
精选1-4 写出图1-4所示各序列的闭合形式表达式。
大学科目《信号与系统》各章节习题答案
第一章 习 题1-1 画出下列各信号的波形：(1) f 1(t)=(2-e -t )U(t); (2) f 2(t)=e -t cos10πt×[U(t -1)-U(t-2)]。
答案（1）)(1t f 的波形如图1.1（a ）所示.(2) 因t π10cos 的周期s T 2.0102==ππ,故)(2t f 的波形如图题1.1(b)所示.1-2 已知各信号的波形如图题1-2所示，试写出它们各自的函数式。
答案)1()]1()([)(1-+--=t u t u t u t t f)]1()()[1()(2----=t u t u t t f)]3()2()[2()(3----=t u t u t t f1-3 写出图题1-3所示各信号的函数表达式。
答案2002121)2(21121)2(21)(1≤≤≤≤-⎪⎩⎪⎨⎧+-=+-+=+=t t t t t t t f)2()1()()(2--+=t u t u t u t f)]2()2([2sin )(3--+-=t u t u t t f π)3(2)2(4)1(3)1(2)2()(4-+---++-+=t u t u t u t u t u t f1-4 画出下列各信号的波形：(1) f 1(t)=U(t 2-1); (2) f 2(t)=(t-1)U(t 2-1);(3) f 3(t)=U(t 2-5t+6); (4)f 4(t)=U(sinπt)。
答案(1) )1()1()(1--+-=t u t u t f ,其波形如图题1.4(a)所示.(2))1()1()1()1()]1()1()[1()(2---+--=--+--=t u t t u t t u t u t t f 其波形如图题1.4(b)所示.(3))3()2()(3-++-=t u t u t f ,其波形如图1.4(c)所示.(4) )(sin )(4t u t f π=的波形如图题1.4(d)所示.1-5 判断下列各信号是否为周期信号，若是周期信号，求其周期T 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
32下信号与线性系统第一、二章练习题一．选择题:1.*()t A e t ε的卷积积分为( A ) A.不存在B.()t Ae t ε-C 。
()t Ae t εﻩD 。
()At e t ε２.若连续LTI 系统的初始状态不为零，当激励信号增大一倍时，其零状态响应( A ) A.增大一倍B ．保持不变C 。
增大，但不能确定增大倍数D 。
增大两倍3．式0(2)sin (3)t t dt δω∞--⎰的值是（ B )Ａ。
cos ω- B.sin ω- C.cos ωﻩD ．sin ω4.已知ｆ (t )的傅里叶变换为()F j ω,则函数()()()y t f t t a δ=-的傅里叶变换()Y j ω为( B )Ａ。
()ja F j e ωω-ﻩB 。
()ja f a e ω- C 。
()ja F j e ωωﻩD 。
()ja f a e ω5．已知信号ｆ（ｔ)如题７图所示,则其傅里叶变换F (j ω）为( B )Ａ。
1cos 2ωτB.2cos ωτ Ｃ。
1sin 2ωτD.2sin ωτ6.下列各表达式正确的是( B )A.(t -1）δ（t ）=δ(t )ﻩB ．(1—t )δ(１—t )＝0 C.⎰∞∞-=+)()()1(t dt t t δδD.⎰∞∞-=++1)1()1(dt t t δ7．信号f (—２t +4）是下列哪种运算的结果（ ） Ａ.ｆ (—2t ）右移2 B.f （-2ｔ)左移2 C ．f (—２t ）右移４D.ｆ (－2ｔ）左移21８.设某线性电路的单位冲激响应为h (ｔ），ｆ （t ）为输入,则⎰-=t d h t f t y 0)()()(τττ是系统的( ）A ．自由响应ﻩB ．零输入响应 Ｃ．完全响应ﻩD ．零状态响应９．信号)(2t e t j δ'的傅里叶变换为（ )A ．j (ω－2） B.ｊ （ω＋2） C ．2+ｊωD ．-２＋j ω10.已知f (t )的傅里叶变换为)(ωj F ,则ｆ （1-ｔ)的傅里叶变换为（ ） Ａ．ωωj e j F )(--Ｂ.ωωj e j F -)(C ．ωωj e j F --)(ﻩD.ωωj e j F )(-11.若周期信号f (t ）为对称于原点的奇函数,则其傅里叶级数展开式的结构特点是( ) A.只有正弦项 B ．只有余弦项 C ．有直流分量ﻩD.只含偶次谐波12.设f （t ）为系统输入,y (t )为系统输出,则下列关系式中为线性时不变系统的是( ) Ａ。
y （t )=x (t )f (t ) B.y (t ）=t ｆ (ｔ）C ．)()()()(22t f t f dt d t y t y dtd +=+D 。
y (t )＝f （2t ） 1３。
式⎰∞∞-⎪⎭⎫⎝⎛-+6)sin (πδt t t d ｔ的值是( ）A ．6πﻩＢ.6π—1 C 。
6π-21ﻩＤ.6π+21１4。
已知f （t )的傅里叶变换为Ｆ（j ω），y (t ）=f ⎪⎭⎫ ⎝⎛+b a t ，其中a 、b 为常数，则Y （ｊω）为( ） A 。
|a |F （ｊω）ωjab e B ．|ａ|Ｆ(j ａω)ωjab e - C.||1a F (j aω）ωa b j e Ｄ．||1a Ｆ⎪⎭⎫ ⎝⎛a j ωωa bj e -１5.已知信号f （t )如题7图所示，其傅里叶变换为F (j ω),则F （0)为( ) Ａ。
２Ｂ。
πC 。
π21ﻩＤ。
416。
积分f (t ）=⎰-11(2t 2+1)δ（t －2)ｄt 的结果为（ )A.1 Ｂ。
３ C 。
9Ｄ.０17。
设激励为f 1（ｔ)、ｆ 2(ｔ）时系统产生的响应分别为y l (t ）、y 2（t ),并设ａ、b 为任意实常数,若系统具有如下性质：ａf 1(t ）+bf 2（t ）↔ay l （t )＋ｂy 2（t ），则系统为（ ) A 。
线性系统 Ｂ。
因果系统 Ｃ。
非线性系统Ｄ。
时不变系统18。
周期信号的频谱特点是( ） A 。
周期连续谱ﻩB.周期离散谱 C 。
非周期连续谱D 。
非周期离散谱 19。
卷积积分f (t -ｔ1)*δ(t —t 2)的结果为( ) A 。
f (t —t 1—t 2）ﻩB. δ（ｔ-t １-t ２） C 。
f (t +ｔ1＋ｔ２)ﻩＤ。
δ(t +t l ＋ｔ2）20。
信号ｆ (t ）的带宽为20ＫH ｚ，则信号ｆ （2ｔ)的带宽为( ) A.20KHz ﻩB.４0KHz C.1０KHz ﻩD.30KHz21．已知信号f (t ）的傅里叶变换为F ( j ω)，则t dtt df )(的傅里叶变换为（ ) A 。
ωωωωd j dF j F )(-)( B 。
ωωωωd j dF j F )()(+- C ．ωωωωd j dF j F )(-)(-ﻩＤ。
ωωωωd j dF j F )()(+ 22。
已知信号f(t)的波形如题3图所示,则=dt )t (df （ ) A 。
0Ｂ。
)2t ()t (-δ-δ C 。
)2t (2)t (2-δ+δD 。
)2t (2)t (2-δ-δ２3.离散信号f （n ＋i ）,（ｉ≥０)，表示( ） Ａ。
信号f （n)的左移序i B.信号f （n)的右移序i C 。
信号f （n)的折叠ﻩD.信号ｆ(n ）的折叠再移序ｉ2４。
下列表达式中错误的是( ) Ａ。
)t ()t (-δ=δ Ｂ。
)t t ()t t (00-δ=-δ C 。
)t ()t (δ-=δﻩＤ.)t (21)t 2(δ=-δ 2５.信号f １(ｔ)、f 2（ｔ)的波形如题6图所示,则f （ｔ)=f 1（ｔ）＊f 2(t ）的表达式为（ ) Ａ。
)1t ()1t (-ε-+ε B 。
)2t ()2t (-ε-+ε Ｃ.)1t ()1t (+ε--ε D 。
)2t ()2t (+ε--ε 2６．周期信号ｆ（ｔ)=—f （t 2T±）,(T —周期），则其傅里叶级数展开式的结构特点是（ )A.只有正弦项ﻩB 。
只有余弦项C.只含偶次谐波ﻩＤ。
只含奇次谐波2７。
已知f （t)↔F(ｊω),则ｆ（２t+4）的傅里叶变换为（ ） A ．ωω2j e )2j (F 21ﻩＢ.2j e )2j (F 21ωωC.ωω2j e )2j (F 2ﻩD 。
2j e )j (F 2ωω二、填空题:1.连续信号是指___＿__＿＿的信号,通常表示为f (t )。
2.计算33cos ()t t dt δπ--=⎰_＿______。
3.若某系统在信号()f t 激励下的零状态响应()()tf y t f t dt -∞=⎰，则该系统的冲激响应()h t =_____＿__。
4.设周期信号的角频率为ω，则其频谱的谱线只出现在0、ω、2ω、……等__＿__＿＿_频率上,即周期信号的频谱是____＿___谱．５.若某滤波器的频率响应()H j j ωω=,则其冲激响应()h t =__＿_＿_＿_.6．设两子系统的频率响应分别为1()H j ω和2()H j ω，则由其串联组成的复合系统的频率响应()H j ω=__＿_＿___。
7.计算)3()()2(---t t e t δε=＿______＿. 8.计算⎰∞∞----dt t e t )1()2(δ＝___＿＿＿__。
9．激励为f (t )，响应为ｙ(t ）的线性非时变因果系统由下式描述：)()(3)(2)(t f t f t y t y +'=+',则系统的单位冲激响应为h (t ）=＿_______.10.写出题17图所示信号的时域表达式ｆ (t )＝_＿___＿_＿。
１1.函数)(t te atε-的傅里叶变换为＿_＿___＿＿。
12.卷积积分f (ｔ-t 1)*(t +t 2）=__＿＿＿___。
1３．一周期电流为A t t i )15cos(234)(︒++=,则电流有效值为_＿____＿＿． 1４．⎰--⋅65)(cos dt t t πδ=_＿_______＿__＿__＿＿。
1５．冲激响应h (ｔ)与阶跃响应ｇ(ｔ)的关系为__＿______＿___＿＿__。
16．设两子系统的冲激响应分别为h 1(t ）和h 2（t ）,则由其并联组成的复合系统的冲激响应ｈ(t )＿____＿＿___＿___＿__。
１7.已知信号f (t ）=ｃos ω0t ,则其傅里叶变换为__＿_＿_＿___＿＿_＿___．18.周期为T 的连续信号的频谱是一系列______＿______＿_的谱线,谱线间的间隔为_＿________＿_。
１9.信号f （t )=cos επt (t ）的拉普拉斯变换为＿_____＿＿___＿_。
20.信号ｆ (ｔ）=δ(t ）—ε（t ）—ε(t-t ０)的拉普拉斯变换为________＿________。
21。
2sin 2 δtt ⎰∞∞-(t ）dt =______＿_＿_____＿_.22。
信号f (t )到f (at ）的运算中，若ａ>1,则信号时间尺度扩大a 倍,其结果是将信号波形沿时间轴_______＿＿＿a 倍。
23。
周期奇函数的傅里叶级数的特点是_______＿_＿________．２4。
由傅里叶变换的尺度特性可知,信号的持续时间与信号占有频带宽度成＿＿____＿____. 25.已知ｆ （t ）的傅里叶变换为Ｆ（ｊω），则（t —3）ｆ （t ）的傅里叶变换为_____＿＿＿_。
26.若已知ｆ (t )=ε（ｔ）-ε(t —2）,则ｆ (t ）*δ（t —2）=__＿_________。
27。
信号时移只改变信号的_＿_______＿_频谱；不改变信号的__________＿频谱。
28.已知某系统的冲激响应h(t)＝２e -２t ε(ｔ），若激励f(ｔ)= ε(t)，则该系统的零状态响应为___＿_______.２９．周期信号的平均功率等于它的___＿＿_____＿之和。
30．１的傅里叶变换为_______＿___。
３１.c ｏs （2ω)的傅里叶反变换为＿_＿_______＿。
32．系统的完全响应可以表示为零状态响应和___＿＿______之和．33.⎰∞∞-∞<dt )t (f 是f(ｔ)的傅里叶变换存在的_＿______条件。
34.对于正弦序列f （n ）=sin n Ω，若Ωπ2为＿＿＿＿_____时,ｆ(n)为非周期序列。
3５.f （t)*δ（ｔ－t 0）＝＿__＿＿_＿＿_.三、简答题:１．已知信号()[()(1)](1)(2)f t t t t t t εεεε=--+---,绘出(12)f t -的波形。
2.名词解释：简述“单位序列”的概念。
简述“系统的频响函数”的概念。