2019人教新版数学九年级上学期《24.4弧长和扇形面积》同步练习精品教育.doc
人教版九年级上册数学 24.4弧长和扇形面积 同步训练

人教版九年级上册数学弧长和扇形面积同步训练一.选择题(共5小题)1.如图,⊙O的半径为12,点A、B是圆上的两点,∠AOB=120°,则的长为()A.6πB.8πC.10πD.12π2.如图,四边形OABC1是正方形,曲线C1C2,C2C3,C3C4,C4C5,⋯叫作“正方形的渐开线”,其中C1C2,C2C3,C3C4,C4C5,的圆心依次按O,A,B,C1循环,当OA=1时,弧C2024C2025的长为()A.1012πB.1022.5πC.2024πD.2025π3.如图,将含60°角的直角三角板ABC绕顶点A顺时针旋转45°后得到△AB'C',点B经过的路径为弧BB′,若∠BAC=60°,AC=3,则图中阴影部分的面积是()A.B.C.D.3π4.中国美食讲究色香味美,优雅的摆盘造型能让美食锦上添花.图1中的摆盘,其形状是扇形的一部分,图2是其几何示意图(阴影部分为摆盘),通过测量得到AC=BD=10cm,C,D两点之间的距离是3cm,∠AOB=60°,则摆盘的面积是()A.B.C.D.5.如图,汽车雨刮器摆动的轨迹是以点O为圆心的扇形,已知雨刮器OB的总长为5dm,其中橡胶部分AB 的长为3dm.若其中一个雨刮器在车窗上从OB位置摆动60°至OD位置,则橡胶部分扫过的图形面积为()A.B.C.D.二.填空题(共5小题)6.一个扇形的圆心角为60°,该扇形面积为6πcm2,则该扇形的半径为cm.7.一圆锥的底面半径为3,母线长为6,则这个圆锥的侧面积为.8.如图,AB=8,以AB为直径的半圆绕A点逆时针旋转60°,此时点B到了点B′,则图中阴影部分的面积是.9.如图,将半径OB=6的半圆绕点B按顺时针方向旋转30°,此时点A到了点A',则图中涂色部分的面积为.10.如图,在Rt△ABC中,∠CAB=90°,AB=4,,以点A为圆心,AB长为半径作圆弧交AC于点D,交BC于点E,则阴影部分的面积为.三.解答题(共4小题)11.如图,在△ABC中,AB=AC=6cm,∠BAC=45°,以AB为直径作半圆,交BC于点D,交AC于点E.(1)求线段CE的长;(2)求弧DE的长.12.某面粉厂有一个容积是24m3的长方体储粮池,它的长是宽的2倍,高与宽相等.当贴着它最大的内侧面将面粉堆成一个最大的半圆锥时,这堆面粉的体积是多少立方米?13.如图,圆锥可以看作以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转一周形成的面所围成的旋转体.旋转轴叫做圆锥的轴,垂直于轴的边(另一条直角边)旋转而成的圆面叫做圆锥的底面,斜边旋转而成的曲面叫做圆锥的侧面,无论旋转到什么位置,斜边都叫做圆锥的母线.圆锥的侧面展开图是扇形.若扇形的半径为R,圆心角为α°,面积为S,弧长为l,则有.如果某圆锥的母线长是5,底面半径是3.(1)求该圆锥侧面展开图的面积;(2)PA是圆锥的一条母线,过圆锥底面圆心O作PA的垂线,垂足为M,求OM绕圆锥的轴旋转一周所得曲面将圆锥分成两部分的体积比.14.如图,在平面直角坐标系中,A(1,3),B(﹣2,0),C(4,0)是⊙M上的三个点,D为的中点.(1)直接写出圆心M的坐标:,这个圆的半径为.(2)求扇形BMD的面积.。
人教版九年级数学上册24.4 弧长和扇形面积同步练习带答案【优】

第24章 24.4《弧长和扇形面积》同步练习及答案(2)第1题. 一条弧所对的圆心角是90o,半径是R ,则这条弧的长是 .答案:12R π 第2题. 若»AB 的长为所对的圆的直径长,则»AB 所对的圆周角的度数为 .答案:180πo第3题. 如图,AB 是半圆O 的直径,以O 为圆心,OE 为半径的半圆交AB 于E ,F 两点,弦AC 是小半圆的切线,D 为切点,若4OA =,2OE =,则图中阴影部分的面积为 .答案:43π+第4题. 如果一条弧长等于l ,它的半径等于R ,这条弧所对的圆心角增加1o,则它的弧长增加( ) A.lnB.180R π C.180lRπ D.360l答案:B第5题. 在半径为3的O e 中,弦3AB =,则»AB 的长为( )A.π2B.πC.32π D.2π答案:B第6题. 扇形的周长为16,圆心角为360πo,则扇形的面积是()A.16 B.32 C.64 D.16π答案:A第7题. 如图,扇形OAB 的圆心角为90o,且半径为R ,分别以OA ,OB 为直径在扇形内作半圆,P 和Q 分别表示两个阴影部分的面积,那么P 和Q 的大小关系是( ) A.P Q =B.P Q >C.P Q <D.无法确定答案:A第8题. 如图,矩形ABCD 中,1AB =,BC =,以BC 的中点E 为圆心的¼MPN与AD 相切,则图中的阴影部分的面积为( )A.23π B.34πD.π3答案:D第9题. 如图所示,正方形ABCD 是以金属丝围成的,其边长1AB =,把此正方形的金属丝重新围成扇形的ADC ,使AD AD =,DC DC =不变,问正方形面积与扇形面积谁大?大多少?由计算得出结果. 答案:1S =正方形,121122ADC S lR 1==⨯⨯=扇形,∴面积没有变化.第10题. 如图,O e 的半径为1,C 为O e 上一点,以C 为圆心,以1为半径作弧与O e 相交于A ,B 两点,则图中阴影部分的面积为.答案:2π3第11题. 如图,△ABC 中,105A ∠=o ,45B ∠=o,AB =AD BC ⊥,D 为垂足,以A为圆心,以AD 为半径画弧»EF,则图中阴影部分的面积为( )MC A DA.76πB.76-π+2C.56πD.56-π+2答案:B第12题. 如图,半径为r 的1O e 与半径为3r 的2O e 外切于P 点,AB 是两圆的外公切线,切点分别为A ,B ,求AB 和»PA,»PB 所围成的阴影部分的面积.答案:连结2O B ,1O A ,过1O 作12O H O B ⊥,垂足为H ,则得矩形1ABHO , 1BH O A r ∴==,1AB O H =.在Rt △21O HO 中,2232O H O B BH r r r =-=-=,122134O O O P O P r r r =+=+=,1O H ==,2211221cos 42O H r HO O O O r ∠===,2160HO O ∴∠=o ,1120AO P ∠=o .21212111()(3)22ABO O S O A O B O H r r =+=+=g 梯形,26033606BO P O B r r S 222π()π(3)π===2g 2扇形,122120AO P O A S r π()π==3603扇形、,212122223ABO O BO P AO P S S S S r r ππ=--=--=23阴影梯形扇形扇形.第13题. 圆周角是90o,占整个周角的90360,因此它所对的弧长是圆周长的 . 答案:14第14题. 圆心角是45o,占整个周角的 ,因此它所对的弧长是圆周长的 . 答案:45360,18第15题. 圆心角是1o,占整个周角的 ,因此它所对的弧长是圆周长的 .C D B EAF答案:1360,1360第16题. 扇形的圆心角为210o,弧长是28π,求扇形的面积.答案:336π第17题. 一个扇形的半径等于一个圆的半径的2倍,且面积相等.求这个扇形的圆心角.答案:90o第18题. 一服装厂里有大量形状为等腰直角三角形的边角布料(如图),现找出其中的一种,测得90C ∠=o ,4AC BC ==.今要从这种三角形中剪出一种扇形,做成不同形状的玩具,使扇形的边缘半径恰好都在ABC △的边上,且扇形的弧与ABC △的其他边相切,请设计出所有可能符合题意的方案示意图,并求出扇形的半径(只要求画出图形,并直接写出扇形半径).答案:第19题.90o,半径为R A.2R πB.3R πC.4R πD.6R答案:A第20题. 已知一条弧长为l ,它所对圆心角的度数为n o,则这条弦所在圆的半径为( ).A.180n lπ B.180ln πC.360ln πD.180lnπ答案:B第21题. 半径为6cm 的圆中,60o的圆周角所对的弧的弧长为 .答案:4cm π第22题. 半径为9cm 的圆中,长为12cm π的一条弧所对的圆心角的度数为 .答案:240o第23题. 已知圆的面积为281cm π,若其圆周上一段弧长为3cm π,则这段弧所对的圆心角的度42r =24r =1r =数为 .答案:60o第24题. 若扇形的圆心角为120o,弧长为6cm π,则这个扇形的面积为 .答案:227cm π第25题. 弯制管道时,先按中心线计算其“展直长度”,再下料.根据如图所示的图形可算得管道的展直长度为 .(单位:mm ,精确到1mm )答案:389mm第26题. 如图,在Rt △ABC 中,90C ∠=o,60A ∠=o,3cm AC =,将△ABC 绕点B 旋转至△A BC ''的位置,且使点A ,B ,C '三点在同一直线上,则点A 经过的最短路线长是cm . 答案:53π第27题. 一块等边三角形的木板,边长为1,若将木板沿水平线翻滚(如图),则点B 从开始至结束走过的路径长度为( ). A.3π2B.4π3C.4D.322+π答案:B第28题. 如图,扇形AOB 的圆心角为60o,半径为6cm ,C ,D 是»AB 的三等分点,则图中阴影部分的面积和是 .A ' C ' B C A BC答案:22cm π第29题. 如图,已知在扇形AOB 中,若45AOB ∠=o,4cm AD =,3cm CD =π,则图中阴影部分的面积是 .答案:214cm π第30题. 如图4,在两个同心圆中,三条直径把大圆分成相等的六部分,若大圆的半径为2,则图中阴影部分的面积为 .答案:14.2π.图4。
人教版九年级上 24.4弧长及扇形面积同步练习(人教新课标九年级上)

21.5 弧长和扇形面积一、双基整合:1.若扇形面积为3π,半径为3,则弧长为_______,圆心角是________.2.有一段弯道是圆弧形的,如图1,道长是12m,弧所对的圆心角是81°,•求这段弧的半径R为________.(精确到0.1m)(1) (2) (3)3.如图2,正△ABC的边长AB=2,以A为圆心的圆切BC于点D,交AB于点E,交AC•于点F,则EF的长=_________.4.如图3所示,三个圆是同心圆,图中阴影部分的面积为______.5.如图4,Rt△ABC中,∠C=90°,AC=2,AB=4,分别以AC、BC为直径作半圆,•则图中阴影部分的面积为________.(4) (5) (6)6.已知一弧的半径为3,弧长为2π,则此弧所对的圆心角为()A.(23π)° B.240° C.120° D.60°7.如图5,矩形ABCD中,AB=1,AD=3,以BC的中点E为圆心的¼MPN与AD相切,则图中阴影部分的面积为()A.23B.34C.54D.3π8.秋千拉绳长3米,静止时踩板离地面0.5米,某小朋友荡该秋千时,•秋千在最高处踩板离地面2米(左右对称),则该秋千所荡过的圆弧长为()A .π米B .2π米C .43π米 D .32π米 9.正三角形ABC 内接于半径为2cm 的圆,则AB 所对弧的长为( ) A .23π B .43π C .83π D .43π或83π10.如图6所示的5个半圆,邻近的两半圆相切,两只小虫同时出发,•以相同的速度从A 点到B 点,甲虫沿¼¼¼¼112233,,,ADA A EA A FA A GB 的路线爬行,乙虫沿ACB 的路爬行,则下列结论正确的是( )A .甲先到B 点 B .乙先到B 点C .甲、乙同时到B 点D .无法确定 11.有一圆形的马戏帐篷,其半径为20m ,从A 到B 有一笔直的栅栏,长为203m .(1)试求∠ACB 的度数.(2)某学校的学生在阴影区域里看马戏,设每平方米中有两个学生,•试问该校有多少学生在看马戏?(π取3.14,3取1.73)ABC二、拓广探索:12.如图,⊙O 1的半径O 1A 是⊙O 2的直径,⊙O 1的半径O 1C 交⊙O 2于点B ,则»AC 和»AB 的长度的大小关系为________. 13.如图,⊙A 、⊙B 、⊙C 、⊙D 、⊙E 相互外离,它们的半径都是1,顺次连接五个圆心得到五边形ABCDE ,则图中五个扇形(阴影部分)的面积之和是( )A .πB .1.5πC .2πD .2.5π14.如图,把直角三角形ABC 的斜边AB 放在直线L 上,按顺时针方向在L 上转动两次,使它转到△A ″B ″C ″的位置上,设BC=1,AC=3,则顶点A 运动到A ′的位置时,点A 经过的路线有多长,点A 经过的路线与直线L 所围成的面积有多大?O 1AB O 2CB ''A''C'A 'lBAC三、智能升级:15.如图,一块边长为10cm 的正方形木板ABCD ,在水平桌面上绕点D 按顺时针方向旋转到A ′B ′C ′D ′的位置时,顶点B 从开始到结束所经过的路程长为( ) A .20cm B .202cm C.10cm D .52cm16.农村常常建横截面积为半圆形的全封闭塑料薄膜蔬菜大棚,如图所示,•如图不考虑塑料薄膜接头重合及埋在土里的部分,•那么搭建一个这样的蔬菜大棚需要用塑料薄膜的面积是( )A .64πm 2B .72πm 2C .78πm 2D .80πm217.将三根直径为a 的圆柱形钢管用铁丝捆扎,现设计了两种方案,如图所示,•请你探索,宜采用哪一种方案.(1) (2)答案:1.2π 120° 2.8.5m 3.33π 4.14π 5.2π-23 6.C 7.D 8.B 9.D 10.C11.(1)∠ACB=120° (2)约491人 12.相等 13.B14.Rt △A BC 中, BC=1,AC=3,则可得AB=2,∠CAB=30°,则点A 到A ″所经过的路线为¼¼''''l AA l A A +=1202180π⨯+903π⨯=(43+3)π; 点A 经过的路线与直线L 围成的面积为21202360π⨯⨯+12×1×3+290(3)π⨯=2512π+315.D 16.A17.如图(1)中铁丝长应为半圆¼¼,AmD BnC的长度与线段AB 、CD 之和, 因为¼AmD 的长=¼BnC 的长=12πa ,AB=CD=2a , 所以,铁丝长=2a ×2+12πa ×2=(π+4)a . 如图(2)中,•将铁丝长分为六段,易知AB=CD=EF=a ,»AF 的长=»BC 的长=»DE 的长=11202180aπ⨯=3πa , 所以铁丝长=3a+3×3πa=(π+3)a ,故最少要用(π+3)a 的铁丝,宜采用后一种捆法.。
人教版九年级上数学册24.4弧长和扇形面积同步练习含答案
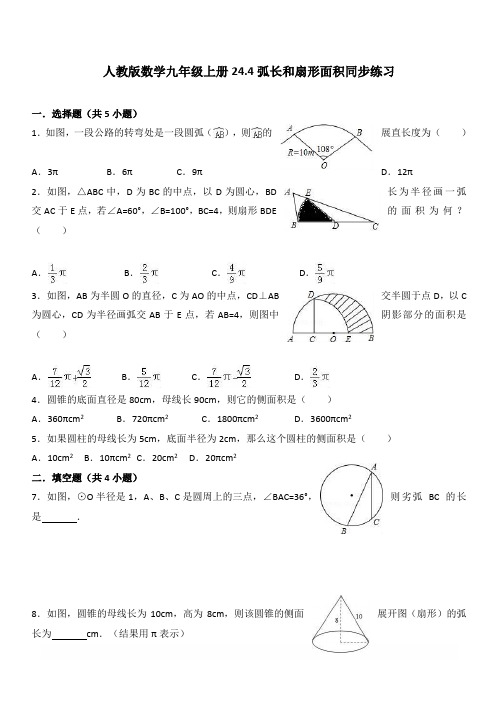
人教版数学九年级上册24.4弧长和扇形面积同步练习一.选择题(共5小题)1.如图,一段公路的转弯处是一段圆弧(),则的展直长度为()A.3πB.6πC.9πD.12π2.如图,△ABC中,D为BC的中点,以D为圆心,BD长为半径画一弧交AC于E点,若∠A=60°,∠B=100°,BC=4,则扇形BDE的面积为何?()A.B.C.D.3.如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧交AB于E点,若AB=4,则图中阴影部分的面积是()A.B.C.D.4.圆锥的底面直径是80cm,母线长90cm,则它的侧面积是()A.360πcm2 B.720πcm2C.1800πcm2D.3600πcm25.如果圆柱的母线长为5cm,底面半径为2cm,那么这个圆柱的侧面积是()A.10cm2B.10πcm2C.20cm2D.20πcm2二.填空题(共4小题)7.如图,⊙O半径是1,A、B、C是圆周上的三点,∠BAC=36°,则劣弧BC的长是.8.如图,圆锥的母线长为10cm,高为8cm,则该圆锥的侧面展开图(扇形)的弧长为cm.(结果用π表示)9.用一块圆心角为216°的扇形铁皮,做一个高为40cm的圆锥形工件(接缝忽略不计),那么这个扇形铁皮的半径是cm.10.如图,两圆半径均为1,且图中两块阴影部分的面积相等,那OO1的长度是.三.解答题(共4小题)11.如图所示,将直角△ABC向下旋转90°,已知BC=5厘米,AB=4厘米,AC=3厘米,求△ABC扫过的面积.12.如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E.(1)求证:DE=AB;(2)以D为圆心,DE为半径作圆弧交AD于点G,若BF=FC=1,试求的长.13.如图,锚标浮筒是打捞作业中用来标记锚或沉船位置的,它的上下两部分是圆柱,中间是一个圆柱(如图,单位:mm).电镀时,如果每平方米用锌0.11kg,要电镀1000个这样的锚标浮筒需要用多少锌?(精确到1kg)14.已知如图,在直角坐标系xOy中,点A,点B坐标分别为(﹣1,0),(0,),连结AB,OD由△AOB绕O点顺时针旋转60°而得.(1)求点C的坐标;(2)△AOB绕点O顺时针旋转60°所扫过的面积;(3)线段AB绕点O顺时针旋转60°所扫过的面积.参考答案一.选择题 1.B . 2.C . 3.A . 4.D . 5.D . 二.填空题7.=π.8.12π. 9.50.10..三.解答题 11.解:∵将此三角形绕点A 顺时针旋转90°到直角△AB′C′的位置, ∴∠BAB′=90°,∴直角△ABC 扫过的面积是:S 扇形BAB′+S △ACB′=+×3×4=+6.12.(1)证明:∵四边形ABCD 是矩形, ∴∠B=∠C=90°,AB=DC ,BC=AD ,AD ∥BC , ∴∠EAD=∠AFB , ∵DE ⊥AF , ∴∠AED=90°,在△ADE 和△FAB 中,,∴△ADE ≌△FAB (AAS ),∴DE=AB;(2)连接DF,如图所示:在△DCF和△ABF中,,∴△DCF≌△ABF(SAS),∴DF=AF,∵AF=AD,∴DF=AF=AD,∴△ADF是等边三角形,∴∠DAE=60°,∵DE⊥AF,∴∠AED=90°,∴∠ADE=30°,∵△ADE≌△FAB,∴AE=BF=1,∴DE=AE=,∴的长=.13.解:由图形可知圆锥的底面圆的半径为0.4m,圆锥的高为0.3m,则圆锥的母线长为:=0.5m.∴圆锥的侧面积S1=π×0.4×0.5=0.2π(m2),∵圆柱的高为0.8m.圆柱的侧面积S2=2π×0.4×0.8=0.64π(m2),∴浮筒的表面积=2S1+S2=1.04π(m2),∵每平方米用锌0.11kg,∴一个浮筒需用锌:1.04π×0.11kg,∴1000个这样的锚标浮筒需用锌:1000×1.04π×0.11=11.44π≈359(kg).答:1000个这样的锚标浮筒需用锌359kg.14.解:(1)如图1,过C作CE⊥OA于E,∵点A,点B坐标分别为(﹣1,0),(0,),∴OA=1,OB=,∵△AOB绕点O顺时针旋转60°得到△COD,∴∠AOC=∠BOD=60°,AO=OC=1,∴OE=OC=,CE=OC=,∴C(﹣,);(2)△AOB绕点O顺时针旋转60°所扫过的面积=++×=π+;(3)如图2,线段AB绕点O顺时针旋转60°所扫过的面积═(﹣1×)+(﹣)+(﹣)=π﹣.。
2019年秋人教版九年级上册数学同步练习(PDF,无答案):24.4 弧长和扇形面积

结束所走过的路径长度为( )ꎮ
A������
3π 2
B������
4π 3
C������ 4
D������
2
+
3π 2
图 24 ̄4 ̄15
— 59 —
((
12������ 如图 24 ̄4 ̄16 所示ꎬ点 D 在☉O 的直径 AB 的延长线上ꎬ点 C 在☉O 上ꎬ且 AC = CDꎬ∠ACD = 120°ꎮ (1) 求证:CD 是☉O 的切线ꎻ(2) 若☉O 的半径为 2ꎬ求图中阴影部分的面积ꎮ
6������ 如果一个扇 形 的 面 积 和 一 个 圆 面 积 相 等ꎬ 且 扇 形 的 半 径 为 圆 半 径 的 2 倍ꎬ 这 个 扇 形 的 中 心 角
为 ꎮ
7������ 如图 24 ̄4 ̄12 所示ꎬAꎬBꎬC 三点在半径为 1 的☉O 上ꎬ若∠BAC = 60°ꎬ则扇形 OBC 的
图 24 ̄4 ̄36
— 61 —
( a) 的路线:线段 AC→CD→线段ꎮ ( b) 的路线:线段 AE→EF→线段 FB( 其中 E、F 为切点) ꎮ
(a) (b) 图 24 ̄4 ̄17
第二课时 圆锥的侧面积和全面积
基础练习 1������ 圆锥的母线长为 13 cmꎬ底面半径为 5 cmꎬ则此圆锥的高线为 ꎮ 2������ 一个圆锥的侧面展开图的弧长为 12πꎬ则这个圆锥的地面半径为 ꎮ 3������ 已知圆锥的侧面积为 8π cm 2 ꎬ侧面展开图的圆心角为 45°ꎬ则该圆锥的母线为 ꎮ 4������ 一个圆锥的底面圆的周长是 2πꎬ母线长是 3ꎬ则它的侧面展开图的圆心角等于 ꎮ 5������ 粮仓顶部是一个圆锥形ꎬ其底面周长为 36 mꎬ母线长为 8 mꎬ为防雨需在粮仓顶部铺上油毡ꎬ如果按
人教版九年级数学上册24.4弧长和扇形面积同步测试及答案【优】

弧长和扇形面积第1课时 弧长和扇形面积 [见B 本P48]1.若扇形的半径为6,圆心角为120°,则此扇形的弧长是( B )A .3πB .4πC .5πD .6π2.按图24-4-1(1)的方法把圆锥的侧面展开,得到图24-4-1(2)所示的扇形,其半径OA =3,120°,则AB ︵的长为( B )(1) 图24-4-1A .πB .2πC .3πD .4π3.如果一个扇形的半径是1,弧长是π3,那么此扇形的圆心角的大小为( C ) A .30° B .45° C .60° D .90°4.[2012·兰州]如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”,则半径为2的“等边扇形”的面积为( C )A .πB .1C .2 D.23π 【解析】 设扇形的半径为r ,弧长为l ,根据扇形的面积公式得S =12lr =12r 2=2. 5.钟面上的分针的长为1,从9点到9点30分,分针在钟面上扫过的面积是( A ) A.12π B.14π C.18π D .π 【解析】 从9点到9点30分分针扫过的扇形的圆心角是180°,则分针在钟面上扫过的面积是:180π×12360=12π. 6.如图24-4-2,AB 与⊙O 相切于点B ,AO 的延长线交⊙O 于点C ,连接BC ,若∠ABC =120°,OC =3,则BC ︵的长为( B )3π D .5π第6【解析】 如图,连接OB ,∵AB 与⊙O 相切于点B ,∴∠ABO =90°.∵∠ABC =120°,∴∠OBC =30°.∵OB =OC ,∴∠OCB =30°,∴∠BOC =120°,∴BC ︵的长为n πr 180=120π×3180=2π. 7.如图24-4-3,水平地面上有一面积为30π cm 2的扇形OAB ,半径OA =6 cm ,且OA 与地面垂直.在没有滑动的情况下,将扇形向右滚动至OB 与地面垂直为止,则O 点移动的距离为( C )图24-4-3A .20 cmB .24 cmC .10π cmD .30π cm 【解析】 点O 移动的距离就是扇形的弧长,设扇形弧长为l ,根据题意可得12l ×6=30π,解得l =10π cm.8.在半径为6 cm 的圆中,60°的圆心角所对的弧长等于__2π__cm(结果保留π).【解析】 弧长为60π×6180=2π(cm). 9.一个扇形的圆心角为120°,半径为3,则这个扇形的面积为__3π__(结果保留π).【解析】 由题意得n =120°,R =3,故S 扇形=n πR 2360=120π×32360=3π.图24-4-4 10.如图24-4-4,AB 切⊙O 于点B ,OA =2,∠OAB =30°,弦BC ∥OA ,劣弧BC ︵的弧长为__π3__.(结果保留π)11.如图24-4-5,在3×3的方格中(共有9个小格),每个小方格都是边长为1的正方形,O ,B ,C 是格点,则扇形OBC 的面积等于__54π__(结果保留π).12. 如图24-4-6,在边长为1的小正方形组成的方格纸上,将△ABC 绕着点A 顺时针旋转90°.(1)画出旋转后的△AB ′C ′;(2)求线段AC 在旋转过程中所扫过的扇形的面积.图24-4-6解:(1)如图;(2)线段AC 在旋转过程中所扫过的扇形的面积=S 扇形ACC ′=90π·22360=π. 13.如图24-4-7,一根5 m 长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只小羊A (羊),那么小羊A 在草地上的最大活动区域面积是( D )图24-4-7A.1712π m 2B.176π m 2 C.254π m 2 D.7712π m 2 14.如图24-4-8,△ABC 是正三角形,曲线CDEF 叫做正三角形的渐开线,其中弧CD ,弧DE ,弧EF 的圆心依次是A ,B ,C ,如果AB =1,那么曲线CDEF 的长是__4π__.图24-4-815.如图24-4-9,在矩形ABCD 中,AB =2DA ,以点A 为圆心,AB 为半径的圆弧交DC 于点E ,交AD 的延长线于点F ,设DA =2.(1)求线段EC 的长;(2)求图中阴影部分的面积.图24-4-9解:(1)∵在矩形ABCD 中,AB =2DA ,∴AE =2AD ,且∠ADE =90°.又DA =2,∴AE =AB =4,∴DE =AE 2-AD 2=16-4=23,∴EC =DC -DE =4-2 3.(2)S 阴影=S 扇形AEF -S △ADE =60°×π×42360°-12×2×23=83π-2 3. 16.如图24-4-10,已知AB 是⊙O 的直径,弦CD ⊥AB ,垂足为E ,∠AOC =60°,OC =2.(1)求OE 和CD 的长;【解析】 ∵∠CAD ,∠DBE ,∠ECF 是等边三角形的外角,∴∠CAD =∠DBE =∠ECF =120°,又∵AC =1,∴BD =2,CE =3,∴弧CD 的长=13×2π×1, 弧DE 的长=13×2π×2,弧EF 的长=13×2π×3, ∴曲线CDEF 的长=13×2π×1+13×2π×2+13×2π×3=4π. 解:(1)在△OCE 中,∵∠CEO =90°,∠EOC =60°,∴∠OCE =30°.∵OC =2,∴OE =12OC =1, ∴CE =OC 2-OE 2= 3.∵OA ⊥CD ,∴CE =DE ,∴CD =2CE =2 3.(2)∵S △ABC =12AB ·CE =12×4×3=23, ∴S 阴影=S 半圆-S △ABC =12π×22-23=2π-2 3. 17.如图24-4-11,AB 是⊙O 的直径,C 是半圆O 上的一点,AC 平分∠DAB ,AD ⊥CD ,垂足为D ,AD 交⊙O 于E ,连接CE .(1)判断CD 与⊙O 的位置关系,并证明你的结论;(2)若E 是AC ︵的中点,⊙O 的半径为1,求图中阴影部分的面积.图24-4-11解:(1)CD 与圆O 相切,理由为:∵AC 为∠DAB 的平分线,∴∠DAC =∠BAC ,∵OA =OC ,∴∠OAC =∠OCA ,∴∠DAC =∠OCA ,∴OC ∥AD ,∵AD ⊥CD ,∴OC ⊥CD ,∴CD 与圆O 相切;(2)连接EB ,由AB 为直径,得到∠AEB =90°,∴EB ∥CD ,F 为EB 的中点,∴OF 为△ABE 的中位线,∴OF =12AE =12,即CF =DE =12, 在Rt △OBF 中,根据勾股定理得:EF =FB =DC =32, 则S 阴影=S △DEC =12×12×32=38.。
(人教版数学)初中9年级上册-同步练习-人教版九年级数学上册:24.4+弧长和扇形面积(含答案)
24.4 弧长和扇形面积知识点1.在半径为R 的圆中,1°的圆心角所对的弧长是____________,n °的圆心角所对的弧长是______________.2.在半径为R 的圆中,1°的圆心角所对的扇形面积是____________,n °的圆心角所对的扇形面积S 扇形=______________.3.半径为R ,弧长为l 的扇形面积S 扇形=________.一、选择题1.(2013•潜江)如果一个扇形的弧长是34π,半径是6,那么此扇形的圆心角为( ) A .︒40B .︒45C .︒60D .︒802.(2013•南通) 如图,已知□ABCD 的对角线BD =4cm ,将□ABCD 绕其对称中心O 旋转180°,则点D 所转过的路径长为( ) A .4π cmB .3π cmC .2π cmD .π cm3.(2013•宁夏)如图,以等腰直角△ABC 两锐角顶点A 、B 为圆心作等圆,⊙A 与⊙B 恰好外切,若AC=2,那么图中两 个扇形(即阴影部分)的面积之和为( )A.4π B.2π C.22π D.2π 4.(2013•资阳)钟面上的分针的长为1,从9点到9点30分,分针在钟面上扫过的面积是 ( )A .12πB .14π C. 18πD .π 5.(2013•荆州)如图,将含60°角的直角三角板ABC 绕顶点A 顺时针旋转45°度后得到△AB 'C ',点B 经过的路径为弧BB ',若角∠BAC =60°,AC =1,则图中阴影部分的面积是 ( )A .2πB . 3πC . 4πD . π6.(2013•恩施州)如图所示,在直角坐标系中放置 一个边长为1的正方形ABCD ,将正方形ABCD 沿 x 轴的正方向无滑动的在x 轴上滚动,当点A 离开 原点后第一次落在x 轴上时,点A 运动的路径线与第2题ABCDO第3题C ′B ′C B A第5题第6题x 轴围成的面积为( ) A.122π+B. 12π+ C.1π+ D. 12π+7.(2013•德州)如图,扇形AOB 的半径为1,∠AOB =90°,以AB 为直径画半圆.则图中阴影部分的面积为( )A .14π B .π12-C .12D .1142π+8.(2013•襄阳)如图,以AD 为直径的半圆O 经过Rt △ABC 斜边AB 的两个端点,交直角边AC 于点E ,B 、E 是半圆弧的 三等分点,弧BE 的长为π,则图中阴影部分的面积为 ( ) A.9π B.39πC.33322π- D.33223π-二、填空题9.(2013•茂名)如图是李大妈跳舞用的扇子,这个扇形 AOB 的圆心角120O ∠=,半径OA=3,则弧.AB ..的长 度为 (结果保留π).10.(2013•遂宁)如图,△ABC 的三个顶点都在5×5 的网格(每个小正方形的边长均为1个单位长度)的 格点上,将△ABC 绕点B 逆时针旋转到△A ′BC ′的位 置,且点A ′、C ′仍落在格点上,则图中阴影部分的面积 约是___________.(π≈3.14,结果精确到0.1)11.(2013•玉林)如图,实线部分是半径为15m 的两条等弧 组成的游泳池,若每条弧所在的圆都经过另一个圆的圆心, 则游泳池的周长是 _______ m .OAB 第7题第8题第10题第11题12.(2013•眉山)如图,以BC为直径的⊙O与△ABC的另两边分别相交于点D、E。
人教版九年级上册数学 弧长和扇形的面积 同步训练(含答案)
人教版九年级上册数学24.4 弧长和扇形的面积同步训练一、单选题1.如图,AB 切⊙O 于点B ,连接OA 交⊙O 于点C ,连接OB .若30A ∠︒=,OA =4,则劣弧BC 的长是( )A .13πB .23π C .π D .43π 2.已知扇形的半径为6,圆心角为120︒,则它的弧长是( )A .2πB .4πC .6πD .8π3.如图,要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底面圆周长为20πcm,侧面积为240πcm 2,则这个扇形的圆心角的度数是( )度.A .120°B .135°C .150°D .160° 4.如图,将ABC 绕点C 旋转60得到A B C '',已知6AC =,4BC =,则线段AB 扫过的图形面积为( )A .32πB .83πC .6πD .103π 5.如图,圆锥的高AO 为4,母线AB 长为5,则该圆锥展开图的弧长等于( )A .9πB .15πC .6πD .12π 6.如图,矩形ABCD 中,4BC =,2CD =,以AD 为直径的半圆O 与BC 相切于点E ,连接BD ,则阴影部分的面积为( )A .πB .2π-C .2π+D .4π+ 7.如图,在⊙ABC 中,AB =AC =10,BC =12,分别以点A ,B ,C 为圆心,12AB 的长为半径画弧,与该三角形的边相交,则图中阴影部分的面积为( )A .96﹣252πB .96﹣25πC .48﹣254πD .48﹣252π 8.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B 点从开始至结束所走过的路径长度为( )A .32πB .42πC .4D .322π+二、填空题9.一圆锥的底面半径为2,母线长3,则这个圆锥的表面积为_________.10.若圆锥侧面展开图是面积为265cm π的扇形,扇形的弧长为10cm π,则圆锥的高为______.11.如图,在由边长为1的小正方形组成的网格中,一条弧经过格点(网格线的交点)A ,B ,D ,点C 为弧BD 上一点.若30CAD ∠=︒,则弧CD 的长为__________.12.如图,在Rt⊙ABC 中,⊙ACB =90°,AC =BC =2,以BC 为直径作半圆,交AB 于点D ,则阴影部分的面积是 _________13.若圆锥的母线为6,底面圆的半径为3,则此圆锥的侧面积为________.14.若一个圆锥的母线长为5cm ,它的半径为3cm ,则这个圆锥的全面积为________2cm . 15.用一个圆心角为120︒,半径为2的扇形做一个圆锥的侧面,则这个圆锥的侧面积为______.16.若圆锥的侧面积为 9π,底面半径为 3,则该圆锥的母线长是_____.三、解答题17.将图中的破轮子复原,已知弧上三点A ,B ,C .(1)画出该轮的圆心;(2)若ABC 是等腰三角形,底边BC =腰AB =10cm,求弧BC 的长.18.如图,BE 是⊙O 的直径,点A 和点D 是⊙O 上的两点,过点A 作⊙O 的切线交BE 延长线于点C .(1)若⊙ADE =25°,求⊙C 的度数;(2)若AC =CE =4,求阴影部分的面积.19.如图,AB 是⊙O 的直径,点D 是弦BC 延长线上一点,且BC CD =.(1)证明:AB AD =;(2)若8BD =,OD =求弓形BMC (阴影区域)的面积.20.如图,AB 是圆O 的直径,弦CD 交AB 于点E ,60ACD ∠=︒,50ADC ∠=︒.(1)求CEB ∠的度数;(2)若AD =求扇形AOC 的面积.参考答案:1.B2.B3.C4.D5.C6.A7.D8.B9.10π10.12cm1112.3π24 -13.18π14.24π15.4 3π16.317.(2)203πcm18.(1)⊙C=40°;(2)阴影部分的面积为83π.19.(2)24π-20.(1)100°;(2)109π.答案第1页,共1页。
【精品试卷】人教版数学九年级上册《24.4 弧长和扇形面积》练习
13
A.
6
13
π
B.
4
π
5
C.
3
π
5
D.
2
π
⏜
3.把一个弧长AC为10π cm的扇形AOC围成一个圆锥,测得母线OA = 13cm,则圆锥的
高ℎ为( )
A. 12cm
B. 10cm
C. 6cm
D. 5cm
4.如图,正方形ABCD的边长为8,以点为圆心,AD为半径,画圆弧DE得到扇形
∴ 由勾股定理得:ℎ = 12.
故选:.
根据扇形的弧长求得圆锥的底面半径,然后利用勾股定理求得高即可.
考查了圆锥的计算,解答该题的关键是了解圆锥的底面周长等于扇形的弧长,难度不
大.
4.【答案】D;
【解析】解:设圆锥的底面圆的半径为,
根据题意可知:
AD = AE = 8,∠DAE = 45°,
答案和解析
1.【答案】B;
【解析】解:设弧所在圆的半径为 cm,
135πr
由题意得, 180
= 2π × 3 × 5
,
解得, = 40.
故选:.
设出弧所在圆的半径,由于弧长等于半径为3cm的圆的周长的5倍,所以根据原题所给
出的等量关系,列出方程,解方程即可.
解决本题的关键是熟记圆周长的计算公式和弧长的计算公式,根据题意列出方程.
故选:.
从2:00到4:00,这根分针的尖走了2圈,根据圆的周长 = 2πr,计算即可.
此题主要考查弧长的计算,解答该题的关键是理解题意,灵活运用所学知识解决问
题.
10.【答案】B;
阴影 = 2扇形 ‒ 正方形 = 2 ×
人教版数学九年级上册:24.4 弧长和扇形面积 同步练习(附答案)
24.4 弧长和扇形面积第1课时 弧长和扇形面积1.一个扇形的半径为8 cm ,弧长为163π cm ,则扇形的圆心角为( )A .60°B .120°C .150°D .180°2.如图,⊙O 是△ABC 的外接圆,BC =2,∠BAC =30°,则劣弧BC ︵的长等于( )A.2π3 B.π3 C.23π3 D.3π33.如图,一块含有30°角的直角三角板ABC ,在水平桌面上绕点C 按顺时针方向旋转到A ′B ′C ′的位置.若BC =12 cm ,则顶点A 从开始到结束所经过的路径长为 cm.4.如图,⊙O 的半径为6 cm ,直线AB 是⊙O 的切线,切点为B ,弦BC ∥AO.若∠A =30°,求劣弧BC 的长.5.若扇形的面积为3π,圆心角为60°,则该扇形的半径为( )A .3B .9C .2 3D .3 26. 如图,扇形AOB 中,半径OA =2,∠AOB =120°,C 是AB ︵的中点,连接AC ,BC ,则图中阴影部分的面积是( )A.4π3-2 3 B.2π3-2 3 C.4π3- 3 D.2π3- 37.如图,AB 是⊙O 的直径,弦CD ⊥AB ,∠C =30°,CD =23,则阴影部分的面积为 .8.如图,一扇形纸扇完全打开后,外侧两竹条AB 和AC 的夹角为120°,AB 长为25 cm ,贴纸部分的宽BD 为15 cm.若纸扇两面贴纸,则贴纸的面积为 cm 2.9.如图,在6×6的方格纸中,每个小方格都是边长为1个单位长度的正方形,其中A ,B ,C 为格点.作△ABC 的外接圆⊙O ,则劣弧AC 的长等于( )A.34π B.54π C.32π D.52π 10.如图,已知AB 是⊙O 的直径,弦CD ⊥AB ,垂足为E.若∠AOC =60°,OC =2 cm ,则阴影部分的面积是( )A .(π-3)cm 2B .(π+3)cm 2C .(2π+23)cm 2D .(2π-23)cm 211.如图,在扇形AOB 中,∠AOB =90°,半径OA =6,将扇形AOB 沿过点B 的直线折叠,点O 恰好落在AB ︵上点D 处,折痕交OA 于点C ,则整个阴影部分的面积为 .12.如图,在边长为1个单位长度的正方形网格中,△ABC的顶点均在格点上.(1)画出△ABC关于原点成中心对称的△A′B′C′,并直接写出△A′B′C′各顶点的坐标;(2)求点B旋转到点B′的路径(结果保留π).13.如图,C,D是半圆O上的三等分点,直径AB=4,连接AD,AC,DE⊥AB,垂足为E,DE交AC于点F.(1)求∠AFE的度数;(2)求阴影部分的面积(结果保留π和根号).第2课时圆锥的侧面积和全面积1.已知圆柱的底面半径为3 cm,母线长为5 cm,则圆柱的侧面积是( )A.30 cm2 B.30π cm2 C.15 cm2 D.15π cm22.如图是一个有盖子的圆柱体水杯,底面周长为6π cm,高为18 cm,若盖子与杯体的重合部分忽略不计,则制作10个这样的水杯至少需要的材料是( )A.108π cm2 B.1 080π cm2 C.126π cm2 D.1 260π cm23.一个圆柱的底面直径为6 cm,高为10 cm,则这个圆柱的全面积是cm2(结果保留π).4.下列图形中,是圆锥侧面展开图的是( )5.已知圆锥的母线长为6 cm,底面的半径为3 cm,则此圆锥侧面展开图的圆心角的度数为( ) A.30° B.60° C.90° D.180°6.如图,用一张半径为24 cm的扇形纸板制作一顶圆锥形帽子(接缝忽略不计),如果圆锥形帽子的底面半径为10 cm,那么这张扇形纸板的面积是( )A.240π cm2 B.480π cm2 C.1 200π cm2 D.2 400π cm27.已知圆锥的底面圆半径为3,母线长为5,则圆锥的侧面积是.8.有一圆锥,它的高是8 cm,底面半径是6 cm,则这个圆锥的侧面积是cm2.(结果保留π)9.已知圆锥的侧面展开图是一个半径为12 cm、弧长为12π cm的扇形,求这个圆锥的侧面积及高.10.一个几何体由圆锥和圆柱组成,其尺寸如图所示,该几何体的全面积(即表面积)是多少?(结果保留π)11.已知一个圆柱的侧面展开图为如图所示的矩形,则其底面圆的面积为.12.若要用一个底面直径为10,高为12的实心圆柱体,制作一个底面半径和高分别与圆柱底面半径和高相同的圆锥,则该圆锥的侧面积为( )A.60π B.65π C.78π D.120π13.如图,从一张腰长为60 cm、顶角为120°的等腰三角形铁皮OAB中剪出一个最大的扇形OCD,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的高为( )A.10 cm B.15 cm C.10 3 cm D.20 2 cm14.一个圆锥形漏斗,某同学用三角板测得其高度的尺寸如图所示,则该圆锥形漏斗的侧面积为cm2.15.如图,在菱形ABCD 中,AB =23,∠C =120°,以点C 为圆心的EF ︵与AB ,AD 分别相切于点G ,H ,与BC ,CD 分别相交于点E ,F.若用扇形CEF 作一个圆锥的侧面,则这个圆锥的高是 .16.如图1是某校存放学生自行车的车棚的示意图(尺寸如图所示,单位:m),车棚顶部是圆柱侧面的一部分,其展开图是矩形.如图2是车棚顶部截面的示意图,AB ︵所在圆的圆心为点O ,车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积.(不考虑接缝等因素,计算结果保留π)17.如图,有一直径是1米的圆形铁皮,圆心为O ,要从中剪出一个圆心角是120°的扇形ABC. (1)求被剪掉阴影部分的面积;(2)若用所留的扇形ABC 铁皮围成一个圆锥,该圆锥底面圆的半径是多少?参考答案:24.4 弧长和扇形面积第1课时 弧长和扇形面积1.B2. A3.16π.4.解:连接OB ,OC.∵AB 是⊙O 的切线, ∴AB ⊥BO.∵∠A =30°,∴∠AOB =60°. ∵BC ∥AO ,∴∠OBC =∠AOB =60°. 又∵OB =OC ,∴△OBC 是等边三角形. ∴∠BOC =60°.∴劣弧BC 的长为60×π×6180=2π(cm ).5.D 6. A 7.2π3.8.350π . 9.D 10.D1112.解:(1)如图所示,A ′(4,0),B ′(3,3),C ′(1,3). (2)由图可知:OB =32+32=32, ∴BB ′︵=n πr 180=180×π×32180=32π.13.解:(1)连接OD ,OC.∵C ,D 是半圆O 上的三等分点, ∴AD ︵=CD ︵=BC ︵.∴∠AOD =∠DOC =∠COB =60°. ∴∠CAB =30°. ∵DE ⊥AB , ∴∠AEF =90°.∴∠AFE =90°-30°=60°. (2)由(1)知,∠AOD =60°, ∵OA =OD ,AB =4,∴△AOD 是等边三角形,OA =2. ∵DE ⊥AO , ∴DE = 3.∴S 阴影=S 扇形AOD -S △AOD =60×π×22360-12×2× 3=23π- 3.第2课时 圆锥的侧面积和全面积1.B 2.D 3.78π.4.B 5.D 6.A 7.15π. 8.60π9.解:侧面积为12×12×12π=72π(cm 2).设底面半径为r cm ,则有2πr =12π,∴r =6.由于高、母线、底面半径恰好构成直角三角形,根据勾股定理可得,高为122-62=63(cm ). 10.解:圆锥的母线长是: 32+42=5. 圆锥的侧面积是: π×82×5=20π.圆柱的侧面积是:8π×4=32π. 几何体的下底面面积是:π×42=16π. 所以该几何体的全面积(即表面积)为: 20π+32π+16π=68π. 11.π或4π. 12.B 13.D14.15π.1516.解:连接OB ,过点O 作OF ⊥AB ,垂足为E ,交AB ︵于点F ,由垂径定理,知E 是AB 的中点,F 是AB ︵的中点,从而EF 是弓形的高.∴AE =12AB =2 3 m ,EF =2 m.设半径为R m ,则OE =(R -2)m. 在Rt △AOE 中,由勾股定理,得 R 2=(R -2)2+(23)2.解得R =4. ∴OE =4-2=2(m ). 在Rt △AEO 中,AO =2OE , ∴∠OAE =30°,∠AOE =60°. ∴∠AOB =120°.∴AB ︵的长为120×4π180=8π3(m ).故帆布的面积为8π3×60=160π(m 2).17.解:(1)连接OA ,OB.由∠BAC =120°,可知AB =12米,点O 在扇形ABC 的BC ︵上.∴扇形ABC 的面积为120360π·(12)2=π12(平方米).∴被剪掉阴影部分的面积为π·(12)2-π12=π6(平方米).(2)由2πr =120180π·12,得r =16,即圆锥底面圆的半径是16米.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人教新版数学九年级上学期《24.4弧长和扇形面积》同步练习一.选择题(共10小题)
1.如图,在4×4的方格中(共有16个小方格),每个小方格都是边
长为1的正方形,O,A,B分别是小正方形的顶点,则扇形OAB的弧
长等于()
A.2πB.πC.2π
D.π
2.如图,Rt△AB′C′是Rt△ABC以点A为中心逆时针旋转90°而得到的,其
中AB=1,BC=2,则旋转过程中弧CC′的长为()
A.πB.πC.5πD.π
3.如图,AB是⊙O的直径,点D为⊙O上一点,且∠ABD=30°,BO=4,则
的长为()
A.B.C.2πD.
4.如图,⊙O
与⊙O2的半径均为5,⊙O1的两条弦长
分别为6和8,⊙O2的两条弦长均为7,则图中阴影部
分面积的大小关系为()
A.S1>S2B.S1<S2C.S1=S2
D.无法确定
5.如图,在Rt△ABC中,∠ABC=90°,AC=4,AB=2,以点B为圆
心,AB为半径画弧,交AC于点D,交BC于点E,连接BD,则图
中阴影部分面积为()
A.B.C.
D.
6.圆锥的底面直径是80cm,母线长90cm,则它的侧面积是()A.360πcm2B.720πcm2C.1800πcm2D.3600πcm2 7.用半径为8的半圆围成一个圆锥的侧面,则圆锥的底面半径等于()A.4 B.6 C.16πD.8
8.小洋用一张半径为24cm的扇形纸板做一个如图
所示的圆锥形小丑帽子侧面(接缝忽略不计),如
果做成的圆锥形小丑帽子的底面半径为10cm,那么
这张扇形纸板的面积是()
A.120πc m2B.240πcm2
C.260πcm2D.480πcm2
9.圆柱底面半径为3cm,高为2cm,则它的体积为()
A.97πcm3B.18πcm3C.3πcm3D.18π2cm3
10.如图1所示,一只封闭的圆柱形水桶内盛了半桶水
(桶的厚度忽略不计),圆柱形水桶的底面直径与母线
长相等,现将该水桶水平放置后如图2所示,设图1、
图2中水所形成的几何体的表面积分别为S1、S2,则S1
与S2的大小关系是()
A.S1≤S2B.S1<S2C.S1>S2D.S1≥S2
二.填空题(共8小题)
11.已知扇形的圆心角为120°,弧长是40πcm,则扇形的半径是cm.12.已知圆锥的侧面展开图的扇形的弧长为12π,面积为60π,则圆锥的高是.
13.如图,正方形ABCD的边长为4,点O是AB的中点,
以点O为圆心,4为半径作⊙O,分别与AD、BC相交于点E、
F,则劣弧的长为
14.如图,以AD为直径的半圆O经过Rt△ABC的斜边A的两个
端点,交直角边AC于点
E.B、E是半圆弧的三等分点,若OA=2,则图中阴影部分的面
积为.
15.如图,在Rt△AOB中,∠AOB=90°,OA=2,OB=1,将Rt△
AOB绕点O顺时针旋转90°后得到Rt△FOE,将线段EF绕点E逆时针旋转90°后得到线段ED,分別以O、E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分的面积是.
16.如图,扇形的半径为6,圆心角θ为120°,用这
个扇形围成一个圆锥的侧面,所得圆锥的底面半径
为.
17.用半径为10,圆心角为54°的扇形纸片围成一个圆锥的侧面,
这个圆锥的底面圆半径等于.
18.图1是三个直立于水平面上的形状完全相同的由圆柱切割得到
的几何体(单位:cm).将它们拼成如图2的新几何体,则该新几何体的体积为cm3.(计算结果保留π)
三.解答题(共6小题)
19.如图,已知四边形ABCD内接于圆O,且∠A=105°,BD=CD
(1)求∠DBC的度数
(2)若⊙O的半径为3,求的长.
20.如图,AB是⊙O的直径,点C是圆上一点,连接CA、CB,过点O作弦的垂线,交B»C于点D,连接AD.
(1)求证:∠CAD=∠BAD;
(2)若⊙O的半径为1,∠B=50°,求的长.
21.如图,已知圆上两点A,B.
(1)用直尺和圆规求作圆心(保留作图痕迹,不写画法);
(2)若AB=6,此圆的半径为2,求弦AB与劣弧AB所组成的弓形面积.
22.如图,半圆的直径AB=40,C,D是半圆的三等分点,求弦AC,AD与围成的阴影部分的面积.
23.如图,将一个圆锥沿母线AB展开后得到一个扇形,
(1)若圆锥的高AO为2,底面半径为1,求扇形的面积;
(2)若扇形的弧长BC恰好等于圆锥母线AB和AC的长度之
和,求圆锥的母线AB与地面圆半径OB之比.
24.一个盖着瓶盖的瓶子里面装着一些水(如下图所示),
请你根据图中标明的数据,计算瓶子的容积.
参考答案
一.选择题)
1.B.
2.A.
3.D.
4.B.
5.B.
6.D.
7.A.
8.B.
9.B.
10.B.
二.填空题
11.60.
12.8.
13..
14.﹣.
15..
16.2.
17.1.5.
18.189π.
三.解答题
19.解:(1)∵四边形ABCD内接于圆O,∴∠DCB+∠BAD=180°,
∵∠A=105°,
∴∠C=180°﹣105°=75°,
∵BD=CD,
∴∠DBC=∠C=75°;
(2)连接BO、CO,
∵∠C=∠DBC=75°,
∴∠BDC=30°,
∴∠BOC=60°,
故的长l==π.
20.(1)证明:∵点O是圆心,OD⊥BC,
∴∠CAD=∠BAD;
(2)连接CO,
∵∠B=50°,
∴∠AOB=100°,
∴的长为:L=.
21.解:(1)如图所示,点O即为所求;
(2)如图,连接OA,OB,
∵OC⊥AB,
∴AC=BC,
而弦AB=6,
∴AD=3,
又∵⊙O的半径长为2,
∴OD==,
∴∠OAB=30°,
∴∠AOB=120°,
=S扇形OAB﹣S△AOB=﹣××6=4π﹣3.∴S
弓形AB
所以弓形AB的面积4π﹣3.
22.解:连接OC、OD、CD.
∵△COD和△CDA等底等高,
=S△ACD.
∴S
△COD
∵点C,D为半圆的三等分点,
∴∠COD=180°÷3=60°,
==π.
∴阴影部分的面积=S
扇形COD
23.解:(1)∵圆锥的高AO为2,底面半径为1,
∴圆锥的母线长为3,
∴圆锥的侧面积为πrl=π×1×3=3π;
(2)设圆锥的母线长为l,根据题意得:AB=AC=l,
所以2πr=2l
所以=π;
24.解:由已知条件知,第二个图上部空白部分的高为7﹣5=2cm,
从而水与空着的部分的体积比为4:2=2:1.
由第一个图知水的体积为10×4=40,所以总的容积为40÷2×(2+1)=60立方厘米.。
