北师大版七年级数学下册第二章 相交线与平行线练习(含答案)
北师大版七年级下册数学第二章相交线与平行线测试题(附答案)

北师大版七年级下册数学第二章相交线与平行线测试题(附答案)北师大版七年级下册数学第二章相交线与平行线测试题(附答案)一、单选题1.如图,已知直线l1∥l2,将一块直角三角板ABC按如图所示方式放置,若∠1=39°,则∠2等于()A。
39° B。
45° C。
50° D。
51°2.如图.直线a∥b,直线L与a、b分别交于点A,B,过点A作AC⊥b于点C.若∠1=50°,则∠2的度数为()A。
130° B。
50° C。
40° D。
25°3.如图,三点共线A、B、C,D、E、F三点共线,且AD∥CF,BE∥CD,下列结论错误的是()A。
∠ABE=∠XXX∠ABE=∠CDEC。
∠ABE=∠XXX∠ABE=∠BDF4.如图,平行线AB∥CD,EF⊥CD,垂足为G,图中∠AGE=()A。
90° B。
45° C。
30° D。
60°5.如图,互余的角有()A。
1个 B。
2个 C。
3个 D。
4个6.如图,AB∥CD,EF∥GH,则下列等式正确的是()A。
∠AEF=∠GHF B。
∠AEF=∠HGFC。
∠XXX∠GHF D。
∠XXX∠HGF7.已知同一平面内的三条直线AB,CD,EF,AB∥CD,CD∥EF,则下列结论错误的是()A。
AB∥EF B。
AB∥CD C。
EF∥CD D。
AB∥EF8.如果a<b,且a+b=5c,如果c<a,b<c,比a与b 的和的3倍少2,那么a与b的位置关系是()A。
a<b B。
a>b C。
a=b D.无法确定9.如图,已知AB∥CD,AE=2cm,EC=3cm,则图中互相平行的线段是()A。
AB//CD B。
AE//DC C。
BE//CD D。
AB//EC10.如图,AB∥CD,点E在直线AD上,且∠AEC=34°,则∠BED的大小为()A。
北师大版七年级数学下册第二章相交线与平行线综合训练试卷(含答案解析)

北师大版七年级数学下册第二章相交线与平行线综合训练考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、如图,AB∥EF,则∠A,∠C,∠D,∠E满足的数量关系是()A.∠A+∠C+∠D+∠E=360°B.∠A+∠D=∠C+∠EC.∠A﹣∠C+∠D+∠E=180°D.∠E﹣∠C+∠D﹣∠A=90°2、如图,O是直线AB上一点,OE平分∠AOB,∠COD=90°,则图中互余的角有()对.A.5 B.4 C.3 D.23、如图,∠1与∠2是同位角的是()① ② ③ ④A.①B.②C.③D.④4、如图,在直角三角形ABC中,∠BAC=90°,AD⊥BC于点D,则下列说法错误的是()A.线段AC的长度表示点C到AB的距离B.线段AD的长度表示点A到BC的距离C.线段CD的长度表示点C到AD的距离D.线段BD的长度表示点A到BD的距离5、若∠A与∠B互为补角,且∠A=28°,则∠B的度数是()A.152°B.28°C.52°D.90°6、下列语句中叙述正确的有()①画直线3AB cm;②连接点A与点B的线段,叫做A、B两点之间的距离;③等角的余角相等;④射线AB与射线BA是同一条射线.A.0个B.1个C.2个D.3个7、已知40A∠=︒,则A∠的余角的补角是()A.130︒B.120︒C.50︒D.60︒8、如图,将矩形纸条ABCD折叠,折痕为EF,折叠后点C,D分别落在点C′,D′处,D′E与BF交于点G.已知∠BGD′=26°,则∠α的度数是()A.77°B.64°C.26°D.87°9、如果两个角的两边两两互相平行,且一个角的12等于另一个角的13,则这两个角的度数分别是()A.48°,72°B.72°,108°C.48°,72°或72°,108°D.80°,120°10、若∠α=55°,则∠α的余角是()A.35°B.45°C.135°D.145°第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、如图,直线a b∥,三角尺(30°,60,90°)如图摆放,若∠1=52°,则∠2的度数为 _____.2、∠1与∠2的两边分别平行,且∠2的度数比∠1的度数的3倍少40°,那么∠2的度数为 ___.3、如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=40°,则∠AEC=_____度.4、图中∠AOB的余角大小是_____°(精确到1°).5、判断正误:(1)如果两个角有公共顶点且没有公共边,那么这两个角是对顶角()(2)如果两个角相等,那么这两个角是对顶角()(3)有一条公共边的两个角是邻补角()(4)如果两个角是邻补角,那么它们一定互补( )(5)有一条公共边和公共顶点,且互为补角的两个角是邻补角( )三、解答题(5小题,每小题10分,共计50分)1、已知AB ∥CD ,点E 在AB 上,点F 在DC 上,点G 为射线EF 上一点.(基础问题)如图1,试说明:∠AGD =∠A +∠D .(完成图中的填空部分).证明:过点G 作直线MN∥AB ,又∵AB∥CD ,∴MN∥CD ( )∵MN∥AB ,∴∠A =( )( )∵MN∥CD ,∴∠D = ( )∴∠AGD =∠AGM +∠DGM =∠A +∠D .(类比探究)如图2,当点G 在线段EF 延长线上时,直接写出∠AGD 、∠A 、∠D 三者之间的数量关系.(应用拓展)如图3,AH 平分∠GAB ,DH 交AH 于点H ,且∠GDH =2∠HDC ,∠HDC =22°,∠H =32°,直接写出∠DGA 的度数.2、已知:如图,AB ∥CD ∥EF ,点G 、H 、M 分别在AB 、CD 、EF 上.求证:GHM AGH EMH ∠∠∠=+.3、如图,①过点Q作QD⊥AB,垂足为点D;②过点P作PE⊥AB,垂足为点E;③过点Q作QF⊥AC,垂足为点F;④连P,Q两点;⑤P,Q两点间的距离是线段______的长度;⑥点Q到直线AB的距离是线段______的长度;⑦点Q到直线AC的距离是线段______的长度;⑧点P到直线AB的距离是线段______的长度.4、已知直线AB和CD交于点O,∠AOC=α,∠BOE=90°,OF平分∠AOD.(1)当α=30°时,则∠EOC=_________°;∠FOD=_________°.(2)当α=60°时,射线OE′从OE开始以12°/秒的速度绕点O逆时针转动,同时射线OF′从OF 开始以8°/秒的速度绕点O顺时针转动,当射线OE′转动一周时射线OF′也停止转动,求经过多少秒射线OE′与射线OF′第一次重合?(3)在(2)的条件下,射线OE′在转动一周的过程中,当∠E′OF′=90°时,请直接写出射线OE′转动的时间为_________秒.5、如图,直线DE上有一点O,过点O在直线DE上方作射线OC,∠COE比它的补角大100°,将一直角三角板AOB的直角点放在点O处,一条直角边OA在射线OD上,另一边OB在直线DE上方,将直角三角板绕点O按每秒10°的速度逆时针旋转一周.设旋转时间为t秒.(1)求∠COE的度数;(2)若射线OC的位置保持不变,在旋转过程中,是否存在某个时刻,使得∠BOC=∠BOE?若存在,请求出t的取值,若不存在,请说明理由;(3)若在三角板开始转动的同时,射线OC也绕O点以每秒10°的速度顺时针旋转一周.从旋转开始多长时间.射线OC平分∠BOE.直接写出t的值.(本题中的角均为大0°且小180°的角)-参考答案-一、单选题1、C【分析】如图,过点C作CG∥AB,过点D作DH∥EF,根据平行线的性质可得∠A=∠ACG,∠EDH=180°﹣∠E,根据AB∥EF可得CG∥DH,根据平行线的性质可得∠CDH=∠DCG,进而根据角的和差关系即可得答案.【详解】如图,过点C作CG∥AB,过点D作DH∥EF,∴∠A=∠ACG,∠EDH=180°﹣∠E,∵AB∥EF,∴CG∥DH,∴∠CDH=∠DCG,∴∠ACD=∠ACG+∠CDH=∠A+∠CDE﹣(180°﹣∠E),∴∠A﹣∠ACD+∠CDE+∠E=180°.故选:C.【点睛】本题考查了平行线的性质,两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;熟练掌握平行线的性质,正确作出辅助线是解题关键.2、B【分析】根据余角的定义找出互余的角即可得解.【详解】解:∵OE平分∠AOB,∴∠AOE=∠BOE=90°,∴互余的角有∠AOC和∠COE,∠AOC和∠BOD,∠COE和∠DOE,∠DOE和∠BOD共4对,故选:B.【点睛】本题考查了余角的定义,从图中确定余角时要注意按照一定的顺序,防止遗漏.3、B【分析】同位角就是两个角都在截线的同旁,又分别处在被截线的两条直线的同侧位置的角.【详解】根据同位角的定义可知②中的∠1与∠2是同位角;故选B.【点睛】本题主要考查了同位角的判断,准确分析判断是解题的关键.4、D【分析】根据直线外一点,到这条直线的垂线段的长度是这点到直线的距离判断即可.【详解】解:A. 线段AC的长度表示点C到AB的距离,说法正确,不符合题意;B. 线段AD的长度表示点A到BC的距离,说法正确,不符合题意;C. 线段CD的长度表示点C到AD的距离,说法正确,不符合题意;D. 线段BD的长度表示点B到AD的距离,原说法错误,符合题意;故选:D.【点睛】本题考查了点到直线的距离,解题关键是准确识图,正确进行判断.5、A【分析】根据两个角互为补角,它们的和为180°,即可解答.【详解】解:∵∠A与∠B互为补角,∴∠A+∠B=180°,∵∠A=28°,∴∠B=152°.故选:A【点睛】本题考查了补角,解决本题的关键是熟记补角的定义.6、B【分析】根据直线的性质判断①,根据两点间距离的定义判断②,根据余角的性质判断③,根据射线的表示方法判断④.【详解】解:因为直线是向两端无限延伸的,所以①不正确;因为连接两点间的线段的长度,叫做这两点间的距离,所以②不正确;③正确;因为射线AB和射线BA的端点不同,延伸方向也不同,所以④不正确.故选:B.【点睛】本题考查直线的性质,两点间的距离的定义(连接两点间的线段的长度,叫做这两点间的距离),余角的性质,射线的表示方法,熟练掌握这些知识点是解题关键.7、A【分析】根据余角和补角定义解答.解:A ∠的余角的补角是180(9040)130︒-︒-︒=︒,故选:A .【点睛】此题考查余角和补角的定义:和为90度的两个角互为余角,和为180度的两个角是互为补角.8、A【分析】本题首先根据∠BGD ′=26°,可以得出∠AEG =∠BGD ′=26°,由折叠可知∠α=∠FED ,由此即可求出∠α=77°.【详解】解:由图可知: AD∥BC∴∠AEG =∠BGD ′=26°,即:∠GED =154°,由折叠可知: ∠α=∠FED , ∴∠α=12GED ∠=77°故选:A .【点睛】本题主要考察的是根据平行得性质进行角度的转化.9、B【分析】根据题意可得这两个角互补,设其中一个角为x ,则另一个角为()180x ︒-,由两个角之间的数量关系列出一元一次方程,求解即可得.解:∵两个角的两边两两互相平行,∴这两个角可能相等或者两个角互补, ∵一个角的12等于另一个角的13,∴这两个角互补,设其中一个角为x ,则另一个角为()180x ︒-, 根据题意可得:()1118023x x =︒-,解得:72x =︒,180108x ︒-=︒,故选:B .【点睛】题目主要考查平行线的性质、角的数量关系、一元一次方程等,理解题意,列出方程是解题关键.10、A【分析】根据余角的定义即可得.【详解】由余角定义得∠α的余角为90°减去55°即可.解:由余角定义得∠α的余角等于90°﹣55°=35°.故选:A .【点睛】本题考查了余角的定义,熟记定义是解题关键.二、填空题【分析】如图,标注字母,过B 作,BC a ∥ 再证明,BC b ∥证明12,EBD从而可得答案.【详解】解:如图,标注字母,过B 作,BC a ∥1=,EBC,a b ∥,BC b ∥2=,DBC12,EBD∠1=52°,90,EBD ∠=︒2=905238.故答案为:38︒【点睛】本题考查的是平行公理的应用,平行线的性质,掌握“两直线平行,内错角相等”是解本题的关键.2、20°或125°或20°【分析】根据∠1,∠2的两边分别平行,所以∠1,∠2相等或互补列出方程求解则得到答案.【详解】解:∵∠1与∠2的两边分别平行,∴∠1,∠2相等或互补,①当∠1=∠2时,∵∠2=3∠1-40°,∴∠2=3∠2-40°,解得∠2=20°;②当∠1+∠2=180°时,∵∠2=3∠1-40°,∴∠1+3∠1-40°=180°,解得∠1=55°,∴∠2=180°-∠1=125°;故答案为:20°或125°.【点睛】本题考查了平行线的性质的运用,关键是注意:同一平面内两边分别平行的两角相等或互补.3、70【分析】根据平行线性质求出∠CAB的度数,根据角平分线求出∠EAB的度数,再根据平行线性质求出∠AEC的度数即可.【详解】解:∵AB//CD,∴∠C+∠CAB=180°,∵∠C=40°,∴∠CAB=180°-40°=140°,∵AE平分∠CAB,∴∠EAB=70°,∵AB//CD,∴∠AEC=∠EAB=70°,故答案为70.【点睛】本题考查角平分线的定义和平行线的性质,解题的关键是熟练掌握两条平行线被第三条直线所截,同旁内角互补.4、63【分析】根据余角的定义:如果两个角的度数和为90度,那么这两个角互为余角,进行求解即可.【详解】解:由量角器上的度数可知,∠AOB=27°,∴∠AOB的余角的度数=90°-∠AOB=63°,故答案为:63.【点睛】本题主要考查了量角器测量角的度数和求一个角的余角,熟知余角的定义是解题的关键.5、(1)×;(2)×;(3)×;(4)√;(5)×【分析】根据对顶角与邻补角的定义与性质分析判断即可求解.【详解】(1)如果两个角有公共顶点且没有公共边,那么这两个角是对顶角,错误;(2)如果两个角相等,那么这两个角不一定是对顶角,错误;(3)有一条公共边的两个角不一定是邻补角,错误;(4)如果两个角是邻补角,那么它们一定互补,正确;(5)有一条公共边和公共顶点,且互为补角的两个角不一定是邻补角,错误;故答案为:(1)×;(2)×;(3)×;(4)√;(5)×.【点睛】本题主要考查了对顶角的与邻补角的性质,是基础题,熟记概念与性质是解题的关键,如果一个角的两边分别是另一个角两边的反向延长线,且这两个角有公共顶点,那么这两个角是对顶角,两个角有一条公共边,它们的另一条边互为反向延长线,具有这种关系的两个角,叫做邻补角.三、解答题1、基础问题:平行于同一条直线的两条直线平行;∠AGM;两直线平行,内错角相等;∠DGM,两直线平行,内错角相等;类比探究:∠AGD=∠A-∠D;应用拓展:42°.【分析】基础问题:由MN∥AB,可得∠A=∠AGM,由MN∥CD,可得∠D=∠DGM,则∠AGD=∠AGM+∠DGM=∠A +∠D;类比探究:如图所示,过点G作直线MN∥AB,同理可得∠A=∠AGM,∠D=∠DGM,则∠AGD=∠AGM-∠DGM=∠A-∠D.应用拓展:如图所示,过点G作直线MN∥AB,过点H作直线PQ∥AB,由MN∥AB,PQ∥AB,得到∠BAG =∠AGM,∠BAH=∠AHP,由MN∥CD,PQ∥CD,得到∠CDG=∠DGM,∠CDH=∠DHP,再由∠GDH=2∠HDC,∠HDC=22°,∠AHD=32°,可得∠GDH=44°,∠DHP=22°,则∠CDG=66°,∠AHP=54°,∠DGM=66°,∠BAH=54°,再由AH平分∠BAG,即可得到∠AGM=108°,则∠AGD=∠AGM-∠DGM=42°.【详解】解:基础问题:过点G作直线MN∥AB,又∵AB∥CD,∴MN∥CD(平行于同一条直线的两条直线平行),∵MN∥AB,∴∠A=∠AGM(两直线平行,内错角相等),∵MN∥CD,∴∠D=∠DGM(两直线平行,内错角相等),∴∠AGD=∠AGM+∠DGM=∠A+∠D.故答案为:平行于同一条直线的两条直线平行;∠AGM;两直线平行,内错角相等;∠DGM,两直线平行,内错角相等;类比探究:如图所示,过点G作直线MN∥AB,又∵AB∥CD,∴MN∥CD,∵MN∥AB,∴∠A=∠AGM,∵MN∥CD,∴∠D=∠DGM,∴∠AGD=∠AGM-∠DGM=∠A-∠D.应用拓展:如图所示,过点G作直线MN∥AB,过点H作直线PQ∥AB,又∵AB∥CD,∴MN∥CD,PQ∥CD∵MN∥AB,PQ∥AB,∴∠BAG=∠AGM,∠BAH=∠AHP,∵MN∥CD,PQ∥CD,∴∠CDG=∠DGM,∠CDH=∠DHP,∵∠GDH=2∠HDC,∠HDC=22°,∠AHD=32°,∴∠GDH=44°,∠DHP=22°,∴∠CDG=66°,∠AHP=54°,∴∠DGM=66°,∠BAH=54°,∵AH平分∠BAG,∴∠BAG=2∠BAH=108°,∴∠AGM=108°,∴∠AGD=∠AGM-∠DGM=42°.【点睛】本题主要考查了平行线的性质,平行公理,解题的关键在于能够熟练掌握平行线的性质.2、见解析【分析】由AB ∥CD ∥EF 可得,1AGH ∠=∠,2EMH ∠=∠,即可证明.【详解】证明:∵AB ∥CD (已知)∴1AGH ∠=∠(两直线平行,内错角相等)又 ∵CD ∥EF (已知)∴2EMH ∠=∠,(两直线平行,内错角相等)∵12GHM ∠∠∠=+(已知)∴GHM AGH EMH ∠∠∠=+(等式性质)【点睛】本题主要考查平行线的性质,准确观察图形,推出角之间的关系是解题关键.3、①②③④作图见解析;⑤PQ;⑥QD;⑦QF;⑧PE【分析】由题意①②③④根据题目要求即可作出图示,⑤⑥⑦⑧根据两点之间距离及点到直线的距离的定义即可得出答案.【详解】①②③④作图如图所示;⑤根据两点之间距离即可得出P,Q两点间的距离是线段PQ的长度;⑥根据点到直线的距离可得出点Q到直线AB的距离是线段QD的长度;⑦根据点到直线的距离可得出点Q到直线AC的距离是线段QF的长度;⑧根据点到直线的距离可得出点P到直线AB的距离是线段PE的长度.【点睛】本题主要考查基本作图和两点之间距离及点到直线的距离,熟练掌握相关概念与作图方法是解题的关键.4、(1)60,75;(2)152秒;(3)3或12或21或30【分析】(1)根据题意利用互余和互补的定义可得:∠EOC与∠FOD的度数.(2)由题意先根据60α=︒,得出∠EOF=150°,则射线OE'、OF'第一次重合时,其OE'运动的度数+OF '运动的度数=150,列式解出即可;(3)根据题意分两种情况在直线OE 的左边和右边,进而根据其夹角列4个方程可得时间.【详解】解:(1)∵∠BOE =90°,∴∠AOE =90°,∵∠AOC=α=30°,∴∠EOC =90°-30°=60°,∠AOD =180°-30°=150°,∵OF 平分∠AOD ,∴∠FOD =12∠AOD =12×150°=75°;故答案为:60,75;(2)当60α=︒,9060150EOF ∠=︒+︒=︒.设当射线OE '与射线OF '重合时至少需要t 秒,可得128150t t +=,解得:152t =; 答:当射线OE '与射线OF '重合时至少需要152秒; (3)设射线OE '转动的时间为t 秒,由题意得:12815090t t +=-或12815090t t +=+或81236015090t t +=+-或12836015090t t +=++, 解得:3t =或12或21或30.答:射线OE '转动的时间为3或12或21或30秒.【点睛】本题考查对顶角相等,邻补角互补的定义,角平分线的定义,角的计算,第三问有难度,熟记相关性质是解题的关键,注意要分情况讨论.5、(1)140゜(2)存在,t=2秒或20秒;(3)533秒【分析】(1)设∠COE=x度,则其补角为(180−x)度,根据∠COE比它的补角大100°列方程即可求得结果;(2)存在两种情况:当OC在直线DE上方时;当OC在直线DE下方时;就这两种情况考虑即可;(3)画出图形,结合图形表示出∠COE与∠COB,根据角平分线的性质建立方程即可求得t值.【详解】(1)设∠COE=x度,则其补角为(180−x)度,由题意得:x−(180−x)=100解得:x=140即∠COE=140゜(2)存在当OC在直线DE上方时,此时OB平分∠BOC∵∠COE=140゜∴1702BOC COE∠=∠=︒当OB没有旋转时,∠BOC=50゜所以OB旋转了70゜−50゜=20゜则旋转的时间为:t=20÷10=2(秒)当OC在直线DE下方时,如图由图知:∠BOE+∠BOC+∠COE=360゜即:2∠BOE+∠COE=360゜∵OB旋转了10t度∴∠BOE=(10t−90)度∴2(10t−90)+140=360解得:t=20综上所述,当t=2秒或20秒时,∠BOC=∠BOE(3)OB、OC同时旋转10t度如图所示,∠COE=(180゜+40゜)−(10t)゜=(220−10t)゜∵2×(10t)゜−∠COB+50゜=360゜∴∠COB=2× (10t)゜−310゜∵∠COB=∠COE∴2× 10t−310=220-10t解得:533 t即当t的值为533秒时,满足条件.【点睛】本题考查了角平分线的性质,角的和差运算,补角的概念,解一元一次方程等知识,注意数形结合及分类讨论.。
北师大版七年级数学下册第二章《相交线与平行线》单元同步练习题(含答案)
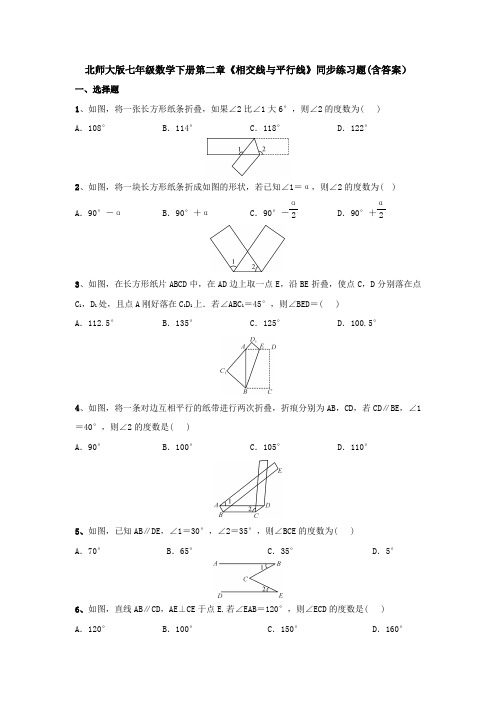
北师大版七年级数学下册第二章《相交线与平行线》同步练习题(含答案)一、选择题1、如图,将一张长方形纸条折叠,如果∠2比∠1大6°,则∠2的度数为( ) A .108°B .114°C .118°D .122°2、如图,将一块长方形纸条折成如图的形状,若已知∠1=α,则∠2的度数为( ) A .90°-αB .90°+αC .90°-α2D .90°+α23、如图,在长方形纸片ABCD 中,在AD 边上取一点E ,沿BE 折叠,使点C ,D 分别落在点C 1,D 1处,且点A 刚好落在C 1D 1上.若∠ABC 1=45°,则∠BED =( ) A .112.5°B .135°C .125°D .100.5°4、如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB ,CD ,若CD ∥BE ,∠1=40°,则∠2的度数是( ) A .90°B .100°C .105°D .110°5、如图,已知AB ∥DE ,∠1=30°,∠2=35°,则∠BCE 的度数为( ) A .70°B .65°C .35°D .5°6、如图,直线AB ∥CD ,AE ⊥CE 于点E.若∠EAB =120°,则∠ECD 的度数是( ) A .120°B .100°C .150°D .160°二、填空题7、如图,将长方形ABCD沿EF折叠,点D落在AB边上的H点处,点C落在点G处.若∠AEH =30°,则∠EFC等于______.8、如图a是长方形纸带,∠DEF=15°,将纸带沿EF折叠成图b,则∠AEG=______.度,再沿BF折叠成图c.则图中的∠CFE=______度.9、已知:如图,AB∥EF,∠ABC=75°,∠CDF=135°,则∠BCD=______度.10、如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=______.11、如图,AB∥CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD=______.12、如图是我们生活中经常接触的小刀,刀片的外壳是一个直角梯形,刀片上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2=______.三、解答题13、如图,在Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°.点D 在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,当旋转了多少秒时,边CD恰好与边AB平行?14、问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.(1)按小明的思路,易求得∠APC的度数为______度;(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P 在B,D两点之间运动时,问∠APC与α,β之间有何数量关系?请说明理由;(3)在(2)的条件下,如果点P在B,D两点外侧运动时(点P与点O,B,D三点不重合),请直接写出∠APC与α,β之间的数量关系.15、已知AM∥CN,点B为平面内一点,AB⊥BC于点B.(1)如图1,直接写出∠A和∠C之间的数量关系;(2)如图2,过点B作BD⊥AM于点D,∠BAD与∠C有何数量关系,并说明理由;(3)如图3,在(2)问的条件下,点E,F在DM上,连接BE,BF,CF,BF平分∠DBC,BE平分∠ABD.若∠FCB+∠NCF=180°,∠BFC=5∠DBE,求∠EBC的度数.参考答案一、选择题1、如图,将一张长方形纸条折叠,如果∠2比∠1大6°,则∠2的度数为(D) A .108°B .114°C .118°D .122°2、如图,将一块长方形纸条折成如图的形状,若已知∠1=α,则∠2的度数为(C) A .90°-αB .90°+αC .90°-α2D .90°+α23、如图,在长方形纸片ABCD 中,在AD 边上取一点E ,沿BE 折叠,使点C ,D 分别落在点C 1,D 1处,且点A 刚好落在C 1D 1上.若∠ABC 1=45°,则∠BED =(A) A .112.5°B .135°C .125°D .100.5°4、如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB ,CD ,若CD ∥BE ,∠1=40°,则∠2的度数是(B) A .90°B .100°C .105°D .110°5、如图,已知AB ∥DE ,∠1=30°,∠2=35°,则∠BCE 的度数为(B) A .70°B .65°C .35°D .5°6、如图,直线AB ∥CD ,AE ⊥CE 于点E.若∠EAB =120°,则∠ECD 的度数是(C) A .120°B .100°C .150°D .160°二、填空题7、如图,将长方形ABCD沿EF折叠,点D落在AB边上的H点处,点C落在点G处.若∠AEH =30°,则∠EFC等于105°.8、如图a是长方形纸带,∠DEF=15°,将纸带沿EF折叠成图b,则∠AEG=150度,再沿BF折叠成图c.则图中的∠CFE=135度.9、已知:如图,AB∥EF,∠ABC=75°,∠CDF=135°,则∠BCD=30度.10、如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=140°.11、如图,AB∥CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD=125°.12、如图是我们生活中经常接触的小刀,刀片的外壳是一个直角梯形,刀片上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2=90°.三、解答题13、如图,在Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°.点D 在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,当旋转了多少秒时,边CD恰好与边AB平行?解:分两种情况:当两三角形在点O的同侧时,如图1,设CD与OB相交于点E.∵AB∥CD,∴∠CEO=∠B=40°.∵∠C=60°,∴∠OOE=180°-60°-40°-80°.∴∠DOE=∠COD-∠COE=10°.∴旋转角∠AOD=∠AOB+∠DOE=90°+10°=100°.∵每秒旋转10°,∴旋转的时间为100÷10=10(秒).当两三角形在点O的异侧时,如图2,延长BO与CD相交于点E.∵AB∥CD,∴∠CEO=∠B=40°.∵∠C=60°,∴∠COE=180°-60°-40°=80°.∴旋转角为360°-∠COE=360°-80°=280°.∵每秒旋转10°,∴旋转的时间为280÷10=28(秒).综上所述,当旋转了10秒或28秒时,边CD恰好与边AB平行.14、问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.(1)按小明的思路,易求得∠APC的度数为110度;(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P 在B,D两点之间运动时,问∠APC与α,β之间有何数量关系?请说明理由;(3)在(2)的条件下,如果点P在B,D两点外侧运动时(点P与点O,B,D三点不重合),请直接写出∠APC与α,β之间的数量关系.图1 图2解:∠APC=α+β.理由:过点P作PE∥AB交AC于点E,∵AB∥CD,∴AB∥PE∥CD.∴α=∠APE,β=∠CPE.∴∠APC=∠APE+∠CPE=α+β.(3)如图3,当P在BD延长线上时,∠CPA=α-β;如图4,当P在DB延长线上时,∠CPA=β-α.图3 图415、已知AM∥CN,点B为平面内一点,AB⊥BC于点B.(1)如图1,直接写出∠A和∠C之间的数量关系;(2)如图2,过点B作BD⊥AM于点D,∠BAD与∠C有何数量关系,并说明理由;(3)如图3,在(2)问的条件下,点E,F在DM上,连接BE,BF,CF,BF平分∠DBC,BE平分∠ABD.若∠FCB+∠NCF=180°,∠BFC=5∠DBE,求∠EBC的度数.解:(1)∠A+∠C=90°(2)过点B作BG∥DM,∵BD⊥AM,∴∠ABD+∠BAD=90°,DB⊥BG,即∠ABD+∠ABG=90°.又∵AB⊥BC,∴∠CBG+∠ABG=90°.∴∠ABD=∠CBG.∵AM∥CN,BG∥AM,∴CN∥BG.∴∠C=∠CBG.∴∠ABD=∠C.∴∠C+∠BAD=90°.(3)过点B作BG∥DM,∵BF平分∠DBC,BE平分∠ABD,∴∠DBF=∠CBF,∠DBE=∠ABE,由(2)可得∠ABD=∠CBG.∴∠ABF=∠GBF.设∠DBE=α,∠ABF=β,则∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC =5∠DBE=5α,∴∠AFC=5α+β.∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,∴∠FCB=∠AFC=5α+β.在△BCF中,由∠CBF+∠BFC+∠BCF=180°,可得(2α+β)+5α+(5α+β)=180°.①由AB⊥BC,可得β+β+2α=90°.②由①②联立方程组,解得α=9°.∴∠ABE=9°.∴∠EBC=∠ABE+∠ABC=9°+90°=99°.。
北师大版七年级下册第二章-平行线与相交线同步练习题(含答案)

第二章 平行线与相交线同步练习题2.1两条直线的位置关系一、选择题(共18小题) 1 .下列说法正确的是( )A .两条不相交的线段叫平行线B .过一点有且只有一条直线与已知直线平行 C. 线段与直线不平行就相交D. 与同一条直线相交的两条直线有可能平行2 .如果线段AB 与线段CD 没有交点,则( A .线段AB 与线段CD 一定平行 C .线段AB 与线段CD 可能平行3.如图,在方格纸上给出的线中,平行的有( )4.已知Z1 + Z 2=90° Z3+)B .线段AB 与线段CD 一定不平行 D .以上说法都不正确0=180 °下列说法正确的是()A. Z1是余角C. Z1是的余角 D . Z3和也都是补角5. 下列说法错误的是()题(含答案)6. 下列说法正确的是()A.两个互补的角中必有一个是钝角B . 一个锐角的余角一定小于这个角的补角C. 一个角的补角一定比这个角大D. 一个角的余角一定比这个角小7. 如果Z aZ =90°,而/与/互余,那么/o与/Y勺关系为()A.互余 B .互补C.相等9.下列说法正确的是()A.如果两个角相等,那么这两个角是对顶角B .有公共顶点并且相等的两个角是对顶角C.如果两个角不相等,那么这两个角不是对顶角D .以上说法都不对A •两个互余的角相加等于90°C.互为补角的两个角不可能都是钝角B .钝角的平分线把钝角分为两个锐角D .两个锐角的和必定是直角或钝角D .不能确定A. 60 ° B . 45 C. 30° D . 90°8—个角的余角是它的补角的11.(2007?济南)已知:如图,AB J CD ,垂足为O,EF 为过点O 的一条直线,则J 与的关系一定成立的是 ( )12. (2003?杭州)如图所示立方体中,过棱 BB 1和平面CD 1垂直的平面有(C . 3个15. 如图,已知 0A J m , OB J m ,所以OA 与OB 重合,其理由是□EmC .互补D .互为对顶角ZPQR 等于 138° SQ J QR , QTZPQ .贝U zSQT 等于(B . 64 °C . 48°D . 24°14. (2005?哈尔滨)过一个钝角的顶点作这个角两边的垂线,若这两条垂线的夹角为 40°则此钝角为( 140° B . 160° C . 120° D . 110°A •相等A . 1个B •过一点只能作一条垂线C. 经过一点只有一条直线垂直于已知直线D. 垂线段最短16. 如图,ZBAC=90 ° AD ZBC,则下列的结论中正确的个数是()①点B到AC的垂线段是线段AB ;②线段AC是点C到AB的垂线段;③线段AD是点D到BC的垂线段;④线段BD是点B到AD的垂线段.C. 3个17. 如图,把水渠中的水引到水池C,先过C点向渠岸AB画垂线,垂足为D,再沿垂线CD开沟才能使沟最短,A.垂线最短B .过一点确定一条直线与已知直线垂盲C. 垂线段最短D. 以上说法都不对18 .已知线段AB=10cm,点A , B至煩线I的距离分别为6cm, 4cm .符合条件的直线I有()C. 3条、填空题(共12小题)19.已知Z1=43°7',则Z1的余角是_____________ ,补角是20.若一个角的余角是30°则这个角的补角为_________________21•两个角互余或互补,与它们的位置 ________________ (填有”或无”)关.22. 一个角的补角是它的余角的4倍,则这个角等于_______________ 度.23•若/o和/匝为余角,并且/a匕/大20° /和/互为补角,贝y Z = _______________________ , Z= _____________ ,那么,/ 丫 / = ______________ .24.如图,已知ZCOE= ZBOD= zAOC=90 °则图中与ZBOC相等的角为_________________ ,与ZBOC互补的角为—___________ ,与ZBOC互余的角为______________ .O,左OC=6O ° OA平分zEOC,那么ZBOD的度数是26. (2006?宁波)如图,直线azb, Z=50° 则/2= _ _ 度.27.如图,点 A ,B ,C 在一条直线上,已知 21=53° Z2=37°贝U CD 与CE 的位置关系是 ____________________28 .老师在黑板上随便画了两条直线 AB , CD 相交于点0,还作/BOC 的平分线0E 和CD 的垂线OF (如图),量得zDOE 被一直线分成2: 3两部分,小颖同学马上就知道 2AOF 等于 __ .30. 如图,已知 BA zBD , CB 2CD , AD=8 , BC=6,则线段 BD长的取值范围是29 .如图,2ADB=90 ° 贝^ AD ____________ B D ;用 匕”连接AB , AC , AD ,结果是三、解答题(共9小题)31. 已知一个角的补角加上 10。
北师大版七年级数学下《相交线与平行线》附答案

北师大版七年级数学下册第二章——余角、补角、邻补角和相交线一.选择题(共9小题)1.(2012•孝感)已知∠α是锐角,∠α与∠β互补,∠α与∠γ互余,则∠β﹣∠γ的值等于()A.45°B.60°C.90°D.180°2.(2012•北京)如图,直线AB,CD交于点O,射线OM平分∠AOC,若∠BOD=76°,则∠BOM等于()A.38°B.104°C.142°D.144°3.(2011•柳州)如图,在所标识的角中,互为对顶角的两个角是()A.∠2和∠3 B.∠1和∠3 C.∠1和∠4 D.∠1和∠24.(2008•资阳)如图,CA⊥BE于A,AD⊥BF于D,下列说法正确的是()A.α的余角只有∠B B.α的邻补角是∠DAC C.∠ACF是α的余角D.α与∠ACF互补5.(2008•湘西州)如图,直线AB,CD相交于O点,若∠1=30°,则∠2,∠3的度数分别为()A.120°,60°B.130°,50°C.140°,40°D.150°,30°6.(2008•西宁)如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③(∠α+∠β);④(∠α﹣∠β).正确的有()A.4个B.3个C.2个D.1个7.(2007•襄阳)如图,直线AB、CD相交于点O,OE⊥AB于O,∠COE=55°,则∠BOD的度数是()A.40°B.45°C.30°D.35°8.(2007•济南)已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是()A.相等B.互余C.互补D.互为对顶角9.(2006•西岗区)如图,直线AB,CD相交于点O,OM⊥AB,若∠COB=135°,则∠MOD等于()A.45°B.35°C.25°D.15°二.填空题(共16小题)10.(2012•泰州)已知∠α的补角是130°,则∠α=_________度.11.(2012•厦门)已知∠A=40°,则∠A的余角的度数是_________.12.(2011•梧州)如图,直线a、b相交,∠1=65°,则∠2的度数是_________°.13.(2011•芜湖)一个角的补角是36°5′,这个角是_________.14.(2011•江西)一块直角三角板放在两平行直线上,如图所示,∠1+∠2=_________度.15.(2010•娄底)如图,直线AB、CD相交于点O.OE平分∠AOD,若∠BOD=100°,则∠AOE=_________度.16.(2009•资阳)若两个互补的角的度数之比为1:2,则这两个角中较小角的度数是_________度.17.(2009•营口)如图,将直尺与三角尺叠放在一起,在图中标记的所有角中,与∠2互余的角是_________.18.(2008•十堰)如图,直线AB、CD相交于点O,OE⊥AB,垂足为O,如果∠EOD=42°,则∠AOC= _________度.19.(2006•海南)如图,△ABC中,∠ACB=90°,CD⊥AB于D,则图中所有与∠B互余的角_________.20.(2004•南平)如图,将两块三角板的直角顶点重合后重叠在一起,如果∠1=40°,那么∠2=_________度.21.(2002•岳阳)如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=76°,则∠BOD=_________.22.若∠1+∠2=90°,∠3+∠2=90°,∠1=40°,则∠3=_________°,依据是_________.23.已知∠1与∠2互补,∠1与∠3互余,若∠2=130°,则∠3=_________.24.一个角的余角比它的补角的多1°,则这个角的度数为_________度.25.已知∠1与∠2互补,∠1又与∠3互补,若∠2=150°,则∠3=_________.三.解答题(共5小题)26.如图,点A、O、E在同一直线上,∠AOB=40°,∠COD=28°,OD平分∠COE.(1)求∠COB的度数(2)求∠AOD的度数.27.如图所示,直线AB、CD相交O,OE⊥AB于O,且∠DOE=3∠COE,求∠AOD的度数.28.如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.29.一个角的余角比它的补角的还少20°,求这个角.30.如图,∠AOC和∠BOD都是直角,如果∠AOB=150°,求∠COD的度数.参考答案与试题解析一.选择题(共9小题)1.(2012•孝感)已知∠α是锐角,∠α与∠β互补,∠α与∠γ互余,则∠β﹣∠γ的值等于()A.45°B.60°C.90°D.180°考点:余角和补角.专题:计算题.分析:根据互余两角之和为90°,互补两角之和为180°,结合题意即可得出答案.解答:解:由题意得,∠α+∠β=180°,∠α+∠γ=90°,两式相减可得:∠β﹣∠γ=90°.故选C.点评:此题考查了余角和补角的知识,属于基础题,掌握互余两角之和为90°,互补两角之和为180°,是解答本题的关键.2.(2012•北京)如图,直线AB,CD交于点O,射线OM平分∠AOC,若∠BOD=76°,则∠BOM等于()A.38°B.104°C.142°D.144°考点:对顶角、邻补角;角平分线的定义.专题:常规题型.分析:根据对顶角相等求出∠AOC的度数,再根据角平分线的定义求出∠AOM的度数,然后根据平角等于180°列式计算即可得解.解答:解:∵∠BOD=76°,∴∠AOC=∠BOD=76°,∵射线OM平分∠AOC,∴∠AOM=∠AOC=×76°=38°,∴∠BOM=180°﹣∠AOM=180°﹣38°=142°.故选C.点评:本题考查了对顶角相等的性质,角平分线的定义,准确识图是解题的关键.3.(2011•柳州)如图,在所标识的角中,互为对顶角的两个角是()A.∠2和∠3 B.∠1和∠3 C.∠1和∠4 D.∠1和∠2考点:对顶角、邻补角.分析:两条直线相交后,所得的只有一个公共顶点,且两个角的两边互为反向延长线,这样的两个角叫做互为对顶角.解答:解:根据同位角、同旁内角、邻补角、对顶角的定义进行判断,A、∠2和∠3是对顶角,正确;B、∠1和∠3是同旁内角,错误;C、∠1和∠4是同位角,错误;D、∠1和∠2的邻补角是内错角,错误.故选A.点评:解答此类题确定三线八角是关键,可直接从截线入手.对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义.4.(2008•资阳)如图,CA⊥BE于A,AD⊥BF于D,下列说法正确的是()A.α的余角只有∠B B.α的邻补角是∠DAC C.∠ACF是α的余角D.α与∠ACF互补考点:垂线;对顶角、邻补角.分析:根据余角、补角、邻补角的定义来判断.解答:解:∵∠α+∠DAC=90°,∴选项A错误;α的邻补角为∠DAE,∴选项B错误;由同角的余角相等知∠α=∠ACD,而∠ACF+∠ACD=180°,∴∠ACF是α的补角,不是余角.∴选项C错误,选项D正确.故选D.点评:主要考查了余角和补角的概念以及运用.互为余角的两角的和为90°,互为补角的两角之和为180°.解此题的关键是把握余角、补角、邻补角的定义,同时应注意认真审图,准确找出两个角之间的数量关系,从而判断出两角之间的关系.5.(2008•湘西州)如图,直线AB,CD相交于O点,若∠1=30°,则∠2,∠3的度数分别为()A.120°,60°B.130°,50°C.140°,40°D.150°,30°考点:对顶角、邻补角.专题:计算题.分析:首先判断所求角与∠1的关系,然后利用对顶角、邻补角的性质求解.解答:解:∵∠1与∠3是对顶角,∴∠3=∠1=30°,∵∠1与∠2是邻补角,即∠1+∠2=180°,∴∠2=180°﹣30°=150°.故选D.点评:熟练掌握邻补角及对顶角的性质.6.(2008•西宁)如果∠α和∠β互补,且∠α>∠β,则下列表示∠β的余角的式子中:①90°﹣∠β;②∠α﹣90°;③(∠α+∠β);④(∠α﹣∠β).正确的有()A.4个B.3个C.2个D.1个考点:余角和补角.分析:根据角的性质,互补两角之和为180°,互余两角之和为90,可将,①②③④中的式子化为含有∠α+∠β的式子,再将∠α+∠β=180°代入即可解出此题.解答:解:∵∠α和∠β互补,∴∠α+∠β=180度.因为90°﹣∠β+∠β=90°,所以①正确;又∠α﹣90°+∠β=∠α+∠β﹣90°=180°﹣90°=90°,②也正确;(∠α+∠β)+∠β=×180°+∠β=90°+∠β≠90°,所以③错误;(∠α﹣∠β)+∠β=(∠α+∠β)=×180°﹣90°=90°,所以④正确.综上可知,①②④均正确.故选B.点评:本题考查了角之间互补与互余的关系,互补两角之和为180°,互余两角之和为90度.7.(2007•襄阳)如图,直线AB、CD相交于点O,OE⊥AB于O,∠COE=55°,则∠BOD的度数是()A.40°B.45°C.30°D.35°考点:垂线;对顶角、邻补角.专题:计算题.分析:由已知OE⊥AB,∠COE=55°,利用互余关系求∠AOC,再利用对顶角相等求∠BOD的度数.解答:解:∵OE⊥AB,∠COE=55°,∴∠AOC=90°﹣∠COE=35°;∵∠BOD与∠AOC是对顶角,∴∠BOD=∠AOC=35°.故选D.点评:此题主要考查了余角和对顶角的关系.8.(2007•济南)已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是()A.相等B.互余C.互补D.互为对顶角考点:垂线;余角和补角;对顶角、邻补角.分析:根据图形可看出,∠2的对顶角∠COE与∠1互余,那么∠1与∠2就互余.解答:解:图中,∠2=∠COE(对顶角相等),又∵AB⊥CD,∴∠1+∠COE=90°,∴∠1+∠2=90°,∴两角互余.故选B.点评:本题考查了余角和垂线的定义以及对顶角相等的性质.9.(2006•西岗区)如图,直线AB,CD相交于点O,OM⊥AB,若∠COB=135°,则∠MOD等于()A.45°B.35°C.25°D.15°考点:垂线;对顶角、邻补角.分析:已知∠COB与∠BOD是邻补角,且∠COB=135°,可求∠BOD,再利用互余关系求∠MOD.解答:解:∵∠COB与∠BOD是邻补角,∠COB=135°,∴∠BOD=180°﹣∠COB=180﹣135°=45°.又∵OM⊥AB,∴∠MOD=90°﹣∠BOD=45°.故选A.点评:本题先根据平角的定义求出∠BOD的度数,再根据余角的定义求出∠MOD的度数.二.填空题(共16小题)10.(2012•泰州)已知∠α的补角是130°,则∠α=50度.考点:余角和补角.分析:根据补角的和等于180°列式计算即可得解.解答:解:∵∠α的补角是130°,∴∠α=180°﹣130°=50°.故答案为:50.点评:本题考查了余角与补角的定义,熟记补角的和等于180°是解题的关键.11.(2012•厦门)已知∠A=40°,则∠A的余角的度数是50°.考点:余角和补角.分析:设∠A的余角是∠B,则∠A+∠B=90°,再根据∠A=40°求出∠B的度数即可.解答:解:设∠A的余角是∠B,则∠A+∠B=90°,∵∠A=40°,∴∠B=90°﹣40°=50°.故答案为:50°.点评:本题考查的是余角的定义,即如果两个角的和等于90°(直角),就说这两个角互为余角.即其中一个角是另一个角的余角.12.(2011•梧州)如图,直线a、b相交,∠1=65°,则∠2的度数是65°.考点:对顶角、邻补角.分析:根据对顶角相等解答即可.解答:解:∵∠1=65°,∴∠2=∠1=65°.故答案为:65.点评:本题主要考查了对顶角相等的性质,熟记性质并认准对顶角是解题的关键,是基础题,比较简单.13.(2011•芜湖)一个角的补角是36°5′,这个角是143°55′.考点:余角和补角;度分秒的换算.专题:计算题.分析:根据补角的定义,用180°减36°5′即可得到该角.解答:解:180°﹣36°5′=143°55′.故答案为:143°55′.点评:此题考查了补角的定义,属于基础题,较简单,主要记住互为补角的两个角的和为180度.14.(2011•江西)一块直角三角板放在两平行直线上,如图所示,∠1+∠2=90度.考点:对顶角、邻补角;余角和补角.专题:计算题.分析:根据对顶角相等得到∠1=∠3,∠2=∠4,而三角形尺为直尺,即可得到∠1+∠2=90°.解答:解:如图,∵∠1=∠3,∠2=∠4,而∠3+∠4=90°,∴∠1+∠2=90°.故答案为:90.点评:本题考查了对顶角的性质:对顶角相等.15.(2010•娄底)如图,直线AB、CD相交于点O.OE平分∠AOD,若∠BOD=100°,则∠AOE=40度.考点:对顶角、邻补角;角平分线的定义.专题:计算题.分析:首先利用邻补角互补求出∠AOD,再利用角平分线的定义计算.解答:解:∵∠AOD与∠BOD互为邻补角,∠BOD=100°,∴∠AOD=180°﹣∠BOD=80°,又OE平分∠AOD,∴∠AOE=40°.点评:本题考查了利用邻补角和角平分线的定义,在相交线中角的度数的求解方法.16.(2009•资阳)若两个互补的角的度数之比为1:2,则这两个角中较小角的度数是60度.考点:余角和补角.专题:计算题.分析:根据补角定义列方程解答.解答:解:设这两个角的度数为x°、2x°.列方程得:x°+2x°=180°,解得x=60°.即较小的角的度数是60°.点评:此题比较容易,考查了互补的概念,是送分题.17.(2009•营口)如图,将直尺与三角尺叠放在一起,在图中标记的所有角中,与∠2互余的角是∠4,∠5,∠6.考点:余角和补角.分析:本题要注意到∠2与∠4互余,并且直尺的两边互相平行,可以考虑平行线的性质.解答:解:与∠2互余的角有∠4,∠5,∠6;一共3个.点评:正确观察图形,由图形联想到学过的定理是数学学习的一个基本要求.18.(2008•十堰)如图,直线AB、CD相交于点O,OE⊥AB,垂足为O,如果∠EOD=42°,则∠AOC= 48度.考点:垂线;对顶角、邻补角.专题:计算题.分析:由OE⊥AB,∠EOD=42°,利用互余关系求∠BOD,再利用对顶角相等求∠AOC.解答:解:∵OE⊥AB,∠EOD=42°,∴∠BOD=90°﹣∠EOD90°﹣42°=48°,∵∠BOD与∠AOC是对顶角,∴∠BOD=∠AOC=48°.点评:利用垂直的定义及对顶角相等求解.19.(2006•海南)如图,△ABC中,∠ACB=90°,CD⊥AB于D,则图中所有与∠B互余的角∠A与∠2.考点:余角和补角.分析:利用“直角三角形两锐角之和为90°”的性质来解题.解答:解:∵∠ACB=90°,∴∠A+∠B=90°;又∵CD⊥AB于D,∴∠2+∠B=90°.根据互余定义,与∠B互余的角为∠A、∠2.点评:根据互余定义,找出与∠B和为90°的角即可.其间,要利用直角三角形的性质.20.(2004•南平)如图,将两块三角板的直角顶点重合后重叠在一起,如果∠1=40°,那么∠2=40度.考点:余角和补角.专题:计算题.分析:由于∠1与∠2都与∠AOB互余,根据余角的性质可知∠2=∠1,从而得出∠2的度数.解答:解:∵∠1+∠AOB=90°,∠2+∠AOB=90°,∴∠1=∠2.∵∠1=40°,∴∠2=40°.故答案为40.点评:本题主要考查了余角的性质:同角或等角的余角相等.21.(2002•岳阳)如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=76°,则∠BOD=38°.考点:对顶角、邻补角;角平分线的定义.专题:计算题.分析:根据角平分线的定义可判断∠AOC=∠EOC=×76°=38°,根据对顶角的定义可知∠BOD=∠AOC=38°.解答:解:∵OA平分∠EOC,∴∠AOC=∠EOC=×76°=38°,∴∠BOD=∠AOC=38°.故答案为38°.点评:本题考查了对顶角、角平分线的定义,知道角平分线平分一个角、对顶角相等即可解答.22.若∠1+∠2=90°,∠3+∠2=90°,∠1=40°,则∠3=40°,依据是同角的余角相等.考点:余角和补角.分析:若∠1+∠2=90°,∠3+∠2=90°,根据余角的性质可知,∠1=∠3,由∠1的度数可以求出∠3的度数.解答:解:∵∠1+∠2=90°,∠3+∠2=90°,∴∠1=∠3(同角的余角相等),∵∠1=40°,∴∠3=40°.故答案是40°,同角的余角相等.点评:本题重点考查了余角的性质,即同角的余角相等,等角的余角也相等.23.已知∠1与∠2互补,∠1与∠3互余,若∠2=130°,则∠3=40°.考点:余角和补角.分析:根据∠2=150°,∠1与∠2互补可先求出∠1.再根据∠1又与∠3互补求出∠3的度数.解答:解:∵∠2=130°,∠1与∠2互补,∴∠1=180°﹣∠2=50°,又∵∠1又与∠3互余,∴∠3=90°﹣∠1=40°.点评:此题属于基础题,较简单,互补即两角的和为180°,互余即两角的和为90°,先求出∠1是解题的关键.24.一个角的余角比它的补角的多1°,则这个角的度数为63度.考点:余角和补角.专题:计算题.分析:根据余角、补角的定义计算.解答:解:设这个角为x°,则它的余角为(90﹣x)°,补角为(180﹣x)°.根据题意有:(90﹣x)=(180﹣x)+1解得x=63,故这个角的度数为63度.点评:此题综合考查余角与补角,属于基础题中较难的题,解答此类题一般先用未知数表示所求角的度数,再根据一个角的余角和补角列出代数式和方程求解.25.已知∠1与∠2互补,∠1又与∠3互补,若∠2=150°,则∠3=150°.考点:余角和补角.专题:计算题.分析:互补即两角的和为180°,根据∠2=150°,∠1与∠2互补可先求出∠1.再根据∠1又与∠3互补求出∠3的度数.解答:解:∵∠2=150°,∠1与∠2互补,∴∠1=180°﹣∠2=30°,又∵∠1又与∠3互补,∴∠3=180°﹣∠1=150°.故答案为150°.点评:此题属于基础题,较简单,先求出∠1是解题的关键.三.解答题(共5小题)26.如图,点A、O、E在同一直线上,∠AOB=40°,∠COD=28°,OD平分∠COE.(1)求∠COB的度数(2)求∠AOD的度数.考点:角平分线的定义;余角和补角.专题:探究型.分析:(1)先根据OD平分∠COE得出∠DOE=∠COD,再由∠COD=28°可得出∠DOE=28°,再根据平角的性质即可得出∠COB的度数;(2)根据∠AOD=180°﹣∠DOE即可得出答案.解答:解:(1)∵OD平分∠COE,∴∠DOE=∠COD,∵∠COD=28°,∴∠DOE=28°,∵∠AOB+∠BOC+∠COD+∠DOE=180°,∴∠BOC=180°﹣(∠AOB+∠COD+∠DOOE),=180°﹣(40°+28°+28°),=84°;(2)∠AOD=180°﹣∠DOE,=180°﹣28°,=152°.点评:本题考查的是角平分线的定义及补角的性质,解答此题的关键是熟知从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线.27.如图所示,直线AB、CD相交O,OE⊥AB于O,且∠DOE=3∠COE,求∠AOD的度数.考点:角的计算;余角和补角;垂线.专题:计算题.分析:先根据∠DOE=3∠COE,和平角等于180°,可求出∠DOE,又OE⊥AB,故可得出∠DOB,再根据平角关系,即可得出∠AOD的度数.解答:解:∵∠DOE=3∠COE,∠DOE+∠COE=180°,∴∠DOE=135°,∵OE⊥AB,∴∠BOD=45°,∵∠AOB=180°,∴∠AOD=∠AOB﹣∠BOD=135°.点评:此题主要考查角的计算,注意垂直和平角的灵活运用.28.如图,已知O为AD上一点,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°,试求∠AOC与∠AOB的度数.考点:余角和补角;角平分线的定义.专题:计算题.分析:解此类题目关键在于:结合图形,根据余角、补角的定义,有时还需考虑角平分线的性质,分析并找到角与角之间的关系,再进行计算得出答案.解答:解:设∠AOB=x°,因为∠AOC与∠AOB互补,则∠AOC=180﹣x°.由题意,得.∴180﹣x﹣x=80,∴﹣2x=﹣100,解得x=50故∠AOB=50°,∠AOC=130°.点评:此题结合图形考查余角、补角的定义;涉及了角平分线的性质,及角的运算.在图形中,找补角、余角关系时,除了借助图形外,还需考虑等量关系即有没有相等的角.29.一个角的余角比它的补角的还少20°,求这个角.考点:余角和补角.专题:计算题.分析:首先根据余角与补角的定义,设这个角为x,则它的余角为(90°﹣x),补角为(180°﹣x),再根据题中给出的等量关系列方程即可求解.解答:解:设这个角为x,则它的余角为(90°﹣x),补角为(180°﹣x),根据题意可,得90°﹣x=(180°﹣x)﹣20°,解得x=75°.故答案为75°.点评:此题综合考查余角与补角,属于基础题中较难的题,解答此类题一般先用未知数表示所求角的度数,再根据一个角的余角和补角列出代数式和方程求解.30.如图,∠AOC和∠BOD都是直角,如果∠AOB=150°,求∠COD的度数.考点:余角和补角.专题:计算题.分析:由于∠AOC和∠BOD都是直角,如果∠AOB=150°,可求出∠AOD=60°,进而可以求出∠COD=30°.解答:解:∵∠BOD是直角,∴∠BOD=90°,∵∠AOB=150°,∴∠AOD=60°,又∵∠AOC是直角,∴∠AOC=90°,∴∠COD=30°.故答案为30°.点评:本题主要考查角余角和补角的知识点,比较简单.。
北师大版七年级下册数学第二章 相交线与平行线含答案【通用】

北师大版七年级下册数学第二章相交线与平行线含答案一、单选题(共15题,共计45分)1、已知两个角的两边分别平行,并且这两个角的差是90°,则这两个角分别等于()A.60°,150°B.20°,110°C.30°,120°D.45°,135°2、如图,AB//CD,∠1+∠2=110°,则∠GEF+∠GFE的度数为()A.110°B.70°C.80°D.90°3、下列命题是真命题的是()A.邻补角相等B.对顶角相等C.内错角相等D.同位角相等4、下列命题中,是假命题的是().A.在同一平面内,过一点有且只有一条直线与已知直线垂直.B.同旁内角互补,两直线平行.C.如果两条直线都与第三条直线平行,那么这两条直线也互相平行.D.两条直线被第三条直线所截,同位角相等.5、如图,AB∥CD,AC⊥BC,∠BAC=65°,则∠BCD的度数等于()A.20°B.25°C.35°D.50°6、如图,给出如下推理:①∠1=∠3.∴AD∥BC;②∠A+∠1+∠2=180°,∴AB∥CD;③∠A+∠3+∠4=180°,∴AB∥CD;④∠2=∠4,∴AD∥BC其中正确的推理有()A.①②B.③④C.①③D.②④7、如图,BC⊥AE于点C,CD∥AB,∠B=60°,则∠1等于()A.30°B.40°C.50°D.60°8、如图,已知直线a,b被直线c所截,若a∥b,∠1=110°,∠2=40°,则∠3=()A.40°B.50°C.60°D.70°9、如图,梯形ABCD中,AD∥BC,AB=,BC=4,连结BD,∠BAD的平分线交BD于点E,且AE∥CD,则AD的长为()A. B. C. D.1210、如图,CD∥AB,∠1=120°,∠2=80°,则∠E的度数是( )A.40°B.60°C.80°D.120°11、如图,将一张矩形纸片折叠,若∠1=80°,则∠2的度数是()A.50°B.60°C.70°D.80°12、下列条件不能够证明a∥b的是()A.∠2+∠3=180°B.∠1=∠4C.∠2+∠4=180°D.∠2=∠313、下列命题中,为真命题的是()A. 是13的算术平方根B.三角形的一个外角大于任何一个内角C. 是最简二次根式D.两条直线被第三条直线所截,内错角相等14、将一副三角板和一张对边平行的纸条按图所示方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则的度数是()度A.5B.10C.15D.2015、如图是一张足够长的长方形纸条ABCD,沿点A所在直线折叠纸条,使点B 落在边AD上,折痕与边BC交于点E;然后将其展平,再沿点E所在直线折叠纸条,使点A落在边BC上,折痕EF交边AD于点F,则∠AFE的大小是( )A.22.5°B.45°C.60°D.67.5°二、填空题(共10题,共计30分)16、某同学在研究传统文化“抖空竹”时有一个发现:他把它抽象成数学问题,如图所示:已知AB∥CD,∠BAE=87°,∠DCE=121°,则∠E的度数是________.17、如图所示,已知∠A=∠F,∠C=∠D,把下面的空填写完整.解:因为∠A=∠F(已知)所以DF∥AC(________)所以∠D=∠ABD(________)又因为∠D=∠C(已知)所以∠C=∠ABD(________)所以________∥________(________)18、如图,直线AB、CD相交于点O,∠COE是直角,OF平分∠AOD,若∠BOE=42°,则∠AOF的度数是________.19、小明在玩“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题,如图,若AB∥CD,∠BAE=92°,∠DCE=121°,则∠AEC=________°。
北师大版七年级数学下册第二章相交线与平行线练习题(有答案)
第二章检测卷一.选择题(每小题4分,共32分)1.如图,用数字表示的各角中,∠1的同位角为()A.∠2B.∠3C.∠4D.∠5第1题图第3题图第4题图第6题图2.下列说法正确的是()①两条直线相交,所成的四个角中有一个角是90°,那么这两条直线一定互相垂直;②两条直线的交点叫垂足;③直线AB⊥CD,也可以说成是CD⊥AB;④两条直线不是互相平行就是互相垂直.A.1个B.2个C.3个D.4个3.如图,点O为直线AB上一点,∠AOC=90°,∠DOE=90°,图中互余的角有几对?()A.2对B.3对C.4对D.5对4.如图,直线a∥b,直线c与直线a、b分别相交于A、B两点,若∠1=60°,则∠2=()A.60°B.120°C.50°D.30°5.如图,若∠1=∠2,则下列选项中可以判定AB∥CD的是()A.B.C.D.6.如图,一副直角三角板按如图所示的方式摆放,其中点C在FD的延长线上,且AB∥FC,则∠CBD的度数为()A.15°B.30°C.45°D.60°7.如图,如果AB∥EF,EF∥CD,下列各式正确的是()A.∠1+∠2﹣∠3=90°B.∠1﹣∠2+∠3=90°C.∠1+∠2+∠3=90°D.∠2+∠3﹣∠1=180°第7题图第8题图第9题图8.如图,是一张长方形纸片(其中AB∥CD),点E,F分别在边AB,AD上.把这张长方形纸片沿着EF折叠,点A落在点G处,EG交CD于点H.若∠BEH=4∠AEF,则∠CHG的度数为()A.108°B.120°C.136°D.144°二.填空题(每小题5分,共25分)9.如图,AH⊥BC,若AB=3cm、AC=4.5cm、AH=2cm,则点A到直线BC的距离为.10.如图,直线AB,CD相交于点O,OE⊥CD,∠BOE=38°,则∠AOC等于度.第10题图第11题图第12题图11.如图所示,FE⊥CD,∠2=25°,猜想当∠1=时,AB∥CD.12.如图,若∠1=∠3,∠2=60°,则∠4的大小为度.13.已知A,B,C三点及直线EF,过B点作AB∥EF,过B点作BC∥EF,那么A,B,C 三点一定在同一条直线上,依据是.三.解答题(共43分)14.(10分)已知:直线L和L外一点P,根据所学的“用尺规作一个角等于已知角”求作:一条直线AB,使它经过点P,并与已知直线L平行,保留作图痕迹,不要求写作法.15.(10分)如图,∠EBC+∠EF A=180°,∠A=∠C.求证:AB∥CE.16.(10分)如图,AB∥CD,点E在线段AB上,连接EC、ED、AD,且AD⊥CE于F,ED平分∠CEB,若∠ADC=40°,∠A﹣∠B=10°,求∠BDE的度数.17.(13分)如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为;(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.答案1.B 2.B 3.C 4.A 5.D 6.A 7.D 8.B9.2cm 10.52 11.65°12.12013.过直线外一点,有且只有一条直线与已知直线平行.14.解:如图,直线PN∥L(10分).15.解:∵∠EBC+∠EF A=180°,∠DFB=∠EF A,∴∠EBC+∠DFB=180°,∴BC∥AD,∴∠EDA=∠C.∵∠A=∠C,∴∠EDA=∠A,∴AB∥CE.(10分)16.解:∵AB∥CD,∴∠ADC=∠A=40°,∵∠A﹣∠B=10°,∴∠B=30°,∵AD ⊥EF,∴∠AFE=90°,∴∠AEF=50°,∴∠BEC=130°,∵DE平分∠BEC,∴∠BED=∠BEC=65°,∴∠BDE=180°﹣30°﹣65°=85°.(10分)17.解:(1)作PG∥AB,如图①所示:则PG∥CD,∴∠PFD=∠1,∠2=∠AEM,∵∠1+∠2=∠P=90°,∴∠PFD+∠AEM=∠1+∠2=90°,故答案为:∠PFD+∠AEM =90°.(4分)(2)如图②所示:∵AB∥CD,∴∠PFD+∠BHF=180°,∵∠P=90°,∴∠BHF+∠2=90°,∵∠2=∠AEM,∴∠BHF=∠PHE=90°﹣∠AEM,∴∠PFD+90°﹣∠AEM =180°,∴∠PFD﹣∠AEM=90°.(8分)(3)如图③所示:∵∠P=90°,∴∠PHE=90°﹣∠FEB=90°﹣15°=75°,∵AB ∥CD,∴∠PFC=∠PHE=75°,∵∠PFC=∠N+∠DON,∴∠N=75°﹣30°=45°.(13分)。
北师大版七年级下册数学第二章 相交线与平行线含答案【可修改】
北师大版七年级下册数学第二章相交线与平行线含答案一、单选题(共15题,共计45分)1、如图,若a∥b,∠1=58°,则∠2的度数是()A.58°B.112°C.122°D.142°2、如图,直线a∥b,CD⊥AB于点D,若∠1=36°,则∠2等于()A.54°B.126°C.136°D.144°3、如图,AB∥CD,BF平分∠ABE,且BF∥DE,则∠ABE与∠D的关系是()A.∠ABE=3∠DB.∠ABE+∠D=90°C.∠ABE+3∠D=180°D.∠A BE=2∠D4、如图,CD∥AB,∠1=120°,∠2=80°,则∠E的度数是()A.40°B.60°C.80°D.120°5、下列结论正确的是()A.两直线被第三条直线所截,同位角相等B.三角形的一个外角等于两个内角的和C.多边形最多有三个外角是钝角D.连接平面上三点构成的图形是三角形6、如图,AB∥CD,∠BAC与∠DCA的平分线相交于点G,GE⊥AC于点E,F为AC上的一点,且FA=FG=FC,GH⊥CD于H.下列说法:①AG⊥CG;②∠BAG=∠CGE;③S△AFG =S△CFG;④若∠EGH:∠ECH=2:7,则∠EGF=50度.其中正确的有()A.①②③④B.②③④C.①③④D.①②④7、下面四个图形中关于∠1与∠2位置关系表述错误的是()。
A.互为对顶角B.互为邻补角C.互为内错角D.互为同位角8、如图,直线a∥b,∠1=70°,那么∠2等于( )A.70°B.100°C.110°D.20°9、如图所示,,,,.则()A. B. C. D.10、如图,把长方形ABCD沿EF折叠后使两部分重合,若,则()A.100°B.150°C.110°D.105°11、如图,已知∠1=∠2,∠3=30°,则∠B的度数是( )A. B. C. D.12、下列命题中,正确的是( )A.对顶角相等B.同位角相等C.内错角相等D.同旁内角互补13、如图,小明从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处此时需把方向调整到与出发时一致,则方向的调整应是()A.右转80°B.左转80°C.右转100°D.左转100°14、在平行四边形中,下列结论一定成立的是()A. B. C. D.15、如图,AD是的中线,E、F分别是AD和AD延长线上的点,且,连结BF、CE.下列说法:①CE=BF②△ABD和△ACD面积相等;③BF∥CE;④△BDF≌△CDE.其中正确的有()A.1个B.2个C.3个D.4个二、填空题(共10题,共计30分)16、如图,AB∥EF,若∠C=90°,那么x、y和z的关系是________17、如图,一条公路修到湖边时,需拐弯绕湖而过;如果第一次拐角∠A是120°,第二次拐角∠B是150°,第三次拐角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是________18、如图,l∥m,矩形ABCD的顶点B在直线m上,则∠α=________度.19、如图,已知∠1+∠2=180°,∠3=108°,则∠4=________°.20、推理填空:已知:如图AB⊥BC于B,CD⊥BC于C,∠1=∠2,求证:BE∥CF.证明:∵ AB⊥BC于B,CO⊥BC于C (已知)∴∠1+∠3=90°,∠2+∠4=90°∴∠1与∠3互余,∠2与∠4互余又∵∠1=∠2(________),∴________=________(________)∴BE∥CF(________) .21、已知,如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.证明:∵DG⊥BC,AC⊥BC,(已知)∴DG∥AC(________ )∴∠2=________ (________ )∵∠1=∠2(已知)∴∠1=∠DCA(等量代换)∴EF∥CD(________ )∴∠AFE=∠ADC(________ )∵EF⊥AB(已知)∴∠AEF=90°(________ )∴∠ADC=90°(等量代换)∴CD⊥AB(垂直定义)22、如图,将一块三角板的直角顶点放在直尺的一边上,当∠1=40°时,那么∠2的度数是________.23、如图,AB∥CD, AF=EF,若∠C=62°,则∠A=________度.24、如图,是的直径,弦,垂足为点,连接、.如果,图中阴影部分的面积是,则的长为________.25、如图,直线a,b相交,若∠1与∠2互余,则∠3=________.三、解答题(共5题,共计25分)26、如图,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.试求∠COE的度数.27、如图,EF∥AD,∠1=∠2,∠BAG=60°,求∠G的度数.28、如图,AB是☉O的直径,OD垂直弦AC于点E,且交☉O于点D,F是BA的延长线上一点,若∠CDB=∠BFD,求证:FD是☉O的切线.29、如图,A,B,C,D是同一条直线上的点,AC=BD,AE∥DF,∠1=∠2.求证:BE = CF.30、如图,已知:∠1=∠2,∠3=108°,求∠4的度数.参考答案一、单选题(共15题,共计45分)1、C2、B3、D4、A5、C6、A7、D8、C9、A10、D11、B13、A14、D15、D二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、28、29、30、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 相交线与平行线
一、单选题
1.如图,直线,AB CD 相交于点,50,O AOC OE AB ︒∠=⊥,则DOE ∠的大小是( )
A .40︒
B .50︒
C .70︒
D .90︒
2.如图CD⊥AB,⊥C=90°,线段AC 、BC 、CD 中最短的是( )
A .AC
B .B
C C .C
D D .不能确定 3.如图,下列说法正确的是( )
A .A ∠与⊥1与是内错角
B .A ∠与2∠是同旁内角
C .⊥1与2∠是内错角
D .A ∠与3∠是同位角
4.下列说法正确的是( )
A .一条直线的平行线有且只有一条
B .经过一点有且只有一条直线与已知直线平行
C .经过一点有两条直线与已知直线平行
D .过直线外一点有且只有一条直线与已知直线平行
5.如图,能判定EB ⊥AC 的条件是( )
A .⊥C =⊥ABE
B .⊥A =⊥EBD
C .⊥C =⊥ABC
D .⊥A =⊥AB
E 6.如图,点E 在AD 的延长线上,下列条件中能判断AB ⊥CD 的是( )
A .⊥3=⊥4
B .⊥1=⊥2
C .⊥C =⊥CDE
D .⊥C +⊥ADC =180° 7.AF 是BAC ∠的平分线,//,DF AC 若70,BAC ∠=︒则1∠的度数为( )
A .17.5o
B .35o
C .55o
D .70o
8.如图,直线,a b 被直线,c d 所截,1110,270,360︒︒︒∠=∠=∠=,则4∠的大小是( )
A .60︒
B .70︒
C .110︒
D .120︒
9.下列对尺规作图步骤的描述不准确的是( )
A .作ABC ∠,使ABC αβ∠=∠+∠
B .作AOB ∠,使2AOB α∠=∠
C .以点A 为圆心,线段a 的长为半径作弧
D .以点O 为圆心作弧
10.如图,已知直线AB 、CD 被直线AC 所截,AB⊥CD ,E 是平面内任意一点(点E 不在直线AB 、CD 、AC 上),设⊥BAE=α,⊥DCE=β.下列各式:⊥α+β,⊥α﹣β,⊥β﹣α,⊥360°﹣α﹣β,⊥AEC 的度数可能是( )
A .⊥⊥⊥
B .⊥⊥⊥
C .⊥⊥⊥
D .⊥⊥⊥⊥
二、填空题 11.如图,直线AB 、CD 相交于点O ,OA 平分⊥EOC ,⊥EOC=80°,则⊥BOD=_____.
12.如图,两只手的食指和大拇指在同一个平面内,它们构成的一对角可看成是___.
13.如图,已知AB ,CD ,EF 互相平行,且⊥ABE =70°,⊥ECD =150°,则⊥BEC =________°.
14.如图,AB //CD BED 110BF o ,,∠=平分ABE DF ∠,平分CDE ∠,则BFD ∠= ______ .
三、解答题
15.如图,直线AB ,CD 相交于点O ,OE AB ⊥,垂足为O .
(1)直接写出图中AOC ∠的对顶角为 ,BOD ∠的邻补角为 ; (2)若:1:2BOD COE ∠∠=,求AOD ∠的度数.
16.如图,已知四边形ABCD ,AB⊥CD ,点E 是BC 延长线上一点,连接AC 、AE ,AE 交CD 于点F ,⊥1=⊥2,⊥3=⊥4.
证明:
(1)⊥BAE=⊥DAC;
(2)⊥3=⊥BAE;
(3)AD⊥BE.
17.如图,已知AB⊥CD,⊥B=60°,CM平分⊥ECB,⊥MCN=90°,求⊥DCN的度数.
18.如图,已知BC⊥GE,AF⊥DE,点D在直线BC上,点F在直线GE上,且⊥1=50°.(1)求⊥AFG的度数;
(2)若AQ平分⊥FAC,交直线BC于点Q,且⊥Q=18°,则⊥ACB的度数为______°.(直接写出答案)
答案
1.A
2.C
3.D
4.D
5.D
6.B
7.B
8.A
9.D
10.D
11.40°
12.内错角
13.40
14.125o
15.(1)⊥AOC 的对顶角为:⊥BOD ⊥BOD 的邻补角为:⊥BOC ,⊥AOD (2)⊥:1:2BOD COE ∠∠=
设⊥BOD=x,则⊥COE=2x
⊥OE⊥AB
⊥⊥EOB=90°
⊥⊥COE+⊥BOD=90°,即x+2x=90°解得:x=30°
⊥⊥BOD=⊥COA=30°
⊥⊥AOD=150°
16.证明:(1)⊥⊥1=⊥2,
⊥⊥1+⊥CAE=⊥2+⊥CAE,
即⊥BAE=⊥DAC;
(2)⊥AB⊥CD,
⊥⊥4=⊥BAE,
⊥⊥3=⊥4,
⊥⊥3=⊥BAE;
(3)⊥⊥3=⊥BAE,⊥BAE=⊥DAC,⊥⊥3=⊥DAC,
⊥AD⊥BE.
17.⊥AB⊥CD,
⊥⊥B+⊥BCE=180°,⊥BCD=⊥B,
⊥⊥B=60°,
⊥⊥BCE=120°,⊥BCD=60°,
⊥CM平分⊥BCE,
⊥⊥ECM=1
2
⊥BCE=60°,
⊥⊥MCN=90°,
⊥⊥DCN=180°-60°-90°=30°.
18.(1)⊥BC⊥EG,
⊥⊥E=⊥1=50°.
⊥AF⊥DE,
⊥⊥AFG=⊥E=50°;
(2)作AM⊥BC,
⊥BC⊥EG,
⊥AM⊥EG,
⊥⊥FAM=⊥AFG=50°.
⊥AM⊥BC,
⊥⊥QAM=⊥Q=18°,
⊥⊥FAQ=⊥FAM+⊥QAM=68°.⊥AQ平分⊥FAC,
⊥⊥QAC=⊥FAQ=68°,
⊥⊥MAC=⊥QAC+⊥QAM=86°.⊥AM⊥BC,
⊥⊥ACB=⊥MAC=86°。
