西北工业大学机械原理课后标准答案第11章
机械原理 第七版西北工业大学课后习题答案(7-11章)

第7章课后习题参考答案7—1等效转动惯量和等效力矩各自的等效条件是什么?7—2在什么情况下机械才会作周期性速度波动?速度波动有何危害?如何调节?答: 当作用在机械上的驱动力(力矩)周期性变化时,机械的速度会周期性波动。
机械的速度波动不仅影响机械的工作质量,而且会影响机械的效率和寿命。
调节周期性速度波动的方法是在机械中安装一个具有很大转动惯量的飞轮。
7—3飞轮为什么可以调速?能否利用飞轮来调节非周期性速度波动,为什么?答:飞轮可以凋速的原因是飞轮具有很大的转动惯量,因而要使其转速发生变化.就需要较大的能量,当机械出现盈功时,飞轮轴的角速度只作微小上升,即可将多余的能量吸收储存起来;而当机械出现亏功时,机械运转速度减慢.飞轮又可将其储存的能量释放,以弥补能最的不足,而其角速度只作小幅度的下降。
非周期性速度波动的原因是作用在机械上的驱动力(力矩)和阻力(力矩)的变化是非周期性的。
当长时问内驱动力(力矩)和阻力(力矩)做功不相等,机械就会越转越快或越转越慢.而安装飞轮并不能改变驱动力(力矩)或阻力(力矩)的大小也就不能改变驱动功与阻力功不相等的状况,起不到调速的作用,所以不能利用飞轮来调节非周期陛速度波动。
7—4为什么说在锻压设备等中安装飞轮可以起到节能的作用?解:因为安装飞轮后,飞轮起到一个能量储存器的作用,它可以用动能的形式把能量储存或释放出来。
对于锻压机械来说,在一个工作周期中,工作时间很短.而峰值载荷很大。
安装飞轮后.可以利用飞轮在机械非工作时间所储存能量来帮助克服其尖峰载荷,从而可以选用较小功率的原动机来拖动,达到节能的目的,因此可以说安装飞轮能起到节能的作用。
7—5由式J F =△W max /(ωm 2 [δ]),你能总结出哪些重要结论(希望能作较全面的分析)?答:①当△W max 与ωm 一定时,若[δ]下降,则J F 增加。
所以,过分追求机械运转速度的均匀性,将会使飞轮过于笨重。
②由于J F 不可能为无穷大,若△W max ≠0,则[δ]不可能为零,即安装飞轮后机械的速度仍有波动,只是幅度有所减小而已。
机械原理第11章作业答案 王德伦版 课后习题

12-1如图所示为几何对称钳式握持器,转动副处摩擦圆半径为ρ,夹起重物后两钳夹角为α,重物重力为G 。
试对该夹持器进行受力分析(画出作用力方向,写出力平衡方程,并画出力多边形),根据自锁条件确定钳口处摩擦系数多大才能保证重物安全夹持?FGα图12.31 习题1图 夹钳式握持器解:设钳口与重物之间的正压力为N F ,摩擦力为f F ,钳口处的摩擦系数为f 。
要保证重物安全夹持,则根据自锁条件有2f F G ≥ , f N F fF =设N F ,f F 的合力为R 1,其方向与水平方向成φ 角。
则tan()f φ= 即arctan()f φ= (1)取夹持器的一半进行受力分析如图所示。
转动副处的力R 2与摩擦圆相切,方向根据力矢量三角形确定如图示。
设R 2与水平方向成δ角 力的平衡方程21cos(/2)sin()sin()o F R R αδφ+= (2) 12sin(/2)cos()cos()o F R R αφδ+= (3)力矩平衡有21112cos()sin()R R L R L ρφφ+= (4) 对圆环处受力分析 见图2中a)。
则2sin(/2)o F F G α==(5)2sin(/2)o GF α=12-2 机床滑板与床身的接触形式如图所示,机床滑板的运动方向垂直于纸面,测定接触面间的滑动摩擦系数为f =0.1。
试求滑板的当量摩擦系数f e 的大小。
图12.32 习题2图 机床滑板解:设山形导轨一般的角度为а,如图所示。
受力图如上。
可以知道1212F F Q ==12sin()2N F Q α=4sin()N QF α=122sin()f N fQF fF α==212f F fQ =设当量摩擦系数f e 则12e f f f Q F F =+12sin()211(1)22sin()10.05(1)2sin()e e e fQ f Q fQf f f ααα=+=+=+12-3 图12-28所示鼓式制动器,设计的制动力矩要求为为3500Nm ,制动蹄上有摩擦衬片的当量摩擦系数f =0.25,摩擦面作用的平均半径R =120mm ,制动时轮缸活塞压迫制动鼓的最大径向紧力为20KN 。
机械设计第十一章课后习题答案

械设计第十一章课后习题答案11-1 解1)由公式可知:轮齿的工作应力不变,则则,若,该齿轮传动能传递的功率11-2解由公式可知,由抗疲劳点蚀允许的最大扭矩有关系:设提高后的转矩和许用应力分别为、当转速不变时,转矩和功率可提高69%。
11-3解软齿面闭式齿轮传动应分别验算其接触强度和弯曲强度。
(1)许用应力查教材表11-1小齿轮45钢调质硬度:210~230HBS取220HBS;大齿轮ZG270-500正火硬度:140~170HBS,取155HBS。
查教材图11-7,查教材图11-10 , 查教材表11-4取,故:(2)验算接触强度,验算公式为:其中:小齿轮转矩载荷系数查教材表11-3得齿宽中心距齿数比则:、,能满足接触强度。
(3)验算弯曲强度,验算公式:其中:齿形系数:查教材图11-9得、则:满足弯曲强度。
11-4解开式齿轮传动的主要失效形式是磨损,目前的设计方法是按弯曲强度设计,并将许用应力降低以弥补磨损对齿轮的影响。
(1)许用弯曲应力查教材表11-1小齿轮45钢调质硬度:210~230HBS取220HBS;大齿轮45钢正火硬度:170~210HBS,取190HBS。
查教材图11-10得,查教材表11-4 ,并将许用应用降低30% 故(2)其弯曲强度设计公式:其中:小齿轮转矩载荷系数查教材表11-3得取齿宽系数齿数,取齿数比齿形系数查教材图11-9得、因故将代入设计公式因此取模数中心距齿宽11-5解硬齿面闭式齿轮传动的主要失效形式是折断,设计方法是按弯曲强度设计,并验算其齿面接触强度。
(1)许用弯曲应力查教材表11-1,大小齿轮材料40Cr 表面淬火硬度:52~56HRC,取54HRC。
查教材图11-10得,查材料图11-7得。
查教材表11-4 ,因齿轮传动是双向工作,弯曲应力为对称循环,应将极限值乘70%。
故(2)按弯曲强度设计,设计公式:其中:小齿轮转矩载荷系数查教材表11-3得取齿宽系数齿数,取齿数比齿形系数应将齿形系数较大值代入公式,而齿形系数值与齿数成反比,将小齿轮的齿形系数代入设计公式,查教材图11-9得因此取模数(3)验算接触强度,验算公式:其中:中心距齿宽,取满足接触强度。
西北工业大学机械原理习题答案

p'=0F'=1
F=3n-(2pl+ph-p′)-F′
=3×10-(2×13+2-0)-1=1
机构原动件数目=1
机构有无确定运动?有确定运动
1—91)按传动顺序用数字1、2、3…在图示机构上给构件编号。
2)计算自由度,并判断机构有无确定运动:
在图中指明:复合铰链、局部自由度和虚约束
2为了使冲头6得到上下运动,只要有机构CDE即可,为什还要引入机构ABC?(可在学过第三章后再来想想)
1—5图a)所示为一简易冲床的初拟设计方案。设计者的思路是:动力由齿轮1输入,使轴A连续回转;而固装在轴A上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动,以达到冲压的目的。试绘出其机构运动简图(各尺寸由图上量取),分析是否能实现设计意图,并提出修改方案。
2.计算机构自由度的目的是什么?
3.当机构的自由度小于1时,可通过哪些途径来增加自由度?本题中还可列出哪些简单而又适用的修改方案?
计算1-6~1-9题各机构的自由度。
1—61)按传动顺序用数字1、2、3…在图示机构上给构件编号。
2)计算自由度,并机构判断有无确定运动:
在图中指明复合铰链、局部自由度和虚约束
解:属于两构件间重合点的问题
思路:因已知B2点的运动,故通过B2点求B3点的运动。
1)速度分析
方向:⊥BD ⊥AB ∥CD
大小: ? ω12l?
在速度多边形中,∵b3与极点p重合,∴vB3=0
且ω3=vB3/lBD=0,由于构件2与构件3套在一起,∴ω2=ω3=0
2) 加速度分析
方向: ⊥BD B→A ∥CD
p'=0F'=0
F=3n-(2pl+ph-p′)-F′
机械原理,孙恒,西北工业大学版第11齿轮系及其设计
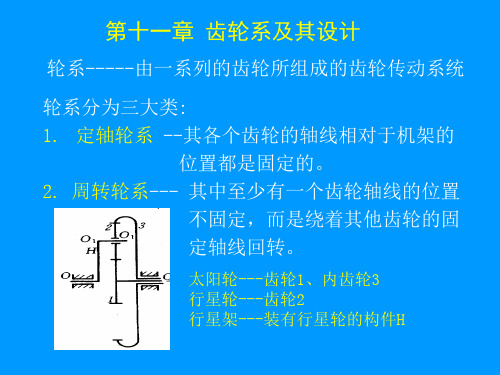
定轴轮系的传动比 =
所有主动轮齿数连乘积
规定:首、末两轮转向相同时, 其传动比为“+” ,反之为“— ”。 当有空间齿轮时,转向关系 的确定,只能画箭头
本例中,轮2为惰轮 (或程过桥轮、中介轮)
§11-3 周转轮系的传动比 11给整个周转轮系加上 一个公共角速度“ωH” ωH -ωH=0 ,即行星 架“静止不动”,周 转轮系转化为定轴轮 系 (转化轮系) ω1H=ω1-ωH ω2H=ω2-ωH ω3H=ω3-ωH ωHH=ωH-ωH=0
特别注意:“±” ,须由转化轮系中m、n两轮的 转向关系来确定
§11—4 复合轮系的传动比 11 4
注意几点: 1.必须正确地将轮系中的各组成部分加以划分 (找出行星架,并注意行星架往往是由轮 系 中具有其他功用的构件所兼任) 2.列出各组成轮系的传动比计算公式。 3.联解方程
例1. 图示的轮系,设已知各轮齿数,试求其 传动比 i1H
,
(3)联解方程
ω1 −ωH z2 z3 = ω3 −ωH z1z2
200 −ωH 40 ⋅ 24 = −100 −ωH 30 ⋅ 20
nH = −600
§11—5 轮系的功用
1.实现分路传动 2.获得较大的传动比 3. 实现变速传动 4.实现换向传动 5.用作运动的合成和分解 6.在尺寸及重量较小的条件下,实现 大功率传动
解: (1)区分轮系
2’—3 — 4 — H 周转轮系 1 — 2 定轴轮系
(2)列方程
n1 z2 40 i12 = = − = − = −2 n2 z1 20
i2′H = 1 − i2′4 = 1 − (−z4 / z2′ ) = 1 + 80 / 20 = 5
西工大版机械设计答案解析(第八版)

第三章机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-σ,取循环基数60105⨯=N ,9=m ,试求循环次数N分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。
[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N σσN MPa 3.324105.2105180946920112=⨯⨯⨯==--N N σσN MPa 0.227102.6105180956930113=⨯⨯⨯==--N N σσN 3-2已知材料的力学性能为MPa 260=s σ,MPa 1701=-σ,2.0=σΦ,试绘制此材料的简化的等寿命寿命曲线。
[解] )170,0('A )0,260(C12σσσΦσ-=-Θ σΦσσ+=∴-121MPa 33.2832.0117021210=+⨯=+=∴-σΦσσ得)233.283,233.283(D ',即)67.141,67.141(D '根据点)170,0('A ,)0,260(C ,)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4圆轴轴肩处的尺寸为:D =72mm ,d =62mm ,r =3mm 。
如用题3-2中的材料,设其强度极限σB =420MPa ,精车,弯曲,βq =1,试绘制此零件的简化等寿命疲劳曲线。
[解] 因2.14554==d D ,067.0453==d r ,查附表3-2,插值得88.1=ασ,查附图3-1得78.0≈σq ,将所查值代入公式,即()()69.1188.178.0111k =-⨯+=-α+=σσσq查附图3-2,得75.0=σε;按精车加工工艺,查附图3-4,得91.0=σβ,已知1=q β,则35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=qσσσσββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴ 根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5如题3-4中危险截面上的平均应力MPa 20m =σ,应力幅MPa 20a =σ,试分别按①C r =②C σ=m ,求出该截面的计算安全系数ca S 。
机械原理第八版课后练习答案(西工大版)(孙恒等)

解:
f 3324112 图示机构为一凸轮齿轮连杆组合机构,试绘制其机构示意简图并计算自由度。
解:
f 38210211
2-16 试计算图示凸轮-连杆组合机构的自由度 (a)
解: (b)
解:(1) n=11, p1=17, ph=0, p`=2p1`+ph-3n`=2, F`=0 F=3n-(2p1+ph-p`)-F`=3×11-(2×17+0-2)-0=1 (2) 去掉虚约束后 F=3n-(2pl+ph) =3×5-(2×7+0) =1
(d)A、B、C 处为复合铰链。自由度为:F=3n-(2p1+ph-p`)-F`=3×6-(2×7+3)-0=1
(10 分)
3-4 标出图示的齿轮一连杆组合机构中所有瞬心,并用瞬心法求齿轮 1 与齿轮 3 的传动比 ω1/ω3。
答:1)瞬新的数目: K=N(N-1)/2=6(6-1)/2=15
2)为求ω1/ω3需求 3 个瞬心 P16、P36、P13的位置
(2 分)
3) ω1/ω3= P36P13/P16P13=DK/AK 由构件 1、3 在 K 点的速度方向相同,可知ω3与ω1同向。 3-6 在图示的四杆机构中, LAB=60mm, LCD=90mm,LAD=LBC=120mm, ω2=10rad/s,试用瞬心法求: 1)当φ=165°时,点的速度 vc; 2)当φ=165°时,构件 3 的 BC 线上速度最小的一点 E 的位置及速度的大小; 3)当 VC=0 时,φ角之值(有两个解)。
F=3n- (2pl+ph- p’)- F’=3ⅹ7- (2ⅹ8+2-0)- 2=1 (2)如将 D 处结构改为如图 b 所示形式,即仅由两个移动副组成。注意,此时在该处 将带来一个虚约束。因为构件 3、6 和构件 5、6 均组成移动副,均要限制构件 6 在图纸平面 内转动,这两者是重复的,故其中有一个为虚约束。经分析知这时机构的活动构件数为 6, 低副数为 7,高副数和局部自由度数均为 2,虚约束数为 1,故机构的自由度为
机械原理课后答案第十一章作业
11-5 图a 、 b所示为两个不同结构的圆锥齿轮周转轮系,已知z1=20, z2=24,z2′=30,z3=40,n1=200r/min,n3= -100r/min。求两轮系 nH= ?(下面给出了计算结果,请检查所列算式、计算结果、 转向的判断是否正确,若正确请打“√”。)
解:1)图a: n1 n H = i13 H = n3 n H
z 2 z 3 24 40 =1.6 = z1 z 2 20 30
nH = (i13 H n3- n1) / (i13 H - 1) = [1.6×(-100) -200] / (1.6 - 1) = - 600 r/min
25 24 121 =5.6 30 24 18
n6 = ( n1 - nH) / i16 H + nH 当n1=48~200r/min时,则
n6 = ( 48 - 316) / 5.6 + 316 ~ ( 200 - 316) / 5.6 + 316
= 268.14 ~ 295.29 (r/min)
3. 由演算结果可见,若转化轮系传动比的“±”号判断错误,不仅会 影响到 周转轮系传动比大小 ,还会影响到 周转轮系中构件的转向 。
11-6 图示为纺织机中的差动轮系,设z1=30,z2=25,z3 = z 4= 24, z5=18,z6=121, n1=48~200r/min,nH= 316r/min。求n6= ? 解:差动轮系:1—2=3—4=5—6(H) z2 z4 z6 n1 n H H i16 = = - z1 z 3 z 5 n6 nH =
n1 n H - z 2 z 4 z 6 z 7 = z1 z 3 z 5 z 6 n7 nH
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第11章课后参考答案11-1在给定轮系主动轮的转向后,可用什么方法来确定定轴轮系从动轮的转向?周转轮系中主、从动件的转向关系又用什么方法来确定?答:参考教材216~218页。
11-2如何划分一个复合轮系的定轴轮系部分和各基本周转轮系部分?在图示的轮系中,既然构件5作为行星架被划归在周转轮系部分中,在计算周转轮系部分的传动比时,是否应把齿轮5的齿数,Z5计入?答:划分一个复合轮系的定轴轮系部分和各基本周转轮系部分关键是要把其中的周转轮系部分划出来,周转轮糸的特点是具有行星轮和行星架,所以要先找到轮系中的行星轮,然后找出行星架。
每一行星架,连同行星架上的行星轮和与行星轮相啮合的太阳轮就组成一个基本周转轮糸。
在一个复合轮系中可能包括有几个基本周转轮系(一般每一个行星架就对应一个基本周转轮系),当将这些周转轮一一找出之后.剩下的便是定轴轮糸部分了。
在图示的轮系中.虽然构件5作为行星架被划归在周转轮系部分中,但在计算周转轮系部分的传动比时.不应把齿轮5的齿数计入。
11-3在计算行星轮系的传动比时,式i mH=1-i H mn只有在什么情况下才是正确的? 答在行星轮系,设固定轮为n, 即ωn=0时, i mH=1-i H mn公式才是正确的。
11-4在计算周转轮系的传动比时,式i H mn=(n m-n H)/(n n-n H)中的i H mn是什么传动比,如何确定其大小和“±”号?答: i H mn是在根据相对运动原理,设给原周转轮系加上一个公共角速度“-ωH”。
使之绕行星架的固定轴线回转,这时各构件之间的相对运动仍将保持不变,而行星架的角速度为0,即行星架“静止不动”了.于是周转轮系转化成了定轴轮系,这个转化轮系的传动比,其大小可以用i H mn=(n m-n H)/(n n-n H)中的i H mn公式计算;方向由“±”号确定,但注意,它由在转化轮系中m. n两轮的转向关系来确定。
11-5用转化轮系法计算行星轮系效率的理论基础是什么?为什么说当行星轮系为高速时,用它来计算行星轮系的效率会带来较大的误差?答: 用转化轮系法计算行星轮系效率的理论基础是行星轮系的转化轮系和原行”。
经过这样星轮系的差别,仅在于给整个行星轮系附加了一个公共角速度“-ωH的转化之后,各构件之间的相对运动没有改变,而轮系各运动副中的作用力(当不考虑构件回转的离心惯性力时)以及摩擦因数也不会改变。
因而行星轮系与其转化轮系中的摩擦损失功率P H f应相等。
用转化轮系法计算行星轮系效率没有考虑由于加工、安装和使用情况等的不同,以及还有一些影响因素如搅油损失、行星轮在公转中的离心惯性力等,因此理论计算的结果并不能完全正确地反映传动装置的实际效率。
11-6何谓正号机构、负号机构?各有何特点?各适用于什么场合?答: 行星轮系的转化轮系中当传动比i H1n>o,称为正号机构;当传动比i H1n<o,称为负号机构。
正号机构效率随着l i H1l的增大而降低,其效率可能出现负值而发生自锁,其主要用于传递运动,如用在传动比大而对效率要求不高的辅助装置中;负号机构由于在任何情况下都不会出现自锁,效率较高,主要用于动力传动。
11-7何谓封闭功率流?在什么情况下才会出现?有何危害?答: 在选用封闭式行星轮系时,如其型式及有关参数选择不当,可能会形成有一部分功率只在轮系内部循环,而不能向外输出的情况,即形成所谓的封闭功率流。
当i aⅢ和i bⅢ异号,且l i aⅢl>l i bⅢl时,出现封闭功率流。
这种封闭的功率流将增大摩擦功率损失,使轮系的效率和强度降低,对于传动极为不刊。
11-8在确定行星轮系各轮齿数时,必须满足哪些条件,为什么?答设计行星轮系时,各轮齿数的选择应满足四个条件;对于不同的轮系,这四个条件具体表达式不尽相同,下面以内齿轮3固定,各轮均为标准齿轮的2K—H型轮系为例加以说明。
(1)保证实现给定的传动比:z3=(i1H-1)z1(2)满足同心条件(即保证两太阳轮和系杆的轴线重合): Z3=z1+2z2(3)满足k个行星轮均布安装(即满足装配条件):N=(z3+z1)/k (n 为整数)(4)满足邻接条件(即保证相邻行星轮不致相互碰撞):(z1+z2)sin(180º/k)>z2+2h a*11-9在行星轮系中采用均载装置的目的何在?采用均载装置后会不会影响该轮系的传动比?答在行星轮系中,常把某些构件作成可以浮动的.在轮系运转中,如各行星轮受力不均匀。
这些构件能在一定的范围内自由浮动,以达到自动调节各行星轮载荷的目的。
采用均载装置后不会影响该轮系的传动比。
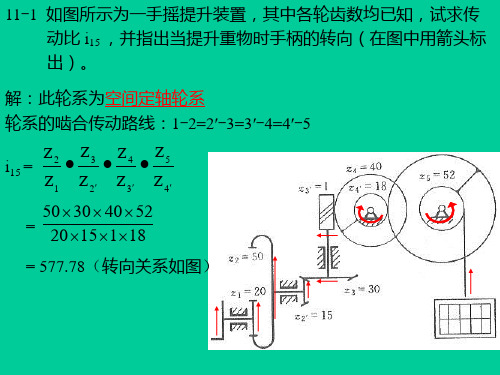
11-10何谓少齿差行星传动?摆线针轮传动的齿数差是多少?在谐波传动中柔轮与刚轮的齿数差如何确定?答少齿差行星传动是指在行星轮系中.当行星轮1与内齿轮2的齿数差△z=z2-z1=1~4时.就称为少齿差行星传动;摆线针轮传动的齿数差是1;在谐波传动中柔轮与刚轮的齿距相同.但齿数不等,刚轮与柔轮的齿数差通常等于波数n,即z r-z s=n011-11图示为一手摇提升装置,其中各轮齿数均为已知,试求传动比i 15并指出当提升重物时手柄的转向。
解:23451512'3'4'50304052577.782015118z z z z i z z z z ⨯⨯⨯===⨯⨯⨯当提升重物时手柄的转向逆时针(从左向右看手柄)。
11-12图示为一千分表的示意图,已知各轮齿数如图,模数m=0.11mm(为非标准模数)若要测量杆1每移动0.001 mm 时,指针尖端刚好移动一个刻度(s=1.5 mm)。
问指针的长度尺等于多少?(图中齿轮5和游丝的作用是使各工作齿轮始终保持单侧接触,以消除齿侧间隙对测量精度的影响。
)解:由图可知,轮2(2`)、3、(3`)、4、5组成定轴轮系且n 2=n 2`, n 3=n 3`33422`442`3``16121(1)120160100z z n i n z z -⨯==-=-=-⨯ n 4=-100n`2杆1和齿轮2是一对齿条与齿轮的外啮合,设杆1每移动0.001时间为t12212242212220.001/0.20.112931920100`100319v n mz v t n mz tn n n t =⨯===⨯=-=-=-由图知,指针摆一个刻度的s=1.5mm则摆角θ有关系式 θ=s/R即 θ=n 4t=s/R则 41523.92520319s R mm n t t t ===11-13图示为绕线机的计数器。
图中1为单头蜗杆,其一端装手把,另一端装绕制线圈。
2、3为两个窄蜗轮,z 2=99,.Z 3=100。
在计数器中有两个刻度盘,在固定刻度盘的一周上有100个刻度,在与蜗轮2固连的活动刻度盘的一周上有99个刻度,指针与蜗轮3固连。
问指针在固定刻度盘上和活动刻度盘上的每一格读数各代表绕制线圈的匝数是多少?又在图示情况下,线圈已绕制了多少匝? 解: 因i 13=n l /n 3=z 3/z 1=100,故n 3=n 1/100,即蜗杆每转一转,蜗轮3转过1/100转,指针相对固定刻度盘转过一个格度,说明指针在固定刻度盘上的每一格读数代表被绕制线圈绕制了一匝。
i 12=n l /n 2=z 2/z 1=99,故n 2=n 1/99,即蜗杆转一转,蜗轮2转过l /99转。
由于蜗轮2、3转向相同,故蜗杆每转一转,指针相对活动刻度盘转过l /100-1/99= -1/9 900转(即相对向后倒转,所以活动刻度盘刻度的增大方向与固定刻度盘者相反),因活动刻度盘上有99个刻度,故指针在活动刻度盘上的每一格读数,代表被绕制线圈已绕制了9 900/99=100匝。
今指针在活动刻度盘上的读数为13.××,在固定刻度盘上的读数为5.×,所以线圈已绕制的匝数为活动刻度盘上的整数读数×100+固定刻度盘上的整数读数=13×100+5=1 305匝11-14图示为一装配用电动螺丝刀的传动简图。
已知各轮齿数为z 1=z 4=7,z 3=z 6=39。
若n 1=3 000 r /min ,试求螺丝刀的转速。
解:此轮系为一复合周转轮系。
在1-2-3-H 1行星轮系中1111333911117h H z i i z =-=+=+ 在4-5-6-H 2行星轮系中2424663911147H H Z i i Z =-=+=+12114243.18H H H I I I =⨯==239(1+)7故 n H2=n 1/i 1H2=3000/43.18=69.5r/min 转向以n 1相同 11-16如图所示为两个不同结构的锥齿轮周转轮系,已知z 1=20,z 2=24,z 2,=30,z 3=40,n 1=200 r /min ,n 3=-100 r /min 。
求n H 等于多少?(a)解: 231133122440 1.62030H H H z z n n i n n z z -⨯====-⨯‘131331[1.6]/1H h H i n n n i -==⨯-(100)-200(1.6-1)=-600r/min(b)解:231133122440 1.62030H H H z z n n i n n z z -⨯==-==--⨯‘131331[ 1.6]/1H h H i n n n i -==-⨯-(-100)-200(-1.6-1)=15.385r/min11-17在图示的电动三爪卡盘传动轮系中,设已知各轮齿数为z 1=6,z 2=z 2,=25,z 3=57,z 4=56。
试求传动比i 14。
解 : 图示轮系为一周转轮系(整个轮系只有一个行星架,去掉周转轮系部分后,无定轴轮系部分,故整个轮系为一周转轮系)。
该轮系共有三个中心轮,故称之为3K型行星传动。
此轮系的右端由轮2’、4和件H组成一差动轮系,左端由轮1、2、3和件H 组成一行星轮系,此行星轮系将差动轮系中的构件2’和H封闭起来(即使构件2和H之间有固定速比关系),整个轮系类似于一个封闭式行星轮系。
此轮系也可认为是由轮1、2、3和行星架H组成的行星轮系与由轮4、2’、2、3和行星架H 组成的另一行星轮系组合而成。
故为求解此轮系的传动比,必须列出两个方程。
如下的解法,求解最简便。
在轮1、2、3及行星架H组成的行星轮系中,轮3为固定轮,故11-18图示为手动起重葫芦,已知z1=Z2,=10,z2=20,z3=40。
设各级齿轮的传动效率(包括轴承损失)η1=0.98,曳引链的传动效率η2=0.97。
为提升重G=10 kN 的重物,求必须施加于链轮A上的圆周力F。
解:42314141312'11()z zi w w iz z==-=--=2040191010⨯+=⨯所以411440160Qp iw m Qw m Pη∂==414/4710/40.99308.64p Q I N==⨯⨯=11-19图示为纺织机中的差动轮系,设z1=30,z2=25,z3=z4=24,z5=1 8,z6=121,n1=48~200 r/rain,n H=316 r/min,求n6等于多少?解:246 16135125241215.66302418HZ Z ZN NHIN NH Z Z Z-⨯⨯====-⨯⨯2(-1)1616HNI=1H H(N-N)+N当n1=48 ~200r/min 时116(48316)316(200316)3165.6 5.6268.14295.29(/min)nr=-++=:::N6与n1及n H的转向相同11-20图示为建筑用绞车的行星齿轮减速器。
