西北工业大学机械原理课后答案第3章-1
《机械原理》第七版西北工业大学习题答案 特别全答案详解
题 2-8 图示为一刹车机构。刹车时，操作杆 1 向右拉，通过构件 2、3、4、5、6 使两闸瓦刹住车轮。试计 算机构的自由度，并就刹车过程说明此机构自由度的变化情况。（注：车轮不属于刹车机构中的构件。）
解：1)未刹车时，刹车机构的自由度
n 6 pl 8 ph 0
F 3n 2 pl ph 3 6 28 0 2
F 3n 2 pl ph 35 2 7 0 1
所设计的一种假肢膝关节机构，该机构能 为机架，
自由度，并作出大腿弯曲 90 度时的机构
简图。大腿弯曲 90 度时的机构运动简图
题 2-6 试计算如图所示各机构的自由度。图
a、d 为齿轮-连杆组合机构；图 b 为凸轮-连
杆组合机构（图中在 D 处为铰接在 题2-5
移动副。 解法一：
n 13 pl 17 ph 4
虚约束：
因为 AB BC CD AD ，4 和 5，6 和 7、8 和 9 为不影响机构传递运动的重复部分，与连杆 10、
11、12、13 所带入的约束为虚约束。机构可简化为图 2-7（b）
重复部分中的构件数 n 10 低副数 pl 17 高副数 ph 3 局部自由度 F 3
p5 3 p4 1 F 1
5
F 6 mn i mpi F 6 3 3 5 3p5 4 3p4 F 1 i m1
F0 6n ipi F 6 3 5 3 411 2 将平面高副改为空间高副，可消除虚约束。
题 2-10 图示为以内燃机的机构运动简图，试计算自由度，并分析组成此机构的基本杆组。如在该机构中 改选 EG 为原动件，试问组成此机构的基本杆组是否与前者不同。 解：1)计算此机构的自由度
p 2 pl ph 3n 2 17 3 310 3 4 局部自由度 F 4
西北工业大学机械原理课后答案第3章
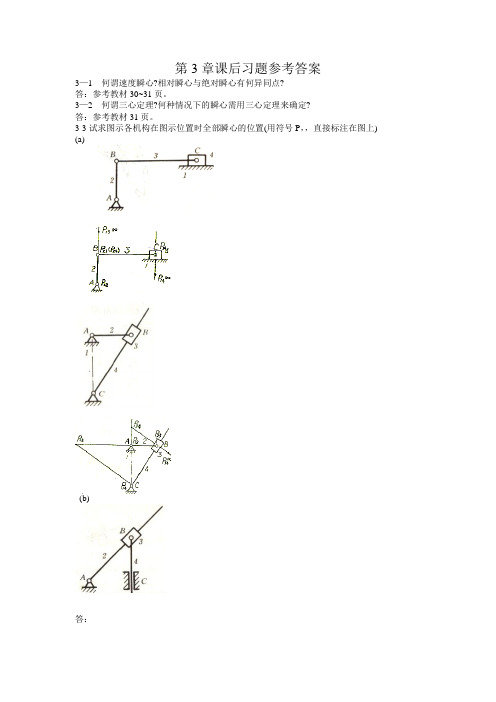
答：
（1分） （1分）
Vc3=VB+VC3B=VC2+VC3C2（2分）
aC3=aB+anC3B+atC3B=aC2+akC3C2+arC3C2（3分）
VC2=0 aC2=0（2分）
VC3B=0 ω3=0 akC3C2=0（3分）
(b)
答：
（2分）
（2分）
VC2=VB+VC2B=VC3+Vc2C3（2分）
解：(1)以μl作机构运动简图如(a)所示。
(2)速度分斫：
此齿轮连杆机构可看作，ABCD受DCEF两个机构串联而成，则可写出：
vC=vB+vCB
vE=vC+vEC
以μv作速度多边形如图(b)所示．由图得
vE=μvpe m/S
取齿轮3与齿轮4的啮合点为k，根据速度影像原理，作△dck∽△DCK求得k点。然后分别以c，e为圆心，以ck．ek为半径作圆得圆g3和圆g4。圆g3代表齿轮3的速度影像，圆g4代表齿轮4的速度影像。
解1）以μl作机构运动简图．如图(a)。
2）利用瞬心多边形图(b)依次定出瞬心P36,P13.P15
vC=vP15=ω1AP15μl=1.24 m/S
3 -19图示齿轮一连杆组合机构中，MM为固定齿条，齿轮3的直径为齿轮4的2倍．设已知原动件1以等角速度ω1顺时针方向回转，试以图解法求机构在图示位置时E点的速度vE以及齿轮3，4的速度影像。
aD=μap`d`=0.6 4m/S2
aE=μap`e`=2.8m/s2
α2=atC2B/lBC=μan`2C`2/lBC=8.36rad/s2(顺时针) i
3- l5在图（a）示的机构中，已知lAE=70 mm,；lAB=40mm，lEF=60mm,
机械原理第八版课后练习答案(西工大版)(孙恒等)
齿轮 3、5 和齿条 7 与齿轮 5 的啮合高副所提供的约束数目不同，因为齿轮 3、5 处只有一个 高副，而齿条 7 与齿轮 5 在齿的两侧面均保持接触，故为两个高副。 2-13 图示为一新型偏心轮滑阎式真空泵。其偏心轮 1 绕固定轴心 A 转动，与外环 2 固连在一 起的滑阀 3 在可绕固定轴心 C 转动的圆柱 4 中滑动。当偏心轮按图示方向连续回转时可将设 备中的空气吸入，并将空气从阀 5 中排出，从而形成真空。(1)试绘制其机构运动简图；(2) 计算其自由度。
解：
f 37210 1 2-18 图示为一刹车机构。刹车时，操作杆 j 向右拉，通过构件 2、3、4、5、6 使两闸瓦刹住 车轮。试计算机构的自由度，并就刹车过程说明此机构自由度的变化情况。(注；车轮不属于 刹车机构中的构件。
（1)未刹车时，刹车机构的自由度 2)闸瓦 G、J 之一剃紧车轮时．刹车机构的自由度 3)闸瓦 G、J 同时刹紧车轮时，刹车机构的自由度
解：
1> f 3628 2
2> f 3527 1
3> f 3426 1
2-23 图示为一内然机的机构运动简图，试计算自由度 t 并分析组成此机构的基本杆组。如在 该机构中改选 EG 为原动件，试问组成此机构的基本杆组是否与前者有所不同。
解：
f 37210 1
2-21
图示为一收放式折叠支架机构。该支架中的件 1 和 5 分别用木螺钉连接于固定
收起(如图中双点划线所示)。现已知机构尺寸 lAB=lAD=90 mm；lBC=lCD=25 mm，其余尺寸
见图。试绘制该机构的运动简图，并计算其自由度。
解：机械运动简图如下：
F=3n-(2p1+pb-p`)-F`=3×5-(2×6+1-0)-1=1
机械原理第2、3、4、6章课后答案西北工业大学(第七版)
第二章 机构的结构分析题2-11 图a 所示为一简易冲床的初拟设计方案。
设计者的思路是：动力由齿轮1输入，使轴A 连续回转；而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动，以达到冲压的目的。
试绘出其机构运动简图（各尺寸由图上量取），分析是否能实现设计意图，并提出修改方案。
解：1)取比例尺,绘制机构运动简图。
(图2-11a)2)要分析是否能实现设计意图,首先要计算机构的自由度。
尽管此机构有4个活动件，但齿轮1和凸轮2是固装在轴A 上，只能作为一个活动件，故 3=n 3=l p 1=h p01423323=-⨯-⨯=--=h l p p n F原动件数不等于自由度数，此简易冲床不能运动，即不能实现设计意图。
分析：因构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架。
故需增加构件的自由度。
3)提出修改方案：可以在机构的适当位置增加一个活动构件和一个低副，或用一个高副来代替一个低副。
(1) 在构件3、4之间加一连杆及一个转动副(图2-11b)。
(2) 在构件3、4之间加一滑块及一个移动副(图2-11c)。
(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-11d)。
11(c)题2-11(d)5364(a)5325215436426(b)321讨论：增加机构自由度的方法一般是在适当位置上添加一个构件（相当于增加3个自由度）和1个低副（相当于引入2个约束），如图2-1（b ）（c ）所示，这样就相当于给机构增加了一个自由度。
用一个高副代替一个低副也可以增加机构自由度，如图2-1（d ）所示。
题2-12 图a 所示为一小型压力机。
图上，齿轮1与偏心轮1’为同一构件，绕固定轴心O 连续转动。
在齿轮5上开有凸轮轮凹槽，摆杆4上的滚子6嵌在凹槽中，从而使摆杆4绕C 轴上下摆动。
同时，又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。
机械设计基础第三章(西北工业大学)
第三章机械零件的强度3-1 材料的疲劳特性§3-2 机械零件的疲劳强度计算§3-3 机械零件的抗断裂强度§3-4 机械零件的接触强度疲劳曲线机械零件的疲劳大多发生在s －N 曲线的CD 段，可用下式描述：)(D C m rN N N N C N ≤≤= s )D r rN N N >=∞ （s s D 点以后的疲劳曲线呈一水平线，代表着无限寿命区其方程为：由于N D 很大，所以在作疲劳试验时，常规定一个循环次数N 0(称为循环基数)，用N 0及其相对应的疲劳极限σr 来近似代表N D 和σr∞，于是有：CN N ==0m rm rN s s 有限寿命区间内循环次数N 与疲劳极限s rN 的关系为：式中，s 、N 及m 的值由材料试验确定。
二、s －N 疲劳曲线m0r rN N N s s =0mrN r N N ⎪⎪⎭⎫ ⎝⎛=s s s －N 疲劳曲线详细说明极限应力线图三、等寿命疲劳曲线（极限应力线图）机械零件材料的疲劳特性除用s －N 曲线表示外，还可用等寿命曲线来描述。
该曲线表达了不同应力比时疲劳极限的特性。
在工程应用中，常将等寿命曲线用直线来近似替代。
用A 'Ｇ'C 折线表示零件材料的极限应力线图是其中一种近似方法。
A 'Ｇ'直线的方程为：m a1s ψs s s '+'=-s m as s s ='+'C Ｇ'直线的方程为：12s s s ψs -=-ψσ为试件受循环弯曲应力时的材料常数，其值由试验及下式决定：详细介绍对于碳钢，ψ≈0.1~0.2，对于合金钢，ψ≈0.2~0.3。
机械零件的疲劳强度计算1一、零件的极限应力线图由于零件几何形状的变化、尺寸大小、加工质量及强化因素等的影响，使得零件的疲劳极限要小于材料试件的疲劳极限。
以弯曲疲劳极限的综合影响系数Ｋσ表示材料对称循环弯曲疲劳极限σ-1与零件对称循环弯曲疲劳极限σ-1e 的比值，即e11--=s s s K 在不对称循环时，Ｋσ是试件与零件极限应力幅的比值。
机械原理第三章习题答案
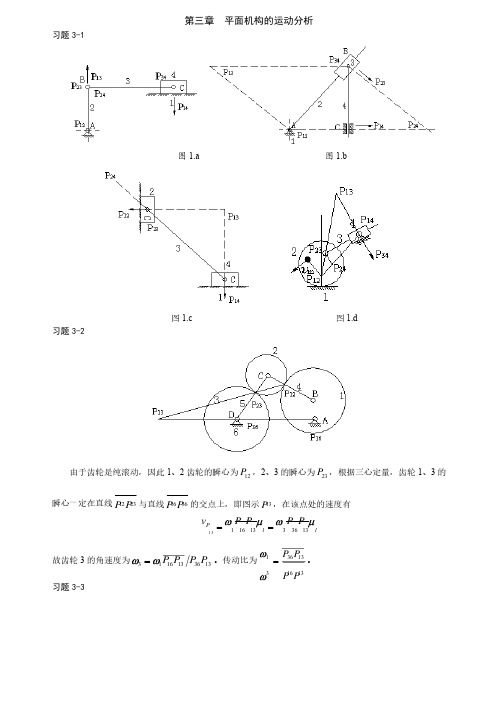
第三章平面机构的运动分析习题3-1 图1.a 图1.b 图1.c 图1.d 习题3-2 由于齿轮是纯滚动，因此1、2齿轮的瞬心为12P ，2、3的瞬心为23P ，根据三心定量，齿轮1、3的瞬心一定在直线2312P P与直线3616P P 的交点上，即图示13P ，在该点处的速度有ll P PP P P P v m w m w 133631316113==故齿轮3的角速度为1336131613P P P P w w =。
传动比为1316133631P P P P =w w 。
习题3-3答：1)三个瞬心中，14P、12P 为绝对瞬心，24P 为相对瞬心。
2)不利用其它的三个瞬心，因为它们全是相对瞬心。
3)构件2和4之间的转向关系可以根据瞬心24P 的瞬时绝对速度方向判断。
的瞬时绝对速度方向判断。
习题3-4取比例尺为mmm l 003.0=m ，作图如下，作图如下1) 由图上可知：l l P P P P P v m w m w 241442412224==，根据量得的长度，得，根据量得的长度，得s rad P P P P/455.414.72/14.32102414241224=´==w w 可计算出C 点的速度为：s m CD v l C /4.0003.030455.44=´´==m w2) 构件1、3的瞬心在点13P 处，且为绝对瞬心，因此构件3的角速度为的角速度为()s rad C P v l c /53.2)67.52003.0/(4.0133=´==mw 显然构件3上速度最小点在E 点，则其速度为点，则其速度为s m EP v l E /36.0003.04.4753.2133=´´==mw 3) 要使0=C v ，需瞬心12P 、24P 重合(如图)，两位置分别为0126'=Ð=DAB j ，02227''=Ð=DAB j 。
机械原理第七版西北工业大学课后习题答(1-8章)
机械原理作业集答案详解 第二章平面机构的结构分析题2-1 图a 所示为一简易冲床的初拟设计方案。
设计者的思路是：动力由齿轮1输入，使轴A 连续回转；而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动，以达到冲压的目的。
试绘出其机构运动简图（各尺寸由图上量取），分析是否能实现设计意图，并提出修改方案。
解：1)取比例尺,绘制机构运动简图。
(图2-1a) 2)要分析是否能实现设计意图,首先要计算机构的自由度。
尽管此机构有4个活动件，但齿轮1和凸轮2是固装在轴A 上，只能作为一个活动件，故3=n 3=l p 1=h p01423323=-⨯-⨯=--=h l p p n F原动件数不等于自由度数，此简易冲床不能运动，即不能实现设计意图。
分析：因构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架。
故需增加构件的自由度。
3)提出修改方案：可以在机构的适当位置增加一个活动构件和一个低副，或用一个高副来代替一个低副。
(1) 在构件3、4之间加一连杆及一个转动副(图2-1b)。
(2) 在构件3、4之间加一滑块及一个移动副(图2-1c)。
(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-1d)。
11(c)题2-1(d)54364(a)5325215436426(b)321讨论：增加机构自由度的方法一般是在适当位置上添加一个构件（相当于增加3个自由度）和1个低副（相当于引入2个约束），如图2-1（b ）（c ）所示，这样就相当于给机构增加了一个自由度。
用一个高副代替一个低副也可以增加机构自由度，如图2-1（d ）所示。
题2-2 图a 所示为一小型压力机。
图上，齿轮1与偏心轮1’为同一构件，绕固定轴心O 连续转动。
在齿轮5上开有凸轮轮凹槽，摆杆4上的滚子6嵌在凹槽中，从而使摆杆4绕C 轴上下摆动。
同时，又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。
机械原理_课后习题答案免费(全面)高教版 西北工大
2) 求vC2
v C 2 = v B + v C 2 B = v C 3 + vC 2 C 3
方向： 大小： ⊥AB
√
⊥BC ?
0 0
∥BC ?
取
μv = 0.005
m/s mm
作速度图
b
题3-10 解(续2)
[解] （2）速度分析
v B → vC 2 → v D , v E → ω 2
1) 求vB 2) 求vC2 3) 求vD 和求vE 用速度影像法
C
E
vC = v B + vCB v D = v B + v DB
(2) 求vE
D p(a, f )
v E = vC + v EC = v D + v ED
b d e c
题3-5 解
b) 解: 顺序 (1) 求vC
v B → vC → v E → v F
D B vB A E G F C
vC = v B + vCB
√
0 0
∥CD ?
b2 (b1) (b3)
其中 a B3B2 = 2ω2 v B3B2 = 0(∵ v B3B2 = 0)
a B1 ⎛ m / s 2 ⎞ 取 μa = ⎜ ⎟ 作加速度图 p ' b '1 ⎝ mm ⎠
题3-8 c) 解(续2)
[解] （3）加速度分析 a B 2 ( = a B1 ) → a B 3 → a C 3 1) 求aB2 A 1 ω1 2) 求aB3
取
√ v ⎛m/s⎞ μ v = B1 ⎜ ⎟ 作速度图 pb1 ⎝ mm ⎠
3) 求vC3 : 用速度影像法
v C 3 = 0 同时可求得 ω3 =
西工大版机械原理第3章
1 2
1
2 A(A1A2)
VA2、VA1为两构件上A点的绝对速度，VA2A1为相对速度
VA2A1方向为平行于导路方向。
（2）加速度分析
r aA2 aA1 ak a A2 A1 A2 A1
1 2
aA2、aA1为两构件上A点的绝对加速度
科氏加速度： a k A2 A1 21VA2 A1， 方向为将相对速度VA2 A1沿1转过90
大小 方向
？ ⊥C P14 ？
？
⊥AB ⊥BC
vS 4 vC vS 4C vE vS 4 E
vS 4 vB vCB vS 4C vE vS 4 E
大小 方向
（1）用瞬心法确定C点方向
⊥AB
？
⊥CB
？
⊥SE
借助速度瞬心法
VC ?
= VB
+ VCB
P36 E • C G 3 5 A D 2 1 4 F B 6 即：VS3 = VB
vK 3 vK 2 2lOK
（2）用影像原理求vB
⊥OK
vC vB vCB
vB v pb
vC v pc 6 lCD lCD
例 3 – 3 图示为6杆（Ⅲ级）机构，已知2 ，作速度多边形
d
c p
b （2）利用特殊点S减少未知量
S
p14
e
vC vB vCB
n t k r aB3 aB 3 aB3 aB2 aB3B2 aB3B2
大小： 方向：
2 3 lBC
?
⊥BC
2 1 l AB
23VB3B 2
?
' ' b（ ） 2 b1
机械设计(第八版)课后习题答案(最新,参考答案)
3到13章答案 免费下载 0财富值西北工业大学机械原理及机械零件教研室 编著第三章 机械零件的强度习题答案3-1某材料的对称循环弯曲疲劳极限MPa 1801=-ζ，取循环基数60105⨯=N ，9=m ，试求循环次数N 分别为7 000、25 000、620 000次时的有限寿命弯曲疲劳极限。
[解] MPa 6.373107105180936910111=⨯⨯⨯==--N N ζζNM P a 3.324105.2105180946920112=⨯⨯⨯==--N N ζζNM P a 0.227102.6105180956930113=⨯⨯⨯==--N N ζζN3-2已知材料的力学性能为MPa 260=s ζ，MPa 1701=-ζ，2.0=ζΦ，试绘制此材料的简化的等寿命寿命曲线。
[解] )170,0('A )0,260(C 0012ζζζΦζ-=-ζΦζζ+=∴-1210M P a 33.2832.0117021210=+⨯=+=∴-ζΦζζ得)233.283,233.283(D '，即)67.141,67.141(D '根据点)170,0('A ，)0,260(C ，)67.141,67.141(D '按比例绘制该材料的极限应力图如下图所示3-4 圆轴轴肩处的尺寸为：D =72mm ，d =62mm ，r =3mm 。
如用题3-2中的材料，设其强度极限σB =420MPa ，精车，弯曲，βq =1，试绘制此零件的简化等寿命疲劳曲线。
[解] 因2.14554==d D ，067.0453==d r ，查附表3-2，插值得88.1=αζ，查附图3-1得78.0≈ζq ，将所查值代入公式，即()()69.1188.178.0111k =-⨯+=-α+=ζζζq查附图3-2，得75.0=ζε；按精车加工工艺，查附图3-4，得91.0=ζβ，已知1=q β，则 35.211191.0175.069.1111k =⨯⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=q ζζζζββεK ()()()35.267.141,67.141,0,260,35.2170,0D C A ∴根据()()()29.60,67.141,0,260,34.72,0D C A 按比例绘出该零件的极限应力线图如下图3-5 如题3-4中危险截面上的平均应力MPa 20m =ζ，应力幅MPa 20a =ζ，试分别按①C r =②C ζ=m ，求出该截面的计算安全系数ca S 。
西北工业大学机械原理课后答案第3章1
第三章 平面机构的运动分析题3-３ 试求图示各机构在图示位置时全部瞬心的位置(用符号P ｉｊ直接标注在图上) 解:1P 13(P 34)13∞题3-4 在图示在齿轮-连杆机构中,试用瞬心法求齿轮1与齿轮3 的传动比w １／ｗ3、P 13P 23P 363D 652C 4B P 16A 1P 12解:1)计算此机构所有瞬心的数目152)1(=-=N N K2)为求传动比31ωω需求出如下三个瞬心16P 、36P 、13P 如图3-2所示。
3)传动比31ωω计算公式为:1316133631P P P P =ωω题3－６在图ａ所示的四杆机构中,ｌA Ｂ＝60m ｍ,ｌCD =90mm,l ＡＤ=l BC =12０mm,ω２＝10r ａd/s,试用瞬心法求:231） 当φ＝165°时,点C 的速度Vc;2） 当φ=165°时,构件3的BC 线上速度最小的一点E 的位置及速度的大小; 3） 当Ｖc=0时,φ角之值(有两个解)解:１) 以选定比例尺,绘制机构运动简图。
(图３-３ ) 2)求V C ,定出瞬心Ｐ13的位置。
如图3-3(a)s rad BP ll v l AB AB B 56.21323===μωω s m CP v l C 4.0313==ωμ 3)定出构件3的BC 线上速度最小的点E 的位置。
因为ＢC 线上速度最小的点必与P 1３点的距离最近,所以过P 1３点引BC 线延长线的垂线交于E 点。
如图3-3(ａ)s m EP v l E 375.0313==ωμ4)当0=C v 时,P 13与Ｃ点重合,即AB 与BC 共线有两个位置。
作出0=C v 的两个位置。
量得 ︒=4.261φ ︒=6.2262φ题3-１2 在图示的各机构中,设已知各构件的尺寸、原动件1以等角速度ω1顺时针方向转动。
试用图解法求机构在图示位置时构件3上C 点的速度及加速度。
解:a)速度方程:32233C C C B C B C v v v v v +=+=加速度方程:r C C k C C C t B C n B C B t C nC a a a a a a a a 232323333++=++=+ｂ) 速度方程:2323B B B B v v v +=加速度方程:r B B K B B B t B nB a a a a a 2323233++=+c) 速度方程:2323B B B B v v v +=加速度方程:r B B K B B B t B nB a a a a a 2323233++=+题3-１4 在图示的摇块机构中,已知l ＡB ＝３0ｍｍ,l ＡＣ=10０mm,ｌBD =5０mm,ｌDE =４0mm 。
机械原理第八版课后练习答案(西工大版)(孙恒等)
解：(1) n=11, p1=17, ph=0, p`=2p1`+ph-3n`=2, F`=0 F=3n-(2p1+ph-p`)-F`=3×11-(2×17+0-2)-0=1 (2) 去掉虚约束后 F=3n-(2pl+ph) =3×5-(2×7+0) =1 （d）A、B、C 处为复合铰链。自由度为：F=3n-(2p1+ph-p`)-F`=3×6-(2×7+3)-0=1
（3 分）
3-8 机构中，设已知构件的尺寸及点 B 的速度 vB(即速度矢量 pb)，试作出 各机构在图示位置时的速度多边形。
答：
（10 分） （b）
答：
答：
3—11 速度多边形和加速度多边彤有哪些特性?试标出图中的方向。 答 速度多边形和加速度多边形特性参见下图，各速度方向在图中用箭头标出。
3-12 在图示的机构中，设已知构件的尺寸及原动件 1 的角速度ω1 (顺时针)，试用图解法求机 构在图示位置时 C 点的速度和加速度。 (a)
齿轮 3、5 和齿条 7 与齿轮 5 的啮合高副所提供的约束数目不同，因为齿轮 3、5 处只有一个 高副，而齿条 7 与齿轮 5 在齿的两侧面均保持接触，故为两个高副。 2-13 图示为一新型偏心轮滑阎式真空泵。其偏心轮 1 绕固定轴心 A 转动，与外环 2 固连在一 起的滑阀 3 在可绕固定轴心 C 转动的圆柱 4 中滑动。当偏心轮按图示方向连续回转时可将设 备中的空气吸入，并将空气从阀 5 中排出，从而形成真空。(1)试绘制其机构运动简图；(2) 计算其自由度。
解：
1> 2>
f 3628 2 f 3527 1
f 3426 1 3> 2-23 图示为一内然机的机构运动简图，试计算自由度 t 并分析组成此机构的基本杆组。如在 该机构中改选 EG 为原动件，试问组成此机构的基本杆组是否与前者有所不同。
西北工业大学机械原理习题答案
2－3在图a所示的四杆机构中，lAB=60mm,lCD=90mm，lAD=lBC=120mm，ω2=10rad/s，试用瞬心法求：
1）当φ＝165°时，点C的速度vC；
2）当φ＝165°时，构件3的BC线上速度最小的一点E的位置及速度的大小；
何进一步的认识?
1—4图a所示为一具有急回作用的冲床。图中绕固定轴心A转动的菱形盘1为原动件，其与滑块2在B点铰接，通过滑块2推动拨叉3绕固定轴心C转动，而拨叉3与圆盘4为同一构件。当圆盘4转动时，通过连杆5使冲头6实现冲压运动。试绘制其机构运动简图，并计算自由度。
解：1)选取适当比例尺μl，绘制机构运动简图(见图b)
10．平面机构是指组成机构的各个构件均在同一个平面上运动。
11．在平面机构中，平面低副提供2个约束，平面高副提供1个约束。
12．机构具有确定运动时所必须给定的独立运动参数的数目称为机构的自由度。
13．机构具有确定运动的条件是机构的原动件数目应等于机构的自由度的数目。
1—2试画出图示平面机构的机构示意图，并计算自由度（步骤：1）列出完整公式，2）带入数据，3）写出结果）。其中：
解：自由度计算：画出机构示意图：
n=3
pL=4pH=0
p'=0F'=0
F=3n－(2pl＋ph－p′)－F′
=3×3－(2×4＋0－0)－0
=1
1—3 试绘出图a)所示偏心回转油泵机构的运动简图(各部分尺寸由图中直接量取)。图中偏心轮1绕固定轴心A转动，外环2上的叶片a在可绕轴心c转动的圆柱3中滑动，将低压油从右湍吸入，高压油从左端排出。
2)分析是否能实现设计意图
n=3
机械原理第八版课后练习答案(西工大版)(孙恒等)ppt课件
编辑版pppt
2-14 图示是为高位截肢的人所设汁的一种假肢膝关节机构。该机构能保持人行走的稳定性。 若以胫骨 1 为机架，试绘制其机构运动简图和计一算其自由度，并作出大腿弯曲时的机构运 动简图。 解 把胫骨 l 相对固定作为机架．假肢膝关节机构的机构运动简图如图
1)取比例尺绘制机构运动简图 2)分析是否能实现设计意图
f 33241 0不合理
∵ f 0，可改为
2-12 图示机构为一凸轮齿轮连杆组合机构，试绘制其机构示意简图并计算自由度。
解：
编辑版pppt
f 38210211 2-16 试计算图示凸轮-连杆组合机构的自由度
解： （b）
f 342511
(2)速度分析： 以 C 为重合点，有
vC2= vB+ vC2B= vC3+ vC2C3
大小 ?ω1lAB
?0’
方向 ? ┴AB ┴BC //BC
以μl作速度多边形图 (b)，再根据速度影像原理，作△bde∽／△BDE 求得 d 及 e，由图可得 vD=μvpd=0．23 m／s
vE=μvpe=0.173m/s ω2=μvbc2/lBC=2 rad/s(顺时针)
F=3n- (2pl+ph- p’)- F’ =3×6- (2ⅹ7+2-1)- 2=1 上述两种结构的机构虽然自由度均为一，但在性能上却各有千秋：前者的结构较复杂，但没 有虚约束，在运动中不易产生卡涩现象；后者则相反，由于有一个虚约束，假如不能保证在
运动精度要求 较高。 （c）
（2 分）
（2 分） （2 分）
机械原理课后答案3章
3-2 在如图所示的齿轮-连杆组合机构中，试用瞬心法求齿轮1与3的传动比ω1/ω3。
顺时针）(v 1613361331361331613113P P P PP P P P P ===ωωωω3-3在如图3-32所示的四杆机构中，LAB=60mm ，LCD=90mm ，LAD=LBC=120mm ，ω2=rad/s ，试用瞬心法求：（1） 当φ=165°时，点C 的速度vc;（2） 当φ=165°时，构件3的BC 线上（或延长线上）速度最小的一点E 的位置及其速度的大小；（3） 当vC=0时，φ角之值（有两个解）。
sm EP P P v P P v s m v s rad P P P P P P P P E C C CD C P /36.0143.055.2v (rad/s 55.2158.0403.0/403.009.048.4(/48.438.21738.9710v 133133431334341424122424142441224224=⨯=======⨯=⨯==⨯====ωωωωωωωω顺时针）顺时针）3-4在如图3-33所示的凸轮机构中，已知r=50mm ，LOA=30mm ，LAC=90mm ，φ1=90°，凸轮1以角速度ω1=10rad/s 逆时针转动。
试用瞬心法求从动件的角速度ω2。
顺时针）(/79.286.12486.3410v 2312131212231221312112s rad P P P P P P P P P =⨯====ωωωω 3-5在如图3-34所示的各机构中，已知各构件的尺寸及B 点的速度vB ，试作出其如图3-34所示位置时的速度多边形。
3-6在如图3-35所示的各机构中，已知各构件的尺寸，原动件1以等角速度ω1顺时针方向转动，试以图解法求机构在如图3-35所示位置时构件3上C 点的速度及角速度。
3-8A BCDEbk ec3。
西北工业大学机械原理课后答案第3章-1
第三章 平面机构的运动分析题3-3 试求图示各机构在图示位置时全部瞬心的位置(用符号P ij 直接标注在图上) 解：1P 13(P 34)13∞题3-4 在图示在齿轮-连杆机构中,试用瞬心法求齿轮1与齿轮3 的传动比w1/w3.P 13P 23P 363D 652C 4B P 16A 1P 12解：1〕计算此机构所有瞬心的数目152)1(=-=N N K2〕为求传动比31ωω需求出如下三个瞬心16P 、36P 、13P 如图3-2所示。
3〕传动比31ω计算公式为：1316133631P P P P =ωω题3-6在图a 所示的四杆机构中，l AB =60mm ，l CD =90mm ，l AD =l BC =120mm ，ω2=10rad/s ，试用瞬心法求：231） 当φ=165°时，点C 的速度Vc ；2） 当φ=165°时，构件3的BC 线上速度最小的一点E 的位置及速度的大小； 3） 当Vc=0时，φ角之值〔有两个解〕 解：1) 以选定比例尺,绘制机构运动简图。
(图3-3 ) 2〕求V C ，定出瞬心P 13的位置。
如图3-3〔a 〕s rad BP ll v l AB AB B 56.21323===μωω s m CP v l C 4.0313==ωμ 3〕定出构件3的BC 线上速度最小的点E 的位置。
因为BC 线上速度最小的点必与P 13点的距离最近，所以过P 13点引BC 线延长线的垂线交于E 点。
如图3-3〔a 〕s m EP v l E 375.0313==ωμ4〕当0=C v 时，P 13与C 点重合，即AB 与BC 共线有两个位置。
作出0=C v 的两个位置。
量得 ︒=4.261φ ︒=6.2262φ题3-12 在图示的各机构中，设已知各构件的尺寸、原动件1以等角速度ω1顺时针方向转动。
试用图解法求机构在图示位置时构件3上C 点的速度及加速度。
解：a)速度方程：32233C C C B C B C v v v v v +=+=加速度方程：r C C k C C C t B C n B C B t C nC a a a a a a a a 232323333++=++=+b) 速度方程：2323B B B B v v v +=加速度方程：r B B K B B B t B nB a a a a a 2323233++=+c) 速度方程：2323B B B B v v v +=加速度方程：r B B K B B B t B nB a a a a a 2323233++=+题3-14 在图示的摇块机构中，已知l AB =30mm ，l AC =100mm ，l BD =50mm ，l DE =40mm 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章 平面机构的运动分析题3-3 试求图示各机构在图示位置时全部瞬心的位置(用符号P ij 直接标注在图上) 解：1P 13(P 34)13∞题3-4 在图示在齿轮-连杆机构中,试用瞬心法求齿轮1与齿轮3 的传动比w1/w3.P 13P 23P 363D 652C 4B P 16A 1P 12解：1）计算此机构所有瞬心的数目152)1(=-=N N K2）为求传动比31ωω需求出如下三个瞬心16P 、36P 、13P 如图3-2所示。
3）传动比31ω计算公式为：1316133631P P P P =ωω题3-6在图a 所示的四杆机构中，l AB =60mm ，l CD =90mm ，l AD =l BC =120mm ，ω2=10rad/s ，试用瞬心法求：231） 当φ=165°时，点C 的速度Vc ；2） 当φ=165°时，构件3的BC 线上速度最小的一点E 的位置及速度的大小； 3） 当Vc=0时，φ角之值（有两个解） 解：1) 以选定比例尺,绘制机构运动简图。
(图3-3 ) 2）求V C ，定出瞬心P 13的位置。
如图3-3（a ）s rad BP ll v l AB AB B 56.21323===μωω s m CP v l C 4.0313==ωμ 3）定出构件3的BC 线上速度最小的点E 的位置。
因为BC 线上速度最小的点必与P 13点的距离最近，所以过P 13点引BC 线延长线的垂线交于E 点。
如图3-3（a ）s m EP v l E 375.0313==ωμ4）当0=C v 时，P 13与C 点重合，即AB 与BC 共线有两个位置。
作出0=C v 的两个位置。
量得 ︒=4.261φ ︒=6.2262φ题3-12 在图示的各机构中，设已知各构件的尺寸、原动件1以等角速度ω1顺时针方向转动。
试用图解法求机构在图示位置时构件3上C 点的速度及加速度。
解：a)速度方程：32233C C C B C B C v v v v v +=+=加速度方程：r C C k C C C t B C n B C B t C nC a a a a a a a a 232323333++=++=+b) 速度方程：2323B B B B v v v +=加速度方程：r B B K B B B t B nB a a a a a 2323233++=+c) 速度方程：2323B B B B v v v +=加速度方程：r B B K B B B t B nB a a a a a 2323233++=+题3-14 在图示的摇块机构中，已知l AB =30mm ，l AC =100mm ，l BD =50mm ，l DE =40mm 。
曲柄以等角速度ω1=10rad/s 回转，试用图解法求机构在φ1=45°位置时，点D 和点E 的速度和加速度，以及构件2的角速度和角加速度。
解： 1) 选定比例尺, mm mAB l AB l 002.01503.0===μ 绘制机构运动简图。
(图 (a)) 2）速度分析：图（b ）s m l v AB B 3.003.0101=⨯==ω速度方程32322C C C B C B C v v v v v +=+=mm s m pb v B v 005.0603.0===μ由速度影像法求出V E 速度多边形如图3-6 (b)s m pd v V D 224.083.44005.0=⨯==μ sm pe v V E 171.018.34005.0=⨯==μs l bc l v Bc v BC CB 1253.61002.05.49005.023=⨯⨯===μω （顺时针）3）加速度分析：图3-6（c ） mm s m b p a B a 2204.0753==''=μrC C k C C C t B C n B C B C a a a a a a a 32323222++=++=由加速度影像法求出a E 加速度多边形如图 (c)2221303.0101s m l a AB B =⨯==ω 222225.0122.021s m l a CB B C ==⨯==ω23223327.0175.0.222s m v a C C k C C =⨯⨯==ω 26.26504.0s m d p a a D =⨯=''=μ28.27104.0s me p a a E =⨯=''=μ 22222139.853.61002.06.2504.0s BC c c l a l a BC tBC =⨯⨯='''==μμα （顺时针）(a)题3-15在图示的机构中，已知l AE =70mm ，l AB =40mm ，l EF =60mm ，l DE =35mm ，l CD =75mm ，l BC =50mm ，原动件1以等角速度ω1=10rad/s 回转，试以图解法求点C 在φ1=50°时的速度Vc 和加速度a c 。
解：1) 速度分析：以F 为重合点(F 1、F 5、、F 4) 有速度方程：15154F F F F F v v v v +==以比例尺mm sm v 03.0=μ速度多边形如图3-7 (b)，由速度影像法求出V B 、V DCD D CB B C v v v v v +=+=2) 加速度分析：以比例尺mm s m a 26.0=μ有加速度方程：rF F k F F F t F n F F a a a a a a 15151444++=+= 由加速度影像法求出a B 、a DtCD n CD D t CB n CB B C a a a a a a a ++=++=s m pc v V C 69.0==μ23s mc p a a C =''=μ题3-16 在图示的凸轮机构中，已知凸抡1以等角速度s rad 101=ω转动，凸轮为一偏心圆，其半径︒====90,50,15,251ϕmm l mm l mm R AD AB ，试用图解法求构件2的角速度2ω与角加速度2α 。
解：1) 高副低代，以选定比例尺,绘制机构运动简图。
2) 速度分析：图（b ）s m l v v AB B B 15.0015.010114=⨯===ω 取B 4、、B 2为重合点。
速度方程：4242B B B B v v v +=速度多边形如图(b)s m pb v V B 1175.05.23005.022=⨯==μ sm b b v V B B 16.032005.02442=⨯==μs l pb l v BD v BD B 129.2400125.01175.0222=⨯===μω 转向逆时针3）加速度分析：图（c ）rB B K B B B t B n B a a a a a 4242422++=+2221145.1015.0101s m l a a AB n B n B =⨯===ω 22222269.04100125.029.21s m l a Bdn B =⨯⨯==ω 242242732.016.029.222s m v a B B k B B =⨯⨯==ω 22222136.94100125.01204.0s BD b b l a l a BD tB =⨯⨯='''==μμα 转向顺时针。
Bω11ACD 234ω22′′′′题3-18 在图a 所示的牛头刨床机构中，h=800mm ，h 1=360mm ，h 2=120mm ，l AB =200mm ，l CD =960mm ，lDE=160mm ，设曲柄以等角速度ω1=5rad/s 逆时针方向回转，试用图解法求机构在φ1=135°位置时，刨头上点C 的速度Vc 。
解： 选定比例尺,mm mAB l AB l 001.01212.0===μ 绘制机构运动简图。
(图 (a)) 解法一：速度分析：先确定构件3的绝对瞬心P 36，利用瞬心多边形，如图（b ）由构件3、5、6组成的三角形中，瞬心P 36、P 35、P 56必在一条直线上，由构件3、4、6组成的三角形中，瞬心P 36、P 34、P 46也必在一条直线上，二直线的交点即为绝对瞬心P 36。
速度方程2323B B B B v v v +=mm sm pb v B v 05.0201===μ s m l v v AB B B 12.05112=⨯===ω 方向垂直AB 。
V B3的方向垂直BG （BP 36），V B3B2的方向平行BD 。
速度多边形如图 (c) 速度方程33CB B Cv v v += sm pc v V C 24.1==μ(e)453162(d)∞P 56453621解法二：确定构件3的绝对瞬心P 36后，再确定有关瞬心P 16、P 12、P 23、P 13、P 15，利用瞬心多边形，如图3-9（d ）由构件1、2、3组成的三角形中，瞬心P 12、P 23、P 13必在一条直线上，由构件1、3、6组成的三角形中，瞬心P 36、P 16、P 13也必在一条直线上，二直线的交点即为瞬心P 13。
利用瞬心多边形，如图3-9（e ）由构件1、3、5组成的三角形中，瞬心P 15、P 13、P 35必在一条直线上，由构件1、5、6组成的三角形中，瞬心P 56、P 16、P 15也必在一条直线上，二直线的交点即为瞬心P 15。
如图3-9 (a) P 15为构件1、5的瞬时等速重合点sm AP v v l P C 24.115115===μω题3-19 在图示的齿轮-连杆组合机构中，MM 为固定齿条，齿轮3的齿数为齿轮4的2倍，设已知原动件1以等角速度ω1顺时针方向回转，试以图解法求机构在图示位置时，E 点的速度V E 以及齿轮3、4的速度影像。
解： 1) 选定比例尺l μ 绘制机构运动简图。
(图 (a))2）速度分析：此齿轮-连杆机构可看成ABCD 及DCEF 两个机构串联而成。
则 速度方程：CB B C v v v += EC C E v v v +=以比例尺v μ作速度多边形，如图 (b)pe vV E μ=取齿轮3与齿轮4的啮合点为K ，根据速度影像原理，在速度图(b)中作DCK dck ∆∆∽，求出k 点，以c 为圆心，以ck 为半径作圆g 3即为齿轮3的速度影像。
同理FEK fek ∆∆∽，以e 为圆心，以ek 为半径作圆g 4即为齿轮4的速度影像。
MM(a)(b)FEB A 61Cω1D2K453题3-20 如图a 所示的摆动式飞剪机用于剪切连续运动中的钢带。
设机构的尺寸为l AB =130mm ，l BC =340mm ，l CD =800mm 。