机械原理课后答案第章
机械原理习题册答案

参考答案 第一章 绪论一,填空题1.1 能量,物料,信息1.2运动,动力 1.3制造,运动,装配 二、选择题2.1 D 2.2 B 三,简答题第二章 机械的结构分析二、综合题1.n = 7 ,p l = 9 ,p h = 121927323=-⨯-⨯=--=h l P P n F从图中可以看出该机构有2个原动件,而由于原动件数与机构的自由度数相等,故该机构具有确定的运动。
2. (a )D 、E 处分别为复合铰链(2个铰链的复合);B 处滚子的运动为局部自由度;构件F 、G 及其联接用的转动副会带来虚约束。
n = 8 ,p l = 11 ,p h = 1111128323=-⨯-⨯=--=h l P P n F3. (c )n = 6 ,p l = 7 ,p h = 313726323=-⨯-⨯=--=h l P P n F(e )n = 7 ,p l = 10 ,p h = 0101027323=-⨯-⨯=--=h l P P n F 4. (a )n = 5 ,p l = 7 ,p h = 010725323=-⨯-⨯=--=h l P P n FⅡ级组 Ⅱ级组 因为该机构是由最高级别为Ⅱ级组的基本杆组构成的,所以为Ⅱ级机构。
(c )n = 5 ,p l = 7 ,p h = 010725323=-⨯-⨯=--=h l P P n FⅢ级组因为该机构是由最高级别为Ⅲ级组的基本杆组构成的,所以为Ⅲ级机构。
5. n = 7 ,p l =10 ,p h = 0101027323=-⨯-⨯=--=h l P P n FⅡ级组 Ⅲ级组当以构件AB 为原动件时,该机构为Ⅲ级机构。
Ⅱ级组 Ⅱ级组 Ⅱ级组当以构件FG 为原动件时,该机构为Ⅱ级机构。
可见同一机构,若所取的原动件不同,则有可能成为不同级别的机构。
6. (a )n = 3 ,p l = 4 ,p h = 101423323=-⨯-⨯=--=h l P P n F因为机构的自由度为0,说明它根本不能运动。
机械原理习题及答案
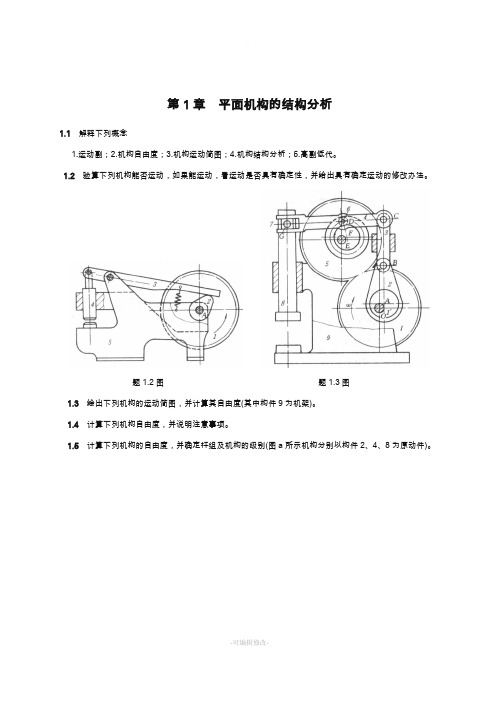
第1章平面机构的结构分析1.1解释下列概念1.运动副;2.机构自由度;3.机构运动简图;4.机构结构分析;5.高副低代。
1.2验算下列机构能否运动,如果能运动,看运动是否具有确定性,并给出具有确定运动的修改办法。
题1.2图题1.3图1.3 绘出下列机构的运动简图,并计算其自由度(其中构件9为机架)。
1.4 计算下列机构自由度,并说明注意事项。
1.5计算下列机构的自由度,并确定杆组及机构的级别(图a所示机构分别以构件2、4、8为原动件)。
题1.4图题1.5图第2章平面机构的运动分析2.1试求图示各机构在图示位置时全部瞬心。
题2.1图2.2在图示机构中,已知各构件尺寸为l AB=180mm , l BC=280mm , l BD=450mm ,l CD=250mm ,l AE =120mm ,φ=30º, 构件AB上点E的速度为v E=150 mm /s ,试求该位置时C、D两点的速度及连杆2的角速度ω2。
2.3 在图示的摆动导杆机构中,已知l AB=30mm , l AC=100mm , l BD=50mm ,l DE=40mm ,φ1=45º,曲柄1以等角速度ω1=10 rad/s沿逆时针方向回转。
求D点和E点的速度和加速度及构件3的角速度和角加速度(用相对运动图解法)。
题2.2图题2.3图2.4 在图示机构中,已知l AB =50mm , l BC =200mm , x D =120mm , 原动件的位置φ1=30º, 角速度ω1=10 rad/s ,角加速度α1=0,试求机构在该位置时构件5的速度和加速度,以及构件2的角速度和角加速度。
题2.4图2.5 图示为机构的运动简图及相应的速度图和加速度图。
(1)在图示的速度、加速度多边形中注明各矢量所表示的相应的速度、加速度矢量。
(2)以给出的速度和加速度矢量为已知条件,用相对运动矢量法写出求构件上D 点的速度和加速度矢量方程。
机械原理课后答案
习题解答第一章绪论1-1 答:1 )机构是实现传递机械运动和动力的构件组合体。
如齿轮机构、连杆机构、凸轮机构、螺旋机构等。
2 )机器是在组成它的实物间进行确定的相对运动时,完成能量转换或做功的多件实物的组合体。
如电动机、内燃机、起重机、汽车等。
3 )机械是机器和机构的总称。
4 )a. 同一台机器可由一个或多个机构组成。
b. 同一个机构可以派生出多种性能、用途、外型完全不同的机器。
c. 机构可以独立存在并加以应用。
1-2 答:机构和机器,二者都是人为的实物组合体,各实物之间都具有确定的相对运动。
但后者可以实现能量的转换而前者不具备此作用。
1-3 答:1 )机构的分析:包括结构分析、运动分析、动力学分析。
2 )机构的综合:包括常用机构设计、传动系统设计。
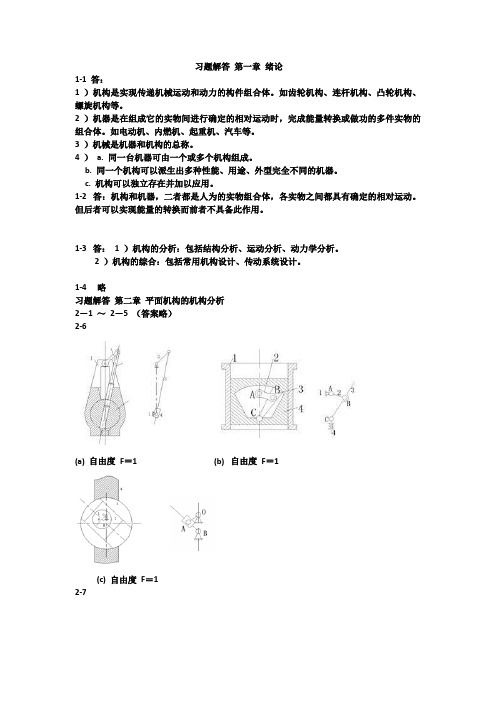
1-4 略习题解答第二章平面机构的机构分析2-1 ~2-5 (答案略)2-6(a) 自由度F=1 (b) 自由度F=1(c) 自由度F=12-7题2 -7 图F =3 × 7 -2 × 9 -2 =12 -8a) n =7 =10 =0 F =3×7-2×10 =1b) B 局部自由度n =3 =3 =2 F=3×3 -2×3-2=1c) B 、D 局部自由度n =3 =3 =2 F=3×3 -2×3-2 =1d) D( 或C) 处为虚约束n =3 =4 F=3×3 -2×4=1e) n =5 =7 F=3×5-2×7=1f) A 、B 、C 、E 复合铰链n =7 =10 F =3×7-2×10 =1g) A 处为复合铰链n =10 =14 F =3×10 -2×14=2h) B 局部自由度n =8 =11 =1 F =3×8-2×11-1 =1i) B 、J 虚约束C 处局部自由度n =6 =8 =1 F =3×6 -2×8-1=1j) BB' 处虚约束A 、C 、D 复合铰链n =7 =10 F =3×7-2×10=1 k) C 、D 处复合铰链n=5 =6 =2F =3×5-2×6-2 =1l) n =8 =11 F =3×8-2×11 =2m) B 局部自由度I 虚约束4 杆和DG 虚约束n =6 =8 =1 F =3×6-2×8-1 =12-9a) n =3 =4 =1 F =3 × 3 -2 × 8 -1 =0 不能动。
机械原理课后习题答案(朱理)

机械原理作业(部分答案)第一章结构分析作业1.2 解:F = 3n-2P L-P H = 3×3-2×4-1= 0该机构不能运动,修改方案如下图:1.2 解:(a)F = 3n-2P L-P H = 3×4-2×5-1= 1 A点为复合铰链。
(b)F = 3n-2P L-P H = 3×5-2×6-2= 1B、E两点为局部自由度, F、C两点各有一处为虚约束。
(c)F = 3n-2P L-P H = 3×5-2×7-0= 1 FIJKLM为虚约束。
1.3 解:F = 3n-2P L-P H = 3×7-2×10-0= 11)以构件2为原动件,则结构由8-7、6-5、4-3三个Ⅱ级杆组组成,故机构为Ⅱ级机构(图a)。
2)以构件4为原动件,则结构由8-7、6-5、2-3三个Ⅱ级杆组组成,故机构为Ⅱ级机构(图b)。
3)以构件8为原动件,则结构由2-3-4-5一个Ⅲ级杆组和6-7一个Ⅱ级杆组组成,故机构为Ⅲ级机构(图c)。
(a) (b) (c)第二章 运动分析作业2.1 解:机构的瞬心如图所示。
2.2 解:取mmmm l /5=μ作机构位置图如下图所示。
1.求D 点的速度V D13P D V V =而 25241314==P P AE V V E D ,所以 s mm V V E D /14425241502524=⨯==2. 求ω1s r a d l V AE E /25.11201501===ω3. 求ω2因 98382412141212==P P P P ωω ,所以s rad /46.0983825.1983812=⨯==ωω 4. 求C 点的速度V Csmm C P V l C /2.10154446.0242=⨯⨯=⨯⨯=μω2.3 解:取mmmm l /1=μ作机构位置图如下图a 所示。
1. 求B 2点的速度V B2V B2 =ω1×L AB =10×30= 300 mm/s 2.求B 3点的速度V B3V B3 = V B2 + V B3B2大小 ? ω1×L AB ? 方向 ⊥BC ⊥AB ∥BC 取mm s mm v /10=μ作速度多边形如下图b 所示,由图量得:mmpb 223= ,所以smm pb V v B /270102733=⨯=⨯=μ由图a 量得:BC=123 mm , 则mmBC l l BC 1231123=⨯=⨯=μ3. 求D 点和E 点的速度V D 、V E利用速度影像在速度多边形,过p 点作⊥CE ,过b 3点作⊥BE ,得到e 点;过e 点作⊥pb 3,得到d 点 , 由图量得:mmpd 15=,mmpe 17=,所以smm pd V v D /1501015=⨯=⨯=μ , smm pe V v E /1701017=⨯=⨯=μ;smm b b V v B B /17010173223=⨯=⨯=μ4. 求ω3s rad l V BC B /2.212327033===ω5. 求n B a 222212/30003010smm l a AB n B =⨯=⨯=ω6. 求3B aa B3 = a B3n + a B3t = a B2 + a B3B2k + a B3B2τ 大小 ω32L BC ? ω12L AB 2ω3V B3B2 ?方向 B →C ⊥BC B →A ⊥BC ∥BC 22233/5951232.2s mm l a BC n B =⨯=⨯=ω223323/11882702.222s mm V a B B k B B =⨯⨯=⨯=ω取mm s mm a 2/50=μ作速度多边形如上图c 所示,由图量得:mmb 23'3=π ,mmb n 20'33=,所以233/11505023's mm b a a B =⨯=⨯=μπ2333/10005020's mm b n a at B =⨯=⨯=μ7. 求3α233/13.81231000s rad l a BC tB ===α8. 求D 点和E 点的加速度a D 、a E利用加速度影像在加速度多边形,作e b 3'π∆∽CBE ∆, 即 BE eb CE e CB b 33''==ππ,得到e 点;过e 点作⊥3'b π,得到d 点 , 由图量得:mme 16=π,mmd 13=π,所以2/6505013s mm d a a D =⨯=⨯=μπ ,2/8005016s mm e a a E =⨯=⨯=μπ 。
机械原理第七版西北工业大学课后习题答案(2—8章)

机械原理课后习题答案第二章 机构的结构分析题2-11 图a 所示为一简易冲床的初拟设计方案。
设计者的思路是:动力由齿轮1输入,使轴A 连续回转;而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动,以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取),分析是否能实现设计意图,并提出修改方案。
解:1)取比例尺,绘制机构运动简图。
(图2-11a)2)要分析是否能实现设计意图,首先要计算机构的自由度。
尽管此机构有4个活动件,但齿轮1和凸轮2是固装在轴A 上,只能作为一个活动件,故 3=n 3=l p 1=h p01423323=-⨯-⨯=--=h l p p n F原动件数不等于自由度数,此简易冲床不能运动,即不能实现设计意图。
分析:因构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架。
故需增加构件的自由度。
3)提出修改方案:可以在机构的适当位置增加一个活动构件和一个低副,或用一个高副来代替一个低副。
(1) 在构件3、4之间加一连杆及一个转动副(图2-11b)。
(2) 在构件3、4之间加一滑块及一个移动副(图2-11c)。
(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-11d)。
11(c)题2-11(d)54364(a)5325215436426(b)321讨论:增加机构自由度的方法一般是在适当位置上添加一个构件(相当于增加3个自由度)和1个低副(相当于引入2个约束),如图2-1(b )(c )所示,这样就相当于给机构增加了一个自由度。
用一个高副代替一个低副也可以增加机构自由度,如图2-1(d )所示。
题2-12 图a 所示为一小型压力机。
图上,齿轮1与偏心轮1’为同一构件,绕固定轴心O 连续转动。
在齿轮5上开有凸轮轮凹槽,摆杆4上的滚子6嵌在凹槽中,从而使摆杆4绕C 轴上下摆动。
同时,又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。
《机械原理》第八版课后习题答案

第2章 机构的结构分析(P29)2-12:图a 所示为一小型压力机。
图上,齿轮1与偏心轮1’为同一构件,绕固定轴心O 连续转动。
在齿轮5上开有凸轮轮凹槽,摆杆4上的滚子6嵌在凹槽中,从而使摆杆4绕C 轴上下摆动。
同时,又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。
试绘制其机构运动简图,并计算自由度。
解:分析机构的组成:此机构由偏心轮1’(与齿轮1固结)、连杆2、滑杆3、摆杆4、齿轮5、滚子6、滑块7、冲头8和机架9组成。
偏心轮1’与机架9、连杆2与滑杆3、滑杆3与摆杆4、摆杆4与滚子6、齿轮5与机架9、滑块7与冲头8均组成转动副,滑杆3与机架9、摆杆4与滑块7、冲头8与机架9均组成移动副,齿轮1与齿轮5、凸轮(槽)5与滚子6组成高副。
故解法一:7=n 9=l p 2=h p12927323=-⨯-⨯=--=h l p p n F解法二:8=n 10=l p 2=h p 局部自由度1='F11210283)2(3=--⨯-⨯='-'-+-=F p p p n F h l(P30) 2-17:试计算如图所示各机构的自由度。
图a 、d 为齿轮-连杆组合机构;图b 为凸轮-连杆组合机构(图中在D 处为铰接在一起的两个滑块);图c 为一精压机机构。
并问在图d 所示机构中,齿轮3与5和齿条7与齿轮5的啮合高副所提供的约束数目是否相同?为什么?解: a) 4=n 5=l p 1=h p11524323=-⨯-⨯=--=h l p p n Fb) 5=n 6=l p 2=h p12625323=-⨯-⨯=--=h l p p n F12625323=-⨯-⨯=--=h l p p n Fc) 5=n 7=l p 0=h p10725323=-⨯-⨯=--=h l p p n Fd) 6=n 7=l p 3=h p13726323=-⨯-⨯=--=h l p p n F(C 可看做是转块和导块,有1个移动副和1个转动副)齿轮3与齿轮5的啮合为高副(因两齿轮中心距己被约束,故应为单侧接触)将提供1个约束。
机械原理课后习题答案
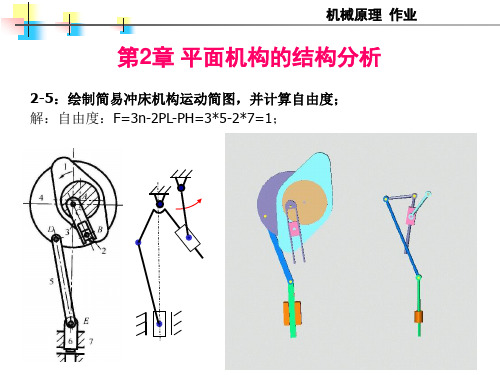
inva )
=6.8mm
分度圆半径r=mz/2=10*18/2=90mm
齿槽宽:ea=2π ra/z-sa
分度圆齿厚s=π m/2=15.7mm
=28.1mm
齿顶圆半径ra=r+ha*m=90+10=100mm
基圆半径rb=rcosα=90cos200=84.57mm
inv200=0.0148
齿顶圆压力角
第2章 平面机构的结构分析
2-7:计算自由度,指出所有的复合铰链、局部自由度和虚约束,判定运动 是否确定; 解:自由度:
a) F=3n-2PL-PH=3*3-2*4=1;确定 b) F=3n-2PL-PH=3*6-2*8=2;不确定 c) F=3n-2PL-PH=3*4-2*5-1=1;确定 d) F=3n-2PL-PH=3*4-2*5-1=1;确定
从而lAB+lBC, lBC-lAB可求得,最后确定lAB和lBC; 设计步骤:
①取一点A,并定D点; ②以D为圆心,作圆; 根据CD摆角15°定C1,C2点; ③ 量取lAC1,lAC2
lAB+lBC=430 lBC-lAB=348
C2 15° 15°C1
B A
lAB=41
A
B1
D
lBC=389
B2
虚约束
局部自由度
复合铰链
a)
b)
c)
d)
机械原理 作业
第2章 平面机构的结构分析
2-8:计算自由度;确定机构所含杆组的数目与级别;确定机构级别。画出 瞬时替代机构; 解:自由度:
a) F=3n-2PL-PH=3*7-2*10=1;Ⅱ级 b) F=3n-2PL-PH=3*6-2*8-1=1;Ⅲ级
机械原理第七版课后答案

机械原理第七版课后答案
1. 机械原理是工程学中的重要基础课程,它涉及到机械结构、运动学、动力学等方面的知识,对于理解和设计各种机械系统都具有重要意义。
在学习机械原理的过程中,课后习题是检验学生对知识掌握程度的重要手段。
因此,以下是机械原理第七版课后答案,供大家参考。
2. 第一章机械原理基础知识。
1. 什么是机械原理?
答,机械原理是研究机械运动规律和机械结构工作原理的科学。
2. 机械原理的研究对象包括哪些方面?
答,机械原理的研究对象包括机械结构、运动学、动力学等方面的知识。
3. 第二章机械结构。
1. 什么是机械结构?
答,机械结构是由零件和零件之间的连接构成的整体。
2. 机械结构的作用是什么?
答,机械结构的作用是传递和转换力、运动和能量。
4. 第三章运动学。
1. 什么是运动学?
答,运动学是研究物体运动状态、运动轨迹和运动规律的学科。
2. 运动学的研。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第8章作业8-l 铰链四杆机构中,转动副成为周转副的条件是什么?在下图所示四杆机构ABCD 中哪些运动副为周转副?当其杆AB 与AD 重合时,该机构在运动上有何特点?并用作图法求出杆3上E 点的连杆曲线。
答:转动副成为周转副的条件是:(1)最短杆与最长杆的长度之和小于或等于其他两杆长度之和;(2)机构中最短杆上的两个转动副均为周转副。
图示ABCD 四杆机构中C 、D 为周转副。
当其杆AB 与AD 重合时,杆BE 与CD 也重合因此机构处于死点位置。
8-2曲柄摇杆机构中,当以曲柄为原动件时,机构是否一定存在急回运动,且一定无死点?为什么? 答:机构不一定存在急回运动,但一定无死点,因为:(1)当极位夹角等于零时,就不存在急回运动如图所示,(2)原动件能做连续回转运动,所以一定无死点。
8-3 四杆机构中的极位和死点有何异同?8-4图a 为偏心轮式容积泵;图b 为由四个四杆机构组成的转动翼板式容积泵。
试绘出两种泵的机构运动简图,并说明它们为何种四杆机构,为什么?解 机构运动简图如右图所示,ABCD 是双曲柄机构。
因为主动圆盘AB 绕固定轴A 作整周转动,而各翼板CD 绕固定轴D 转动,所以A 、D 为周转副,杆AB 、CD 都是曲柄。
8-5试画出图示两种机构的机构运动简图,并说明它们各为何种机构。
图a 曲柄摇杆机构图b 为导杆机构。
8-6如图所示,设己知四杆机构各构件的长度为240a mm =,600b =mm ,400,500c mm d mm ==。
试问:1)当取杆4为机架时,是否有曲柄存在?2)若各杆长度不变,能否以选不同杆为机架的办法获得双曲柄机构和双摇杆机构?如何获得?3)若a 、b ﹑c 三杆的长度不变,取杆4为机架,要获得曲柄摇杆机构,d 的取值范围为何值? :解 (1)因a+b=240+600=840≤900=400+500=c+d 且最短杆 1为连架轩.故当取杆4为机架时,有曲柄存在。
(2)、能。
要使此此机构成为双曲柄机构,则应取1杆为机架;两使此机构成为双摇杆机构,则应取杆3为机架。
(3)要获得曲柄摇杆机构, d 的取值范围应为440~760mm 。
8-7图示为一偏置曲柄滑块机构,试求杆AB 为曲柄的条件。
若偏距e=0,则杆AB 为曲柄的条件是什么? 解 (1)如果杆AB 能通过其垂直于滑块导路的两位置时,则转动副A 为周转副,故杆AB 为曲柄的条件是AB+e ≤BC 。
(2)若偏距e=0, 则杆AB 为曲柄的条件是AB≤BC8-8 在图所示的铰链四杆机构中,各杆的长度为1l 28mm =,2l 52mm =, 3l 50mm =,4l 72mm =,试求:1)当取杆4为机架时,该机构的极位夹角θ、杆3的最大摆角ϕ、最小传动角min γ和行程速比系数K;2)当取杆1为机架时,将演化成何种类型的机构?为什么?并说明这时C 、D 两个转动副是周转副还是摆转副;3)当取杆3为机架时,又将演化成何种机构?这时A 、B 两个转动副是否仍为周转副?解 (1)怍出机构的两个极位,如图, 并由图中量得:θ=,φ=, γmin= o(2)①由l1+l4 ≤l2+l3可知图示铰链四杆机构各杆长度符合杆长条件;小②最短杆l 为机架时,该机构将演化成双曲柄机构;③最短杆1参与构成的转动副A 、B 都是周转副而C 、D 为摆转副;(3)当取杆3为机架时,最短杆变为连杆,又将演化成双摇杆机构,此时A 、B 仍为周转副。
8-9 在图示的连杆机构中,已知各构件的尺寸为160,AB l mm =BC l =260,mm200,CD l mm =80,AD l mm =构件AB 为原动件,沿顺时针方向匀速回转,试确定:1)四杆机构ABCD 的类型;2)该四杆机构的最小传动角min γ;3)滑块F 的行程速比系数K 。
解 (1)由l AD +l BC <l AB +l CD 且最短杆AD 为机架可知,图中四杆ABCD 为双曲柄机构;(2)作出四杆机构ABCD 传动角最小时的位置。
见图并量得γmin =12o(3)作出滑块F 的上、下两个极位及原动件AB 与之对应的两个极位,并量得θ=47o 。
求出滑块F 的行程速比系数为8-10试说明对心曲柄滑块机构当以曲柄为主动件时,其传动角在何处最大?何处最小?解 在曲柄与导轨共线的两位置之一传动角最大,γmax =90 o ;在曲柄与机架共线的两位置之一传动角最小,γmin =arcos(L AB /l BC )。
8-11正弦机构(图8一15b)和导杆机构(图8—22a)中,当以曲柄为主动件时,最小传动角γmin 为多少?传动角按什么规律变化?解 γmin =90o ;传动角恒定不变。
8-12图示为偏置导杆机构,试作出其在图示位置时的传动角以及机构的最小传动角及其出现的位置,并确定机构为回转导杆机构的条件。
解 传动角以及机构最小传动角及其出现的位置如下图所示。
机构为回转导杆机构的条件: AB≤AC8-13如图8—57所示,当按给定的行程速度变化系数K 设计曲柄摇杆机构时,试证明若将固定铰链A 的中心取在FG 弧段上将不满足运动连续性要求。
答 因这时机构的两极位DC 1, DC 2将分别在两个不连通的可行域内。
8-14图示为一实验用小电炉的炉门装置,关闭时为位置E 1,开启时为位置E 2。
试设计一个四杆机构来操作炉门的启闭(各有关尺寸见图)。
(开启时,炉门应向外开启,炉门与炉体不得发生干涉。
而关闭时,炉门应有一个自动压向炉体的趋势(图中S 为炉门质心位置)。
B 、C 为两活动铰链所在位置。
解 (1)作出B 2C 2的位置;用作图法求出A 及D 的位置,并作出机构在E 2位置的运动简图,见下图,并从图中量得l AB ==μ=95 mml AD =μ =335mml CD =μ=290mm(2)用怍图法在炉门上求得B 及C 点位置,并作出机构在位置的运动图(保留作图线)。
作图时将位置E1转至位置E2,见图并量得l AB =μ= mml BC =μl BC=l rnml CD =μ= mn8-15 图示为公共汽车车门启闭机构。
已知车门上铰链C 沿水平直线移动,铰链B 绕固定铰链A 转动,车门关闭位置与开启位置夹角为a=115 o ,AB 11C D 2C D 3C D 1F 2F 3F 2F30mm 75CD l mm =100AD l mm =45ψ=︒AB l BC l 1 1.51180180361 1.51k k θ--===++o o o 图可得两个解: (1) l AB =μl. (AC 2-AC 1)/2 =, l BC =μl . (AC 2+AC 1)/2=(2) l AB =μl. (AC 1-AC 2)/2 =22mm, l BC =μl . (AC 2+AC 1)/2=48mm8-24如图所示,设已知破碎机的行程速度变化系数K=,颚板长度l CD =300 mm 颚板摆角φ=35o ,曲柄长度l AD =80 mm 。
求连杆的长度,并验算最小传动角γmin 是否在允许的范围内。
解:先计算1 1.51180180361 1.51k k θ--===++o o o取相应比例尺μl 作出摇杆CD 的两极限位置C 1D 及C 2D 和固定铰链A 所在圆s 1(保留作图线)。
-如图所示,以C 2为圆心、2AB 为半径作圆,同时以F 为圆心2FC 2为半径作圆,两圆交于点E ,作C 2E 的延长线与圆s 1的交点,即为铰链A 的位置。
由图知: l BC =μl . AC 1+l AB =310mmγmin =γ``=45o>40o8-25图示为一牛头刨床的主传动机构,已知l AB =75 mm ,l DE =100 mm ,行程速度变化系数K=2,刨头5的行程H=300 mm 。
要求在整个行程中,推动刨头5有较小的压力角,试设计此机构。
解 先算导杆的摆角12118018060121k k ϕθ--====++o o o取相应比例尺μl 作图,由图可得导杆机构导杆和机架的长度为:L CD =μ=300mm, l AC =μ=150mm;导杆端点D 的行程 D 1D 2=E 1E 2=H/μl为了使推动刨头5在整行程中有较小压力角,刨头导路的位置h 成为H=l CD (1+cos(φ/2))/2=300[(1+cos(60/2))/2=点津 本题属于按行程速比系数K 设计四杆机构问题,需要注意的是:①导杆CD 的最大摆角与机构极位夹角相等:②因H=300mm ,且要求在整个行中刨头运动压力角较小。
所以取CD 1=CD 2=300mm, 则D 1D 2=H=300mm 。
8-26某装配线需设计一输送工件的四杆机构,要求将工件从传递带C 1经图示中间位置输送到传送带C 2上。
给定工件的三个方位为:M 1(204,-30),θ21=0o ;M 2(144,80),θ22=22 o ;M 3(34,100),θ23=68 o 。
初步预选两个固定铰链的位置为A(0,0)、D(34,一83)。
试用解析法设计此四杆机构。
解 由题可知, 本题属于按预定的连杆位置用解析法设汁四杆机构问题,N=3,并已预选x A , y A 和x D , y D 坐标值,具体计算过程略。
8-27 如图所示,设要求四杆机构两连架杆的三组对应位置分别为:135α=︒,150ϕ=︒,280α=︒,275ϕ=︒,3α=125︒,3105ϕ=︒。
试以解析法设计此四杆机构。
解:(1)将α, φ 的三组对应值带入式(8-17)(初选α0=φ0=0)Cos(α+α0)=p 0cos(φ+φ0)+p 1cos[(φ+φ0)-(α+α0)]+p 2 得 012012012cos35cos50cos(5035)cos80cos 75cos(7580)cos125cos105cos(105125)p p p p p p p p p ⎧=+-+⎪=+-+⎨⎪=+-+⎩o o o o o o o o o o o解之得(计算到小数点后四位)p 0=, p 1=, p 2=(2)如图所示,求各杆的相对长度,得n=c/a=p 0=, l=-n/p=(3)求各杆的长度:得d=a=d/l=80/=b=ma=ⅹ=c=na=ⅹ=8-28试用解析法设计一曲柄滑块机构,设已知滑块的行程速度变化系数K=1.5,滑块的冲程H=50 mm ,偏距e=20 mm 。
并求其最大压力角αmax 。
解:计算1 1.51180180361 1.51k k θ--===++o o o 并取相应比例尺μl 根据滑块的行程H 作出极位及作θ圆,作偏距线,两者的交点即铰链所在的位置,由图可得:l AB =μl. (AC 2-AC 1)/2 =17mm, l BC =μl . (AC 2+AC 1)/2=36mm8-29试用解析法设计一四杆机构,使其两连架杆的转角关系能实现期望函数y=^,l ≤z ≤10。
