机械原理课后答案第章
《机械原理》第十三、十四章课后答案（孙恒版）
第13章
第14章机械系统的方案设计
(2)工作循环图有3种形式:直线式工作循环图、圆周式工作循环图、直角坐标式工作循环图。
(3)工作循环图在机械传动系统设计中的作用:
①保证各执行构件的动作相互协调、紧密配合，使机械顺利实现预期的工艺动作;
②为进-步设计各执行机构的运动尺寸提供重要依据;
③为机械系统的安装、调试提供依据。
(4)不是。
在设计某些机械系统时，其各执行构件间的运动具有协调配合关系，因此在设计这类机械时应编制出工作循环图:反之，如果在某些机械中各执行构件之间的运动是彼此独立的，不需要协调配合，则不需要编制工作循环图。
14-4机构选型有哪几种途径?在选型时应考虑哪些问题?
答: (1)机构选型的途径:
①从常用机构中选择;
②机构变异;
③机构组合;
④利用最小阻力定律使传动机构简化。
(2)在选型时应考虑机构的工作特点、性能和工作场合、动力等要求。
14-5机构的变异与组合各有哪几种方式?
答: (1)机构的变异方式。
机械原理第八版课后练习答案西工大
解：
1> 2>
f 3 6 2 8 2 f 3 5 2 7 1
f 3 4 2 6 1 3> 2-23 图示为一内然机的机构运动简图，试计算自由度 t 并分析组成此机构的基本杆组。如在 该机构中改选 EG 为原动件，试问组成此机构的基本杆组是否与前者有所不同。
解：机械运动简图如下：
F=3n-(2p1 +pb-p`)-F`=3×5-(2×6+1-0)-1=1
第3章 3—1 何谓速度瞬心?相对瞬心与绝对瞬心有何异同点? 答：参考教材 30~31 页。 3—2 何谓三心定理?何种情况下的瞬心需用三心定理来确定? 答：参考教材 31 页。 3-3 试求图示各机构在图示位置时全部瞬心的位置(用符号 P， ，直接标注在图上) (a)
3） ω1 /ω3 = P36 P13 /P16P13=DK/AK 由构件 1、3 在 K 点的速度方向相同，可知ω3 与ω1 同向。 3-6 在图示的四杆机构中， LAB=60mm， LCD=90mm,LAD=LBC=120mm, ω2 =10rad/s,试用瞬心法求： 1)当φ=165°时，点的速度 vc； 2)当φ=165°时，构件 3 的 BC 线上速度最小的一点 E 的位置及速度的大小； 3)当 VC=0 时，φ角之值(有两个解)。
A 为复合铰链
解： （1） 图示机构在 D 处的结构与图 2-1 所示者一致，经分析知该机构共有 7 个活动构件， 8 个低副(注意移动副 F 与 F’ ，E 与 E’均只算作一个移动副 )，2 个高副；因有两个滚子 2、4， 所以有两个局部自由度，没有虚约束，故机构的自由度为 F=3n- (2pl+ph- p’)- F’=3ⅹ7- (2ⅹ8+2-0)- 2=1 （2）如将 D 处结构改为如图 b 所示形式，即仅由两个移动副组成。注意，此时在该处 将带来一个虚约束。因为构件 3、6 和构件 5、 6 均组成移动副，均要限制构件 6 在图纸平面 内转动，这两者是重复的，故其中有一个为虚约束。经分析知这时机构的活动构件数为 6， 低副数为 7，高副数和局部自由度数均为 2，虚约束数为 1，故机构的自由度为 F=3n- (2pl+ph - p’)- F’ =3×6- (2ⅹ7+2-1)- 2=1 上述两种结构的机构虽然自由度均为一，但在性能上却各有千秋：前者的结构较复杂，但没 有虚约束，在运动中不易产生卡涩现象；后者则相反，由于有一个虚约束，假如不能保证在 运动过程中构件 3、5 始终垂直，在运动中就会出现卡涩甚至卡死现象，故其对制造精度要求 较高。 （c）
机械原理 第七版西北工业大学课后习题答案(7-11章)(DOC)
第7章课后习题参考答案7—1等效转动惯量和等效力矩各自的等效条件是什么?7—2在什么情况下机械才会作周期性速度波动?速度波动有何危害?如何调节?答: 当作用在机械上的驱动力（力矩)周期性变化时，机械的速度会周期性波动。
机械的速度波动不仅影响机械的工作质量，而且会影响机械的效率和寿命。
调节周期性速度波动的方法是在机械中安装一个具有很大转动惯量的飞轮。
7—3飞轮为什么可以调速?能否利用飞轮来调节非周期性速度波动，为什么?答： 飞轮可以凋速的原因是飞轮具有很大的转动惯量，因而要使其转速发生变化．就需要较大的能量，当机械出现盈功时，飞轮轴的角速度只作微小上升，即可将多余的能量吸收储存起来；而当机械出现亏功时，机械运转速度减慢．飞轮又可将其储存的能量释放，以弥补能最的不足，而其角速度只作小幅度的下降。
非周期性速度波动的原因是作用在机械上的驱动力(力矩)和阻力(力矩)的变化是非周期性的。
当长时问内驱动力(力矩)和阻力(力矩)做功不相等，机械就会越转越快或越转越慢．而安装飞轮并不能改变驱动力(力矩)或阻力(力矩)的大小也就不能改变驱动功与阻力功不相等的状况，起不到调速的作用，所以不能利用飞轮来调节非周期陛速度波动。
7—4为什么说在锻压设备等中安装飞轮可以起到节能的作用?解： 因为安装飞轮后，飞轮起到一个能量储存器的作用，它可以用动能的形式把能量储存或释放出来。
对于锻压机械来说，在一个工作周期中，工作时间很短．而峰值载荷很大。
安装飞轮后．可以利用飞轮在机械非工作时间所储存能量来帮助克服其尖峰载荷，从而可以选用较小功率的原动机来拖动，达到节能的目的，因此可以说安装飞轮能起到节能的作用。
7—5由式J F =△W max ／(ωm 2 [δ])，你能总结出哪些重要结论(希望能作较全面的分析)?答：①当△W max 与ωm 一定时，若[δ]下降，则J F 增加。
所以，过分追求机械运转速度的均匀性，将会使飞轮过于笨重。
②由于J F 不可能为无穷大，若△W max ≠0，则[δ]不可能为零，即安装飞轮后机械的速度仍有波动，只是幅度有所减小而已。
机械原理第2、3、4、6章课后答案西北工业大学(第七版)
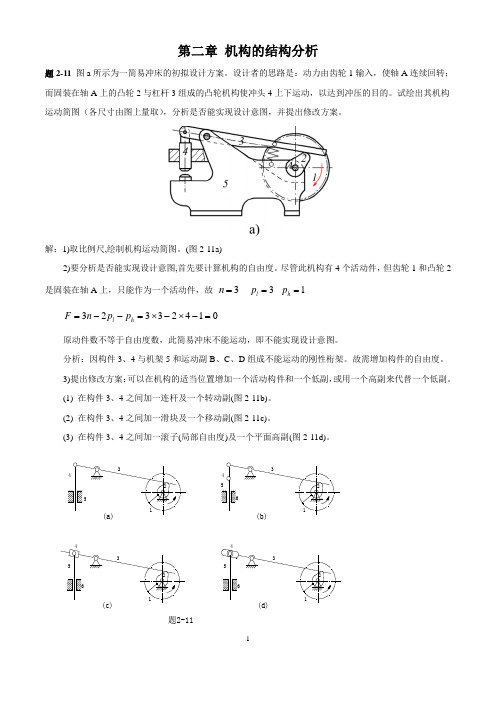
第二章 机构的结构分析题2-11 图a 所示为一简易冲床的初拟设计方案。
设计者的思路是：动力由齿轮1输入，使轴A 连续回转；而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动，以达到冲压的目的。
试绘出其机构运动简图（各尺寸由图上量取），分析是否能实现设计意图，并提出修改方案。
解：1)取比例尺,绘制机构运动简图。
(图2-11a)2)要分析是否能实现设计意图,首先要计算机构的自由度。
尽管此机构有4个活动件，但齿轮1和凸轮2是固装在轴A 上，只能作为一个活动件，故 3=n 3=l p 1=h p01423323=-⨯-⨯=--=h l p p n F原动件数不等于自由度数，此简易冲床不能运动，即不能实现设计意图。
分析：因构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架。
故需增加构件的自由度。
3)提出修改方案：可以在机构的适当位置增加一个活动构件和一个低副，或用一个高副来代替一个低副。
(1) 在构件3、4之间加一连杆及一个转动副(图2-11b)。
(2) 在构件3、4之间加一滑块及一个移动副(图2-11c)。
(3) 在构件3、4之间加一滚子(局部自由度)及一个平面高副(图2-11d)。
题2-11讨论：增加机构自由度的方法一般是在适当位置上添加一个构件（相当于增加3个自由度）和1个低副（相当于引入2个约束），如图2-1（b ）（c ）所示，这样就相当于给机构增加了一个自由度。
用一个高副代替一个低副也可以增加机构自由度，如图2-1（d ）所示。
题2-12 图a 所示为一小型压力机。
图上，齿轮1与偏心轮1’为同一构件，绕固定轴心O 连续转动。
在齿轮5上开有凸轮轮凹槽，摆杆4上的滚子6嵌在凹槽中，从而使摆杆4绕C 轴上下摆动。
同时，又通过偏心轮1’、连杆2、滑杆3使C 轴上下移动。
最后通过在摆杆4的叉槽中的滑块7和铰链G 使冲头8实现冲压运动。
试绘制其机构运动简图，并计算自由度。
华科机械原理课后习题答案第五六七章_
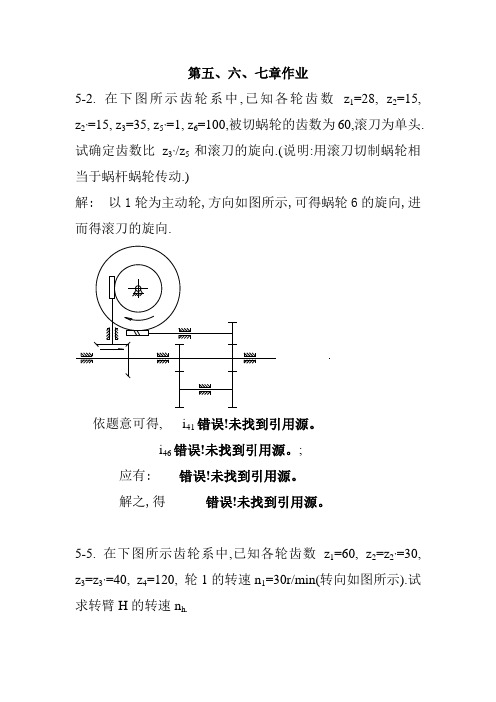
第五、六、七章作业5-2. 在下图所示齿轮系中,已知各轮齿数z1=28, z2=15, z2’=15, z3=35, z5’=1, z6=100,被切蜗轮的齿数为60,滚刀为单头.试确定齿数比z3’/z5和滚刀的旋向.(说明:用滚刀切制蜗轮相当于蜗杆蜗轮传动.)解: 以1轮为主动轮,方向如图所示,可得蜗轮6的旋向,进而得滚刀的旋向.依题意可得, i41错误!未找到引用源。
i46错误!未找到引用源。
;应有: 错误!未找到引用源。
解之,得错误!未找到引用源。
5-5. 在下图所示齿轮系中,已知各轮齿数z1=60, z2=z2’=30, z3=z3’=40, z4=120, 轮1的转速n1=30r/min(转向如图所示).试求转臂H的转速n h.解:图中的周转齿轮系,其转化轮系的传动比的计算公式为i H14错误!未找到引用源。
由此可解得: 错误!未找到引用源。
(负号表示与n1反向) ;5-8. 在下图所示齿轮系中,已知各轮齿数z1=20, z2=40, z3=20, z4=80, z4’=60, z5=50,z5’=55, z6=65, z6’=1, z7=60, 轮1、3的转速n1=n3=3000r/min(转向如图所示). 试求转速n7.解依题意, 错误!未找到引用源。
n2错误!未找到引用源。
i 34错误!未找到引用源。
对于周围齿轮系4’-5-5’-6; 此转化轮系的传动比计算公式为:i H 36错误!未找到引用源。
;由此解出 错误!未找到引用源。
(负号表示与n 2反向);进而n 7=错误!未找到引用源。
;5.12 在如图所示齿轮系中，已知各轮齿数1z =20，2z =40，3z =35，'3z =30，''3z =1，4z =20，5z =75，'5z =80，6z =30，7z =90，8z =30，9z =20，10z =50，轮1的转速1n =100r/min,试求轮10的转速10n 。
机械原理包含课后答案
第一章绪论一、教学要求（1）明确本课程研究的对象和内容，及其在培养机械类高级工程技术人才全局中的地位、任务和作用。
（2）对机械原理学科的发展现状有所了解。
二、主要内容1．机械原理课程的研究对象机械原理（Theory of Machines and Mechanisms）是以机器和机构为研究对象，是一门研究机构和机器的运动设计和动力设计，以及机械运动方案设计的技术基础课。
机器的种类繁多，如内燃机、汽车、机床、缝纫机、机器人、包装机等，它们的组成、功用、性能和运动特点各不相同。
机械原理是研究机器的共性理论，必须对机器进行概括和抽象内燃机与机械手的构造、用途和性能虽不相同，但是从它们的组成、运动确定性及功能关系看，都具有一些共同特征：1）人为的实物（机件）的组合体。
2）组成它们的各部分之间都具有确定的相对运动。
3）能完成有用机械功或转换机械能。
机构是传递运动和动力的实物组合体。
最常见的机构有连杆机构、凸轮机构、齿轮机构、间歇运动机构、螺旋机构、开式链机构等。
它们的共同特征是：（1）人为的实物（机件）的组合体。
（2）组成它们的各部分之间都具有确定的相对运动。
2．机械原理课程的研究内容1、机构的分析1）机构的结构分析（机构的组成、机构简图、机构确定运动条件等）；2）机构的运动分析（机构的各构件的位移、速度和加速度分析等）；3）机构的动力学分析（机构的受力、效率、及在外力作用下机构的真实运动规律等）；2、机构的综合（设计）：创新的过程1）常用机构的设计与分析（连杆机构、凸轮机构、齿轮机构、常用间歇机构等）；2）传动系统设计（选用、组装、协调机构）通过对机械原理课程的学习，应掌握对已有的机械进行结构、运动和动力分析的方法，以及根据运动和动力性能方面的设计要求设计新机械的途径和方法。
3 机械原理课程的地位和作用机械原理是以高等数学、物理学及理论力学等基础课程为基础的，研究各种机械所具有的共性问题；它又为以后学习机械设计和有关机械工程专业课程以及掌握新的科学技术成就打好工程技术的理论基础。
机械原理课后全部习题解答
机械原理课后全部习题解答文档编制序号：[KKIDT-LLE0828-LLETD298-POI08]《机械原理》习题解答机械工程学院目录第1章绪论 (1)第2章平面机构的结构分析 (3)第3章平面连杆机构 (8)第4章凸轮机构及其设计 (15)第5章齿轮机构 (19)第6章轮系及其设计 (26)第8章机械运动力学方程 (32)第9章平面机构的平衡 (39)第一章绪论一、补充题1、复习思考题1)、机器应具有什么特征机器通常由哪三部分组成各部分的功能是什么2）、机器与机构有什么异同点3）、什么叫构件什么叫零件什么叫通用零件和专用零件试各举二个实例。
4）、设计机器时应满足哪些基本要求试选取一台机器，分析设计时应满足的基本要求。
2、填空题1)、机器或机构，都是由组合而成的。
2）、机器或机构的之间，具有确定的相对运动。
3）、机器可以用来人的劳动，完成有用的。
4）、组成机构、并且相互间能作的物体，叫做构件。
5）、从运动的角度看，机构的主要功用在于运动或运动的形式。
6）、构件是机器的单元。
零件是机器的单元。
7）、机器的工作部分须完成机器的动作，且处于整个传动的。
8）、机器的传动部分是把原动部分的运动和功率传递给工作部分的。
9）、构件之间具有的相对运动，并能完成的机械功或实现能量转换的的组合，叫机器。
3、判断题1)、构件都是可动的。
（）2）、机器的传动部分都是机构。
（）3）、互相之间能作相对运动的物件是构件。
（）4）、只从运动方面讲，机构是具有确定相对运动构件的组合。
（）5）、机构的作用，只是传递或转换运动的形式。
（）6）、机器是构件之间具有确定的相对运动，并能完成有用的机械功或实现能量转换的构件的组合。
（）7）、机构中的主动件和被动件，都是构件。
（）2 填空题答案1）、构件 2）、构件 3）、代替机械功 4）、相对运动 5）、传递转换6）、运动制造 7）、预定终端 8）、中间环节 9）、确定有用构件3判断题答案1）、√ 2）、√ 3）、√ 4）、√ 5）、× 6）、√ 7）、√第二章 机构的结构分析2-7 是试指出图2-26中直接接触的构件所构成的运动副的名称。
机械原理第八版课后练习答案
<机械原理>第八版西工大教研室编第2章2-1 何谓构件何谓运动副及运动副元素运动副是如何进行分类的答：参考教材5~7页。
2-2 机构运动简图有何用处它能表示出原机构哪些方面的特征答：机构运动简图可以表示机构的组成和运动传递情况，可进行运动分析，而且也可用来进行动力分析。
2-3 机构具有确定运动的条件是什么当机构的原动件数少于或多于机构的自由度时，机构的运动将发生什么情况答：参考教材12~13页。
2-4 何谓最小阻力定律试举出在机械工程中应用最小阻力定律的1、2个实例。
2-5 在计算平面机构的自由度时，应注意哪些事项答：参考教材15~17页。
2-6 在图2-20所示的机构中，在铰链C、B、D处，被连接的两构件上连接点的轨迹都是重合的，那么能说该机构有三个虚约束吗为什么答：不能，因为在铰链C、B、D中任何一处，被连接的两构件上连接点的轨迹重合是由于其他两处的作用，所以只能算一处。
2-7 何谓机构的组成原理何谓基本杆组它具有什么特性如何确定基本杆组的级别及机构的级别答：参考教材18~19页。
2-8 为何要对平面高副机构进行“高副低代"“高副低代”应满足的条件是什么答：参考教材20~21页。
2-9 任选三个你身边已有的或能观察到的下列常用装置(或其他装置)，试画出其机构运动简图，并计算其自由度。
1)折叠桌或折叠椅；2)酒瓶软木塞开盖器；3)衣柜上2-11图示为一简易冲床的初拟设计方案。
设计者的思路是：动力由齿轮j输入，使轴A连续回转；而固装在轴^上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动，以达到冲压的目的。
试绘出其机构运动简图(各尺寸由图上量取)，分析是否能实现设计意图，并提出修改方案。
1)取比例尺绘制机构运动简图2)分析是否能实现设计意图解：不合理∵，可改为试绘制其机构示意简图并计算自由度。
解：2-16试计算图示凸轮-连杆组合机构的自由度（a）解： A为复合铰链（b）解：（1）图示机构在D处的结构与图2-1所示者一致，经分析知该机构共有7个活动构件，8个低副(注意移动副F与F’，E与E’均只算作一个移动副)，2个高副；因有两个滚子2、4，所以有两个局部自由度，没有虚约束，故机构的自由度为F=3n- (2p l+p h- p’)- F’=3ⅹ7- (2ⅹ8+2-0)- 2=1（2）如将D处结构改为如图b所示形式，即仅由两个移动副组成。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第6章作业
6—1什么是静平衡?什么是动平衡?各至少需要几个平衡平面?静平衡、动平衡的力学条件
各是什么?
6—2动平衡的构件一定是静平衡的，反之亦然，对吗?为什么?在图示 （a）（b）两根曲
轴中，设各曲拐的偏心质径积均相等，且各曲拐均在同一轴平面上。试说明两者各处于何
种平衡状态?
答：动平衡的构件一定是静平衡的，反之不一定。因各偏心质量产生的合惯性力为零时，
合惯性力偶不一定为零。（a）图处于动平衡状态，（b）图处于静平衡状态。
6一3既然动平衡的构件一定是静平衡的，为什么一些制造精度不高的构件在作动平衡
之前需先作静平衡?
6—4为什么作往复运动的构件和作平面复合运动的构件不能在构件本身内获得平衡，而
必须在基座上平衡?机构在基座上平衡的实质是什么?
答 由于机构中作往复运动的构件不论其质量如何分布，质心和加速度瞬心总是随着机械
的运动周期各沿一条封闭曲线循环变化的，因此不可能在一个构件的内部通过调整其质量
分布而达到平衡，但就整个机构而言．各构件产生的惯性力可合成为通过机构质心的的总
惯性力和总惯性力偶矩，这个总惯性力和总惯性力偶矩全部由机座承受，所以必须在机座
上平衡。机构在基座上平衡的实质是平衡机构质心的总惯性力，同时平衡作用在基座上的
总惯性力偶矩、驱动力矩和阻力矩。
6—5图示为一钢制圆盘，盘厚b=50 mm。位置I处有一直径φ=50 inm的通孔，位置Ⅱ
处有一质量m2=0.5 kg的重块。为了使圆盘平衡，拟在圆盘上r=200 mm处制一通孔，试求
此孔的直径与位置。(钢的密度ρ=7.8 g／em3。)
解 根据静平衡条件有:
m1rI+m2rⅡ+mbrb=0
m2rⅡ=0.5×20=10 kg.cm
m1r1=ρ×(π/4) ×φ2×b×r1=7.8 ×10-3×(π/4)×52×5 ×l0=7.66 kg.cm
取μW=4(kg.cm)／cm，作质径积矢量多边形如图所示，所添质量为:
m b=μwwb／r=4×2.7／20=0.54 kg，θb=72o，可在相反方向挖一通孔
其直径为：
6—6图示为一风扇叶轮。已知其各偏心质量为m1=2m2=600 g，其矢径大小为r1=r2=200 mm，
方位如图。今欲对此叶轮进行静平衡，试求所需的平衡质量的大小及方位(取rb=200 mm)。
(注：平衡质量只能加在叶片上，必要时可将平衡质量分解到相邻的两个叶片上。)
解 根据静平衡条件有:
m1r1+m2r2+mbrb=0
m1r1=0.6×20=1 2 kg.cm
m2r2=0.3×20=6 kg.cm
取μW=4(kg.cm)/cm作质径积矢量多边形如图
mb=μWWb/r=4×2.4／20=0.48 kg，θb =45o
分解到相邻两个叶片的对称轴上
6—7在图示的转子中，已知各偏心质量m1=10 kg，m2=15 k，m3=20 kg，m4=10 kg它们的
回转半径大小分别为r1=40cm，r2=r4=30cm，r3=20cm，方位如图所示。若置于平衡基面I及
Ⅱ中的平衡质量mbI及mbⅡ的回转半径均为50cm，试求mbI及mbⅡ的大小和方位(l12=l23=l34)。
解 根据动平衡条件有
以μW作质径积矢量多边形，如图所示。则
mbI=μWWbI/rb=5.6 kg，θbI =6o
mbⅡ=μWWbⅡ/rb=5.6 kg，θbⅡ=145o
6—8图示为一滚筒，在轴上装有带轮现已测知带轮有一偏心质量。另外，根据该滚筒的结
构知其具有两个偏心质量m2=3 kg，m3=4，各偏心质量的方位如图所示（长度单位为）。若
将平衡基面选在滚筒的两端面上，两平衡基面中平衡质量的回转半径均取为，试求两平衡
质量的大小和方位。若将平衡基面Ⅱ改选在带轮宽度的中截面上，其他条件不变，两平衡
质量的大小和方位作何改变？
解 (1)以滚筒两端面为平衡基面时，其动平衡条件为
以μW作质径极矢量多边形．如图 (a)，(b)，则
mbI=μWWbI/rb==1.45 kg， θbI =145o
mbⅡ=μWWbⅡ/rb=0.9kg，θbⅡ=255o
(2)以带轮中截面为平衡基面Ⅱ时，其动平衡条件为
以μw=2 kg.crn／rnm，作质径积矢量多边形，如图 (c)，(d)，则
mbI=μWWbI/rb==2×27/40=1.35 kg，θbI =160o
mbⅡ=μWWbⅡ/rb=2×14/40=0.7kg，θbⅡ=-105o
6—9 已知一用于一般机器的盘形转子的质量为30 kg，其转速n=6 000 r／min，试确定
其许用不平衡量。
解 (1)根据一般机器的要求，可取转子的平衡精度等级为G6.3，对应平衡精度A=6.3。
(2) n=6000 r／min， ω=2πn/60=628.32 rad/s
[e]=1 000A／ω=10.03μm
[mr]=m[e]=30×10.03×10-4=0.03 kg.cm
6—10 图示为一个一般机器转子，已知转子的质量为15 kg，其质心至两平衡基面I
及Ⅱ的距离分别为l1=100 mm，12=200 mm，转子的转速n=3 000 r／min，试确定在两个平
衡基面I及Ⅱ内的许用不平衡质径积。当转子转速提高到6 000 r／min时，其许用不平衡
质径积又各为多少?
解 (1)根据一般机器的要求，可取转子的平衡精度等级为G6.3，对应平衡精度A=6.3mm／s。
(2)n=3000r／min, ω=2πn/60= 314.16 rad／s
[e]=1 000A／ω=20.05μm
[mr]=m[e]=15×20.05×10-4=0.03 kg.cm
可求得两平衡基面I及Ⅱ中的许用不平衡质径积为
(3) n=6000 r／min， ω=2πn/60=628.32 rad/s
[e]=1 000A／ω=10.025μm
[mr]=m[e]=15×10.025×10--4=15g.cm
可求得两平衡基面I及Ⅱ中的许用不平衡质径积为
6—11 有一中型电机转子其质量为m=50 kg，转速n=3 000 r／min，已测得其
不平衡质径积mr=300 g·mm，试问其是否满足平衡精度要求?
6—12在图示的曲柄滑块机构中，已知各构件的尺寸为lAB=100 mm, lBC=400 mm；连杆
2的质量m2=12 kg，质心在s2处，lBS2=400／3 mm；滑块3的质量m3=20 kg，质心在C点处；
曲柄1的质心与A点重合。今欲利用平衡质量法对该机构进行平衡，试问若对机构进行完
全平衡和只平衡掉滑块3处往复惯性力的50％的部分平衡，各需加多大的平衡质量mC`和
mC``(取lBC``=1AC``=50 mm)?
解 (1)完全平衡需两个平衡质量，各加在连杆上C’点和曲柄上C``点处，平衡质量
的大小为：
mC` =(m2lBS2+m3lBC)/lBC`=(12×40／3+20×40)／5=192 kg
mC``=(m`+m2+m3) lAB/lAC``=(1 92十12+20)×10／5=448 kg
(2)部分平衡需一个平衡质量。应加在曲柄延长线上C``点处。平衡质量的大小为：
用B、C为代换点将连杆质量作静代换得
mB2=m2lS2C/lBC=1 2×2／3=8 kg
mC2=m2lBS2.lBC=1 2×4=4 kg
mB=mB2=8kg, mC=mC2+m3=24 kg
故下衡质量为
mC``=(mB+mC/2)lAB/lAC``=(8+24/2) ×10/5=40kg
6—13在图示连杆一齿轮组合机构中，齿轮a与曲柄1固连，齿轮b和c分别活套在
轴C和D上，设各齿轮的质量分别为m。=10 kg，m b=12 kg，m。=8 kg，其质心分别与轴
心B、c、D重合，而杆1、2、3本身的质量略去不计，试设法平衡此机构在运动中的惯性
力。
解 如图所示，用平衡质量m’来平衡齿轮a的质量，r`=lAB；
m`=malAB/r`=10kg
用平衡质量，m”来平衡齿轮b的质量，r``=l
CD
m``=mblCD/r``
齿轮c不需要平衡。
6—14 图a所示为建筑结构抗震试验的振动发生器。该装置装在被试建筑的屋顶。由
一电动机通过齿轮拖动两偏心重异向旋转(偏心重的轴在铅垂方向)，设其转速为150 r／
min，偏心重的质径积为500kg.m求两偏心重同相位时和相位差为180o时，总不平衡惯性
力和惯性力矩的大小及变化情况。
图b为大地重力测量计(重力计)的标定装置，设r=150 mm，为使标定平台的向心加速
度近似于重力加速度(9.81 m／s2)，同步带轮的角速度应为多大?为使标定平台上升和下降
均能保持相同的匀速回转，在设计中应注意什么事项?