2018美赛数学建模A题
2018数学建模a题优秀论文

2018数学建模a题优秀论文Background: On high frequencies (HF, defined to be 3 –30 mHz), radio waves can travel long distances (from one point on the earth’s surface to another distant point on the earth’s surface) by multiple reflections off the ionosphere and off the earth. For frequencies below the maximum usable frequency (MUF), HF radio waves from a ground source reflect off the ionosphere back to the earth, where they may reflect again back to the ionosphere, where they may reflect again back to the earth, and so on, travelling further with each successive hop. Among other factors, the characteristics of the reflecting surface determine the strength of the reflected wave and how far the signal will ultimately travel while maintaining useful signal integrity. Also, the MUF varies with the season, time of day, and solar conditions. Frequencies above the MUF are not reflected/refracted, but pass through the ionosphere into space. In this problem, the focus is particularly on reflections off the ocean surface. It has been found empirically that reflections off a turbulent ocean are attenuated more than reflections off a calm ocean. Ocean turbulence will affect the electromagnetic gradient of seawater, altering the local permittivity and permeability of the ocean, and changing the height and angle of the reflection surface. A turbulent ocean is one in which wave heights, shapes, and frequencies change rapidly, and the direction of wavetravel may also change.Problem:Part Ⅰ: Develop a mathematical model for this signal reflection off the ocean. For a 100-watt HF constant-carrier signal, below the MUF, from a point source on land, determine the strength of the first reflection off a turbulent ocean and compare it with the strength of a first reflection off a calm ocean. (Note that this means that there has been one reflection of this signal off the ionosphere.) If additional reflections (2 through n) take place off calm oceans, what is the maximum number of hops the signal can take before its strength falls below a usable signal-to-noise ratio (SNR) threshold of 10 dB?Part Ⅱ: How do your findi ngs from Part I compare with HF reflections off mountainous or rugged terrain versus smooth terrain?Part Ⅲ: A ship travelling across the ocean will use HF for communications and to receive weather and traffic reports. How does your model change to accommodate a shipboard receiver moving on a turbulent ocean? How long can the ship remain in communication using the same multi-hop path?Part Ⅳ: Prepare a short (1 to 2 pages) synopsis of your results suitable for publication as a short note in IEEE Communications Magazine.Your submission should consist of:One-page Summary Sheet,Two-page synopsis,Your solution of no more than 20 pages, for a maximum of 23 pages with your summary and synopsis.Note: Reference list and any appendices do not count toward the 23-page limit and should appear after your completed solution.中文赛题:多跳高频无线电传播背景:在高频时(HF,定义为3 - 30 mhz),无线电波可以通过电离层和地球的多次反射,传播很长的距离(从地球表面的一个点到地球表面的另一个遥远的点)。
历年美国数学建模(AMCM)问题

AMCM85问题-A 动物群体的管理在一个资源有限,即有限的食物、空间、水等等的环境里发现天然存在的动物群体。
试选择一种鱼类或哺乳动物(例如北美矮种马、鹿、免、鲑鱼、带条纹的欧洲鲈鱼)以及一个你能获得适当数据的环境,并形成一个对该动物群体的捕获量的最佳方针。
AMCM85问题-B 战购物资储备的管理钴对许多工业是必不可少的(1979年仅国防需要就占了全世界钴生产量的17%),但是钴不产生在美国。
大部分钴来自政治上不稳定的构F地区。
见图85B-1,85B-2,85B-3。
1946年制订的战略和稀有作战物资存贮法令要求钴的储存量应保证美国能渡过三年战争时期。
50年代政府按要求存贮了,并在70年代卖掉了大部分贮量,而在70年代后期决定重新贮存,贮存的指标是8540万磅,到1982年获得了贮量的一半。
试建立一个战略金属钴的储存管理数学模型。
你需要考虑诸如以下的问题;贮量应多大?应以多大的比率来获得贮量?买这些金属的合理价格应该是多少?还要求你考虑诸如以下的问题,贮量达到多大时应开始减少贮存量?应以多大的比率来减少?卖出这些金属的合理价格应该是多少?应该怎样分配(附页中有关于钴的资源、价格、需求及再循环等方面的信息)关于钴有用信息:1985年政府计划需要2500万磅钴。
进行周而复始的生产经营,从而每年可生产600万磅钴。
1980年占总消耗量70银的120万磅钴再循环了,得到了重新处理。
AMCM86问题-A 水道测量数据表86A-1给出了在以码为单位的直角坐标为X,Y的水面一点处以英尺计的水Z.水深数据是在低潮时测得的。
船的吃水深度为5英尺。
在矩形区域(75,200)×(-50,150)里的哪些地方船要避免进入。
本题是由加州海军研究生院数学系的Richard Franke提供的,可阅他的论文Scattered Data Interpolation,Math,Comput.,38(1982),18l-200。
数学建模期末考试2018A试的题目与答案

数学建模期末考试2018A试的题⽬与答案华南农业⼤学期末考试试卷(A卷)2012-2013学年第⼆学期考试科⽬:数学建模考试类型:(闭卷)考试考试时间:120 分钟学号姓名年级专业⼀、(满分12分)⼀⼈摆渡希望⽤⼀条船将⼀只狼.⼀只⽺.⼀篮⽩菜从河岸⼀边带到河岸对⾯.由于船的限制.⼀次只能带⼀样东西过河.绝不能在⽆⼈看守的情况下将狼和⽺放在⼀起;⽺和⽩菜放在⼀起.怎样才能将它们安全的带到河对岸去? 建⽴多步决策模型,将⼈、狼、⽺、⽩菜分别记为i = 1.2.3.4.当i在此岸时记x i = 1.否则为0;此岸的状态下⽤s =(x1.x2.x3.x4)表⽰。
该问题中决策为乘船⽅案.记为d = (u1, u2, u3, u4).当i 在船上时记u i = 1.否则记u i = 0。
(1) 写出该问题的所有允许状态集合;(3分)(2) 写出该问题的所有允许决策集合;(3分)(3) 写出该问题的状态转移率。
(3分)(4) 利⽤图解法给出渡河⽅案. (3分)解:(1) S={(1,1,1,1), (1,1,1,0), (1,1,0,1), (1,0,1,1), (1,0,1,0)} 及他们的5个反状(3分)(2) D = {(1,1,0,0), (1,0,1,0), (1,0,0,1), (1,0,0,0)} (6分)(3) sk+1 = sk+ (-1) k dk(9分)(4)⽅法:⼈先带⽺.然后回来.带狼过河.然后把⽺带回来.放下⽺.带⽩菜过去.然后再回来把⽺带过去。
或: ⼈先带⽺过河.然后⾃⼰回来.带⽩菜过去.放下⽩菜.带着⽺回来.然后放下⽺.把狼带过去.最后再回转来.带⽺过去。
(12分). .21、⼆、(满分12分) 在举重⽐赛中.运动员在⾼度和体重⽅⾯差别很⼤.请就下⾯两种假设.建⽴⼀个举重能⼒和体重之间关系的模型:(1)假设肌⾁的强度和其横截⾯的⾯积成⽐例。
6分(2)假定体重中有⼀部分是与成年⼈的尺⼨⽆关.请给出⼀个改进模型。
全国大学生数学建模比赛题目(18年数学建模)

• (5) 连带消费是购物中心经营的核心,如果商家将策划某次促销活 动,如何根据会员的喜好和商品的连带率来策划此次促销活动?
全国大学生数学建模比赛题目(18年数学建模)
• 由于该公司的生产线24小时不间断作业,以上总装线和喷涂线的 各项要求对相邻班次(包括当日晚班与次日白班)的车辆同样适 用。
全国大学生数学建模比赛题目(18年数学建模)
不同颜色汽车在总装线上排列时的 具体要求如下:
• (a)黑色汽车连续排列的数量在50-70辆之间,两批黑色汽车在总装线上需 间隔至少20辆。
• (2) 针对会员的消费情况建立能够刻画每一位会员购买力的数学模 型,以便能够对每个会员的价值进行识别。
全国大学生数学建模比赛题目(18年数学建模)
• (3) 作为零售行业的重要资源,会员具有生命周期(会员从入会到 退出的整个过程),会员的状态(比如活跃和非活跃)也会发生变 化。试在某个时间窗口,建立会员生命周期和状态划分的数学模 型,使商场管理者能够更有效地对会员进行管理。
• 为设计专用服装,将体内温度控制在37ºC的假人放置在实验室的 高温环境中,测量假人皮肤外侧的温度。为了降低研发成本、缩 短研发周期,请你们利用数学模型来确定假人皮肤外侧的温度变 化情况,并解决以下问题:
• 附件1. 专用服装材料的参数值 • 附件2. 假人皮肤外侧的测量温度
全国大学生数学建模比赛题目(18年数学建模)
• 公司每天可装配各种型号的汽车460辆,其中白班、晚班(每班12小 时)各230辆。每天生产各种型号车辆的具体数量根据市场需求和销售 情况确定。附件给出了该企业2018年9月17日至9月23日一周的生产计 划。
大学生数学建模竞赛A题参考答案

2018高教社杯全国大学生数学建模竞赛题目<请先阅读“全国大学生数学建模竞赛论文格式规范”)A题城市表层土壤重金属污染分析随着城市经济的快速发展和城市人口的不断增加,人类活动对城市环境质量的影响日显突出。
对城市土壤地质环境异常的查证,以及如何应用查证获得的海量数据资料开展城市环境质量评价,研究人类活动影响下城市地质环境的演变模式,日益成为人们关注的焦点。
按照功能划分,城区一般可分为生活区、工业区、山区、主干道路区及公园绿地区等,分别记为1类区、2类区、……、5类区,不同的区域环境受人类活动影响的程度不同。
现对某城市城区土壤地质环境进行调查。
为此,将所考察的城区划分为间距1公里左右的网格子区域,按照每平方公里1个采样点对表层土<0~10 厘M深度)进行取样、编号,并用GPS记录采样点的位置。
应用专门仪器测试分析,获得了每个样本所含的多种化学元素的浓度数据。
另一方面,按照2公里的间距在那些远离人群及工业活动的自然区取样,将其作为该城区表层土壤中元素的背景值。
附件1列出了采样点的位置、海拔高度及其所属功能区等信息,附件2列出了8种主要重金属元素在采样点处的浓度,附件3列出了8种主要重金属元素的背景值。
现要求你们通过数学建模来完成以下任务:(1> 给出8种主要重金属元素在该城区的空间分布,并分析该城区内不同区域重金属的污染程度。
(2> 通过数据分析,说明重金属污染的主要原因。
(3> 分析重金属污染物的传播特征,由此建立模型,确定污染源的位置。
(4> 分析你所建立模型的优缺点,为更好地研究城市地质环境的演变模式,还应收集什么信息?有了这些信息,如何建立模型解决问题?题目A题城市表层土壤重金属污染分析摘要:本文研究的是某城区警车配置及巡逻方案的制定问题,建立了求解警车巡逻方案的模型,并在满足D1的条件下给出了巡逻效果最好的方案。
在设计整个区域配置最少巡逻车辆时,本文设计了算法1:先将道路离散化成近似均匀分布的节点,相邻两个节点之间的距离约等于一分钟巡逻路程。
2018数学建模美赛题目

2018数学建模美赛题目
2018年数学建模美赛题目如下:
A题是多跳高频(HF)广播传播问题。
在高频(HF,定义为3-30 MHz)上,无线电波可以通过电离层和地球以外的多次反射传播很长的距离。
对于低于最大可用频率(MUF)的频率,来自地面源的HF无线电波从电离层反射回地球,在此它们可能再次反射回电离层,在此又可能反射回地球,依此类推。
随着每个连续的跃点走得更远。
除其他因素外,反射表面的特性决定了反射波的强度以及信号最终传播的距离,同时又保持了有用的信号完整性。
而且,MUF随季节、一天中的时间和太阳条件而变化。
MUF上方的频率不会被反射/折射,而是通过电离层进入太空。
在这个问题中,重点特别放在
海洋表面的反射上。
C题是能源生产问题。
能源生产和使用是任何经济结构的主要部分。
这个问题提供了一个数据集,包含了美国四个州在过去50年的能源生产和消费数据,以及一些人口和经济信息。
参赛者需要使用这些数据来回答以下问题:这四个州的能源生产和消费模式有何不同?这些模式如何随时间变化?这些模式如何与人口和经济活动相关联?如何预测未来的能源生产和消费趋势?如何优化能源生产和消费以减少对环境的影响?
以上内容仅供参考,建议查阅美赛官网获取更准确的信息。
2018电子科技大学数学建模校内赛A题:健身计划制定,女性身体形态数学建模设想
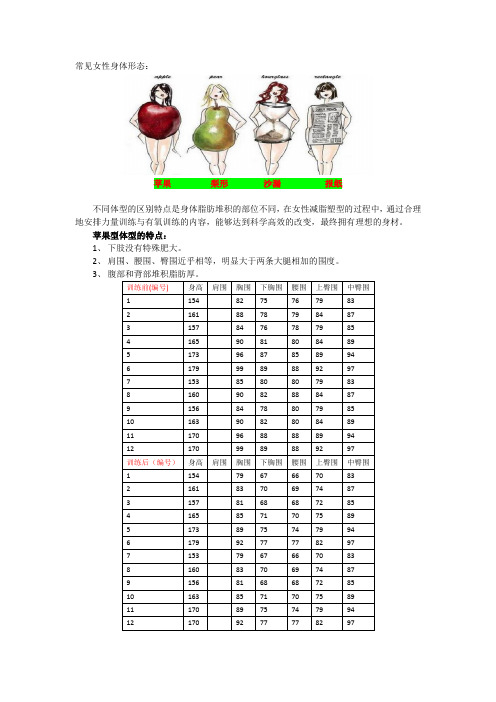
常见女性身体形态:
苹果梨形沙漏报纸
不同体型的区别特点是身体脂肪堆积的部位不同,在女性减脂塑型的过程中,通过合理地安排力量训练与有氧训练的内容,能够达到科学高效的改变,最终拥有理想的身材。
苹果型体型的特点:
1、下肢没有特殊肥大。
2、肩围、腰围、臀围近乎相等,明显大于两条大腿相加的围度。
3、
梨形体型的特点:
1、肩围小于胸围和腰围臀围。
2、胸围小于腰围,腰围小于臀围。
3、臀围是整个身体最肥大的地方。
1、胸部饱满。
2、腰部纤细。
3
1、整体很瘦削。
2、肩围、胸围、腰围、臀围相差不大。
2018AMC12即将开赛啦(A题)

Problem 1Pablo buys popsicles for his friends. The store sells single popsicles for $1 each, 3-popsicle boxes for $2, and 5-popsicle boxes for $3. What is the greatest number of popsicles that Pablo can buy with $8?Problem 2The sum of two nonzero real numbers is 4 times their product. What is the sum of the reciprocals of the two numbers?Problem 3Ms. Carroll promised that anyone who got all the multiple choice questions right on the upcoming exam would receive an A on the exam. Which one of these statements necessarily follows logically?Problem 4Jerry and Silvia wanted to go from the southwest corner of a square field to the northeast corner. Jerry walked due east and then due north to reach the goal, but Silvia headed northeast and reached the goal walking in a straight line. Which of the following is closest to how much shorter Silvia's trip was, compared to Jerry's trip?Problem 5At a gathering of people, there are people who all know each other and people who know no one. People who know each other hug, and people who do not know each other shake hands. How many handshakes occur?Problem 6Joy has thin rods, one each of every integer length from through . She places the rods with lengths , , and on a table. She then wants to choose a fourth rod that she can put with these three to form a quadrilateral with positive area. How many of the remaining rods can she choose as the fourth rod?Problem 7Define a function on the positive integers recursively by , if is even, andif is odd and greater than . What is ?Problem 8The region consisting of all points in three-dimensional space within units of line segment has volume . What is the length ?Problem 9Let be the set of points in the coordinate plane such that two of the three quantities , , and are equal and the third of the three quantities is no greater than the common value. Which of the following is a correct description of ?Problem 10Chloé chooses a real number uniformly at random from the interval . Independently, Laurent chooses a real number uniformly at random from the interval . What is the probability that Laurent's number is greater than Chloe's number?Problem 11Claire adds the degree measures of the interior angles of a convex polygon and arrives at a sum of . She then discovers that she forgot to include one angle. What is the degree measure of the forgotten angle?Problem 12There are horses, named Horse 1, Horse 2, , Horse 10. They get their names from how many minutes it takes them to run one lap around a circular race track: Horse runs one lap in exactly minutes. At time 0 all the horses are together at the starting point on the track. The horses start running in the same direction, and they keep running around the circular track at their constant speeds. The least time , in minutes, at which all horses will gain simultaneously be at the starting point is . Let be the least time, in minutes, such that at least of the horses are again at the starting point. What is the sum of the digits of ?Problem 13Driving at a constant speed, Sharon usually takes minutes to drive from her house to her mother's house. One day Sharonbegins the drive at her usual speed, but after driving of the way, she hits a bad snowstorm and reduces her speed by miles per hour. This time the trip takes her a total of minutes. How many miles is the drive from Sharon's house to her mother's house?Problem 14Alice refuses to sit next to either Bob or Carla. Derek refuses to sit next to Eric. How many ways are there for the five of them to sit in a row of chairs under these conditions?Problem 15Let , using radian measure for the variable . In what interval does the smallest positive value of for which lie?Problem 16In the figure below, semicircles with centers at and and with radii 2 and 1, respectively, are drawn in the interior of, and sharing bases with, a semicircle with diameter . The two smaller semicircles are externally tangent to each other and internally tangent to the largest semicircle. A circle centered at is drawn externally tangent to the two smaller semicircles and internally tangent to the largest semicircle. What is the radius of the circle centered at ?Problem 17There are different complex numbers such that . For how many of these is a real number?Problem 18Let equal the sum of the digits of positive integer . For example, . For a particular positive integer , . Which of the following could be the value of ?Problem 19A square with side length is inscribed in a right triangle with sides of length , , and so that one vertex of the square coincides with the right-angle vertex of the triangle. A square with side length is inscribed in another right triangle with sides of length , , and so that one side of the square lies on the hypotenuse of the triangle. What is ?Problem 20How many ordered pairs such that is a positive real number and is an integer between and , inclusive, satisfy the equationProblem 21A set is constructed as follows. To begin, . Repeatedly, as long as possible, if is an integer root of some polynomial for some , all of whose coefficients are elements of , then is put into . When no more elements can be added to , how many elements does have?Problem 22A square is drawn in the Cartesian coordinate plane with vertices at , , , . A particle starts at . Every second it moves with equal probability to one of the eight lattice points (points with integer coordinates) closest to its current position, independently of its previous moves. In other words, the probability is that the particle will move from to each of , , , , , , , or . The particle will eventually hit the square for the first time, either at one of the 4 corners of the square or at one of the 12 lattice points in the interior of one of the sides of the square. The probability that it will hit at a corner rather than at an interior point of a side is , where and are relatively prime positive integers. What is ?Problem 23For certain real numbers , , and , the polynomial has three distinct roots, and each root of isalso a root of the polynomial What is ?Problem 24Quadrilateral is inscribed in circle and has side lengths , and . Let and be points onsuch that and . Let be the intersection of line and the line through parallel to . Let be the intersection of line and the line through parallel to . Let be the point on circle other than that lies on line . What is ?Problem 25The vertices of a centrally symmetric hexagon in the complex plane are given byFor each , , an element is chosenfrom at random, independently of the other choices. Let be the product of the numbers selected. What is the probability that ?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018MCM
Problem A: 多跳短波无线电传播
背景:在高频率(HF,定义为3 - 30兆赫),无线电波可以长途旅行(从地球表面的
一个点到地球表面的另一个遥远的地方)通过电离层和地球以外的多次反射。
下面的最高可用频率(MUF),高频无线电波从地面源反映了电离层返回地球,在那里他们可以
再次回到电离层反射,在那里他们可以再次回到地球的反映,等等,旅行还与每个连
续跳。
在其他因素中,反射表面的特性决定了反射波的强度,以及信号在保持有用信
号完整性的情况下最终会传播多远。
而且,随着季节的变化,白天的时间和太阳的条
件也不同。
上面的MUF频率不是反射和折射,但通过电离层进入太空。
在这个问题上,重点特别是海面上的反射。
经验发现,在汹涌的海洋中,反射比平静的海面上的反射
减弱。
海洋湍流将影响海水的电磁梯度,改变海洋的局部介电常数和磁导率,改变反
射面的高度和角度。
一个汹涌的海洋,其中浪高、形状和频率变化很快,波的传播方向也可能改变。
问题:
第一部分:建立海洋信号反射的数学模型。
一个100瓦的高频恒定载波信号,低于MUF,从陆地上的点源,确定第一反射强度和湍流海洋用了平静的海洋的第一反射强度的比较。
(注意,这意味着这个信号在电离层上有一次反射)如果额外的反射(2到n)在平静
的海洋上发生,那么信号在强度低于可用的信噪比(SNR)阈值10分贝之前,可以达到的最大跳数是多少?
第二部分:你如何从第一部分的调查结果与HF反射在山区或崎岖的地形与光滑的地形
比较?
第三部分:穿越海洋的船将使用短波进行通信,并接收天气和交通报告。
你的模型如何改变以适应船上的接收器在湍流的海洋上行驶?使用相同的多跳路径,船舶能保持多长时间通信?
第四部分:准备一份简短的(1到2页)你的结果概要,适合作为IEEE通讯杂志中的简短说明发表。
您的提交应包括:
•一页摘要表,
•两页简介,
•你的解决方案不超过20页,最多有23页的摘要和概要。
注:参考清单和任何附录不计入23页的限制,并应在您完成的解决方案之后出现。
