非线性方程组牛顿迭代法(1)
牛顿法及基于牛顿算法下的Steffensen加速法求解非线性方程组方法例题及答案
1. 非线性方程组求解1.分别用牛顿法,及基于牛顿算法下的Steffensen 加速法。
(1) 求ln(sin )x x +的根。
初值0x 分别取0.1,1,1.5,2,4进行计算。
(2) 求sin =0x 的根。
初值0x 分别取1,1.4,1.6,1.8,3进行计算。
分析其中遇到的现象与问题。
(1)牛顿法牛顿法实质上是一种线性化方法,其基本思想是将非线性方程()0f x =逐步归结为某种线性方程来求解。
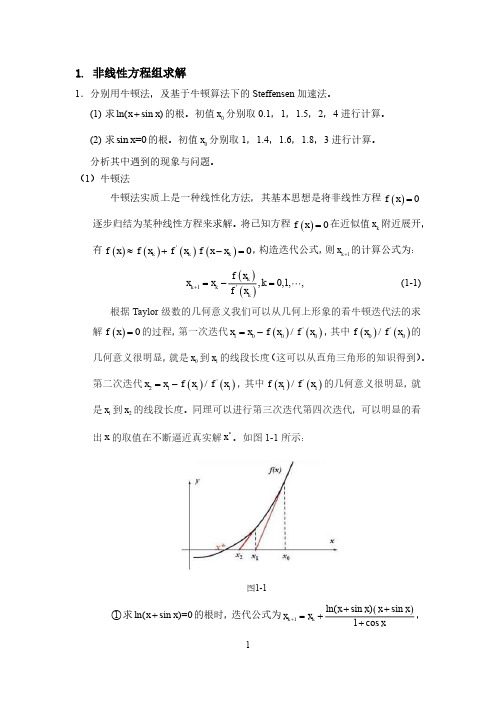
将已知方程()0f x =在近似值k x 附近展开,有()()()()'0k k k f x f x f x f x x ≈+-=,构造迭代公式,则1k x +的计算公式为:()()1',0,1,,k k k k f x x x k f x +=-= (1-1)根据Taylor 级数的几何意义我们可以从几何上形象的看牛顿迭代法的求解()0f x =的过程,第一次迭代()()'1000/x x f x f x =-,其中()()'00/f x f x 的几何意义很明显,就是0x 到1x 的线段长度(这可以从直角三角形的知识得到)。
第二次迭代()()'2111/x x f x f x =-,其中()()'11/f x f x 的几何意义很明显,就是1x 到2x 的线段长度。
同理可以进行第三次迭代第四次迭代,可以明显的看出x 的取值在不断逼近真实解*x 。
如图1-1所示:图1-1○1求ln(sin )=0x x +的根时,迭代公式为()1ln(sin )sin 1cos k k x x x x x x x+++=++,0示。
计算结果见附录1表F.1-1所示。
初值取1.5,2,4进行计算时结果不收敛。
表 1-1 牛顿法计算结果○2求sin =0x 的根时,迭代公式为1cos k k x x x+=+,初值0x 分别取1、1.4、1.6、1.8、3计算时结果收敛,误差小于510-时,近似解如表1-2所示。
1 牛顿迭代法的简介

1 牛顿迭代法的简介1.1 牛顿迭代法的概述牛顿迭代法(Newton's method)又称为牛顿-拉夫逊方法(Newton-Raphson method),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法。
多数方程不存在求根公式,因此求精确根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要。
方法使用函数f(x)的泰勒级数的前面几项来寻找方程f(x) = 0的根。
设r是f(x) = 0的根,选取x0作为r初始近似值,过点(x0,f(x0))做曲线y = f(x)的切线L,L的方程为y = f(x0)f'(x0)(x-x0),求出L与x轴交点的横坐标x1 = x0-f(x0)/f'(x0),称x1为r的一次近似值。
过点(x1,f(x1))做曲线y = f(x)的切线,并求该切线与x轴的横坐标x2 = x1-f(x1)/f'(x1),称x2为r的二次近似值。
重复以上过程,得r的近似值序列,其中x(n+1)=x(n)-f(x(n))/f'(x(n)),称为r的n+1次近似值,上式称为牛顿迭代公式。
解非线性方程f(x)=0的牛顿法是把非线性方程线性化的一种近似方法。
把f(x)在x0点附近展开成泰勒级数f(x) = f(x0)+(x -x0)f'(x0)+(x-x0)^2*f''(x0)/2! +… 取其线性部分,作为非线性方程f(x) = 0的近似方程,即泰勒展开的前两项,则有f(x0)+f'(x0)(x-x0)=f(x)=0 设f'(x0)≠0则其解为x1=x0-f(x0)/f'(x0) 这样,得到牛顿法的一个迭代序列:x(n+1)=x(n)-f(x(n))/f'(x(n))。
1.2 牛顿迭代法的优点迭代法是求方程近似根的一个重要方法,也是计算方法中的一种基本方法,它的算法简单,是用于求方程或方程组近似根的一种常用的算法设计方法。
非线性方程求根—牛顿迭代法(新)

非线性方程求根——牛顿迭代法一、牛顿迭代法的基本思想基本思想:将非线性方程逐步归结为某种线性方程求解。
设方程f (x )=0有近似根x k (f `(x k )≠0),将f (x )在x k 展开:(ξ在x 和x k 之间)2()()()()()()2!k k k k f f x f x f x x x x x ξ'''=+-+-()()()()k k k f x f x f x x x '≈+-可设记该线性方程的根为x k +1,则()()()0k k k f x f x x x '+-=1()()k k k k f x x x f x +=-'故f (x )=0可近似表示为即为Newton 法迭代格式。
(k =0,1,……)例:用Newton 迭代法求方程310x x --=在x 0=1.5附近的近似实根。
解:32()1,()31f x x x f x x '=--=-迭代公式为312131kk k k k x x x x x +--=--计算步骤如下:(1)取初值x 0=1.5;(2)按照迭代公式计算x 1;(3)若|x 1-x 0|<=0.00001,终止迭代;否则,x 0=x 1;转(2);(4)输出迭代次数和近似根.二、牛顿迭代法的实现MATLAB求解程序设计:方程及一阶导数函数:function[fun,dfun]=fun0(x)fun=x^3-x-1;%求原函数的值dfun=3*x^2-1;%求一阶导数的值计算主程序:clearx0=1.5;[fun,dfun]=fun0(x0);x1=x0-fun/dfun;i=1;while abs(x1-x0)>1e-5x0=x1;[fun,dfun]=fun0(x0);x1=x0-fun/dfun;i=i+1;enddisp('the solution is x1=')x1disp('the iter time is ')i计算结果为:the solution is x1=x1 =1.3247the iter time isi =4可见经过4次迭代即到达要求的精度,原方程的一个近似实数根为1.3247.三、牛顿迭代法的收敛性牛顿迭代法的迭代函数:)()()(x f x f x x '-=ϕ222)]([)()()]([)()()]([1)(x f x f x f x f x f x f x f x '''='''-'-='ϕ设f (x *)=0,f `(x *)≠0,则ϕ`(x *)=0,故Newton 迭代法在x *附近至少平方收敛。
研究生数值分析(5)牛顿(Newton)迭代法

z
0.612547 0.641384 0.641186
6 求方程 m重根的Newton法 设 s 是方程 f(x)=0 的 m 重根(m≥2), f(x)
在 s 的某邻域内有m阶连续导数 ,这时
f (s) f (s) f (m1) (s) 0, f (m) (s) 0
由Taylor公式,得
设 f '(x) 0 ,上式解为
x
xk
f (xk ) f ' (xk )
于是方程 f(x)=0的新的近似根xk+1,可由牛顿
迭代公式
xk 1
xk
f (xk ) f ' (xk )
k 0,1, 2,
求出
牛顿迭代公式具有明显的几何意义。 方程 y f (xk ) f '(xk )(x xk ) 是曲线 y=f(x)在点 (xk , f (xk )) 处的切线方程,迭代公式就是切线与x轴 交点的横坐标。因此,牛顿迭代法又称为切线法。
这表明牛顿迭代法用于求单根时至少是二阶收敛的。
(2)若 x* 是方程 f (x) 0 的 m(m 2) 重根,
即
f (x) (x x*)m q(x)
(q(x*) 0)
此时有
g ' (x*) lim g ' (x) lim
x x*
x x*
f (x) f '' (x) [ f ' (x)]2
k
xk
k
xk
4 0.635498 8 0.640964
5 0.643719 9 0.641285
6 0.640061 10 0.641142
第7章非线性方程组的数值解法

f 1 y f 2 2 y
2 y ( 1,1 ) 2
( 1,1 )
( y 3) ( 1, 1 )
( 1, 1 )
( x 1) ( 1 , 1 ) 2
( 1,1 )
f 1 f 2 2 2[ 2 * ( 3) ( 2 ) * ( 2 )] 4 f1 f2 g10 x ( 1,1) x ( 1,1) x f 1 f 2 g 2 2[ 2 * ( 3) 2 * ( 2 )] 20 20 y y f 1 y f 2 ( 1, 1 ) ( 1, 1 )
完
f ( x0 h, y0 k ) f ( x0 , y0 ) ( h k ) f ( x0 , y0 ) x y 1 2 ( h k ) f ( x 0 , y0 ) 2! x y 1 n ( h k ) f ( x 0 , y0 ) n! x y 1 n 1 ( h k ) f ( x0 h, y0 k ) ( n 1)! x y
2
2
令
0
得 f 1 f 1 ( g10 x g 20 y ) f 1 ( g10 ( g f 1 g f 1 ) 2 ( g 10 20 10 x y f 2 g 20 x f 2 g 20 x f 2 ) f2 y f 2 2 ) ( x y
1
f 1 ( x 0 , y0 ) f ( x , y ) 2 0 0
从n到n+1的迭代格式为:
f 1 ( x n , y n ) xn 1 x n x y y f 2 ( xn , yn ) n 1 n x
5-非线性方程组的数值解法及最优化方法

1 4 0
非线性方程组的数值解法
x10=0; x20=0; k=0; while 1 k=k+1; x1k=(1+x20-0.1*exp(x10))/4; x2k=(x10-x10^2/8)/4; %雅克比迭代法 %x2k=(x1k-x1k^2/8)/4; %高斯-赛德尔迭代法 err1=abs(x1k-x10); err2=abs(x2k-x20); err=max(err1,err2); if err<=0.00000000005 break; end x10=x1k; x20=x2k; end
0.0000055305 0.0000001511 0.0000000041 0.0000000001
非线性方程组的数值解法
牛顿迭代法:根据求解非线性方程的牛顿迭代法,如果已经 k k T ,则 ,, xn 给出方程组 Fx 0 的一个近似根 xk x1k , x2 可把函数 Fx 的分量 fi x, i 1,2,, n 在 x k 处按多元函数泰 勒公式展开,取其线性部分做近似,得
(0.2325668498,0.0564514831) (0.2325670008,0.0564515487) (0.2325670050,0.0564515196) (0.2325670051,0.0564515197) (0.2325670051,0.0564515197)
0.0002023950
所以有
1 x φx 1 2 x1
0
T
取初值 x 代公式收敛。
T 0 x 0 , 0 附近 φx 1,所以迭 0,0 ,在
1 1 x 1 e 40 x2 2 1 1 x1 x2 4 16
牛顿-拉夫森(Newton-Raphson)迭代法

§3.4 牛顿迭代法牛顿迭代法也称为牛顿-拉夫森(Newton-Raphson)迭代法,它是数值分析中最重要的方法之一,它不仅适用于方程或方程组的求解,还常用于微分方程和积分方程求解。
3.4.1 牛顿迭代法用迭代法解非线性方程时,如何构造迭代函数是非常重要的,那么怎样构造的迭代函数才能保证迭代法收敛呢?牛顿迭代法就是常用的方法之一,其迭代格式的来源大概有以下几种方式:1设],[)(2b a C x f ∈,对)(x f 在点],[0b a x ∈作泰勒展开: !2))((''))((')()(20000x x f x x x f x f x f -+-+=ξ略去二次项,得到)(x f 的线性近似式:))((')()(000x x x f x f x f -+≈。
由此得到方程=)(x f 0的近似根(假定≠)('0x f 0),)(')(000x f x f x x -=即可构造出迭代格式(假定≠)('k x f 0):)(')(1k k k k x f x f x x -=+ 公式(3.4.1)这就是牛顿迭代公式,若得到的序列{k x }收敛于α,则α就是非线性方程的根。
2 牛顿迭代法也称为牛顿切线法,这是由于)(x f 的线性化近似函数)(x l =))((')(000x x x f x f -+是曲线y =)(x f 过点))(,(00x f x 的切线而得名的,求)(x f 的零点代之以求)(x l 的零点,即切线)(x l 与x 轴交点的横坐标,如右图所示,这就是牛顿切线法的几何解释。
实际上,牛顿迭代法也可以从几何意义上推出。
利用牛顿迭代公式,由k x 得到1+k x ,从几何图形上看,就是过点))(,(k k x f x 作函数)(x f 的切线k l ,切线k l 与x 轴的交点就是1+k x ,所以有1)()('+-=k k k k x x x f x f ,整理后也能得出牛顿迭代公式: )(')(1k k k k x f x f x x -=+。
牛顿-拉夫森(Newton-Raphson)迭代法

§3.4 牛顿迭代法牛顿迭代法也称为牛顿-拉夫森(Newton-Raphson)迭代法,它是数值分析中最重要的方法之一,它不仅适用于方程或方程组的求解,还常用于微分方程和积分方程求解。
3.4.1 牛顿迭代法用迭代法解非线性方程时,如何构造迭代函数是非常重要的,那么怎样构造的迭代函数才能保证迭代法收敛呢?牛顿迭代法就是常用的方法之一,其迭代格式的来源大概有以下几种方式:1设],[)(2b a C x f ∈,对)(x f 在点],[0b a x ∈作泰勒展开: !2))((''))((')()(20000x x f x x x f x f x f -+-+=ξ略去二次项,得到)(x f 的线性近似式:))((')()(000x x x f x f x f -+≈。
由此得到方程=)(x f 0的近似根(假定≠)('0x f 0),)(')(000x f x f x x -=即可构造出迭代格式(假定≠)('k x f 0):)(')(1k k k k x f x f x x -=+ 公式(3.4.1)这就是牛顿迭代公式,若得到的序列{k x }收敛于α,则α就是非线性方程的根。
2 牛顿迭代法也称为牛顿切线法,这是由于)(x f 的线性化近似函数)(x l =))((')(000x x x f x f -+是曲线y =)(x f 过点))(,(00x f x 的切线而得名的,求)(x f 的零点代之以求)(x l 的零点,即切线)(x l 与x 轴交点的横坐标,如右图所示,这就是牛顿切线法的几何解释。
实际上,牛顿迭代法也可以从几何意义上推出。
利用牛顿迭代公式,由k x 得到1+k x ,从几何图形上看,就是过点))(,(k k x f x 作函数)(x f 的切线k l ,切线k l 与x 轴的交点就是1+k x ,所以有1)()('+-=k k k k x x x f x f ,整理后也能得出牛顿迭代公式: )(')(1k k k k x f x f x x -=+。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
华中师范大学课程结业论文题目:非线性方程组牛顿法及MATLAB程序院系:数学与统计学学院专业:数学与应用数学年级:2014级课堂名称:数值分析(1)实验学生姓名:杨帅学号:20142126432016年6月18非线性方程组牛顿法及其MATLAB 程序〔摘要〕学了《数值分析》这门课,了解到非线性方程的数值解法有:对分区间法、简单迭代法、Aitken-Steffensen 加速法、Newton 迭代法、正割法等,自然就会想到非线性方程组的数值解法有哪些呢?和非线性方程的数值解法有哪些不不同呢?在研究非线性方程组的数值解法之前,首先要给非线性方程组下一个合理定义;n 个变量n 个方程(n>1)的方程组表示为0),...,,(21=nix x x f (其中i=1,2...,n ),若if 中至少有一个是非线性函数,则称上述的表示为非线性方程组。
在R 中记,T nx x x f f ),...,,(21=,其中记),...,()(1n i i i x x f x f f ==且D x ∈。
若存在尣∈D ,使ƒ(尣)=0,则称尣为非线性方程组的解。
上述方程组可能有一个解或多个解,也可能有无穷多解或无解。
对非线性方程组解的存在性的研究远不如线性方程组那样成熟,现有的解法也不象线性方程组那样有效。
除极特殊的方程外,一般不能用直接方法求得精确解,目前主要采用迭代法求近似解。
根据不同思想构造收敛于解尣的迭代序列{尣}(k=0,1,…),即可得到求解非线性方程组的各种迭代法;但研究数学问题的时候,一般是由简单到复杂,由特殊到一般。
因此要在研究非线性方程组牛顿解法的时候,首先要探究非线性方程的牛顿解法。
1.1求解线性方程组的牛顿法及其MATAB 程序 1.1.1程序设计思路输入的量:初始值0x 、近似根kx 的误差限tol ,近似根kx 的函数值)(kx f 得误差限ftol ,迭代次数的最大值gxmax 、函数fnq (x )=)(x f及其导数dfnq (x )=f ’(x )。
输出的量:迭代序列{kx }、迭代k 次得到的迭代值kx (迭代次数超过gxmax 时,运行后输出信息'请注意:迭代次数超过给定的最大值gxmax')、相邻两次迭代的偏差piancha=|1-k kx -x |和它的偏差的相对误差xdpiancha=|1-k kx -x |/|kx |的值。
1.1.2具体操作现提供名为newtonqx.m 的M 文件:function [k,xk,yk,piancha,xdpiancha]=newtonqx(x0,tol,ftol,gxmax) x(1)=x0; for i=1: gxmaxx(i+1)=x(i)-fnq(x(i))/(dfnq(x(i))+eps); piancha=abs(x(i+1)-x(i)); xdpiancha= piancha/( abs(x(i+1))+eps); i=i+1; xk=x(i);yk=fnq(x(i)); [(i-1) xk yk piancha xdpiancha] if (abs(yk)<ftol)&((piancha<tol)|(xdpiancha< tol)) k=i-1; xk=x(i);[(i-1) xk yk piancha xdpiancha] return ; end end if i>gxmaxdisp('请注意:迭代次数超过给定的最大值gxmax 。
') return ; end[(i-1),xk,yk,piancha,xdpiancha]';1.1.3例题分析用牛顿法求解方程2x^3-3x^2+1=0在0x = -0.4和0.9的近似根,要求精度ε = 10^(-3).然后判断此方法分别在方程的根*x = -0.5和1处的收敛速度. (1),先求方程的近似根. 在MATLAB 工作窗口输入程序>>[k,xk,yk,piancha,xdpiancha]=newtonqx(-0.4,0.001, 0.001,100)运行后输出初始值0x = -0.4的迭代结果如表所示.迭代次数k = 3,根的近似值kx =-0.500,它的函数值ky =-1.759e-013,偏差piancha =1.712e-007和相对误差xdpiancha =3.423e-007如果将-0.4改作0.9,则运行后输出初始值0x = -0.4的迭代结果为k =7;piancha =7.290e-004;xdpiancha =7.295e-004;kx = 0.999;ky=1.590e-006. (2),再讨论收敛速度比较初始值分别是0x = -0.4和0.9的两组结果,在0x = -0.4处迭代 3 次就得到单根*x = -0.5的近似值 kx =-0.500;而在x 0 = 0.9处迭代 7 次才得到二重根*x = 1的近似值kx =0.999.可见,牛顿切线迭代法在单根处的迭代速度比二重根处的迭代速度快很多.这正如前面讨论的结果一样,即若 *x 是 f (x ) = 0的单根,则牛顿切线法是平方收敛的;若*x 是f (x ) = 0的二重根,则牛顿切线法是线性收敛的;2.1,求解二元非线性方程组的牛顿法及其MATLAB 程序2.1.1程序设计思路:输入的量:初始值X =[0,y x ],要求的近似根(kky x ,)的误差tol ,(kky x ,)的函数值 2,1),,(=i y x f kk i 的误差限ftol ,迭代次数的最大值ngmax 和函数 2,1),,(=i y x f kki及其一阶偏导数:输出的量:迭代k c i=次数得到的迭代向量值X=(0,y x )、向量的函数值Y={),(),,(21kkkky x f y x f }、Y 的2范数hanfan 、迭代方程组的系数行列式D 的值、相邻两次迭代向量的2范数danfan=norm(k k X X-+1)和它的2范数的相对误差xddf=danfan/norm(1+k X )的值(当迭代次数超过最大值ngmax 时运行后输出’请注意:迭代次数超过给定的最大值namax,请重新输入初始值0x ’:当D=0时,运行后输出信息’请注意!迭代方程组的系数行列式的值等于零’) 2.1.2具体操作:使用两个初始值0,y x ,现提供名为newtonzu2.m 的M 文件function [ci,D,danfan,xddf,hanfan,Xk,Yk]=newtonzu2(X,tol,ftol,ngmax) Y=Z(X); for i=1:ngmax dY=JZ(X);D=det(dY);A1=[Y(1),dY(1,2); Y(2),dY(2,2)]; A=det(A1);B1=[dY(1,1), Y(1); dY(2,1), Y(2)];B=det(B1);Xk=X-[A,B]/D; hanfan=norm(Y);danfan=norm(Xk-X); xddf=danfan/(norm(Xk)+eps); X=Xk;Y=Z(X);ci=i; if D~=0ci=i; Xk=X-[A,B]/D;Yk=Y; [ci,D,danfan, xddf, hanfan , X, Y]; elsedisp('请注意!迭代方程组的系数行列式的值等于零.') endif (hanfan <ftol)&(( danfan <tol)|( xddf < tol)) [ci,D,danfan, xddf, hanfan , X, Y]; return ; end if i>gxmaxdisp('请注意:迭代次数超过给定的最大值ngmax,请重新输入初始值x0.') return ; end end2.1.3例题分析:用上述迭代法求解方程组x^2+y^2=16与x^2-y^2=2 (1)设)(1x f =x^2+y^2-16)(2x f =x^2-y^2-2则y yy x f x x y x f y y y x f x x y x f 2),(,2),(,2),(,2),(2211-=∂∂=∂∂=∂∂=∂∂ (2)作函数)(1x f 和)(2x f>>syms x yF1=x^2-y^2-2;F2=x^2+y^2-16; ezplot(F1,[-4.5,4.5]), hold on ezplot(F2,[-4.5,4.5]) ,hold off运行后屏幕显示如右图, 取两个初始值2,20==y x(3),建立并保存名为Z.m 的M 文件function F=Z(X)x=X(1);y=X(2); F=zeros(1,2); F(1)= x^2+y^2-16; F(2)= x^2-y^2-2;(4),建立并保存名为JZ.m 的M 文件function dF=JZ(X)x=X(1);y=X(2); dF=zeros(2,2); dF(1,1)=2*x; dF(1,2)=2*y; dF(2,1)=2*x; dF(2,2)=-2*y;(5),保存名为newtonzu2.m 的M 文件;(6),在MATLAB 工作窗口输入程序:>>X=[2,2]; [k,D,danfan, xddf, hanfan , Xk, Yk]= newtonzu2 (X,1e-4,1e-4,100)(7),运行后输出结果k = 5 D =-63.49803146638493 danfan =3.932201289951168e-011 xddf =9.830503224877920e-012 hanfan =3.336593498083849e-010Xk =2.99999999996068 2.64575131106449 Yk = 1.0e-015 *0 -0.888178419700132.2求解n 元非线性方程组的牛顿法及其MATLAB 程序 2.2.1程序设计思路输入的量:初始值0X ,要求的近似根k x 的误差限 tol ,k x 的函数值if(k x ),n ,...,2,1i =的误差限ftol , 迭代次数的最大值gxmax 和函数if (k x ), n ,...,2,1i =及其一阶偏导数;输出的量:迭代k 次数得到的迭代向量值k x 、向量的函数值if(k x ),n ,...,2,1i =及其2范数hanfan 、迭代方程组的雅可比矩阵的行列式D 的值、相邻两次迭代向量的2范数danfan=norm )(k k x x -+1和它的2范数的相对误差xddf=danfan/norm(1+k x )的值。
