§分波面双光束干涉资料
合集下载
分波振面干涉

··光源原子1原子2随时间迅变。
2ϕ很难保持恒定21ϕ−ϕ在眼睛的响应时间10(二)干涉原理致。
很近,振动方向近似一与;,它们永远有相同的相位的同一波面上,发出的光波由它们的频率相同;位于、212121S S S S S ϕ=ϕ因为两孔发出的两束光波来自同一波面上的不同部分, 故称分波振面干涉。
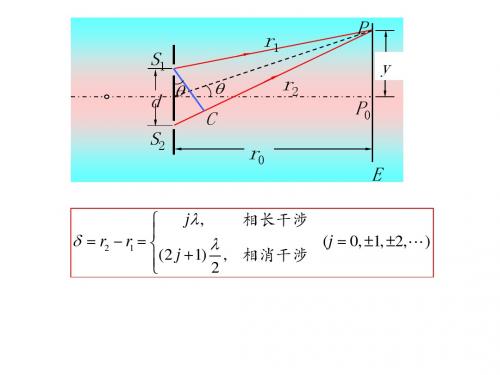
Flashd1、两光束的光程差NO 是s 1s 2连线的垂直平分线;两缝的间距为d ,观察屏到双缝的距离为r 0 ;观察面上Y 轴向上为正,P 为观察点,其坐标为y ;两束光在P 点处的光程差为:δ=r 2-r 1(n 1=n 2=1);θ是NP 与NO 的夹角。
sin d yd r r ≈⋅≈−=θδ光程差:dθS'() ,2,1,0 22 0⋅⋅⋅±±=⋅=j j d r y λ光强极大值的位置:双缝遮光板观察屏d2y=0 处为亮条纹,往两侧依次称为一级(明或暗)条纹,二级(明或暗)条纹。
的。
0r d≈Δθ∵又 y θλΔ≈Δ∴反映光波的空间周期性增大(缩小)时,条纹宽度和条纹间距减小(增大)。
增大(缩小)时,条纹宽度和条纹间距增大(减小)。
5、白光光源:央是白色条纹,其它级次为彩色条纹。
零级条纹-2、-3级条纹重叠1级条纹-1级条纹2、3级条纹重叠λ⋅=Δdr y 002 2r y j d λ=⋅明条纹中心的位置:条纹宽度:y如果S1、S2是两个小孔,则屏幕上得到的是一组如右图所示的双曲线。
前面所求的光强极大值与极小值分别为亮条纹与暗条纹中心点(双曲线的顶点)。
例:25页1.1SdS'r0为光源,S'为光源S 对MM' 的镜像。
发出的光,一部分直接照射到屏幕上;另一部分MM'反射后射向屏幕,相当于从S'发出。
还有许多分波面的干涉装置,如菲涅耳双棱镜,比累双切透镜等。
分波面法双光束干涉

求 (1) d =1.0 mm 和 d =10 mm两种情况下,相邻明条纹间距分 别为多大?(2) 若相邻条纹的最小分辨距离为 0.065 mm, 能分清干涉条纹的双缝间距 d 最大是多少?
解 (1) 明纹间距分别为
x D 600 5.893104 0.35mm
d
1.0
x D 600 5.893104 0.035mm
x D
d
一系列平行的 明暗相间条纹
(2) 已知 d , D 及Δx,可测 ;
(3) Δx 正比于 和 D ,反比于 d ;
(4) 当用白光作为光源时,在零级白色中央条纹两边对称地 排列着几条彩色条纹。
5
2021/3/11
红光入射的杨氏双缝干涉照片
白光入射的杨氏双缝干涉照片
6
2021/3/11
您能判断0级 条纹在哪吗?
§19.2 分波面法双光束干涉 一、杨氏实验 二、其他类似装置
干涉主要包含以下几个主要问题
•实验装置;
•确定相干光束,求出光程差(相位差);
•分析干涉花样,给出强度分布; •应用及其他。
杨(T.Young)在1801 年首先发现光的干涉
现象,并首次测量了
1
2021/3/11
光波的波长。
一、 分波阵面法(杨氏实验)
1. 实验装置 ( 点源 分波面 相遇)
s1
S
s2
2. 强度分布 步骤
2
2021/3/11
明条纹位置
明条纹位置
明条纹位置
确定相干光束 计算光程差 根据相长、相消条件确定坐标
•理论分析
r12
D2
y2
(x
d )2 2
S2 •
r22
物理光学 双光束干涉(1)

D = S2Q2 (n n)l
零级条纹出现条件是
D = ml = 0
即
D = S2Q2 (n n)l = 0 S 2Q2 = (n n)l
考虑到
n n S 2Q2 0
于是,零级条纹(因而所有条纹)应当上移。
(2) 考察屏幕上的一个固定点移动一个条纹,表明光 程差相差一个波长,因此
因此干涉图样可见度变低。
洛埃镜
S
d
S’
M
D 洛 埃 镜 的 干 涉
1.分波面法双光束干涉 这些实验的共同点是: ①在两束光的叠加区内,到处都可以观察到干涉条 纹,只是不同地方条纹的间距、形状不同而已。这 种在整个光波叠加区内随处可见干涉条纹的干涉, 称为非定域干涉。 ②在这些干涉装置中,都有限制光束的狭缝或小孔, 因而干涉条纹的强度很弱,以致于在实际上难以应 用。
2π 2π
Dr dy / D
2π yd = D = (Dr DR) ( DR) ( 10 ) l l l D
1.分波面法双光束干涉
①如果 S1、S2 到 S 的距离相等,DR=0, 则对应 = 2mπ (m=0, 1, 2) 的空间点
Dl y=m d (11)
为光强极大,呈现干涉亮条纹;
I = I1 I 2 2 I1I 2 cosq cos = I1 I 2 +2 I12 (3)
1.分波面法双光束干涉
对应 = (2m+1)π (m=0, 1, 2) 的空间点
1 Dl y = (m ) 2 d
(12)
为光强极小,呈现干涉暗条纹。
1.分波面法双光束干涉
1 l y = (m ) = (m ) 2 d 2
双光束干涉1.
因此干涉图样可见度变低。
I = I1 I2 2 I1I2 cos
P = IM Im = 4 =1 IM Im 4
使一个狭缝加宽一倍,振幅变为原来的 2 倍,光强 变为原来的 4 倍,相干度为
I = I1 4I1 2 4I1I1 cos = 5I1 4I1 cos
P = IM Im = 8 = 0.8 IM Im 10
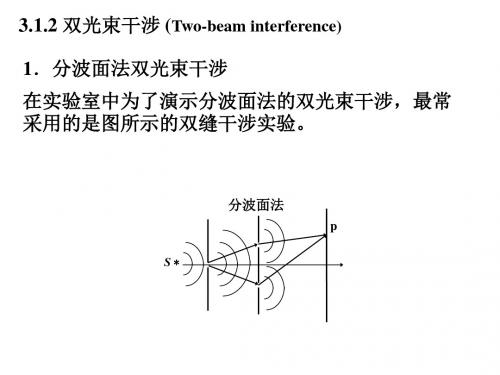
3.1.2 双光束干涉 (Two-beam interference) 1.分波面法双光束干涉 在实验室中为了演示分波面法的双光束干涉,最常 采用的是图所示的双缝干涉实验。
分波面法
p S*
激
S1*
光
S2 *
x
k=+2
k=+1
k= 0
I
k=-1
k=-2
1.分波面法双光束干涉
Sl 和 S2 双缝从来自狭缝 S 的光波波面上分割出很小的 两部分作为相干光源,它们发出的两列光波在观察屏 上叠加,形成干涉条纹。
1.分波面法双光束干涉 对应 = (2m+1)π (m=0, 1, 2 ) 的空间点
y = (m 1 ) Dl (12)
2d
为光强极小,呈现干涉暗条纹。
1.分波面法双光束干涉
相邻两亮(暗)条纹间的距离是条纹间距为,且
= Dy = Dl = l (13) d
其中 = d/D 叫光束会聚角。在实验中,可以通过 测量 D、d 和 ,计算求得光波长 l。
于是,零级条纹(因而所有条纹)应当上移。
(2) 考察屏幕上的一个固定点移动一个条纹,表明光 程差相差一个波长,因此
(n n)l = 20l n = n 20l
进而可得
I = I1 I2 2 I1I2 cos
P = IM Im = 4 =1 IM Im 4
使一个狭缝加宽一倍,振幅变为原来的 2 倍,光强 变为原来的 4 倍,相干度为
I = I1 4I1 2 4I1I1 cos = 5I1 4I1 cos
P = IM Im = 8 = 0.8 IM Im 10
3.1.2 双光束干涉 (Two-beam interference) 1.分波面法双光束干涉 在实验室中为了演示分波面法的双光束干涉,最常 采用的是图所示的双缝干涉实验。
分波面法
p S*
激
S1*
光
S2 *
x
k=+2
k=+1
k= 0
I
k=-1
k=-2
1.分波面法双光束干涉
Sl 和 S2 双缝从来自狭缝 S 的光波波面上分割出很小的 两部分作为相干光源,它们发出的两列光波在观察屏 上叠加,形成干涉条纹。
1.分波面法双光束干涉 对应 = (2m+1)π (m=0, 1, 2 ) 的空间点
y = (m 1 ) Dl (12)
2d
为光强极小,呈现干涉暗条纹。
1.分波面法双光束干涉
相邻两亮(暗)条纹间的距离是条纹间距为,且
= Dy = Dl = l (13) d
其中 = d/D 叫光束会聚角。在实验中,可以通过 测量 D、d 和 ,计算求得光波长 l。
于是,零级条纹(因而所有条纹)应当上移。
(2) 考察屏幕上的一个固定点移动一个条纹,表明光 程差相差一个波长,因此
(n n)l = 20l n = n 20l
进而可得
1.3_分波面双光束
光学
1.3 分波面双光束干涉
一、光源的发光机制
通常情况下,当两个光源同时照明同一区域时,观 察不到干涉图样,说明通常两个独立的普通光源之间的 叠加是非相干叠加,即它们是非相干光源。为什么普通 的独立光源是非相干光源呢?这是由它们的发光机制决 定的。
3
光学
1.3 分波面双光束干涉
凡能发光的物体称为光源。光源的最基本发光单元是分子、原子。
r2 r1 7
d r1
1
P
插入云母片后,P 点为 0 级明纹。s
r2 r1 d nd 0 7
d n 1 6.6 m
r2
本节结束
s2
o
例 1 杨氏双缝的间距为 0.2 mm ,双缝与屏的距离为 1 m . 若 第 1 级明纹到第 4 级明纹的距离为 7.5 mm ,求光波波长。 解: d y 0.2 7.5 0.5 10 3 (mm ) 500nm 3
r0
10
3
例 2 用云母片( n = 1.58 )覆盖在杨氏双缝的一条缝上,这时 屏上的零级明纹移到原来的第 7 级明纹处。若光波波长为 550 nm ,求云母片的厚度。 解:插入云母片前,P 点为 7 级明纹。
二、光源和机械波源的区别
机械波源:容易实现干涉
表面上 光源:难于观察到干涉现象 机械波源:振动是连续的,是位移的振动 本质上 光源:物质原子或分子辐射引起,辐射不连续的
光学
1.3 分波面双光束干涉
三、获得稳定干涉图样的条件和方法
相干光的产生: ①原则:将同一光源同一点发出的光波列,即某个原子某次 发出的光波列分成两束,使其经历不同的路径之后相遇叠加。
S1 d
1.3 分波面双光束干涉

§1-3
1.3.1
分波面双光束干涉
通常的独立光源是不相干的
光的辐射起源于物质的原子(或分子) 一般, 原子的辐射互不相关的 一批发出辐射的原子里, 由于能量的损失或由于周围原子的作用, 辐射过程常常中段,延续时间很短(约10^-8s)
另一批原子发光,但已具有新的初相位了, 因此不同原子所发出的辐射之间的相位差, 将在每一次新的辐射开始时发生改变
4.维纳驻波实验 入射波和反射波相遇在一起时,也会发生相 干性叠加而形成驻波。
值得注意的地方是乳胶片和反射平面MMˊ接触的 地方没有感光。表示这里不是波腹,而是波节。 也就是说,入射光和反射光在介质表面上叠加时, 振动方向总是相反的,或者说光在介质表面上垂 直反射时,也产生了半波损失。
例1-1 杨氏实验装置中,两小孔的间距为0.5mm, 光屏离小孔距离为50cm,当以折射率为1.60的透 明薄片贴住小孔s2时,发现屏上条纹移动了1cm, 试确定该薄片的厚度。
d d 2 解: r r ( y r ) r y 2 1 2 r 0 d 2 2 2 r1 r0 ( y ) 有薄片时, 2 d d d2 ) r ( y y ' ) 2 nd 2 (r 2 1 r2 r0 0 ( y )0 r 0 2
2 2 无薄片时 2 0,
也就是说每经过一个极短的时间隔 (太短的时间间隔,人眼和仪器不可分辩), 相位差就会改变, 所以这样的光源是不相干的 六十年代激光的问世, 使光源的相干性大大地提高
1.3.2 获得稳定干涉花样的条件,典型的干涉实验
这个条件就是:在任何时刻到达观察点的, 应该是从同一批原子发射出来但经过不同 光程的两列光波。各原子的发光尽管迅速 地改变,但任何相位改变总是同时发生在 这两列波中,因而到达同一观察点时总是 保持着不变的相位差,只有经过这样特殊 装置的两束光才可能是相干的。
1.3.1
分波面双光束干涉
通常的独立光源是不相干的
光的辐射起源于物质的原子(或分子) 一般, 原子的辐射互不相关的 一批发出辐射的原子里, 由于能量的损失或由于周围原子的作用, 辐射过程常常中段,延续时间很短(约10^-8s)
另一批原子发光,但已具有新的初相位了, 因此不同原子所发出的辐射之间的相位差, 将在每一次新的辐射开始时发生改变
4.维纳驻波实验 入射波和反射波相遇在一起时,也会发生相 干性叠加而形成驻波。
值得注意的地方是乳胶片和反射平面MMˊ接触的 地方没有感光。表示这里不是波腹,而是波节。 也就是说,入射光和反射光在介质表面上叠加时, 振动方向总是相反的,或者说光在介质表面上垂 直反射时,也产生了半波损失。
例1-1 杨氏实验装置中,两小孔的间距为0.5mm, 光屏离小孔距离为50cm,当以折射率为1.60的透 明薄片贴住小孔s2时,发现屏上条纹移动了1cm, 试确定该薄片的厚度。
d d 2 解: r r ( y r ) r y 2 1 2 r 0 d 2 2 2 r1 r0 ( y ) 有薄片时, 2 d d d2 ) r ( y y ' ) 2 nd 2 (r 2 1 r2 r0 0 ( y )0 r 0 2
2 2 无薄片时 2 0,
也就是说每经过一个极短的时间隔 (太短的时间间隔,人眼和仪器不可分辩), 相位差就会改变, 所以这样的光源是不相干的 六十年代激光的问世, 使光源的相干性大大地提高
1.3.2 获得稳定干涉花样的条件,典型的干涉实验
这个条件就是:在任何时刻到达观察点的, 应该是从同一批原子发射出来但经过不同 光程的两列光波。各原子的发光尽管迅速 地改变,但任何相位改变总是同时发生在 这两列波中,因而到达同一观察点时总是 保持着不变的相位差,只有经过这样特殊 装置的两束光才可能是相干的。
13分波面双光束干涉(精)

4
所以,普通光源的光波特点: 1º 原子振动时随机的发出“有限长的波列” 2º 各波列之间没有恒定的位相关系,即:每个波列的初位相 各不相同。 3º 自然光:E矢量振动方向包含与传播方向垂直的一切可能的 振动方向。
两个独立的光源不可能成为一对相干光源
原因:原子发光是随机的,间歇性的,两列光波的振 动方向不可能一致,位相差不可能恒定。 两束光 不相干!
暗纹
d
光程差: r r2 r1 d sin 相位差:
程差条件
位置条件 暗纹
y (2 j 1)
r0 2d
(j 0,1,2)
13
条纹间距:
r0 y yk 1 yk d
y y P r1 ·y r2 0 r0
d
r
y0
y I
14
15
条纹分布区域在光线相遇的阴影区内。
28
3、洛埃镜
▲
实验装置
S1
① ①
M
P
y
P
②
d
S2
②
L
o
r0
最小
最大
最小
29
条纹特点 在光线相遇的阴影区内,干涉花样为与狭缝光源平 行、等间距、明暗相间条纹。 把屏幕 P 移到和镜面相接触的位置P ,s1 和s 2 到接 触点 L 的路程相等,似乎接触点应出现亮纹,实验事实 是接触点是暗纹。
8
(二)、几种典型的分波面干涉实验
1、杨氏实验 杨氏实验是分波面干涉最著名的例子,分析 杨氏实验,可了解分波面干涉的一些共同特点。 ▲ 实验装置 r1 单色光入射
d
r
P y r2
0
·y
所以,普通光源的光波特点: 1º 原子振动时随机的发出“有限长的波列” 2º 各波列之间没有恒定的位相关系,即:每个波列的初位相 各不相同。 3º 自然光:E矢量振动方向包含与传播方向垂直的一切可能的 振动方向。
两个独立的光源不可能成为一对相干光源
原因:原子发光是随机的,间歇性的,两列光波的振 动方向不可能一致,位相差不可能恒定。 两束光 不相干!
暗纹
d
光程差: r r2 r1 d sin 相位差:
程差条件
位置条件 暗纹
y (2 j 1)
r0 2d
(j 0,1,2)
13
条纹间距:
r0 y yk 1 yk d
y y P r1 ·y r2 0 r0
d
r
y0
y I
14
15
条纹分布区域在光线相遇的阴影区内。
28
3、洛埃镜
▲
实验装置
S1
① ①
M
P
y
P
②
d
S2
②
L
o
r0
最小
最大
最小
29
条纹特点 在光线相遇的阴影区内,干涉花样为与狭缝光源平 行、等间距、明暗相间条纹。 把屏幕 P 移到和镜面相接触的位置P ,s1 和s 2 到接 触点 L 的路程相等,似乎接触点应出现亮纹,实验事实 是接触点是暗纹。
8
(二)、几种典型的分波面干涉实验
1、杨氏实验 杨氏实验是分波面干涉最著名的例子,分析 杨氏实验,可了解分波面干涉的一些共同特点。 ▲ 实验装置 r1 单色光入射
d
r
P y r2
0
·y
《双光束干涉》PPT课件

18
返回
菲涅耳双面镜装置示意图
P
s
P1
M1
L
s1
d
s2
C
M2
P2
11/24/2020
r0
19
返回
劳埃德镜示意图
P'
P
s1
d
ML
P0
s2
d'
狭缝S1被强单色光照射,作为单色线状光源;
S1经M所成的虚像S2与S1构成相干光源;
入射角i1接近90o-掠射,可使很小。
注意
•1当1/2屏4/2与020M接触时,P0点出现暗纹,原因是光在M
• 也就是说,凡入射角相同的光,形成同一干涉 条纹。通常把这种干涉条纹称为等倾干涉。
11/24/2020
25
从点光源发出的单条光线的光路
11/24/2020
26
等倾干涉 从点光源发出的锥面上光线的光路
11/24/2020
27
(2) 等倾干涉条纹的特性
• 一等倾干涉条纹的 形状与观察透镜放 置的方位有关。
时,肉眼或探测仪器就将观察不到稳定的条纹分布。 • 因此11/,24为/20了20 产生干涉现象,要求两叠加光束的频率尽量相等6。
(2) 对叠加光束振动方向的要求
• 当两光束光强相等,则条纹可见度为V=cosθ
• 若θ=0,两光束的振动方向相同时,V=1,干涉条纹最
清晰; • 若θ=π/2,两光束正交振动时,V=0,不发生干涉; • 当0<θ<π/2时,0<V<1,干涉条纹清晰度介于上
• 对应于光源S发出的同一入射角的光束,经平板产生的两束透射
光和两束反射光的光程差恰好相差λ/2,相位差相差π; • 透射光与反射光的等倾干涉条纹是互补的,即对应反射光干涉条
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(4)
(1)最大位置:
= r2r1drx 02j 2 xM j 2jr d 0 2
(5)
Im paxA 1 2A 2 22A 1A 2A 1A 22
(j0,1 , 2, )
(2)最小位置:
= r2r1drx 0(2j1) 2 xm j (2j1)r d 0 2
(6)
Im pinA 1 2A 2 22A 1A 2A 1A 22
r2r12xrd0 2
原为明纹处:xd 2 j 时 (2j 1) 暗
r0
2
2
原为暗纹处: xd (2j 1)
r0
2
时 2 j
2
明
5、维纳驻波实验。
h 2
l
2 sin
l
h
图3.6维纳驻波实验 结论:直射时产生了半波损失。
四、半波损失的解释 1、理论:菲涅耳公式如下 反射: A S 1 sin (i1 i2)
lim Ap1 lim tg(i1 i2) = ctgi2 =1
A i1900
p1
i1900 tg(i1 i2) ctgi2
(2)正射——维纳驻波实验。
图3.8 A S 1 sin (i1 i2) A S 1 sin (i1 i2)
A p 1tg (i1 i2) A p 1 tg (i1 i2)
2、发光机理 处于激发态的原子或分子的自发辐射。
3、普通光源发出的光的特性
所以,一般光源发出的光波往往可以看作是大量的有许多断
续的、彼此独立的波列构成,各波列的频率、振动方向、初
相等彼此独立随几分布。
I
(1) 不恒定。
I0
(2)非单色性。
(3)单色性量度
o
二、获得稳定干涉花样的方法
(j0,1,2, )
(3)条纹间距:
xxj1
xj
r0
d
(7)
(4)干涉图样:
这些点的轨迹是以s 1 s 2 为轴线的双叶旋转双曲面. 图3.3
5、特征:
(1)各级亮条纹的光强相等,条纹间距相等
(2) xr0/d
(3)
d x r0
(4)复色光(白光):彩色条纹,“红外紫
内”
红
大
K+1
紫
红
K
小
紫
1、基本设想:
2、实现方法 (1)分波振面法——从光源发出的同一波的波面上取出两个 次波源。(杨氏干涉)。 (2)分振幅法——把同一波列的波分为两束。(薄膜干涉)。
振幅分割法
波阵面分割法
s1
光源 *
s2
三、分波面法干涉实验
1、杨氏干涉实验:
x x
p
(1)装置
r1
·
R1
S1 d
s
R2
S2
x
r2
0
x0
x
I
r0
图3.2 杨氏实验装置
装置中的数据一般可取:
双孔(缝)间隔:d0.1mm1mm 横向观察范围:x1cm10cm 双孔与屏的距离:r0 1m10m
(2)实验原理的分析
120000((tt))22R R1220102(R2R1)
(1)
(3)实验结果——干涉强度分布
kn2r2n1r12 (r1r2)
(2)
r 2 r 1 d sin d x/r 0
(3)
或
r r 1 2 2 2 r r0 0 2 2 ( (x x d d//2 2 ) )2 2 r2 2 r 1 2 (r2 r 1 )(r2 r 1 ) 2 x d
光程差:
r2r1r2 2x dr1 r 2D r 1 d 2r0 drx0
xr d 0r2 c r o s sin l r 2 r l
x r d 0 r 2 c r o s s in l 即 平 r行 光 入 射 2 s in
4、 洛埃镜
图3.5洛埃镜实验 揭示了光在介质表面上反射,且入射角接近90°(掠射) 时,产生了半波损失。
(5)由合振幅的平均光强公式可说明,干涉图样实质上体现了参 与相干叠加的光波间相位差的空间分布。即干涉图样的强度记 录了相位差的信息,这也就是全息照相的原理。
2、菲涅耳双面镜
d 2 r s i n ; r 0 r c o s l
类似于杨氏双缝(或双孔)干涉实验,菲涅耳双面镜干涉 条纹的间隔:
A S 1 sin (i1 i2) 2、解释 (1)掠射——在洛埃镜实验中。
A p 1tg (i1 i2) A p 1 tg (i1 i2)
n2 n1 1 n1sini1n2sini2
i190 ,i1i290
令: As1,Ap1 0 As10, Ap10
lim As1 lim sin(i1 i2) = cosi2 1 A i1900 s1 i1900 sin(i1 i2) cosi2
§1.3分波面双光束干涉
一、普通光源的发光机理及特性
1、光源——发射光波的物质。 (1)热辐射。热能转化为光能。如太阳、白炽灯都属热辐射发
光光源。 (2)电致发光。电能直接转换为光能;如闪电、通电稀薄气体
发出的辉光 。
(3)光致发光。用光激发引起的放光现象。如日光灯。 荧光物质、磷光物质。
(4)化学发光。由于化学反应而发光的过程 ;例如燃烧过程
i1 0 0 n1 n2 As1 0, Ap1 0
| Ap1 | n2 n1 | Ap1 | n2 n1
| As1 | n2 n1 | As1 | n2 n1
直射时产生了半波损失。
作业:《光学教程》 姚启均 1.1——1.6 题
