方格网法土方计算公式
方格网计算土方量原理

方格网计算土方量原理方格网法是一种用于测量土地表面不规则形状的土方量的方法。
它是一种简单而有效的方法,可以帮助工程师和土木工程师快速准确地计算土地表面的土方量。
接下来,我们将介绍方格网法的原理和计算步骤。
方格网法的原理是将土地表面划分为一个个小方格,并通过对每个小方格的测量来计算土方量。
首先,需要在土地表面建立一个方格网,网格的大小可以根据实际情况来确定,一般情况下,网格大小为1米×1米或2米×2米。
然后,对每个小方格的高程进行测量,可以使用全站仪或其他测量仪器来进行高程测量。
通过对每个小方格的高程测量,可以得到土地表面的高程数据。
在进行高程测量之后,需要对每个小方格的面积进行测量。
可以通过测量每个小方格的边长来计算出每个小方格的面积。
在测量完所有小方格的高程和面积之后,就可以利用这些数据来计算土方量了。
土方量的计算公式为,土方量 = Σ(高程差×面积)。
其中,Σ表示对所有小方格进行求和,高程差表示每个小方格的最大高程和最小高程之差,面积表示每个小方格的面积。
通过对所有小方格的高程差和面积进行求和,就可以得到土地表面的土方量。
在实际应用中,方格网法可以帮助工程师和土木工程师快速准确地计算土地表面的土方量,特别是对于不规则形状的土地表面,方格网法可以更加方便地进行土方量的计算。
通过合理设置方格网的大小和密度,可以得到更加精确的土方量计算结果。
总之,方格网法是一种简单而有效的土方量计算方法,通过对土地表面进行方格划分和测量,可以快速准确地得到土方量的计算结果。
在工程实践中,方格网法可以帮助工程师和土木工程师更加方便地进行土方量的计算,为工程设计和施工提供重要的参考依据。
用方格网法计算土方步骤

用方格网法计算土方步骤方格网法是一种常用的土方计算方法,可以用于计算土方的体积和步骤。
方格网法的基本原理是将土地划分为一系列方格,并测量每个方格的高程差。
然后,通过计算每个方格的体积,并将其累加,即可得到土方的总体积。
下面将详细介绍方格网法的计算步骤。
第一步:测量区域边界首先,需要准确测量土地或施工场地的边界线,并在各个角点处标记测量点。
这些测量点将作为方格网中每个方格的角点。
第二步:确定网格间距根据实际情况,确定方格网的间距。
间距的选择应该根据场地尺寸和地形的复杂程度进行合理调整。
通常情况下,间距可以选择为1米或更小。
第三步:建立方格网使用测量点确定的位置,可以使用绳子或钉子等工具在地面上建立方格网。
确保方格网的边缘和角点都严格平行和垂直。
第四步:测量高程差使用水准仪或其他测量工具,对方格网中的每个角点进行高程测量。
记录每个位置的高程数值。
第五步:计算体积根据高程差测量结果,可以计算每个方格的土方体积。
通常情况下,每个方格的土方体积计算公式为:V=(A1+A2+A3+A4)/4*h,其中A为方格四个角点的高程数值,h为方格中心点的高程数值。
第六步:累加体积将每个方格的土方体积累加,即可得到整个土地或施工场地的土方体积。
如果方格网是等距的,可以直接将每个方格的体积相加。
如果方格网是非等距的,需要按照实际情况进行体积调整。
方格网法可以用于计算多个区域的土方体积。
例如,可以将场地划分为不同的区域,然后按照上述步骤逐个计算每个区域的土方体积,并将结果累加得到总体积。
需要注意的是,方格网法只适用于地形平坦的场地。
如果场地地形复杂或存在斜坡等情况,则需要使用其他方法进行土方计算,如三角测量法或通过地形测量仪器获取高程数据。
总结起来,方格网法是一种简单而实用的土方计算方法,适用于平坦的场地。
通过将场地划分为一系列方格,并测量各个角点的高程数值,然后计算每个方格的土方体积并累加,可以得到土方的总体积。
方格网法计算土方

方格网法常用方格网计算公式横截面计算步骤及方法1.方格网法方格网计算步骤及方法图示计算步骤方法适用范围1.划方格网根据地形图划分方格网,尽量使其与测量或施工坐标网重合,方格一般采用20m×20m~40m×40m,将相应设计标高和自然地面标高分别标注在方格点的右上角和右下角,求出各点的施工高度(挖或填),填在方格网左上角,挖方为(+),填方为(-)。
2.计算零点位置计算确定方格网中两端角点施工高度符号不同的方格边上零点位置,标于方格网上,联接零点,即得填方与挖方区的分界线。
零点的位置按下式计算,见图(a):;式中、——角点至零点的距离 m;、——相邻两角点的高程 m,均用绝对值;a——方格网的边长 m。
零点亦可采用图解法求出,如图(b)用尺在各角上标出相应比例,用尺相接,与方格相交点即为零点位置。
3.计算土方工程量按方格网底面图形和下表体积计算公式,计算每个方格内的挖方或填方量。
4.汇总分别将挖方区和填方区所有方格计算土方量汇总,即得该建筑场地挖方区和填方区的总土方量。
适于地形较平缓或台阶宽度较大的地段采用计算方法较为复杂,但作为平整场地土方量计算,精度较高。
2. 常用方格网计算公式项目图示计算公式一点填方或挖方(三角形)当时,二点填方或挖方(梯形)三点填方或挖方(五角形)四点填方或挖方(正方形)注:1)a——方格网的边长,m;b、c——零点到一角的边长,m;h1,h2,h3,h4——方格网四角点的施工高程,m,用绝对值代入;Σh——填方或挖方施工高程的总和 ,m,用绝对值代入;——挖方或填方体积,m。
2)本表公式是按各计算图形底面积乘以平均施工高程而得出的。
3. 横截面计算步骤及方法图示计算步骤方法适用范围1.划分横截面根据地形图、竖向布置图或现场检测,将要计算的场地划分为若干个横截面; ; ……,使截面尽量垂直等高线或建筑物边长;截面间距可不等,一般取10 m或20 m,但最大不大于100 m.2.划横截面按比例绘制每个横截面的自然地面和设计地面的轮廓线。
方格网法[1]
![方格网法[1]](https://img.taocdn.com/s3/m/1741b01f0029bd64793e2c55.png)
【例】厂房场地平整,部分方格网如图所示,方格边长为20m×20m,试计算挖填总土方工程量。
方格网法计算土方量(a)方格角点标高、方格编号、角点编号图;(b)零线、角点挖、填高度图(图中I、II、III等为方格编号;1、2、3等为角点号)常用方格网点计算公式注:1.a ——方格网的边长(m );b 、c ——零点到一角的边长(m );h 1、h 2、h 3、h 4——方格网四角点的施工高程(m ),用绝对值代入;Σh ——填方或挖方施工高程的总和(m ),用绝对值代入;V ——挖方或填方体积(m 3)。
2.本表公式是按各计算图形底面积乘以平均施工高程而得出的。
[解] ①划分方格网、标注高程。
根据图(a)方格各点的设计标高和自然地面标高,计算方格各点的施工高度,标注于图(b)中各点的左角上。
②计算零点位置。
从图(b)中可看出1~2、2~7、3~8三条方格边两端角的施工高度符号不同,表明此方格边上有零点存在,由公式:1~2线 13.010.02013.01+⨯=x =11.30(m ) 2~7线 13.041.02013.01+⨯=x =4.81(m ) 3~8线 15.021.02015.01+⨯=x =8.33(m ) 将各零点标注于图(b ),并将零点线连接起来。
③计算土方工程量 方格I 底面为三角形和五角形,由表中第1、3项公式:三角形200土方量 81.430.11613.0⨯⨯=+V =1.18(m 3) 五角形16700土方量 )541.052.010.0()81.430.112120(2++⨯⨯⨯--=-V =-76.80(m 3)方格II 底面为二个梯形,由表中第2项公式:梯形2300土方量 V +=820(4.81+8.33)(0.13+0.15)=9.20(m 3) 梯形7800土方量 V -=-820(15.19+11.67)(0.41+0.21)=-41.63(m 3) 方格III 底面为一个梯形和一个三角形,由表中第1、2项公式:梯形3400土方量 V +=820(8.33+20)(0.15+0.12)=19.12(m 3)④汇总全部土方工程量全部挖方量 ΣV -=-76.80-41.63-8.17-147-164-115-21.33=-573.93(m 3)全部填方量 ΣV +=1.18+9.20+19.12+55.0+15.33=99.83(m 3)。
土方方格网计算公式图示及推导
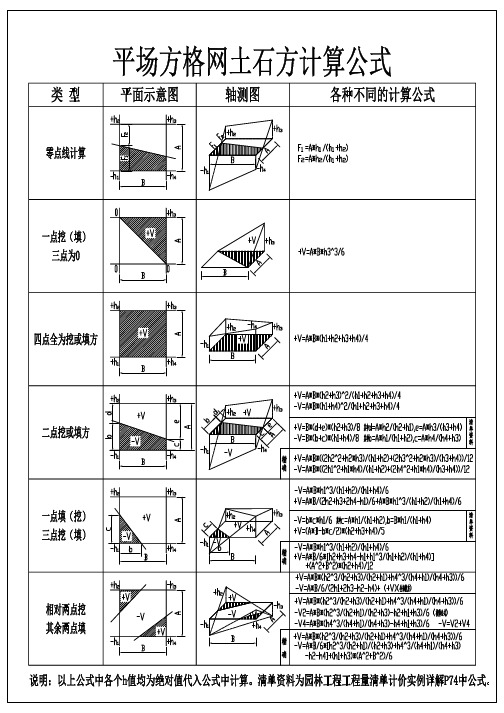
方格网土方计算公式推导:1、两点开挖工程量计算公式:如上图示:d=A*h2/(h1+h2); e=A*h3/(h3+h4); S1=d*h2/2; S2=e*h3/2S0=(d+e)/2*(h2+h3)/2/2根据拟柱体体积计算公式:V=B/6*(S1+4*S0+S2)将上面已知数代入公式可得:V=B/6*{A*h2/(h1+h2)*h2/2+4*[A*h2/(h1+h2)+A*h3/(h3+h4)]/2*(h2+h3)/2/2+h3*A*h3/(h3+h4)/2}=A*B/6*{h2*h2/(h1+h2)+ h2*(h2+h3)/(h1+h2)+ h3*(h2+h3)/(h3+h4)+h3*h3/(h3+h4)}/2=A*B/12*{(2h2^2+h2*h3)/ (h1+h2)+(2*h3^2+h2*h3)/(h3+h4)}2、三点开挖的挖方量计算公式:由图分解可得,挖方体积=v1+v2-(v3-v4),由拟柱体体积计算公式可以得出:V1={A*(h3+h4)/2+4*A/2*(h3+h2+h2+h4)/4}*B/6=A*B/12*{h3+h4+2*h2+h3+h4}=A*B*(h2+h3+h4)/6V2、V3、V4分别按四棱锥、三棱锥、三棱锥体积计算公式进行计算(体积=底面积*高/3)V2= [√(A^2+B^2)]*1/2*1/3*[√(A^2+B^2)]*(h2+h4)/2= (A^2+B^2)*(h2+h4) /12V3=A*B/2/3*h1=A*B*h1/6V4=h1/3*(B*h1/(h1+h4)*A*h1/(h1+h2)/2=A*B/6*h1^3/(h1+h2)/(h1+h4)V=V1+V2-V3+V4= A*B*(h2+h3+h4)/6+(A^2+B^2)*(h2+h4) /6+A*B/6*h1^2/(h1+h2)/(h1+h4)- A*B*h1/6= A*B /6*[ h2+h3+h4-h1+h1^3/(h1+h2)/(h1+h4)] +(A^2+B^2)*(h2+h4) /123、不机邻两点回填方量计算公式推导:如图示:从h1和h3处将图形分成平面为两个直角三角形体:h4侧的体积公式如下:Vh4=V1+V3-V2根据锥体体积公式:底面积*高/3可得V1=(h1+h3)/2*[√(A^2+B^2)] /3*[√(A^2+B^2)]/2=(h1+h3)*(A^2+B^2) /12 V2=A*B/2*h4/3= A*B*h4/6V3= h4/3*(B*h4/(h4+h1)*A*h4/(h4+h3)/2=A*B/6*h4^3/(h4+h1)/(h4+h3) V=(h1+h3)*(A^2+B^2) /12- A*B*h4/6+ A*B/6*h4^3/(h4+h1)/(h4+h3)= A*B/6*[h4^3/(h4+h1)/(h4+h3)-h4]+ (h1+h3)*(A^2+B^2) /12h2侧的体积公式推导方法h4侧的体积公式:Vh2=A*B/6*[h2^3/(h2+h1)/(h2+h3)-h2]+ (h1+h3)*(A^2+B^2) /12V=Vh2+Vh4=A*B/6*[h2^3/(h2+h1)/(h2+h3)-h2]+ (h1+h3)*(A^2+B^2) /12+ A*B/6*[h4^3/(h4+h1)/(h4+h3)-h4]+ (h1+h3)*(A^2+B^2) /12= A*B/6*[ h2^3/(h2+h1)/(h2+h3) + h4^3/(h4+h1)/(h4+h3) -h2-h4]+ (h1+h3)*(A^2+B^2) /6。
方格网土方计算公式

方格网土方计算公式
11.2.1 方格网法土方计算
方格网法土方计算适用于地形变化比较平缓的地形情况,用于计算场地平整的土方量计算较为精确。
具体做法如下:
首先建立地形的坐标方格网,方格网的一边与地形等高线或场地坐标网平行,大小根据地形变化的复杂程序和设计要求的精度确定,边长一般常采用20m×20m 或40m×40m(地形平坦、机械化施工时也可采用100m×100m)。
然后求出方格各个角点的自然标高、设计标高以及施工高程。
计算零点位置,在每相邻的填方点和挖方点之间总存在一个零点,零点的确定方法如下:
说明:
X:零点据填方角顶的距离;X:零点据挖方角顶的距离 tw
h:填方高度;h:挖方高度;a:方格边长 tw
连接每个方格上的相邻两个零点,根据零线将方格划分的情况,采用相应公式来计算,如表 11-2所示。
汇总,分别将填方区、挖方区所有土方汇总,得到填、挖土方总量。
四个角点全填方(或全挖方)
一个角点填方(或挖方),另外三个角点挖方(或填方)
一侧两个角点填方(或挖方),另一侧两个角点挖方(或填方)
相对两个角点填方(或挖方),另外相对两个角点挖方(或填方)
表 11-2 方格网法土方计算公式说明:
a:方格边长(m)
h、h、h、h:方格网角点的施工高度,正值代表填方,负值代表挖方 12343V、V-:填方(或挖方)的体积(m) +。
(整理)方格网法计算土方

方格网法常用方格网计算公式横截面计算步骤及方法1.方格网法方格网计算步骤及方法图示计算步骤方法适用范围1.划方格网根据地形图划分方格网,尽量使其与测量或施工坐标网重合,方格一般采用20m×20m~40m×40m,将相应设计标高和自然地面标高分别标注在方格点的右上角和右下角,求出各点的施工高度(挖或填),填在方格网左上角,挖方为(+),填方为(-)。
2.计算零点位置计算确定方格网中两端角点施工高度符号不同的方格边上零点位置,标于方格网上,联接零点,即得填方与挖方区的分界线。
零点的位置按下式计算,见图(a):;式中、——角点至零点的距离 m;、——相邻两角点的高程 m,均用绝对值;a——方格网的边长 m。
零点亦可采用图解法求出,如图(b)用尺在各角上标出相应比例,用尺相接,与方格相交点即为零点位置。
3.计算土方工程量按方格网底面图形和下表体积计算公式,计算每个方格内的挖方或填方量。
4.汇总分别将挖方区和填方区所有方格计算土方量汇总,即得该建筑场地挖方区和填方区的总土方量。
适于地形较平缓或台阶宽度较大的地段采用计算方法较为复杂,但作为平整场地土方量计算,精度较高。
2. 常用方格网计算公式项目图示计算公式一点填方或挖方(三角形)当时,二点填方或挖方(梯形)三点填方或挖方(五角形)四点填方或挖方(正方形)注:1)a——方格网的边长,m;b、c——零点到一角的边长,m;h1,h2,h3,h4——方格网四角点的施工高程,m,用绝对值代入;Σh——填方或挖方施工高程的总和 ,m,用绝对值代入;——挖方或填方体积,m。
2)本表公式是按各计算图形底面积乘以平均施工高程而得出的。
3. 横截面计算步骤及方法图示计算步骤方法适用范围1.划分横截面根据地形图、竖向布置图或现场检测,将要计算的场地划分为若干个横截面; ; ……,使截面尽量垂直等高线或建筑物边长;截面间距可不等,一般取10 m或20 m,但最大不大于100 m.2.划横截面按比例绘制每个横截面的自然地面和设计地面的轮廓线。
土方工程量计算-方格网法

绘制土方平衡表、土方调配表及土方调配图
从土方平衡表上可以一目了然地了解各个区的出土量和需土量、调拨关系和土方平衡情况。在土方调配表上则可更清楚地看到各区的土方盈缺情况。土方调配图上清楚地看到土方的调拨量,调拨方向和距离。
挖填方区划图
方格编号
挖方/m3
填方/m3
备注
VⅠ
32.3
16.5
VⅡ
17.6
施工标高+0.80
设计标高36.00
⑨ 角点编号
35.00 原地形标高
Hx=Ha±xh/L
当方格交叉点不在等高线上就要采用插入法计算出原地形标高。插入法求标高公式如下:
Ha——位于低边的等高线高程(m); x——角点至低边等高线的距离(m); h——等高距(m); L——相邻两等高线间最短距离(m)。
1
1
假设4-3点的设计标高是x,根据场地的坡度求出其他点的标高,标在角点上,如图;再求出每角点的设计标高。
5.求各角点的设计标高
H0′=4N(∑h1′+2∑h2′+3∑h3′+4∑h4′) ∑h1′=x-0.8+x-0.8+x-1.1+x-1.1+x-1.3+x-1.3 =6x-6.4m 2∑h2′=(x-0.4+x+x-0.4+x-1.0+x-1.0+x-0.9)×2 =12x-7.4m 3∑h3′=(x-0.7+x-0.7) ×3 =6x-4.2m 4∑h4′=(x-0.3+x-0.6)×4 =8x-3.6m H0′=4*8 (6x-6.4+12x-7.4+6x-4.2+8x-3.6)= x-0.675 H0′=X-0.675=H0 ∵ H0 ≈ 20.06 ∴ X=20.06+0.675≈20.74
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
方格网法土方计算公式(原理)__飞时达土方计算
飞时达土方计算软件采用双向切分三棱锥平均值计算土方量。
希望大家好好对照方格网计算公式,手工计算和我们软件计算,好好对比下,计算出来结果是一样的。
根据各角点施工高度的不同,零线(即方格边上施工高度为零、不填不挖的点的连线)可能将三角形划分为两种情况:三角形全部为挖方或全部为填方以及部分挖方和部分填方。
土方计算软件产品经理QQ:124230688 (各种各样土方工程量计算项目都有涉及)注:更详细计算方法可参见《建筑施工》(第三版)P11~13页
1、全填全挖的计算公式:
V=[a2*(h1+h2+h3)]/6
a:指方格的边长
h1 h2 h3 值的三角形的各点的施工高度。
举例:下面是一个全填方的网格(20*20),请看软件详细的计算过程:
第一种对角线
第一种对角线的情况:V1=[202*(6.61+5.84+10.88)]/6 =1555.3333333333 V2=[202*(10.62+5.84+10.88)]/6 =1822.66666666
总量:3377.9999999
第二种对角线
第二种对角线的情况:V1=[202*(6.61+5.84+10.62)]/6 =1538
V2=[202*(10.62+6.61+10.88)]/6 =1874
总量:3412
【第一种情况+第二种情况】/ 2 =(3378+3412)/2=3395 (正好和网格里的对上了) 全挖的情况和全填的情况是一样的计算过程。
2、部分填部分挖的计算公式:
由于零线将三角形划分成底面为三角形的锥体和底面为四边形的锲体,锥体和楔体体积公式分别:
锥体的体积计算公式:
V锥体=(a2/6)×{h33/[(h1+h3) ×(h2+h3)]}
楔体的体积计算公式:
V楔体=(a2/6)×{h33/ [(h1+h3) ×(h2+h3)]-h3+h2+h1}
注意:h1、h2、h3—三角形角点的施工高度(均用绝对值代入),但是h3恒指锥体顶点的施工高度,a指的是网格的边长
举例:下面是一个部分填部分挖的情况的网格,网格大小(20*20),请看软件详细的计算过程:
第一种对角线
对角线的第一种情况:
V1:
V锥体=(a2/6)×{h33/[(h1+h3) ×(h2+h3)]}
=(202/6)×{0.253/[(0.25+2.77) ×(0.97+0.25)] }
=(400/6) ×0.00424
=0.283 (挖方)
V楔体= (a2/6)×{h33/ [(h1+h3) ×(h2+h3)]-h3+h2+h1}
=(202/6)×{0.253/(0.25+2.77) ×(0.97+0.25)-0.25+2.77+0.97} = (400/6) ×3.494
=232.933 (填方)
V2:
V楔体= (a2/6)×{h33/ [(h1+h3) ×(h2+h3)]-h3+h2+h1}
=(400/6) ×{0.973/ [2.3×1.22]-0.97+0.25+1.33}
=62.351 (挖方)
V锥体=(a2/6)×{h33/[(h1+h3) ×(h2+h3)]}
=(400/6) ×{0.973/[2.3×1.22] }
=21.684 (填方)
总填方=21.684+232.933=254.617
总挖方=0.283+62.351=62.634
第二种对角线
对角线的第二种情况:
V1:
V锥体=(a2/6)×{h33/[(h1+h3) ×(h2+h3)]}
=(400/6)×{2.773/[(0.25+2.77) ×(1.33+2.77)]
=(400/6)×{2.773/[3.02×4.1]
=114.435 (填方)
V楔体= (a2/6)×{h33/ [(h1+h3) ×(h2+h3)]-h3+h2+h1}
=(400/6)×{2.773 /[(0.25+2.77) ×(1.33+2.77)]-2.77+0.25+1.33}
=(400/6)×{0.5265}
=35.101 (挖方)
V2:
V锥体=(a2/6)×{h33/[(h1+h3) ×(h2+h3)]}
=(400/6)×{1.333/[(1.33+0.97) ×(1.33+2.77)]
=(400/6)×{1.333/[2.3×4.1]
=16.632 (挖方)
V楔体= (a2/6)×{h33/ [(h1+h3) ×(h2+h3)]-h3+h2+h1}
=(400/6)×{1.333 /[(1.33+0.97) ×(1.33+2.77)]-1.33+2.77+0.97} =(400/6)×{ 2.659}
= 177.2666(填方)
总填方=177.2666+114.435=291.7016
总挖方=16.632+35.101=51.733
最后,我们取两种情况的平均值:
挖方=(51.733+62.634)/2≈57.18
填方=(291.702+254.617)/2≈273.18。
