(完整)暨南大学09-10高等数学试卷__A_5附答案
2009级高等数学(下)考试试题及参考答案_A_

扬州大学2009级《高等数学I (2)》统考试题(A)卷班级班级 学号学号 姓名姓名 得分得分一、单项选择题(每小题3分,共18分) 1.设函数),(y x f 在),(00y x 处不连续,则【处不连续,则【 】(A)),(y x f 在),(00y x 处必不可微处必不可微 (B)),(lim ),(),(00y x f y x y x ®必不存在必不存在 (C)),(0y x f 必不存在必不存在 (D)),(0y x f x¢与),(00y x f y¢必不存在必不存在2.设函数),(y x f z =在点)0 ,0(处具有偏导数,且3)0 ,0(=¢xf ,1)0 ,0(=¢yf ,则【则【 】(A) yx z d d 3d )0,0(+=(B) 曲面),(y x f z =在点))0 ,0(,0,0(f 的法向量为)1 ,1 ,3( (C) 曲线îíì==0),(y y x f z 在点))0 ,0(,0 ,0(f 的切向量为)3 ,0 ,1( (D) 曲线îíì==0),(y y x f z 在点))0 ,0(,0 ,0(f 的切向量为)1 ,0 ,3( 3.设L 是2y x =上从)0,0(O 到)1,1(A 的一段弧,则22d d Lxy x x y +=ò【 】(A) 2 (B) 1- (C) 0 (D) 1 4.设函数),(y x f 连续,且y x y x f xy yx f Ddd ),(),(òò+=,其中D 是由是由 2 ,1 ,0x y x y ===所围成的闭区域,则=),(y x f 【 】(A) 81+xy (B) xy (C) xy 2 (D)1+xy 5.下列级数中,发散的是【.下列级数中,发散的是【 】(A) å¥=+1)11ln(1n nn (B) å¥=++112 2n nn n n (C) å¥=12sin n nn (D) å¥=1!n nn n 6.若幂级数nn n x a )1(1+å¥=的收敛半径为R ,则nn n x a 21å¥=的收敛半径为【的收敛半径为【 】 (A) R (B) 2R (C) 1-R (D) R题号题号 选择题选择题 填空题填空题 13~14 15~16 17~19 20~21 22~23 扣分扣分扣分2-e xy-..被三坐标面割下的面积为..处取得极大值.处取得极大值.的收敛区间为.,yxxyz15.计算y x y x Dd d )cos(òò+,其中D 是由直线x y =,0=y 及2p=x 所围成的闭区域.所围成的闭区域.16.计算曲线积分s e Ly xd22ò+,其中L 为圆周222a y x =+, 直线x y =及x 轴在第一象限内所围成的扇形的整个边界.轴在第一象限内所围成的扇形的整个边界.扣分扣分17. 求半球面223y x z --=与旋转抛物面)(2122y x z +=所围立体的体积.所围立体的体积.18.计算曲面积分S z xòòSd 2,其中S 为球面4222=++z y x被平面1=z 截出的顶部.截出的顶部.19. 计算曲面积分y x z z x z y z y x d )d 3( d d 2 d d 2-++òòS, 其中S 是锥面22y x z +=位于平面1=z 下方部分的下侧.下方部分的下侧.扣分扣分扣分20.求幂级数å¥=----112112)1(n n n n x 的收敛域及和函数,并求å¥=----1113 )12()1(n n n n .21.将函数2234)(x x x f -+=展开成)2(-x 的幂级数,并指出展开式的成立范围.扣分扣分( -nnz z 6¶¶222000z y x 0z y x 000z y x xyz z y x z y x 222z y x z y x l l l15.原式y x y x D d d )cos(1òò+=y x y x D d d )cos(2òò+-+…………………………………………………………(2(2分) 其中}40 ,2|),{(1pp££-££=y y x y y x D }24 ,2|),{(2pp p££££-=x x y x y x D x y x y yy d )cos(d 240òò-+=p py y x xx xd )cos(d 224òò--+-p p p ……………………………………(4(4分))421()214(pp---=12-=p ……………………………………………………………………………………(6(6分)16.s e Ly x d22ò+s e s e s e L y x L y x Ly x d d d 322222122òòò+++++=………………………………(1(1分)其中其中 )0( 0 :1a x y L ££=,)40( sin ,cos :2p ££==t t a y t a x L ,)220( :3a x x y L ££= 且 1d d 1d 002122-==×=òòò++aax ax L y x e x e x es ea a Lyxae t a e s e 4d d 42220p p=×=òò+1d 2d 22022322-=×=òò++aa x x L y x e x es e…………………………………………………………(5(5分) 故 s e Ly xd22ò+aaa a aae e e ae e 4)1(2141pp+-=-++-= ……………………(6(6分)17.所围立体W 在xOy 面上的投影区域2:2222£+y x Dxy.òòòW =V V d …………………………………………………………………………………………………………………………………………(1(1分)z d d d 222132020òòò-=r r pr r q ………………………………………………………………………………………………(4(4分) r r r r p )d 21-3(22220-=òp )3532(-=……………………………………………………(6(6分)18.原式y x y x y x x xyD d d 42422222----=òòy x x y x d d 23222òò£+=……………………(3(3分)òò×=302220d cos d 2r r q r q pp 29=…………………………………………………………………………(6(6分) 19.设1S 为平面) 1 ( 122£+=y x z 的上侧,W 为S 和1S 所围成的空间闭区域,所围成的空间闭区域,则y x z z x z y z y x d )d 3( dd 2 d d 21-++òòS +S v z d 2òòòW=y x z z zD d d 2 d 1òòò=ò×=102d 2 z z z p 2p= ……………………………………(3(3分)又y x z z x z y z y x d )d 3( d d 2 d d 21-++òòS y x y x d d 2122òò£+-=p 2-=故原式)2(2p p--=p 25=……………………………………………………………………………………………………(6(6分)20.nn n u u1lim+¥®12)1(12)1(lim 12112--+-=--+¥®n x nx n nn n n =2x 当12<x 即1<x 时,幂级数绝对收敛;当12>x 即1>x 时,幂级数发散;时,幂级数发散;所以收敛半径1=R ,收敛区间)1 ,1(-. 当1=x 时,原级数为å¥=---1112)1(n nn ,收敛;,收敛; 当1-=x 时,原级数为å¥=--112)1(n nn ,收敛;,收敛;故原级数的收敛域为]1 ,1[- ……………………………………………………………………………………………………(3(3分)设 å¥=----=112112)1()(n n n n x x S ,)1 ,1(-Îx , 则 å¥=---=¢1221)1()(n n nxx S 211x +=, x x S a r c t an )(=Þå¥=----=112112)1(n n n n x ,)1 ,1(-Îx ……………………………………(5(5分) 在上式中,令31=x 得 6)31()31(121)1(1211p==---¥=-åS n n n n 故 å¥=----1113 )12()1(n n nn p 63=……………………………………………………………………………………………………(6(6分)3x (32-)p d )(4òxy p 214ò=21tan ò21ò=å--11)1(nn å11n 发散;发散; å-1)1(n 为一交错级数,收敛;为一交错级数,收敛; nn+. 。
暨南大学考试试卷(参考答案)

暨 南 大 学 考 试 试 卷(参考答案)一、单项选择题(请将最恰当的选择项写在每小题中的括号内。
共15小题,每小题2分,共30分) B )。
A 、技能组合法、德尔菲法、问卷调查法 B 、德尔菲法、工作研究法、描述法 C 、技能组合法、德尔菲法、专家评估法 D 、工作研究法、描述法、回归分析法 2、人力资源管理七大模块中,最基础的两大模块是( B )。
A 、绩效管理、薪酬管理B 、职位分析、胜任力模型C 、培训开发体系、人力资源规划D 、晋升机制、人员甄选与招聘3、一个完整的人力资源规划一般表现在( A )等几个方面。
A 、管理体制调整计划、人员补充调配计划、素质提升计划、接替晋升计划和退休解聘计划B 、人员补充调配计划、素质提升计划、接替晋升计划C 、管理体制调整计划、人员补充调配计划、素质提升计划D 、需求计划、供给计划 4、下列关于素质(胜任力)的描述不正确的是( B )。
A 、素质(胜任力)是通过对行为的引导而最终影响绩效的B 、素质(胜任力)研究即通过测量一个人的智商来预测其未来工作绩效的方法C 、麦克利兰的素质(胜任力)研究更关注那些工作成功人士所特有的行为和能力特征的发掘D 、素质(胜任力)是驱动一个人产生优秀工作绩效的知识、技能、个性和驱动力等特征的集合。
5、下列不属于评价中心技术(Assessment Center )的人员测量手段的是(B/C )。
A 、公文处理、角色扮演 B 、案例分析 C 、心理问卷测验 D 、无领导小组讨论6、下列不属于内部招聘的优点的是( B )。
A 、组织对候选人的能力有较清晰的认识B 、利于把新想法、新理念带入组织,使组织产生鲶鱼效应C 、利于鼓舞内部员工的士气D 、更低的招聘和甄选成本7、根据霍兰德的职业性向维度理论,与现实型(R)性向差距最大的是( D )。
A、艺术型(A)B、常规型(C)C、企业型(E)D、社会型(S)8、根据沙恩(E.H Shein)的职业发展路径理论,组织内的个人职业生涯发展有几种选择,它们是( D )。
0910高等数学A(二)答案

0910高等数学A(二)答案第一篇:0910高等数学A(二)答案济南大学2009~2010学年第二学期课程考试试卷评分标准(含参考答案)A卷课程名称:高等数学A(二)任课教师:张苏梅等一、填空题(每小题3分,共18分)1.yzez-xy;2.y=2x3-x2;3.2xdx+2ydy;π∞(-1)n(2x)2n4.0;5.2;6..12(1-n∑=0(2n)!),(-∞,+∞)二、选择题(每小题3分,共18分)C;D;C;B;A;B.三、计算题(每小题8分,共32分)1.解:∂z∂x=1ycosxy;.....4分∂2z1xxx∂x∂y=-y2cosy+y3siny.....8分2.解:⎰⎰xydσ=⎰2dx⎰xxydy.....4分D0=12⎰20x3dx=2.....8分 3.解:dS=+x2x2+y+y2x2+ydxdy=2dxdy.....2分⎰⎰zdS=⎰⎰x2+y22dxdy.....5分∑Dxy=⎰2πdθ⎰2r2dr=π.....8分 4.解:⎰⎰(x2+y2+z2)dxdy=dxdy=πa4...........8分∑D⎰⎰axy四、应用题(每小题8分,共16分)1.解:由椭球的对称性,不妨设(x,y,z)是该椭球面上位于第Ⅰ卦限的任一点,内接长方体的相邻边长为2x,2y,2z(x,y,z>0),其体积为:V=8xyz构造拉格朗日函数F(x,y,z,λ)=8xyz-λ(x2y2a+b+z2c-1)......4分∂F∂x=8yz-λ2xa2=0令∂F2y∂y=8xz-λb2=0........6分∂F∂z=8xy-λ2zc2=0求得(x,y,z)=⎛a,b,c⎫⎪,V=8xyz=8abc......8分⎝33⎪⎭332.解:Iz=⎰⎰⎰(x2+y2)dv.........3分Ω=⎰2π2430dθ⎰0dr⎰r2rdz.........6分=2π⎰2r3(4-r2)dr=03π.........8分五、(8分)解:因为limana=limn=1,所以收敛半径为1.n→∞n+1n→∞n+1又x=±1时,级数均发散,故级数的收敛域为(-1,1).....3分n=1∑nx∞n=x∑nxn=1∞n-1=x(∑xn)'......6分 n=1∞xx=x()'=,x∈(-1,1).........8分 21-x(1-x)六、(8分)解:① 设u=x2+y2,则∂zx=f'(u);∂xu∂2zx21x2=()f''(u)+f'(u)-3f'(u)........2分 2uu∂xuy21y2同理,2=()f''(u)+f'(u)-3f'(u)uu∂yu由∂2z∂2z∂x2+∂2z∂y2=0⇒f''(u)+1f'(u)=0.....4分 u② 设f'(u)=p,f''(u)=dp,du则原方程化为:dp1dpdu+p=0⇒=-duupu积分得:p=CC,即f'(u)=,........6分 uu由f'(1)=1,得C=1.于是f(u)=ln|u|+C1代入f(1)=0得:C1=0.函数f(u)的表达式为:f(u)=ln|u|.......8分第二篇:1112高等数学B(二)答案济南大学2011~2012学年第二学期课程考试试卷评分标准(含参考答案)A卷课程名称:高等数学B(二)任课教师:一、填空题(每小题2分,共10分)1、2dx+dy,2、-5,3、1,4、⎰10dy⎰1yf(x,y)dx5、1二、选择题(每小题2分,共10分)1、A2、B3、C4、C5、D三、计算题(每小题8分,共40分)1、解:令F=x2+y2+z2-2z,则Fx=2x,Fz=2z-2.....2分∴∂zFx∂x=-xF=z.....4分z1-∂2z∂x(1-z)2+x2∴∂x2=∂x(1-z)=(1-z)3.....8分2、解:⎰⎰(x+6y)dxdy=⎰1dx5x76D0⎰x(x+6y)dy=3.....8分π3、解:⎰⎰+x2+y2dxdy=D⎰2dθ⎰1+r2rdr=π(22-1).....8分4、解:ux(2,1,3)=4,uy(2,1,3)=5,uz(2,1,3)=3 方向lϖ=(3,4,12)cosα=313,cosβ=413,cosγ=12 .....6分∂z∂l=uu68xcosα+ycosβ+uzcosγ=13.....8分5、解:收敛域为(0,2).....2分∞∞令S(x)=∑(n+1)(x-1)n=(1)n+1)'.....6分n=0∑(x-n=0S(x)=(x-12-x)'=1(2-x)2x∈(0,2).....8分四、解答题(每小11分,共33分)ϖ1、解:交线的方向向量为nϖiϖjkϖ=1-4=(-4,-3,-1).....8分2-1-5所求直线方程为x+3y-2z-54=3=1.....11分2、解:令f(x)=xx-1,则f'(x)=-1-x2x(x-1)<0x>1 所以un单调递减且limn→∞un=0∞所以级数∑(-1)nnn=2n-1.....6分n∞由于limn→∞=1,且∑1发散n=2nn∑∞(-1)n所以级数n.....11分n=2n-13、解:旋转曲面方程为z=x2+y2.....3分投影区域D:x2+y2≤1.....5分V=⎰⎰(1-x2-y2)dxdy=⎰2πdθ⎰1π(1-r)rdr=D.....11分五、证明题(每小题7分,共7分)ff(x,0)-f(0,0)x(0,0)=lim证:x→0x=0f(0,0)=limf(x,0)-f(0,0)xx→0x=0所以函数f(x,y)在(0,0)处可导.....3分lim∆z-fx(0,0)∆x-fy(0,0)∆yρ→0ρ=limf(∆x,∆y)∆x∆yρ→0∆x2+∆y2=limρ→0∆x2+∆y2取∆y=k∆x,得极限为k1+k,说明极限不存在所以函数f(x,y),在(0,0)点不可微.....7分第三篇:专升本高等数学(二)成人高考(专升本)高等数学二第一章极限和连续第一节极限[复习考试要求]1.了解极限的概念(对极限定义等形式的描述不作要求)。
高等数学下考试题库(附答案)

《高等数学》试卷1(下)一.选择题(3分⨯10)1.点1M ()1,3,2到点()4,7,22M 的距离=21M M ( ).A.3 B 。
4 C 。
5 D 。
62.向量j i b k j i a+=++-=2,2,则有( ).A 。
a ∥bB 。
a ⊥b C.3,π=b a D 。
4,π=b a3.函数1122222-++--=y x y x y 的定义域是( ).A 。
(){}21,22≤+≤y x y x B 。
(){}21,22<+<y x y xC 。
(){}21,22≤+<y xy x D (){}21,22<+≤y x y x4。
两个向量a 与b垂直的充要条件是( ).A 。
0=⋅b a B.0 =⨯b a C 。
0 =-b a D.0 =+b a5。
函数xy y x z 333-+=的极小值是( )。
A.2 B.2- C 。
1 D.1- 6。
设y x z sin =,则⎪⎭⎫ ⎝⎛∂∂4,1πyz =( ).A 。
22B.22-C.2 D 。
2-7。
若p 级数∑∞=11n p n 收敛,则( ). A 。
p 1< B 。
1≤p C 。
1>p D.1≥p8。
幂级数∑∞=1n nnx 的收敛域为( )。
A 。
[]1,1-B ()1,1- C.[)1,1- D 。
(]1,1-9。
幂级数nn x ∑∞=⎪⎭⎫⎝⎛02在收敛域内的和函数是( ).A.x -11 B 。
x -22 C.x -12 D.x-21 10.微分方程0ln =-'y y y x 的通解为( )。
A 。
xce y = B 。
xe y = C.xcxe y = D.cxe y =二.填空题(4分⨯5)1.一平面过点()3,0,0A 且垂直于直线AB ,其中点()1,1,2-B ,则此平面方程为______________________. 2。
函数()xy z sin =的全微分是______________________________。
暨南大学08-09高数II(A)参考答案word精品文档6页

暨 南 大 学 考 试 试 卷1. 两平行平面23490x y z -++=与234150x y z -+-=的距离为( C ). (A)629 (B) 2429 (C) 2. 二元函数极限32lim2++∞→→y xyy x 的值为 ( A ). (A) 4 (B) ∞+ (C) 34(D) 0 3.下列说法正确的是( C ).(A) 若∑∞=1n n u ,∑∞=1n n v 都发散,则∑∞=+1)(n n n v u 发散;(B) 若∑∞=1n n u ,∑∞=1n n v 都发散, 则∑∞=1)(n n n v u 发散;(C) 若∑∞=1n n u 收敛, 则∑∞=11n n u 发散; (D) 若∑∞=1n n u 发散, 则∑∞=11n n u 收敛;4. 函数x e y y y x 2cos 52=+'-''的一个特解应具有形式:( C )(C) )2sin 2cos (x B x A xe x + (D) )2sin 2cos (2x B x A e x x + 5. 设曲线积分ydy x f ydx e x f cx cos )(sin ])([--⎰与路径无关,其中)(x f 具有一阶连续导数,且0)0(=f ,则)(x f 等于( D )(A))(21x x e e -- (B) )(21x x e e --(C) 1)(1---x x e e (D) )(211x x e e ---二、填空题(共5小题,每小题3分,共15分)1、曲面3=+-xy z e z 在点)0,1,2(处的切平面方程为240x y +-=。
2、曲线积分dx y x L⎰-)(22=5615-,其中L 是抛物线2x y =上从点)0,0(到)4,2(的一段弧。
3、交换二次积分⎰⎰⎰⎰+121212212),(),(yydx y x f dy dx y x f dy 的积分顺序为211(,)xdx f x y dy⎰⎰。
考研真题:广东暨南大学2022年[高等数学]考试真题
![考研真题:广东暨南大学2022年[高等数学]考试真题](https://img.taocdn.com/s3/m/4b7492427f21af45b307e87101f69e314332fa0f.png)
考研真题:暨南大学2022年[高等数学]考试真题一、填空题1. 若,则_____________________________.Q x x Q Px x =-+-+→11)8(lim 221=P =Q 2. 二次型为正定型,那么的取值范围3231212322213212245),,(x x x x x x ax x x x x x f --+++=a 是_________________3.若 ,则__________________________.03275=--+x x y y ==0|x dy 4. ______________________.=++++++∞→)...2211(lim 222nn n n n n 5.以函数作为通解的微分方程是_______________________.12C x C y +=6.二次积分___________________________.⎰⎰≤++=+1)(22222)(y x y x dxdy e y x 7.函数展开成正弦级数为_________________________.π<<=x x f 0,1)(8.曲面在点处的切平面方程为_______.532+=+++z y e z y x )2,2,1(-9.设在上可导,且,则)(x f ),(+∞-∞⎰≠=xx dt t f x x F 10)0()()(=)(''x F __________________.二、选择题1. 行列式_____________=v u d c yx b a 00000000(A)xyuv abcd -(B)bcuv adxv -(C)))((yu xv bc ad --(D) ))((uv xy cd ab --2. 四元线性方程组的基础解系是__________⎪⎩⎪⎨⎧=-==+00041241x x x x x (A)T )0,0,0,0((B)T )0,2,0,0((C)T )1,0,1(-(D) 和T )0,2,0,0(T)1,0,0,0(3. 设可导,,则是在处可导的)(x f |))1ln(|1)(()(x x f x F +-=0)0(=f )(x F 0=x ________________(A) 充要条件(B) 充分不必要条件(C) 必要不充分条件(D) 既不充分也不必要4. 若级数收敛,那么说法正确的是___________)(1n n n b a +∑∞=(A)和中至少有一个收敛 ∑∞=1n n a ∑∞=1n n b (B)和有相同的敛散性∑∞=1n n a ∑∞=1n n b (C)和都收敛 ∑∞=1n n a∑∞=1n n b (D) 收敛||1n n n b a +∑∞=5. 设是以为顶点的正方形,其方向为逆时针方向,那L )1,0(),0,1(),1,0(),0,1(--D C B A么___________⎰=-+Ly x d y x )()((A)0(B)2-(C)4-(D) 8-6. 设在上可导且其反函数也可导,已知则)(x f ),0(+∞,3)1(=f ,1)1('=f ,3)3('=f ___________==-31|)(x dxx df (A)1/3(B)3(C)1(D) 不能确定7. 设为正整数,那么 _______________.n m ,=→nx mx x sin sin lim π(A). n m nm --)1((B) nm (C) n m -(D) 不存在8. 将XOZ 坐标面上的抛物线绕Z 轴旋转一周得到的方程是__________.x z =2(A)222y x z +=(B)x y x =+22(C)y x z +±=2(D) xz y =+22三 、计算题1.,求.⎪⎪⎪⎭⎫ ⎝⎛-=6/10013/10212/1A n n A ∞→lim 2. 设向量组,,,。
暨南大学高数考试题及答案

暨南大学高数考试题及答案一、选择题(每题4分,共20分)1. 下列函数中,哪一个是奇函数?A. f(x) = x^2B. f(x) = x^3C. f(x) = x^4D. f(x) = sin(x)答案:B2. 计算定积分∫(0,π) sin(x) dx的结果是多少?A. 2B. 0C. -2D. π答案:B3. 微分方程y'' - 4y' + 4y = 0的通解是?A. y = e^(2x) + e^(-2x)B. y = e^(2x) - e^(-2x)C. y = 2e^(2x) + e^(-2x)D. y = 2e^(2x) - e^(-2x)答案:A4. 以下哪个极限不存在?A. lim(x→0) (sin(x)/x)B. lim(x→0) (1 - cos(x))/x^2C. lim(x→0) (1 - cos(x))/xD. lim(x→0) (tan(x)/x)答案:C5. 以下哪个级数是收敛的?A. 1 + 1/2 + 1/4 + 1/8 + ...B. 1 - 1/2 + 1/4 - 1/8 + ...C. 1 + 1/2^2 + 1/3^2 + 1/4^2 + ...D. 1 + 1/2 + 1/3 + 1/4 + ...答案:B二、填空题(每题3分,共15分)1. 函数f(x) = x^2 + 3x + 2的导数是______。
答案:2x + 32. 函数f(x) = ln(x)的不定积分是______。
答案:x*ln(x) - x + C3. 曲线y = x^3 - 3x^2 + 2在x = 1处的切线斜率是______。
答案:-44. 微分方程y' + 2y = e^(-2x)的特解是______。
答案:y = -1/2 * e^(-2x) + C * e^(-2x)5. 级数1/2 + 1/4 + 1/8 + ...的和是______。
高数IIA参考答案
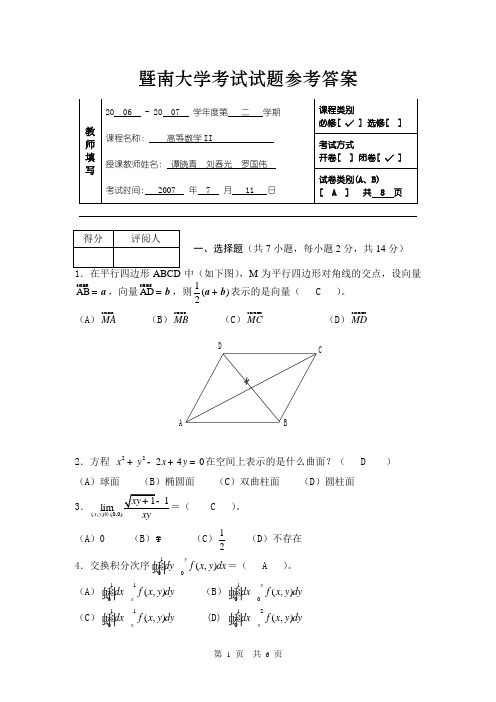
暨南大学考试试题参考答案一、选择题(共7小题,每小题2分,共14分)中(如下图),M 为平行四边形对角线的交点,设向量AB a = ,向量AD b = ,则1()2a b +表示的是向量( C )。
(A )MA(B )MB (C )MC (D )MDACD2.方程22240x y x y +-+=在空间上表示的是什么曲面?( D ) (A )球面 (B )椭圆面 (C )双曲柱面 (D )圆柱面 3.(,)(0,0)limx y ® C )。
(A )0 (B )¥ (C )12(D )不存在 4.交换积分次序100(,)y dyf x y dx 蝌=( A )。
(A )110(,)x dxf x y dy 蝌 (B )10(,)x dxf x y dy 蝌 (C )110(,)xdxf x y dy 蝌 (D) 120(,)xdxf x y dy 蝌5.设()f x 以2π为周期,且它在一个周期内的定义为1,0()1,0x f x x ππì--?ïï=íï?ïî,则它的傅里叶级数展开式在x π=处收敛于( D )。
(A )-1 (B )1 (C )12 (D )06.级数21sin n n n α¥=å(α为常数)( A )。
(A )绝对收敛 (B )条件收敛 (C )发散 (D )收敛性与α的取值有关7.曲线23x t y t z t ì=ïïï=íïï=ïïî在点(1,1,1)处的法平面方程为( B )。
(A )236x y z -+= (B )236x y z ++= (C )236x y z +-= (D )236x y z --=二、填空题(共8小题,每小题2分,共16分)1.平行于向量(2,2,1)的单位向量为221221(,,)(,,)333333---和。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.对 lim n n a A →∞= 的表述错误的是 ( C )A. 0ε∀>, ∃ N N +∈, 使得对所有 n N ≥ 的 n N +∈, 都有||n a A -<; B. 01ε∀<<, ∃N N +∈, 使得对所有 n N ≥ 的 n N +∈, 都有 2||n a A ε-<; C. 0ε∀>, ∃ N N +∈, 使得对所有 n N ≥ 的 n N +∈, 都有||n a A -<; D. N k +∀∈, ∃ N N +∈, 使得对所有 n N ≥ 的 n N +∈, 都有 1||n a A k-<. 2. 设函数 21sin ,0;()0,0x x f x xx ⎧≠⎪=⎨⎪=⎩, 则 ()f x 在 0x = 处 ( C ) A. 不连续; B. 连续但不可导;C. 连续且可导;D. 导函数连续.3. 设221(),43x f x x x -=-+ 则( B ) A. 1x = 是 ()f x 的跳跃间断点; B. 1x = 是 ()f x 的可去间断点; C. 3x = 是 ()f x 的跳跃间断点; D. 3x = 是 ()f x 的可去间断点.4.下列命题中正确的是 ( D )A. 若在 (a, b) 内 '()0f x >, 则 ()f x 在 [a, b] 上单调递增;B .若 ()f x 在 (a, b) 内单调增加且可导, 则在 (a, b) 内必有 '()0f x >. C. 若 '()0f x >, 则必有 ()0f x >.D. 若函数 ()f x 在 [a, b] 上连续, 在 (a, b) 内 '()0f x ≥, 且'()f x 至多有有限多个零点, 则 ()f x 在 [a, b] 上单调增加.5. 下列关于极值叙述正确的是 ( C ).A. 若 0'()0f x =, 则 0x 为 ()f x 的极值点. B .若 0x 为()f x 的极值点, 则 0'()0f x =. C. ()f x 在 (a, b) 内的极小值可能大于极大值.D. 若 ()f x 在 0x 取得极大值, 则存在 0x 的某邻域, 使得在该邻域内,()f x 在 0x 左侧单调增加, 右侧单调减少.6. 下列各式中正确的是 ( B ).A.'(3)(3)f x dx f x C =+⎰; B.1'(3)(3)3f x dx f x C =+⎰; C. '(3)3(3)f x dx f x ⎡⎤=⎣⎦⎰; D. '1(3)(3)3f x dx f x ⎡⎤=⎣⎦⎰.二、填空题(共6小题,每小题3分,共18分)1. limn →∞= 0 .2. 设xy xe y +=12,则=x dxdy =12. 3. 11lim sin sin x x x x x →∞⎛⎫+ ⎪⎝⎭= 1 .4. 设()x f x xe =, 写出它带 Peano 型余项的三阶麦克劳林公式2331()()2f x x x x o x =+++.5. 100d sin ()d d x x t t x -⎰=100sin x 6.2sin sin cos x dx x x π=+⎰4π.三、计算题(共8小题,每小题5分,共40分)1. 222111lim 2n n n n n n πππ→∞⎛⎫+++⎪+++⎝⎭解:由于22222221112n n n n n n n n n n πππππ⎛⎫<+++< ⎪+++++⎝⎭ ( 2 分)且221lim lim 11n n n n n n ππ→∞→∞==++, 2221lim lim 11n n n n n ππ→∞→∞==++, 由夹逼定理可知222111lim 12n n n n n n πππ→∞⎛⎫+++= ⎪+++⎝⎭( 3 分)2. ⎪⎭⎫ ⎝⎛-→x x x x tan 11lim 203020tan lim tan 11lim x x x x x x x x -=⎪⎭⎫ ⎝⎛-→→解 ( 2 分) 22031sec lim x x x -=→ 313tan lim 220==→xx x( 3 分) 3.20lim(1sin x x e x →+解:由于2112x - (0x →) 22lim(1sin →+x xx e x22sin 1202lim 2→→===x x e xx x x eee( 5 分)4. 1lim 1x x x e x →∞⎡⎤⎛⎫+-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦解:令 1t x=, 则 11200ln(1)1(1)1lim 1lim lim(1)xttx t t tt t e t x e t x t t →∞→→-+⎡⎤+-⎛⎫++-==+⎢⎥ ⎪⎝⎭⎢⎥⎣⎦( 2 分)=2011(1)1lim 2t t te t →-++=211lim2(1)2t e e t →-=-+ ( 3 分)5. 方程 ⎩⎨⎧+==t t t y t x sin cos sin ln 确定 y 为 x 的函数,求 dx dy与 22dx y d . 解:,sin )()(t t t x t y dx dy =''= ( 2 分) .sin tan sin )()sin (22t t t t t x t t dxy d +=''= ( 3 分)6. arctan d xxe x e⎰ 解:2arctan d arctan 1x x x x xx x e e x e e e dx e e --=-++⎰⎰ ( 2 分) =22arctan (1)1xxxxe e e dx e--+-+⎰ =21arctan ln(1)2x x x e e t e C --+-++ ( 3 分)7.x解:242004|sin cos |d (cos sin )d (sin cos )d x x x x x x x x x x ππππ=-=-+-⎰⎰⎰( 2 分)=424(sin cos )|(cos sin )|x x x x πππ++--=1) ( 3 分) 7.ln 0x ⎰解:令t =则 21ln(1)2x t =--, 21tdx dt t=-,2ln 2211)11t x dt dt t t ==-+--⎰( 2 分)=11ln ln(221t t t ⎛---=- +⎝ ( 3 分)四、解答题(共2小题,每小题6分,共12 分)1. 已知 (1, 3) 是曲线 32y x ax bx c =+++ 的拐点, 并且曲线在 2x =处有极值, 求出 ,,a b c 的值, 并画出此曲线的图形.解:由于 2'32y x ax b =++, ''62y x a =+, 由已知条件可得以下方程组131240620a b c a b a +++=⎧⎪++=⎨⎪+=⎩解得 a=-3, b=0, c=5. ( 2 分) 由于 2'36y x x =-, 令 '0y =, 解得 x=0, 2 由于''66y x =-, 解得 x=1.图形略. ( 2 分)2. 求抛物线 21y x =- 在 (0, 1) 内的一条切线, 使得它与两坐标轴和抛物线围成的图形面积最小.解:设切线过抛物线上的点 2(,1)M a a -, 切线方程是2(1)2()y a a x a --=-- ( 1 分)它与两坐标轴的交点分别是, 围成的面积22221(1)(1)21222430()(1)d a a a aS a x x ++=--=-⎰( 1 分) 则22214()(1)(31)aS a a a '=+⋅- ( 1 分) ()0,S a '=令 得到在 [0, 1] 上的唯一驻点 ( 1 分)当当 ( 1 分)且为最小点, 故所求切线方程是 433y x =-+ ( 1 分)五、证明题(共2题,每题6分,共12 分)1. 设)(x f 在区间]1,0[上连续,在区间)1,0(内可导,11(0)0, (1), 1,22f f f ⎛⎫=== ⎪⎝⎭证明在区间)1,0(内至少存在一点ξ,使得()1='ξf证: ()(), () [0,1] 01F x f x x F x =-设 则 在 上连续,在(,)内可导, ( 1 分)1111111(1)(1)10,0, (2 ) 2222211()0. (1 )2F f F f F ξξ⎛⎫⎛⎫=-=-<=-=> ⎪ ⎪⎝⎭⎝⎭⎛⎫∃∈= ⎪⎝⎭分由介值定理,,,使分1 (0)0 (0,)(0,1) ()0() 1.F F f ξξξξ=∃∈⊂''==又,由罗尔定理,,使,即 ( 2 分)2. 设 ()f x 在 [a, b] 上连续, 且单调增加, 证明:()()2bbaa ab xf x dx f x dx +≥⎰⎰. 212(,0),a aA +2(0,1)B a +a =,a <()0S a '<a >()0S a '>()[0,1],a S a =因此是在上的唯一极小点证: 设()()()2xxaa a x x sf s ds f s ds ϕ+=-⎰⎰ ( 1 分) 则1'()()()()22xaa x x xf x f x f s ds ϕ+=--⎰()()22x a x af x f ξ--=- (积分中值定理 (,)a x ξ∈)( 2 分)由于 ()f x 在 [a, b] 上单调增加, 从而 '()0x ϕ>, (,)x a b ∈, ( 1 分)又由于 ()0a ϕ=, ()x ϕ 在 [a, b] 上连续, 则()()0x a ϕϕ≥=, ( 1 分) 特别有()0b ϕ≥ 即()()2bbaa ab xf x dx f x dx +≥⎰⎰ ( 1 分)。
