最短路径问题梳理
最短路径知识点总结

最短路径知识点总结最短路径问题的核心思想是通过某种策略找到两个节点之间的最短路径。
在图的表示方法上,最短路径问题通常使用邻接矩阵或邻接表来表示图的结构。
多种最短路径算法也可以适用于不同的图模型,包括有向图、无向图、带权图等。
常用的最短路径算法包括Dijkstra算法、Bellman-Ford算法、Floyd-Warshall算法等。
下面将对这些算法进行介绍和总结。
Dijkstra算法是一种解决单源最短路径问题的贪心算法。
它的核心思想是通过不断地确定距离源点距离最短的顶点来逐步扩展已知的最短路径集合。
具体步骤包括:初始化距离数组,设置起点距离为0,其他顶点距离为无穷大;选择未访问顶点中距离最短的顶点,并将其标记为已访问;更新与该顶点相邻的顶点的距离;不断重复以上步骤直到所有顶点都被访问。
Dijkstra算法的时间复杂度为O(V^2),其中V表示顶点的个数。
当图比较大时,可以使用堆优化的Dijkstra算法,将时间复杂度优化到O((V+E)logV)。
Bellman-Ford算法是一种解决单源最短路径问题的动态规划算法。
它的核心思想是通过对所有边进行松弛操作,不断更新顶点的最短路径估计值。
具体步骤包括:初始化距离数组,设置起点距离为0,其他顶点距离为无穷大;循环遍历所有边,不断进行松弛操作,直到没有发生变化为止。
Bellman-Ford算法的时间复杂度为O(VE),其中V表示顶点的个数,E表示边的个数。
这个算法可以解决包含负权边的图的最短路径问题,而Dijkstra算法则无法处理负权边。
Floyd-Warshall算法是一种解决多源最短路径问题的动态规划算法。
它的核心思想是通过对所有顶点之间的距离进行不断更新,找到所有顶点之间的最短路径。
具体步骤包括:初始化距离矩阵,设置顶点之间的距离为边的权重,若没有直接相连的边则设置为无穷大;循环遍历所有顶点,尝试将每个顶点作为中转点,并尝试更新所有顶点对之间的距离。
初中数学最短路径问题12种模型

初中数学最短路径问题12种模型
1. 确定起点的最短路径问题:即已知起始结点,求最短路径的问题;
2. 确定终点的最短路径问题:与确定起点的问题相反,该问题是已知终结结点,求最短路径的问题;
3. 确定起点终点的最短路径问题:即已知起点和终点,求两结点之间的最短路径;
4. 全局最短路径问题:求图中所有的最短路径。
问题原型
“将军饮马”,“造桥选址”,“费马点”。
涉及知识:“两点之间线段最短”,“垂线段最短”,“三角形三边关系”,“轴对称”,“平移”。
出题背景
角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等。
解题思路
找对称点实现“折”转“直”,近两年出现“三折线”转“直”等变式问题考查。
12个基本问题
例题一:
已知在平面直角坐标系中,A(2,-3),B(4,-1).
(1) 若点P(x,0)是X轴上的动点,当三角形PAB的周长最短时,求X的值。
(2) 若点C、D是X轴上的两个动点,且D(a,0),当四边形
ABCD的周长最短时,求a的值;
(3) 设M、N分别为X轴、Y轴的动点。
问是否存在这样的点(m,0)和N(0,n)使得四边形ABMN的周长最短?若存在,请求出m、n。
若不存在,请说明理由。
例题二:。
最短路径问题介绍

最短路径问题介绍全文共四篇示例,供读者参考第一篇示例:最短路径问题是指在一个带有边权的图中,寻找连接图中两个特定节点的最短路径的问题。
在实际生活中,最短路径问题广泛应用于交通运输、通信网络、物流配送等领域。
通过解决最短路径问题,可以使得资源的利用更加高效,节约时间和成本,提高运输效率,并且在紧急情况下可以迅速找到应急通道。
最短路径问题属于图论中的基础问题,通常通过图的表示方法可以简单地描述出这样一个问题。
图是由节点和边组成的集合,节点表示不同的位置或者对象,边表示节点之间的连接关系。
在最短路径问题中,每条边都有一个权重或者距离,表示从一个节点到另一个节点移动的代价。
最短路径即是在图中找到一条路径,使得该路径上的边权和最小。
在解决最短路径问题的过程中,存在着多种算法可以应用。
最著名的算法之一是Dijkstra算法,该算法由荷兰计算机科学家Edsger W. Dijkstra于1956年提出。
Dijkstra算法是一种贪心算法,用于解决单源最短路径问题,即从一个给定的起点到图中所有其他节点的最短路径。
该算法通过维护一个距离数组和一个集合来不断更新节点之间的最短距离,直到找到目标节点为止。
除了Dijkstra算法和Floyd-Warshall算法外,还有一些其他与最短路径问题相关的算法和技术。
例如A*算法是一种启发式搜索算法,结合了BFS和Dijkstra算法的特点,对图中的节点进行评估和排序,以加速搜索过程。
Bellman-Ford算法是一种解决含有负权边的最短路径问题的算法,通过多次迭代来找到最短路径。
一些基于图神经网络的深度学习方法也被应用于最短路径问题的解决中,可以获得更快速和精确的路径搜索结果。
在实际应用中,最短路径问题可以通过计算机程序来实现,利用各种算法和数据结构来求解。
利用图的邻接矩阵或者邻接表来表示图的连接关系,再结合Dijkstra或者Floyd-Warshall算法来计算最短路径。
八年级最短路径问题归纳

八年级最短路径问题归纳最短路径问题是图论中的一个经典问题,也是计算机科学中的重要研究领域之一。
在八年级的学习中,我们也会接触到最短路径问题,并且通过一些简单的算法来解决这个问题。
本文将对八年级最短路径问题进行归纳总结,希望能够帮助大家更好地理解和应用这个问题。
一、最短路径问题的定义最短路径问题是指在一个给定的图中,找出两个顶点之间的最短路径,即路径上的边权之和最小。
其中,图由顶点和边组成,顶点表示路径中的点,边表示路径中的通路或连接。
二、最短路径问题的应用最短路径问题在生活中有着广泛的应用,比如导航系统中的最短路径规划、货物运输中的最短路径选择等等。
通过寻找最短路径,可以帮助我们节省时间和资源,提高效率。
三、最短路径问题的解决方法1. 迪杰斯特拉算法迪杰斯特拉算法是解决最短路径问题的一种常用算法。
该算法通过不断更新起点到各个顶点的最短路径,直到找到终点的最短路径为止。
迪杰斯特拉算法的具体步骤如下:- 初始化起点到各个顶点的距离为无穷大,起点到自身的距离为0;- 选择一个未访问的顶点,更新起点到其他顶点的距离;- 重复上述步骤,直到找到终点的最短路径或所有顶点都被访问过。
2. 弗洛伊德算法弗洛伊德算法是解决最短路径问题的另一种常用算法。
该算法通过不断更新任意两个顶点之间的最短路径,直到更新完所有顶点对之间的最短路径为止。
弗洛伊德算法的具体步骤如下:- 初始化任意两个顶点之间的距离,如果两个顶点之间有直接的边,则距离为边的权值,否则距离为无穷大;- 选择一个顶点作为中转点,更新任意两个顶点之间的距离;- 重复上述步骤,直到更新完所有顶点对之间的最短路径。
四、最短路径问题的注意事项在解决最短路径问题时,需要注意以下几点:1. 图的表示方式:可以使用邻接矩阵或邻接表来表示图,根据具体的问题选择合适的表示方式。
2. 边的权值:边的权值可以表示两个顶点之间的距离、时间、花费等等,根据具体的问题选择合适的权值。
初中数学中考复习专题 最短路径问题 (24张PPT)

【例题分层探究】 问题 1:边 CD 是定值,此问题可转化为计算 CE+DE 的最小值问题. 问题 2:线段 CD,EF 均为定值,此问题可借助轴对称 求最短路径的方法计算出 DE+CF 的最小值.
初中数学中考复习专题 最短路径问题 (24张PPT)
初中数学中考复习专题 最短路径问题 (24张PPT) 初中数学中考复习专题 最短路径问题 (24张PPT)
∵C(0,-5) ∴C′(0,5) ∴直线C′D为y=-7x+5
D(2,-9)
ME
x
AO
B
∴y=0 , 即-7x+5=0 ∴m=5 ∕ 7
∴x=5 ∕ 7
C D
初中数学中考复习专题 最短路径问题 (24张PPT)
初中数学中考复习专题 最短路径问题 (24张PPT)
中考链接
24 如图 Z8-3,在平面直角坐标系中,矩形 OACB 的
A
B l
在直线l上求一 点P,使 PA+PB值最小
作B关于l 的对称点 B',连A B'与l交 点即为P
图形
原理
两点之间线段 最短
PA+PB最小值 为AB
原理
两点之间线段 最短
PA+PB最小值 为AB
问题3
作法
l1
P
分别作点P关于
l2
两直线的对称
在直线l1、l2上 点P'和P",连 分别求点M P'P"与两直线
AM+MN+NB的 值最小.
作点A关于l2的 对称点A',作 点B关于l1的对 称点B',连A 'B'交l2于M
,交l1于N.
图形
原理
两点之间线段 最短.
AM+MN+NB 的最小值为线 段A'B'的
12个最短路径问题精华版
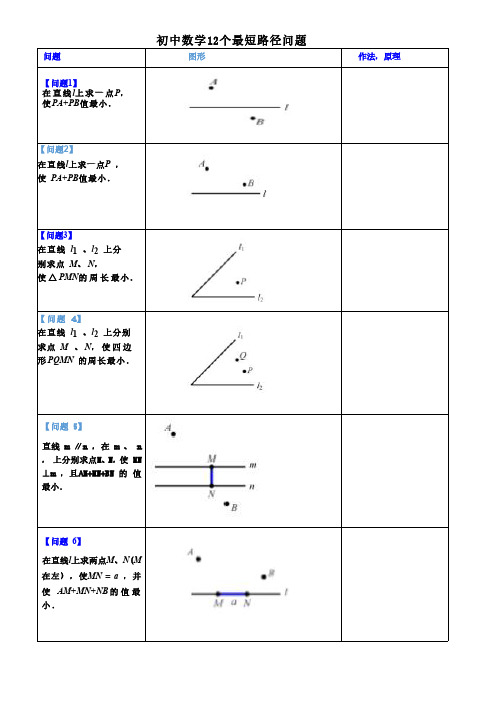
初中数学12个最短路径问题
问题图形作法,原理
【问题1】
在直线l上求一点P,
使PA+PB值最小.
【问题2】
在直线l上求一点P,
使PA+PB值最小.
【问题3】
在直线l1、l2上分
别求点M、N,
使△PMN的周长最小.
【问题4】
在直线l1、l2上分别
求点M、N,使四边
形PQMN的周长最小.
【问题5】
直线m∥n,在m、n
,上分别求点M、N,使MN
⊥m,且AM+MN+BN的值
最小.
【问题6】
在直线l上求两点M、N(M
在左),使MN=a,并
使AM+MN+NB的值最
小.
问题图形作法,原理
【问题7】
在l1上求点A,在l2上求
点B,使PA+AB值最小.
【问题8】
A为l1上一定点,B为l2上
一定点,在l2上求点M,
在l1上求点N,使
AM+MN+NB的值最小.
【问题9】在直线l上求一
点P,使PA一PB的值
最小.
【问题10】
在直线l上求一点P,使
PA一PB的值最大.
【问题11】
在直线l上求一点P,使
PA一PB的值最大.
【问题12】
△ABC中每一内角都小
于120°,在△ABC内求
一点P,使PA+PB+PC
值最小.。
最短路径问题

最短路径问题【基础知识】最短路径问题是一个经典问题,旨在寻找图中两点之间的最短路径,具体有以下几种:1. 确定起点的最短路径问题——即已知起始点,求最短路径;2. 确定终点的最短路径问题;3. 确定起点终点的最短路径问题;4. 全局最短路径问题。
这些问题涉及知识有“两点之间线段最短”、“垂线段最短”、“三角形三边之和大于第三边”、“轴对称”、“平移旋转”等。
问题图形在直线l上求一点P,使得PA+PB值最小在直线l上求一点P,使得PA+PB值最小(将军饮马问题)在直线l1、l2上分别求点M、N,使得∆PMN的周长最小直线m//n,在m、n上分别求点M、N,使MN⊥m,且AM+MN+BN的值最小在直线l上求两点M、N(M在左),使MN=a,并且AM+MN+BN的值最小在直线l1、l2上分别求点M、N,使得四边形PQMN的周长最小在直线l1上求点A,在l2上求点B,使PA+PB最小点A、B分别为直线l1、l2上定点,在l1、l2上分别求点N、M,使AM+MN+NB在直线l上求一点P,使|PA−PB|的值最小在直线l上求一点P,使|PA−PB|的值最大在直线l上求一点P,使|PA−PB|的值最大若∆ABC中每一个内角都小于120°,在∆ABC内求一点P,使得PA+PB+PC的值最小)如图,在△ABC 中,AB =AC =10,tanA =2,BE ⊥AC 于点E ,D 是线段BE 上的一个动点,则CD+√55BD 的最小值是 .如图,半圆的半径为1,AB 为直径,AC 、BD 为切线,AC =1,BD =2,点P 为弧AB 上一动点,求的最小值.。
最短路径与选址问题

第6步:① v6是刚得到P标号的点。因为(v6,v7)∈E, 步 而且v7为T标号,故修改它的T标号为 T(v7)=min[T(v7),P(v6)+w67]=min[14,8+5]=13
② 目前只有v7是T标号,故令:P(v7)=13。
从城镇v1到v7之间的最短路径为(v1,v2,v3,v5,v6, v7),最短路径长度为13。
(二)中位点选址问题
中位点选址问题的质量判据 使最佳选址位置所在的顶点到网络图中 其他各个顶点的最短路径距离的总和(或者 以各个顶点的载荷加权求和)达到最小。
中位点选址问题的数学描述 设G=(V,E)是一个简单连通赋权无 向图,连接两个顶点的边的权值为该两顶点 之间的距离;对于每一个顶点vi(i=1, 2,…,n),有一个正的负荷a(vi),而且它 与其他各顶点之间的最短路径长度为di1, di2,…,din。那么,中位点选址问题,就是 求图G的中位点 vi 0 ,使得
最短路径与选址问题
最短路径问题 选址问题
对于许多地理问题,当它们被抽 象为图论意义下的网络图时,问题的核 心就变成了网络图上的优化计算问题。 其中,最为常见的是关于路径和顶点的 优选计算问题。 在路径的优选计算问题中,最常见 的是最短路径问题;而在顶点的优选计 算问题中,最为常见的是中心点和中位 点选址问题。
S (v1 ) = ∑ a (v j )d1 j = 122.3
j =1 7
S (v 2 ) = ∑ a (v j )d 2 j = 71.3
j =1
7
S (v3 ) = ∑ a (v j )d 3 j = 69.5
j =1
7
7
S (v 4 ) = ∑ a (v j )d 4 j = 69.5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
按照路径最值问题的构成或解答方式分组。
模型组一
1 两点一线异侧和最小值问题 问题:两定点A、B位于直线l异侧,在直线l上找一点P,使PA+PB值最 小. 问题解决:
结论:根据两点之间线段最短,PA+PB的最小值即为线段AB长.
模型组一
2. 两点一线同侧和最小值问题 问题:两定点A、B位于直线l同侧,在直线l上找一点P,使得PA+PB值 最小. 问题解决:
(分析:PQ为定值,只需AP+QB的值最小,可通 过平移,使P、Q“接头”,转化为基本模型)
解:将点A沿着平行于l的方向,向右移至A´, 使AA´=PQ=a,连接A´B交直线l于点Q,在l上截取
PQ=a(P在Q左边),则线段PQ即为所求,此 时
AP+PQ+QB的最小值为A´B+PQ,即A´B+a
ห้องสมุดไป่ตู้
模型组三
解:作点A关于OM的对称点A′,过点A′作AQ⊥ON 于 点Q,A′Q交OM于点P,此时AP+PQ最小;
理由:由轴对称的性质知AP=A′P, 要使AP+PQ最小, 只需A′P+PQ最小,从而 转化为拓展模型1
模型组二
3. “胡不归”问题 基本模型:两定一动,动点在定直线上
问题:点A为直线l上一定点,点B为直线外一定点, P为直线l上一动点,要使 AP+BP最小.
模型组四
2.异侧差最小值问题
问题:两定点A、B位于直线l异侧,在直线l上找一点P,使得|PA-
PB|的值最小. 问题解决:
A▪
B▪
结论:根据垂直平分线上的点到线段两端点的距 离相等,当PA=PB时,|PA-PB|=0.
模型组四总结:
所求问题为两线段之差绝对值最小的问题,解决方式 为作 中垂线找交点。
所求问题为有公共端点的线段之和最小,解决方式 为连接 或作对称点后再连接。
模型组二
1.已知:如图,A为锐角∠MON外一定点; 要求:在射线OM上找一点P,在射线ON上 找一点Q,使 AP+PQ的值最小.
解:过点A作AQ⊥ON于点Q,AQ与OM相 交于点P,此 时,AP+PQ最小;
模型组二
2. 已知:如图,A为锐角∠MON内一定点;要求:在射线 OM上找一点P,在射线ON上找一点Q,使AP+PQ的值最小.
模型组一
4. 两定点与两条直线上两动点问题 问题:点P、Q在∠AOB的内部,在OB上找点D,在OA上找点 C,使得四边形PQDC周长最小. 问题解决:
结论:将问题转化为上一种类型即可,PC+CD+ DQ的最小值为线段P’Q’长,则四边形PQDC的周长 的最小值为P’Q’+PQ的值.
模型组一总结:
此类题的解题步骤: 第一步:以系数不为1的线段的定端点为顶点作一个角,使其正弦值等 于此线段的系数(注意题目中有无特殊角); 第二步:过动点作第一步中角的边的垂线,构造直角三角形; 第三步:根据两点之间线段最短,将“折”变“直”,再利用 “垂线段最短”找到最小值的位置.
模型组二总结:
所求问题为一定点,两动点的两线段之和,解决方式 为作 垂线段或作对称点后再作垂线段。
结论:将两定点同侧转化为异侧问题,PA+PB最小值为AB′.
模型组一
3. 一定点与两条直线上两动点问题 问题:点P在∠AOB的内部,在OB上找一点D,在OA上找一点C, 使得△PCD周长最小. 问题解决:
结论:要使△PCD周长最小,即PC+PD+CD值最小,根据两点之 间线段最短,将三条线段转化到同一直线上即可,则△PCD周长 最小为线段的长.
3. 已知:如图,定点A、B分布于直线l的同侧,长度a
(a为定值)的线段PQ在l上移动(P在Q左边)
将军遛马
要求:确定PQ的位置,使得四边形APQB周长最小
分析:AB长度确定,只需AP+PQ+QB最小,通过作A点 关于l的对称点,转化为上述模型
解:作A点关于l的对称点A´,将点A´沿着平行于l 的方向,向右移至A´´,使A´A´´=PQ=a,连接A´´B 交l于Q,在l上截取QP=a(P在Q左边),线段 PQ即为所求,此时四边形APQB周长的最小值为 A´´B+AB+PQ,即A´´B+AB+a
模型组三总结:
所求问题为无公端点线段之和的最小值问题, 解决方式 为平移或作对称点后再平移。
模型组四
1.同侧差最小值问题 问题:两定点A、B位于直线l同侧,在直线l上找一点P,使得|PA- PB|的值最小. 问题解决:
结论:根据垂直平分线上的点到线段两端点的距 离相等,当PA=PB时,|PA-PB|=0.
模型组三
1. 已知:如图,直线m∥n,A、B分别为m 上方和n下方的定点,(直线AB不与m垂直) 要求:在m、n之间求作垂线段PQ,使得 AP+PQ+BQ最小
将军过桥
模型组三
2.已知:如图,定点A、B分布于直线l两侧,长度为a(a为 定值)的线段PQ在l上移动(P在Q左边) 要求:确定PQ的位置,使得AP+PQ+QB最小
模型组五
1. 同侧差最大值问题 问题:两定点A、B位于直线l同侧,在直线l上找一点P,使得|PA-PB|的值 最大. 问题解决:
结论:根据三角形任意两边之差小于第三边,|PA-PB|≤AB, 则|PA-PB|的最大值为线段AB的长.
模型组五
2.异侧差最大值问题 问题:两定点A、B位于直线l异侧,在直线l上找一点P,使得|PA-PB| 的值最大. 问题解决:
理由.
自练:
如图,已知抛物线y= x2+bx+c与直线y= x+3交于A,B两点,交x轴于 C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).
(1)求此抛物线的解析式; (2)在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个
最大值;
(3)点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴于 点Q,问:是否存在点P,使得以A,P,Q为顶点的三角形与△ABC相 似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理
(1)求此抛物线的解析式; (2)在抛物线对称轴l上找一点M,使|MB﹣MD|的值最大,并求出这个
最大值;
(3)点P为y轴右侧抛物线上一动点,连接PA,过点P作PQ⊥PA交y轴 于点Q,问:是否存在点P,使得以A,P,Q为顶点的三角形与△ABC 相似?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明
由.
结论:将异侧点转化为同侧,同类型4,|PA-PB|的最大值为AB′.
模型组五总结:
所求问题为两线段之差绝对值最大,解决方式 为延长相交 或作对称点后再连接延长。
自练:
如图,已知抛物线y= x2+bx+c与直线y= x+3交于A,B两点,交x轴于 C、D两点,连接AC、BC,已知A(0,3),C(﹣3,0).
