8弯矩分配法分配系数计算过程及结果8
建筑力学(力矩分配法)

第十八章力矩分配法力矩分配法理论基础:位移法;计算对象:杆端弯矩;适用范围:连续梁和无侧移刚架。
一、转动刚度转动刚度表示杆端对转动的抵抗能力。
它在数值上等于使杆端产生单位转角时需要施加的力矩,以SAB表示。
A是施力端(近端),B为远端。
1S AB=4i1S AB=3iS AB= i1S AB=0远端固定远端铰支远端滑动远端自由第一节力矩分配法的基本原理1S AB =4i1S AB =3iS AB = i 1S AB =0远端固定远端铰支远端滑动远端自由转动刚度远端固定,S =4i 远端简支,S =3i 远端定向,S =i 远端自由,S =0S AB 与杆的线刚度i 和远端支承情况有关。
i —杆件的线刚度,lEI i二、传递系数M AB = 4i AB ϕAM BA = 2i AB ϕA21==AB BA ABM M C M AB = 3i AB ϕA 0==ABBA ABM M C M AB = i AB ϕAM BA = -i AB ϕA1-==ABBA ABM M C ϕAlAB远端固定ABϕAϕAAB远端铰支远端滑动M BA = 0远端支承转动刚度传递系数固定S=4i C =1/2简支S=3i C =0定向S=i C = -1自由S=0三、力矩分配法的基本原理杆端弯距:取结点A 作隔离体,由∑M =0,得分配系数CA BDi ABi AC i ADAAB A AB AB S i M ϕϕ==4A AC A AC AC S i M ϕϕ==AAD A AD AD S i M ϕϕ==3}M M ABM ACM ADAAD AC AB S S S M ϕ)(++=∑=++=AAD AC AB A SMS S S M ϕMSSM AADAD ∑=M SS M A ABAB ∑=M S S M AACAC ∑=注:1)分配弯矩是杆端转动时产生的近端弯矩。
2)结点集中力偶顺时针为正。
∑=AAkAkSS μMM Ak Ak μ=分配弯矩A ϕM1321=++=∑A A A Ak μμμμ各杆的远端弯矩M kA 可以利用传递系数求出。
建筑力学弯矩分配法

M M1143
3i131 S131 i141 S141
(a)
M15 4i151 S151
②由结点1的平衡条件:
M1 0
即:
MM12M13M14M150
M12
M(S12S13S14S15)1
得:
1
M S12S13S14S15
(b)
M M13
1
M14
1
M15
得:
M
12
S 12 M S
12 M
200.9 120
B
0.5 0.5 +250.0 -187.5
+32.0 -47.3 -47.3 +4.8 -2.4 -2.4 +0.3 -0.2 -0.2
+237.4 -237.4 237.4
375
300
C
+112.5 -23.7 -1.2
+87.6 87.6
D
M图(kn.m)
§14—3 用力矩分配法计算无侧移刚架
89.83
2042
40kn.m
850.7443.88
C CA
144
B
A
40 D
6.86
固端弯矩 -86.4 +57.6 0.0 -40.0 0.0 0.0
分配传递 -3.43 -6.86 -6.86 -3.83
-3.43
M图(kn.m)
0. 最后弯矩 -89.83 +50.7 -6.86 -43.88 0.0 -3.43
B
Mf BC
MB=
Mf BA
+MBf C
(c)
M’=-MB
A
B C
力矩分配法

1渐近法2用力法、位移法分析超静定结构,都需要求解多元联立方程组,求出基本未知量。
当未知量较多时,计算颇为繁重。
渐近法—采用逐步地逼近真实解的方法。
渐近法主要有:一、渐近法概述(1)力矩分配法:适于连续梁与无侧移刚架。
(2)无剪力分配法:适于规则的有侧移刚架。
(3)迭代法:适于梁的刚度大于柱刚度的各种刚架。
3力矩分配法理论基础:位移法;计算对象:杆端弯矩;计算方法:逐渐逼近的方法;适用范围:连续梁和无侧移刚架。
4只有结点角位移而无结点线位移的梁和刚架。
?力矩分配法的适用范围:力矩分配法的适用范围:5只有结点角位移而无结点线位移的梁和刚架。
√6力矩分配法以杆端弯矩为计算对象,采用:固定放松分配、传递逐次逼近杆端弯矩的精确解。
计算原理及符号规则均与位移法相同,只是计算过程不相同。
7计算过程:1.固定结点求出固定状态的杆端弯矩FijM 附加刚臂处的不平衡弯矩iM依次将结点上的不平衡弯矩反号分配于各杆近端,并传向远端。
2.逐次放松各结点8若干次循环计算= 也即逐次恢复转角的过程直接表达为各杆端弯矩逐次修正的过程放松结束,也即变形(转角)、内力趋于实际状态。
9——基本运算A BCM ABM BAM BC A BCM FAB M FBAM FBCM BM BM F BAM F BCM B =M F BA +M F BCABC-M BBAM ′BCM ′AB M ′0-M BBAM ′BCM ′)(B BA BAM M −⋅=′μ)(B BC BCM M −⋅=′μ+=最后杆端弯矩:M BA =M F BA +BAM ′M BC =M F BC +BCM ′M AB =M F AB +AB M ′然后各跨分别叠加简支梁的弯矩图,即得最后弯矩图。
固端弯矩带本身符号单结点的力矩分配分配系数分配弯矩10例1. 用力矩分配法作图示连续梁的弯矩图。
3m 3m 6m EI EI 200kN 20kN/m (1)固定B 结点A BC 200kN 20kN/m M F AB =M F BA =M F BC=mkN ⋅−=×−15086200m kN ⋅150m kN ⋅−=×−9086202M B =M F BA + M F BC =m kN ⋅60-150150-90(2)放松结点B,即加-60进行分配60A B C-60设i =EI/l 计算转动刚度:S BA =4iS BC =3i分配系数:571.0344=+=i i iBAμ429.073==iiBCμ0.5710.429分配力矩:3.34)60(571.0−=−×=′BAM 7.25)60(429.0−=−×=′BCM -34.3-25.7-17.2+(3) 最后结果。
结构力学次课力矩分配法分配系数结点不平衡力矩

梦想不会逃跑,会逃跑的永远都是自己!结构力学第27次课 第8章力矩分配法 分配系数 结点不平衡力矩2012-6-6第1节课 其他约束情况下 超静定单跨梁的转动刚度1 转动刚度:梁端发生单位转角产生的弯矩。
⎪⎪⎩⎪⎪⎨⎧⇒⇒⇒⇒=∆=远端为自由端远端为平行支链杆远端为铰支端远端为固定端0341ik ikik ik ik ik i i i S S M 2 分配系数:与转动刚度成正比()1==∑∑iikiikikik S S μμ3 传递系数:近端发生转角时,远端弯矩与近端弯矩的比值.⎪⎪⎩⎪⎪⎨⎧⇒-⇒⇒==远端为平行支链杆远端为铰支端远端为固定端1021ikkiik M M C ⏹结构力学第26次课(mardi 5-juin -2012)内容回顾( )( )a b1234AllllBCADE=1i =1i =1i =1i第2节课 结点不平衡力矩求解单结点的力矩分配F P q A原结构=F P qAA 状态-MB 状态+A 点附加刚臂阻止转动,承担汇交杆端的不平衡固端弯矩M 。
在结点上加一个反向的力矩。
(相当于刚臂放松)B 状态的内力——分配弯矩用力矩分配法计算A 状态的内力——固端弯矩查表计算例题-M(作用在结点上)结点不平衡力矩3/74/7i iMiiM BM BM B =-MM1. 直接作用结点力偶分配系数:二、结点不平衡力矩例题3/74/7-ql 2/8固端弯矩qiill分配系数:-ql 2/8结点不平衡力矩8ql ⏹结构力学第27次课(merdredi 5-juin -2012)内容回顾2. 杆上作用荷载MB M B8ql单结点的力矩分配例题-F P l 固端弯矩-F P l 0F P l/2F P l 杆端弯矩0F P l /2F P l分配、传递ll2iiF P10F P lF P l/2M 图3. 带悬臂端杆件分配系数:单结点连续梁的力矩分配法小结2.具有一个结点角位移结构的计算步骤:● 加约束:在刚结点i 处加一附加刚臂,求出固端弯矩,再求出附加刚臂给结点的约束力矩f i M 。
弯矩分配法分配系数计算过程及结果8

弯矩分配法分配系数计算过程及结果:6第层各节点的弯矩分配系数I 节点 0.000μ=上4415.780.43644415.78420.42i i i μ⨯===+⨯+⨯下下下4420.420.56444420.42415.78i i i μ⨯===+⨯+⨯IO 下O 节点 0.000μ=上4415.780.313442415.78420.42228.58i i i i μ⨯===++⨯+⨯+⨯下下下4420.420.404442415.78420.42228.58i i i i μ⨯===++⨯+⨯+⨯左左下4428.580.283442415.78420.42228.58i i i i μ⨯===++⨯+⨯+⨯右右下U 节点 0.000μ=上4415.780.35644415.78428.58i i i μ⨯===+⨯+⨯下下下4428.580.64444428.58415.78i i i μ⨯===+⨯+⨯OU 下第5、4层各节点的弯矩分配系数H 、G 节点 4415.780.304444415.78415.78420.42i i i i μ⨯===++⨯+⨯+⨯上上下上4415.780.304444415.78415.78420.42i i i i μ⨯===++⨯+⨯+⨯下下下上4420.420.392444415.78415.78420.42HN GM i i i i μ⨯===++⨯+⨯+⨯、下上N 、M 节点0.2384442415.78415.78420.42228.58i i i i μ===+++⨯+⨯+⨯+⨯上上下上4415.780.2384442415.78415.78420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯下下下上4420.420.3084442415.78415.78420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯NH 、MG 下上4228.580.2164442415.78415.78420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯NT 、MS 下上T 、S 节点 4415.780.262444415.78415.78428.58i i i i μ⨯===++⨯+⨯+⨯上上下上4415.780.262444415.78415.78428.58i i i i μ⨯===++⨯+⨯+⨯下下下上4428.580.47644415.78415.78428.58i i i μ⨯===+⨯+⨯+⨯TN 、SM 下第3层各节点的弯矩分配系数F 节点 4415.780.266444415.78423.11420.42i i i i μ⨯===++⨯+⨯+⨯上上下上4423.110.390444415.78423.11420.42i i i i μ⨯===++⨯+⨯+⨯下下下上4420.420.344444423.11415.78420.42i i i i μ⨯===++⨯+⨯+⨯FL 下上L 节点4415.780.2154442415.78423.11420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯上上下上4423.110.3144442415.78423.11420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯下下下上4420.420.2774442415.78423.11420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯LF 下上0.1944442415.78423.11420.42228.58i i i i μ===+++⨯+⨯+⨯+⨯LR 下上R 节点 4415.780.234444415.78423.11428.58i i i i μ⨯===++⨯+⨯+⨯上上下上4423.110.343444415.78423.11428.58i i i i μ⨯===++⨯+⨯+⨯下下下上4428.580.42344423.11415.78428.58i i i μ⨯===+⨯+⨯+⨯RL 下第2、1层各节点的弯矩分配系数E 、D 节点 4423.110.347444423.11423.11420.42i i i i μ⨯===++⨯+⨯+⨯上上下上4423.110.347444423.11423.11420.42i i i i μ⨯===++⨯+⨯+⨯下下下上4420.420.306444423.11423.11420.42EK DJ i i i i μ⨯===++⨯+⨯+⨯、下上K 、J 节点4423.110.2864442423.11423.11420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯上上下上4423.110.2864442423.11423.11420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯下下下上4420.420.2524442423.11423.11420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯KE 、JD 下上4228.580.1764442423.11423.11420.42228.58i i i i i μ⨯===+++⨯+⨯+⨯+⨯LR 下上Q 、P 节点 4423.110.309444423.11423.11428.58i i i i μ⨯===++⨯+⨯+⨯上上下上4423.110.309444423.11423.11428.58i i i i μ⨯===++⨯+⨯+⨯下下下上4428.580.38244423.11423.11428.58i i i μ⨯===+⨯+⨯+⨯QK 、PJ 下。
力矩分配法专题知识

BA BC ---分配系数
一种结点上旳各杆端分配系
数总和恒等于1。
SBA 4i SBC 3i
BA 4i /(3i 4i) 4 / 7 0.571 A
B
M
u B
C
B
BC 3i /(3i 4i) 3 / 7 0.429
M
d BA
BA
(
M
u B
)
57.1
M
d BC
BC
(
M
u B
)
10m
M
u 2
B
2
110000
-28.6 -57.1 -42.9
21.4
6.1
-9.2 -12.2 -6.1
1.8
6.1
1.8 3.5 2.6
… … ...
q 12kN / m
A
EI
1 EI
2 EI
B A q 12kN / m
1
2
10m
10m
10m
q 12kN / m
A
M
u 1
ql 2 / 8
S21 4i S2B 3i
21 0.571 2B 0.429
放松结点1(结点2固定):
S12 4i S1A 3i
12 0.571 1A 0.429
q 12kN / m
A
EI
1 EI
B 2 EI
10m
10m
q 12kN / m
A
M1u
ql 2 / 8 28.6
1
ql 2 / 12
50
那么假如外荷载不是结点力偶,情况又怎样呢?
一.基本概念
固定状态:
M
u B
第8章力矩分配法

1 4
传递系数
远端固定,CAB=0.5
远端简支,CAD=0
远端滑动,CAC=-1
D i
分配系数
AB
2 3
AC
1 12
AD
1 4
120kNm
A
2i
i
C
传递系数
CAB=0.5
CAD=0
CAC=-1
B
D
80kNm A 30kNm
B 40kNm
10kNm C
M图
杆端弯矩
M AB
AB M
2 *120
3
固端弯矩
分配和传 递弯矩 杆端弯矩
A -150 -17.2
-167.2
分配系数
4 7
150
3 7
B
-90
-34.3 -25.7
115.7 -115.7
167.2 A
115.7
300
90
B 32.1
158.5
M图(单位kNm)
C 0 0 0 单位kNm
C
单结点力矩分配法计算举例
3)非结点荷载作用刚架
渐近法概述
1、线性代数方程组的解法: 直接法,渐进法
2、结构力学的渐近法:
力学建立方程,数学渐近解 不建立方程式,直接逼近真实受力状态。其 突出的优点是每一步都有明确的物理意义。
3、位移法方程的两个特点:
(1)每个方程一般不超过五项式; (2)主系数大于副系数的总和,即 kii > kij,
适于渐近解法。
80kNm
M AC AC M 10kNm
M AD AD M 30kNm
M BA CAB M AB 40kNm
M CA CAC M AC 10kNm
弯矩分配法计算表格
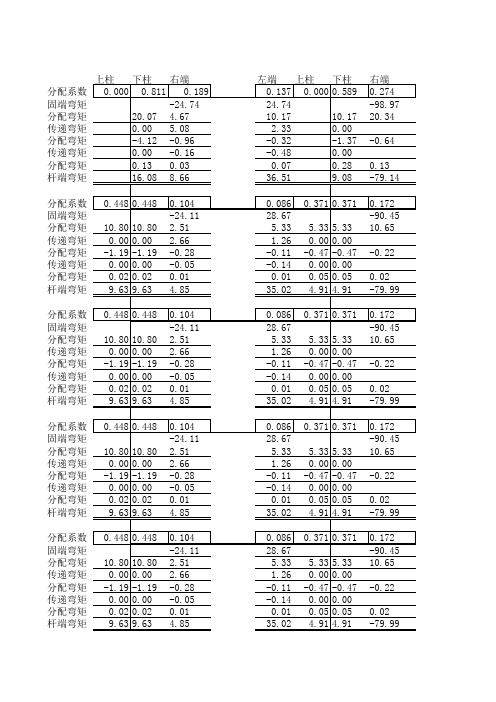
固端弯矩分配弯矩传递弯矩分配弯矩传递弯矩分配弯矩杆端弯矩
分配系数固端弯矩分配弯矩传递弯矩分配弯矩传递弯矩分配弯矩杆端弯矩
分配系数固端弯矩分配弯矩传递弯矩分配弯矩传递弯矩分配弯矩杆端弯矩
分配系数固端弯矩分配弯矩传递弯矩分配弯矩传递弯矩分配弯矩杆端弯矩
分配系数固端弯矩分配弯矩传递弯矩分配弯矩传递弯矩分配弯矩
杆端弯矩
分配系数固端弯矩分配弯矩传递弯矩分配弯矩传递弯矩分配弯矩
杆端弯矩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弯矩分配法分配系数计算过程及结果:
6第层各节点的弯矩分配系数
I 节点 0.000
μ=上 4415.780.43644415.78420.42
i i i
μ⨯=
=
=+⨯+⨯下下下
4420.420.56444420.42415.78
i i i μ⨯=
=
=+⨯+⨯IO 下
O 节点 0.000
μ=上 4415.78
0.313442415.78420.42228.58
i i i i
μ⨯=
=
=++⨯+⨯+⨯下
下下
4420.42
0.404442415.78420.42228.58
i i i i
μ⨯=
==++⨯+⨯+⨯左
左下
4428.58
0.283442415.78420.42228.58
i i i i
μ⨯=
==++⨯+⨯+⨯右
右下
U 节点 0.000
μ=上 4415.780.35644415.78428.58
i i i
μ⨯=
=
=+⨯+⨯下下下
4428.580.64444428.58415.78
i i i μ⨯=
=
=+⨯+⨯OU 下
第5、4层各节点的弯矩分配系数
H 、G 节点 4415.78
0.304
444415.784
15.78420.42
i i i i μ⨯=
=
=++⨯+⨯+⨯
上
上下上 4415.78
0.304444415.78415.78420.42
i i i i
μ⨯==
=++⨯+⨯+⨯下
下下上
4420.42
0.392444415.78415.78420.42
H N G M i i i i
μ⨯=
=
=++⨯+⨯+⨯、下上
N 、M 节点
0.2384442415.78415.78420.42228.58
i i i i
μ=
=
=+++⨯+⨯+⨯+⨯上
上下上
4415.78
0.2384442415.78415.78420.42228.58
i i i i i
μ⨯=
==+++⨯+⨯+⨯+⨯下
下下上
4420.42
0.3084442415.78415.78420.42228.58
i
i i i i
μ⨯=
=
=+++⨯+⨯+⨯+⨯NH 、MG 下上
4228.58
0.216
4442415.784
15.78420.42
228.58
i
i i i i μ⨯=
=
=+++⨯+⨯+⨯
+⨯NT 、MS 下
上
T 、S 节点 4415.78
0.262
444415.784
15.78428.58
i i i i μ⨯=
=
=++⨯+⨯+⨯
上
上下上 4415.78
0.262444415.78415.78428.58
i i i i
μ⨯=
=
=++⨯+⨯+⨯下
下下上
4428.58
0.47644415.78415.78428.58
i i i μ⨯=
=
=+⨯+⨯+⨯TN 、SM 下
第3层各节点的弯矩分配系数
F 节点 4415.78
0.266
444415.784
23.11420.42
i i i i μ⨯=
=
=++⨯+⨯+⨯
上
上下
上 4423.11
0.390444415.78423.11420.42
i i i i
μ⨯=
==++⨯+⨯+⨯下
下下上
4420.42
0.344444423.11415.78420.42
i i i i
μ⨯=
=
=++⨯+⨯+⨯FL 下上
L 节点
4415.78
0.2154442415.78423.11420.42228.58
i i i i i
μ⨯=
=
=+++⨯+⨯+⨯+⨯上
上下上
4423.11
0.3144442415.78423.11420.42228.58
i i i i i
μ⨯=
==+++⨯+⨯+⨯+⨯下
下下上
4420.42
0.2774442415.78423.11420.42228.58
i
i i i i
μ⨯=
=
=+++⨯+⨯+⨯+⨯LF 下上
0.1944442415.78423.11420.42228.58
i i i i
μ=
=
=+++⨯+⨯+⨯+⨯LR 下上
R 节点 4415.78
0.234
444415.784
23.11428.58
i i i i μ⨯=
=
=++⨯+⨯+⨯
上
上下
上 4423.11
0.343444415.78423.11428.58
i i i i
μ⨯=
==++⨯+⨯+⨯下
下下上
4428.58
0.42344423.11415.78428.58
i i i μ⨯=
=
=+⨯+⨯+⨯RL 下
第2、1层各节点的弯矩分配系数
E 、D 节点 4423.11
0.347444423.11423.11420.42
i i i i μ⨯=
==++⨯+⨯+⨯上
上下上
4423.11
0.347444423.11423.11420.42
i i i i
μ⨯=
==++⨯+⨯+⨯下
下下上
4420.42
0.306444423.11423.11420.42
EK D J i i i i
μ⨯=
=
=++⨯+⨯+⨯、下上
K 、J 节点
4423.11
0.2864442423.11423.11420.42228.58
i i i i i
μ⨯=
=
=+++⨯+⨯+⨯+⨯上
上下上
4423.11
0.2864442423.11423.11420.42228.58
i i i i i
μ⨯=
==+++⨯+⨯+⨯+⨯下
下下上
4420.42
0.2524442423.11423.11420.42228.58
i
i i i i μ⨯=
=
=+++⨯+⨯+⨯+⨯KE 、JD 下上
4228.58
0.176
4442423.114
23.114
20.42
228.58
i
i i i i μ⨯=
=
=+++⨯+⨯+⨯
+⨯LR 下
上
Q 、P 节点 4423.11
0.309
444423.114
23.11428.58
i i i i μ⨯=
=
=++⨯+⨯+⨯
上
上下上 4423.11
0.309444423.11423.11428.58
i i i i
μ⨯=
=
=++⨯+⨯+⨯下
下下上
4428.58
0.38244423.11423.11428.58
i i i μ⨯=
=
=+⨯+⨯+⨯QK 、PJ 下。
