串、并联阻抗的等效互换
合集下载
无线电通信-2.2 串、并联阻抗的等效互换与回路抽头时的阻抗变换

为了减小信号源或负载电阻对谐振回路的 影响,信号源或负载电阻不是直接接入回路, 而是经过一些简单的变换电路,将它们部分接 入回路。
常用的电路形式有变压器耦合连接、自耦 变压器抽头电路和双电容抽头电路,下面分别 介绍。首先,讨论负载电阻的部分接入问题。
2.3.3 抽头式并联电路的阻抗变换
1. 变压器耦合连接
振回路相近,谐振阻抗可以通过串联支路的串并联互
换得到。
2.3.2 并联谐振回路的其他形式
当品质因数足够高时
p
1 LC
Zp
(p L)2
R1 R2
1
(R1 R2 )(pC)2
如果R1和R2都不是很大, 则认为都是集中在电感支路内,
这时
Qp
p L
R1 R2
2.3.2 并联谐振回路的其他形式
2.3串、并联阻抗的等效互换与回路 抽头时的阻抗变换
• 2.3.1 串、并联阻抗的等效互换 • 2.3.2 并联谐振回路的其他形式 • 2.3.3 抽头式并联电路的阻抗变换
2.3.1 串、并联阻抗的等效互换
所谓等效,就是指电路工作在某一频率时,不管 其内部的电路形式如何,从端口看过去其阻抗或者导 纳是相等的。
并联谐振频率
fp 2π
1
Lq
CqC0 Cq C0
a
Lq
Cq
C0
rq
b
石英谐振器基频等效电路
2.3串、并联阻抗的等效互换与回路 抽头时的阻抗变换
• 2.3.1 串、并联阻抗的等效互换 • 2.3.2 并联谐振回路的其他形式 • 2.3.3 抽头式并联电路的阻抗变换
2.3.3 抽头式并联电路的阻抗变换
Xp
Rp 1 QL2 Rs
常用的电路形式有变压器耦合连接、自耦 变压器抽头电路和双电容抽头电路,下面分别 介绍。首先,讨论负载电阻的部分接入问题。
2.3.3 抽头式并联电路的阻抗变换
1. 变压器耦合连接
振回路相近,谐振阻抗可以通过串联支路的串并联互
换得到。
2.3.2 并联谐振回路的其他形式
当品质因数足够高时
p
1 LC
Zp
(p L)2
R1 R2
1
(R1 R2 )(pC)2
如果R1和R2都不是很大, 则认为都是集中在电感支路内,
这时
Qp
p L
R1 R2
2.3.2 并联谐振回路的其他形式
2.3串、并联阻抗的等效互换与回路 抽头时的阻抗变换
• 2.3.1 串、并联阻抗的等效互换 • 2.3.2 并联谐振回路的其他形式 • 2.3.3 抽头式并联电路的阻抗变换
2.3.1 串、并联阻抗的等效互换
所谓等效,就是指电路工作在某一频率时,不管 其内部的电路形式如何,从端口看过去其阻抗或者导 纳是相等的。
并联谐振频率
fp 2π
1
Lq
CqC0 Cq C0
a
Lq
Cq
C0
rq
b
石英谐振器基频等效电路
2.3串、并联阻抗的等效互换与回路 抽头时的阻抗变换
• 2.3.1 串、并联阻抗的等效互换 • 2.3.2 并联谐振回路的其他形式 • 2.3.3 抽头式并联电路的阻抗变换
2.3.3 抽头式并联电路的阻抗变换
Xp
Rp 1 QL2 Rs
阻抗的串联与并联

△ ω = ( ω 2- ω 1)
值,对其它频率不会产生这样的结果.因此该电路具 对其它频率不会产生这样的结果. 选频作用.常用于正弦波振荡器. 有选频作用.常用于正弦波振荡器.
1 同相, 仅当 ω = ω0 = RC 时,1与 U2同相,U2=U1/3 为最大 U
3.10.2 串联谐振
谐振的概念: 谐振的概念: 在同时含有L 的交流电路中, 在同时含有 和C 的交流电路中,如果总电压和 总电流同相,称电路处于谐振状态. 总电流同相,称电路处于谐振状态.此时电路与电 源之间不再有能量的交换,电路呈电阻性. 源之间不再有能量的交换,电路呈电阻性. 串联谐振:L 与 C 串联时 u,i 同相 串联谐振: 并联谐振: 并联谐振:L 与 C 并联时 u,i 同相 研究谐振的目的, 研究谐振的目的,就是一方面在生产上充分利 用谐振的特点, 如在无线电工程 如在无线电工程, 用谐振的特点,(如在无线电工程,电子测量技术等 许多电路中应用). 许多电路中应用 .另一方面又要预防它所产生的危 害.
3.8 阻抗的串联与并联 3.8.1阻抗的串联 3.8.1阻抗的串联 I U = U 1 + U 2 = Z 1I + Z 2 I + + Z1 U1 = ( Z 1 + Z 2) I
U
+ Z2 U2
-
Z = Z1 + Z2
通式: 通式 Z =
k
I
∑Z = ∑R + j∑X
k
U I= Z
=
1 1 3 + j( ω R C ) ω RC
频率特性
T (j ω ) =
1 ω 1 ω 3 + j( ω R C ) 3 + j( 0) ω RC ω ω 0 ω ω 0 ω ω 1 0 = arctan 3 2 ω0 2 ω 3 + ω ω 0 =
电阻电路的等效变换技术

不能改变电路的结构和参数
电阻电路等效变换不能改变 电路的电压、电流、功率等 参数。
电阻电路等效变换不能改变 电路的元件参数,如电阻、
电容、电感等。
电阻电路等效变换只能改变 电路的连接方式,不能改变 电路的结构和参数。
电阻电路等效变换不能改变 电路的拓扑结构,如串联、
并联、混联等。
07
电阻电路等效变换的发 展趋势
变换过程中,要保证电路的电源和负载不变,如电压、电流、功率等。
变换过程中,要保证电路的稳定性和可靠性,如电路的稳定性、可靠性、 安全性等。
保持元件连接方式不变的原则
电阻电路等效变换时,应保持元件之间的连接方式不变,避免出现错误。 变换过程中,应遵循电路的基本原理,如欧姆定律、基尔霍夫定律等。 变换过程中,应保持电路的拓扑结构不变,避免出现短路或断路。 变换过程中,应保持电路的功率和能量守恒,避免出现能量损失或增加。
复杂电路的等效变换:对于复杂电路,可以采用分压法、分流法等方法进 行等效变换,将复杂电路简化为简单电路,再进行等效变换。
星形电阻网络的等效变换
星形电阻网络的定义:由多个电阻串联或并联组成的网络
等效变换的方法:将星形电阻网络转换为等效的Y形或△形网络
转换步骤:首先确定星形网络的中心点,然后将每个电阻两端的电压和电流分别相加或相减, 得到等效的Y形或△形网络
电阻电路的等效变换 技术
,a click to unlimited possibilities
汇报人:
目录 /目录
01
点击此处添加 目录标题
04
电阻电路等效 变换的应用
02
电阻电路等效 变换的基本概 念
05
电阻电路等效 变换的注意事 项
1234串、并联阻抗等效互换与抽头变换双调谐
按幅频特性对滤波器的分类
A ( jω ) A ( jω )
低通 高通
ω
A ( jω ) A ( jω )
ω
带通
带阻
ω
ω
按所用器件的特点对滤波器分类
无源滤波器
由无源器件构成(电阻、电感和电容组成的RLC滤 波器)
晶体滤波器
利用石英晶体薄片构成
声表面波滤波器(SAW)
利用压电效应构成的。
有源滤波器
在所构成的滤波器中,除无源器件外还含有放大器 等有源电路。
相对衰减 衰减特性 ( jω ) Vo ( jω )
x(t )
延时与失真
τ
t
信号与延时后的信号(已知一信号是另一信 号的延时)
信号描述: 延时信号: 瞬时相位: 延时量:
x(t ) = A cos(ϕ (t )) = A cos(ωt ) x1(t) = A cos[ϕ1(t)] = x(t − τ ) = A cos(ω(t − τ ))
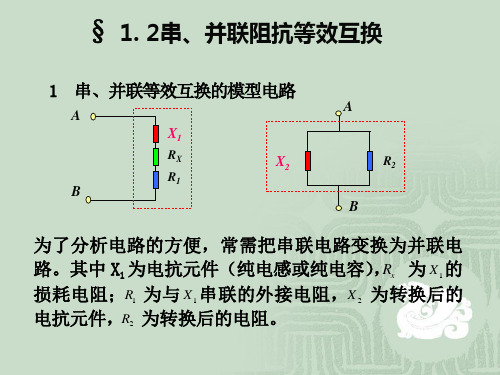
2串 § 1. 2串、并联阻抗等效互换
1 串、并联等效互换的模型电路
A X1
RX R1
A
X2 B
R2
B
为了分析电路的方便, 为了分析电路的方便 ,常需把串联电路变换为并联电 路。其中 X1 为电抗元件(纯电感或纯电容) Rx 为 X 1 的 为电抗元件(纯电感或纯电容) , 串联的外接电阻, 损耗电阻; 损耗电阻; R1 为与 X 1 串联的外接电阻, X 2 为转换后的 电抗元件, 为转换后的电阻。 电抗元件, R2 为转换后的电阻。
+ + Uab
-
+ + Ucb
-
Udb
-
Udb
-
串并联阻抗等效互换

本页完 返回
本 节 学 习 要 点 和 要 求
串 、 并 联 电 阻 等 效 变 换 串 、 并 联 电 抗 等 效 变 换 线 圈 有 抽 头 时 的 阻 抗 等 效 变 换 电容器有抽头时的阻抗等效变换 互 感 变 压 器 的 阻 抗 等 效 变 换
返回
串联谐振回路主页
串、并联阻抗的等效互换 回 路 抽 头 时 的 阻 抗 变 换 主页 互 感 变 压 器 的 阻 抗 变 换
把此式进行变换。 把此式进行变换。 1、推导串、并联阻抗变换计算式 推导串、 A R2·X22 (R1+RX)= ———— R22+X22 电感或 X1 R22·X2 电容 RX X1= ——— R22+X22 R1 对于串联电路来说, 对于串联电路来说,其Q 值为 外电阻
L1
串、并联阻抗等效变换
A
R2
X2
X1 R2 QL1 = ——— = —— RX+R1 X2 2、串、并联电阻变换公式 ·X2
2、串并联电阻变 B 换公式 B
串联回路
并联回路
所谓“等效” 所谓“等效”就是指在电 R2 2 (R1+RX)= ———— 路的频率等于工作频率 ω时 , 2 +X2 R2 2 从串联电路的A 从串联电路的A 、B 端看去 R2 R2 的阻抗与从并联电路的A = ———— = ——— 的阻抗与从并联电路的 A、 端看去的阻抗相等。 1+(R2 / X2)2 1+QL12 B端看去的阻抗相等。 本页完 继续
串、并联阻抗等效变换
1、推导串、并联阻抗变换计算式 推导串、 A R2·X22 (R1+RX)= ———— R22+X22 电感或 X1 R22·X2 电容 RX X1= ——— R22+X22 R1 对于串联电路来说, 对于串联电路来说,其Q 值为 外电阻
高频电子电路1.1.3

抽头处看进去的阻抗较小
关于电容抽头时p的公式
根据接入系数 p的严格定义
L C1 b
C2 a
p
抽头所夹元件阻抗 抽头所在支路总阻抗
1 jC1 1 1 jC1 jC2
C2 C1 C2
√
C1 p是否等于 ? C1 C2
注意课后习题 中C1和C2位置
3)抽头式电路中电压的关系
a
I ac
I bc L2
Vbc L1
b
I k:谐振环路电流 I bc和I ac:支路电流
Vac 回顾谐振时各电 流的大小关系
Ik
C c
可知I k I ac和I bc
从而可近似认为 I L1 I L2 I k
注:高频电路通常工作于谐振状态或接近于谐振状态
4)抽头式电路中电阻的等效变换
a L2 Ri b L1 c 等 效 a R’i L2 根据等效变换时能量守恒定律, C
虚部:
又 回路的品质因数
2 R2 X X1 2 2 2 R2 X 2
2 R2 X 2 R1 RX 2 2 R2 X 2
①
②
X1 R QL2 2 R1 RX X2
R2
QL1
由①式得:
R1 R X
R2 R 1 ( 2 )2 X2
2 L1
= 1 QL 2 1
– 1、减小信号源内阻和负载对回路和影响; – 2、可调抽头还可以实现阻抗匹配功能。
• 常见的抽头电路(电路图见下页):
– 按被抽头的元件分:电感抽头和电容抽头 – 按抽头在整个电路中位置分:源端抽头和负 载端抽头
1 常用的抽头振荡回路
电感抽头部分接入
关于电容抽头时p的公式
根据接入系数 p的严格定义
L C1 b
C2 a
p
抽头所夹元件阻抗 抽头所在支路总阻抗
1 jC1 1 1 jC1 jC2
C2 C1 C2
√
C1 p是否等于 ? C1 C2
注意课后习题 中C1和C2位置
3)抽头式电路中电压的关系
a
I ac
I bc L2
Vbc L1
b
I k:谐振环路电流 I bc和I ac:支路电流
Vac 回顾谐振时各电 流的大小关系
Ik
C c
可知I k I ac和I bc
从而可近似认为 I L1 I L2 I k
注:高频电路通常工作于谐振状态或接近于谐振状态
4)抽头式电路中电阻的等效变换
a L2 Ri b L1 c 等 效 a R’i L2 根据等效变换时能量守恒定律, C
虚部:
又 回路的品质因数
2 R2 X X1 2 2 2 R2 X 2
2 R2 X 2 R1 RX 2 2 R2 X 2
①
②
X1 R QL2 2 R1 RX X2
R2
QL1
由①式得:
R1 R X
R2 R 1 ( 2 )2 X2
2 L1
= 1 QL 2 1
– 1、减小信号源内阻和负载对回路和影响; – 2、可调抽头还可以实现阻抗匹配功能。
• 常见的抽头电路(电路图见下页):
– 按被抽头的元件分:电感抽头和电容抽头 – 按抽头在整个电路中位置分:源端抽头和负 载端抽头
1 常用的抽头振荡回路
电感抽头部分接入
第2章3串并联阻抗的等效互换

性质相同,当 Q 值较大时,电抗 X 基本不变;而并联电路的
电阻 Rp 比串联电路的电阻 Rs 大 Q 2 倍。
[Rp =Rs( 1+Q2)]
12:47
a
[例 ]:
C
a'
L
R
C'
L'
Rp
b
R=
Rp Q2
'
'
b'
Rp =Q 2 R =
C =C
L =L
C =C '
L =L'
L CR
结论2:并联于回路两端的电阻 Rp 越大,就相当于串联于 电感支路中的电阻R越小,回路的Q值就越高;并联于回路 两端的电阻 Rp 越小,就相当于串联于回路中的电阻R越大, 回路的Q值就越低。
为了分析电路的方便有时需要将(a)转换为(b)的等效形式。
Rp
A
Rs
( a)
Xs
B
A'
B'
Xp
( b)
电路工作频率 ,从AB端看进去的阻抗(或导纳),与从A B 端看进去的阻抗(或导纳)相等。 式中:
12:47
2.3 串并联阻抗的等效互换 A
由(a)图得:
Rs -jX s Rs Xs 1 Ys = = = -j Rs +jX s Rs2 +X s2 Rs2 +X s2 Rs2 +X s2
12:47
2.3
阻抗变换电路
Rs与RL满足什么关系时, RL可以获得最大功率传输?
如果RL不能满足最大功率传输条件,该怎么办?
2.3
阻抗变换电路
1.变压器耦合阻抗变换电路 不考虑M
' 折合到1、2两端的等效电阻 RL 所得的功率 P 1 应与负载 RL所获功率 P 2 相等。 2 2 V 2 V1 (P代表功率) P = 2 P = 1 RL R'
串并联电路的等效阻抗变换与回路抽头阻抗变换讲解

➢ 以上基于互感耦合回路的分析与结论对于纯 电抗耦合系统都适用。
➢耦合回路的调谐特性: 电流幅值
I1m I2m
V1m
M 2
2
M 2
2
R11
R222
X
2 22
R22
X11
R222
X
2 22
X 22
V1mM
M 2 2
X
2 p
j
R
2 p
X
p
Rp2
X
2 p
等式两边实部与虚部分别相等,可得:
Rs
Rp
X
2 p
Rp2
X
2 p
Xs
Rp2 X p
Rp2
X
2 p
这说明Xs与Xp电抗性质相同,即同为电感或电 容。
串联电路的有效品质因数: QL1 X s Rs Rp X p 即串联电路的有效品质因数QL1等效于并联电路
的电阻Rp与电抗Xp的比值。
由此可得: Rp Rs 1 QL21
X
p
Xs
1
1 QL21
当QL1的值较大时,有:
Rp Rs QL21 Xp Xs
该结果表明:
(1) 串联电抗Xs和并联电抗Xp性质相同,在高 QL1时X s X p ;
(2) 小的串联电阻Rs可转化为大的并联电阻Rp: Rp 1 QL21 Rs
M 2
X11
X
f1
R222
X
2 22
➢耦合回路的调谐特性: 电流幅值
I1m I2m
V1m
M 2
2
M 2
2
R11
R222
X
2 22
R22
X11
R222
X
2 22
X 22
V1mM
M 2 2
X
2 p
j
R
2 p
X
p
Rp2
X
2 p
等式两边实部与虚部分别相等,可得:
Rs
Rp
X
2 p
Rp2
X
2 p
Xs
Rp2 X p
Rp2
X
2 p
这说明Xs与Xp电抗性质相同,即同为电感或电 容。
串联电路的有效品质因数: QL1 X s Rs Rp X p 即串联电路的有效品质因数QL1等效于并联电路
的电阻Rp与电抗Xp的比值。
由此可得: Rp Rs 1 QL21
X
p
Xs
1
1 QL21
当QL1的值较大时,有:
Rp Rs QL21 Xp Xs
该结果表明:
(1) 串联电抗Xs和并联电抗Xp性质相同,在高 QL1时X s X p ;
(2) 小的串联电阻Rs可转化为大的并联电阻Rp: Rp 1 QL21 Rs
M 2
X11
X
f1
R222
X
2 22
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
等
教
P1 P2
育
Is'
Vab Vdb
Is
pIs
出
版
社
《
高
频
电
子 线
上面分析了外接负载为纯阻的情况。而当外接负
路 》
载包括电抗成分时,上述等效变换关系仍然适用。
(
第
d
d
四
版
)
CP
张
a
CL
R L C L
肃
RL CL
文
主
编
b
b
高 等 教
2
2
RL '
Vdb Vab
RL
N1 N2
RL
1 p2
四 版 ) 张
Rs
jX s
Rp jX p Rp jX p
肃
文 主 编
Rp jX p Rp jX p Rp jX p Rp jX p
高
等 教 育 出
Rp
X
2 p
Rp2
X
2 p
j
Rp2 X p
Rp2
X
2 p
串联串、并联阻抗
版
的等效互换
社
《
高
频
电
子 线 路 》 (
Rs
jX s
C2
C2
C1 C2
《
高
频
电
子 线
以上讨论了负载电阻的部分接入问题,下面,讨
路 》
论信号源及其内阻的部分接入问题。
(
第
d
d
四 版 ) 张
Rs '
1 p2
Rs
Vdb Vab
2 Rs
肃 文
P1 Vdb Is'
Is
a Rs
C RL
I s R s
L C RL
主
编 P2 Vab I s
b
b
高
1 p2
RL
社
C
L
b)
+
R L V
—
功率守恒 P1 P2 接入系数 p VL 1
V
《
高
频
电
子 线
3.
电容抽头电路
路
》
( 第
C1
四
P +
版 )
C2 RL VL
张
肃 文
-
a)
—
主
编
1
高 等 教 育
RL
1
C2
出
p VL C2
V
1
C
版 社
+
C
L
R L V
-
b)
—
C1C2
C C1 C2 C1
RL
育
2
出 版 社
CL'
Vab Vdb
CL
p 2CL
End
N1 1 N2
教
2
2
育 出 版
RL '
V VL
RL
N1 N2
RL
1 p2 RL
接入系数
p VL N 2 1
V
N1
社
《
高
频
电
子 线
3.
电容抽头电路
路
》
( 第
C1
四
P +
版 )
C2 RL VL
张
肃 文
-
a)
—
主
编 高 等
P1
V2 RL '
P2
VL 2 RL
教
2
育 出 版
RL '
V VL
RL
பைடு நூலகம்
编 变压器抽头电路和双电容抽头电路,下面分别
高 等
介绍。首先,讨论负载电阻的部分接入问题。
教
育
出
版
社
《
高
频
电
子
线 1.
变压器耦合连接
路
》
( 第
+L
+
四 版 )
Is
Rp
C VL
P2 RL
P1
Is
Rp C
R L V
张 肃
—
文
(a)
— (b)
主
编 高 等
P1
V2 RL '
P2
VL 2 RL
功率守恒 P1 P2
N1 1 N2
教
接入系数 育
出 版
2
2
RL '
V VL
RL
N1 N2
RL
1 p 2 RL
p VL N 2 1
V
N1
社
《
高
频
电
子 线
2. 自耦合变压器
路
》
(
第
+
四 版
C
P +
C
L
R L V
) 张 肃 文
RL VL
-
a)
—
-
b)
—
主
编 高 等
P1
V2 RL '
P2
VL 2 RL
功率守恒 P1 P2
L Rp
C
肃
文 主 编
p
1 LC
Rp
Qp 2 R
L CR
高 等
对于高Q值并联谐振回路,其谐振频率与串联谐
教 振回路相近,谐振阻抗可以通过串联支路的串并联互
育 出
换得到。
版
社
《
高
频
电
子 线
对于高Q值并联谐振回路,其谐振频率与串联谐
路 》
振回路相近,谐振阻抗可以通过串联支路的串并联互
( 换得到。
第
四
《
高
频
电
子
线
路
》
( 第
2.3.1
四
版
)
张 肃
2.3.2
文
主
编
高 等
2.3.3
教
育
出
版
社
串、并联阻抗的等效互换 并联谐振回路的其他形式 抽头式并联电路的阻抗变换
《
高
频
电
子 线 路
所谓等效,就是指电路工作在某一频率时,不管其内部的 电路形式如何,从端口看过去其阻抗或者导纳是相等的。
》
( 第
要串、并联阻抗等效,即
版
社
End
《
高
频
电
子
线 对于复杂的并联谐振回路,其谐振频率和谐振阻抗的计算
路 》 (
一般更为繁琐。然而,当整个电路满足高Q条件时,计算可以 大大化简。
第
四
版
)
张
肃
文
主
编
高
等
教
育 出
并联电路的
版
广义形式
社
两个支路都有电阻 的并联回路
《
高
频
电
子
线
路
》 (
L C 高Q
第 四
Is
损
版 )
耗 电
R
张
阻
Is
出 版 社
Xp
Xs 1
1 QL21
《
高 频
电
子 线 路 》
Rp 1 QL21 Rs
Xp
Xs 1
1 QL21
(
第 四
QL 1≥10时, Rp RsQL21
版
)
张 肃
Xp Xs
文
主
编 结论:当品质因数足够高时
高
等 教
1)小的串联电阻变为大的并联电阻。
育
出
2)串联电抗变为同性质的并联电抗。
版 )
当品质因数足够高时
张
肃
文 主 编
p
1 LC
高 等 教 育
Gp
Gp1
Gp2
R1 R2
(p L)2
出
版
社
End
《
高
频
电
子
线
路 》
为了减小信号源或负载电阻对谐振回路的
( 第
影响,信号源或负载电阻不是直接接入回路,
四 版
而是经过一些简单的变换电路,将它们部分接
) 入回路。
张
肃
文 主
常用的电路形式有变压器耦合连接、自耦
Rp jX p Rp jX p
Rp
X
2 p
Rp2
X
2 p
j
Rp2 X p Rp2 X
2 p
第 四 版 )
故
Rs
Rp
X
2 p
Rp2
X
2 p
Xs
Rp2 X p
Rp2
X
2 p
张
肃 文
尽管电路形式变化,但是二者的品质因数应该相等。
主 编 高 等 教 育
QL1
Xs Rs
QL2
Rp Xp
所以等效互换的变换关系为: Rp 1 QL21 Rs
