2012届北京市海淀区高三期末数学理科试题(WORD精校版)
2012年北京市高考数学理科试卷及答案解析

2012北京理科高考试卷及答案解析精校版一、选择题共8小题。
每小题5分.共40分.在每小题列出的四个选项中,选出符合胜目要求的一项. 1.已知集合A={x ∈R |3x+2>0﹜,B={x ∈ R |(x+1)(x-3)>0﹜则A ∩B=( ) A .(﹣∞,﹣1) B.{21,3--} C. ﹙2,33-﹚ D.(3,+∝) 2. 设不等式组0202x y ≤≤⎧⎨≤≤⎩表示的平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是( ) A.4π B.22π- C.6πD. 44π-3.设,a b R ∈.“0a =”是‘复数a bi +是纯虚数”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.执行如图所示的程序框图,输出的S 值为( ) A. 2 B .4 C.8 D. 165.如图. ∠ACB=90º,CD ⊥AB 于点D ,以BD 为直径的圆与BC 交于点E.则( ) A. CE ·CB=AD ·DB B. CE ·CB=AD ·AB C. 2AD AB CD =g D.2CE EB CD =g6.从0,2中选一个数字.从1.3.5中选两个数字,组成无重复数字的三位数.其中奇数的个数为( ) A. 24 B. 18 C. 12 D. 67.某三梭锥的三视图如图所示,该三梭锥的表面积是( ) A.2865+ B. 3065+ C.56125+ D.60125+8.某棵果树前n 前的总产量S 与看,前mA.5B.7C.9D.11二.填空题共6小题。
每小题5分。
共30分. 9.直线21x t y t =+⎧⎨=--⎩ (t 为参数)与曲线3cos 3sin x y αα=⎧⎨=⎩(α为参数)的交点个数为10.已知{}n a 等差数列n S 为其前n 项和,若112a =,23S a =,则2a = ,n S =11.在△ABC 中,若2a =,7b c +=,1cos 4B =-,则b =12.在直角坐标系xOy 中,直线l 过抛物线24y x =的焦点F ,且与该抛物线相交于A 、B 两点,其中点A 在x 轴上方,若直线l 的倾斜角为60º.则OAF V 的面积为13.己知正方形ABCD 的边长为1,点E 是AB 边上的动点.则DE CB u u u r u u u rg的值为14.已知()(2)(3)f x m x m x m =-++,()22xg x =-,若同时满足条件:①x R ∀∈,有()0f x <或()0g x <;②(,4)x ∃∈-∞-,使得()()0f x g x <g 则m 的取值范围是三、解答题公6小题,共80分。
2012年全国普通高等学校招生统一考试理科数学(北京卷带解析
第1页 共4页 ◎ 第2页 共4页2012年全国普通高等学校招生统一考试理科数学(北京卷带解析1.已知集合={x R|3x+2>0}A ∈,B={x R|(x+1)(x-3)>0}∈,则A B =( ) A .(,1)-∞- B .2(1,)3-- C .2(,3)3-D .(3,)+∞ 2.设不等式0202x y ≤≤⎧⎨≤≤⎩表示的平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离大于2的是( )A .4π B.22π- C .6π D .44π- 3.设,a b R∈,“0a =”是“复数a bi +是纯虚数”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件 D . 既不充分也不必要条件 4.执行如图所示的程序框图,输出的S 的值是( )A .2B .4C .8D .165.如图,090ACB ∠=,CD AB ⊥于点D ,以BD 为直径的圆与BC 交于点E.则( )A. CE CB AD DB ∙=∙B. CE CB AD AB ∙=∙C. 2AD AB CD ∙= D. 2CE EB CD ∙=6.从0,2中选一个数字.从 1.3.5中选两个数字,组成无重复数字的三位数.其中奇数的个数为( )A. 24B. 18C. 12D. 67.某三棱锥的三视图如图所示,该三棱锥的表面积是( )A .28+.30+ C .56+.60+8.某棵果树前n 年的总产量n S 与n 之间的关系如图所示,从目前记录的结果看,前m 年的年平均产量最高,m 的值为( )A .5B .7C .9D .11A DBCE第3页共4页◎第4页共4页第II卷(非选择题)请点击修改第II卷的文字说明二、填空题(题型注释)9.直线21x ty t=+⎧⎨=--⎩(t为参数)与曲线3cos3sinxyαα=⎧⎨=⎩(“为多α数)的交点个数为10.已知{}na为等差数列,nS为其前n项和,若112a=,23S a=,则2a=nS=11.在△ABC中,若2,7a b c=+=,1cos4B=-,则b=12.在直角坐标系xOy中.直线l过抛物线=4x的焦点F.且与该抛物线相交于A、B两点.其中点A在x轴上方。
2012年高考真题——理数(北京卷)word版

2012年普通高等学校招生全国统一考试数学(理)(北京卷)本试卷共5页. 150分.考试时长120分钟.考试生务必将答案答在答题卡上.在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题共40分)一、选择题共8小题。
每小题5分.共40分.在每小题列出的四个选项中,选出符合胜目要求的一项.1.已知集合A={x∈R|3x+2>0﹜·B={x∈ R|(x+1)(x-3)>0﹜则A∩B=( )A.(﹣∞,﹣1) B.{﹣1,-⅔} C. ﹙﹣⅔,3﹚ D.(3,+∝)2. 设不等式组表示的平面区域为D.在区域D内随机取一个点.则此点到坐标原点的距离大于2的概率是()A. B. C. D.3.设a,b∈R.“a=O”是‘复数a+bi是纯虚数”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件4.执行如图所示的程序框图,输出的S值为()A. 2B .4C.8D. 165.如图. ∠ACB=90º。
CD⊥AB于点D,以BD为直径的圆与BC交于点E.则( )A. CE·CB=AD·DBB. CE·CB=AD·ABC. AD·AB=CD ²D.CE·EB=CD²6.从0,2中选一个数字.从1.3.5中选两个数字,组成无重复数字的三位数.其中奇数的个数为( )A. 24B. 18C. 12D. 67.某三梭锥的三视图如图所示,该三梭锥的表面积是()A. 28+6B. 30+6C. 56+ 12D. 60+128.某棵果树前n前的总产量S与n之间的关系如图所示.从目前记录的结果看,前m年的年平均产量最高。
m值为()A.5B.7C.9D.11第二部分(非选择题共110分)二.填空题共6小题。
每小题5分。
共30分.9.直线(t为参数)与曲线 (“为多α数)的交点个数为10.已知﹛﹜等差数列为其前n项和.若=,=,则=11.在△ABC中,若α=2,b+c=7,=-,则b=12.在直角坐标系xOy中.直线l过抛物线=4x的焦点F.且与该撇物线相交于A、B两点.其中点A在x轴上方。
【精品解析】北京市海淀区2012届高三数学上学期期末考试试题 文(教师版)新人教B版

【精品解析】市海淀区2012届高三政治上学期期末练习试题(教师版)新人教版【试题总体说明】本套试卷严格按照2011年卷的高考题进行命制,题目难度适当,创新度较高。
所命试卷呈现以下几个特点:(1)注重对基础知识、基本能力和基本方法的考查,严格控制试题难度。
如选择题2,4;(2)知识点覆盖全面,既注重对传统知识的考查,又注重对新增内容的考查,更注重对主干知识的考查;(3)遵循源于教材、高于教材的原则,部分试题根据教材中的典型例题或习题改编而成;如选择题3,7.(4)深入探究2011高考试题,精选合适的试题进行改编;如填空题9,11.(5)题型新颖,创新度高,部分试题是原创题,有较强的时代特色.如填空题13和解答题20等;(6)在知识网络的交汇处命题,强调知识的整合,突出考查学生综合运用数学知识分析问题、解决问题的能力。
如17题。
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.(1)复数i(12i)-=(A )2i -+ (B )2i + (C )2i - (D )2i --【答案】B(3)已知数列{}n a 满足:22111, 0, 1(*)n n n a a a a n +=>-=∈N ,那么使5n a <成立的n 的最大值为( )(A )4 (B )5 (C )24 (D )25【答案】C【解析】22222111,{}1,11(1),n n n n a a a a a n n +-=∴=∴=+-=是以为公差的等差数列, 0,.5,5,25.n n n a a n a n n n >∴=<∴<∴<∴的最大值为24,故选C 。
(A )充分不必要条件 (B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件【答案】C【解析】1212121212,11,;,110,.k k l l l l k k k k =≠-∴∴⨯-⨯=∴=∥∥故为充要条件。
2012北京数学理科(纯word版,含答案)
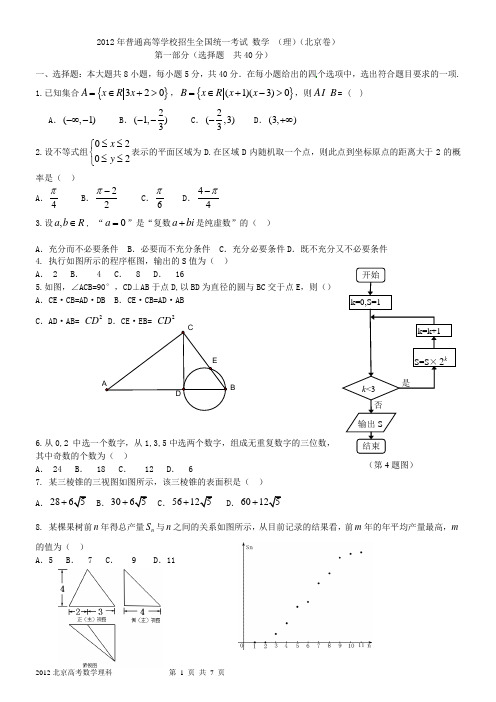
2012年普通高等学校招生全国统一考试 数学 (理)(北京卷)第一部分(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项. 1.已知集合{}320A x R x =∈+>,{}(1)(3)0B x R x x =∈+->,则A B = ( ) A .(,1)-∞- B .2(1,)3-- C .2(,3)3- D .(3,)+∞2.设不等式组0202x y ≤≤⎧⎨≤≤⎩表示的平面区域为D.在区域D 内随机取一个点,则此点到坐标原点的距离大于2的概率是( ) A .4π B .22π- C .6π D .44π- 3.设,a b R ∈, “0a =”是“复数a bi +是纯虚数”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分又不必要条件4. 执行如图所示的程序框图,输出的S 值为( ) A . 2 B . 4 C . 8 D . 165.如图,∠ACB=90°,CD ⊥AB 于点D,以BD 为直径的圆与BC 交于点E ,则() A .CE ·CB=AD ·DB B .CE ·CB=AD ·AB C .AD ·AB= 2CD D .CE ·EB= 2CD6.从0,2 中选一个数字,从1,3,5中选两个数字,组成无重复数字的三位数, 其中奇数的个数为( )A . 24B . 18C . 12D . 67. 某三棱锥的三视图如图所示,该三棱锥的表面积是( ) A.28+ B.30+ C.56+.60+8. 某棵果树前n 年得总产量n S 与n 之间的关系如图所示,从目前记录的结果看,前m 年的年平均产量最高,m 的值为( )A .5B . 7C . 9D .11(第4题图)B第二部分(非选择题 共110分) 二、填空题:本大题共6小题,每小题5分,共30分. 9. 直线2,1x t y t =+⎧⎨=--⎩(t 为参数)与曲线3cos 3sin x y =α⎧⎨=α⎩(α为参数)的交点个数为 .10.已知{}n a 为等差数列,n S 为其前n 项和.若112a =,23S a =,则2a = ;n S = . 11.在△ABC 中,若2a =,7bc +=,1cos 4B =-,则b = . 12.在直角坐标系xoy 中,直线l 过抛物线24y x =的焦点F,且与该抛物线相较于A 、B 两点,其中点A 在x 轴上方,若直线l 的倾斜角为60°,则△OAF 的面积为 .13.已知正方形ABCD 的边长为1,点E 是AB 边上的动点,则DE CB ⋅的值为 ; DE DC ⋅的最大值为 .14.已知()(2)(3)f x m x m x m =-++,()22x g x =-.若同时满足条件:①,()0x R f x ∀∈<或()0g x <;②(,4)x ∃∈-∞- ,()()0f x g x <. 则m 的取值范围是 . 三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题13分) 已知函数(sin cos )sin 2()sin x x xf x x-=.(1)求()f x 的定义域及最小正周期; (2)求()f x 的单调递增区间.16. (本小题14分)如图1,在Rt △ABC 中,∠C=90°,BC=3,AC=6,D,E 分别是AC ,AB 上的点, 且DE ∥BC ,DE=2,将△ADE 沿DE 折起到△A 1DE 的位置,使A 1C ⊥CD ,如图2. (1)求证:A 1C ⊥平面BCDE;(2)若M 是A 1D 的中点,求CM 与平面A 1BE 所成角的大小;(3)线段BC 上是否存在点P,使平面A 1DP 与平面A 1BE 垂直?说明理由. 17.(本小题13分)近年来,某市为促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱,为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1000吨生活垃圾,数(1)试估计厨余垃圾投放正确的概率; (2)试估计生活垃圾投放错误的概率;(3)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投放量分别为,,a b c ,其中0a >,600a b c ++=.当数据,,a b c 的方差2S 最大时,写出,,a b c 的值(结论不要求证明),并求此时2S 的值. (注:方差2222121[()()()]n s x x x x x x n=-+-++- ,其中x 为12,,n x x x 的平均数) 18.(本小题13分)已知函数2()1f x ax =+(0a >),3()g x x bx =+.(1)若曲线()y f x =与曲线()y g x =在它们的交点(1,c )处具有公共切线,求,a b 的值; (2)当24a b =时,求函数()()f x g x +的单调区间,并求其在区间(,1]-∞-上的最大值.19.(本小题14分)已知曲线C: 22(5)(2)8()m x m y m R -+-=∈ (1)若曲线C 是焦点在x 轴的椭圆,求m 的范围;(2)设4m =,曲线C 与y 轴的交点为A,B (点A 位于点B 的上方),直线4y kx =+与曲线C 交于不同的两点M,N,直线1y =与直线BM 交于点G 求证:A,G,N 三点共线. 20.(本小题13分)设A 是由m n ⨯个实数组成的m 行n 列的数表,满足:每个数的绝对值不大于1,且所有数的和为零.记(,)S m n 为所有这样的数表构成的集合.对于(,)A S m n ∈,记()i r A 为A 的第i 行各数之和1i m ≤≤,()j c A 为A 的第j 列各数之和1j n ≤≤; 记()k A 为1|()|r A ,2|()|r A ,…,|()|m r A ,1|()|c A ,2|()|c A ,…,|()|n c A 中的最小值. (1)对如下数表A,求()k A 的值;(2)设数表A=(2,3)S 形如求()k A 的最大值;(3)给定正整数t ,对于所有的A ∈S(2,21t +),求()k A 的最大值.(李国波录入2012-6-8)参考答案 一、选择题1、D2、D3、B4、C5、A6、B7、B8、C 二、填空题9、2;10、1,1(1)4n n +;11、4;1213、1,1;14、(4,2)--; 三、解答题15、解:(1)由sin 0x ≠得,()x k k Z π≠∈,故()f x 的定义域为{|,}x R x k k Z π∈≠∈.因为(sin cos )sin 2()sin x x x f x x -==2cos (sin cos )x x x -=sin 2cos 21x x --)14x π--,所以()f x 的最小正周期22T ππ==. (2)函数sin y x =的单调递减区间为3[2,2]()22k k k Z ππππ++∈. 由222,()242k x k x k k Z ππππππ-≤-≤+≠∈得3,()88k x k x k k Z πππππ-≤≤+≠∈ 所以函数()f x 的单调递增区间为[,)8k k k Z πππ-∈,和3(,]()8k k k Z πππ+∈. 16.解:(1) ,AC BC DE BC ⊥∥∴DE AC ⊥∴1DE A D ⊥,DE CD ⊥(1A D CD D = )又 DE ⊥平面1A DC ,∴DE 1AC ⊥ 又∵1A C CD ⊥,(DE CD D = ) ∴1AC ⊥平面BCDE (2)如图,以C 为坐标原点,建立空间直角坐标系C xyz -,则(100A ,,,()020D ,,,M ,()300B ,,,()220E ,,,设平面1A BE 法向量为()n x y z = ,,,则10,0A B n BE n ⋅=⋅=∴(130A B =- ,,,()120BE =- ,,,∴3020x x y ⎧-=⎪⎨-+=⎪⎩令1y =,则2,x z ==∴(21n = 设CM 与平面1A BE 所成的角为θ∵(0CM =∴sin |cos ,|||||||CM n n CM CM n θ⋅=====⋅CM 与平面1A BE 所成角的大小45︒(3)线段BC 上不存在点P,使平面1A DP 与平面1ABE 垂直。
【精品解析】北京市海淀区2012届高三数学上学期期末考试试题 文(学生版)新人教B版

(Ⅱ)求决赛中甲、乙两支队伍出场顺序相邻的概率.
(17)(本小题满分13分)
在四棱锥 中,底面 是菱形, .
(Ⅰ)若 ,求证: 平面 ;
(Ⅱ)若平面 平面 ,求证: ;
(Ⅲ)在棱 上是否存在点 (异于点 )使得 ∥平面 ,若存在,求 的值;若不存在,说明理由.
(11)若实数 满足 则 的最大值为.
(12)甲和乙两个城市去年上半年每月的平均气温(单位: )用茎叶图记录如下,根据茎叶图可知,两城市中平均温度较高的城市是_____________,气温波动较大的城市是
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
(15)(本小题满分13分)
(3)已知数列 满足: ,那么使 成立的 的最大值为()
(A)4(B)5(C)24(D)25
(4)某程序的框图如图所示,若执行该程序,则输出的 值为
(A)5(B)6
(C)7(D)8
(5)已知直线 : 与直线 : ,那么“ ”是“ ∥ ”的
(A)充分不必要条件(B)必要不充分条件
(C)充要条件(D)既不充分也不必要条件
(6)函数 的部分图象函数 ,则下列结论正确的是
(A) 是偶函数,递增区间是
(B) 是偶函数,递减区间是
(C) 是奇函数,递减区间是
(D) 是奇函数,递增区间是
(9)双曲线 的离心率为.
(10)已知抛物线 过点 ,那么点 到此抛物线的焦点的距离为.
【精品解析】市海淀区2012届高三政治上学期期末练习试题(教师版)新人教版
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
北京市海淀区2012届高三下学期期末练习 文科数学(2012海淀二模)Word版

海淀区高三年级第二学期期末练习数 学(文科)2012.05一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. (1)函数21,12y x x=-+-?的值域是(A )(3,0]- (B ) (3,1]- (C )[0,1] (D )[1,5) (2)已知命题p :1,sin 2x x x $?R . 则p Ø为 (A )1,sin 2x x x $?R (B )1,sin 2x x x "?R (C )1,sin 2x xx $纬R (D )1,sin 2x x x "纬R (3)22cos 15sin 15-的值为(A )12 (B)2 (C)2 (D)2(4)执行如图所示的程序框图,若输入x 的值为10,则输出的x(A )4 (B )2 (C )1 (D )0(5)已知平面,αβ和直线m ,且m Ìα,则“α∥β”是“m ∥β”的(A )充要条件 (B )必要不充分条件 (C )充分不必要条件 (D )既不充分也不必要条件(6)为了得到函数21log (1)2y x =-的图象,可将函数2log y x =的图象上所有的点的 (A )纵坐标缩短到原来的12倍,横坐标不变,再向右平移1个单位长度 (B )纵坐标缩短到原来的12倍,横坐标不变,再向左平移1个单位长度(C )横坐标伸长到原来的2倍,纵坐标不变,再向右平移1个单位长度 (D )横坐标伸长到原来的2倍,纵坐标不变,再向左平移1个单位长度(7)某几何体的主视图与俯视图如图所示,左视图与主视图相同,且图中的四边形都是边长为2的正方形,两条虚线互相垂直,则该几何体的体积是(A )203(B )43(C )6 (D )4(8)点(,)P x y 是曲线1:(0)C y x x=>上的一个动点,曲线C 在点P 处的切线与x 轴、y 轴分别交于,A B 两点,点O 是坐标原点. 给出三个命题:①PA PB =;②OAB ∆的面积为定值;③曲线C 上存在两点,M N ,使得OMN ∆为等腰直角三角形.其中真命题的个数是(A )1 (B )2 (C )3 (D )0二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上. (9)复数31iiz +=,则z = . (10)已知双曲线22221x y a b-=的渐近线方程是2y x =?,那么此双曲线的离心率为 .(11)在ABC ∆中,若120A??,6c =,ABC ∆的面积为,则a = .(12)在面积为1的正方形ABCD 内部随机取一点P ,则PAB ∆的面积大于等于14的概率是_________.左俯视图主视图(13)某同学为研究函数()1)f x x=#的性质,构造了如图所示的两个边长为1的正方形ABCD 和BEFC ,点P 是边BC 上的一个动点,设CP x =,则()AP PF f x +=. 请你参考这些信息,推知函数()f x 的极值点是 ;函数()f x 的值域是 .(14)已知定点(0,2),(2,0)M N -,直线:220l kx y k --+=(k 为常数). 若点,M N 到直线l 的距离相等,则实数k 的值是 ;对于l 上任意一点P ,MPN Ð恒为锐角,则实数k 的取值范围是 .三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)已知等差数列{}n a 的前n 项和为n S ,公差0d ¹,5346S a =+,且139,,a a a 成等比数列.(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)求数列1{}nS 的前n 项和公式.(16)(本小题满分13分)在一次“知识竞赛”活动中,有12,,,A A B C 四道题,其中12,A A 为难度相同的容易题,B 为中档题,C 为较难题. 现甲、乙两位同学均需从四道题目中随机抽取一题作答.(Ⅰ)求甲、乙两位同学所选的题目难度相同的概率; (Ⅱ)求甲所选题目的难度大于乙所选题目的难度的概率.(17)(本小题满分14分)在正方体''''ABCD AB C D 中, 棱,','',''AB BB B C C D 的中点分别是,,,E F G H , 如图所示. (Ⅰ)求证:'AD ∥平面EFG ;EFAB C DPC'C(Ⅱ)求证:'A C ^平面EFG ;(Ⅲ)判断点,',,A D H F 是否共面? 并说明理由.(18)(本小题满分13分)已知函数22()3x af x x a+=+(0a ≠,a ∈R ). (Ⅰ)求函数()f x 的单调区间;(Ⅱ)当1a =时,若对任意12,[3,)x x ∈-+∞,有12()()f x f x m -≤成立,求实数m 的最小值.(19)(本小题满分13分)已知椭圆C :22221(0)x y a b a b +=>>的右焦点为(1,0)F ,且点(-在椭圆C 上.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)已知点5(,0)4Q ,动直线l 过点F ,且直线l 与椭圆C 交于A ,B 两点,证明:QA QB ⋅为定值.(20)(本小题满分14分)将一个正整数n 表示为12(*)p a a a p +++?N 的形式,其中*i a ÎN ,1,2,,i p =,且p a a a ≤≤≤ 21,记所有这样的表示法的种数为)(n f (如4=4,4=1+3,4=2+2,4=1+1+2,4=1+1+1+1,故5)4(=f ).(Ⅰ)写出)5(),3(f f 的值,并说明理由; (Ⅱ)证明:(1)()1f n f n +-?(1,2,n =);(Ⅲ)对任意正整数n ,比较)1(+n f 与)]2()([21++n f n f 的大小,并给出证明.海淀区高三年级第二学期期末练习数 学(文科)参考答案及评分标准 2012.05一.选择题:本大题共8小题,每小题5分,共40分.二.填空题:本大题共6小题,每小题5分,共30分.(9 (11) (12)12(13)12;1](14)1或13;1(,)(1,)7-?+? 注:(13)、(14)题第一空3分;第二空2分.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分) 解:(Ⅰ)因为5346S a =+,所以115454(2)62da a d 创+=++. ①……………………………………3分 因为139,,a a a 成等比数列,所以2111(8)(2)a a d a d +=+. ② ……………………………………5分 由①,②及0d ¹可得:12,2a d ==.……………………………………6分 所以2n a n =. ……………………………………7分 (Ⅱ)由2n a n =可知:2(22)2n n nS n n +?==+.……………………………………9分所以1111(1)1n S n n n n ==-++. ……………………………………11分 所以1211111n nS S S S -++++11111111122311n n n n =-+-++-+--+1111n n n =-=++. ……………………………………13分 所以 数列1{}nS 的前n 项和为1n n +. (16)(本小题满分13分)解:由题意可知,甲、乙两位同学分别从四道题中随机抽取一题,所有可能的结果有16个,它们是:11(,)A A ,12(,)A A ,1(,)A B ,1(,)A C ,21(,)A A ,22(,)A A ,2(,)A B ,2(,)A C ,1(,)B A ,2(,)B A ,(,)B B ,(,)B C ,1(,)C A ,2(,)C A ,(,)C B ,(,)C C . ……………………………………3分(Ⅰ)用M 表示事件“甲、乙两位同学所选的题目难度相同”,则M 包含的基本事件有:11(,)A A ,12(,)A A ,21(,)A A ,22(,)A A ,(,)B B ,(,)C C . 所以63()=168P M =. ……………………………………8分 (Ⅱ)用N 表示事件“甲所选题目的难度大于乙所选题目的难度”,则N 包含的基本事件有:1(,)B A ,2(,)B A ,1(,)C A ,2(,)C A ,(,)C B . 所以5()16P N =. ……………………………………13分 (17)(本小题满分14分)(Ⅰ)证明:连接'BC .在正方体''''ABCD A B C D -中,''AB C D =,AB ∥''C D . 所以 四边形''ABC D 是平行四边形. 所以 'AD ∥'BC .因为 ,F G 分别是',''BB B C 的中点,所以 FG ∥'BC .所以 FG ∥'AD . ……………………………………2分因为 ,'EF AD 是异面直线, 所以 'AD Ë平面EFG .因为 FG Ì平面EFG ,所以 'AD ∥平面EFG .………………………………………4分(Ⅱ)证明:连接'B C .在正方体''''ABCD A B C D -中,''A B ^平面''BCC B ,'BC Ì平面''BCC B , 所以 '''A B BC ⊥.在正方形''BCC B 中,''B C BC ⊥,因为 ''A B Ì平面''A B C ,'B C Ì平面''A B C ,''''A B B C B =,所以'BC ⊥平面''A B C . ……………………………………6分因为 'A C Ì平面''A B C , 所以''BC A C ⊥. ……………………………………7分因为 FG ∥'BC , 所以 'A C FG ⊥.同理可证:'A C EF ⊥.因为 EF Ì平面EFG ,FG Ì平面EFG ,EFFG F =,所以 'A C ^平面EFG . ……………………………………9分 (Ⅲ)点,',,A D H F 不共面. 理由如下: ……………………………………10分 假设,',,A D H F 共面. 连接',,C F AF HF . 由(Ⅰ)知,'AD ∥'BC , 因为 'BC Ì平面''BCC B ,'AD Ë平面''BCC B .所以 'AD ∥平面''BCC B .……………………………………12分 因为 ''C D H Î,所以 平面'AD HF 平面'''BCC B C F =. 因为 'AD Ì平面'AD HF , 所以 'AD ∥'C F .所以 'C F ∥'BC ,而'C F 与'BC 相交,矛盾.所以 点,',,A D H F 不共面. ……………………………………14分 (18)(本小题满分13分) 解:222()(3)'()(3)x a x a f x x a --+=+. HG FED'C'B'A'D C BAHG FED'C'B'A'DC BA令'()0f x =,解得x a =或3x a =-. ……………………………………2分 (Ⅰ)当0a >时,'()f x ,()f x 随着x 的变化如下表函数()f x 的单调递增区间是(3,)a a -,函数()f x 的单调递减区间是(,3)a -∞-,(,)a +∞. ……………………………………4分当0a <时,'()f x ,()f x 随着x 的变化如下表函数()f x 的单调递增区间是(,3)a a -,函数()f x 的单调递减区间是(,)a -∞,(3,)a -+∞. ……………………………………6分(Ⅱ)当1a =时,由(Ⅰ)得()f x 是(3,1)-上的增函数,是(1,)+∞上的减函数.又当1x >时,21()03x f x x +=>+. ……………………………………8分 所以 ()f x 在[3,)-+∞上的最小值为1(3)6f -=-,最大值为1(1)2f =.……………………………………10分 所以 对任意12,[3,)x x ∈-+∞,122()()(1)(3)3f x f x f f -≤--=. 所以 对任意12,[3,)x x ∈-+∞,使12()()f x f x m -≤恒成立的实数m 的最小值为23. ……………………………………13分(Ⅰ)解:由题意知:1c =.根据椭圆的定义得:2a =a = ……………………………………3分 所以 2211b =-=.所以 椭圆C 的标准方程为2212x y +=. ……………………………………4分 (Ⅱ)证明:当直线l 的斜率为0时,(A B . 则557(2,0)(,0)4416QA QB ⋅=⋅=-. ……………………………………6分当直线l 的斜率不为0时,设直线l 的方程为:1x ty =+,()()1122,,,A x y B x y .由221,21x y x ty ìïï+=ïíïï=+ïî可得:22(2)210t y ty ++-=.显然0∆>.1221222,21.2t y y t y y t ìïï+=-ïï+ïíïï=-ïï+ïî……………………………………9分 因为 111x ty =+,221x ty =+,所以 112212125511(,)(,)()()4444x y x y ty ty y y -?=--+ 2121211(1)()416t y y t y y =+-++2221121(1)24216t t t t t =-+++++ 22222172(2)1616t t t --+=+=-+. 即 716QA QB ⋅=-. ……………………………………13分(Ⅰ)解:因为3=3,3=1+2,3=1+1+1,所以3)3(=f .因为5=5,5=2+3,5=1+4,5=1+1+3,5=1+2+2,5=1+1+1+2,5=1+1+1+1+1, 所以7)5(=f . ……………………………………3分 (Ⅱ)证明:因为21≥+n ,把1+n 的一个表示法中11a =的1a 去掉,就可得到一个n 的表示法;反之,在n 的一个表示法前面添加一个“1+”,就得到一个1n +的表示法,即1+n 的表示法中11a =的表示法种数等于n 的表示法种数,所以 )()1(n f n f -+表示的是1+n 的表示法中11a ¹的表示法数.即 (1)()1f n f n +-?. ……………………………………8分 (Ⅲ)结论是)1(+n f )]2()([21++≤n f n f . 证明如下:由结论知,只需证 ).1()2()()1(+-+≤-+n f n f n f n f由(Ⅱ)知:)()1(n f n f -+表示的是1+n 的表示法中11a ¹的表示法数,)1()2(+-+n f n f 是2+n 的表示法中11a ¹的表示法数.考虑到21≥+n ,把一个11a ¹的1+n 的表示法中的p a 加上1,就可变为一个11a ¹的2+n 的表示法,这样就构造了从11a ¹的1+n 的表示法到11a ¹的2+n 的表示法的一个对应,所以有).1()2()()1(+-+≤-+n f n f n f n f ……………………………………14分。
2012年普通高等学校招生全国统一考试理数北京卷pdf版含答案

( )
∴= A1B 0 ,3,− 2 3 , A1E =(−2 ,−1,0)
设平面 A1BE 法向量为 n = ( x ,y ,z)
则
A1B
⋅
n
=0
A1E ⋅ n =0
∴
3
y
−
2
3z
= 0 ∴
z
=
3y 2
−2x − y =0
x
=
−y 2
( )
∴ n = −1,2 , 3
( ) 又∵ M −1,0 , 3
( ) ( ) ( ) (求: s2=
1 n
2
x1 − x +
2
x2 − x + +
xn
−
x
2
,其中
x
为数据
x1
,
x2
,…,
xn
的平均数)
18.(本小题共 13 分)
已知函数 f ( x) = ax2 + 1(a > 0) , g ( x=) x3 + bx . (1)若曲线 y = f ( x) 与曲线 y = g ( x) 在它们的交点 (1,c) 处具有公共切线,求 a ,b 的值;
4
5
6
7
8
答案
D
D
B
C
A
B
B
C
二、填空题
题号 答案
9
10
11
n2 + n
2
1;
4
4
12
13
14
3
1;1
(−4 ,− 2)
三、解答题 15.
解:
= f (x) (sin x − cos x)s= in 2x (sin x − cos x)2sin x= cos x 2(sin x − cos x) cos x
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市海淀区2012届高三上学期期末考试试题数 学(理)2012.01一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. (1)复数52i=+ ( ) (A )2i - (B )21i 55+ (C )105i - (D )105i 33- (2)如图,正方形ABCD 中,点E 是DC 的中点,点F 是BC 的一个三等分点.那么=EF(A )1123AB AD-(B )1142AB AD+(C )1132AB DA+(D )1223AB AD-(3)若数列{}n a 满足:119a =,13(*)n n a a n +=-∈N ,则数列{}n a 的前n 项和数值最大时,n 的值是(A )6 (B )7 (C )8 (D )9(4)已知平面α,β,直线l ,若αβ^,l αβ= ,则(A )垂直于平面β的平面一定平行于平面α (B )垂直于直线l 的直线一定垂直于平面α (C )垂直于平面β的平面一定平行于直线l (D )垂直于直线l 的平面一定与平面α,β都垂直(5)函数()sin(2)(,)f x A x A ϕϕ=+ R 的部分图象如图所示,那么(0)f = ( )(A )12-(B)2-(C )1- (D)-(6)执行如图所示的程序框图,输出的i 值为( )(A )5 (B )6 (C )7 (D )8(7)已知函数2()cos sin f x x x =+,那么下列命题中假命题...是 ( ) (A )()f x 既不是奇函数也不是偶函数 (B )()f x 在[,0]π-上恰有一个零点(C )()f x 是周期函数 (D )()f x 在(,2π5π)6上是增函数(8)点P 到图形C 上每一个点的距离的最小值称为点P 到图形C 的距离,那么平面内到定圆C 的距离与到定点A 的距离相等的点的轨迹不可能...是 ( )(A )圆 (B )椭圆 (C )双曲线的一支 (D )直线 二、填空题:本大题共6小题,每小题5分,共30分,把答案填在题中横线上.(9)51)的展开式中2x 的系数是 . (用数字作答)(10)若实数,x y 满足40,20,250,x y x y x y ì+- ïïï-- íïï+- ïïî则2z x y =+的最大值为 .(11)抛物线2x ay =过点1(1,)4A ,则点A 到此抛物线的焦点的距离为 .甲城市 乙城市(12)甲和乙两个城市去年上半年每月的平均气温(单位:C °)用茎叶图记录如下,根据茎叶图可知,两城市中平均温度较高的城市是____________,气温波动较大的城市是____________.(13)已知圆C :22(1)2x y -+=,过点(1,0)A -的直线l 将圆C 分成弧长之比为1:3的两段圆弧,则直线l 的方程为 . (14)已知正三棱柱'''ABC A B C -的正(主)视图和侧(左)视图如图所示. 设,'''ABC A B C ∆∆的中心分别是,'O O ,现将此三棱柱绕直线'OO 旋转,射线OA 旋转所成的角为x 弧度(x 可以取到任意一个实数),对应的俯视图的面积为()S x ,则函数()S x 的最大值为 ;最小正周期为 .8,3π说明:“三棱柱绕直线'OO 旋转”包括逆时针方向和顺时针方向,逆时针方向旋转时,OA 旋转所成的角为正角,顺时针方向旋转时,OA 旋转所成的角为负角.三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c , 2A B =,sin 3B =. (Ⅰ)求cos A 及sinC 的值; (Ⅱ)若2b =,求ABC ∆的面积.9 0 8 7 7 3 1 2 4 72 2 0 4 7侧(左)视图正(主)视图(16)(本小题满分13分)为加强大学生实践、创新能力和团队精神的培养,促进高等教育教学改革,教育部门主办了全国大学生智能汽车竞赛. 该竞赛分为预赛和决赛两个阶段,参加决赛的队伍按照抽签方式决定出场顺序.通过预赛,选拔出甲、乙等五支队伍参加决赛. (Ⅰ)求决赛中甲、乙两支队伍恰好排在前两位的概率;(Ⅱ)若决赛中甲队和乙队之间间隔的队伍数记为X ,求X 的分布列和数学期望.(17)(本小题满分14分)在四棱锥P ABCD -中,底面ABCD 是直角梯形,AB ∥CD ,90ABC ? ,2AB PB PC BC CD ====,平面PBC ^平面ABCD .(Ⅰ)求证:AB ^平面PBC ;(Ⅱ)求平面PAD 和平面BCP 所成二面角(小于90°)的大小; (Ⅲ)在棱PB 上是否存在点M 使得CM ∥平面PAD ?若存在,求PMPB的值;若不存在,请说明理由.(18)(本小题满分13分)已知函数2()e ()xf x x ax a =+-,其中a 是常数.PABC D(Ⅰ)当1a =时,求曲线()y f x =在点(1,(1))f 处的切线方程;(Ⅱ)若存在实数k ,使得关于x 的方程()f x k =在[0,)+∞上有两个不相等的实数根,求k 的取值范围.(19)(本小题满分14分)已知焦点在x 轴上的椭圆C 过点(0,1),Q 为椭圆C 的左顶点. (Ⅰ)求椭圆C 的标准方程; (Ⅱ)已知过点6(,0)5-的直线l 与椭圆C 交于A ,B 两点. (ⅰ)若直线l 垂直于x 轴,求AQB ∠的大小;(ⅱ)若直线l 与x 轴不垂直,是否存在直线l 使得QAB ∆为等腰三角形?如果存在,求出直线l 的方程;如果不存在,请说明理由.(20)(本小题满分14分)已知集合{1,2,3,,}(*)M n n = N ,若集合12{,,,}(*)m A a a a M m =臀N ,且对任意的b M Î,存在,(1)i j a a A i jm 危#,使得12i j b a a λλ=+(其中12,{1,0,1}λλ?),则称集合A 为集合M 的一个m 元基底.(Ⅰ)分别判断下列集合A 是否为集合M 的一个二元基底,并说明理由; ①{1,5}A =,{1,2,3,4,5}M =;②{2,3}A =,{1,2,3,4,5,6}M =.(Ⅱ)若集合A 是集合M 的一个m 元基底,证明:(1)m m n + ;(Ⅲ)若集合A 为集合{1,2,3,,19}M = 的一个m 元基底,求出m 的最小可能值,并写出当m 取最小值时M 的一个基底A .参考答案及评分标准 2012.01一. 选择题:本大题共8小题,每小题5分,共40分. 题号 (1) (2) (3) (4) (5) (6) (7) (8) 答案ADBDCABD二.填空题:本大题共6小题,每小题5分,共30分. (9)5 (10)7 (11)54(12)乙,乙(13)(1)3y x =+或(1)3y x =-+ (14)8;3π注:(13)题正确答出一种情况给3分,全对给5分;(12)、(14)题第一空3分;第二空2分.三.解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. (15)(本小题满分13分)解:(Ⅰ)因为2A B =,所以2cos cos 212sin A B B ==-. ………………………………………2分因为sin B =, 所以11cos 1233A =-?. ………………………………………3分 由题意可知,(0,)2B πÎ.所以cos B =………………………………………5分因为sin sin 22sin cos A B B B ===.………………………………………6分 所以sin sin[()]sin()C A B A B π=-+=+sin cos cos sin A B A B =+=. ………………………………………8分 (Ⅱ)因为sin sin b aB A=,2b =, ………………………………………10分=.所以3a =. ………………………………………11分所以1sin 29ABC S ab C ∆==. ………………………………………13分 (16)(本小题满分13分)解:(Ⅰ)设“甲、乙两支队伍恰好排在前两位”为事件A ,则()23!15!10P A ⨯==. ………………………………………4分 所以 甲、乙两支队伍恰好排在前两位的概率为110.………………………………………5分(Ⅱ)随机变量X 的可能取值为0, 1, 2, 3. ………………………………………6分()24!205!5P X ⨯===, ()323!315!10P X ⨯⨯===,()22!32!125!5P X ⨯⨯⨯===,()23!135!10P X ⨯===. ………………………………………10分随机变量X 的分布列为:因为 01231510510EX =⨯+⨯+⨯+⨯=,所以 随机变量X 的数学期望为1. ………………………………………13分(17)(本小题满分14分)(Ⅰ)证明:因为 90ABC? ,所以 AB BC ⊥. ………………………………………1分 因为 平面PBC ^平面ABCD ,平面PBC 平面ABCD BC =,AB Ì平面ABCD ,所以 AB ^平面PBC . ………………………………………3分 (Ⅱ)解:取BC 的中点O ,连接PO . 因为PB PC =, 所以 PO BC ⊥.因为 平面PBC ^平面ABCD ,平面PBC 平面ABCD BC =,PO Ì平面PBC , 所以 PO ^平面ABCD . ………………………………………4分 如图,以O 为原点,OB 所在的直线为x 轴,在平面ABCD 内过O 垂直于BC 的直线为y 轴,OP 所在的直线为z 轴建立空间直角坐标系O xyz -.不妨设2BC =.由 直角梯形ABCD 中2AB PB PC BC CD ====可得P ,(1,1,0)D -,(1,2,0)A .所以(1,DP =- ,(2,1,0)DA =.设平面PAD 的法向量(,,)=x y z m .因为 0,0.DP DAìï?ïíï?ïî m m所以(,,)(1,0,(,,)(2,1,0)0,x y z x y z ìï?=ïíï?ïî即0,20.x y x y ìï-+=ïíï+=ïî 令1x =,则2, y z =-=-所以(1,2,=--m . ………………………………………7分取平面BCP 的一个法向量n ()0,1,0=. 所以cos ,⋅==m n m n m n . 所以 平面ADP 和平面BCP 所成的二面角(小于90°)的大小为4π. ………………………………………9分 (Ⅲ)解:在棱PB 上存在点M 使得CM ∥平面PAD ,此时12PM PB =. 理由如 下: ………………………………………10分 取AB 的中点N ,连接CM ,CN ,MN . 则 MN ∥PA ,12AN AB =. 因为 2AB CD =,NMPABCD所以 AN CD =. 因为 AB ∥CD ,所以 四边形ANCD 是平行四边形. 所以 CN ∥AD .因为 , MN CN N PA AD A == ,所以 平面MNC ∥平面PAD . ………………………………………13分 因为 CM Ì平面MNC ,所以 CM ∥平面PAD . ………………………………………14分(18)(本小题满分13分)解:(Ⅰ)由2()e ()xf x x ax a =+-可得2'()e [(2)]xf x x a x =++. ………………………………………2分 当1a =时,(1)e f = ,'(1)4e f =. ………………………………………4分 所以 曲线()y f x =在点(1,(1))f 处的切线方程为()e 4e 1y x -=-,即4e 3e y x =-. ………………………………………5分 (Ⅱ) 令2'()e ((2))0xf x x a x =++=,解得(2)x a =-+或0x =. ………………………………………6分 当(2)0a -+≤,即2a ≥-时,在区间[0,)+∞上,'()0f x ≥,所以()f x 是[0,)+∞上的增函数.所以 方程()f x k =在[0,)+∞上不可能有两个不相等的实数根.………………………………………8分当(2)0a -+>,即2a <-时,()'(),f x f x 随x 的变化情况如下表由上表可知函数()f x 在[0,)+∞上的最小值为2((2))ea f a +-+=. ………………………………………10分 因为 函数()f x 是(0,(2))a -+上的减函数,是((2),)a -++∞上的增函数, 且当x a ≥-时,有()f x e ()aa a -≥->-. ………………………………………11分所以 要使方程()f x k =在[0,)+∞上有两个不相等的实数根,k 的取值范围必须是24(,]e a a a ++-. ……………………………………13分 (19)(本小题满分13分)解:(Ⅰ)设椭圆C 的标准方程为22221(0)x y a b a b+=>>,且222a b c =+.由题意可知:1b =,2c a =. ………………………………………2分 所以24a =.所以,椭圆C 的标准方程为2214x y +=. ……………………………………3分 (Ⅱ)由(Ⅰ)得(2,0)Q -.设1122(,),(,)A x y B x y . (ⅰ)当直线l 垂直于x 轴时,直线l 的方程为65x =-. 由226,514x x y ⎧=-⎪⎪⎨⎪+=⎪⎩ 解得:6,545x y ⎧=-⎪⎪⎨⎪=⎪⎩或6,54.5x y ⎧=-⎪⎪⎨⎪=-⎪⎩即6464(,), (,)5555A B ---(不妨设点A 在x 轴上方).………………………………………5分则直线AQ 的斜率1AQ k =,直线BQ 的斜率1BQ k =-. 因为 1AQ BQ k k ⋅=-, 所以 AQ BQ ^.所以 2AQB π∠=. ………………………………………6分 (ⅱ)当直线l 与x 轴不垂直时,由题意可设直线AB 的方程为6()(0)5y k x k =+≠.由226(),514y k x x y ⎧=+⎪⎪⎨⎪+=⎪⎩消去y 得:2222(25100)2401441000k x k x k +++-=. 因为 点6(,0)5-在椭圆C 的内部,显然0∆>. 21222122240,25100144100.25100k x x k k x x k ⎧+=-⎪⎪+⎨-⎪=⎪+⎩………………………………………8分 因为 1122(2,), (2,)QA x y QB x y =+=+ ,116()5y k x =+,226()5y k x =+,所以 1212(2)(2)QA QB x x y y ⋅=+++121266(2)(2)()()55x x k x k x =++++⋅+ 2221212636(1)(2)()4525k x x k x x k =++++++ 2222222144100624036(1)(2)()402510052510025k k k k k k k -=+++-++=++. 所以 QA QB ⊥.所以 QAB ∆为直角三角形. ………………………………………11分 假设存在直线l 使得QAB ∆为等腰三角形,则QA QB =取AB 的中点M ,连接QM ,则QM AB ^.记点6(,0)5-为N . 另一方面,点M 的横坐标22122212024225100520M x x k k x k k+==-=-++, 所以 点M 的纵坐标266()5520M M ky k x k=+=+. 所以 222221016666(,)(,)520520520520k k k QM NMk k k k+? ++++222601320(520)k k += +. 所以 QM 与NM不垂直,矛盾.所以 当直线l 与x 轴不垂直时,不存在直线l 使得QAB ∆为等腰三角形.………………………………………13分(20)(本小题满分14分)解:(Ⅰ)①{1,5}A =不是{1,2,3,4,5}M =的一个二元基底.理由是 1212315(,{1,0,1})λλλλ棺+孜-;②{2,3}A =是{1,2,3,4,5,6}M =的一个二元基底. 理由是 11213,21203,30213=-????? , 41212,51213,61313=????? .………………………………………3分 (Ⅱ)不妨设12m a a a <<< ,则 形如10i j a a ? (1)ij m # 的正整数共有m 个; 形如11ii a a ? (1)im #的正整数共有m 个;形如11i j a a ? (1)ij m ? 的正整数至多有2mC 个; 形如(1)1i j a a -? (1)ij m ? 的正整数至多有2mC 个. 又集合{1,2,3,,}M n = 含n 个不同的正整数,A 为集合M 的一个m 元基底. 故22m m m m C C n +++ ,即(1)m m n + . ………………………………………8分 (Ⅲ)由(Ⅱ)可知(1)19m m + ,所以4m ³.当4m =时,(1)191m m +-=,即用基底中元素表示出的数最多重复一个. * 假设1234{,,,}A a a a a =为{1,2,3,,19}M = 的一个4元基底, 不妨设1234a a a a <<<,则410a ³. 当410a =时,有39a =,这时28a =或7.如果28a =,则由1109,198,1899,18108=-=-=+=+,与结论*矛盾. 如果27a =,则16a =或5.易知{6,7,9,10A =和{5,7,9,10}A =都不是{1,2,3,,19M = 的4元基底,矛盾. 当411a =时,有38a =,这时27a =,16a =,易知{6,7,8,11}A =不是{1,2,3,,19M = 的4元基底,矛盾.当412a =时,有37a =,这时26a =,15a =,易知{5,6,7,12}A =不是{1,2,3,,19M = 的4元基底,矛盾.当413a =时,有36a =,25a =,14a =,易知{4,5,6,1A =不是{1,2,3,,1M = 的4元基底,矛盾. 当414a =时,有35a =,24a =,13a =,易知{3,4,5,1A =不是{1,2,3,,M = 的4元基底,矛盾.当415a =时,有34a =,23a =,12a =,易知{2,3,4,1A =不是{1,2,3,,1M = 的4元基底,矛盾. 当416a =时,有33a =,22a =,11a =,易知{1,2,3,16}A =不是{1,2,3,,M = 的4元基底,矛盾.当417a ³时,A 均不可能是M 的4元基底.当5m =时,M 的一个基底{1,3,5,9,16}A =;或{3,7,8,9,10};或{4,7,8,9,10}等,只要写出一个即可.综上,m 的最小可能值为5. ………………………………………14分。
