第四版运筹学部分课后习题解答
运筹学(胡运权第四版及答案)

主讲:谢先达
2014.09
联系方式 办公室:QL643 87313663 手机: 13600512360 邮箱: xxdhz@
绪
论
绪论
什么是运筹学?
运筹学发展历史 运筹学主要内容 运筹学的基本特征与基本方法
绪论
什么是运筹学?
定义:为决策机构在对其控制下业务活动进行决策 时,提供以数量化为基础的科学方法。
概念:可行解、最优解、最优值
第一章:线性规划及单纯形法
练习:靠近某河流有两个化工厂,流经第一化工厂的河流流量为每天 500万m3,在两个工厂之间有一条流量为每天200万m3支流,第一化工厂每 天排放含有某种有害物质的工业污水2万m3 ,第二化工厂每天排放这种 工业污水1.4万m3 。从第一化工厂排出的工业污水流到第二化工厂以前, 有20%可自净化。根据环保要求,河流中工业污水的含量应不大于0.2%, 这两个工厂都需各自处理一部分工业污水,第一化工厂处理工业污水的 成本是1000元/万m3 。第二化工厂处理污水的的成本是800元/万m3 。现 问在满足环保要求的条件下,每厂各应处理多少工业污水,使这两个工 厂总的处理工业污水费用最小。
-x1+x2+x3 = 4
-2x1+x2-x3 ≤ 6 x1 ≤ 0,x2 ≥ 0, x3取值无约束
第一章:线性规划及单纯形法
线性规划问题及其数学模型 线性规划图解法
单纯形法原理
单纯形法计算步骤
单纯形法的进一步讨论
第一章:线性规划及单纯形法
x2
目标函数: 约束条件: maxz=50x1+100x2 x1+x2≤300 2x1+x2≤400 x2≤250 x1≥0 ,x2≥0
第四版运筹学部分课后习题解答

运筹学部分课后习题解答P47 1.1 用图解法求解线性规划问题a)12121212min z=23466 ..424,0x xx xs t x xx x++≥⎧⎪+≥⎨⎪≥⎩解:由图1可知,该问题的可行域为凸集MABCN,且可知线段BA上的点都为最优解,即该问题有无穷多最优解,这时的最优值为min 3z=23032⨯+⨯=P47 1.3 用图解法和单纯形法求解线性规划问题a)12121212max z=10x5x349 ..528,0x xs t x xx x++≤⎧⎪+≤⎨⎪≥⎩解:由图1可知,该问题的可行域为凸集OABCO,且可知B点为最优值点,即112122134935282xx xx x x=⎧+=⎧⎪⇒⎨⎨+==⎩⎪⎩,即最优解为*31,2Tx⎛⎫= ⎪⎝⎭这时的最优值为max335z=101522⨯+⨯=单纯形法: 原问题化成标准型为121231241234max z=10x 5x 349..528,,,0x x x s t x x x x x x x +++=⎧⎪++=⎨⎪≥⎩ j c →105B CB Xb 1x2x3x4x0 3x 9 3 4 1 0 04x8[5] 2 0 1 j j C Z -105 0 0 0 3x 21/5 0 [14/5] 1 -3/5 101x8/51 2/5 0 1/5 j j C Z -1 0 -2 5 2x 3/2 0 1 5/14 -3/14 101x11 0 -1/72/7j j C Z --5/14 -25/14所以有*max 33351,,1015222Tx z ⎛⎫==⨯+⨯= ⎪⎝⎭P78 2.4 已知线性规划问题:1234124122341231234max24382669,,,0z x x x x x x x x x x x x x x x x x x x =+++++≤⎧⎪+≤⎪⎪++≤⎨⎪++≤⎪≥⎪⎩求: (1) 写出其对偶问题;(2)已知原问题最优解为)0,4,2,2(*=X ,试根据对偶理论,直接求出对偶问题的最优解。
运筹学基础及应用第四版胡运权主编课后练习答案

运筹学基础及应用习题解答z 3。
(b)用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解。
(a)约束方程组的系数矩阵12 3 6 3 0A 8 1 4 0 23 0 0 0 0基基解是否基可行解目标函数值X1 X2 X3 X4 X5 X6P1 P2 P3163 7-60 0 0否P1 P2 P4 0 10 0 7 0 0 是10P1 P2 P50 3 0 0 72是 3习题一P46x i1-的所有X i,X2,此时目标函数值o(b)约束方程组的系数矩阵A 12 3 4A2 2 12⑻(1)图解法基 基解 是否基可行解 目标函数值X 1X 2X 3X 4P 1P 24 11否"2P 1P 3 2 0 110 是435 ~5~5P 1P 4111否—36P 2P 312是52P 2P 41否22P 3P 40 0 1 1是5最优解xT2 11 5吋omax z 10x 1 5x 2 0x 3 0x 4 3x i 4X 2 X 3st. 5x 1 2x 2 x 48 9 8 12。
min—,— — 5 3 5C j 105 0 0 C B基b X 1X 2X 3X 421143 0 X 3— 1—"5"5582110X 11C j 105 0 0 C B 基bX 1 X 2 X 3 X 4 0 X 3 9 341 0 0X 48[5] 20 1 C j Z j105令 X iX 20,0,9,8,由此列出初始单纯形表最优解即为3x1 4x2 9的解x5x 1 2x 2 81,-,最大值z 竺 2 2(2)单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式则P 3,P 4组成一个基。
得基可行解xC j Z j0 1221 8320,min14 22新的单纯形表为C j 105 0 0 C B基b X 1X 2X 3X 435 3 5X 2— 01— —2141410X 11121—7525c jZ j14 143*35x i 1, x 2 - , X 3 0, X 4 0。
[运筹学第四版课后答案]课后答案
![[运筹学第四版课后答案]课后答案](https://img.taocdn.com/s3/m/24ea5b5d814d2b160b4e767f5acfa1c7aa008294.png)
[运筹学第四版课后答案]课后答案课后答案一:《蜀道难》课后题答案《蜀道难》课后题答案一、这是一首乐府诗,以七言为主,却有不少杂言句,节奏多变化,与散文句法相似。
试给下面的诗句划分节奏,朗读几遍,说说它们对本诗的风格起什么作用。
1.噫吁戏,危乎高哉!蜀道之难,难于上青天!2.上有六龙回日之高标,下有冲波逆折之回川。
3.其险也如此,嗟尔远道之人胡为乎来哉!4.剑阁峥嵘而崔嵬,一夫当关,万夫莫开。
解题指导这首诗较长,且内容有一定难度所以先设计此题,目的是使你初步适应这首诗节奏的变化。
在完成本题时你一定要朗读几遍,读出一点韵味来。
但要注意:不要把这些句子读成散文,这对领会诗人炽烈奔放的感情和飘逸的风格极为必要。
这是一首杂言体诗,但跟其他诗人的这类体裁作品和李白的另一些这类体裁作品(如《将进酒》《梁甫吟》《庐山谣寄卢待御虚舟》等)相比,都有显著的不同。
这不同就在于:其中的某些句子,如练习中所列举的,如果孤立地看,确属散文句。
但我们不这样称它们,因为它们毕竟是诗的整体中的一部分,只能说它们是散文化的诗句,或句法与散文近似。
这当然不能随意而为,没有李白那样的气概,那样的英才,是驾驭不了的。
参考答案这些诗句都仿佛是诗人在炽烈感情的驱动下,不能自已,脱口而出,生动地表现了诗人奔放豪迈的风格。
二、“蜀道之难,难于上青天”这句诗有什么含义它重复出现三次,有什么作用解题指导这道题是为鉴赏诗的内容设计的。
重点是前一问,后一问是对前一问的补充,意思是可以从形式入手鉴赏诗的内容。
因此在完成本题时,你可以先思考后一问,然后分析“蜀道之难”一句的含义。
此题有一定的难度,你最好先理清课文的结构层次并了解诗的大意,在此基础上完成本题。
李白善于从民歌中吸取养料。
这首诗中“一咏三叹”的写法,明显地是对《诗经》中复沓形式的继承,同时又有很大的发展。
这一特点同你已学过的《君子于役》《无衣》等相同。
参考答案诗人创造性地继承了古代民歌中常见的复沓形式(又称反复),主旨句凡三见:开头、中间、结尾各出现一次。
运筹学基础及指导应用第四版胡运权主编课后练习问题详解
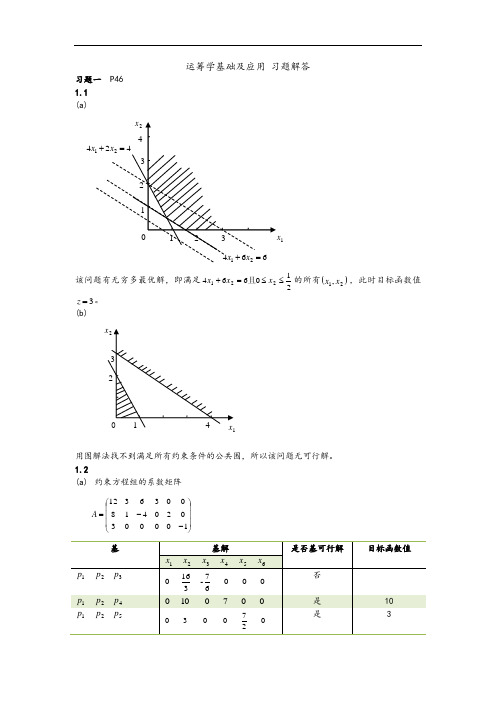
运筹学基础及应用 习题解答习题一 P46 1.1 (a)该问题有无穷多最优解,即满足210664221≤≤=+x x x 且的所有()21,x x ,此时目标函数值3=z 。
(b)用图解法找不到满足所有约束条件的公共围,所以该问题无可行解。
1.2(a) 约束方程组的系数矩阵⎪⎪⎪⎭⎫ ⎝⎛--=1000030204180036312A4最优解()T x 0,0,7,0,10,0=。
(b) 约束方程组的系数矩阵⎪⎪⎭⎫⎝⎛=21224321A最优解Tx ⎪⎭⎫⎝⎛=0,511,0,52。
1.3(a)(1) 图解法最优解即为⎩⎨⎧=+=+8259432121x x x x 的解⎪⎭⎫⎝⎛=23,1x ,最大值235=z(2)单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式 ⎩⎨⎧=++=+++++=825943 ..00510 max 4213214321x x x x x x t s x x x x z则43,P P 组成一个基。
令021==x x得基可行解()8,9,0,0=x ,由此列出初始单纯形表 21σσ>。
5839,58min =⎪⎭⎫ ⎝⎛=θ02>σ,2328,1421min =⎪⎭⎫ ⎝⎛=θ0,21<σσ,表明已找到问题最优解0 , 0 , 231,4321====x x x x 。
最大值 235*=z (b)(1) 图解法最优解即为⎩⎨⎧=+=+524262121x x x x 的解⎪⎭⎫⎝⎛=23,27x ,最大值217=z(2) 单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式1234523124125max 2000515.. 62245z x x x x x x x s t x x x x x x =+++++=⎧⎪++=⎨⎪++=⎩21=+x x 2621+x x则3P ,4P ,5P 组成一个基。
令021==x x得基可行解()0,0,15,24,5x =,由此列出初始单纯形表21σσ>。
管理运筹学(第四版)第三章习题答案

3.1(1)解:, 53351042..715min 212112121≥≥+≥≥++=y y y y y y y t s y y ω(2)解:无限制32132131323213121,0,0 2520474235323..86max y y y y y y y y y y y y y y y t s y y ≤≥=++≤-=+≥+--≤++=ω3.4解:例3原问题6,,1,0603020506070..min 166554433221654321 =≥≥+≥+≥+≥+≥+≥++++++=j x x x x x x x x x x x x x t s x x x x x x z j对偶问题:6,,1,0111111..603020506070max 655443322161654321 =≥≤+≤+≤+≤+≤+≤++++++=j y y y x y y y y y y y y y t s y y y y y y j ω3.5解:(1)由最优单纯形表可以知道原问题求max ,其初始基变量为54,x x ,最优基的逆阵为⎪⎪⎪⎪⎭⎫ ⎝⎛-=-31610211B 。
由P32式(2.16)(2.17)(2.18)可知b B b 1-=',5,,1,,1 ='-=='-j P C c P B P j B j j j j σ,其中b 和j P 都是初始数据。
设⎪⎪⎭⎫ ⎝⎛=21b b b ,5,,1,21 =⎪⎪⎭⎫⎝⎛=j a a P j j j ,()321,,c c c C =,则⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫ ⎝⎛-⇒='-25253161021211b b b B b ,即⎪⎩⎪⎨⎧=+-=2531612521211b b b ,解得⎩⎨⎧==10521b b ⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎭⎫⎝⎛-⇒='-0211121031610212322211312111a a a a a a P B P j j ,即 ⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧=+-=-=+-==+-=03161121213161212113161021231313221212211111a a a a a a a a a ,解得⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧==-====121130231322122111a a a a a a()()()⎪⎪⎪⎪⎭⎫⎝⎛---=---⇒'-=31612102121,0,0,2,4,4132c c c P C c j B j j σ,即 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-=--=+--=+-2314612142121113132c c c c c c ,解得⎪⎩⎪⎨⎧==-=6102132c c c所以原问题为:,, 10352..1026max 32132132321≥≤+-≤++-=x x x x x x x x t s x x x z 对偶问题为:, 102263..105min 212121221≥≥+-≥-≥+=y y y y y y y t s y y ω(2)由于对偶问题的最优解为()()()2,4,,5454*=-=-=σσσc c C Y IB IB3.6解:(1)因为3x 的检验数0353≤⨯-c ,所以3c 的可变范围是153≤c 。
《管理组织运筹学》第四版课后知识题目解析
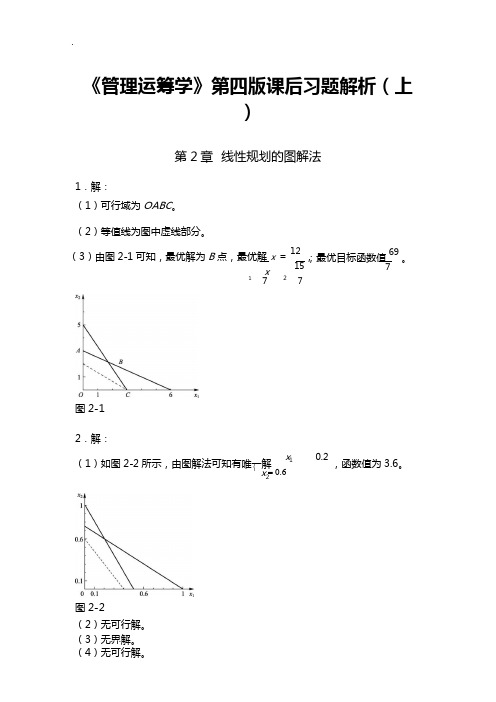
.⎨= 0.6《管理运筹学》第四版课后习题解析(上)第2章 线性规划的图解法1.解:(1)可行域为OABC 。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B 点,最优解 x =12,x15 1727图2-1 ;最优目标函数值 69。
72.解:(1)如图2-2所示,由图解法可知有唯一解 x 10.2,函数值为3.6。
x 2图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
.⎨(5)无穷多解。
x(6)有唯一解 1203 ,函数值为 92 。
8 3 x 233.解:(1)标准形式max f3x 12x 20s 10s 20s 39x 1 2x 2 s 1 30 3x 1 2x 2 s 2 13 2x 12x 2s 39x 1, x 2 , s 1, s 2 , s 3 ≥ 0(2)标准形式min f4x 16x 20s 10s 23x 1 x 2s 1 6 x 12x 2s 210 7x 1 6x 24x 1, x 2 , s 1, s 2 ≥ 0(3)标准形式minfx 12x 22x 20s 1 0s23x 1 5x 25x 2s1702x 15x 25x250 3x 12x 22x 2s 230x 1, x 2, x 2, s 1, s 2 ≥ 04.解:.标准形式max z 10x1 5x2 0s1 0s2 3x1 4x2s1 95x1 2x2 s2 8x1, x2 , s1, s2 ≥0.≤松弛变量(0,0)最优解为 x 1 =1,x 2=3/2。
5.解:标准形式min f11x 18x 20s 10s 20s 310x 1 2x 2 s 1 20 3x 1 3x 2 s 2 18 4x 19x 2s 336x 1, x 2 , s 1, s 2 , s 3 ≥ 0剩余变量(0, 0, 13) 最优解为 x 1=1,x 2=5。
6.解:(1)最优解为 x 1=3,x 2=7。
《管理运筹学》第四版课后习题解析[下]
![《管理运筹学》第四版课后习题解析[下]](https://img.taocdn.com/s3/m/97cbd28969dc5022aaea006f.png)
给 标号 ,同理 标号 。得到最短路线为 ,最短时间为1.35小时。
4.解:
以 为起始点, 标号为 ;
,
边集为 =
且有
所以, 标号(4,1)。
则 ,
边集为
且有
所以, 标号(5,1)。
则 ,
边集为
且有
所以, 标号(7,2)。
则 ,
边集为
且有
所以, 、 标号(8,2)。
则 ,
边集为
且有
所以, 标号(9,4)。
则 ,
边集为
且有
所以, 标号(11.5,6)。
则 ,
边集为
且有
所以, 标号(12,7)。
, 为空集。
所以,最短路径为
5.解:
(1)从 出发,令 ={ },其余点为 ,给 标号 。 的所有边为 ,
累计距离最小为 ,给 标号为 ,令 。
(2) 的所有边为 ,累计距离最小为 ,令 。
(2)
图解法求解如图9-1所示,目标1,2可以达到,目标3达不到,所以有满意解为A点(150,120)。
6、解:
假设甲乙两种产品量为x1,x2,建立数学规划模型如下。
用管理运筹学软件求解得:
所以,甲乙两种产品量分别为8.333吨,3.333吨,该计划内的总利润为250元。
7、解:
设该汽车装配厂为达到目标要求生产产品A 件,生产产品B 件。
图解法略,求解得 。
(2)目标规划模型如下。
图解法略,求解得 。
由此可见,所得结果与(1)中的解是不相同的。
(3)加权目标规划模型如下,
求解得 。
9、解:
假设甲乙两种洗衣机的装配量分别是x1,x2,建立数学规划模型如下。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运筹学部分课后习题解答P47 1、1 用图解法求解线性规划问题a) 12121212min z=23466..424,0x x x x s t x x x x ++≥⎧⎪+≥⎨⎪≥⎩解:由图1可知,该问题的可行域为凸集MABCN,且可知线段BA 上的点都为最优解,即该问题有无穷多最优解,这时的最优值为min3z =23032⨯+⨯=P47 1、3 用图解法与单纯形法求解线性规划问题a)12121212max z=10x 5x 349..528,0x x s t x x x x ++≤⎧⎪+≤⎨⎪≥⎩ 解:由图1可知,该问题的可行域为凸集OABCO,且可知B 点为最优值点,即112122134935282x x x x x x =⎧+=⎧⎪⇒⎨⎨+==⎩⎪⎩,即最优解为*31,2Tx ⎛⎫= ⎪⎝⎭这时的最优值为max 335z =101522⨯+⨯=单纯形法:原问题化成标准型为121231241234max z=10x 5x 349..528,,,0x x x s t x x x x x x x +++=⎧⎪++=⎨⎪≥⎩ j c →105B CB X b 1x2x3x4x0 3x 9 3 4 1 0 04x8[5] 2 0 1 j j C Z -105 0 0 0 3x 21/5 0 [14/5] 1 -3/5 101x8/51 2/5 0 1/5 j j C Z -1 0 -2 5 2x 3/2 0 1 5/14 -3/14 101x11 0 -1/72/7j j C Z --5/14 -25/14所以有*max 33351,,1015222Tx z ⎛⎫==⨯+⨯= ⎪⎝⎭P78 2、4 已知线性规划问题:1234124122341231234max24382669,,,0z x x x x x x x x x x x x x x x x x x x =+++++≤⎧⎪+≤⎪⎪++≤⎨⎪++≤⎪≥⎪⎩求: (1) 写出其对偶问题;(2)已知原问题最优解为)0,4,2,2(*=X ,试根据对偶理论,直接求出对偶问题的最优解。
解:(1)该线性规划问题的对偶问题为:1234124123434131234min8669223411,,,0w y y y y y y y y y y y y y y y y y y y =+++++≥⎧⎪+++≥⎪⎪+≥⎨⎪+≥⎪≥⎪⎩(2)由原问题最优解为)0,4,2,2(*=X ,根据互补松弛性得:12412343422341y y y y y y y y y ++=⎧⎪+++=⎨⎪+=⎩把)0,4,2,2(*=X 代入原线性规划问题的约束中得第四个约束取严格不等号,即4224890y ++=<⇒=从而有12123322341y y y y y y +=⎧⎪++=⎨⎪=⎩得123443,,1,055y y y y ====所以对偶问题的最优解为*43(,,1,0)55T y =,最优值为min 16w =P79 2、7 考虑如下线性规划问题:123123123123123min 6040803224342223,,0z x x x x x x x x x x x x x x x =++++≥⎧⎪++≥⎪⎨++≥⎪⎪≥⎩(1)写出其对偶问题;(2)用对偶单纯形法求解原问题; 解:(1)该线性规划问题的对偶问题为:123123123123123max 2433426022403280,,0w y y y y y y y y y y y y y y y =++++≤⎧⎪++≤⎪⎨++≤⎪⎪≥⎩(2)在原问题加入三个松弛变量456,,x x x 把该线性规划问题化为标准型:123123412351236max 60408032243422230,1,,6j z x x x x x x x x x x x x x x x x j =------+=-⎧⎪---+=-⎪⎨---+=-⎪⎪≥=⎩L*max (,,0),604080063633T x z ==⨯+⨯+⨯=P81 2、12 某厂生产A 、B 、C 三种产品,其所需劳动力、材料等有关数据见下表。
要求:(a)确定获利最大的产品生产计划;(b)产品A 的利润在什么范围内变动时,上述最优计划不变;(c)如果设计一种新产品D,单件劳动力消耗为8单位,材料消耗为2单位,每件可获利3元,问该种产品就是否值得生产? (d) 如果劳动力数量不增,材料不足时可从市场购买,每单位0、4 元。
问该厂要不要购进原材料扩大生产,以购多少为宜。
解:由已知可得,设j x 表示第j 种产品,从而模型为:123123123123max 3463545..34530,,0z x x x x x x s t x x x x x x =++++≤⎧⎪++≤⎨⎪≥⎩ a) 用单纯形法求解上述模型为:得到最优解为*(5,0,3)T x =;最优值为max 354327z =⨯+⨯=b)设产品A 的利润为3λ+,则上述模型中目标函数1x 的系数用3λ+替代并求解得:要最优计划不变,要求有如下的不等式方程组成立20310533053λλλ⎧-+≤⎪⎪⎪--≤⎨⎪⎪-+≤⎪⎩解得:3955λ-≤≤从而产品A的利润变化范围为:39 3,355⎡⎤-+⎢⎥⎣⎦,即242,455⎡⎤⎢⎥⎣⎦C)设产品D用6x表示,从已知可得16661/5Bc c B Pσ-=-='1661128334122555P B P-⎡⎤-⎡⎤⎢⎥⎡⎤⎢⎥===⎢⎥⎢⎥⎢⎥-⎣⎦⎢⎥-⎣⎦⎢⎥⎣⎦把6x加入上述模型中求解得:jc→ 3 1 4 0 0 3 BCBX b1x2x3x4x5x6x31x5 1 -1/3 0 1/3 -1/3 [2]43x3 0 1 1 -1/5 2/5 -4/5j jC Z-0 -2 0 -1/5 -3/5 1/536x5/2 1/2 -1/6 0 1/6 -1/6 143x5 2/5 13/15 1 -1/15 4/15 0j jC Z--1/10 -59/30 0 -7/30 -17/30 0从而得最优解*(0,0,5,0,0,5/2)Tx=;最优值为max45327.5272z=⨯+⨯=>所以产品D值得生产。
P101 3、1已知运输问题的产销量与单位运价如下表所示,用表上作业法求各题的最优解及最小运费。
表3-35B 1 B 2 B 3 B 4 产量 A 1 A 2 A 3 10 12 2 2 7 14 20 9 16 11 20 18 15 25 5 销量5151510解:因为∑∑===4131j j i i b a ,即产销平衡、所以由已知与最小元素法可得初始方案为B1 B2 B3 B4 产量 A1A2 A3 515 0 15 0 10 15 25 5 销量5151510检验:产地 销地 产地 销地B1 B2 B3 B4 产量A1A2A35 1515 1015255销量 5 15 15 10检验:B1 B2 B3 B4 产量A1A2A35 51015 1015255 销量 5 15 15 10 检验:产地销地产地销地从上表可以瞧出所有的检验数都大于零,即为最优方案 最小运费为:min 25257109151110180335z =⨯+⨯+⨯+⨯+⨯+⨯=表 B 1 B 2 B 3 B 4 产量 A 1 A 2 A 3 8 6 5 4 9 3 1 4 4 2 7 3 7 25 26 销量10102015解:因为34115855i j i j a b ===>=∑∑,即产大于销,所以需添加一个假想的销地,销量为3,构成产销平衡问题,其对应各销地的单位运费都为0。
B1 B2B3B4B5 产量 A1A2 A3 8 6 54 9 31 4 42 7 30 0 0 7 25 26 销量10 10 20 153由上表与最小元素法可得初始方案为 B1 B2 B3 B4 B5 产量 A1A2 A3 9 1 107 13 1537 25 26 销量1010 2015 3检验:产地 销地 产地 销地产地 销地从上表可以瞧出所有的检验数都大于零,即为最优方案最小运费为:min 69513101741331503193z =⨯+⨯+⨯+⨯+⨯+⨯+⨯=表3-37B1 B2 B3 B4 B5 产量 A1A2 A3 8 5 6 6 M 3 3 8 9 7 4 6 5 7 8 20 30 30 销量2525201020解:因为351180100i j i j a b ===<=∑∑,即销大于产,所以需添加一个假想的产地,产量为20,构成产销平衡问题,其对应各销地的单位运费都为0。
B1 B2 B3 B4 B5 产量 A1A2 A3 A4 8 5 6 0 6 M 3 0 3 8 9 0 7 4 6 0 5 7 8 0 20 30 30 20 销量2525201020由上表与最小元素法可得初始方案为 B1 B2 B3 B4 B5 产量 A1A2 A3 A4 5 202520 01015 520 30 30 20 销量25 25 20 10 20检验:产地 销地产地 销地产地 销地B1 B2 B3 B4 B5 产量A1A2A3A420525 2010 51520303020 销量25 25 20 10 20B1 B2 B3 B4 B5 产量A1A2A3A420525 2010 02020303020 销量25 25 20 10 20产地销地产地销地从上表可以瞧出所有的检验数都大于零,即为最优方案最小运费为:min 320520410653258002000305z =⨯+⨯+⨯+⨯+⨯+⨯+⨯+⨯=P127 4、8 用割平面法求解整数规划问题。
a) 12121212max 7936735,0,z x x x x x x x x =+-+≤⎧⎪+≤⎨⎪≥⎩且为整数解:该问题的松弛问题为:12121212max 7936735,0z x x x x x x x x =+-+≤⎧⎪+≤⎨⎪≥⎩:j c →7 9 0 0 B C B Xb1x 2x 3x 4x9 2x 7/2 0 1 7/22 1/2271x9/2 10 -1/22 3/22 j j C Z --28/11 -15/11割平面1为:234(31/2)(07/22)(01/22)x x x +=++++3421713022222x x x ⇒--=-≤34571122222x x x ⇒+-= 从而有割平面2为:145(44/7)(01/7)(16/7)x x x +=+++-+451541640x x x x ⇒--=--≤456164x x x ⇒+-=4x4 0 0 0 1 6 -7j jC Z-0 0 0 0 -2 -7,即()*4,3Tx=,最优值为max749355z=⨯+⨯=P144 5、3 用图解分析法求目标规划模型c)解:由下图可知,满足min d1-的满意解为区域X2CDX1;满足min d2+的满意解为闭区域BCDEB;满足min2d3-的满意解为图中的A 点,满足min d4-的满意解为图中的 A 点,所以该问题的满意解为图中的点A(24,26) 。
