极点极线及高中圆锥曲线必备公式

合集下载

圆锥曲线极点极线定理

圆锥曲线极点极线定理圆锥曲线极点极线定理1. 引言圆锥曲线是平面解析几何中的重要概念之一，它包括椭圆、双曲线和抛物线三种类型。

在研究圆锥曲线的性质时，极点和极线是不可避免的概念。

本文将介绍圆锥曲线的极点极线定理，该定理是描述圆锥曲线中极点和极线之间关系的重要结论。

2. 极点和极线的定义在平面直角坐标系中，设有一条直线L和一个点P(x0,y0)。

若从P到L上每一点所引的直线与L垂直，则称P为L的极点，L为P的极线。

3. 圆锥曲线的定义设有一个平面内固定点F（称为焦点）和一条固定直线d（称为准线）。

对于任意一点P，分别以PF和PD（D为d上任意一点）为半径作两个圆，并将这两个圆相切于P处。

则所有这样的P所构成的集合称为圆锥曲线。

4. 圆锥曲线中极点与极轴间关系对于任意一条圆锥曲线，设其焦点为F，准线为d，P为任意一点，则有以下结论：（1）若P在焦点F上，则其极线为准线d；（2）若P在准线d上，则其极线为过该点且垂直于准线的直线；（3）若P不在焦点F和准线d上，则其极轴为PF的中垂线。

5. 圆锥曲线中极轴与极径间关系对于任意一条圆锥曲线，设其焦点为F，准线为d，O为坐标系原点，则有以下结论：（1）若O在焦点F上，则其极径是任意一条过O的直线；（2）若O在准线d上，则其极径是与准线垂直且经过O的直线；（3）若O不在焦点F和准线d上，则其极径是从O出发经过圆锥曲线上任意一点P的直线。

6. 圆锥曲线中两个互异的定理对于任意一条圆锥曲线，设其焦点为F，准线为d，P(x,y)为任意一点。

则有以下两个互异的定理：（1）以FP和PD分别为半径的两个圆相交于点P，则P在圆锥曲线上；（2）以FP和PD分别为半径的两个圆相切于点P，则P在圆锥曲线上。

7. 结论综上所述，圆锥曲线极点极线定理是描述圆锥曲线中极点和极线之间关系的重要结论。

在研究圆锥曲线的性质时，该定理具有重要意义。

一点一线一世界——高考命题中圆锥曲线的极点与极线

线犾上任一点作抛物线的两条切线，则直犕，犖为切点，线犕犖恒过定点．解析：因为抛物线的准线和焦点刚好是一对极点和极线，由定理第（）条知直线犕犖恒过焦点犉（）４１，０．
，动直线犾与椭圆犫＞０）只有一个公共点犘，且犆点犘在第一象限．（ Ⅰ ）已知直线犾的斜率为犽，用犪，犫，犽表示点犘的坐标；图１
）所对应的准线．对于双曲线和抛物线结论类似．犉（犮，０焦点与准线是圆锥曲线的统一定义，我们很多人只知道它的存在，却不知道它们内在的联系，教材中潜形匿迹，但我们也不能对此视而不见，我们也可借此解题．
２例２已知抛物线狔过直＝４狓和直线犾：狓＝－１，
１１２２）即２犕犖的方程为（狋＝ ·２狋狓＋１，狋狓－狔－狋狔＋２２
２２２４狋－狋＋２－狋｜于是犱＝｜＋２＝０，＝２２１＋４狋槡２（），则犱＝＝１＋４狋狊 ≥１
槡
２２（）１＋狋令２．狊１＋４狋
— —极点与极线在高考解题中的３洗尽铅华 — 应用
在近年的各地高考模拟试题中，有关圆锥事实上，曲线的极点与极线问题也屡见不鲜．用普通方法可以
·６４·
数学教育研究
２０１５年第１期
求解，但过程相对繁杂，如果用极点和极线的视角看问题，则事半功倍．定值问题３．１可以解决圆锥曲线中的定点、例３（２０１４稽阳联谊学校高三数学联考２１题）

备战高考数学二轮复习常用的圆锥曲线公式总结

备战 2019 年高考数学二轮复习常用的圆锥曲线公式总结圆锥曲线包含圆，椭圆，双曲线，抛物线。

以下是常用的圆锥曲线公式总结，请考生实时学习。

抛物线： y = ax *+ bx + c就是 y 等于 ax 的平方加上bx 再加上ca0 时张口向上a0 时张口向下c = 0 时抛物线经过原点b = 0 时抛物线对称轴为y 轴还有极点式y = a(x+h)* + k就是 y 等于 a 乘以 (x+h) 的平方 +k-h 是极点坐标的xk 是极点坐标的y一般用于求最大值与最小值抛物线标准方程:y^2=2px它表示抛物线的焦点在x 的正半轴上 ,焦点坐标为 (p/2,0) 准线方程为 x=-p/2因为抛物线的焦点可在随意半轴,故共有标准方程y^2=2px y^2=-2px x^2=2py x^2=-2py圆：体积 =4/3(pi)(r^3)面积 =(pi)(r^2)周长 =2(pi)r圆的标准方程(x-a)2+(y-b)2=r2注：(a,b)是圆心坐标语文课本中的文章都是优选的比较优异的文章 ,还有许多名家名篇。

假如有选择顺序渐进地让学生背诵一些优异篇目、出色段落 ,对提升学生的水平会大有裨益。

此刻 ,许多语文教师在剖析课文时 ,把文章解体的支离破裂 ,总在文章的技巧方面下功夫。

结果教师费力 ,学生头疼。

剖析完以后 ,学生见效甚微 ,没过几日便忘的干干净净。

造成这类事半功倍的难堪局面的重点就是对文章读的不熟。

常言道“书读百遍 ,其义自见”,假如有目的、有计划地指引学生频频阅读课文,或细读、默读、跳读 ,或听读、范读、轮读、分角色朗诵,学生便能够在读中自然意会文章的思想内容和写作技巧,能够在读中自然增强语感 ,增强语言的感觉力。

长此以往,这类思想内容、写作技巧和语感就会自然浸透到学生的语言意识之中,就会在写作中自觉不自觉地加以运用、创建和发展。

唐宋或更早以前，针对“经学”“律学”“算学”和“书学”各科目，其相应教授者称为“博士”，这与此刻“博士”含义已经相去甚远。

极点极线讲稿

一、极点与极线的定义定义 1（代数定义）已知圆锥曲线: Ax2Cy 22Dx2Ey F 0 ,则称点 P(x0 , y0 ) 和直线l : Ax0 x Cy 0 y D ( x x0 ) E( y y0 )F0 是圆锥曲线的一对极点和极线 .事实上，在圆锥曲线方程中，以x0 x 替换 x2，以xx替换 x （另一变量 y 也是如此），2即可得到点 P( x0 , y0 ) 的极线方程.特别地：（ 1）对于椭圆x2y21，与点 P( x0 , y0 ) 对应的极线方程为xxy0 y1；a2b2a2b2221 ，与点 P(x0 , y0 ) 对应的极线方程为xx（2）对于双曲线x2y2y0 y1；a b a2b2（3）对于抛物线y2 2 px ，与点 P( x0 , y0 ) 对应的极线方程为 y0 y p( x0x) .定义 2（几何定义）如图 1，P是不在圆锥曲线上的点，过P点引两条割线依次交圆锥曲线于四点E,F,G,H ,连接 EH ,FG 交于点N ，连接EG , FH交于点 M ，则直线 MN 为点 P 对应的极线 .若 P 为圆锥曲线上的点，则过P 点的切线即为极线.由图 1 可知，同理PM为点 N 对应的极线， PN 为点M所对应的极线 . MNP 称为自极三点形 . 若连接 MN 交圆锥曲线于点A, B, 则 PA, PB 恰为圆锥曲线的两条切线 .二、极点与极线的基本性质、定理定理 1（1）当P在圆锥曲线上时，其极线l是曲线在P点处的切线；（2）当P在外时，其极线l是曲线从点P所引两条切线的切点所确定的直线（即切点弦所在直线）；（3）当P在内时，其极线l是曲线过点P的割线两端点处的切线交点的轨迹.定理2（配极原则）（1）点P 关于圆锥曲线的极线 p 经过点 Q点Q 关于的极线q 经过点P ;（2）直线p 关于的极点P 在直线q 上直线q 关于的极点Q 在直线p 上.由此可知，共线点的极线必共点；共点线的极点必共线.特别地：圆锥曲线的焦点与其相应的准线是该圆锥曲线的一对极点与极线.（1）对于椭圆x 2y 2 1 而言，右焦点 F (c,0) 对应的极线为c x0 y 1，即 x a 2 ，恰a 2b 2a 2b 2c为椭圆的右准线 . 对于椭圆x 2y 2 1 而言，点 M (m,0) 对应的极线方程为 x a 2 ;a 2b 2m（2）对于双曲线x 2y 2 1 而言，点 M (m,0) 对应的极线方程为 x a 2 ；a 2b 2 m（3）对于抛物线 y 22px 而言，点 M (m,0) 对应的极线方程为 xm .定理 3 下面再给出与圆锥曲线的极点和极线有关的性质 .性质 1如图，已知点 A 是椭圆x 2y 2 1(a b 0) 上任一点，极点a 2b 2P(t,0)( ta, t c, t0) ，相应的极线 x a 2 . 椭圆在点 A 处的切线与极线txa 2交于点 N ，过点 N 作直线 AP 的垂线 MN ，垂足为 M ，则直线 MN 恒 t过 x 轴上的一个定点 Q ，且点 M 的轨迹是以 PQ 为直径的圆（点 Q 除外） .性质 2 如图，已知点 A 是双曲线x 2y 2 1( a 0, b 0) 上任一点，极点a 2b 2P(t,0)a 2( ta, t c) ，相应的极线 x. 双曲线在点 A 处的切线与极线txa 2 交于点 N ，过点 N 作直线 AP 的垂线 MN ，垂足为 M ，则直线 MN 恒t过 x 轴上的一个定点 Q ，且点 M 的轨迹是以 PQ 为直径的圆（点 Q 除外） .性质 3 如图，已知点A是抛物线y2 2 px( p 0) 上任一点，极点 P(t,0)(t 0,t p) ，相应的极线为x t . 抛物线在点A处的切线与极线 x t 2交于点 N ，过点 N 作直线AP的垂线 MN ，垂足为M，则直线 MN 恒过x轴上的一个定点 Q ，且点M的轨迹是以 PQ 为直径的圆（点 Q 除外）.定理 4如图，设圆锥曲线的一个焦点为 F ，与 F 相应的准线为l .（1）若过点 F 的直线与圆锥曲线相交于 M,N两点，则在M,N两点处的切线的交点 Q 在准线l上，且 FQ MN ;（2）若过准线 l 上一点Q作圆锥曲线的两条切线，切点分别为M,N ，则直线MN过焦点F，且 FQ MN ；（3）若过焦点 F 的直线与圆锥曲线相交于 M,N 两点，过F作FQ MN 交准线l于 Q ，则连线 QM ,QN 是圆锥曲线的两条切线 .定理 5 设椭圆x2y21(a b 0)的一个焦点为 F ，相应的准线为l，过焦点 F 的直线交a2b2椭圆于 A, B 两点，C是椭圆上任意一点.直线 CA, CB 交准线l于 M , N 两点，则以MN为直径的圆必过 F .三、历年高考题【例 1】（ 2011 年四川高考理数21 题第（ 2）问）如图，椭圆有两顶点A( 1,0) 、B(1,0) ，过其焦点 F (0,1) 的直线l与椭圆交于 C, D 两点，并与 x 轴交于点P .直线AC 与直线BD交于点Q . 当点P异于A, B两点时，求证： OP OQ 为定值 .【例2】（2010 年高考全国卷I 理数21 题第（1）问）已知抛物线 C : y 24x的焦点为 F ，过点K ( 1,0)的直线l 与 C 相交于A, B两点，点 A 关于x 轴的对称点为 D . 证明：点 F 在直线 BD 上.【例 3】（ 2010 江苏卷文理 18）在平面直角坐标系 xOy 中，如图，已知椭圆x 2y 2设过点 T (t , m) 的直线 TA, TB 与此91 的左右顶点为 A, B ，右焦点为 F .5椭圆分别交于点 M ( x , y ), N ( x , y ) ，其中 m 0, y0, y20 . 设t 9 ，求证11221直线 MN 必过 x 轴上一定点（其坐标与 m 无关） .【例 4】（ 2012 年北京卷 19）已知曲线 C : (5 m)x 2(m 2) y 28(mR)（ 1）若曲线 C 是焦点在 x 轴上的椭圆，求 m 的取值范围 .（ 2）设 m 4 ，曲线 C 与 y 轴交点为 A, B （点 A 位于点 B 的上方），直线 y kx 4与曲线 C 交于不同的两点 M , N ，直线 y1 与直线 BM 交于点 G . 求证： A,G,N 三点共线 .【例 5】（ 2012 年福建卷理 19）如图，椭圆 E :x 2y 2 1(a b 0) 的左焦点为 F 1 ，右焦点为a 2b 2F 2 ，离心率 e1，过 F 1 的直线交椭圆于 A, B 两点，且 ABF 2 的周长为 8.2（ 1）求椭圆 E 的方程 . （2）设动直线 l : y kx m 与椭圆 E 有且只有一个公共点 P ，且与直线 x4 相交于点 Q . 试探究：在坐标平面内是否存在定点 M ，使得以 PQ 为直径的圆恒过点 M ？若存在，求出点 M 的坐标；若不存在，说明理由 .【例 6】（2006 年全国卷Ⅱ理 21）已知抛物线 x 2 4 y 的焦点为 F ， A, B 是抛物线上的两动点，且 AFFB (0) ，过 A, B 两点分别作抛物线的切线，并设其交点为P .（ 1）证明 FP AB 为定值；（ 2）设 ABP 的面积为 S ，写出 S f ( ) 的表达式，并求 S 的最小值 .2【例 7】（2014 年江西卷理 20）如图，已知双曲线 C :x2 y 21(a 0) 的右焦点为 F ，点 A, B a分别在 C 的两条渐近线上， AF x 轴， AB OB, BF ∥ OA .（ 1）求双曲线 C 的方程；（ 2）过 C 上一点 P( x 0 , y 0 )( y 0 0) 的直线l :x 0 xy 0 y 1与直线 AF 相交于点 M ，与直线 x3相交于点 N ，证明点a 22P 在 C 上移动时，MF恒为定值，并求此定值 .NF【例 8】（ 2013 年江西卷理 20）椭圆 C :x 2y 21( a b 0) 的离心率 e 3， a b 3 .a 2b 22（ 1）求椭圆 C 的方程；（ 2）如图所示， A, B, D 是椭圆 C 的顶点， P 是椭圆 C 上除顶点外的任意一点，直线 DP 交 x 轴于点 N ，直线 AD 交 BP 于点 M ，设 BP 的斜率为 k ， MN 的斜率为 m ，证明： 2m k 为定值 .【例 9】（ 2009年福建）如图，已知椭圆C 的离心率为e3长轴的左右端点分别为2A 1 ( 2,0), A 2(2,0) .（ 1）求椭圆 C 的方程；（ 2）设直线 xmy 1与椭圆 C 交于 P,Q 两点，直线 A 1P 与 A 2Q 交于点 S . 试问当 m 变化时，点 S 是否恒在一条定直线上？若是，请写出这条直线方程，并证明你的结论；若不是，请说明理由 .【例 10】（ 2006 年全国卷Ⅱ理 21）已知抛物线 x 2 4y 的焦点为 F ， A, B 是抛物线上的两动点，且 AFFB (0) ，过 A, B 两点分别作抛物线的切线，并设其交点为 P .（ 1）证明 FP AB 为定值 ;（ 2）设△ ABP 的面积为 S ，写出 S f ( ) 的表达式，并求 S 的最小值 .。

圆锥曲线的极坐标方程、焦半径公式、焦点弦公式

圆锥曲线的极坐标方程、焦半径公式、焦点弦公式一、圆锥曲线的极坐标方程椭圆、双曲线、抛物线可以统一定义为：与一个定点(焦点)的距离和一条定直线(准线)的距离的比等于常数e 的点的轨迹．以椭圆的左焦点(双曲线的右焦点、抛物线的焦点)为极点，过点F 作相应准线的垂线，垂足为K ，以FK 的反向延长线为极轴建立极坐标系．椭圆、双曲线、抛物线统一的极坐标方程为： θρcos 1e ep -=. 其中p 是定点F 到定直线的距离，p ＞0 ．当0＜e ＜1时，方程表示椭圆；当e ＞1时，方程表示双曲线，若ρ＞0，方程只表示双曲线右支，若允许ρ＜0，方程就表示整个双曲线；当e=1时，方程表示开口向右的抛物线.二、圆锥曲线的焦半径公式设F 为椭圆的左焦点(双曲线的右焦点、抛物线的焦点)，P 为椭圆(双曲线的右支、抛物线)上任一点，则 ∵PQ e PF =，∴)cos (p PF e PF +=θ，其中FH p =，=θ〈x 轴，FP 〉 ∴焦半径θcos 1e ep PF -=．当P 在双曲线的左支上时，θcos 1e ep PF +-=. 推论：若圆锥曲线的弦MN 经过焦点F ，则有ep NF MF 211=+.三、圆锥曲线的焦点弦长若圆锥曲线的弦MN 经过焦点F ，1、椭圆中，cb c c a p 22=-=，θθπθ2222cos 2)cos(1cos 1c a ab e ep e ep MN -=--+-=. 2、双曲线中，若M 、N 在双曲线同一支上，θθπθ2222cos 2)cos(1cos 1c a ab e ep e ep MN -=--+-=；若M 、N 在双曲线不同支上，2222cos 2cos 1cos 1a c ab e ep e ep MN -=--+-=θθθ. 3、抛物线中，θθπθ2sin 2)cos(1cos 1p p p MN =--+-=. 四、直角坐标系中的焦半径公式设P （x,y ）是圆锥曲线上的点，1、若1F 、2F 分别是椭圆的左、右焦点，则ex a PF +=1，ex a PF -=2；2、若1F 、2F 分别是双曲线的左、右焦点，当点P 在双曲线右支上时，a ex PF +=1，a ex PF -=2；当点P 在双曲线左支上时，ex a PF --=1，ex a PF -=2；3、若F 是抛物线的焦点，2p x PF +=.。

高中数学极点极线及高中圆锥曲线必备公式

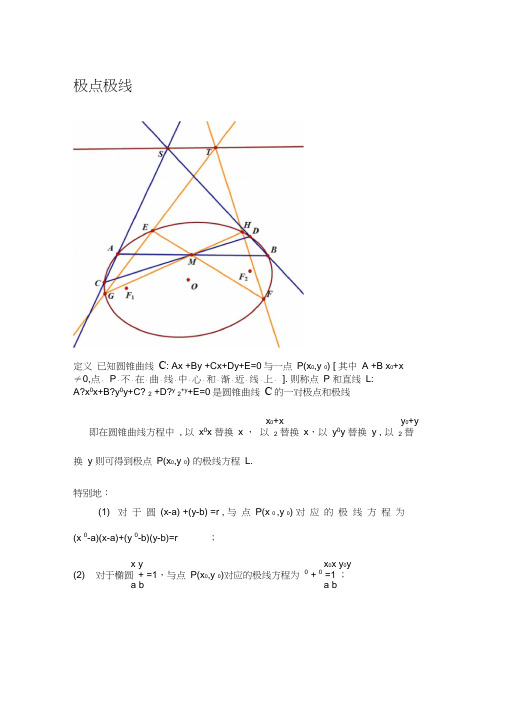
极点极线定义已知圆锥曲线С: Ax +By +Cx+Dy+E=0与一点P(x0,y 0) [ 其中 A +B x0+x≠0,点．P．不．在．曲．线．中．心．和．渐．近．线．上．]. 则称点P 和直线L:A?x0x+B?y0y+C? 2 +D?y2+y+E=0是圆锥曲线С的一对极点和极线x0+x y0+y 即在圆锥曲线方程中, 以x0x 替换x ，以2替换x，以y0y 替换y , 以2替换y 则可得到极点P(x0,y 0) 的极线方程L.特别地：(1) 对于圆(x-a) +(y-b) =r , 与点P(x 0 ,y 0) 对应的极线方程为(x 0-a)(x-a)+(y 0-b)(y-b)=r ；x y x0x y0y(2) 对于椭圆+ =1，与点P(x0,y 0)对应的极线方程为0 + 0 =1 ；a b a bx y x 0x y 0y(3) 对于双曲线 a -b =1，与点 P(x 0,y 0)对应的极线方程为 a 0 -b 0 =1 ；(4) 对于抛物线 y =2px ，与点 P(x 0,y 0) 对应的极线方程为 y 0y=p(x 0+x) ；性质一般地,有如下性质 [焦．点．所．在．区．域．为．曲．线．内．部． ]: ① 若极点 P 在曲线С上,则极线 L 是曲线С在P 点的切线；② 若极点 P 在曲线С外,则极线 L 是过极点 P 作曲线С的两条切线的切点连线；③ 若极点 P 在曲线С内,则极线 L 在曲线С外且与以极点 P 为中点的弦平行 [仅是斜率相等 ]( 若是圆 , 则此时中点弦的方程为(x 0-a)(x-a)+(y 0-b)(y-b)=x 0x y 0y x 0 y 0；若是椭圆,则此时中点弦的方程为 a x x +b y y =x a +y bx 0x y 0y x 0 y 0双曲线,则此时中点弦的方程为 a x0x -b y0y =x a 0 -y b 0 ；若是抛物线 ,则此时中点弦的方程为 y 0y-p(x 0+x)=y 0 -2px 0) ；(x 0-a) +(y 0-b) 若是④当P(x0,y 0)为圆锥曲线的焦点F(c,0) 时，极线恰为该圆锥曲线的准线．．；⑤极点极线的对偶性:Ⅰ.已知点P和直线L是关于曲线С的一对极点和极线,则L上任一点Pn对应的极线Ln必过点P,反之亦然,任意过点P的直线Ln对应的极点Pn必在直线L上[图．Ⅱ.过点P作曲线C的两条割线L1、L2，L1交曲线C于AB，L2交曲线C于MN，则直线AM、BN的交点T，直线AN、BM的交点S必都落在点P 关于曲线C的极线L 上[ 图．中．点．P．与．直．线．S．．T是．一．对．极．点．极．线．；．点．T．与．直．线．S．．P是．一．对．极．点．极．线．] ；即OP = OR OROQⅢ. 点 P 是曲线 C 的极点，它对应的极线为 L ，则有 :1）若C 为椭圆或双曲线，O 是C 的中心，直线 OP 交C 与R ，交L 于Q ，则OP?OQ=OR如图中学数学中极点与极线知识的现状与应用虽然中学数学中没有提到极点极线,但事实上,它的身影随处可见,只是没有点破而已.教材内改名换姓,“视”而不“见” .由④可知椭圆x a +y b =1的焦点的极a线方程为: x= . 焦点与准线是圆锥曲线一章中的核心内容, 它揭示了圆锥曲线c的统一定义, 更是高考的必考知识点. 正是因为它太常见了, 反而往往使我们“视”而不“见” .圆锥曲线基础必备1、长轴短轴与焦距，形似勾股弦定理长轴=2“，短轴= 2b,焦距= 2c.则：a2 =b2 -^c2 1、准线方程准焦距.〃方、"方涂以r..& 0・刁2sm —cos — sm 0_ 2 2 1 +cos0 2 cos 2—2 & 所以：椭圆的焦点三角形的面积为S 胚恶=b tail-.4.焦三角形计面积"半角正切進乘焦三角形：以椭圆的两个焦点巧・耳为顶点，另一个顶点」在椭圆上的三角形称为焦三角形•半角是指—Z 与P 巧的一半. 则焦三角形的面积为：证明：设阿| =小|昭| = S 由余弦定理:m 2 +n 2 - 2mn cos^= 4c 2=4a即：-2mn - = 2mn - 4b 2,故: Sgf =-m n sin0 =-』+ cos& l + cos0又:0 =tan —三、椭圆的相关公式切线平分焦周角, 切点连线求方程, 弦与中线斜率积, 细看中点弦方程,称为弦切角定理① 极线屯理须牢记② 准线去除准焦距③ 恰似弦中点轨迹④艮卩：2D = (1+ cos0)mn .1、切线平分焦周角，称为弦切角定理弦切角定理：切线平分椭圆焦周角的外角，平分双曲线的焦周角.焦周角是焦点三角形中，焦距所对应的角.弦切角是指椭圆的弦与其切线相交于椭圆上时它们的夹角，当弦为焦点弦时（过焦点的弦），那么切线是两个焦点弦的角平分线.第6页2. 切点连线求方程，圾线定理须牢记若旳（X05）在椭圆卡+$ = 1外，则过昨作椭圆的两条切线，切点、为P 』,巧，则点耳和切点弦马•勺分别称为椭圆的极点和极线.切点弦耳乃的直线方程即极线方程是笫？页3、弦与中线斜■率积.准线去涂准焦距|弦指椭圆内的一弦•中线指弦AB 的中点M 与原点O 的连线，即2AB 得中线•这两条直线的斜率的VY - Q 2於乘积，等于准线距离去除准焦^p= — .其k k_ p 结杲是：0M = T =~V第8页（称为极线定理）4、细看中点弦方程，恰似弦中点、轨迹|中点、弦AB 的方程:在椭圆中，若弦的中点、为弦仙称为中点弦，则中点弦的方程就是弦中点M 的轨迹方程：在椭圆中，过椭圆内点 p 皿、m 的弦AB , 其中点、M 的方程就是 S . y o y … /( y 2. 一7*+矿二正+歹，仍为椭圆.这两个方程有些相似，要擦亮眼睛，千万不要搞混了.第9页是直线方程.圆锥曲线必背口诀（红字为口诀）-双曲线一、双曲线定义双曲线有四定义.差比交线反比何1、定义1:（差）平面内，到两个定点唇码的距离之差的绝对值为定值2“（小于这两个定点间的距离冈砂）的点的轨迹称为双曲线。

2024高考数学专项复习圆锥曲线专题：调和点列-极点极线

圆锥曲线专题：调和点列-极点极线一、问题综述(一)概念明晰(系列概念)：1.调和点列：如图，在直线l上有两基点A,B，则在l上存在两点C,D到A,B两点的距离比值为定值，即AC BC =ADBD=λ，则称顺序点列A,C,B,D四点构成调和点列(易得调和关系2AB=1AC+1AD)。

同理，也可以C,D为基点，则顺序点列A,C,B,D四点仍构成调和点列。

所以称A,B和C,D称为调和共轭。

2.调和线束：如图，若A,C,B,D构成调和点列，O为直线AB外任意一点，则直线OA,OC,OB,OD称为调和线束。

若另一直线截调和线束，则截得的四点A ,C ,B ,D 仍构成调和点列。

3.阿波罗尼斯圆：如图，A,B为平面中两定点，则满足APBP=λ(λ≠1)的点P的轨迹为圆O，A,B互为反演点。

由调和点列定义可知，圆O与直线AB交点C,D满足A,C,B,D四点构成调和点列。

4.极点极线：如图，A,B互为阿圆O反演点，则过B作直线l垂直AB，则称A为l的极点，l为A的极线.2024高考数学专项复习5.极点极线推广(二次曲线的极点极线)：(1).二次曲线Ax 2+By 2+Cxy +Dx +Ey +F =0极点P (x 0,y 0)对应的极线为Ax 0x +By 0y +Cx 0y +y 0x 2+D x 0+x2+E y 0+y 2+F =0x 2→x 0x ,y 2→y 0y ,xy →x 0y +y 0x 2,x →x 0+x2,y →y 0+y 2(半代半不代)(2)圆锥曲线的三类极点极线(以椭圆为例)：椭圆方程x 2a 2+y 2b 2=1①极点P (x 0,y 0)在椭圆外，PA ,PB 为椭圆的切线，切点为A ,B 则极线为切点弦AB :x 0xa 2+y 0yb 2=1；②极点P (x 0,y 0)在椭圆上，过点P 作椭圆的切线l ，则极线为切线l :x 0x a 2+y 0y b 2=1；③极点P (x 0,y 0)在椭圆内，过点P 作椭圆的弦AB ，分别过A ,B 作椭圆切线，则切线交点轨迹为极线x 0xa 2+y 0yb 2=1；(3)圆锥曲线的焦点为极点，对应准线为极线.(二)重要性质性质1：调和点列的几种表示形式如图，若A ,C ,B ,D 四点构成调和点列，则有AC BC =AD BD =λ⇔2AB =1AD +1AC⇔OC 2=OB ⋅OA ⇔AC ⋅AD =AB ⋅AO ⇔AB ⋅OD =AC ⋅BD性质2：调和点列与极点极线如图，过极点P作任意直线，与椭圆及极线交点M,D,N则点M,D,N,P成调和点列(可由阿圆推广)性质3：极点极线配极原则若点A的极线通过另一点D，则D的极线也通过A．一般称A、D互为共轭点．推广：如图，过极点P作两条任意直线，与椭圆分别交于点MN,HG，则MG,HN的交点必在极线上，反之也成立。

高中数学圆锥曲线之极点极线微专题一

PART ONE
01 典例导引
高考真题
曲线的极点极线理论
设椭圆 C :
x2 a2
y2 b2
1(a
b
0) 过点 M (
2,1) ，且着焦点为 F1(
2, 0)
（1）求椭圆 C 的方程；
（2）当过点 P(4,1) 的动直线 l 与椭圆 C 相交与两不同点 A, B 时，在线段 AB 上取点 Q ，
则 PA QA ；反之，若 PA QA 成立，则称点 P 与 Q 关于调和共轭.
PB QB
PB QB
P 关于圆锥曲线的调和共轭点的轨迹是一条直线，这条直线就是点 P 的极线.
推论 1 设点 P 关于圆锥曲线的调和共轭点为点 Q ，则有 2 1 1 PQ PA PB
反之，若 2 1 1 成立，则点 P 与 Q 关于调和共轭. PQ PA PB
推论 2： P,Q 是圆锥曲线的一条对称轴 l 上两点（不在上），若 P,Q 关于是圆锥曲线调和共轭，过 Q 任作的一条割线，交于点 A, B ，则 APQ BPQ
推论 3：设点 P 关于有心圆锥曲线（设其中心为 O ）的调和共轭点为点 Q ，直线 PQ 经过圆锥曲线的中心，则有 OR2 OP OQ ，反之若有 OR2 OP OQ ，则点 P 与 Q 关于有心圆锥曲线调和共轭.
PB QB
又 A，P，B，Q 四点共线，从而 AP PB, AQ QB
于是 4 x1 x2 ， 1 y1 y2 ； x x1 x2 ， y y1 y2
1
1
1
1
从而 x12 2 x22 4x ，
①
y12
2y2
2
y
，
②

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

声明: 本容来自网络,感
∙百度贴吧mpc_killer吧的《[选][圆曲]--中点切线王牌杀手--极点极线草稿》∙《漫谈圆锥曲线的极点与极线——两高考试题的统一背景与解法》
∙百度贴吧高中数学吧的《圆锥曲线基础必备》
等优秀容.
极点极线
定义已知圆锥曲线С: A x
+B y
+C x +D y +E=0与一点P(x 0,y 0) [其中A
+B ≠0,点．P ．不在曲线中心和渐近线上．．．．．．．．．．．].则称点P 和直线L: A ∙x 0x +B ∙y 0y +C ∙x 0+x 2
+D ∙y 0+y 2+E=0是圆锥曲线С的一对极点和极线.
即在圆锥曲线方程中,以x 0x 替换x
，以
x 0+x
2
替换x ，以y 0y 替换y ,以
y 0+y
2
替换y 则可得到极点P(x 0,y 0)的极线方程L. 特别地：
(1)对于圆(x-a)
+(y-b)
=r ,与点P(x 0,y 0)对应的极线方程为
(x 0-a)(x-a)+(y 0-b)(y-b)=r ；
(2)对于椭圆x
a+
y
b=1，与点P(x0,y0)对应的极线方程为
x0x
a+
y0y
b=1；
(3)对于双曲线x
a-
y
b=1，与点P(x0,y0)对应的极线方程为
x0x
a-
y0y
b=1；
(4)对于抛物线y=2px，与点P(x0,y0)对应的极线方程为y0y=p(x0+x)；
性质一般地,有如下性质[焦点所在区域为曲线部
．．．．．．．．．．
]:
①若极点P在曲线С上,则极线L是曲线С在P点的切线；
②若极点P在曲线С外,则极线L是过极点P作曲线С的两条切线的切点连线；
③若极点P在曲线С,则极线L在曲线С外且与以极点P为中点的弦平行[仅是斜率相等]( 若是圆,则此时中点弦的方程为(x0-a)(x-a)+(y0-b)(y-b)=
(x 0-a)+(y 0-b)
；若是椭圆,则此时中点弦的方程为x 0x a +y 0y b =
x 0
a +y 0
b
；若是双曲线,则此时中点弦的方程为x 0x a -y 0y b =
x 0
a -y 0
b
；若是抛物线,则此时中点弦的方程为y 0y-p(x 0+x)=y 0-2px 0)；
④当P(x 0,y 0)为圆锥曲线的焦点F(c,0)时，极线恰为该圆锥曲线的准线．．；
⑤极点极线的对偶性:
Ⅰ.已知点P 和直线L 是关于曲线С的一对极点和极线,则L 上任一点Pn 对应的极线Ln 必过点P,反之亦然,任意过点P 的直线Ln 对应的极点Pn 必在直线L 上[图．中点．．Pn ．．与直线．．．Ln ．．是一对极点极线．．．．．．．
]；
Ⅱ.过点P 作曲线C 的两条割线L 1、L 2，L 1交曲线C 于AB ，L 2交曲线C 于MN ，则直线AM 、BN 的交点T ，直线AN 、BM 的交点S 必都落在点P 关于曲线C 的极线L 上 [图中点．．．P ．与直线．．．ST ．．是一对极点极线；点．．．．．．．．．T ．与直线．．．SP ．．是一对极点极线．．．．．．．
] ；
Ⅲ. 点P 是曲线C 的极点，它对应的极线为L ，则有:
1)若C 为椭圆或双曲线，O 是C 的中心，直线OP 交C 与R ，交L 于Q ，则
OP∙OQ=OR即OP
OR= OR OQ
椭圆如图
双曲线如图
2)若曲线为抛物线，过点P作对称轴的平行线交C于R，交L于Q，则PR=QR 如图
中学数学中极点与极线知识的现状与应用
虽然中学数学中没有提到极点极线,但事实上,它的身影随处可见,只是没有点破
而已.教材改名换姓,“视”而不“见”.由④可知椭圆x
a+
y
b=1的焦点的极线
方程为: x=a
c.焦点与准线是圆锥曲线一章中的核心容,它揭示了圆锥曲线的统
一定义,更是高考的必考知识点.正是因为它太常见了,反而往往使我们“视”而不“见”.
圆锥曲线基础必备
极点极线例题。