【解析版】天津市新华中学2013届高三上学期第一次月考数学(理)试题
【解析】天津市新华中学2013届高三上学期第一次月考文科数学

天津新华中学2012-2013学年度第一学期高三年级第一次月考数学试卷(文科)一、选择题(每小题4分,共32分)1. 集合,则()A. (1,2)B.C.D.【答案】C【解析】,,所以,选C.2. 给出如下四个命题①若“且”为假命题,则、均为假命题②命题“若,则”的否命题为“若,则”③“”的否定是“”④在ABC中,“”是“”的充要条件其中不正确...的命题的个数是()A. 4B. 3C. 2D. 1【答案】C【解析】若“且”为假命题,则、至少有一个为假命题,所以①不正确。
②正确。
“”的否定是,所以③不正确。
在ABC中,若,则,根据正弦定理可得,所以④正确,所以不正确的个数为2个,选C.3. 若角的终边上有一点,则的值是()A. B. C. D.【答案】B【解析】因为为第三象限,所以,,所以,选B.4. 公差不为零的等差数列的前项和为。
若是与的等比中项,,则等于()A. 18B. 24C. 60D. 90【答案】C【解析】因为是与的等比中项,所以,又,即,解得,所以,选C.5. 下图是函数在区间上的图象,为了得到这个函数的图象,只要将的图象上所有的点()A. 向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变B. 向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变C. 向左平移个单位长度,再把所得各点的横坐标缩短到原来的倍,纵坐标不变D. 向左平移个单位长度,再把所得各点的横坐标伸长到原来的2倍,纵坐标不变【答案】A【解析】由图象知,,又,所以,所以函数为,当时,,解得,所以函数为所以要得到函数,则只要先向左平移单位,然后再把所得各点的横坐标缩短到原来的倍,纵坐标不变,选A.6. 已知是定义在上的偶函数,且在上是增函数,设,则的大小关系是()A. B. C. D.【答案】C【解析】,,,因为,因为是定义在上的偶函数,且在上是增函数,所以函数在上单调递减,所以,选C. 7. 若向量与不共线,,且,则向量与的夹角为()A. 0B.C.D.【答案】D【解析】因为,所以,所以,即向量夹角为,选D.8. 设定义在R上的函数是最小正周期为的偶函数,是的导函数,当时,;当且时,,则函数在上的零点个数为()A. 2B. 4C. 5D. 8【答案】B【解析】由当x∈(0,π)且x≠时,,知时,为减函数,当。
天津市天津一中2013届高三零月考数学(理)试题(附答案)
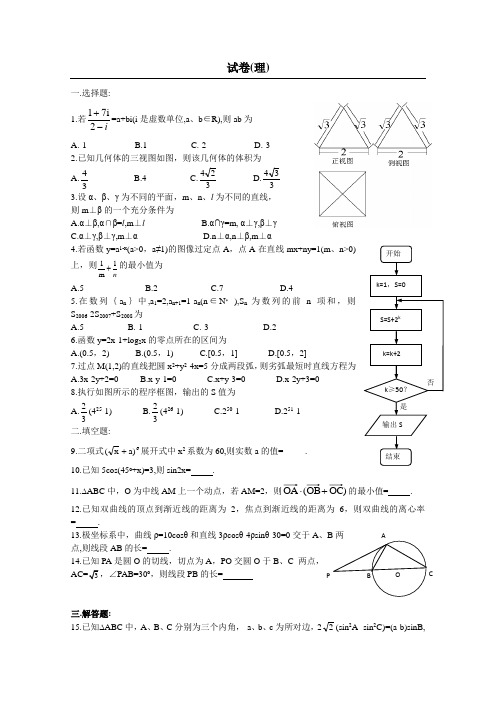
试卷(理)一.选择题: 1.若i-+2i71=a+bi(i 是虚数单位,a 、b ∈R),则ab 为 A.-1 B.1 C.-2 D.-3 2.已知几何体的三视图如图,则该几何体的体积为A.34B.4C.324D.334 3.设α、β、γ为不同的平面,m 、n 、l 为不同的直线, 则m ⊥β的一个充分条件为A.α⊥β,α∩β=l ,m ⊥lB.α∩γ=m, α⊥γ,β⊥γC.α⊥γ,β⊥γ,m ⊥αD.n ⊥α,n ⊥β,m ⊥α4.若函数y=a 1-x (a>0,a ≠1)的图像过定点A ,点A 在直线mx+ny=1(m 、n>0)上,则n1m1+的最小值为A.5B.2C.7D.45.在数列{a n }中,a 1=2,a n+1=1-a n (n ∈N ∗ ),S n 为数列的前n 项和,则S 2006-2S 2007+S 2008为 A.5 B.-1 C.-3 D.26.函数y=2x-1+log 2x 的零点所在的区间为A.(0.5,2)B.(0.5,1)C.[0.5,1]D.[0.5,2]7.过点M(1,2)的直线把圆x 2+y 2-4x=5分成两段弧,则劣弧最短时直线方程为 A.3x-2y+2=0 B.x-y-1=0 C.x+y-3=0 D.x-2y+3=0 8.执行如图所示的程序框图,输出的S 值为A.32(425-1)B.32(426-1) C.250-1 D.251-1 二.填空题:9.二项式6a)x (+展开式中x 2系数为60,则实数a 的值=_____. 10.已知5cos(45o +x)=3,则sin2x= .11.∆ABC 中,O 为中线AM 上一个动点,若AM=2,则)(+⋅的最小值= . 12.已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则双曲线的离心率= .13.极坐标系中,曲线ρ=10cos θ和直线3ρcos θ-4ρsin θ-30=0交于A 、B 两点,则线段AB 的长= .14.已知PA 是圆O 的切线,切点为A ,PO 交圆O 于B 、C 两点,PAB=30o ,则线段PB 的长=三.解答题:15.已知∆ABC 中,A 、B 、C 分别为三个内角, a 、b 、c 为所对边,22(sin 2A- sin 2C)=(a-b)sinB,O B C P APA B CDE∆ABC 的外接圆半径为2,(1)求角C ;(2)求∆ABC 面积S 的最大值.16.右图为一多面体,其底面ABCD 为正方形,PD ⊥平面ABCD ,CE//DP ,且PD=2CE ,(1)求证:BE//平面PDA ;(2)若N 为线段PB 的中点,求证:EN ⊥平面PDB ;(3)若PD=2AD ,求平面PBE 与平面ABCD 所成的二面角的余弦值.17.设有编号为1,2,3,……,n 的n 个学生,编号为1,2,3,……,n 的n 个座位.规定每个学生坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为ξ,已知ξ=2时,共有6种坐法.(1)求n 的值; (2)求随机变量ξ的概率分布列和数学期望.18.数列{a n }的前n 项和S n ,点(a n ,S n )在直线y=2x-3n 上,(1)若数列{a n +c }为等比数列,求常数c 的值;(2)求数列{a n }的通项公式;(3) 数列{a n }中是否存在三项,使它们构成等差数列?若存在,求出一组适合条件的项;若不存在,说明理由.19.已知椭圆C 1:)0(12222>>=+b a b y a x 的离心率为33,直线l : y=x+2与以原点为圆心,以椭圆的短半轴长为半径的圆相切.(1)求椭圆C 1的方程;(2)设椭圆C 1的左、右焦点F 1、F 2,直线l 1过点F 1且垂直于椭圆长轴,动直线l 2垂直l 1于点P ,线段P F 2的垂直平分线交l 2于点M ,求点M 的轨迹C 2方程;(3)设C 2与x 轴交于Q 点,不同的两点R 、S 在C 2上,且满足⋅=0.,求∣QS ∣的取值范围.20.已知函数f(x)=ax 4lnx+bx 4-c (x>0),在x = 1处取得极值-3-c ,其中a,b,c 为常数.(1)试确定a,b 的值;(2)讨论函数f(x)的单调区间;(3)若对任意x>0,不等式f(x)+2c 2≥0恒成立,求c 的取值范围.答案:一、选择题: 1、D 2、C 3、D 4、D 5、C 6、B 7、D 8、A二、填空题: 9、±210、25711、-2 12、3 13、8 14、1三、解答题:15、解:(1))(sin 22)sin (sin )2(2222b a B C A -=-a 2-c 2=ab-b 2即a 2+b 2-c 2=ab ∴2abcosC=ab cosC=21 c=3π(2)S ΔABC =21absinC =21absin 3π=sinAsinB 32 =)32sin(sin 32A A -π=)sin 21cos 23(sin 32A A A + =3sinAcosA+3sin2A=23sin2A+23(1-cos2A) =23sin2A-23cos2A+23=3sin(2A-6π)+23当2A-6π=2π 即A=3π时,S ΔABCmax =233 16、解:(1)取PD 中点F ,则FD //EC ,∴□EFDC ∴EF //CD //AB ∴□EFAB ∴ BE//AF ∴BE//平面PDA AF ⊆面PDA(2)设AC ∩BD=O 则NO //CE ∴□NOCE ∴CO//EN ∵ PD ⊥面ABCD ∴ PD ⊥NE ∴NE ⊥平面PDB PD//CE//NO BD ⊥NE(3)设平面PBE 与平面ABCD 所夹角为α∵PD ⊥平面ABCD 于D ,CE ⊥平面ABCD 于C ,∴PBES ∆∆=BDCS cos αS ΔBDC =2a 2,在ΔPBE 中,PB=2a ,BE=a 26,PE=a 26S ΔPBE =22222)26(22121a a a a EN PB =-⋅⋅=⋅⋅ ∴22222cos 22==a a α 17、解:(1)由ξ=2可知有n-2学生对位,2个错位,选n-2个学生对位 ∴62-n n=C ,∴n=4(2)P(ξ=0)=241144=A ,P (ξ=2)=446A =41P (ξ=3)=3124414=⋅A C ,P (ξ=4)=31944=AE ξ334131201=⨯+⨯+⨯+⨯= 18、把(a n ;S n )代入y=2x-3n 中, S n =2a n -3nS n-1=2a n-1-3(n-1) (n ≥2) 两式相减:a n =2a n-1+3 即a n +3=2(a n-1+3)∴c=3,当n=1时,a 1=3(2)由{a n +3}是首项6公比2的等比数列 ∴a n +3=6·2n-1 ∴a n =3·2n -3(n ∈N*) (3)设0<<βα假设存在 则]323[2)323()323(-⋅=-⋅+-⋅βγα即βγα2222⋅=+222=+--βγβα事实上,0<-βα,0>-βγ∴ 0<12<-βα ∴222>+--βγβα 22>-βγ ∴假设存在不成立 ∴不存在 19、解:(1)由e=33可知 a=c 3 ∴2a 2=3b 2a 2=b 2+c 2由y=x+2与(x 2+y 2=b 2)相切b=22∴ b=2 123x 22=+y 为椭圆C 1的方程a=3(2)F 1(-1,0),F 2(1,0)由已知可知MF 2=MP即点M 到点F 2距离等于点M 到直线l 1:x=-1的距离点M 是焦点为F 2渐近线为x=-1的抛物线,p=2 ∴y 2=4x(3)由(2)可知Q 点为原点O ,设R (x 1,y 1) ,S (x 2,y 2)2221214y ,4y x x ==,由0=⋅RS OR即x 1(x 2-x 1)+y 1(y 2-y 1)=0 x 1x 2-21x +y 1y 2-21y =0, x 1x 2-21x -40x 4x x 121=-0)2(2)-x x (21221=+-x22-x x 121+=x 44112≥+=x x x ,当且仅当x 1=2时,x 2≥16而|QS|=|OS|=2222y x +=2224x x +≥815164162=⨯⨯∴|QS|∈[815,+∞) 另:设直线OR 方程 y=kx ⇒ R(k442,k ),不妨设k>0y 2=4x 直线RS 方程 y-k 4=-)44,)1(4()4(122k k k k s k x k --+⇒- y 2=4x ∴ |QS|=|OS|=4815)1()k 1(k 24≥+++kk (k+k1)2≥420、解:(1)f ’(x )=4ax 3lnx+ax 3+4bx 3 由 f ’(1)=0f(1)=-3-c 即⎩⎨⎧-==∴⎩⎨⎧==+312c --3c -b 04b a b a (2)f(x)=12x 4lnx-3x 4-cf ’(x)=48x 3lnx+12x 3-12x 3=48x 3lnx ,(x>0) f(x)增区间(1,+∞),减区间(0,1) (3)由对x>0,f(x)+2c 2≥0成立即:12x 4lnx-3x 4-c+2c 2≥0对x ∈R 成立 即:c-2c 2≤12x 4lnx-3x 4对x ∈R 成立 必须满足c-2c 2≤{12x 4lnx-3x 4}min设g(x)=12x 4lnx-3x 4 g ’(x)=48x 3lnx ,如图当x=1时,g(x)min =g(1)=-3 ∴c-2c 2≤3 即2c 2-c-3≥0 ∴c ≤-1或c ≥23。
【2013备考】各地名校试题解析分类汇编(一)理科数学:3导数1
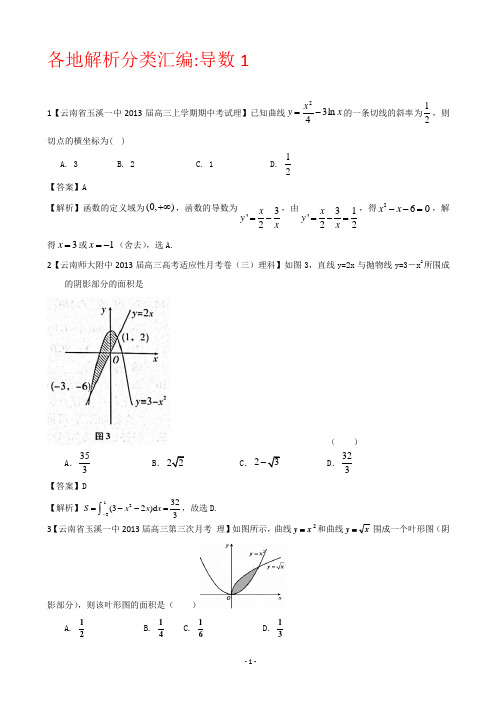
各地解析分类汇编:导数11【云南省玉溪一中2013届高三上学期期中考试理】已知曲线x x y ln 342-=的一条切线的斜率为21,则切点的横坐标为( ) A. 3 B. 2 C. 1 D.21【答案】A【解析】函数的定义域为(0,)+∞,函数的导数为3'2x y x =-,由31'22x y x =-=,得260x x --=,解得3x =或1x =-(舍去),选A.2【云南师大附中2013届高三高考适应性月考卷(三)理科】如图3,直线y=2x 与抛物线y=3-x 2所围成的阴影部分的面积是( )A .353B .C .2D .323【答案】D【解析】12332(32)d 3S x x x -=--=⎰,故选D. 3【云南省玉溪一中2013届高三第三次月考 理】如图所示,曲线2x y =和曲线x y =围成一个叶形图(阴影部分),则该叶形图的面积是( )A.21 B. 41 C. 61 D. 31【答案】D【解析】由2y xy ⎧=⎪⎨=⎪⎩,解得11x y =⎧⎨=⎩或0x y =⎧⎨=⎩,所以根据积分的应用可得阴影部分的面积为3123120021211)()33333x dx x x =-=-=⎰,选D. 4【山东省烟台市莱州一中2013届高三10月月考(理)】由直线2,21==x x ,曲线xy 1=及x 轴所谓成图形的面积为 A.415B.417C.2ln 21D. 2ln 2【答案】D【解析】根据积分的应用可知所求22112211ln ln 2ln2ln 22dx x x==-=⎰,选D. 5【云南师大附中2013届高三高考适应性月考卷(三)理科】已知()f x 为R上的可导函数,且,x R ∀∈均有()f x f>′(x),则有 ( )A.20132013(2013)(0),(2013)(0)e f f f e f -<> B.20132013(2013)(0),(2013)(0)e f f f e f -<< C.20132013(2013)(0),(2013)(0)e f f f e f ->>D .20132013(2013)(0),(2013)(0)e f f f e f -><【答案】A【解析】构造函数()()x f x g x=,则2()()()()()()()x x x x f x e e f x f x f x g x e e ''''--==,6【山东省烟台市莱州一中2013届高三10月月考(理)】曲线x e y 21=在点()2,4e处的切线与坐标轴所围三角形的面积为 A.2eB.24eC.22eD.229e 【答案】A【解析】121'2x y e =,所以在点()2,4e 的导数为142211'22y e e ⨯==,即切线斜率为212k e =,所以切线方程为221(4)2y e e x -=-,令0x =得,2y e =-,令0y =,得2x =.所以三角形的面积为22122e e ⨯⨯=,选A.7【云南省昆明一中2013届高三新课程第一次摸底测试理】函数22ln y x x e ==在处的切线与坐标轴所围成的三角形的面积为A .292e B .212Se =C .22eD .2e【答案】D【解析】212'2y x x x =⨯=,所以在2x e =处的切线效率为22k e =,所以切线方程为2224()y x e e-=-,令0x =,得2y =,令0y =,得2x e =-,所以所求三角形的面积为22122e e ⨯⨯=,选D.8【山东省烟台市莱州一中20l3届高三第二次质量检测 (理)】曲线()ln 2y x =+在点()1,0P -处的切线方程是 A.1y x =+ B.1y x =-+C.21y x =+D.21y x =-+【答案】A 【解析】1'2y x =+,所以在点P 处的切线斜率1112k ==-+,所以切线方程为(1)1y x x =--=+,选A.9【山东省烟台市莱州一中20l3届高三第二次质量检测 (理)】由直线2,,0sin 33x x y y x ππ====与所围成的封闭图形的面积为 A.12B.1C.2【答案】B【解析】由积分的应用得所求面积为2233332sin cos coscos 2cos 1333xdx xπππππππ=-=-+==⎰,选B. 10【天津市新华中学2012届高三上学期第二次月考理】 已知函数))((R x x f ∈满足1)1(=f ,且)(x f 的导函数21)('<x f ,则212)(+<x x f 的解集为 A. {}11<<-x x B. {}1-<x x C. {}11>-<x x x 或 D. {}1>x x【解析】设1()()()22xF x f x =-+, 则11(1)(1)()11022F f =-+=-=,1'()'()2F x f x =-,对任意x R ∈,有1'()'()02F x f x =-<,即函数()F x 在R 上单调递减,则()0F x <的解集为(1,)+∞,即212)(+<x x f 的解集为(1,)+∞,选D.11【山东省烟台市莱州一中20l3届高三第二次质量检测 (理)】函数()32f x x bx cx d =+++的大致图象如图所示,则2212x x +等于A.89B.109C.169D.289【答案】C【解析】函数过原点,所以0d =。
【Word版解析】天津市天津一中2013届高三上学期一月考 理科数学

天津一中2012—2013学年高三数学一月考试卷(理科)一、选择题:(共40分,每小题5分,每小题给出的四个选项中,只有一项符合题目要求) 1.有关下列命题的说法正确的是A.命题“若x 2=1,则x=1”的否命题为:若“x 2=1则x ≠1” B.“1x =-”是“2560x x --=”的必要不充分条件C.命题“∃x ∈R,使得x 2+x+1<0”的否定是:“∀x ∈R,均有x 2+x+1<0” D.命题“若x=y,则sinx=siny ”的逆否命题为真命题 【答案】D【解析】若x 2=1,则x=1”的否命题为21x ≠,则1x ≠,即A 错误。
若2560x x --=,则6x =或1x =-,所以“1x =-”是“2560x x --=”的充分不必要条件,所以B 错误。
∃x ∈R,使得x 2+x+1<0的否定是∀x ∈R,均有210x x ++≥,所以C 错误。
命题若x=y,则sinx=siny 正确,所以若x=y,则sinx=siny 的逆否命题也正确,所以选D.2.定义在R 上的偶函数f(x),当x ∈[0,+∞)时,f(x)是增函数,则f(-2),f(π),f(-3)的大小关系是A.f(π)>f(-3)>f(-2)B.f(π)>f(-2)>f(-3)C.f(π)<f(-3)<f(-2)D.f(π)<f(-2)<f(-3) 【答案】A【解析】因为函数是偶函数,所以(2)(2),(3)(3)f f f f -=-=,又函数在[0,)+∞上是增函数,所以由(2)(3)()f f f π<<,即(2)(3)()f f f π-<-<,选A.3.函数f(x)=sin2x-4sin 3xcosx(x ∈R)的最小正周期为 A.8π B.4π C.2πD.π【答案】C【解析】221()sin 22sin 2sin sin 2(12sin )sin 2cos 2sin 42f x x x x x x x x x =-=-==,所以函数的周期为2242T πππω===,选C.4.设函数sin()3y x π=+(x ∈R),则f(x)A.在区间[-π,2π-]上是减函数 B.在区间27[,]36ππ上是增函数 C.在区间[8π,4π]上是增函数 D.在区间5[,]36ππ上是减函数【答案】B 【解析】当2736x ππ≤≤时,2733363x πππππ+≤+≤+,即332x πππ≤+≤,此时函数sin()3y x π=+单调递减,所以sin()3y x π=+在区间27[,]36ππ上是增函数,选B.5.在∆ABC 中,A,B,C 为内角,且sin cos sin cos A A B B =,则∆ABC 是 A.等腰三角形 B.直角三角形C.等腰直角三角形D.等腰或直角三角形【答案】D【解析】由sin cos sin cos A A B B =得sin 2sin 2sin(2)A B B π==-,所以22A B =或22A B π=-,即A B =或2A B π+=,所以三角形为等腰或直角三角形,选D.6.,,x y z 均为正实数,且22log xx =-,22log yy -=-,22log z z -=,则A. x y z <<B.z x y <<C.z y x <<D.y x z <<【答案】A【解析】因为,,x y z 均为正实数,所以22log 1xx =->,即2log 1x <-,所以102x <<。
天津市天津一中2013届高三(上)零月考数学理试题(WORD解析版)

天津一中2013届高三(上)零月考数学试卷(理科)参考答案与试题解析一、选择题(共8小题,每小题3分,满分24分)1.(3分)若=a+bi(i是虚数单位,a、b∈R),则ab为()A.﹣1 B.1C.﹣2 D.﹣3考点:复数代数形式的乘除运算;复数相等的充要条件.专题:计算题.分析:利用复数的代数形式的乘除运算,知==﹣1+3i=a+bi,由此能求出ab.解答:解:∵====﹣1+3i=a+bi,∴a=﹣1,b=3,∴ab=﹣3.故选D.点评:本题考查复数的代数形式的乘除运算,是基础题.解题时要认真审题,仔细解答.2.(3分)已知几何体的三视图如图,则该几何体的体积为()A.B.4C.D.考点:由三视图求面积、体积.专题:计算题.分析:根据已知的三视图可判断出该几何体是一个正四棱锥,且可得底面棱长为2,侧面高为,由此求出底面面积和棱锥的高,代入棱锥体积公式,可得答案.解答:解:由已知可得该几何体是一个底面棱长为2侧面高为的正四棱锥则棱锥的高h==∴棱锥的高V=Sh=×2×2×=故选C点评:本题考查的知识点是由三视图求体积,其中根据已知分析出几何体的形状是解答的关键.3.(3分)(2005•天津)设α、β、γ为平面,m、n、l为直线,则m⊥β的一个充分条件是()A.α⊥β,α∩β=l,m⊥l B.α∩γ=m,α⊥γ,β⊥γC.α⊥γ,β⊥γ,m⊥αD.n⊥α,n⊥β,m⊥α考点:直线与平面垂直的判定.专题:证明题;转化思想.分析:根据面面垂直的判定定理可知选项A是否正确,根据平面α与平面β的位置关系进行判定可知选项B和C是否正确,根据垂直于同一直线的两平面平行,以及与两平行平面中一个垂直则垂直于另一个平面,可知选项D正确.解答:解:α⊥β,α∩β=l,m⊥l,根据面面垂直的判定定理可知,缺少条件m⊂α,故不正确;α∩γ=m,α⊥γ,β⊥γ,而α与β可能平行,也可能相交,则m与β不一定垂直,故不正确;α⊥γ,β⊥γ,m⊥α,而α与β可能平行,也可能相交,则m与β不一定垂直,故不正确;n⊥α,n⊥β,⇒α∥β,而m⊥α,则m⊥β,故正确故选D点评:本小题主要考查空间线面关系、面面关系以及充分条件的判定等知识,考查化归与转化的数学思想方法,以及空间想象能力、推理论证能力,属于基础题.4.(3分)若函数y=a1﹣x(a>0,a≠1)的图象过定点A,点A在直线mx+ny=1(m、n>0)上,则的最小值为()A.5B.2C.7D.4考点:基本不等式.专题:计算题.分析:函数y=a1﹣x(a>0,a≠1)的图象恒过定点A,知A(1,1),点A在直线mx+ny﹣1=0上,得m+n=1结合mn>0,可得m>0,n>0,利用1的变换构造出可以用基本不等式求最值的形式求最值解答:解:由已知定点A坐标为(1,1),由点A在直线mx+ny﹣1=0上,∴m+n=1,又mn>0,∴m>0,n>0,∴=()(m+n)=2当且仅当即m=n=时取等号故选D点评:本题主要考查了利用基本不等式求解最值,解题的关键是利用1的代换配凑基本不等式应用的条件5.(3分)在数列{a n}中,a1=2,a n+1=1﹣a n(n∈N∗),S n为数列的前n项和,则S2006﹣2S2007+S2008为()A.5B.﹣1 C.﹣3 D.2考点:数列的求和;等差数列.专题:计算题.分析:依题意,可求得a1=a3=…=a2n﹣1=2,a2=a4=…=a2n=﹣1.从而可求得答案.解答:解:∵数列{a n}中,a n+1=1﹣a n(n∈N∗),∴a n+a n+1=1.又a1=2,∴a2=﹣1,∴a3=2,同理可求,a4=﹣1,a5=﹣1,…∴a1=a3=…=a2n﹣1=2,a2=a4=…=a2n=﹣1.∴S2006=1003;同理可求得S2007=1005,S2008=1004,∴S2006﹣2S2007+S2008=﹣3.故选C.点评:本题考查数列的求和,分析出a1=a3=…=a2n﹣1=2,a2=a4=…=a2n=﹣1是关键,考查分析与计算能力,属于中档题.6.(3分)函数y=2x﹣1+log2x的零点所在的区间为()A.(0.5,2)B.(0.5,1)C.[0.5,1]D.[0.5,2]考点:函数的零点.专题:计算题.分析:判断函数在区间端点处函数值的符号,当它们异号时存在零点.解答:解:因为2×0.5﹣1+log20.5=log20.5<0,2×1﹣1+log21=1>0,又在(0.5,1)上函数y=2x﹣1+log2x的图象是连续不断的一条曲线,所以函数y=2x﹣1+log2x在区间(0.5,1)上存在零点.故选B.点评:本题考查函数零点存在的条件,须满足两条:①在区间上图象连续不断;②端点处函数值异号.7.(3分)过点M(1,2)的直线把圆x2+y2﹣4x=5分成两段弧,则劣弧最短时直线方程为()A.3x﹣2y+2=0 B.x﹣y﹣1=0 C.x+y﹣3=0 D.x﹣2y+3=0考点:直线与圆相交的性质.专题:计算题;直线与圆.分析:设已知圆的圆心为C,根据平面几何知识,得劣弧最短时相应的弦长也最短,所以求出过点M,且与CM垂直的直线l即可,根据垂直直线斜率之间的关系算出l的斜率,最后利用点斜式列式,再化成一般式方程,即得所求.解答:解:∵劣弧最短时,相应的弦长也最短∴过点M(1,2)的直线l截圆C:x2+y2﹣4x=5,所得短劣弧对应的直线与CM垂直∵圆x2+y2﹣4x=5的圆心C(2,0)∴CM的斜率k==﹣2,可得直线l的斜率k1=﹣=由此可得直线l方程为:y﹣2=(x﹣1),整理得x﹣2y+3=0故选:D点评:本题给出圆内一点M,求经过点M且被圆截得最短弧的直线l的方程,着重考查了直线的位置关系和直线与圆相交的性质等知识,属于基础题.8.(3分)(2013•甘肃三模)执行如图所示的程序框图,输出的S值为()A.(425﹣1)B.(426﹣1)C.250﹣1 D.251﹣1考点:程序框图.专题:计算题;等差数列与等比数列.分析:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出等比数列的和.解答:解:分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是累加并输出S=0+2+23+…+249==(425﹣1)故选A.点评:本题主要考查了直到型循环结构,直到型循环是先循环后判断.对循环体每次循环需要进行分析并找出内在规律.本题属于基础题二.填空题:9.(3分)的展开式中x2项的系数为60,则实数a=±2.考点:二项式系数的性质.专题:计算题.分析:在的通项公式中,令x的指数等于2,求得r=2,从而得到展开式中x2项的系数为60=C62a2,解方程求得实数a的值.解答:解:的通项公式为T r+1=C6r a r,令=2可得r=2,展开式中x2项的系数为60=C62a2,∴a2=4,a=±2.故答案为:±2.点评:本题主要考查二项式定理,二项展开式的通项公式,求展开式中某项的系数,得到60=C62a2,是解题的关键,属于中档题.10.(3分)已知5cos(45°+x)=3,则sin2x=.考点:二倍角的正弦.专题:三角函数的求值.分析:由题意可得cos(45°+x)=,再利用二倍角的余弦公式求得sin2x=﹣cos(90°+2x)的值.解答:解:由题意可得cos(45°+x)=,∴sin2x=﹣cos(90°+2x)=﹣cos[2(45°+x)]=﹣2cos2(45°+x)+1=﹣2×+1=,故答案为.点评:本题主要考查二倍角的余弦公式的应用,属于基础题.11.(3分)(2005•江苏)在△ABC中,O为中线AM上一个动点,若AM=2,则的最小值是﹣2.考点:平面向量数量积的运算.专题:计算题;压轴题.分析:利用向量的运算法则:平行四边形法则作出,判断出共线,得到的夹角,利用向量的数量积公式将转化成二次函数求出最小值,解答:解:以OB和OC做平行四边形OBNC.则因为M为BC的中点所以且反向∴=,设OA=x,(0≤x≤2)OM=2﹣x,ON=4﹣2x∴=2x2﹣4x(0≤x≤2)其对称轴x=1所以当x=1时有最小值﹣2故答案为﹣2点评:本题考查向量的运算法则、向量共线的充要条件、向量的数量积公式、二次函数最值的求法.12.(3分)(2007•海南)已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则该双曲线的离心率为3.考点:双曲线的简单性质.专题:计算题.分析:过双曲线的顶点A、焦点F分别向其渐近线作垂线,垂足分别为B、C,根据比例线段的性质可知进而求得a和c的关系,则离心率可得.解答:解:如图,过双曲线的顶点A、焦点F分别向其渐近线作垂线,垂足分别为B、C,则:故答案为3点评:本题主要考查了双曲线的简单性质.考查了比例线段的知识和双曲线的离心率问题.13.(3分)极坐标系中,曲线ρ=10cosθ和直线3ρcosθ﹣4ρsinθ﹣30=0交于A、B两点,则线段AB 的长=8.考点:简单曲线的极坐标方程;直线与圆相交的性质.专题:直线与圆.分析:先把曲线和直线的极坐标方程化为普通方程,再利用|AB|=2(d为圆心到直线的距离)即可得出答案.解答:解:∵曲线ρ=10cosθ,∴ρ2=10ρcosθ,化为普通方程:x2+y2=10x,即(x﹣5)2+y2=25,∴圆心C(5,0),半径r=5.∵直线3ρcosθ﹣4ρsinθ﹣30=0,∴普通方程为3x﹣4y﹣30=0.圆心C(5,0)到直线的距离d==3,∴|AB|===8.故答案为8.点评:充分理解|AB|=2(d为圆心到直线的距离)是解题的关键.当然也可以先把交点A、B的坐标求出来,再利用两点间的距离公式即可求出.14.(3分)(2010•怀柔区二模)已知PA是圆O(O为圆心)的切线,切点为A,PO交圆O于B,C两点,,则线段PB的长为1.考点:圆的切线方程.专题:压轴题.分析:利用直径上的圆周角是直角,切点与圆心连线与切线垂直,推出△OAB是正三角形,PB=AB=r (半径),然后求出结果.解答:解:PA是圆O(O为圆心)的切线,切点为A,PO交圆O于B,C两点,∠CAB=90°,又OA⊥AP,∠PAB=30°∴∠CAO=30°△OAB是正三角形,且∠ACO=30°,∠APO=30°∴AB=PB设圆的半径为r,则;PB=1故答案为:1.点评:本题考查圆的切线方程,平面几何知识,是中档题.三.解答题:15.已知△ABC中,A、B、C分别为三个内角,a、b、c为所对边,2(sin2A﹣sin2C)=(a﹣b)sinB,△ABC的外接圆半径为,(1)求角C;(2)求△ABC面积S的最大值.考点:余弦定理;正弦定理.专题:解三角形.分析:(1)利用正弦定理化简已知等式的右边,整理后再利用余弦定理变形,求出cosC的值,由C为三角形的内角,利用特殊角的三角函数值即可求出C的度数;(2)由C的度数求出A+B的度数,用A表示出B,利用三角形的面积公式列出关系式,利用正弦定理化简后,将sinC的值及表示出的B代入,利用两角和与差的正弦函数公式化简,整理后利用二倍角的正弦、余弦函数公式化简,再利用两角和与差的正弦函数公式化为一个角的正弦函数,根据正弦函数的图象与性质即可得出面积的最大值.解答:解:(1)利用正弦定理化简已知的等式得:2(sin2A﹣sin2C)=2sinB(a﹣b),整理得:a2﹣c2=ab﹣b2,即a2+b2﹣c2=ab,∵c2=a2+b2﹣2abcosC,即a2+b2﹣c2=2abcosC,∴2abcosC=ab,即cosC=,则C=;(2)∵C=,∴A+B=,即B=﹣A,∵==2,即a=2sinA,b=2sinB,∴S△ABC=absinC=absin=×2sinA×2sinB×=2sinAsinB=2sinAsin(﹣A)=2sinA(cosA+sinA)=3sinAcosA+sin2A=sin2A+(1﹣cos2A)=sin2A﹣cos2A+=sin(2A﹣)+,则当2A﹣=,即A=时,S△ABCmax=.点评:此题考查了正弦、余弦定理,两角和与差的正弦函数公式,二倍角的正弦、余弦函数公式,以及三角形的面积公式,熟练掌握定理及公式是解本题的关键.16.如图为一多面体,其底面ABCD为正方形,PD⊥平面ABCD,CE∥DP,且PD=2CE.(1)求证:BE∥平面PDA;(2)若N为线段PB的中点,求证:EN⊥平面PDB;(3)若PD=AD,求平面PBE与平面ABCD所成的二面角的余弦值.考点:直线与平面平行的判定;二面角的平面角及求法.专题:综合题;空间角.分析:(1)取PD中点F,证明四边形EFAB为平行四边形,可得BE∥AF,利用线面平行的判定可得BE∥平面PDA;(2)设AC∩BD=O,证明CO∥EN,C0⊥平面PDB,即可得到NE⊥平面PDB;(3)设平面PBE与平面ABCD所夹角为α,利用即可求得结论.解答:(1)证明:取PD中点F,则FD∥EC,FD=EC∴四边形EFDC为长方形∴EF∥CD∥AB∴四边形EFAB为平行四边形∴BE∥AF∵BE⊄面PDA,AF⊂面PDA∴BE∥平面PDA;(2)证明:设AC∩BD=O,则NO∥CE,NO=CE∴四边形NOCE为长方形,∴CO∥EN∵PD⊥面ABCD,∴CO⊂面ABCD∴PD⊥CO,∵CO⊥BD,PD∩BD=D∴C0⊥平面PDB∴NE⊥平面PDB;(3)解:设平面PBE与平面ABCD所夹角为α∵PD⊥平面ABCD于D,CE⊥平面ABCD于C,∴在△PBE中,PB=2a,BE=,PE=,∴S△PBE=∵S△BDC=,∴点评:本题考查线面平行,线面垂直,考查面面角,考查学生分析解决问题的能力,属于中档题.17.(2007•深圳二模)有编号为1,2,3,…,n的n个学生,入坐编号为1,2,3,…n的n个座位.每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为ξ,已知ξ=2时,共有6种坐法.(1)求n的值;(2)求随机变量ξ的概率分布列和数学期望.考点:离散型随机变量及其分布列.专题:计算题.分析:(1)解题的关键是ξ=2时,共有6种坐法,写出关于n的表示式,解出未知量,把不合题意的舍去.(2)学生所坐的座位号与该生的编号不同的学生人数为ξ,由题意知ξ的可能取值是0,2,3,4,当变量是0时表示学生所坐的座位号与该生的编号都相同,当变量是2时表示学生所坐的座位号与该生的编号有2个相同,理解变量对应的事件,写出分布列和期望.解答:解:(1)∵当ξ=2时,有C n2种坐法,∴C n2=6,即,n2﹣n﹣12=0,n=4或n=﹣3(舍去),∴n=4.(2)∵学生所坐的座位号与该生的编号不同的学生人数为ξ,由题意知ξ的可能取值是0,2,3,4,当变量是0时表示学生所坐的座位号与该生的编号都相同,当变量是2时表示学生所坐的座位号与该生的编号有2个相同,当变量是3时表示学生所坐的座位号与该生的编号有1个相同,当变量是4时表示学生所坐的座位号与该生的编号有0个相同,∴,,,,∴ξ的概率分布列为:∴.点评:培养运用从具体到抽象、从特殊到一般的观点分析问题的能力,充分体现数学的化归思想.启发诱导的同时,训练了学生观察和概括归纳的能力.18.数列{a n}的前n项和为S n,S n=2a n﹣3n(n∈N*)(1)若数列{a n+c}成等比数列,求常数c值;(2)求数列{a n}的通项公式a n(3)数列{a n}中是否存在三项,它们可以构成等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.考点:等差数列与等比数列的综合.专题:计算题;压轴题.分析:(1)利用递推公式可得a n=s n﹣s n﹣1,利用等比数列的定义可求c(2)由递推公式a n=s n﹣s n﹣1(n≥2),a1=s1求解(3)假设存在a s,a p,a r成等差数列,则2a p=a s+a r,结合(2)中的通项公式进行推理.解答:解:(1)由S n=2a n﹣3n及S n+1=2a n+1﹣3(n+1)得a n+1=2a n+3∴,∴c=3(2)∵a1=S1=2a1﹣3,∴a1=3,a n+3=(a1+3)•2n﹣1∴a n=3.2n﹣3(n∈N*)(3)设存在S,P,r∈N*,且s<p<r使a s,a p,a r成等差数列∴2a p=a s+a r即2(3•2p﹣3)=(3•2s﹣3)+(3•2r﹣3)∴2p+1=2s+2r∴2p﹣s+1=1+2r﹣s∵s,p,r∈N*且s<p<r∴2p﹣s+1、2r﹣s为偶数1+2r﹣s为奇数矛盾,不存在满足条件的三项点评:本题主要考查了数列的递推关系a n=s n﹣s n﹣1(n≥2),a1=s1的应用及等比数列的定义,而对存在性问题,一般是先假设存在,然后由假设结合已知条件进行推理,看是否产生矛盾,从而判断存在性.19.(2013•梅州二模)已知椭圆的离心率为,直线l:y=x+2与以原点为圆心、椭圆C1的短半轴长为半径的圆相切.(1)求椭圆C1的方程;(2)设椭圆C1的左焦点为F1,右焦点为F2,直线l1过点F1且垂直于椭圆的长轴,动直线l2垂直于直线l1,垂足为点P,线段PF2的垂直平分线交l2于点M,求点M的轨迹C2的方程;(3)设C2与x轴交于点Q,不同的两点R,S在C2上,且满足,求的取值范围.考点:圆与圆锥曲线的综合;平面向量数量积的运算;轨迹方程;椭圆的标准方程.专题:计算题;压轴题.分析:(1)先由离心率为,求出a,b,c的关系,再利用直线l:y=x+2与以原点为圆心、椭圆C1的短半轴长为半径的圆相切,求出b即可求椭圆C1的方程;(2)把题中条件转化为动点M的轨迹是以l1:x=﹣1为准线,F2为焦点的抛物线,即可求点M的轨迹C2的方程;(3)先设出点R,S的坐标,利用求出点R,S的坐标之间的关系,再用点R,S 的坐标表示出,利用函数求最值的方法即可求的取值范围.解答:解:(1)由得2a2=3b2,又由直线l:y=x+2与圆x2+y2=b2相切,得,,∴椭圆C1的方程为:.(4分)(2)由MP=MF2得动点M的轨迹是以l1:x=﹣1为准线,F2为焦点的抛物线,∴点M的轨迹C2的方程为y2=4x.(8分)(3)Q(0,0),设,∴,由,得,∵y1≠y2∴化简得,(10分)∴(当且仅当y1=±4时等号成立),∵,又∵y22≥64,∴当y22=64,即y2=±8时,∴的取值范围是.(13分)点评:本题是对圆与椭圆知识的综合考查.当直线与圆相切时,可以利用圆心到直线的距离等于半径求解.,也可以把直线与圆的方程联立让对应方程的判别式为0求解.20.(2007•重庆)已知函数f(x)=ax4lnx+bx4﹣c(x>0)在x=1处取得极值﹣3﹣c,其中a,b,c 为常数.(1)试确定a,b的值;(2)讨论函数f(x)的单调区间;(3)若对任意x>0,不等式f(x)≥﹣2c2恒成立,求c的取值范围.考点:利用导数研究函数的极值;函数恒成立问题;利用导数研究函数的单调性.专题:计算题.分析:(1)因为x=1时函数取得极值得f(x)=﹣3﹣c求出b,然后令导函数=0求出a即可;(2)解出导函数为0时x的值讨论x的取值范围时导函数的正负决定f(x)的单调区间;(3)不等式f(x)≥﹣2c2恒成立即f(x)的极小值≥﹣2c2,求出c的解集即可.解答:解:(1)由题意知f(1)=﹣3﹣c,因此b﹣c=﹣3﹣c,从而b=﹣3又对f(x)求导得=x3(4alnx+a+4b)由题意f'(1)=0,因此a+4b=0,解得a=12(2)由(I)知f'(x)=48x3lnx(x>0),令f'(x)=0,解得x=1当0<x<1时,f'(x)<0,此时f(x)为减函数;当x>1时,f'(x)>0,此时f(x)为增函数因此f(x)的单调递减区间为(0,1),而f(x)的单调递增区间为(1,+∞)(3)由(II)知,f(x)在x=1处取得极小值f(1)=﹣3﹣c,此极小值也是最小值,要使f(x)≥﹣2c2(x>0)恒成立,只需﹣3﹣c≥﹣2c2即2c2﹣c﹣3≥0,从而(2c﹣3)(c+1)≥0,解得或c≤﹣1所以c的取值范围为(﹣∞,﹣1]∪点评:考查学生利用导数研究函数极值的能力,利用导数研究函数的单调性的能力,函数恒成立时条件的应用能力.。
【2013备考】各地名校试题解析分类汇编(一)理科数学:2函数2

各地解析分类汇编:函数21【云南省玉溪一中2013届高三第四考次月理】函数1()0x f x x ⎧=⎨⎩,为有理数,为无理数 , 则下列结论错误的是 ( ) A . ()f x 是偶函数 B .方程(())f f x x =的解为1x =C . ()f x 是周期函数D .方程(())()f f x f x =的解为1x =【答案】D【解析】则当x 为有有理数时,x -,x T +也为有理数,则()=()f x f x -,()=()f x T f x +; 则当x 为有无理数时,x -,x T +也为无理数,则()=()f x T f x +,所以函数()f x 为偶函数且为周期函数,所以A,C 正确.当x 为有有理数时, (())(1)f f x f x ==,即1x =,所以方程(())f f x x =的解为1x =,C 正确.方程(())()f f x f x =可等价变形为()=1f x ,此时与方程()=1f x 的解为x 为有理数,故D 错误,故选D2【云南省玉溪一中2013届高三上学期期中考试理】已知对数函数()log a f x x =是增函数,则函数(||1)f x +的图象大致是( )【答案】B【解析】因为函数为增函数,所以1a >,又函数(||1)f x +为偶函数。
当0x >时,(||1)(1)log (1af x f x x +=+=+,当0x <时,(||1)(1)log (1)a f x f x x +=-+=-+,选B. 3【云南师大附中2013届高三高考适应性月考卷(三)理科】下列函数中既不是奇函数也不是偶函数的是 ( ) A.||2x y =B.1(y g x =+C.22x x y -=+D.111y gx =+【解析】根据奇偶性定义知,A 、C 为偶函数,B 为奇函数,D 定义域为{|1}x x >-不关于原点对称,故选D.4【云南省玉溪一中2013届高三第三次月考 理】若)(x f 是偶函数,且当0)1(,1)(,),0[<--=+∞∈x f x x f x 则时的解集是( )A .(-1,0)B .(-∞,0) (1,2)C .(1,2)D .(0,2)【答案】D【解析】 根据函数的性质做出函数()f x 的图象如图.把函数()f x 向右平移1个单位,得到函数(1)f x -,如图,则不等式(1)0f x -<的解集为(0,2),选D.5【云南省玉溪一中2013届高三第三次月考 理】已知在函数||y x =([1,1]x ∈-)的图象上有一点(,||)P t t ,该函数的图象与 x 轴、直线x =-1及 x =t 围成图形(如图阴影部分)的面积为S ,则S 与t 的函数关系图可表示为( )【答案】B【解析】由题意知,当10t -<<时,面积原来越大,但增长的速度越来越慢.当0t >时,S 的增长会越来越快,故函数S 图象在y 轴的右侧的切线斜率会逐渐增大,选B .6【云南省玉溪一中2013届高三第三次月考 理】定义在R 上的函数()f x 满足()(),(2)(2)f x f x f x f x -=--=+且(1,0)x ∈-时,1()2,5xf x =+则2(log 20)f =A .1B .45C .1-D .45- 【答案】C【解析】由()(),(2)(2),f x f x f x f x -=--=+可知函数为奇函数,且(4)()f x f x +=,所以函数的周期为4,24log 205<<,20log 2041<-<,即225log 204log 4-=,所以22222554(log 20)(log 204)(log )(log )(log )445f f f f f =-==--=-,因为241l og 05-<<,所以24lo g 524141(l o )215555f =+=+=,所以2224(lo g 20)(l o g 204)(log5f ff =-=-=-,选C. 7【云南省昆明一中2013届高三新课程第一次摸底测试理】函数()2x f x e x =+-的零点所在的区间是A .1(0,)2B .1(,1)2C .(1,2)D .(2,3)【答案】A【解析】函数()2x f x e x =+-,在定义域上单调递增,(0)120f =-<,(1)10f e =->,13()022f ==>,由跟的存在定理可知函数的零点在区间1(0,)2上选A. 8【云南省昆明一中2013届高三新课程第一次摸底测试理】已知偶函数(),(2)(),[1,0]f x x R f x f x x ∀∈-=-∈-对都有且当时 ()2,(2013)x f x f =则=A .1B .—1C .12D .12-【答案】C【解析】由(2)()f x f x -=-得(4)()f x f x -=,所以函数的周期是4,所以11(2013)(45031)(1)(1)22f f f f -=⨯+==-==,选C. 9【天津市耀华中学2013届高三第一次月考理科】已知函数2()=f x x cos x -,则(0.6),(0),(-0.5)f f f 的大小关系是A 、(0)<(0.6)<(-0.5)f f fB 、(0)<(-0.5)<(0.6)f f fC 、(0.6)<(-0.5)<(0)f f fD 、(-0.5)<(0)<(0.6)f f f 【答案】B 【解析】因为函数2()=f x x cos x -为偶函数,所以(0.5)(0.5)f f -=,()=2f 'x x sin x +,当02x π<<时,()=20f 'x x s i n x +>,所以函数在02x π<<递增,所以有(0)<(0.5)<(0.6)f f f ,即(0)<(0.5)<(0.6)f f f -,选B.10【天津市耀华中学2013届高三第一次月考理科】在下列区间中,函数()=+43x f x e x -的零点所在的区间为 A 、(1-4,0) B 、(0,14) C 、(14,12) D 、(12,34)【答案】C 【解析】1114441()=2=1604f e e --<,121()=102f e ->,所以函数的零点在11(,)42,选C.11【天津市新华中学2013届高三上学期第一次月考数学(理)】 已知函数()()2531m f x m m x --=--是幂函数且是()0,+∞上的增函数,则m 的值为A. 2B. -1C. -1或2D. 0【答案】B【解析】因为函数为幂函数,所以211m m --=,即220m m --=,解得2m =或1m =-.因为幂函数在(0,)+∞,所以530m -->,即35m <-,所以1m =-.选B. 12【天津市新华中学2013届高三上学期第一次月考数学(理)】 已知定义在区间[0,2]上的函数=()y f x 的图象如图所示,则=(2-)y f x 的图象为【答案】A【解析】当0x =时,(20)(2)1y f f =-==,排除B,C,D,选A.13【天津市新华中学2013届高三上学期第一次月考数学(理)】给定函数①12=y x -,②23+3=2xx y -,③12=log |1-|y x ,④=sin2xy π,其中在(0,1)上单调递减的个数为A. 0B. 1 个C. 2 个D. 3个【答案】C【解析】①为幂函数,102-<,所以在(0,1)上递减.②223333()24x x x -+=-+,在(0,1)上递减,所以函数23+3=2x x y -在(0,1),递减.③1122log 1log 1y x x =-=-,在(0,1)递增.④sin2y x π=的周期,4T =,在(0,1)上单调递增,所以满足条件的有2个,选C.14【天津市新华中学2013届高三上学期第一次月考数学(理)】设3=2a log ,=2b ln ,12=5c -,则 A. <<a b c B. <<b c aC. <<c a bD. <<c b a【答案】C【解析】321log 2log 3=,21ln 2log e =,125-=222log 3log 0e >>>>,所以22110log 3log e<<<,即c a b <<。
【解析】天津市新华中学2013届高中三年级上学期第一次月考-历史试题

新华中学2012-2013学年度第一学期高三年级第一次月考历史试卷一、选择题(本大题共32小题,每小题1.5分,共48分)1. 下图是汉墓画像石中的《周公辅佐成王图》。
对这幅图历史涵的推测与历史事实基本吻合的应是A. 图中诸侯四方来朝,反映了成王时期中央集权制度已经形成B. 图中成王地位至尊,说明成王时已经实现了权力的高度集中C. 图中成王厉行分封制,诸侯对周王的义务得到了严格履行D. 图中成王勤政爱民,统治者的品行成为政治权利之间的主要纽带【答案】C【解析】考察商周时期的政治制度,周推行宗法制、分封制、礼乐制度。
商周时期尚未实现权力的高度集中,中央集权制尚未形成,血缘关系与政治关系相结合,政治权利之间的主要纽带是血缘关系。
2. 《中国文化史》“盖宋之政治,士大夫之政治也。
”能够支撑这个观点的史实是A. 中书门下和枢密院分割相权B. 派文臣到地方做知州C. 置通判监督地方长官D. 设转运使将财权收归中央【答案】B【解析】考察宋加强中央集权的措施,宋为加强中央集权,削弱地方势力,派文臣任地方官,出现了“士大夫之政治”。
3. 唐朝某中央机构的职能为:“凡百官奏钞(文书),侍中审定,则先读而署之,以驳正违失。
”该机构是A. 尚书省B. 中书省C. 门下省D. 御史台【答案】C【解析】考察隋唐时期的三省六部制的。
三省分工明确,中书省起草诏令,门下省封驳审议、尚书省下设六部负责执行,所以该机构应为门下省。
4. 我国是一个重视制度创新的国度。
分封制、郡县制、行省制都对我国的政治发展产生过深远影响。
对于这三种政治制度,下列说确的是A. 都是与宗法制互为表里的制度B. 都加强了中央集权C. 地方长官都通过任命产生D. 都为历代统治者的持久统治提供了制度保障【答案】D【解析】考察中国古代地方制度的演变。
分封制与宗法制互为表里,分封制实行层层分封,不利于加强中央集权,分封制下地方长官世袭而来,但三者都为历代统治者的持久统治提供了制度保障。
天津市新华中学高三数学上学期第一次月考试题理(最新整理)

天津市新华中学2018届高三数学上学期第一次月考试题 理一、选择题(每小题4分,共32分)1. 设集合{}()=⋂⎭⎬⎫⎩⎨⎧≤--=>=B A C x x x B x x A R ,则041|,3|( ) A ()3,1 B []3,1 C ()4,3 D [)4,32. 函数()22-+=x x f x 的零点所在的区间是( )A ()1,-∞-B ()0,1-C ()1,0D ()2,13. 下列命题中,说法正确的个数是( )(1)若q p ∨为真命题,则q p ,均为真命题(2)命题“02,00≤∈∃x R x ”的否定是“02,>∈∀x R x " (3)“5≥a ”是“[]恒成立0,2,12≤-∈∀a x x "的充分条件(4)在””是“中,“B A b a ABC sin sin >>∆的必要不充分条件(5)命题“1,12==x x 则若”的否命题为:“1,12≠=x x 则若” A 0 B 1 C 2 D 34. a A b B A c b a C B A ABC 2cos sin asin ,,,,2=+∆,所对的边分别为的三个内角,则ab=( ) A 32 B 22 C 3 D 25. 若将函数()x x x f 2cos 2sin +=的图像向右平移ϕ个单位,所得图像关于y 轴对称,则ϕ的最小正值是( ) A8π B 4π C 83π D 43π 6. 已知正方形ABCD 的中心为O 且其边长为1,则()()BC BA OA OD +⋅-=( )A 3B 21C 2D 17. 函数)(x f 是R 上的增函数且())(cos sin )cos ()(sin ωωωωf f f f +->-+ ,其中ω是锐角,并且使得函数()⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+=πππω,24sin 在x x g 上单调递减。
则ω的取值范围是( )A ⎥⎦⎤ ⎝⎛45,4πB ⎪⎭⎫⎢⎣⎡4,45πC ⎪⎭⎫⎢⎣⎡4,21πD ⎥⎦⎤⎢⎣⎡45,218. 已知定义在R 上的函数)(x f y =满足:函数)1(+=x f y 的图像关于直线1-=x 对称,且当()0)()(,0,<'+∞-∈x f x x f x ()(x f '是函数)(x f 的导函数)成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
天津新华中学2012-2013学年度第一学期高三年级第一次月考数学试卷(理科)一、选择题:(本大题共8小题,每小题4分,共32分.)在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合2A={|log <1},B={x|0<<c}x x x ,若=A B B ,则c 的取值范围是A. (0,1]B. [1,+)∞C. (0,2]D. [2,+)∞【答案】D【解析】2{log 1}{01}A x x x x =<=<<.因为AB B =,所以A B ⊆.所以1c ≥,即[1,)+∞,选B.2. 已知命题:"[1,2],-0"2p x x a ∀∈≥,命题:"R,+2+2=0"2q x x ax -a ∃∈使,若命题“p q 且”是真命题,则实数a 的取值范围是A. {|-2=1}a a a ≤或B. {|-2}a a ≤C. {|-22}a a a ≤≤≤或1D. {|-21}a a ≤≤ 【答案】A【解析】由20x a -≥,得2,[1,2]a x x ≤∈,所以1a ≤.要使q 成立,则有244(2)0a a ∆=--≥,即220a a +-≥,解得1a ≥或2a ≤-.因为命题“p q 且”是真命题,则,p q 同时为真,即112a a a ≤⎧⎨≥≤-⎩或,即2a ≤-或1a =,选A.3. 已知函数()()2531m f x m m x --=--是幂函数且是()0,+∞上的增函数,则m 的值为 A. 2 B. -1 C. -1或2 D. 0【答案】B【解析】因为函数为幂函数,所以211m m --=,即220m m --=,解得2m =或1m =-.因为幂函数在(0,)+∞,所以530m -->,即35m <-,所以1m =-.选B.4. 已知定义在区间[0,2]上的函数=()y f x 的图象如图所示,则=(2-)y f x 的图象为【答案】A【解析】当0x =时,(20)(2)1y f f =-==,排除B,C,D,选A.5. 给定函数①12=y x -,②23+3=2xx y -,③12=log |1-|y x ,④=sin2xy π,其中在(0,1)上单调递减的个数为 A. 0 B. 1 个 C. 2 个 D. 3个【答案】C【解析】①为幂函数,102-<,所以在(0,1)上递减.②223333()24x x x -+=-+,在(0,1)上递减,所以函数23+3=2xx y -在(0,1),递减.③1122log 1log 1y x x =-=-,在(0,1)递增.④sin 2y x π=的周期,4T =,在(0,1)上单调递增,所以满足条件的有2个,选C. 6. 设3=2a log ,=2b ln ,12=5c -,则A. <<a b cB. <<b c aC. <<c a bD. <<c b a【答案】C【解析】321l o g 2l o g 3=,21ln 2log e =,12155-=。
因为2252log 3log 0e >>>>,所以221110log 3log 5e<<<,即c a b <<。
选C. 7. 函数()f x 的定义域为R ,若(1)f x +与(1)f x -都是奇函数,则 A. ()f x 是偶函数 B. ()f x 是奇函数 C. ()(2)f x f x =+ D. (3)f x +是奇函数【答案】D【解析】函数(1)f x +,(1)f x -都为奇函数,所以(1)(1)f x f x -+=-+,(1)(1)f x f x -=---,所以 函数()f x 关于点(1,0),(1,0)-对称,所以函数的周期4T =,所以(14)(14)f x f x -+=---+,即(3)(3)f x f x +=--+,所以函数(3)f x +为奇函数,选D.8. 设函数1(1)|-1|)=1(=1)x x f x x ⎧≠⎪⎨⎪⎩(,若关于x 的方程2[()]+()+c=0f x bf x 有三个不同的实数根123,,x x x ,则222123++x x x 等于A. 13B. 5C. 223c +2c D. 222b +2b【答案】B【解析】做出函数()f x 的图象如图,要使方程2[()]+()+c=0f x bf x 有三个不同的实数根,结合图象可知,()1f x =,所以三个不同的实数解为0,1,2,所以2221235x x x ++=,选B.二、填空题:(本大题共6小题,每小题4分,共24分.)把答案填在题中横线上. 9. 若121()=log (2+1)f x x ,则()f x 的定义域为 .【答案】1(,0)2-【解析】要使函数有意义,则有12210log (21)0x x +>⎧⎪⎨+>⎪⎩,即12211x x ⎧>-⎪⎨⎪+<⎩,所以解得102x -<<,即不等式的定义域为1(,0)2-. 10. 已知(+1)=1f x x -,则()=f x (x ∈ ). 【答案】2()2f x x x =-,[1,)x ∈+∞ 【解析】令1t x =+,则1t ≥,2(1)x t =-,所以22()(1)12f t t t t =--=-,所以2()2f x x x =-,[1,)x ∈+∞.11. 函数212()=log (-2-3)f x x x 的单调递减区间为 .【答案】(3,)+∞【解析】令223t x x =--,则12log y t =在定义域上为减函数.由2230t x x =-->得,3x >或1x <-,当3x >时,函数223t x x =--递增,根据复合函数的单调性可知,此时函数()y f x =单调递减,所以函数的递减区间为(3,)+∞.12. 已知函数2=+-1+2y x ax a 的值域为[0,+)∞,则a 的取值范围是 . 【答案】423a ≥+或423a ≤-【解析】令2()12t g x x ax a ==+-+,要使函数y t =的值域为[0,)+∞,则说明[0,){()}y y g x +∞⊆=,即二次函数的判别式0∆≥,即24(21)0a a --≥,即2840a a -+≥,解得423a ≥+或423a ≤-,所以a 的取值范围是423a ≥+或423a ≤-.13. 已知x R ∀∈,(1+)=(1-)f x f x ,当1x ≥时,()=(1)f x ln x+,则当<1x 时,()=f x . 【答案】ln (3-x)【解析】由(1)(1)f x f x +=-,可知函数关于1x =对称,当1x <时,21x ->,所以()(2)l n [(2)1]lf x f x x x =-=-+=-. 14. 定义:如果函数)(x f y =在定义域内给定区间b][,a 上存在)(00b x a x <<,满足ab a f b f x f --=)()()(0,则称函数)(x f y =是b][,a 上的“平均值函数”,0x 是它的一个均值点,如4x y =是]1,1[-上的平均值函数,0就是它的均值点.现有函数1)(2++-=mx x x f 是]1,1[-上的平均值函数,则实数m 的取值范围是 . 【答案】(0,2)【解析】因为函数1)(2++-=mx x x f 是]1,1[-上的平均值函数,所以(1)(1)1(1)f f m --=--,即关于x 的方程21x mx m -++=,在(1,1)-内有实数根,即210mx mx m -+-=,若0m =,方程无解,所以0m ≠,解得方程的根为11x =或21x m =-.所以必有111m -<-<,即02m <<,所以实数m 的取值范围是02m <<,即(0,2).三、解答题:(本大题共4小题,共44分.)解答应写出文字说明,证明过程或演算步骤. 15. (本小题满分10分)已知(+1)(2-)0x x ≥的解为条件p ,关于x 的不等式222+-2-3-1<0(>-)3x mx m m m 的解为条件q . (1)若p 是q 的充分不必要条件时,求实数m 的取值范围. (2)若p ⌝是q ⌝的充分不必要条件时,求实数m 的取值范围. 16. (本小题满分10分)已知={()|1},B={()|3,0x 3}2A x,y y =-x +mx -x,y x+y =≤≤,若AB ⋂是单元素集,求实数m 的取值范围.17. (本小题满分12分)已知函数()f x 对任意实数,x y 恒有()()()f x y f x f y +=+,且当x >0时,()0f x <又(1)2f =-.(1)判断()f x 的奇偶性;(2)求证:()f x 是R 上的减函数; (3)求()f x 在区间[-3,3]上的值域;(4)若x R ∀∈,不等式2()2()()4f ax f x f x -<+恒成立,求a 的取值范围. 18. (本小题满分12分)对于函数()f x 若存在0x R ∈,00()=f x x 成立,则称0x 为()f x 的不动点.已知2()=(1)-1(0)f x ax b x b a +++≠(1)当=1,=-2a b 时,求函数(f x )的不动点;(2)若对任意实数b ,函数()f x 恒有两个相异的不动点,求a 的取值范围;(3)在(2)的条件下,若=()y f x 图象上A 、B 两点的横坐标是函数()f x 的不动点,且A 、B 两点关于直线2121y kx a =++对称,求b 的最小值.【试题答案】一、选择题: 题号 1 2 3 4 5 6 7 8 答案 D ABACCDB二、填空题: 9. 1(-,0)210. 2-2x x ,[1,+)∞ 11. (3,+)∞12. 4+234-23a a ≥≤或 13. ln (3-x) 14. (0,2)三、解答题:15. 解:(1)设条件p 的解集为集合A,则2}x -1|{x ≤≤=A 设条件q 的解集为集合B,则1}m x 1--2m |{x +<<=B 若p 是q 的充分不必要条件,则A 是B 的真子集13211221>⇒⎪⎪⎩⎪⎪⎨⎧->-<-->+m m m m (2)若p ⌝是q ⌝的充分不必要条件, 则B 是A 的真子集0323211221≤<-⇒⎪⎪⎩⎪⎪⎨⎧->-≥--≤+m m m m16. 解:A B ⋂是单元素集[]3,0,3y x x ∴=-∈与21y mx x =-+-有一个交点即方程2(1)40m x x-++=在[]0,3有一个根,0(1)1032m ∆=⎧⎪⎨+≤≤⎪⎩ 解得3m =(2)(0)(3)f f ⋅< 解得103m >(3)若0x =,方程不成立(4)若3x =,则103m =,此时方程213403x x -+=根为3x =或43x = 在[]0,3上有两个根 ,不符合题意 综上103m >或3m = 17.(1)解:取,0==y x 则0)0()0(2)00(=∴=+f f f取)()()(,x f x f x x f x y -+=--=则)()(x f x f -=-∴对任意R x ∈恒成立 ∴)(x f 为奇函数.18. 解:(1)2,1-==b a 时,3)(2--=x x x f ,3,1032)(2=-=⇒=--⇒=x x x x x x f∴函数)(x f 的不动点为-1和3;(2)即x b x b ax x f =-+++=1)1()(2有两个不等实根,转化为012=-++b bx ax 有两个不等实根,需有判别式大于0恒成立即10044)4(0)1(422<<⇒<⨯--=∆⇒>--a a a b a b ,a ∴的取值范围为10<<a ; (3)设),(),,(2211x x B x x A ,则abx x -=+21, A ,B 的中点M 的坐标为)2,2(2121x x x x ++,即)2,2(aba b M - B A 、 两点关于直线1212++=a kx y 对称,又因为A ,B 在直线x y =上,1-=∴k ,A ,B 的中点M 在直线1212++=a kx y 上.aa a a a ab a b 121121212222+-=+-⇒=++=∴, 利用基本不等式可得当且仅当22=a 时,b 的最小值为221.。
