第八讲期权二叉树定价模型
第八章 期权及其二叉树模型

二、以债券为标的资产的期权定价
设以例[8-8]中的债券 为标的资产、执行价X=100的 看涨期权, 在t时期市场上价格为Ct,它的收益如下: 图 8-48
Cd,1m ax(Bd,1票 息 -X,0) =13.77
?
Cu,1max(Bu,1票 息 -X,0) =15.22
为了达到期权定价的目的。与以股票为标的看涨期 权定价理论一样,构造一个无风险套期保值债券组合;购 买一份债券,出售m份看涨期权(以该债券为标的的看 涨期权)。
若是无风险套期保值,此债券组合在到期时的支付 (收益)是一样的。设看涨期权在t期执行,则此债券组 合在t+1期时两个状态的收益相等 。
Bd,t+1 +票息- mCd,t+1= B u,t+1 +票息- mCu,t+1
m= Bdt1 But1 Cdt1 Cut1
由于是无风险债券组合,故有 (Bt- mCt )(1+rt/2)= Bd t+1 +票息- mCdt+1
t 期债券价格:
BpBdt11pBut1票息
t
1rt
2
例 [8-8] 设初始利率为r=10%,在第二期以q=0.5的概 率上升到12%,以0.5的概率下降到d=8.5%。同时假设债 券的面值D=100在一年期半内每半年支付的红利10, 而 每期初债券的价值是期末支付的期望值的折现,求债券 的价格。如图 8-47
第八章 期权及其二叉树模型
金融期权(financial option)简称为期权是主要的金 融衍生产品,它是金融工程的主要工具,也是构成金融工程 其它金融衍生产品的基础。
期权合约是买卖双方签定的一种协议,该协议赋予期 权购买者在未来某一时刻以事先约定的价格购买(或出售) 某一资产的权利。但是,那时他可以行使他的权利也可 以不行使这个权利。
金融工程学(期货)第八单元:二叉树模型

股票价格=$22 期权价格=$1 股票价格 =$20 现时刻 T时刻 股票价格=$18 期权价格=$0
无风险利率为12%(年率),期权期限是三个月
一个无风险证券组合为 多头:0.25股股票 空头:一个期权 如果股票价格上升到$22,或股票价格下降到 $18,该组合的价值都为$4.5 无套利机会存在,则无风险证券组合的收益率 也是无风险利率。 该组合的现值为:4.5e-0.12*0.25=4.367 即:20*0.25-f=4.367,f是期权的价格 f=0.633
复制组合(Synthetic Portfolio): 持有N股股票的多头,并出售一个看涨期权, 在一个时期后,将得到确定的收益。也可以通 过投资于无风险债券而获得确定的收益。 N股股票的多头+1个看涨期权的空头=无风险借款 稍加变形我们得到:股票+债券可以复制期权Βιβλιοθήκη ② 一般结论 S 现时刻 f
Su fu
f=e-2rΔt[p2fuu+2p(1-p)fud+(1-p)2fdd] 结论:衍生工具的价格等于它在风险中性世界的 预期收益按无风险利率贴现值.
多步二叉树
• 股票价格树图
SU3 SU2 SU2 SU SU S SD S
SU5
SU4
SU3
SU
S
SD SD2 SD3
SD2
SD
SD2
SD4 SD5
• • •
节点B,提前执行期权的损益为-$8,按公式计算 值为$1.4147.选择$1.4147. 节点C,提前执行期权的损益为$12.0,按公式计 算值为$9.4636.选择$12.0. 节点A,提前执行期权的损益为$2.0,按公式计算 值为$5.0894.选择$5.0894. 72
期权定价二叉树模型

9 e
0.10.25
8.78
• 这也应该是期初用于投资组合的资金,由 此得:
1 30 C 8.78, C 10 8.78 1.22 3 • 买入期权的价格应该定为1.22元
三、期权定价的二项式公式
符号: S 0 股票在期初的价格, S X 期权确定的执行价格, u 股票价格在单个时间阶段内的上升因子 d 股票价格在单个时间阶段内的下降因子(-) Ru 期权在股票价格上升状态下的收益 Rd 期权在股票价格下降状态下的收益 r 年无风险收益率 T 期权的期限
7.14 qu max{ S 0 (1 u ) 3 (1 d ) S X ,0} q d max{ S 0 (1 u ) 2 (1 d ) 2 S X ,0}
0.33 qu max{ S 0 (1 u ) 2 (1 d ) 2 S X ,0} q d max{ S 0 (1 u )(1 d ) 3 S X ,0}
n n i i n i i C i qu q d max{ S 0 (1 u ) (1 d ) S X ,0} i 0
n
n n! n (n 1) (n i 1) , n 0,1, i (i 1) 1 i (n i )!i !
0 qu max{ S 0 (1 u ) 3 (1 d ) S X ,0} qd max{ S 0 (1 d ) 4 S X ,0}
对于第2阶段各状态期权价值有
2 13.7 qu 18.03 q d 7.14 qu max{ S 0 (1 u ) 4 S X ,0}
计算相关数据
u (e rT 1) ud 0.1 (e 0.05 1) 0.1 0.05 0.324859
期权二叉树定价模型

期权二叉树定价模型期权二叉树定价模型是一种常用的金融衍生品定价模型,用于计算期权合约的公平价格。
该模型基于二叉树的数据结构,将时间分为离散的步长,在每个步长上模拟期权的价格变化。
在期权二叉树定价模型中,二叉树的每个节点表示期权的一个可能价格,树的每一层表示时间的一个步长。
从根节点开始,根据期权的流动性和到期前可执行的次数,构建二叉树模型。
在每个节点上,计算期权的价值,以确定其合理价格。
在构建二叉树模型时,需要考虑期权的标的价格、波动率、到期时间和无风险利率等因素。
这些因素将被用来计算每个节点上的期权价格。
在每个步长上,通过向上或向下移动树的节点,模拟标的价格的波动,从而更新节点上的期权价格。
在二叉树的叶子节点上,期权的价值是已知的,可以直接计算。
在其他节点上,通过对未来价格的概率分布进行加权,计算期权的合理价格。
树的最后一层即为到期时间,即期权到期时的状态。
根据到期状态计算出期权的现值,并通过向根节点回溯,确定期权的公平价格。
期权二叉树定价模型的优点在于能够在离散时间步长上快速确定期权的价格,并且可以灵活地应用于不同类型的期权合约。
此外,该模型对于包含多个期权合约的复杂结构,如欧洲期权、美式期权和亚洲期权等,也具有较高的适用性。
然而,期权二叉树定价模型也存在一些局限性。
首先,该模型假设标的价格的波动服从几何布朗运动,这在实际市场中并不成立,因此模型的有效性有一定的限制。
其次,通过选择适当的步长数和树的深度来平衡精确度和计算效率是一个挑战。
总的来说,期权二叉树定价模型是一个常用且有效的金融工具,可以用于估计期权合约的公平价格。
该模型基于二叉树的数据结构,通过离散时间步长模拟期权的价格变化,并通过回溯计算确定期权的公平价格。
虽然该模型存在一定的局限性,但在实际应用中仍被广泛应用。
期权二叉树定价模型是一种基于离散时间步长和二叉树结构的金融衍生品定价模型。
它是Black-Scholes模型的一种改进方法,通过模拟期权价格的变化来计算期权的公平价格。
期权定价的二叉树模型
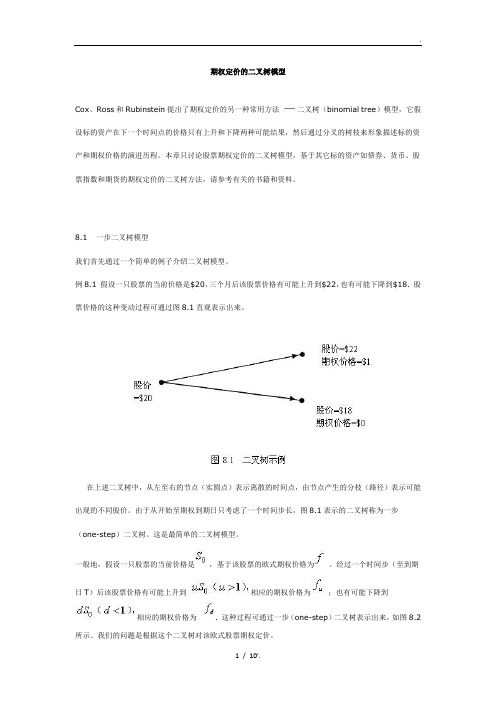
期权定价的二叉树模型Cox、Ross和Rubinstein提出了期权定价的另一种常用方法二叉树(binomial tree)模型,它假设标的资产在下一个时间点的价格只有上升和下降两种可能结果,然后通过分叉的树枝来形象描述标的资产和期权价格的演进历程。
本章只讨论股票期权定价的二叉树模型,基于其它标的资产如债券、货币、股票指数和期货的期权定价的二叉树方法,请参考有关的书籍和资料。
8.1 一步二叉树模型我们首先通过一个简单的例子介绍二叉树模型。
例8.1 假设一只股票的当前价格是$20,三个月后该股票价格有可能上升到$22,也有可能下降到$18. 股票价格的这种变动过程可通过图8.1直观表示出来。
在上述二叉树中,从左至右的节点(实圆点)表示离散的时间点,由节点产生的分枝(路径)表示可能出现的不同股价。
由于从开始至期权到期日只考虑了一个时间步长,图8.1表示的二叉树称为一步(one-step)二叉树。
这是最简单的二叉树模型。
一般地,假设一只股票的当前价格是,基于该股票的欧式期权价格为。
经过一个时间步(至到期日T)后该股票价格有可能上升到相应的期权价格为;也有可能下降到相应的期权价格为. 这种过程可通过一步(one-step)二叉树表示出来,如图8.2所示。
我们的问题是根据这个二叉树对该欧式股票期权定价。
为了对该欧式股票期权定价,我们采用无套利(no arbitrage)假设,即市场上无套利机会存在。
构造一个该股票和期权的组合(portfolio),组合中有股的多头股票和1股空头期权。
如果该股票价格上升到,则该组合在期权到期日的价值为;如果该股票价格下降到,则该组合在期权到期日的价值为。
根据无套利假设,该组合在股票上升和下降两种状态下的价值应该相等,即有由此可得(8.1)上式意味着是两个节点之间的期权价格增量与股价增量之比率。
在这种情况下,该组合是无风险的。
以表示无风险利率,则该组合的现值(the present value)为,又注意到该组合的当前价值是,故有即将(8.1)代入上式,可得基于一步二叉树模型的期权定价公式为(8.2)(8.3)需要指出的是,由于我们是在无套利(no arbitrage)假设下讨论欧式股票期权的定价,因此无风险利率应该满足: .现在回到前面的例子中,假设相应的期权是一个敲定价为$21,到期日为三个月的欧式看涨权,无风险的年利率为12%,求该期权的当前价值。
期权定价的二叉树模型

03
二叉树模型在期权定价中 的应用
二叉树模型在欧式期权定价中的应用
欧式期权定义
二叉树模型原理
欧式期权是一种只能在到期日行权的期权。
二叉树模型是一种离散时间模型,通过构造 一个二叉树来模拟股票价格的演变过程。
模型参数
定价过程
包括无风险利率、股票波动率、期权行权价 等。
从到期日逆推至起始时间,考虑各种可能的 价格路径,计算期权的预期收益,并使用无 风险利率折现至起始时间。
与其他理论的结合
二叉树模型与其它金融理论的结合也是理论研究的一个重要方向,如将二叉 树模型与随机过程理论、博弈论等相结合,以提供更深入、更全面的分析框 架。
二叉树模型的应用研究进展
扩展到其他金融衍生品
二叉树模型在期权定价方面的应用已经非常成熟,研究者们正在将其应用于其他金融衍生品的定价,如期货、 掉期等。
案例一:某公司股票期权定价
背景介绍
某上市公司股票期权激励计划需要为期权定价,以确定向员工发 放的期权数量和行权价格。
模型应用
根据二叉树模型,预测股票价格的上涨和下跌幅度,并计算期权 的内在价值和时间价值。
结论分析
根据计算结果,确定期权的行权价格和数量,实现了员工激励与公 司发展的双赢。
案例二:某交易所债券期权定价
调整利率和波动率
根据市场数据和实际情况,调整利率和波动率的参数,可以提 高模型的拟合度。
模型的选择与比较
1 2
基于误差
比较不同模型的预测误差,选择误差最小的模 型。
基于风险
比较不同模型的风险指标,选择风险最小的模 型。
3
基于解释性
选择更具有解释性的模型,以便更好地理解市 场行为和风险。
05
期权定价的二叉树模型介绍

计算期权的价值
计算期权的现值
根据预期收益和折现率,我们可以计算出期权的现值。 看涨期权的现值是每个节点的股票价格与执行价格的差 值与风险中性概率的乘积之和;看跌期权的现值是每个 节点的执行价格与股票价格的差值与风险中性概率的乘 积之和。
校准二叉树模型参数
为了使模型的预测结果与实际期权价格一致,我们需要 校准模型参数。通常,我们使用历史数据来估计参数, 例如股票价格的波动率和无风险利率。
建立二叉树
以时间步长为单位,从最后一个时间步长开始,依 次向前建立二叉树,每个节点代表一个时间步长。
确定初始股票价格
确定股票的当前价格
通常以市场价格为基础确定初始股票价格 。
考虑股息
如果股票在期权有效期内发放股息,需要 在每个时间步长上调整股票价格。
确定无风险利率与时间步长
要点一
确定无风险利率
无风险利率是投资者在相同风险水平下可以获得的最低 回报率。
05
二叉树模型的结果分析
模拟结果展示
假设一个股票价格变动模型,通过二叉树模型模拟股 票价格的涨跌情况,并计算期权的价值。
根据不同的利率和波动率等参数设置,模拟不同的股 票价格路径,从而得到期权价格的模拟结果。
结果分析与比较
将模拟结果与实际期权价格进行比较,分析二叉树模型 定价的准确性。
对比不同参数设置下的模拟结果,分析利率和波动率等 因素对期权价格的影响。
期权定价的二叉树模型介绍
2023-11-06
目 录
• 引言 • 二叉树模型基本原理 • 构建二叉树模型 • 计算期权价值 • 二叉树模型的结果分析 • 二叉树模型在金融实践中的应用 • 结论与展望
01
引言
研究背景与意义
期权二叉树定价模型

84 美式期权估值8.4.1 方法 二叉树模型可以用于为美式期权估值。方法是:从树图的最后末端向开始的起点倒推计算。在每个节点检验提前执行是否最佳。在最后节点的期权价值与欧式期权在最后节点的期权价值相同。在较早的一些节点,期杈的价值是取如下两者之中较大者: 1)由式(9.2)求出的值。 2)提前执行所得的收益。
8.2 风险中性估值8.2.1 风险中性估值原理 式(9.2)中的变量p可以解释为股票价格上升的概率,于是变量1—p就是股票价格下降的概率。这样, pfu+(1-p)fd 就是衍生证券的预期收益。于是,式(9.2)可以表述为:衍生证券的价值是其未来预期值按无风险利率贴现的值 。
当两个价值相等时 即 (9.1) 该组合是无风险的,收益必得无风险利率。在T时刻的两个节点之间运动时,Δ是衍生证券价格变化与股票价格变化之比。
最后股票的可能价格为$72、$48和$32。在这种情况下,fuu=0,fud=4,fdd=20,Δt=1,利用公式(9.8),得到看跌期权的价格 f=e-2×0.05×1(0.62822×0+ 2×0.6282×0.3718×4+0.37182×20)=4.1923 利用每个单步二步二叉树向回倒推算,也可以得到这个结果。 实际上,如果股票价格的变化是二值的,那么任何基于该股票的衍生证券都可以运用二叉树模型进行估值。
u=1.1,d=0.9,r=0.12,T=0.25,p=0.6523. 在节点B的期权价格为: e-0.12×0.25(0.6523×3.2十0.3477×0)=2.0257 在节点C,期权价格为0。 在节点A的期权价格为:e-0.12×0.25(0.6523×2.0257十0.3477×0)=1.2823 在构造这个例子时,u和d(股票价格上升和下降的比率)在树图的每个节点上是相同的,每个单步二叉树的时间长度是相等的。由式(9.3)可得风险中性的概率p,它在每个节点都是相同的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
22Δ—1=18Δ 得
Δ=0.25
是否一定为正?
因此,一个无风险的组合由0.25股股票和一个期权空头 构成。通过计算可知,无论股票价格是上升还是下降,在期
权有效期的末尾,该组合的价值总是$4.5。 第八讲期权二叉树定价模型
在无套利假设下,无风险证券组合的盈利必定为无风险 利率。
假设无风险利率为年率12%。则该组合的现值应为:
第八讲期权二叉树定价模型
第八讲期权二叉树定价模型
最后股票的可能价格为$72、$48和$32。在这种情况下, fuu=0,fud=4,fdd=20,Δt=1,利用公式(9.8),得到看跌期权的 价格
f=e-2×0.05×1(0.62822×0+ 2×0.6282×0.3718×4+0.37182×20)=4.1923
构造一个证券组合,该组合包含一个Δ股股票多头头寸 和一个看涨期权的空头头寸。是否可有多种构造方法?
第八讲期权二叉树定价模型
第八讲期权二叉树定价模型
由图8-1可知,当股票价格从$20上升到$22时,该证券组 合的总价值为22Δ-1;当股票价格从$20下降到$18时,该证 券组合的总价值为18Δ。
完全可以选取某个Δ值,使得该组合的终值对在上述两 种情况下是相等的。这样,该组合就是一个无风险组合。 由
¡ 式(9.4)说明,当设定上升运动的概率为p时,我们就在假设一个风险 中性世界 。
¡ 式(9.2)说明,衍生证券的价值是其预期收益在风险中性世界中按无 风险利率贴现的值。
¡ 以上过程表明,当为期权和其它衍生证券估值时,完全可以假设世界 是风险中性的。这就是所谓风险中性(risk-neutral valuation)原理。 在风险中性世界中得到的价格,在现实世界中也是正确的。
第八讲期权二叉树定价模型
将式(9.5)和(9.6)代入式(9.7),得到:
式中,p2,2p(1-p)和(1-p)2是达到最后上、中、下三个 节点的概率。衍生证券的价格等于它在它在风险中性世界 的预期收益按无风险利率贴现的值。
如果在树图中加入更多的步(step)以推广应用二叉树图 方法,风险中性估值的原理一直是成立的。衍生证券的价 格总是等于它在风险中性世界的预期收益按无风险利率贴 现的值。
衍生证券定价公式(9.2)并没有用到股票上升和下降 的概率。这似乎不符合人们的直觉,因为人们很自然地假 设假设如果股票价格上升的概率增加,基于该股票的看涨 期权价值也增加,看跌期权的价值则减少。
之所以如此,原因在于,我们并不是在完全的条件下为 期权估值,而只是根据标的股票的价格估计期权的价值。 未来上升和下降的概率已经包含在股票的价格中。它说明, 当根据股票价格为期权估值时,我们不需要股票价格上涨 下降的概率。
一个证券组合由Δ股的股票多头和一个衍生证券空头构 成。
如果股票价格上升,在有效期末该组合的价值为:
如果股票价格下降,在有效期末该组合的价值为:
第八讲期权二叉树定价模型
第八讲期权二叉树定价模型
当两个价值相等时 即
(9.1)
该组合是无风险的,收益必得无风险利率。在T时刻的 两个节点之间运动时,Δ是衍生证券价格变化与股票价格变 化之比。
如图8-6所示,在节点B,期权的价值为$1.4147,而 提前执行期权的损益为负值(-$8)。在节点B提前执行不是 明智的,此时期权价值为1.4147。在节点C,期权的价值 为$9.4636,而提前执行期权的损益为$12.0。在这种情况 下,提前执行是最佳的,因此期权的价值为$12.0。
第八讲期权二叉树定价模型
第八讲期权二叉树定价 模型
2020/11/27
第八讲期权二叉树定价模型
§8.1 单步二叉树图
Ø 8.1.1 二叉树图的构造
¡问题 假设一种股票当前价格为$20,三个月后的价格
将可能为$22或$18。假设股票三个月内不付红利。有 效期为3个月的欧式看涨期权执行价格为$21。如何对 该期权进行估值?
第八讲期权二叉树定价模型
第八讲期权二叉树定价模型
§8.2 风险中性估值
Ø 8.2.1 风险中性估值原理
式(9.2)中的变量p可以解释为股票价格上升的概率, 于是变量1—p就是股票价格下降的概率。这样,
pfu+(1-p)fd 就是衍生证券的预期收益。于是,式(9.2)可以表述为: 衍生证券的价值是其未来预期值按无风险利率贴现的值 。
第八讲期权二叉树定价模型
§ 9.6 二叉树模型在实际中的应用
在实际中应用二叉树图方法时,通常将期权有效期分 成30或更多的时间步。在每一个时间步,就有一个二叉树 股票价格运动。30个时间步意味着最后有31个终端股票价 格(terminal stock prices),并且230即大约10亿个可能的股 票价格路径。
如果在第一个时间步之后,还有一个向下的运动,则 在第二个时间步股票价格变动的Delta为:
第八讲期权二叉树定价模型
在图8-5中,第一个时间步的Delta为:
在第二个时间步,有两个Delta:
或者
第八讲期权二叉树定价模型
上面的两个例子说明,Delta值随时间而变化。这意味 着利用期权和标的股票来保持一个无风险对冲,我们需要 定期调整我们所持有的股票数量。
第八讲期权二叉树定价模型
同样,按照上式对p的解释,在T时刻预期的股票价格
即
将式(9.2)中的p代入上式,得
E(ST)=SerT
(9.4)
这表明,平均来说,股票价格以无风险利率增长。因
此,设定上升运动的概率等于p就是等价于假设股票收益等
于无风险利率。
第八讲期权二叉树定价模型
¡ 我们把每一个人是风险中性的世界称为风险中性世界( risk-neutral world )。在这样的世界中,投资者对风险不要求补偿,所有证券的预 期收高效益是无风险利率。
第八讲期权二叉树定价模型
在初始节点A,求出的期权价值为: f= e-0..05×1(0.6282×1.4147+0.3718×12.0) =5.0894
而提前执行的价值为$2.0。在这种情况下,提前执行是不 明智的。因此期权的价值为$5.0894。
第八讲期权二叉树定价模型
8.5 Delta
8.5.1 Delta的含义
Ø 股票期权的Delta是股票期权价格的变化与标的股票价格 的变化之比,是为了构造一个无风险对冲,对每一个卖 空的期权头寸我们应该持有的股票数目。
Ø 构造无风险对冲有时就称之为Delta对冲(delta hedging)。 Ø 看涨期权的Delta是正值,而看跌期权的Delta是负值。
第八讲期权二叉树定价模型
第八讲期权二叉树定价模型
Ø 8.3.2 一般结论
如图8-4所示,初始股票价格为S。在每个单步二叉树 中,股票价格或者上升到初始值的u倍,或下降到初始值 的d倍。假设无风险利率是r。每个单步二又树的时间长 度是Δt年。
重复式(9.2)的计算,给出: (9.5)
(9.6)
(9.7)
第八讲期权二叉树定价模型
假设在每个单步二叉树的步长是三个月,无风险利 率是年率12%。考虑一个执行价格为$21的期权。
在图8-3中,很容易得到,在节点D,期权价格为 $3.2;在节点E和F,期权价格为零。
在节点B的期权价格计算如下:
第八讲期权二叉树定价模型
第八讲期权二叉树定价模型
u=1.1,d=0.9,r=0.12,T=0.25,p=0.6523. 在节点B的期权价格为: e-0.12×0.25(0.6523×3.2十0.3477×0)=2.0257 在节点C,期权价格为0。 在节点A的期权价格为: e-0.12×0.25(0.6523×2.0257十0.3477×0)=1.2823 在构造这个例子时,u和d(股票价格上升和下降的比率) 在树图的每个节点上是相同的,每个单步二叉树的时间长 度是相等的。由式(9.3)可得风险中性的概率p,它在每个 节点都是相同的。
从股票价格波动率,可以确定u和d的值。可以有许多 种不同的方式做到这一点。
第八讲期权二叉树定价模型
3rew
演讲完毕,谢谢听讲!
再见,see you again
2020/11/27
第八讲期权二叉树定价模型
第八讲期权二叉树定价模型
Ø 8.3.3 看跌期权的例子
考虑一个两年期欧式看跌期权,股票的执行价格为 $52,当前价格为$50。
假设价格为两步二叉树,每个步长为一年。在每个单 步二叉树中股票价格或者按比率上升20%,或者按比率 下降20%。无风险利率为5%。
构造如图8-5所示的两步二叉树图。风险中性概率P的 值为:
Ø 8.5.2 Delta的计算
以图8-2所示的看涨期权估值为例,该看涨期权的 Delta计算如下:
这是因为当股票价格从18变化到22时,期权价格从0 变化到1。
在图8-3中,对于第一个时间步,股票价格变动的 Delta为:
第八讲期权二叉树定价模型
如果在第一个时间步之后,还有一个向上的运动,则 在第二个时间步股票价格变动的Delta为:
第八讲期权二叉树定价模型
用r表示无风险利率,该组合的现值应为: 而构造该组合的成本是:
因此
第八讲期权二叉树定价模型
将式(9.1)代入上式,得到
其中
(9.3)风险中性概率
运用单步二叉树图方法,式(9.2)和(9.3)就可为衍 生证券估值。
第八讲期权二叉树定价模型
Байду номын сангаас
Ø 8.1.3 股票预期收益的无关性
¡思路 根据期权的特性,显然可以用图8-1所示的二叉树图来描
述股票和期权的价格运动。 如果能够用这种股票和期权构造一个组合,使得在三个
月末该组合的价值是确定的,那么,根据该组合的收益率等 于无风险收益率(无套利假设),可以得到构造该组合所需 成本(现值),而组合中股票的价格是已知的,于是可以得 出期权的价格。
