自动控制原理-matlab_simulink自控实验作业-范云飞
2016 《自动控制原理》实验指导书 simulink版_电气专业_看图王

点击工具栏中的 Simulink 选项 能够进入仿真环境,如图所示。
、或者在编辑区命令行>>后键入 simulink↲,就
Simulink
图 启动 SIMULINK
模块库浏览器展示了在你的系统中已经安装的 Simulink 模块库。你需要从模块库中复 制模块到模型窗口。
如果划线错误,先鼠标左键选中连线,然后点击 delete 键。 划线连接 sum 和 gain 模块。 同样划线连接 gain 到 pi controller,pi controller 到 plant,plant 到 scope。现在完成的 连线如图所示。
剩余的线是反馈信号的连接,需要连接 plant 到 sum。这条线不同的是:首先因为这条 线,并不一定简单地按照最短(直角)的路线,所以它需要在几个不同的地方绘制。其次, 没有一个模块具有多余的输出端,所以这一行必须从现有的线中引出。
关闭对话框,注意现在 simulink 模型的 gain 模块显示的是变量 k 而不是数字了。
11
山东科技大学
自动控制原理实验指导书
[Simulink 仿真]
现在你可以再次运行仿真,观察 scope 输出去下,你发现结果是和刚才一样的。
如果 MATLAB 中任何计算修改了变量,下一次运行 simulink 模型仿真的时候会使用 新的变量值。例如在 MATLAB 命令行提示符>>后输入 k=5。再次运行仿真,观察 scope 窗 口,单击 sutoscale 按钮,你会发现输出变大了。
双击文字 PID Controller 修改名称为 PI Controller 。
《自动控制原理》控制系统的simulink仿真实验一

《自动控制原理》控制系统的simulink仿真实验一、实验目的1.初步了解Matlab中Simulink的使用方法,熟悉simulink模块的操作和信号线的连接。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,熟悉各种典型环节的响应曲线。
3.定性了解各参数变化对典型环节动态特性的影响。
二、实验仪器Matlab7.0 , 计算机三、实验原理Simulink是MATLAB中的一种可视化仿真工具。
Simulink是一个模块图环境,用于多域仿真以及基于模型的设计。
它支持系统设计、仿真、自动代码生成以及嵌入式系统的连续测试和验证。
四、实验内容及步骤1、建立仿真模型系统1.1 运行Matlab,在命令窗口“Command Window”下键入“Simulink”后回车,则打开相应的系统模型库;或者点击工具栏上的“Simulink”图标,进入系统仿真模型库,然后点击左上角“新文件”图标,打开模型编辑窗口。
1.2 调出模块在系统仿真模型库中,把要求的模块都放置在模型编辑窗口里面。
从信号源模块包(Sources)中拖出1个阶跃信号(step)和1个白噪声信号发生器(band-limited white noise);从数学运算模块包(Math Operations)中拖出1个比例环节(gain)和1个加法器(sum);从连续系统典型环节模块包(Continuous) 中拖出1个微分环(Derivative)和3个传函环节(transfer Fcn);从信号与系统模块包(Signals Routing) 拖出1个汇流排(mux);从输出模块包(Sinks)中拖出1个示波器(scope);所有模块都放置在模型编辑窗口里面。
1.3 模块参数设置(鼠标左键双击各典型环节,则可进行参数设置)双击打开白噪声信号发生器,设定功率(Noise power)为0.0001,采样时间(Sample time)为0.05。
打开比例环节,设定比例增益为2;打开3个传函环节(transfer Fcn),通过参数设定,分别构成积分、惯性和二阶环节。
自动控制原理作业
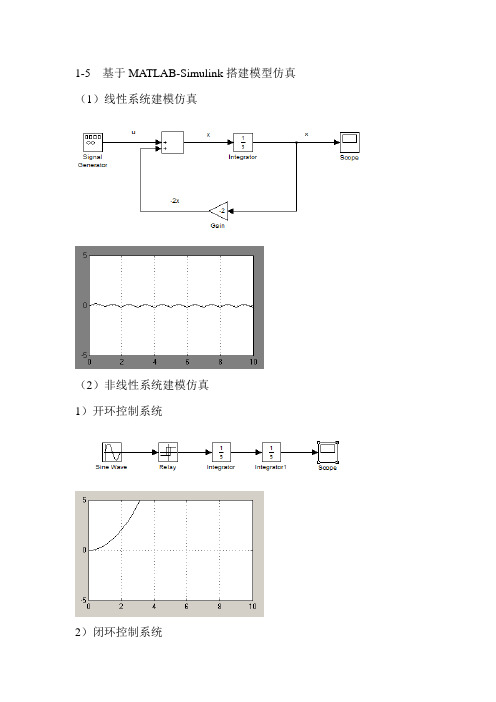
1-5 基于MATLAB-Simulink搭建模型仿真(1)线性系统建模仿真
(2)非线性系统建模仿真
1)开环控制系统
2)闭环控制系统
(3)基于simulink的非线性自激震荡的仿真含继电器特性的非线性系统的simulink模型图
含饱和特性的离散非线性系统
习题1.9
习题1.10
习题1.11
2.6应用matlab处理系统数学模型2.6.1模型建立
(1)并联
(2)串联
(3)闭环
(4)反馈
2.6.2模型简化
3.7应用MATLAB进行时域分析例18
分析:从系统的零极点分布图,可以看出系统有在S有半平面的闭环极点,系统不稳定。
3.7.2应用matlab分析系统的动态特性
分析:从图中可以看出,在过阻尼和临界阻尼曲线中,临界阻尼响应具有最短的上升时间,度最快;在欠阻尼的响应曲线中,阻尼系数越
小,超调量越大,上升时间越短,通常取kosi=0.4~0.8。
例20。
MATLAB自动控制原理实验

实验七 控制系统的MATLAB 分析一、 实验目的1)、掌握如何使用Matlab 进行系统的时域分析 2)、掌握如何使用Matlab 进行系统的频域分析 3)、掌握如何使用Matlab 进行系统的根轨迹分析 4)、掌握如何使用Matlab 进行系统的稳定性分析 5)、掌握使用Bode 图法进行控制系统设计的方法 二、 实验内容 1、时域分析法根据下面传递函数模型:绘制其单位阶跃响应曲线并从图上读取最大超调量,绘制系统的单位脉冲响应、零输入响应曲线。
1)、某单位负反馈系统传递函数为:8106)65(5)(232+++++=s s s s s s Gt (seconds)c (t )t (seconds)c (t )结论:2)、典型二阶系统传递函数为:2222)(nn nc s s s G ωξωω++= 当ζ=0.7,ωn 取2、4、6、8、10、12的单位阶跃响应。
Step ResponseTime (seconds)00.51 1.52 2.53 3.54结论:3)、典型二阶系统传递函数为:2222)(nn nc s s s G ωξωω++= 当ωn =6,ζ取0.2、0.4、0.6、0.8、1.0、1.5、2.0的单位阶跃响应。
Time (seconds)结论:2、频率分析法根据下面传递函数模型,绘制出系统的频率响应曲线,包括Bode 图和Nyquist 图,并从图上读取相角交接频率、截止频率,并求出幅值裕度和相角裕度。
1)、典型二阶系统传递函数为:2222)(nn nc s s s G ωξωω++= 当ζ=0.7,ωn 取2)、4)、6)、8、1)0、1)2)的伯德图和奈奎斯特图。
Wn=2M a g n i t u d e (d B )10101010P h a s e (d e g )Bode DiagramGm = Inf dB (at Inf rad/s) , Pm = 164 deg (at 0.4 rad/s)Frequency (rad/s)Real AxisI m a g i n a r y A x i sWn=4M a g n i t u d e (d B )10101010P h a s e (d e g )Bode DiagramFrequency (rad/s)Real AxisI m a g i n a r y A x i sWn=6M a g n i t u d e (d B )1010101010P h a s e (d e g )Bode DiagramFrequency (rad/s)Real AxisI m a g i n a r y A x i sWn=8M a g n i t u d e (d B )1010101010P h a s e (d e g )Bode DiagramFrequency (rad/s)Real AxisI m a g i n a r y A x i sWn=10M a g n i t u d e (d B )1010101010P h a s e (d e g )Bode DiagramFrequency (rad/s)Real AxisI m a g i n a r y A x i sWn=12M a g n i t u d e (d B )1010101010P h a s e (d e g )Bode DiagramFrequency (rad/s)Real AxisI m a g i n a r y A x i s2)、典型二阶系统传递函数为:2222)(nn nc s s s G ωξωω++= 当ωn =6,ζ取0.2、0.4、0.6、0.8、1.0、1.5、2.0的伯德图和奈奎斯特图。
哈工大自控实验—基于MATLABSimulink的控制系统分析

Harbin Institute of Technologyb/;;/自动控制理论实验报告院系:电气工程及自动化学院班级:姓名:学号:实验名称:基于MATLAB/Simulink的控制系统分析同组人:实验时间:2015年11月11日哈尔滨工业大学实验五 线性系统的时域分析一、实验目的1、学会使用MATLAB 绘制控制系统的单位阶跃响应曲线;2、研究二阶控制系统中 、 对系统阶跃响应的影响3、掌握系统动态性能指标的获得方法及参数对系统动态性能的影响。
二、 实验设备Pc 机一台,MATLAB 软件。
三、实验内容1、已知二阶单位反馈闭环传递函数系统:求:(1)当 及 时系统单位阶跃响应的曲线。
① 时系统单位阶跃响应的曲线。
Time (seconds)A m p l i t u d e② 时系统单位阶跃响应的曲线。
Time (sec)A m p l i t u d eTime (sec)01020304050607080(2)从图中求出系统的动态指标: 超调量M p、上升时间t p及过渡过程调节时间t s。
,超调量=30.9%,上升时间=3,48s,=27.5s;,超调量=16.3%,=4.1s,=20.2s。
,=30.9%,=6.95s,=54.9s;,=30.9%,=2.33s,=18.3s。
(3)分析二阶系统中、的值变化对系统阶跃响应曲线的影响。
当不变,变大,系统的上升时间减小,最大超调量变小,调整时间减小。
当,变大,系统的上升时间减小,最大超调量不变,调整时间减小。
2、已知三阶系统单位反馈闭环传递函数为(1)求取系统闭环极点及其单位阶跃响应,读取动态性能指标。
(2)将原极点 S=-4 改成 S=-0.5,使闭环极点靠近虚轴,观察单位阶跃响应和动态性能指标的变化。
Time (sec)=7.26%,=1.03s,=3.64s;将原极点 S=-4 改成 S=-0.5(绿线)后, ,=4.12s,过渡过程调节时间=7.84s(3)改变系统闭环零点的位置将原零点 S=-2 改成 S=-1, 观察单位阶跃响应和动态性能指标的变化。
自动控制原理的MATLAB仿真与实践第9章 基于simulink的系统建模与仿真分析

(1)提高开环增益可以提高系统的稳定精度和快速性,
能够减小静态误差,但是却不能从根本上消除静差。
(2)若比例系数过大,也会使系统产生较大的超调,
使振荡次数增多,调节时间加长,甚至可能造成系统
的不稳定;
(20131.0)5 若比例系数过小,系统会动作迟缓。
36
9.4.2 比例积分(PI)控制
比例积分控制的传递函数:
果将显示在模型中的输出模块中。
注意: (1)对于循环运行的模型,若在仿真过程中需要终止 时,可选择Simulation下拉菜单中的Stop。 (2)如果输出模块为示波器scope,则在运行结束后 双击scope模块,即可显示运行结果。
2011.05
9
9.2 Simulink模块库及其分类
9.2.1 输入模块 9.2.2 输出模块 9.2.3 功能运算模块
(2)命令方式 在命令窗口中键入“simulink”后回车。
2011.05
4
2.模块库的打开
(1)用鼠标左键单击类模块库列表。Simulink浏 览器右边窗口会显示该模块库中的全部子模块。
(2)用鼠标选择右侧的类模块图,标双击左键会 直接显示其所有子模块;或者,单击鼠标右键并单 击确认,则会弹出一个子模块窗口。
2011.05
14
9.2.3 功能运算模块
1.连续型模块Continuous:显示指定模块的输出 数值。常用模块有:
(1)
微分环节。其输出为其输入信号的微分。
(2)
积分环节。其输出为其输入信号的积分。
(3)
分子分母为多项式形式的传递函数。
(4)
零极点增益形式的传递函数。
2011.05
15
2.数学运算模块Math,该库中模块的功能就是将输 入信号按照模块所描述的数学运算函数计算,并把运算 结果作为输出信号输出。
自动控制原理MATLAB实验报告
实验一典型环节的 MATLAB 仿真一、实验目的1.熟悉 MATLAB 桌面和命令窗口,初步了解SIMULINK功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、实验原理1.比例环节的传递函数为Z 2R22 R1 100K , R2200KG( s)R1Z1其对应的模拟电路及 SIMULINK图形如图 1 所示。
图 1 比例环节的模拟电路及SIMULINK图形2.惯性环节的传递函数为R2Z2R12 G ( s)R2C1 1R1 100K , R2 200K , C1 1ufZ10.2s 1其对应的模拟电路及SIMULINK图形如图 2 所示。
图 2 惯性环节的模拟电路及SIMULINK图形3.积分环节 (I) 的传递函数为Z211 G(s)R1C1s R1 100K ,C1 1ufZ10.1s其对应的模拟电路及SIMULINK图形如图3所示。
图 3积分环节的模拟电路及及SIMULINK图形4.微分环节 (D) 的传递函数为G( s)Z 2R1C1 s s R1 100K, C110uf C2C1 0.01uf Z1其对应的模拟电路及 SIMULINK图形如图 4所示。
图 4 微分环节的模拟电路及及SIMULINK 图形5.比例 +微分环节( PD)的传递函数为G( s)Z 2R2(R1C1 s1)(0.1s1)Z1R1R1 R2100K , C110uf C2C10.01uf 其对应的模拟电路及 SIMULINK图形如图 5 所示。
实验报告6.比例 +积分环节( PI)的传递函数为R21(1 1)R1 R2 100K , C1 10ufG( s)Z2C1sZ1R1s其对应的模拟电路及SIMULINK图形如图 6 所示。
图 6 比例 +积分环节的模拟电路及SIMULINK图形曲三、实验内容按下列各典型环节的传递函数,建立相应的 SIMULINK 仿真模型,观察并记录其单位阶跃响应波形。
自动控制原理MATLAB仿真实验报告
实验一 典型环节的MATLAB 仿真 一、实验目的1.熟悉MATLAB 桌面和命令窗口,初步了解SIMULINK 功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
3.定性了解各参数变化对典型环节动态特性的影响。
二、实验内容① 比例环节1)(1=s G 和2)(1=s G ;Simulink 图形实现:示波器显示结果:② 惯性环节11)(1+=s s G 和15.01)(2+=s s GSimulink 图形实现:示波器显示结果:③ 积分环节s s G 1)(1Simulink 图形实现:示波器显示结果:④ 微分环节s s G )(1Simulink 图形实现:波器显示结果:⑤ 比例+微分环节(PD )2)(1+=s s G 和1)(2+=s s G1)、G1(s )=s+2Simulink 图形实现:示波器显示结果:2)、G2(s)=s+1 Simulink图形实现:示波器显示结果:⑥ 比例+积分环节(PI )s s G 11)(1+=和s s G 211)(2+=1)、G1(1)=1+1/sSimulink 图形实现:示波器显示结果:2)G2(s)=1+1/2s Simulink图形实现:示波器显示结果:三、心得体会通过这次实验我学到了很多,对课本内容加深了理解,熟悉MATLAB桌面和命令窗口,初步了解SIMULINK功能模块的使用方法,加深对各典型环节响应曲线的理解,这为对课程的学习打下了一定基础。
实验二线性系统时域响应分析一、实验目的1.熟练掌握step( )函数和impulse( )函数的使用方法,研究线性系统在单位阶跃、单位脉冲及单位斜坡函数作用下的响应。
2.通过响应曲线观测特征参量ζ和nω对二阶系统性能的影响。
3.熟练掌握系统的稳定性的判断方法。
二、实验内容1.观察函数step( )的调用格式,假设系统的传递函数模型为243237()4641s s G s s s s s ++=++++绘制出系统的阶跃响应曲线?2.对典型二阶系统222()2n n n G s s s ωζωω=++1)分别绘出2(/)n rad s ω=,ζ分别取0,0.25,0.5,1.0和2.0时的单位阶跃响应曲线,分析参数ζ对系统的影响,并计算ζ=0.25时的时域性能指标,,,,p r p s ss t t t e σ。
2018-东南大学自控实验报告 Matlab-Simulink_仿真实验 (1000字)-范文word版 (8页)
本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!== 本文为word格式,下载后可方便编辑和修改! ==东南大学自控实验报告 Matlab-Simulink_仿真实验(1000字)东南大学仪器科学与工程学院学院实验报告课程名称:自动控制原理实验名称: Matlab/Simulink 仿真实验院(系):仪器科学与工程学院专业:测控技术与仪器姓名:刘XX 学号: 2201XXX实验室:机电实验平台实验组别:同组人员:实验时间:201X 年 11 月20 日评定成绩:审阅教师:目录一、实验目的 (3)二、预习要求 (3)三、实验内容 (3)四、实验总结 (14)一、实验目的:1.学习系统数学模型的多种表达方法,并会用函数相互转换。
2.学习模型串并联及反馈连接后的系统传递函数。
3.掌握系统BODE图,根轨迹图及奈奎斯特曲线的绘制方法。
并利用其对系统进行分析。
4.掌握系统时域仿真的方法,并利用其对系统进行分析。
二、预习要求:借阅相关Matlab/Simulink参考书,熟悉能解决题目问题的相关Matlab函数。
三、实验内容:1.已知H(s)=0.05s?1,求H(s)的零极点表达式和状态空间表达式。
(0.2s?1)(0.1s?1)答:(1)零极点表达式:>> num=[0.05 1];den=conv([0.2 1],[0.1 1]);sys1=tf(num,den)sys2=zpk(sys1)sys1 =0.05 s + 1--------------------0.02 s^2 + 0.3 s + 1Continuous-time transfer function.sys2 =2.5 (s+20)------------% 零极点表达式(s+10) (s+5)Continuous-time zero/pole/gain model.状态空间表达式:>> num=[0.05 1];den=conv([0.2 1],[0.1 1]);sys1=tf(num,den);sys3=ss(sys1)sys3 =a =x1 x2x1 -15 -6.25x280b =u1x1 4x2 0c =x1 x2y1 0.625 1.562d =u1y1 0Continuous-time state-space model.2.已知H1(s)?1s?5,H2(s)?。
自动控制原理实验报告MATHLAB建模.doc
自动控制原理实验报告学院:机电工程学院班级:姓名:学号:指导老师:实验一:在MATLAB中创建系统模型一、实验目的:1.熟悉MATLAB桌面和命令窗口,初步了解SIMULINK功能模块的使用方法。
2.通过观察典型环节在单位阶跃信号作用下的动态特性,加深对各典型环节响应曲线的理解。
二、实验过程:1.传递函数模型的建立1)多项式形式的传递函数①课本例2.23上机操作过程如下:②课本P62,习题2-3上机操作过程如下:2)零、极点形式的传递函数课本例2.24上机操作过程如下:3)分子、分母为因式乘积形式的传递函数课本例2.25上机操作过程如下:2.Simulink 建模①课本例题上机操作如下:设单位反馈系统的开环传递函数为:)1(1)(+=s s s G将其转换成Simulink 框图,输入为阶跃信号,它的Simulink 框图如下所示:② 比例环节1)(1=s G 和2)(1=s G 的SIMULINK 图形建模操作如下;比例环节1)(1=s G 的SIMULINK 图形如下图所示:比例环节2)(1=s G 的SIMULINK 图形3.课后练习用matlab求下列函数的拉氏变换(习题2-1),上机操作过程如图所示:实验二:在MATLAB中算特征根及绘制根轨迹图一、实验目的:1.掌握MATLAB下的根轨迹绘制方法;2.学会利用根轨迹进行系统分析。
二、实验过程:1)例3-21 试利用MATLAB函数求例3.1中k=2.k=20时系统的特征根,并分别判定稳定性。
上机操作过程如下:>> num=[2];den=conv([1 0],conv([0.1 1],[0.25 1]));g=tf(num,den);sys=feedback(g,1);>> pzmap(sys)p=pole(sys)p =-11.0314-1.4843 + 2.2470i-1.4843 - 2.2470i2)例3-22 二阶系统如图3.13所示,设Wn=1,试研究系统的单位阶跃响应与参数ξ的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验概述:
【实验目的及要求】
本部分的目的在于学习matlab中有关simulink的正确使用及其应用,包括:simulink的基本使用、模型的建立、模型的复制剪切粘贴、命名等、线的基本使用、子系统的建立、属性的设置、参数的设置与应用、simulink仿真运行参数的设置等。
通过该实验,要求能够做到不查参考书,能熟练编写基本的simulink应用。
实验内容:
[1]建立如图1所示系统结构的Simulink模型,并用示波器(Scope)观测其单
位阶跃和斜坡响应曲线。
101
s
101
s
1.414
R(t)C(t)
-
-
输入信号为阶跃信号:
图 1
输入信号为单位斜坡信号:
[2] 建立如图2所示PID 控制系统的Simulink 模型,对系统进行单位阶跃响
应仿真,用plot 函数绘制出响应曲线。
其中p
k =10,i k =3,d k
=2。
要
求PID 部分用subsystem 实现,参数p
k 、i k 、d k
通过subsystem 参数输入
来实现。
p
k
i
k
d
k 1s
/du dt
324327242410355024
s s s s s s s +++++++R(s)
C(s)
图 2
plot(aa(:,1),aa(:,2))
[3]建立如图3所示控制系统的Simulink模型,并用示波器(Scope)观测其单
位阶跃响应曲线。
4
8 s
8
400
s
43
0.001671
s+
0.0873
0.0132
0.168
0.0171
s+
14.35
s
13.514
-
-
-++
R(t)
图3
[4] 图4所示为弹簧—质量—阻尼器机械位移系统。
请建立此动态系统的Simulink 仿真模型,然后分析系统在外力F(t)作用下的系统响应(即质量块的位移y(t))。
其中质量块质量m=5kg,阻尼器的阻尼系数f=0.5,弹簧的弹性系数K=5;并且质量块的初始位移与初始速度均为0。
说明:外力F(t)由用户自己定义,目的是使用户对系统在不同作用下的性能有更多的了解。
图4 弹簧-质量-阻尼器机械位移系统示意图
提示:
(1)首先根据牛顿运动定律建立系统的动态方程,如下式所示:
()()()()22
d y t dy t m f ky t F t dt dt
++= (2)由于质量块的位移()y t 未知,故在建立系统模型时.使用积分模块Integrator 对位移的微分进行积分以获得位移()y t ,且积分器初估值均为0。
为建立系统模型.将系统动态方程转化为如下的形式:
()()()()22
d y t F t dy t f k y t dt m m dt m
=--
然后以此式为核心建立系统模型。
得到阶跃、速度、加速度、正弦四种信号作用下的示波器显示结果输出。
拉氏变换后:
55.0511)()()()()(1)(2
22++=++=⇒--=
s s k fs ms s F s Y s Y m k
s sY m f s F m s Y s 输入信号为阶跃信号:
输入信号为速度信号:
输入信号为加速度信号:
输入信号为正弦信号:
机自1201 范云飞 41240171
- 11
-
【小结】
初步学会了如何用simulink 进行系统响应的仿真,遇到不会的地方通过查书和上网搜索基本明白,对课本上学到的东西理解更加深刻。
正确的建立模型很重要。
1、 将每一道题的程序、建立的模型放置在该题目下方;
2、 小结部分为对本次实验的心得体会、思考和建议。
