spss主成分分析(PCA)PPT课件
合集下载
主成分分析法PPT课件
6
3.832E-16
2.017E-15 100.000
7
3.351E-16
1.764E-15 100.000
8
2.595E-16
1.366E-15 100.000
000
10
1.683E-16
8.860E-16 100.000
11
7.026E-17
3.698E-16 100.000
• 因子分析是要利用少数几个公共因子去解释较多个要观测 变量中存在的复杂关系,它不是对原始变量的重新组合,而 是对原始变量进行分解,分解为公共因子与特殊因子两部分. 公共因子是由所有变量共同具有的少数几个因子;特殊因 子是每个原始变量独自具有的因子.
3、应用中的优缺点比较
• 主成分分析 优点:首先它利用降维技术用少数几个综合变量来代替 原始多个变量,这些综合变量集中了原始变量的大部分信 息.其次它通过计算综合主成分函数得分,对客观经济现象 进行科学评价.再次它在应用上侧重于信息贡献影响力综 合评价. 缺点:当主成分的因子负荷的符号有正有负时,综合评价 函数意义就不明确.命名清晰性低.
12
2.750E-19
1.447E-18 100.000
13
-7.503E-17 -3.949E-16 100.000
14
-1.291E-16 -6.794E-16 100.000
15
-1.742E-16 -9.168E-16 100.000
16
-2.417E-16 -1.272E-15 100.000
四、主成分分析法的步骤
1数据归一化处理:数据标准化Z 2计算相关系数矩阵R: 3计算特征值;
特征值越大说明重要程度越大.
4计算主成分贡献率及方差的累计贡献率; 5计算主成分载荷与特征向量:
《主成分分析》课件

投资组合优化
通过主成分分析,找到不同投 资标的之间的关系,优化投资 组合的效益。
主成分分析在市场调研中的应用
1
偏好分析
通过主成分分析,找到消费者的特征
产品定位
2
和偏好,精准制定相应的市场策略。
通过主成分分析,找到消费者对产品
的不同评价因素,合理确定产品的定
位。
3
竞品分析
通过主成分分析,评估竞争对手的优 势和劣势,为企业提供相应的决策依 据。
慕课在线学习行业民调
通过主成分分析,找到影响学 习者的因素,比如课程质量、 师资水平、学习难度等方面。
降水量分析和气候变化
通过主成分分析和时间序列分 析,找到影响气象预测和气候 变化的主要原因和特征。
食品市场调查分析
通过主成分分析,找到影响消 费者购买健康食品的因素,制 定相应的市场营销策略。
标准化数据
通过Z-score标准化数据,去除不同变 量的量纲影响。
提取主成分
根据协方差矩阵的特征值和特征向量, 提取主成分。
如何选择主成分数量
特征值
根据特征值大于1的原则,选择主成分的数量。
累计贡献率
当累计贡献率到达一定阈值后,选择主成分数量。
图形分析
通过屏幕图和贡献率图来选择主成分数量。
主成分分析的优点和缺点
应用
主成分分析适用于变量之间没有明确因果关系 的情况下,提取它们的主成分;而因子分析需 要基于理论或先验知识,对变量进行选择和定 量,发现变量间的潜在因子。
主成分分析在金融分析中的应用
股票指数分析
通过主成分分析,找到影响整 个股票市场的因素,快速判断 股票市场的健康状况。
信用卡违约风险评估
通过主成分分析,找到导致信 用卡违约的因素,提高信用卡 贷款的质量。
spss主成分分析(PCA)

2019/9/12
3
cxt
在进行主成分分析后,竟以97.4%的精度, 用三新变量就取代了原17个变量。根据经济 学知识,斯通给这三个新变量分别命名为总 收入F1、总收入变化率F2和经济发展或衰退 的趋势F3。
2019/9/12
4
cxt
主成分分析:将原来较多的指标简化为少数 几个新的综合指标的多元统计方法。
2019/9/12
11
cxt
如果我们将xl 轴和x2轴先平移,再同时按 逆时针方向旋转角度,得到新坐标轴Fl和
F2。Fl和F2是两个新变量。
2019/9/12
12
cxt
x2
平移、旋转坐标轴
F1
F2
•• • • •
••
•• •••
•• •
• •
• •
• •••
•• •
•
•
• •••
•
••
x1
2019/9/12
8
cxt
这种由讨论多个指标降为少数几个综合指 标的过程在数学上就叫做降维。主成分分 析通常的做法是,寻求原指标的线性组合
Fi。
F1 u11X1 u21X 2 u p1X p
F2 u12 X1 u22 X 2 u p2 X p
Fp u1p X1 u2 p X 2 u pp X p
15
cxt
根据旋转变换的公式:
y1 y2
x1 cos x2 s x1 sin x2
in cos
y1 cos sin x1 Ux y2 sin cos x2
U为旋转变换矩阵,它是正交矩阵,即有 U U1, UU I
spss主成分分析(PCA)

第一和第二主成分的累计贡献率:
(5.83 2) /(5.83 2 0.17) 0.97875
由此可将以前三元的问题降维为两维问题.第一和第 二主成分包含了以前变量的绝大部分信息97.87 5%.
2014-11-28
28 cxt
从协方差矩阵出发求解主成分的步骤:
1、求解各观测变量 Xl x1l,x2l, ,x pl (l 1, 2, ,n) 的协方差矩阵。 2、由X的协方差阵Σx,求出其特征根,即解方 程 I 0 ,可得特征根 1 2 p 0 。 3、求解 ui i ui 可得各特征根对应的特征向量U1, U2,…,Up 。
2014-11-28
24 cxt
' x ( x , x , x ) 例:设 的协方差矩阵为: 1 2 3
1 2 2 5 0 0
0 0 2
从协方差矩阵出发,求解主成分. (1)求协方差矩阵的特征根 依据 I 0 求解.
2014-11-28 25 cxt
2014-11-28
4 cxt
主成分分析:将原来较多的指标简化为少数 几个新的综合指标的多元统计方法。 主成分:由原始指标综合形成的几个新指标。 依据主成分所含信息量的大小成为第一主成 分,第二主成分等等。
2014-11-28
5 cxt
主成分分析得到的主成分与原始变量之间的关 系:
1、主成分保留了原始变量绝大多数信息。
13 cxt
x1
2014-11-28
平移、旋转坐标轴
F2
x2
• •• • • • • •••• • • • • •• • • • •• • • • •• • • • •• •• • ••
《主成分分析》幻灯片PPT

PCA的实质——简化数据
用尽可能少的变量〔主成分〕反映原始数据中尽 可能多的信息,以简化数据,突出主要矛盾。
反映原始数据特征的指标:方差-离散度 主成分:原始变量的最优加权线性组合 最优加权:
第一主成分:寻找原始数据的一个线性组合,使 之具有最大方差〔数据离散度最大的方向〕
第二主成分:寻找原始数据的一个线性组合,使 之具有次大方差,且与第一主成分无关
12.00
14.00
16.00
run100m
18.00
20.00
二、PCA的模型与算法
设:x为标准化变量, 原始数据阵 X s [x 1 ,x 2 , x p ] PCA目标:找到原始数据方差最大的线性组合
❖设:线性组合系数为p×1=[1, 2, … p]T
❖即:要找一个 使z=Xs= 1x1+ 2x2 +…+ pxp具有
What does PCA do?
Original data matrix, say n by p 正交旋转
New data matrix, say n by q, with q < p:
例:研究55个国家运发动径赛 能力,用8项径赛成绩
经PCA得到新数据阵: z55×2:选取2个主成分, 其中第一主成分表示综合
0.0
1
第一主成分-1.0包0 含的信0.0息0 量显然1.00
-21..000
售 电 量
Z2
大于第二主成分,因而忽略s 第
二主成分信息损失不大 -2.0
-2
-1
Ma Xin, North China Electric Power University
0
1
2
3
主成分分析之PCAppt课件

•• •
•
• • •• •
•• • •
•
•
•• •
•• •
•• • • • • •
•
•• •
•
•
•
• ••
• • ••
•
•• • •
•
•• •
•• •
•
x1
释
•
••
• •
•
3.2. PCA: 进一步解释
椭圆有一个长轴和一 个短轴。在短轴方向上, 数据变化很少;在极端的 情况,短轴如果退化成一 点,那只有在长轴的方向 才能够解释这些点的变化 了;这样,由二维到一维 的降维就自然完成了。
(3)如何解释主成分所包含的几何意义或 经济意义或其它。
实例1: 经济分析
美国的统计学家斯通(Stone)在1947年关于国民 经济的研究是一项十分著名的工作。他曾利用美国 1929一1938年各年的数据,得到了17个反映国民收 入与支出的变量要素,例如雇主补贴、消费资料和 生产资料、纯公共支出、净增库存、股息、利息、 外贸平衡等等。
(1) 如何作主成分分析?
当分析中所选择的变量具有不同的量纲,变 量水平差异很大,应该选择基于相关系数矩阵 的主成分分析。
各个变量之间差异很大
(2) 如何选择几个主成分。
主成分分析的目的是简化变量,一般情况 下主成分的个数应该小于原始变量的个数。 关于保留几个主成分,应该权衡主成分个数 和保留的信息。
33
• 如果我们将xl 轴和x2轴先平移,再同时 按逆时针方向旋转角度,得到新坐标轴Fl和 F2。Fl和F2是两个新变量。
34
Fl,F2除了可以对包含在Xl,X2中的信息起着 浓缩作用之外,还具有不相关的性质,这就使得 在研究复杂的问题时避免了信息重叠所带来的虚 假性。二维平面上的个点的方差大部分都归结在 Fl轴上,而F2轴上的方差很小。Fl和F2称为原始 变量x1和x2的综合变量。
PCA主成分分析 ppt课件
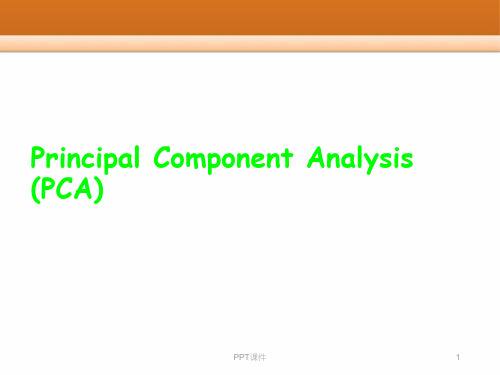
ordered such that principal axis 1 has the highest variance, axis 2 has the next highest variance, .... , and axis p has the lowest variance covariance among each pair of the principal axes is zero (the principal axes are uncorrelated).
1 2 X im X i Vi n 1 m 1
n
PPT课件
6
Geometric Rationale of PCA
degree to which the variables are linearly correlated is represented by their covariances.
best possible representation of their squared Euclidean distances in the full p dimensions.
PPT课件
17
Covariance vs Correlation
using covariances among variables only makes sense if they are measured in the same units
10 12 14 16 18 20
Variable X1
件
C1, 2 3.42
9
Configuration is Centered
each variable is adjusted to a mean of zero (by subtracting the mean from each value).
1 2 X im X i Vi n 1 m 1
n
PPT课件
6
Geometric Rationale of PCA
degree to which the variables are linearly correlated is represented by their covariances.
best possible representation of their squared Euclidean distances in the full p dimensions.
PPT课件
17
Covariance vs Correlation
using covariances among variables only makes sense if they are measured in the same units
10 12 14 16 18 20
Variable X1
件
C1, 2 3.42
9
Configuration is Centered
each variable is adjusted to a mean of zero (by subtracting the mean from each value).
spss主成分分析(PCA)PPT课件

0.924 u30.383
0.000
zf
26
(3)主成分:
F 10 .38 x 1 3 0 .92 x 24
F2 x3 F 30.92x1 40.38x23
(4)各主成分的贡献率及累计贡献率: 第一主成分贡献率: 5.8/35 (.8 320.1)7 0.72875 第二主成分贡献率: 2/5 (.8 3 20.1)7 0.25 第三主成分贡献率:0.1/75 (.8 320.1)7 0.02125
zf
23
(二) 第二主成分
coF 1,v F 2)(0 F 2 u 1X 2 1 u p 2 X p
F 2 u 1 X 2 1 u 2 X 2 2 u p 2 X p
在约束条件 下,寻找第二主成分
zf
24
例:设 x(x1,x2,x3)' 的协方差矩阵为:
1 2 0
2
5
0
当分析中所选择的变量具有不同的量纲,变量水平差异 很大,应该选择基于相关系数矩阵的主成分分析。 2、如何确定主成分个数? 主成分分析的目的是简化变量,一般情况下主成分的个数 应该小于原始变量的个数。关于保留几个主成分,应该 权衡主成分个数和保留的信息。
zf
20
5.3 总体主成分的求解及其性质
❖ 主成分分析的目标:
U为旋转变换正 矩交 阵矩 ,阵 它, 是即有 U U 1,U U I
zf
16
❖ 旋转变换的目的:为了使得n个样品点在Fl 轴方向上的离散程度最大,即Fl的方差最大。
❖ (变量Fl代表了原始数据的绝大部分信息,在 研究某问题时,即使不考虑变量F2也无损大 局)。经过上述旋转变换原始数据的大部分 信息集中到Fl轴上,对数据中包含的信息起 到了浓缩作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
p
F1、F2….Fp分别称为原变量的第一、第二….第p个主成分。
zf
10
5.2 数学模型与几何解释-几何解释
❖ 为了方便,我们在二维空间中讨论主成分的几 何意义: 设有n个样品,每个样品有两个观测变量xl和x2, 在由变量xl和x2 所确定的二维平面中,n个样本 点所散布的情况如椭圆状。由图可以看出这n个 样本点无论是沿着xl 轴方向或x2轴方向都具有 较大的离散性,其离散的程度可以分别用观测 变量xl 的方差和x2 的方差定量地表示。显然, 如果只考虑xl和x2 中的任何一个,那么包含在 原始数据中的经济信息将会有较大的损失。
zf
18
❖ 由此可概括出主成分分析的几何意义:
主成分分析的过程也就是坐标旋转的过程,各主 成分表达式就是新坐标系与原坐标系的转换关 系,新坐标系中各坐标轴的方向就是原始数据 方差最大的方向。
zf
19
❖ 了解了主成分分析的基本思想、数学和几何意义后,问 题的关键:
1、如何进行主成分分析?(主成分分析的方法) 基于相关系数矩阵还是基于协方差矩阵做主成分分析。
zf
4
❖ 主成分分析:将原来较多的指标简化为少数 几个新的综合指标的多元统计方法。
❖ 主成分:由原始指标综合形成的几个新指标。 依据主成分所含信息量的大小成为第一主成 分,第二主成分等等。
zf
5
❖ 主成分分析得到的主成分与原始变量之间的关 系: 1、主成分保留了原始变量绝大多数信息。
2、主成分的个数大大少于原始变量的数目。
3、各个主成分之间互不相关。
4、每个主成分都是原始变量的线性组合。
zf
6
❖ 主成分分析的运用: 1、对一组内部相关的变量作简化的描述
2、用来削减回归分析或群集分析(Cluster)中 变量的数目
zf
7
二、数学模型与几何解释-数学模型
❖ 假设我们所讨论的实际问题中,有p个指标,我 们把这p个指标看作p个随机变量,记为X1, X2,…,Xp,主成分分析就是要把这p个指标的 问题,转变为讨论p个指标的线性组合的问题, 而这些新的指标F1,F2,…,Fk(k≤p),按照 保留主要信息量的原则充分反映原指标的信息, 并且相互独立。
主成分分析
zf
主成分分析的重点
❖ 1、掌握什么是主成分分析? ❖ 2、理解主成分分析的基本思想和几何意义? ❖ 3、理解主成分求解方法:协方差矩阵与相
关系数矩阵的差异? ❖ 4、对结果进行正确分析
zf
2
5.1 主成分分析的基本思想
一项十分著名的工作是美国的统计学家斯通
(stone)在1947年关于国民经济的研究。他
U为旋转变换正 矩交 阵矩 ,阵 它, 是即有 U U 1,U U I
zf
16
❖ 旋转变换的目的:为了使得n个样品点在Fl 轴方向上的离散程度最大,即Fl的方差最大。
❖ (变量Fl代表了原始数据的绝大部分信息,在 研究某问题时,即使不考虑变量F2也无损大 局)。经过上述旋转变换原始数据的大部分 信息集中到Fl轴上,对数据中包含的信息起 到了浓缩作用。
1、从相关的X1, X2,… Xk,求出相互独立的新综合变 量(主成分)Y1,Y2…Yk。
2、X与Y之间的计算关系是:
Y1 a11 a1kX1
即Y=AX
Yk ak1 akkXk
如何求解主成分?
zf
21
❖ 一、从协方差矩阵出发求解主成分
(一)第一主成分: 11 12 1P
曾利用美国1929一1938年各年的数据,得
到了17个反映国民收入与支出的变量要素,
例如雇主补贴、消费资料和生产资料、纯公
共支出、净增库存、股息、利息外贸平衡等
等。
zf
3
❖ 在进行主成分分析后,竟以97.4%的精度, 用三新变量就取代了原17个变量。根据经济 学知识,斯通给这三个新变量分别命名为总 收入F1、总收入变化率F2和经济发展或衰退 的趋势F3。
u1 2 iu2 2i u2 pi1
2、主成分之间相互独立,即无重叠的信息。即
C ( F i , F o j ) 0 , v i j , i , j 1 , 2 , , p
3、主成分的方差依次递减,重要性依次递减,即
V ( F a ) V r( F a ) r V ( F a ) r
1
F1
F2
•
•••
•••
• •
•
•••••••••••••••••••••••
• •
x1
•••
zf
14
平移、旋转坐标轴
x 2
F1
F
2
•
••••••••
••
••••••••••
••••
•••••••••
•
x 1
zf
15
❖ 根据旋转变换的公式:
yy12x1xc1soisnx2xs2cinos
y y1 2 cso in sc sio n sx x1 2 U x
当分析中所选择的变量具有不同的量纲,变量水平差异 很大,应该选择基于相关系数矩阵的主成分分析。 2、如何确定主成分个数? 主成分分析的目的是简化变量,一般情况下主成分的个数 应该小于原始变量的个数。关于保留几个主成分,应该 权衡主成分个数和保留的信息。
zf
20
5.3 总体主成分的求解及其性质
❖ 主成分分析的目标:
zf
11
❖ 如果我们将xl 轴和x2轴先平移,再同时按逆 时针方向旋转角度,得到新坐标轴Fl和F2。 Fl和F2是两个新变量。
zf
12
x2
平移、旋转坐标轴
F1
F2
•• • • •
•• • •
•• •
•
• •
•
• •
•
•
•
• •••
• •• •
•• •
• ••
x 1
••
zf
13
平移、旋转坐标轴
x 2
zf
8
❖ 这种由讨论多个指标降为少数几个综合指 标的过程在数学上就叫做降维。主成分分 析通常的做法是,寻求原指标的线性组合
Fi。
F1 u11X1 u21X2 up1Xp
F2 u12X1 u22X2 up2Xp
Fp u1p X1 u2p X2 uppXp
zf
9
❖ 满足如下的条件:
1、每个主成分的系数平方和为1。即
zf
17
❖ Fl,F2除了可以对包含在Xl,X2中的信息起着浓 缩作用之外,还具有不相关的性质,这就使得 在研究复杂的问题时避免了信息重叠所带来的 虚假性。二维平面上的个点的方差大部分都归 结在Fl轴上,而F2轴上的方差很小。Fl和F2称为 原始变量x1和x2的综合变量。F简化了系统结构, 抓住了主要矛盾。
