弹性力学本构关系
第11章-弹塑性力学--本构关系
xy c41 x c42 y c43 z
y y
图4-2
(a)
z
x
x
z
现在引进坐标系 Ox’y’z’, 原坐 标系 Oxyz 绕 y 轴转动 1800 后可与之重合 (图4-2)
新旧坐标轴间的方向余弦
l11 l33 cos180
1 0 0 1 l22 cos 0 1 0 0 l21 l31 l12 l32 l13 l23 cos 90 0
(11-13)
平面应力问题 用应变分量表示 应力分量
E y x 1 2 x E (11-14) y y x 1 2 G
ij ije 2 ij
(11-3’)
以上证明了各向同性的均匀弹性体的弹性常数只有 两个。
现在考虑一种物体各边平行于坐标轴的特殊情况,并 由此导出工程上常用的弹性常数和广义胡克定律。当物 体边界法线方向与 z 轴重合的两对边上有均匀的σz 作 用,其他边均为自由边时,则由材料力学知道
第11章 本构关系
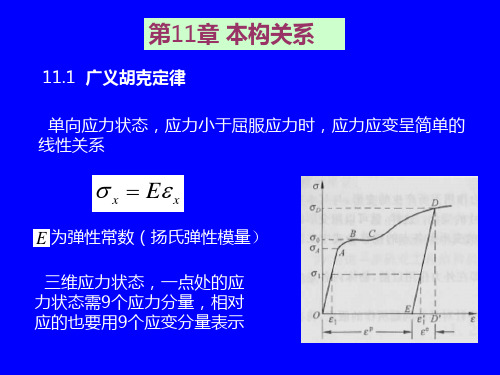
11.1 广义胡克定律 单向应力状态,应力小于屈服应力时,应力应变呈简单的 线性关系
x E x
E 为弹性常数(扬氏弹性模量)
三维应力状态,一点处的应 力状态需9个应力分量,相对 应的也要用9个应变分量表示
弹性力学 总结

弹性力学总结弹性力学概述弹性力学是研究物体在受力作用下的变形和恢复行为的物理学分支。
它主要研究物体在力的作用下如何发生形变,并在去除外力后如何回复到原来的状态。
弹性力学在工程、材料科学和地震学等领域都有广泛的应用。
弹性力学的基本原理弹性力学的基本原理主要包括胡克定律和变形的描述。
胡克定律胡克定律是弹性力学研究的基石之一,它描述了弹性物质的应力和应变之间的关系。
根据胡克定律,弹性物体在小应变范围内,应力与应变成正比。
公式表示为:σ = Eε其中,σ代表应力,E代表弹性模量,ε代表应变。
胡克定律适用于各向同性的线性弹性材料。
变形的描述弹性变形通常分为线弹性和非线性弹性两种情况。
线弹性是指应力与应变之间成线性关系的弹性变形,而非线性弹性则是指应力与应变之间存在非线性关系的弹性变形。
在弹性力学中,常用的变形描述方法有拉伸、压缩、剪切和扭转等。
这些变形可以通过位移场、应变场和应力场来描述。
弹性体的应力分析弹性体在受力作用下会发生应力分布。
根据应力的分布规律,可以得出一些重要结论。
平面应力和轴对称应力问题在平面应力问题中,物体受力平面上只有两个应力分量,另一个应力分量为零。
这种情况下,可以根据累积概率法或复数变量法求解。
轴对称应力问题是较为常见的一类问题,这类问题的特点是应力场只与径向位置有关。
通过解析方法或数值方法,可以得到轴对称弹性体的应力分布。
弹性体的本构关系弹性体的本构关系以描述应力和应变之间的关系。
弹性体的本构关系可以是线性的或非线性的。
常见的线性弹性体本构关系有:胡克弹性体、准胡克弹性体和线弹性体。
这些本构关系常用于弹性力学计算中,可以通过试验数据或材料参数得到。
非线性弹性体的本构关系较为复杂,常用的描述方法有牛顿-拉普森方程和本构方程等。
弹性力学应用弹性力学在各个领域都有广泛的应用。
以下是几个常见领域:工程领域在工程领域中,弹性力学主要用于材料的强度计算、结构的稳定性分析和振动问题的研究。
通过弹性力学的理论,工程师可以预测材料在受力下的变形和破坏情况,并设计出更加安全和可靠的结构。
弹性力学_第四章 本构关系

y ν x
其中 是弹性常数,称为泊松比。
Chapter 5.1
§4-1 本构关系概念
线弹性叠加原理
先考虑在各正应力作用
z
z
x
下沿 x 轴的相对伸长,它
由三部分组成,即
y
o
y
z
Chapter 5.1
y
x x x x
x
x
§4-1 本构关系概念
§4-2 广义胡克定律
其中
c11 C11 , c12 C1122 , c14 C1112 , c56 C2331…
即c 的下角标1、2、3、4、5、6分别对应于C 的双指
标11、22、33、12、23、31。应该指出,改写后的
cmn (m, n=1~6) 并不是张量。 由于存在Voigt对称性,所以对于最一般的各向异性 材料,独立的弹性常数共有21个。
弹性张量,共有81个分量。
• 弹性张量的Voigt对称性
Cijkl C jikl Cijlk Cklij
Chapter 5.1
§4-2 广义胡克定律
ij ji
Cijkl kl C jikl kl kl
Cijkl C jikl
kl lk
Cijkl kl Cijlk lk Cijlk kl kl
x x x x
是由于x的作用所产生的相对伸长 其中 x
x
x
E
ν 是由于y的作用所产生的相对缩短 x x E
ν 是由于z的作用所产生的相对缩短 x x
y
z
E
Chapter 5.1
§4-1 本构关系概念
弹性力学-本构关系

c12 = c21 ⋯⋯ c56 = c65
∴
σ x c11 c12 σ c22 y σ z = τ xy 对 τ yz τ zx
c13 c23 c33
称
c14 c24 c34 c44
c15 c25 c35 c45 c55
弹性对称
弹性 有 个对 向, 称 向, 对称 向上弹性 性 , 力 关系 。 称为弹性对称 弹性对称。 称为弹性对称。
弹性
弹性对称
向
相应的对称方向和对称面称为弹性对称方向 弹性对称面。 弹性对称方向和 相应的对称方向和对称面称为弹性对称方向和弹性对称面。 垂直于弹性对称面的方向称为弹性主轴 弹性主轴。 垂直于弹性对称面的方向称为弹性主轴。
第四章 本构关系
物体的弹性性质和广义 广义胡克定律 §4-1 物体的弹性性质 广义 §4-2 线弹性材料的本构关系 各向同性线弹性材料的物理方程 §4-3 各向同性线弹性材料的物理方程
物体的弹性性质 广义Hooke定律 弹性性质·广义 §4-1 物体的弹性性质 广义 定律
一. 弹性的概念
一般情况下,物体的应力与应变呈某一函数关系,可表示为: 一般情况下,物体的应力与应变呈某一函数关系,可表示为: σ ij = f ( ε ij ) 应力与应变张量均为六个独立分量。 应力与应变张量均为六个独立分量。则 σ x = f1 ( ε x , ε y , ε z , γ xy , γ yz , γ zx )
一. 横观各向异性材料
仅具有一个弹性对称面的材料称为横观各向异性材料。 横观各向异性材料 仅具有一个弹性对称面的材料称为横观各向异性材料。 平面为材料的弹性对称面, 轴为弹性主轴。 设Oxy平面为材料的弹性对称面,z轴为弹性主轴。 平面为材料的弹性对称面 轴为弹性主轴 体内一点P(x, y, z)的应力和应变 体内一点 的应力和应变 为{σ } 和{ε }。则 则 {σ } = [C ]{ε } 其中[C]为各向异性的弹性矩阵 其中 为各向异性的弹性矩阵 现将z轴反向, 现将 轴反向,考 轴反向 察其本构关系
弹塑性力学第四章弹性本构关系资料

产生的x方向应变:
叠加
产生的x方向应变:
同理:
剪应变:
物理方程:
说明:
1.方程表示了各向同性材料的应力与应 变的关系,称为广义Hooke定义。也称 为本构关系或物理方程。
2.方程组在线弹性条件下成立。
. 体积应变与体积弹性模量
令: 则: 令:
sm称为平均应力; q 称为体积应变
eij
1 2G
sij
(4.40)
因为 J1 0, J1' 0 ,所以以上六个式子中独立变量只有5个
因此应力偏张量形式的广义虎克定律,即
eij
1 2G
sij
em
1 3K
sm
(4.41)
用应变表示应力:
或: ✓ 各种弹性常数之间的关系
§4-2 线弹性体本构方程的一般表达式
弹性条件下,应力与应变有唯一确定的对应关系,三维 应力状态下,一点的应力取决于该点的应变状态,应力是应 变的函数(或应变是应力的函数) 6个应力分量可表述为6个应变分量的函数。
式(2)中的系数 有36个.
称为弹性常数,共
由均匀性假设,弹性体各点作用同样应力 时,必产生同样的应变,反之亦然.因此 为 常数,其数值由弹性体材料的性质而定.
式(2)推导过程未引用各向同性假设, 故可适用于极端各向异性体、正交各向异性体、 二维各向同性体以及各向同性体等.
式(2)可用矩阵表示
式(3)可用简写为 称为弹性矩阵.
三、. 弹性常数
1. 极端各向异性体:
物体内的任一点, 沿各个方向的性能都不相 同, 则称为极端各向异性体. (这种物体的材料极 少见)
即使在极端各向异性条件下, 式(2)中的36个 弹性常数也不是全部独立.
弹塑性本构关系简介

2) 势能原理的数学表达
应变能
总势能
Ve=Vε+VP =1/2∫VσijεijdV 外力势能
-∫VFbiuidV- ∫SσFsiuidS = min
2 虚力原理
1)虚力原理的表述
给定位移状态协调的充分必要条件为:对 一切自平衡的虚应力,恒有如下虚功方程成 立(矩阵)
∫V[ε]Tδ[σ]dV=∫Su([L]δ[σ])T [u ]0dS
收敛准则
1、位移模式必须包含单元的刚体位移
2、位移模式必须能包含单元的常应变
3、位移模式在单元内要连续、并使相邻单元间的位移必须协调
满足条件1、2的单元为完备单元
满足条件3的单元为协调单元 多项式位移模式阶次的选择——按照帕斯卡三角形选
几何各向同性:位移模式应与局部坐标系的方位无关
多项式应有偏惠的坐标方向,多项式项数等于单元边界结点的自由度总
变间关系为 octσoct
GKtt
oct 3K s oct oct Gs oct
并有
Gs G
1
a
oct
B c
m
KGss
εoct
oct
K G e s
s (c oct ) p
KG
其中G、K分别为初始切线剪切和体积模量,
B c
为混凝土单轴抗压强度,a、m、c和p为由试验
确定的常数。
POCT
弹性张量Dijkl
ij
Dijkl kl
( 2G 1 2
ij kl
2Giklj ) kl
i 1, j 2, k 1,l 2
12
D1212 12
( 2G 1 2
1212
2G1122 )12
11 1 12 0 22 1
弹塑性力学本构关系1资料.

在
平面上任取一点,坐标为 (1, 2 , 3 )
它代表一个应力状态,对应的应力张量分量为 ij
相应的平均应力为 m 易见有
m
1 2
3
3
0
将应力张量分解为应力球张量和应力偏张量,即
ij m ij sij sij
上式表明,与此应力状态相应的应力球张量为零,应力张量
等于应力偏张量。 平面上每一点对应的应力张量是应力偏张量。
• Drucker把它引伸到复杂应力 情况,这就是Drucker公设.
0 d p 0
ij
0 ij
d
p ij
0
d d p 0
第二式中的等号适用于理想 塑性材料.
d
ij
d
p ij
0
Drucker公设在塑性力学中有
重要意义.
屈服面的外凸性和塑性应变增量的法向性
•我们如将塑性应变空间与应力空间重合起来,由Drucker公 设的第一式, 把它看成是两个矢量的点积.
在应力空间中代表一曲面,此曲面称为屈服曲面。
屈服曲面内的点满足不等式
f (1, 2,3) c 时,代表弹性状态。 屈服曲面上及屈服曲面外的点满足 f (1, 2,3) c
时,代表塑性状态。因此,屈服曲面是弹、塑性状态的分界面。
4.2.3 等倾线与 平面
1.等倾线 在应力空间中,过坐标原点与三个坐标轴成相同倾角的直线 叫等倾线。
PR线上每一点都代表一个应力状态。 PR线上的点有相同的应力偏张量和不同的应力球张量。
因为应力球张量不影响屈服,所以如果P点在屈服曲面上, 那么PR线上所有点都应该在屈服面上。因此屈服曲面实际上 是一个柱面,并且柱面的母线平行于等倾线OL
P
弹性力学本构关系

本构关系1. 各向同性线性弹性本构方程及其中的物理常数G、λ、K 与E、μ的关系式;2. 球量和偏量的本构方程。
对于每一种材料,在一定的温度下,应力和应变之间有着完全确定的关系。
这是材料的固有特性,因此称为物理方程或者本构关系。
一般情况下,材料的应力与应变呈某一函数关系,可表示为:当式中的自变量:x、y、z、yz、zx、xy为小量时,可对其按Taylor级数展开,并略去二阶以上小量,如第一式,有上式中(f 1)0表达了函数f 1在应变分量为零时的值,根据应力应变的一般关系式可知,它代表了初始应力。
而表示函数f1 对应变分量的一阶偏导数,在小变形条件下,它们均为常数,这样可得一线性方程组:上述关系式是胡克(Hooke)定律在复杂应力条件下的推广,因此又称作广义胡克定律。
广义胡克定律中的系数Cmn(m,n=1,2,…,6)称为弹性常数,一共有36个,但可以证明,只有21个常数独立。
如果物体是非均匀材料构成的,物体内各点受力后将有不同的弹性效应,因此一般的讲,Cmn是坐标x,y,z的函数。
但是如果物体是由均匀材料构成的,那么物体内部各点,如果受同样的应力,将有相同的应变;反之,物体内各点如果有相同的应变,必承受同样的应力。
这一条件反映在广义胡克定理上,就是Cmn 为弹性常数。
对于完全的各向异性弹性体,本构关系有21个弹性常数,对于具有一个弹性对称面的各向异性材料,本构各向具有13个弹性常数。
对于正交各向异性材料,弹性常数有9个。
正交各向异性材料的本构方程中,正应力仅与正应变有关,切应力仅与对应的切应变有关,因此拉压与剪切之间,以及不同平面内的剪切之间将不存在耦合作用。
1. 极端各向异性体的弹性常数为21个。
2.具有一个对称面的各向异性材料正交各向异性体:物体内的任一点存在三个弹性对称平面,在每一个对称平两侧对称方向上各自具有相同的弹性性质,这种物体称为正交各向异性体。
正交各向异性体的弹性常数为9个。
3.横观各向同性体若物体内的任一点在平行于某一平面的所各方向都具有相同的弹性性质,而垂直于该面的弹性性质不同,这种正交异性体称为横观各向同性体。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本构关系
1. 各向同性线性弹性本构方程及其中的物理常数G 、λ、K 与 E 、μ的关系式;
2. 球量和偏量的本构方程。
对于每一种材料,在一定的温度下,应力和应变之间有着完全确定的关系。
这是材料的固有特性,因此称为物理方程或者本构关系。
一般情况下,材料的应力与应变呈某一函数关系,可表示为:
当式中的自变量: εx 、εy 、εz 、 γyz 、 γzx 、 γxy 为小量时,可对其按Taylor 级数展开,并略去二阶以上小量,如第一式,有
上式中(f 1)0表达了函数 f 1 在应变分量为零时的值,根据应力应变的一般关系式可知,它代表了初始应力。
而,,01 ⎪⎪⎭⎫ ⎝⎛∂∂x f ε表示函数 f 1 对应变分量的一阶偏导数,在小变形条件下,它们均为常数,这样可得一线性方程组:
上述关系式是胡克(Hooke )定律在复杂应力条件下的推广,因此又称作广义胡克定律。
广义胡克定律中的系数C mn (m ,n=1,2,…,6)称为弹性常数,一共有36个,但可以证明,只有21个常数独立。
如果物体是非均匀材料构成的,物体内各点受力后将有不同的弹性效应,因此一般的讲,C mn 是坐标x ,y ,z 的函数。
但是如果物体是由均匀材料构成的,那么物体内部各点,如果受同样的应力,将有相同的应变;反之,物体内各点如果有相同的应变,必承受同样的应力。
这一条件反映在广义胡克定理上,就是C mn 为弹性常数。
对于完全的各向异性弹性体,本构关系有21个弹性常数,
对于具有一个弹性对称面的各向异性材料,本构各向具有13个弹性常数。
对于正交各向异性材料,弹性常数有9个。
正交各向异性材料的本构方程中,正应力仅与正应变有关,切应力仅与对应的切应变有关,因此拉压与剪切之间,以及不同平面内的剪切之间将不存在耦合作用。
1.极端各向异性体的弹性常数为21个。
2.具有一个对称面的各向异性材料
正交各向异性体:物体内的任一点存在三个弹性对称平面,在每一个对称平两侧对称方向上各自具有相同的弹性性质,这种物体称为正交各向异性体。
正交各向异性体的弹性常数为9个。
3.横观各向同性体
若物体内的任一点在平行于某一平面的所各方向都具有相同的弹性性质,而垂直于该面的弹性性质不同,这种正交异性体称为横观各向同性体。
如:层状岩层、复合板材等。
横观各向同性体的弹性常数为5个。
4. 各向同性体:各向同性体的弹性常数仅为2个。
这两个常数可用弹性模量 E 和泊松比 μ 表示。
为了使得各向同性材料的本构关系公式表达简洁,令
C 11−C 12=2ν ;ν=G C 12=λ
体积应变:
体积弹性模量:
[]Θz y x 3
13
10=++=σσσσ
后文进行推导这个用体应变表示的方程
另一说法:
(2)物理方程的主应力形式
若将三个坐标轴方向设为三个主应力方向,则有:
表明:三个主应力方向与三个主应变方向重合。
3
)体积应力形式与体积弹性模量
)
(21z y x E
σσσμ
++-=
注:这里的e 就是体积应变θ
,0===xy zx yz τττ0
===xy zx yz γγγz
y x εεε++[])(2)(1z y x z y x E σσσμσσσ++-++=
令
μ
21-=
E
K —— 体积弹性模量
(4)物理方程的应变表示形式 将物理方程的基本形式中解出xy
zx yz z y x τττσσσ,,,,,将其用应变表示。
从中解出 σx ,有
⎪⎪⎭⎫
⎝⎛+-+=
x x e E
εμμμσ211
—— 用应变量表示的物理方程
进一步引入 拉梅常数
())
1(2,)
21(1μμμμ
λ+=
-+=
E
G E 则
方程中 λ 、G 称为Lame 系数。
至此,上面的结论得以验证
例:如图所示钢制圆柱,其直径为d ,外面套有一厚度为t 的钢制圆筒(圆柱和圆筒间无摩擦),沿圆柱
轴向施加均匀压力q ,求刚柱内的应力(E 、μ已知)。
ΘE e μ
21-=
e
E
Θμ
21-=
[])(1
z y x
x E
σσμσ
ε+-=[]
)()1(1
z y x x
E
σσσμσμ++-+=
[]
ΘE
x
μσμ-+=
)1(1
⎥⎦
⎤
⎢⎣⎡--+=
e E
E x μ
μσμ21)1(1
讨论
(1)如果外筒为刚性筒,怎么办? (2)如果是立方体外套刚性筒,怎么办? (3)如果均匀压力q 变成集中力P ,有什么变化? 总结 1本构方程
2.球量和偏量的本构方程:
体积弹性模量:
五个弹性常数: E 、μ、G 、λ、K ,只有两个独立。
注意:这里的K 和上面K 另一个定义二者意义差不多,但是有差别,差了三倍,
原因在于湖大固体力学版本的
中σ0是平均正应力[]Θz y x 3
1310=++=
σσσσ 而其他版本中e
E
Θμ21-=,因此两个版本中K 的定义不同, []Θz y x 3
13
10=++=σσσσ表示应力球张量,
而
e
E
Θμ21-=被定义为第一应力不变量,称为体积应力。
