信号与系统考研复习思维导图——系统函数H(s)
系统函数(网络函数)H(S)

p1 , p 2 p n 系统函数的极点
在s平面上,画出H(s)的零极点图: 极点:用×表示,零点:用○表示
第
例:
s( s 1 j1)( s 1 j1) H ( s) ( s 1) 2 ( s j 2)( s j 2)
sE s e 0 3E s
零输入响应/零状态响应
2 s 3s 2 R s s 3 E s sr 0 r 0 3r 0
第
21 页
则
sr 0 r 0 3r 0 Rzi s s2 3s 2
§4.6 系统函数(网络函数) H(s)
一.系统函数
系统的零状态响应:
e t
第 2 页
时域:
h( t )
r t
r t e t h t ,其中 h(t) 称为单位冲激响应
复频域:
E s
H s
Rs
R s E s H s
R( s ) H ( s) E ( s)
U C ( s) I L ( s) 1 H 2 (s) 2 X ( s) X ( s)( R2 sL) s 2s 2
例:
I 2 ( s) 求下图所示电路的转移 导纳函数Y21 ( s ) 。 1 V1 ( s )
I 3 s
V1 s
1 s 1 s
1
第 7 页
s 3E s Rzs s 2
s
3s 2
零输入响应为:
rzi (t ) 4 e t 3 e2t
t 0
信号与系统系统函数与信号流图

G2
1 Li LiLj 1 (L1 L2 L3 L4 ) (L1L4 )
1 H4G1 H2H3H4H5G2 H5H6G2 H2H7G2 H2H4H7G1G2
三条前向通路之(1)
X X1 X2 X3 X4 Y
P1 H1H2H3H4H5
其中(L1、L2),(L1、L3)是两两不接触的回路,没有三三不接触的 回路。
信号与系统
三.Mason公式
G1
H1
H2
H3
G4
H5
Y
X
X1 G2 X 2
X 3 H4 X 4 G5
所以流图的特征式为
(s) 1 Li LiLj 1 (L1 L2 L3 L4) (L1L2 L1L3)
信号与系统
§5.6.4 系统函数和信号流图
信号与系统
主要内容
•系统方框图 •信号流图 •Mason公式 •系统模拟(第5.8节)
信号与系统
一.系统方框图
一个系统的方框图可由许多子系统的框图作适当联接组成。
子系统的基本联接方式有级联、并联和反馈三种。
(1)级联 等效系统函数为
(2)并联 等效系统函数为
1 (H2G2 H4G4 H5G5 H2H3H4H5G1) (H2H4G2G4 H2G2H5G5)
前向通路只有一条,即 X X1 X 2 X 3 X 4 Y
所有回路都和这条前向通路接触,所以
P1 H1H2H3H4H5
1 1 0 0 1
L3 (X1 X4 Y X1) H5H6G2 L4 (X1 X2 Y X1) H2H7G2
“信号与系统”中系统稳定性分析

“信号与系统”中系统稳定性分析巩亚楠 魏德旺 刘俊良 李淑晴 吕海燕*(临沂大学 山东临沂 276000)摘要:“信号与系统”是电子信息类本科阶段的专业基础课。
在学习的过程中,很多同学只是记住知识点,不明白它们之间的逻辑关系,不会灵活运用。
该文旨在利用思维导图的方式对系统稳定性分析方法进行总结,描述了连续时间系统和离散时间系统的稳定性,对每个系统提出了两种分析方法,即时域分析法和变换域分析法,对两种方法的具体分析过程做出了详细的说明,并对系统稳定性给出了4种判别方法。
借助思维导图,帮助学生更好地理解知识,充分调动学生学习的积极性。
关键词:信号与系统 思维导图 系统稳定性分析 连续时间系统 离散时间系统中图分类号:G64文献标识码:A 文章编号:1672-3791(2023)18-0078-04 Analysis of the System Stability in "Signals and Systems"GONG Yanan WEI Dewang LIU Junliang LI Shuqing LYU Haiyan*(Linyi University, Linyi, Shandong Province, 276000 China) Abstract:"Signals and systems" i s a professional basic course of the undergraduate level of electronic information. In the process of learning, many students just remember knowledge points, but they don't understand the logic rela‐tionship among them and cannot use them freely. This paper aims to summarize the analytical method of the system stability by mind mapping, describes the stability of the continuous-time system and the discrete-time system, puts forward two analytical methods for each system, namely the time-domain analysis method and the transform-domain analysis method, explains in detail the specific analytical process of the two methods, and also presents four discriminant methods for the system stability. With the help of mind mapping, students can better comprehend knowledge and fully mobilize their enthusiasm for learning.Key Words: Signals and Systems; Mind mapping; System stability analysis; Continuous-time system; Discrete-time system1 “信号与系统”课程地位“信号与系统”作为信息、电子、自控、通信等专业的专业基础课,是为后续数字信号处理、数字图像处理、通信原理、自动控制等课程的学习打下基础,“信号与系统分析”被认为是一门理解困难、计算繁杂、偏理论模型的课程。
信号与系统§4.06-系统函数(网络函数)H(S)

R(s) H(s) r(t) h(t) 则L[h(t)] H(s)
2.H(s)的几种情况
策动点函数:激励与响应在同一端口时
1 I1s V1 s
1
单端口 网络
策动点导纳
转移函数:激励和响应不在同一端口
1 I1s
2 I2s
V1 s
双端口 网络
1
H(s) I2(s) V1 (s)
转移导纳
2
H(s) V2 (s) I1(s)
转移阻抗Biblioteka V2 s H (s) V2(s) V1 ( s )
电压比
H(s) V1 (s) I1(s)
策动点阻抗
H(s) I2(s) I1(s)
电流比
3.求H(s)的方法
ht Hs
微分方程两端取拉氏变换→
H s
H1(s)E(s) H1(s)E2(s)
所以
H1(s)E(s) H1(s)H2 (s) R(s)
H (s) R(s)
H1(s)
E(s) 1 H1(s)H2(s)
4.结论
在s域可进行代数运算:
已知子系统的hi (t)或Hi (s),可以求出整个系统的Hs。
已知总的H(s)及部分系统的H i (s),也可以求出另一个 子系统的H j (s)。
Es
H1s
H 2 s
Rs
时域 : h(t) h1(t) h2(t) 频域: H(s) H1(s) H2(s)
3.LTI系统的反馈连接
Es E1s H1s
Rs
E2s
H 2 s
E1(s) E(s) E2 (s)
E2 (s) R(s) H2 (s)
信号与系统知识点图谱
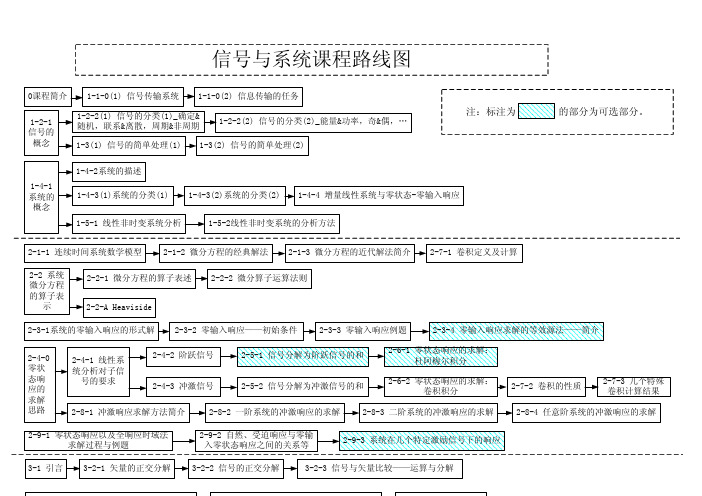
6-6-1 稳定系统的定义 6-6-2 系统稳定的充分必要条件 6-6-3 极点与系统稳定性的关系
6-6-4-1 罗斯-霍维茨判据
6-6-4-2 罗斯-霍维茨判据应用—— 确定使得系统稳定的参数取值范围
6-7-1 反馈系统及其稳定性
6-7-2 反馈系统与控制论简介
6-6-4-3罗斯-霍维茨判据— —出现首例为0情况的处理
7-2-2 抽样定理
7-2-3 实际应用中的抽样与恢复
7-3-1 离散时间系统的数学模型 7-3-2 离散时间系统的框图
7-4-1 差分算子描述 7-4-2 差分方程零输入响应的求解 7-4-3 离散时间系统的特征根与稳定性
7-5-1 差分方程零状态响应的卷积和求解法 7-5-2 卷积和的计算 7-5-3 卷积和的性质
2-8-3 二阶系统的冲激响应的求解
2-7-2 卷积的性质
2-7-3 几个特殊 卷积计算结果
2-8-4 任意阶系统的冲激响应的求解
2-9-1 零状态响应以及全响应时域法 求解过程与例题
2-9-2 自然、受迫响应与零输 入零状态响应之间的关系等
2-9-3 系统在几个特定激励信号下的响应
3-1 引言 3-2-1 矢量的正交分解 3-2-2 信号的正交分解
注:标注为
1-4-1 系统的
概念
1-4-2Байду номын сангаас统的描述 1-4-3(1)系统的分类(1)
1-4-3(2)系统的分类(2) 1-4-4 增量线性系统与零状态-零输入响应
1-5-1 线性非时变系统分析
1-5-2线性非时变系统的分析方法
的部分为可选部分。
2-1-1 连续时间系统数学模型 2-1-2 微分方程的经典解法 2-1-3 微分方程的近代解法简介 2-7-1 卷积定义及计算
