再论含特大洪水系列的频率计算问题

合集下载

库漠屯水文站洪水频率计算

库漠屯水文站洪水频率计算作者：魏艳凤孙卓来源：《科技创新与应用》2015年第20期摘要：2013年8月10日是库漠屯水文站建站以来出现的第一号洪水，水位235.29米，为此做一次洪水频率计算，该站为五十年一遇的特大洪水。

了解掌握该测站洪水重现期，为水文的中长期预报作参考，为修建水利工程防洪安全标准和设计标准提供重要依据，使水利工程发挥重要作用。

关键词：频率；偏差系数；离差系数；均值；模比系数库漠屯水文站是嫩江上游重要把口站，中央、省、地、市重要报汛站。

1950年8月建站，测站位于东经125°11′，北纬49°24′，集水面积32229平方公里。

建站六十四年发生较大洪水有十余次（233.50m以上洪水），一般3-5年出现一次，大洪水约10年左右出现一次，特大洪水约30年左右出现一次。

2013年8月10日，是建站以来出现的第一号洪水（235.29m），为此有必要对该站重做一次洪水频率计算，掌握洪水重现期，为水文的中长期预报作参考。

1 流域自然地理概况嫩江发源于大兴安岭北邻伊勒呼里山中段南坡，源头左有南瓮河，右有南阳河，二源与二根河汇合后称嫩江。

河流全长1416公里，流域面积为24.39万平方公里。

上源流经山区，属山区性河流。

由库漠屯水文站以下进入平原，属平原性河流。

流域呈树枝状，支流众多，较大支流右岸有卧都河、门鲁河、泥鳅河、科洛河，左岸有古里河、那都河、多布库尔河、甘河等。

流域成扇形，由北向南倾斜，地形变化较大，平均海拔高200-300m，流域植被良好，坡度较大，径流条件良好。

2 气候特征和洪水形成来源该站地处高纬度，冬季严寒少雪，夏季湿润多雨。

冬季最低气温零下47℃，夏季最高气温达38℃左右，流域内无霜期120天左右，最大冻土为2.5-3.0m，最大冰厚为1.3-1.5m左右。

流域内多年平均降水量为490mm，雨量分布不均，6-9月占全年降水量的80%以上，冬季11月-3月降水量较少，不足全年降水量的10%。

洪水频率计算

21 附录A 洪水频率计算A1 洪水频率曲线统计参数的估计和确定A1.1 参数估计法A1.1.1 矩法。

对于n年连序系列可采用下列公式计算各统计参数: 均值niiXnX11 A1 均方差niiXXnS1211 或niniiiXnXnS1212111 A2 变差系数XSCv A3 偏态系数331321vniisCXnnXXnC 或33131121322123vniniiniiniiisCXnnnXXXnXnC A4 式中Xi——系列变量i1??n n——系列项数。

对于不连序系列其统计参数的计算与连序系列的计算公式有所不同。

如果在迄今的N年中已查明有a个特大洪水其中有l个发生在n年实测或插补系列中假定n-l年系列的均值和均方差与除去特大洪水后的N-a年系列的相等即lnanlnaNSSXX可推导出统计参数的计算公式如下111nliiajjXlnaNXNX A5 nliiajjvXXlnaNXXNXC1212111 A633131321vnliiajjsCXNNXXlnaNXXNC A7 22 式中Xj——特大洪水变量j1??a Xi——实测洪水变量il1??n。

A1.1.2 概率权重矩法。

概率权重矩定义为10dFxxFMjj j012?? A8 皮尔逊Ⅲ型频率曲线的三个统计参数不能用概率权重矩的显式表达。

但经推导有oMX A9 2101MMHCv A10 2/3/0102MMMMR A11 式中H和R都和Cs有关并已有近似的经验关系如下4313/4154.9472.1051.1341.1612.0432RRRuuuuuCs A12 3413/4160938.36315.2985.29545.314.02432RRRVVVVVH A13 为保证Cv和Cs有二位小数准确要求在用式A11计算R时M0、M1和M2的计算值至少达到5位有效数字。

1 根据连序系列计算概率权重矩。

将洪水系列按从大到小顺序排列样本概率权重矩按下式计算niiniiniionnininXnMninXnMXnM121112111111 A142 根据含历史洪水特大值的不连序样本计算概率权重矩。

洪水频率计算规范方法

洪水频率计算规范方法 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】附录A 洪水频率计算A1 洪水频率曲线统计参数的估计和确定参数估计法A1.1.1 矩法。

对于n 年连序系列，可采用下列公式计算各统计参数: 均值 ∑==ni i X n X 11（A1）均方差 ∑=--=ni i X X n S 12)(11或 ⎥⎦⎤⎢⎣⎡--=∑∑==n i n i i i X n X n S 1212)(111（A2）变差系数 XSC v =（A3）偏态系数 3313)2)(1()(vni i sCX n n X X n C ---=∑=或 3313112132)2)(1()(23vni ni i n i i ni i i s CX n n n X X X n X n C --+⋅-=∑∑∑∑====（A4）式中 X i ——系列变量（i=1，…，n ）； n ——系列项数。

对于不连序系列，其统计参数的计算与连序系列的计算公式有所不同。

如果在迄今的N 年中已查明有a 个特大洪水（其中有l 个发生在n年实测或插补系列中），假定（n-l ）年系列的均值和均方差与除去特大洪水后的（N-a ）年系列的相等，即l n a n l n a N S S X X ----==,，可推导出统计参数的计算公式如下：)(111∑∑+==--+=nl i i a j j X l n a N X N X （A5）⎥⎦⎤⎢⎣⎡---+--=∑∑++==n l i i a j jv X X l n a N X X N XC 1212)()(111（A6）331313)2)(1()()(vn l i ia j j s C X N N X X l n a N X X N C --⎥⎦⎤⎢⎣⎡---+-=∑∑+==（A7）式中 X j ——特大洪水变量（j=1，…，a ）；X i ——实测洪水变量（i=l +1，…，n ）。

洪水频率计算(要求规范方法)

附录A 洪水频率计算A1 洪水频率曲线统计参数的估计和确定A1.1 参数估计法A1.1.1 矩法。

对于n 年连序系列，可采用下列公式计算各统计参数: 均值∑==ni i X n X 11 （A1）均方差 ∑=--=ni i X X n S 12)(11或 ⎥⎦⎤⎢⎣⎡--=∑∑==n i n i i i X n X n S 1212)(111 （A2）变差系数XSC v =（A3）偏态系数3313)2)(1()(vni i s CX n n X X n C ---=∑=或3313112132)2)(1()(23vni ni i n i i ni i i s CX n n n X X X n X n C --+⋅-=∑∑∑∑==== （A4）式中 X i ——系列变量（i=1，…，n ）； n ——系列项数。

对于不连序系列，其统计参数的计算与连序系列的计算公式有所不同。

如果在迄今的N 年中已查明有a 个特大洪水（其中有l 个发生在n 年实测或插补系列中），假定（n-l ）年系列的均值和均方差与除去特大洪水后的（N-a ）年系列的相等，即l n a n l n a N S S X X ----==,，可推导出统计参数的计算公式如下：)(111∑∑+==--+=nl i i a j j X l n a N X N X （A5）⎥⎦⎤⎢⎣⎡---+--=∑∑++==n l i i a j jv X X l n a N X X N XC 1212)()(111 （A6）331313)2)(1()()(vn l i ia j j s C X N N X X l n a N X X N C --⎥⎦⎤⎢⎣⎡---+-=∑∑+== （A7）式中 X j ——特大洪水变量（j=1，…，a ）；X i ——实测洪水变量（i=l +1，…，n ）。

A1.1.2 概率权重矩法。

概率权重矩定义为⎰=10)(dF x xF M j j j=0,1,2,… （A8）皮尔逊Ⅲ型频率曲线的三个统计参数不能用概率权重矩的显式表达。

洪峰流量及时段洪量的频率分析

Qm＝110000m3/s
1153
1870
1992 n
N
说明确定特大洪水的重现期具有相当大的不稳定性。要准确地确定重现期就要追溯到更远的年代，但追溯的年代愈远，河道情况与当前差别越大，记载愈不详尽，计算精度亦愈差。一般地，以明、清两代六百年为宜。
三、洪水经验频率计算（一）连序系列的经验频率计算
③ 代表性：现有n年实测洪水资料组成的特定样本系列和总体接近。样本的代表性决
定抽样误差的大小。
④ 由于水文系列的总体不可能取得，若仅有 n个样本系列，无法检验其代表性，通常只能通过与临近相似流域较长期系列作比较来间接衡量： • 参证站长系列比短系列的代表性好，可用长系列为基础来检验短系列的代表性； • 气候相同的区域内，参证站与设计站年径流的时序变化具有同步性（同枯或同丰）。可把参证站的代表期直接移用于设计站。
所以历史洪水加入系列后，样本成为不连序系列，其经验频率和统计参数的计算与连序系列不同。这样就要研究有历史洪水时的经验频率和统计参数的计算方法，称为特大洪水处理。
例如某站 1940—1982 年有实测洪水资料。其中1963年洪水最大，1940年次大；另调查到自1903年以来，为首的三次大洪水的排位为1921年、1963年、1903年，且在此80年间不会漏掉比1903年更大的洪水。另通过文献考证，1903年以前还有三次大于1921年的洪水，其排位为1867年、1852 年、1832年，但小于1921年的洪水，则无法查清。该站的洪峰流量即为不连序系列。
Q（m3/s）
同一年内所选取的各种洪水特征值可以在同一场洪水中取，也可以在不同场洪水中选取，只需遵循“最大”的原则即可。
Qm

洪水频率计算(规范方法)

附录A 洪水频率计算A1 洪水频率曲线统计参数的估计和确定A1.1 参数估计法A1.1.1 矩法。

对于n 年连序系列，可采用下列公式计算各统计参数: 均值∑==ni i X n X 11 （A1）均方差 ∑=--=ni i X X n S 12)(11或 ⎥⎦⎤⎢⎣⎡--=∑∑==n i n i i i X n X n S 1212)(111 （A2）变差系数XSC v =（A3）偏态系数3313)2)(1()(vni i s CX n n X X n C ---=∑=或3313112132)2)(1()(23vni ni i n i i ni i i s CX n n n X X X n X n C --+⋅-=∑∑∑∑==== （A4）式中 X i ——系列变量（i=1，…，n ）； n ——系列项数。

对于不连序系列，其统计参数的计算与连序系列的计算公式有所不同。

如果在迄今的N 年中已查明有a 个特大洪水（其中有l 个发生在n 年实测或插补系列中），假定（n-l ）年系列的均值和均方差与除去特大洪水后的（N-a ）年系列的相等，即l n a n l n a N S S X X ----==,，可推导出统计参数的计算公式如下：)(111∑∑+==--+=nl i i a j j X l n a N X N X （A5）⎥⎦⎤⎢⎣⎡---+--=∑∑++==n l i i a j jv X X l n a N X X N XC 1212)()(111 （A6）331313)2)(1()()(vn l i ia j j s C X N N X X l n a N X X N C --⎥⎦⎤⎢⎣⎡---+-=∑∑+== （A7）式中 X j ——特大洪水变量（j=1，…，a ）；X i ——实测洪水变量（i=l +1，…，n ）。

A1.1.2 概率权重矩法。

概率权重矩定义为⎰=10)(dF x xF M j j j=0,1,2,… （A8）皮尔逊Ⅲ型频率曲线的三个统计参数不能用概率权重矩的显式表达。

洪水频率计算(规范方法)

附录A 洪水频率计算A1 洪水频率曲线统计参数的估计和确定A1.1 参数估计法A1.1.1 矩法。

对于n 年连序系列，可采用下列公式计算各统计参数: 均值∑==ni i X n X 11 （A1）均方差 ∑=--=ni i X X n S 12)(11或 ⎥⎦⎤⎢⎣⎡--=∑∑==n i n i i i X n X n S 1212)(111 （A2）变差系数XSC v =（A3）偏态系数3313)2)(1()(vni i s CX n n X X n C ---=∑=或3313112132)2)(1()(23vni ni i n i i ni i i s CX n n n X X X n X n C --+⋅-=∑∑∑∑==== （A4）式中 X i ——系列变量（i=1，…，n ）； n ——系列项数。

对于不连序系列，其统计参数的计算与连序系列的计算公式有所不同。

如果在迄今的N 年中已查明有a 个特大洪水（其中有l 个发生在n 年实测或插补系列中），假定（n-l ）年系列的均值和均方差与除去特大洪水后的（N-a ）年系列的相等，即l n a n l n a N S S X X ----==,，可推导出统计参数的计算公式如下：)(111∑∑+==--+=nl i i a j j X l n a N X N X （A5）⎥⎦⎤⎢⎣⎡---+--=∑∑++==n l i i a j jv X X l n a N X X N XC 1212)()(111 （A6）331313)2)(1()()(vn l i ia j j s C X N N X X l n a N X X N C --⎥⎦⎤⎢⎣⎡---+-=∑∑+== （A7）式中 X j ——特大洪水变量（j=1，…，a ）；X i ——实测洪水变量（i=l +1，…，n ）。

A1.1.2 概率权重矩法。

概率权重矩定义为⎰=10)(dF x xF M j j j=0,1,2,… （A8）皮尔逊Ⅲ型频率曲线的三个统计参数不能用概率权重矩的显式表达。

洪峰流量频率计算

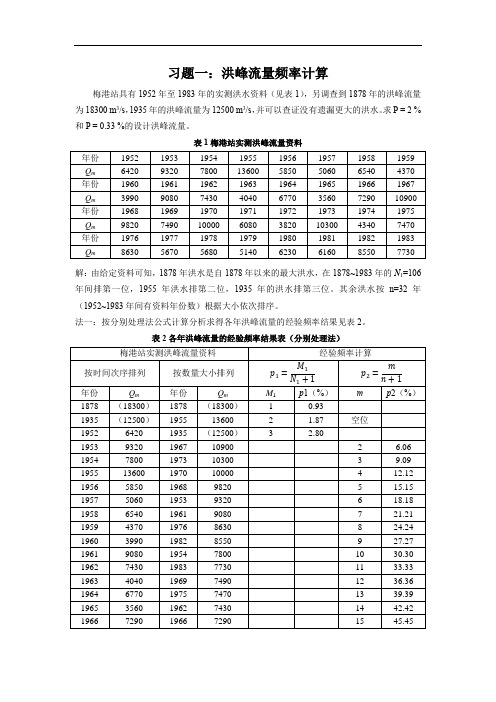
习题一：洪峰流量频率计算梅港站具有1952年至1983年的实测洪水资料（见表1），另调查到1878年的洪峰流量为18300 m3/s，1935年的洪峰流量为12500 m3/s，并可以查证没有遗漏更大的洪水。

求P = 2 %和P = 0.33 %的设计洪峰流量。

表1梅港站实测洪峰流量资料解：由给定资料可知，1878年洪水是自1878年以来的最大洪水，在1878~1983年的N1=106年间排第一位，1955年洪水排第二位，1935年的洪水排第三位。

其余洪水按n=32年（1952~1983年间有资料年份数）根据大小依次排序。

法一：按分别处理法公式计算分析求得各年洪峰流量的经验频率结果见表2。

表2各年洪峰流量的经验频率结果表（分别处理法）根据表2中的流量数据和计算的经验频率，点绘经验点据，如图1中圆形点据所示。

图1分别处理法求得的频率曲线经过调整，参数最终选用Q̅=7146.25 m3/s， C v=0.38，C s=1.32 ，拟合度达96.79%。

经检验，当P = 2 %时的设计洪峰流量为14408.97 m3/s>13900 m3/s，故成果合理。

据此组参数求得P = 2 %和P = 0.33 %的设计洪峰流量分别为14408.97 m3/s和18227.16 m3/s。

法二：按统一处理法公式计算分析求得各年洪峰流量的经验频率结果见表3。

表3各年洪峰流量的经验频率结果表（统一处理法）根据表3中的流量数据和计算的经验频率，点绘经验点据，如图2中圆形点据所示。

图2统一处理法绘制的频率曲线经过调整，参数最终选用Q̅=7080.47 m3/s， C v=0.38，C s=1.33 ，拟合度达96.70%。

经检验，当P = 2 %时的设计洪峰流量为14286.92 m3/s>13900 m3/s，故成果合理。

据此组参数求得P = 2 %和P = 0.33 %的设计洪峰流量分别为14286.92 m3/s和18085.61 m3/s。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

Ａｂｔａｔｈｍｐｒｃｌｑｅｃａｃｌｔｎ，￣ｅｕｎｙｃｒｅｄａｎｎａａｔｒｅｔｔｎｏｅｄｓｏｔｕｕｏｄｓｒｃ：Ｔｅｅｉａ￣ｅｕｎｙｃｌｕａｉｉｏｑｅｃｕｖｒｗｉｇａｄｐｒｍｅｅｓｉｉｆｈｉｃｎｉｏｓｆｏｍａｏｔｎｌ
值系列），通常由调查大洪水的痕迹或考证历史文献等资料，经过整理、分析、计算而获得，其系列
为（：１２，，… ，）ｎ（）１
频率曲线所含统计参数（均值、ｃ、ｃ）的估计，现采用适线法 … 。所谓适线法，就是将所选线型（现
水利水电技术
第４２卷
２１０１年第８期
再论含特大洪水系列的频率计算问题
金光炎
（秉淮
摘
员水科研院安蚌３。墓开学究，徽埠２。ＩＪ３）。
要：叙述了不连序洪水系列（特大洪水和实测洪水系列）的经验频率计算、频率曲线绘制和参数
估计等问题。认为在研制方法时应以不确定性较小的事件为主，并提出了评析意见及改进的建议。由于水文频率计算具有一定的不确定性、随机性和经验性，故需对计算结果进行综合平衡，通过合理性
分析后取用。
关键词：特大洪水；实测洪水；水文频率计算；经验频率；适线法
中图分类号：Ｐ３３３文献标识码：Ａ文章编号：１０ —８０２１）８０７－４０００６（０１０ —０５０
Ｆｒｈｒｄｓｕｓｏｎｐｏｌｍｓｆｏａｃｌｔｎｏｒｑｅｃｆｆｏｅｉｓｃｎａｎｎｘｒｏｄｎｒｖｎｕｔｅｉｃｓｉｎｏｒｂｅｒｍｃｌｕａｉｎｆｅｕｎｙｏｏｄｓｒｅｏｔｉｉｇｅｔａｒｉａｙｅｅｔｏｌ
ｐａｓｎｏｒｉｉｇｃｍｍｅｔｎｍｐｏｉｇｓｇｅｔｎｒｕｏｗａｄａｅ１Ａｓｔｅｈｄｏｏｉ￣ｑｅｃａｃｌｔｎｈｓｃｒｉｎｓａｄｉｒｖｎｕｇｓｉｓａｅｐｔｆｒｒｓｗｌｏ．ｈｙｒｌｇｃｅｕｎｙｃｌｕａｉａｅａｎｏｔｕｃｒａｎｙ，ｒｎｏｅｓａｄｅｉｉａｉｎｅｔｉｔａｄｍｎｓｎｍｐｒｃｌｙ，ｔｅｃｌｕａｉｎｒｓｌｓｅｕｅｆｒｒｔｎｌａａｙｉｈｏｇｏｒｈｎｔｈａｃｌｔｅｕｔｍｕｔｂｓｄａｔａｉａｎｌｓｓｔｒｕｈａｃｍｐｅｅ — ｏｓｅｏ
用Ｐ３型）经验频率点子在概率格纸上进行拟合，与取拟合较好者作为参数的结果。因此，经验频率的选择，显得十分重要。
ＪＮＧｕｎｙｎＩａｇａ
（ｔｅｏｒｅＲｓａｃｓｔｔｏｎｕｒｖｃｎｕｉｅＲｖｒｏｍｓｏ，ＷａｅＲｓｕｃｓｅｅｒｈＩｔｕｅｆｈｉｏｉｅａｄＨａｈｉｍｉｉｎＭＷＲ，Ｂｎｂ２３０，ｎｕ，ＣｉａｒｎｉＡＰｎｅＣｓ．ｅｇｕ３００Ａｈｉｈｎ）
ｔｏｅｅｅｔｗｉｅｓｕｃｒｉｔｅｓｅｍａｎｙｔｋｎｆｒｔｅｄｖｌｐｎｆｔｅｍｅｈｄｃｎｅｎｄ，ａｄｔｅｏｐｈｓｖｎｓｔｌｓｎｅｔｎｉｓｍｕｔｂｉｌａｅｏｈｅｅｏｍｅｔｏｔｏｏｃｒｅｈａｈｎｈｎｓｍｅａ —
般，在频率计算中，收集到的洪水系列包含两种类型：特大洪水系列和实测洪水系列。
一Байду номын сангаас
当单独考虑两个洪水系列中的一个系列时，称其为连序系列；当两个洪水系列合并处理时，称为不连
序系列。
特大洪水系列（称历史洪水系列，简称特大亦
ｓｒｓ（ｎｌｄｎｘｒｏｄｎｒｆｏｅｉｓａｄａｔａｍａｕｅｏｄｓｒｓａｅｄｓｒｅｅｅｎＩｉｃｎｉｅｅｈｔｅｉｉｃｉｇｅｔｒｉａｏｄｓｒｎｃｌｅｓｒｄｆｏｅｅ）ｒｅｃｉｄｈｒｉ．ｔｓｏｓｒｄｔａｅｕａｙｌｅｕｌｉｂｄ
ｓｖｌｃ．ｉｅｂａａｎｅ
Ｋｅｒｓｘｒｏｄｎｒｏｄ；ａｔａｅｓｒｄｆｏｙｗｏｄ：ｅｔｒｉａｙｆｏａｌｃｕｌｍａｕｅｏｄ；ｈｄｏｏｉｒｑｅｃａｃｌｔｎ；ｍｐｒａｒｑｅｃｃｒｅｆｔｇｍｅｈｄｌｙｒｌｇｃｆｅｕｎｙｃｕａｉｌｏｅｉｃｆｕｎｙ；ｕｖ — ｔｎｔｏｉｌｅｉｉ