大学光学经典课件L6_定态光波及其复振幅描述
合集下载
大学物理波动光学一PPT课件

超快光谱技术
介绍超快光谱技术的原理、方法及应 用,如泵浦-探测技术、时间分辨光谱 技术等。
超短脉冲激光技术
详细介绍超短脉冲激光技术的原理、 实现方法及应用领域,如飞秒激光技 术、阿秒激光技术等。
未来光学技术挑战和机遇
光学技术的挑战
阐述当前光学技术面临 的挑战,如光学器件的 微型化、集成化、高性 能化等。
大学物理波动光学一 PPT课件
目录
• 波动光学基本概念与原理 • 干涉原理及应用 • 衍射原理及应用 • 偏振现象与物质性质研究 • 现代光学技术进展与挑战
01
波动光学基本概念与原理
光波性质及描述方法
光波是一种电磁波,具有波动性 质,可以用振幅、频率、波长等
物理量来描述。
光波在真空中的传播速度最快, 且在不同介质中传播速度不同。
01
02
03
04
摄影
利用偏振滤镜消除反射光和散 射光,提高照片清晰度和色彩
饱和度。
液晶显示
利用液晶分子的旋光性控制偏 振光的透射和反射,实现图像
显示。
光学仪器
如偏振光显微镜、偏振光谱仪 等,利用偏振光的特性进行物
质分析和检测。
其他领域
如生物医学、材料科学、环境 科学等,利用偏振光的特性进
行研究和应用。
01
牛顿环实验装置与步骤
介绍牛顿环实验的基本装置和操作步骤,包括凸透镜、平面镜、光源等
。
02
牛顿环测量光学表面反射相移
阐述如何通过牛顿环实验测量光学表面反射相移的原理和方法。
03
等厚干涉原理及应用
探讨等厚干涉的基本原理,以及其在光学测量和光学器件设计中的应用
。
多光束干涉及其应用
2-2定态光波

2.2定态光波
2.2.1定态光波: ⑴定态光波定义:
空间各点均为同频率的简谐振动; 空间各点振动的振幅不随时间变化。
⑵定态光波可用标量波来处理。 ⑶定态光波表示式:
U ( p, t ) A( p) cos[t ( p)]
2.2.2定态光波波函数中各个 物理量的含义
⑴ U ( p, t ) 电场矢量的瞬时值。 ⑵ A( p) 是电场矢量的振幅。 ⑶ ( p) 是初相位,与时间无关。 ⑷ 是简谐振动的频率。
2.2.Байду номын сангаас波矢、光程及相位:
r v 2 v ˆ ˆ k k kk r v 2 v ˆ ˆ k0 其中: k nk0 真空中的波矢: 0 k0 k0 k 0 v v ˆ 的方向为波的传播方向 ˆ 单位矢量 k 或 k0
0
Q
r
P
v v 2 v v 2 v v ˆ k r (k r ) (nk0 r ) k0 ( L)
⑴ 球面波的复振幅表达式:
( P) a ei ( P ) a exp(i ( P)) U r r v
v ( P) k r 0 kr 0
r ( x x0 ) 2 ( y y 0 ) 2 ( z z 0 ) 2
( P) a ei ( P ) a exp(i kr ) 发散球面波: U 0 r r 会聚球面波:U ( P) a ei ( P ) a exp(i kr 0 ) r r
U ( P) A( P)ei ( P ) A( P) exp(i ( P)) U ( P ) 称为定态光波的复振幅
⑵引入定态光波复振幅的意义: 为了运算的方便 ⑶注意: ①两种关系式只是对应关系, 不是相等关系 ②复振幅只用于运算 ③对应成相应的简谐式后 再讨论物理意义
2.2.1定态光波: ⑴定态光波定义:
空间各点均为同频率的简谐振动; 空间各点振动的振幅不随时间变化。
⑵定态光波可用标量波来处理。 ⑶定态光波表示式:
U ( p, t ) A( p) cos[t ( p)]
2.2.2定态光波波函数中各个 物理量的含义
⑴ U ( p, t ) 电场矢量的瞬时值。 ⑵ A( p) 是电场矢量的振幅。 ⑶ ( p) 是初相位,与时间无关。 ⑷ 是简谐振动的频率。
2.2.Байду номын сангаас波矢、光程及相位:
r v 2 v ˆ ˆ k k kk r v 2 v ˆ ˆ k0 其中: k nk0 真空中的波矢: 0 k0 k0 k 0 v v ˆ 的方向为波的传播方向 ˆ 单位矢量 k 或 k0
0
Q
r
P
v v 2 v v 2 v v ˆ k r (k r ) (nk0 r ) k0 ( L)
⑴ 球面波的复振幅表达式:
( P) a ei ( P ) a exp(i ( P)) U r r v
v ( P) k r 0 kr 0
r ( x x0 ) 2 ( y y 0 ) 2 ( z z 0 ) 2
( P) a ei ( P ) a exp(i kr ) 发散球面波: U 0 r r 会聚球面波:U ( P) a ei ( P ) a exp(i kr 0 ) r r
U ( P) A( P)ei ( P ) A( P) exp(i ( P)) U ( P ) 称为定态光波的复振幅
⑵引入定态光波复振幅的意义: 为了运算的方便 ⑶注意: ①两种关系式只是对应关系, 不是相等关系 ②复振幅只用于运算 ③对应成相应的简谐式后 再讨论物理意义
第1章 波动光学基础 1-2 光波的函数表述 物理光学课件

r x x0 2 y y0 2 z z0 2
发散柱面波波函数:
会聚柱面波波函数:
结论:平面波可以看成是构成空间任何复杂波动的基元波。
1 波动光学基础
1.2 光波的函数表述
1.2.4.波前与波面
• 1.波前函数
•
广义波前:光波场内任意考察面(平面、曲面)。
•
波前函数:光波场内任意考察面(平面、曲面)上的复振幅分布函数。
S (b) 球面波
θ θθ
图10-10只考虑平面上的复振幅分布时,共轭波有两个
•
若考虑某一平面的复振幅分布,则产生其共轭复振幅
的共轭波有两个。
•例:传播方向平行于xoz平面,且与z轴夹角为θ的平面波在z=0平面上 波前函数的共轭波前函数.
1 波动光学基础
1.2 光波的函数表述
作业三:入射光波是圆频率为ω的平面波
•和
E
E0
cos
k
r t
H H0 cos k r t
E
E0
cos
kr
t
H
r H0
cos kr t
r
• 其中:
•
k 和ω分别为波的空间角频率和时间角频率(又称
•
圆频率)。
E0 , H0
E0 , H0 rr
称为振动的振幅矢量; 把上式中余弦
函数的宗量称为振动的相位。
1 波动光学基础
• 真空中光速
C 1 2.99792 108 m / s
0 0
• 介质中光速
C C rr n
• 介质折射率
n rr
• 对光学波段,近似有 r 1 ,故 n εr
•
折射率是随光波的频率改变的.
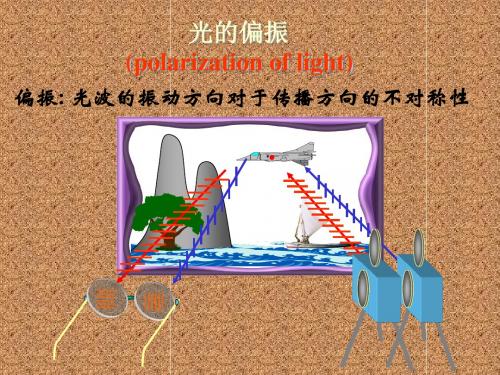
第六章 光的偏振及晶体光学基础 波动光学课件(共102张PPT)

振光
第六页,共102页。
第 六 章 光的偏振及晶体(jīngtǐ)光学根底
2.完全(wánquán)偏振光
由光于波介的质的各向异性,使得(shǐ de) D和 E
不再是同方向的了。而 D是和光波的波矢 k
有关的,所以我们用 D 作为光波的电矢量来讨论。
光波沿z方向传播,那么在z方向的分量为0,在x, y方向的分量为:Dx Dx0cos(kztx0)
x
旋圆偏振光。
当sinδ>0时,为左旋椭圆偏
振光。当sinδ<0时,为右旋椭圆 左旋椭圆偏振光电矢量随
偏振光。
时间(shíjiān)逆时针旋转
第十页,共102页。
第 六 章 光的偏振(piān zhèn)及晶体光学根底
(2)正椭圆偏振光:
当 m /2 (m=0, ±1, ±2, …)
式(6.4)变成了一个正椭圆(tuǒyuán)方程:
D0
e jx0
cos
sin
其中,θ的取值范围为 〔-π/2,π/2〕,并且有:
cos D x0(D x 20D y 20)1/2 sin D y0(D x 2 0D y 20) 1/2
〔3〕圆偏振光: δ=±π/2,两个分量的振幅(zhènfú)相
同,
D0
2 2
e jx0
1
j
第二十二页,共102页。
三、偏振的描述和分类 ➢ 就光的偏振特性而言,光可以被分为偏振光、自然光
和局部偏振光。 ➢ 光矢量的方向和大小有规律(guīlǜ)变化的光称为偏振
光。线偏振光的轨迹是一条直线;圆偏振光端点的轨 迹是一个圆;椭圆偏振光的光矢量的大小和方向在传 播过程中均有规那么的变化,光矢量端点沿椭圆轨迹 转动。 ➢ 任一偏振光都可以用两个振动方向互相垂直、相位有 关联的线偏振光来表示。
大学物理第6章-光的偏振-PPT精选文档36页
n1
反射光中: 垂直振动 多于平行振动。
n2
i r
折射光中: 平行振动多于垂直振动。
(10)
2.布儒斯特定律(Brewster’s law) 当入射角i = i0 时
使之满足:
tan
i0
n2 n1
i0
n1
1)反射光为线偏振光, 只有垂直振动;
n2
r0
i0为起偏角(布儒斯特角)
2)折射光为部分偏振光,
(14)
主截面: 晶体中光的传播方向与晶体光轴构成的平面
o光的 主截面
···e主·光截的面
光轴 o光 光轴
主截面
入射面 e光
e光 o光
光轴在入 射面内
实验表明: 1)o光和e光都是线偏振光, 但光矢量的振动 方向不同, o光的振动方向垂直于自己的主截面, 而e光 的振动平行于自己的主截面。
2)当光轴在入射面内时, o光与e光的主截面相重合, o光与e光的振动方向相互垂直。 在一般情况下, o光与e光的振动方向并不完全垂直。
5.光在单轴晶体中的传播方向
以方解石为例, 用作图法(惠更斯原理)确定o光和e 光在晶体内的传播方向 1)光轴平行晶体表面, 且在入射面内,自然光入射
cΔt
光轴
光轴
voΔt
veΔt
o oo e ee
o
o
ee
由 光 ,得 程 :c Δ tn 相 o vo Δ t 等 n ocvo
思考: (1)线偏光通过1/4波片后, 出射光的偏振态和
光强如何? (正椭圆或圆偏光, 光强不变)
(2)自然光通过1/4波片后, 出射光的偏振态和
光强如何? (自然光, 光强不变)
光波场的复振幅描述 PPT课件

并求出Tx、 Ty、T 和fx 、fy和 f。
(2)画出y = y1平面上间隔为2p的等相线族,
并求出Tx、 Tz 和fx 、fz.
光波场的复振幅描述
平面波的空间频率-信息光学中最基本的概念
如果平面波传播方向在xz平面(或yz平面),
与z轴夹角为q, 则此平面波复振幅沿x方向
(或y方向)的空间频率为:
复振幅分布: U (x, y) Aexp( jkxcosa)
等位相面是平行于y 轴的一系列平面, 间隔为l
等位相面与x-z平面相交 等位相面与x-y平面相交
形成平行直线
形成平行于y轴的直线
沿x方向的等相线 间距:
z
X 2p l
k cosa cosa
光波场的复振幅描述
四、平面波的空间频率
复振幅分布: U (x, y) Aexp( jkxcosa)
§1-1光波场的复振幅描述
光振动的复振幅表示
为了导出a(P)、n、 j(P)必须满足的关系,将光场用复数表
示,以利于简化运算
u(P,t) = a(P)cos[2pnt - j(P)]}
= e{a(P)e-j[2pnt -j(P)] } 复数表示有利于
= e{a(P) e . jj(P) e -j2pnt } 将时空变量分开
j2p
(
fxx
f y y)]dfxdf y
光波场的复振幅描述
平面波的空间频率-信息光学中最基本的概念
三个空间频率不能相互独立:l2 f x 2 l2 f y 2 l2 f z 2 1
因此 f z ( 1 l2 f x 2 l2 f y 2 ) l
这样平面波的复振幅即平面波方程可以写为 :
即
(x x0 )2 ( y z2
(2)画出y = y1平面上间隔为2p的等相线族,
并求出Tx、 Tz 和fx 、fz.
光波场的复振幅描述
平面波的空间频率-信息光学中最基本的概念
如果平面波传播方向在xz平面(或yz平面),
与z轴夹角为q, 则此平面波复振幅沿x方向
(或y方向)的空间频率为:
复振幅分布: U (x, y) Aexp( jkxcosa)
等位相面是平行于y 轴的一系列平面, 间隔为l
等位相面与x-z平面相交 等位相面与x-y平面相交
形成平行直线
形成平行于y轴的直线
沿x方向的等相线 间距:
z
X 2p l
k cosa cosa
光波场的复振幅描述
四、平面波的空间频率
复振幅分布: U (x, y) Aexp( jkxcosa)
§1-1光波场的复振幅描述
光振动的复振幅表示
为了导出a(P)、n、 j(P)必须满足的关系,将光场用复数表
示,以利于简化运算
u(P,t) = a(P)cos[2pnt - j(P)]}
= e{a(P)e-j[2pnt -j(P)] } 复数表示有利于
= e{a(P) e . jj(P) e -j2pnt } 将时空变量分开
j2p
(
fxx
f y y)]dfxdf y
光波场的复振幅描述
平面波的空间频率-信息光学中最基本的概念
三个空间频率不能相互独立:l2 f x 2 l2 f y 2 l2 f z 2 1
因此 f z ( 1 l2 f x 2 l2 f y 2 ) l
这样平面波的复振幅即平面波方程可以写为 :
即
(x x0 )2 ( y z2
大学光学经典课件L6_定态光波及其复振幅描述

(平面波面)
3)振幅特点: A(P) A
8、相位的物理意义
1)相位表示一个振动的状态(振动 方向,大小,变化趋势)
2)可以比较两个振动的超前和落后 (谁先振动谁就超前)
3)通过比较初相位确定两个振动的 超前与落后
4)初相位 (P) 越小 振动越超前,初相位越大 振动越落后。
9、光程的表示式及其物理意义
面波的复振幅分布
1)已知一列平面波的传播方向平行于x z面,
与 z 轴成倾角 ,设坐标原点所在波面的位相
为 0 0 ,写出它在波前
振幅分布。
X
z k
0平面上的复
lP
x
Oz
Z
解:
E(P) Aexp(i(P))
首先分析在 z 0平面上的复振幅分布。
具体求解为:
X
k
(P) k r 0 kx x ky y kz z 0 l P
(1)两种关系式只是对应关系, 不是相等关系
(2)复振幅只用于运算 (3)对应成相应的简谐式后
再讨论物理意义
11、平面波和球面波的复振幅表达式
1) 球面波的复振幅表达式
E(P) a ei(P) a exp(i(P))
r
r
(P) k r 0 kr 0
r (x x0 )2 ( y y0 )2 (z z0 )2
r
QP
rrˆ
k kkˆ krˆ
(P) k r 0 kr 0 k r kr
(球面波面)
4)振幅特点:
A(P) a r
证明:由能量守恒定律:
I1 4r12 I 2 4r22
设:
r1 1 I1 a2 r2 r
A(P) a r
I1 r1
大学物理下光的偏振PPT课件

反射和折射
当光线从一个介质传播到另一个介质时,在分界面上反
射和折射的光线通常是部分偏振的。这是因为在分界面
上,电矢量的振动方向受到限制,只有某些方向上的振
动能够通过。
双折射
在某些晶体中,光线传播时会分成两束不同速度的光,
这两束光的振动方向互相垂直。这种现象称为双折射,
它是产生偏振光的另一种方式。
偏振光在日常生活中的应用
03
利用法布里-珀罗干涉仪产生的多光束干涉现象,根据透射光强
随角度或波长的变化曲线,可求得光波长。
实验数据处理与结果分析
数据处理
结果分析
注意事项
记录实验数据,包括干涉条纹间
距、角度、双缝间距、缝宽等,
并进行计算处理。
将实验数据与理论值进行比较,
分析误差来源,如光源单色性、
双缝间距和缝宽的准确性、测量
01
圆偏振光概念
光矢量端点在垂直于传播方向的平面上描绘出圆形轨迹,称为圆偏振光。
02
椭圆偏振光概念
光矢量端点在垂直于传播方向的平面上描绘出椭圆形轨迹,称为椭圆偏
振光。
03
产生条件
当两个频率相同、振动方向互相垂直的线性偏振光振幅相等,相位差为
π/2时,可产生圆偏振光;若振幅不相等或相位差不为π/2,则产生椭
旋光度、分析物质的成分等。
光子晶体器件
利用光子晶体对光的调控作用制成的器件,具有体积小、重量轻、
易于集成等优点,被广泛应用于光通信、光计算等领域。
THANKS
感谢观看
产生方式
通过反射、折射、双折射和选择性吸收等方法可
以获得线性偏振光。
马吕斯定律及其物理意义
马吕斯定律
强度为I0的线偏振光,透过检偏器后,透射光的强度(不考虑吸收)为:I=I0cos2。其中为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2)定态光波表示式:v v E ( p ,t) A ( p ) c o s [t ( p ) ]
3)单色波列是无限长的。 4)在傍轴条件下,可以把矢量波看成标量波。
2020/3/10
4、定态光波波函数中各个
物理量的含义
1)
v E(
p,
t
)
电场矢量的瞬时值。
2) A v(p)E v0(p)是电场的振幅矢量。
r
•
P
E (P ,t) A (P )c o s [( t )0 ]
r r2 r2 r
2020/3/10
定义波矢:
r k
kkvˆ
2
kvˆ
真单空位中矢其的量中波:kvˆ 矢或k:kvˆ 0krn的0k0方k向0kvˆ0为 波20的kvˆ 0传播方向
3) ( p ) 是初相位,与时间无关。
4)是简谐振动的频率。
v v
E ( p ,t) A ( p ) c o s [t ( p ) ]
2020/3/10
5、波函数中初相位的具体形式
已知Q点振动的表达式:
E (Q ,t) A (Q )c o s[t0 ] 0
则P点振动表达式是: Q
2020/3/10
E °(P ,t)A (P )ei[t (P )]
E ° (P ) A (P )e i(P ) A (P )e x p ( i(P ) )
称为定态光波的复振幅
2)引入定态光波复振幅的意义: 为了运算的方便
3)注意: (1)两种关系式只是对应关系, 不是相等关系 (2)复振幅只用于运算 (3)对应成相应的简谐式后 再讨论物理意义
且 k v r v k rc o s k l
E ( P , t ) A ( P ) c o s [ t ( k l 0 ) ] A ( P ) c o s [ t ( k v r v 0 ) ]
2020/3/10
2)初相位的特点 rvO uuP urrrv ˆ
E ( P ,t) A ( P ) c o s [t ( k 0 n r 0 ) ]
A A((P P))ccooss[[ tt((kkvrrv0)]0)]
2020/3/10
6、球面波的波函数的具体表达式
1)发散球面波
0 Q
rv v
•
P
k
E ( P , t ) A ( P ) c o s [ t ( k v r v 0 ) ] A ( P ) c o s [ t ( P ) ]
X
l
P
0Prk
O
Z
( 2L 020) /3/ 10 n k v ˆ 0 r v n r c o s n l n ( x c o s y c o s z c o s )
10、定态光波的复振幅描述
1)定态光波的复振幅 将简谐式对应成复指数形式
E (P ,t) A (P )c o s [t(P ) ]
2、标量波与矢量波
标量波:波场中物理态的扰动可用标量场描述的 如密度波,温度波
矢量波:波场中物理状态的扰动需用矢量场描述的
如电磁波,
v vv SEH
2020/3/10
3、定态光波
1)定态光波定义:
空间各点的扰动均为同频率的简谐振动 (频率与振源相同),
波场中各点扰动的振幅不随时间变化, 在空间形成一个稳定的振幅分布。
其中: rvˆ kvˆ
2020/3/10
2) 会聚球面波:
E (P ,t) A A ( ( P P ) ) c c o o s s [ [t( t( k v ) r v 0 0 ] ) ]
其中:rvˆ kvˆ
rv
•
v k
P
0 Q
3) 初相位的特点:
rv( P ) Q Pk v r v r rvˆ 0 kk vr kk0 vˆkvkrvˆrvkr
2020/3/10
(球面波面)
4)振幅特点:
A(P) a r
证明:由能量守恒定律:
I14r12I24r2 2
设:
r1 1 I1 a2 r2 r
2020/3/10
9、光程的表示式及其物理意义
1)光程的表达式: 0
Q
r Pk
k vr v2 (k v ˆr v)2 0(nk v ˆ0r v)k0(L )
(L) nkvˆ0 rv
2020/3/10
2)球面波的光程表达式: (L)nkvˆ0rvnr
3)平面波的光程表达式:
2020/3/10
A(P) a r
I 1 r1
Q I 2 r2
I2 A2(P)
7、平面波的具体表达式
1)选坐标原点为计算起点
rvO uuP urrrv ˆ
设:
X
P0 k
l Pr
E (O ,t) A (O )c o s[ t 0 ]
O
Z
E ( P 0 ,t) A ( P 0 )c o s [t ( k l 0 ) ]
(kxxkyykzz)0
(平面波面)
3)振幅特点: 2020/3/10 A(P) A
8、相位的物理意义
1)相位表示一个振动的状态(振动 方向,大小,变化趋势)
2)可以比较两个振动的超前和落后 (谁先振动谁就超前)
3)通过比较初相位确定两个振动的 超前与落后
4)初相位 ( P ) 越小 振动越超前,初相位越大 振动越落后。
第二章 波动光学基本原理
§1 定态光波及其复振幅描述
1、波动及其时空双重周期性
波动定义:振动在空间的传播形成波动。
(波场中每点的物理状态随时间作周期性的变化,而在每一 瞬时波场中各点物理状态的空间分布也呈现一定的周期性)
构成波动的三个条件(波动的基本特征):
时间周期性,空间周期性,伴随着能量的传输
2020/3/10
v k
kkvˆ
v kxi ky
vv j kzk
v
v
v
k(cosi cos j cosk)
r v rr v ˆxiv y v j zk v ( P ) k v r v 0 k r c o s 0 k z 0
(P)k(xcosycoszcos)0
3)单色波列是无限长的。 4)在傍轴条件下,可以把矢量波看成标量波。
2020/3/10
4、定态光波波函数中各个
物理量的含义
1)
v E(
p,
t
)
电场矢量的瞬时值。
2) A v(p)E v0(p)是电场的振幅矢量。
r
•
P
E (P ,t) A (P )c o s [( t )0 ]
r r2 r2 r
2020/3/10
定义波矢:
r k
kkvˆ
2
kvˆ
真单空位中矢其的量中波:kvˆ 矢或k:kvˆ 0krn的0k0方k向0kvˆ0为 波20的kvˆ 0传播方向
3) ( p ) 是初相位,与时间无关。
4)是简谐振动的频率。
v v
E ( p ,t) A ( p ) c o s [t ( p ) ]
2020/3/10
5、波函数中初相位的具体形式
已知Q点振动的表达式:
E (Q ,t) A (Q )c o s[t0 ] 0
则P点振动表达式是: Q
2020/3/10
E °(P ,t)A (P )ei[t (P )]
E ° (P ) A (P )e i(P ) A (P )e x p ( i(P ) )
称为定态光波的复振幅
2)引入定态光波复振幅的意义: 为了运算的方便
3)注意: (1)两种关系式只是对应关系, 不是相等关系 (2)复振幅只用于运算 (3)对应成相应的简谐式后 再讨论物理意义
且 k v r v k rc o s k l
E ( P , t ) A ( P ) c o s [ t ( k l 0 ) ] A ( P ) c o s [ t ( k v r v 0 ) ]
2020/3/10
2)初相位的特点 rvO uuP urrrv ˆ
E ( P ,t) A ( P ) c o s [t ( k 0 n r 0 ) ]
A A((P P))ccooss[[ tt((kkvrrv0)]0)]
2020/3/10
6、球面波的波函数的具体表达式
1)发散球面波
0 Q
rv v
•
P
k
E ( P , t ) A ( P ) c o s [ t ( k v r v 0 ) ] A ( P ) c o s [ t ( P ) ]
X
l
P
0Prk
O
Z
( 2L 020) /3/ 10 n k v ˆ 0 r v n r c o s n l n ( x c o s y c o s z c o s )
10、定态光波的复振幅描述
1)定态光波的复振幅 将简谐式对应成复指数形式
E (P ,t) A (P )c o s [t(P ) ]
2、标量波与矢量波
标量波:波场中物理态的扰动可用标量场描述的 如密度波,温度波
矢量波:波场中物理状态的扰动需用矢量场描述的
如电磁波,
v vv SEH
2020/3/10
3、定态光波
1)定态光波定义:
空间各点的扰动均为同频率的简谐振动 (频率与振源相同),
波场中各点扰动的振幅不随时间变化, 在空间形成一个稳定的振幅分布。
其中: rvˆ kvˆ
2020/3/10
2) 会聚球面波:
E (P ,t) A A ( ( P P ) ) c c o o s s [ [t( t( k v ) r v 0 0 ] ) ]
其中:rvˆ kvˆ
rv
•
v k
P
0 Q
3) 初相位的特点:
rv( P ) Q Pk v r v r rvˆ 0 kk vr kk0 vˆkvkrvˆrvkr
2020/3/10
(球面波面)
4)振幅特点:
A(P) a r
证明:由能量守恒定律:
I14r12I24r2 2
设:
r1 1 I1 a2 r2 r
2020/3/10
9、光程的表示式及其物理意义
1)光程的表达式: 0
Q
r Pk
k vr v2 (k v ˆr v)2 0(nk v ˆ0r v)k0(L )
(L) nkvˆ0 rv
2020/3/10
2)球面波的光程表达式: (L)nkvˆ0rvnr
3)平面波的光程表达式:
2020/3/10
A(P) a r
I 1 r1
Q I 2 r2
I2 A2(P)
7、平面波的具体表达式
1)选坐标原点为计算起点
rvO uuP urrrv ˆ
设:
X
P0 k
l Pr
E (O ,t) A (O )c o s[ t 0 ]
O
Z
E ( P 0 ,t) A ( P 0 )c o s [t ( k l 0 ) ]
(kxxkyykzz)0
(平面波面)
3)振幅特点: 2020/3/10 A(P) A
8、相位的物理意义
1)相位表示一个振动的状态(振动 方向,大小,变化趋势)
2)可以比较两个振动的超前和落后 (谁先振动谁就超前)
3)通过比较初相位确定两个振动的 超前与落后
4)初相位 ( P ) 越小 振动越超前,初相位越大 振动越落后。
第二章 波动光学基本原理
§1 定态光波及其复振幅描述
1、波动及其时空双重周期性
波动定义:振动在空间的传播形成波动。
(波场中每点的物理状态随时间作周期性的变化,而在每一 瞬时波场中各点物理状态的空间分布也呈现一定的周期性)
构成波动的三个条件(波动的基本特征):
时间周期性,空间周期性,伴随着能量的传输
2020/3/10
v k
kkvˆ
v kxi ky
vv j kzk
v
v
v
k(cosi cos j cosk)
r v rr v ˆxiv y v j zk v ( P ) k v r v 0 k r c o s 0 k z 0
(P)k(xcosycoszcos)0
