小波去噪阈值确定和分解层数确定
合集下载
小波分析的语音信号噪声消除方法
小波分析的语音信号噪声消除方法小波分析是一种有效的信号处理方法，可以用于噪声消除。
在语音信号处理中，噪声常常会影响语音信号的质量和可理解性，因此消除噪声对于语音信号的处理非常重要。
下面将介绍几种利用小波分析的语音信号噪声消除方法。
一、阈值方法阈值方法是一种简单而有效的噪声消除方法，它基于小波变换将语音信号分解为多个频带，然后通过设置阈值将各个频带的噪声成分消除。
1.1离散小波变换（DWT）首先，对语音信号进行离散小波变换（DWT），将信号分解为近似系数和细节系数。
近似系数包含信号的低频成分，而细节系数包含信号的高频成分和噪声。
1.2设置阈值对细节系数进行阈值处理，将细节系数中幅值低于设定阈值的部分置零。
这样可以将噪声成分消除，同时保留声音信号的特征。
1.3逆变换将处理后的系数进行逆变换，得到去噪后的语音信号。
1.4优化阈值选择为了提高去噪效果，可以通过优化阈值选择方法来确定最佳的阈值。
常见的选择方法有软阈值和硬阈值。
1.4.1软阈值软阈值将细节系数进行映射，对于小于阈值的细节系数，将其幅值缩小到零。
这样可以在抑制噪声的同时保留语音信号的细节。
1.4.2硬阈值硬阈值将细节系数进行二值化处理，对于小于阈值的细节系数，将其置零。
这样可以更彻底地消除噪声，但可能会损失一些语音信号的细节。
二、小波包变换小波包变换是对离散小波变换的改进和扩展，可以提供更好的频带分析。
在语音信号噪声消除中，小波包变换可以用于更精细的频带选择和噪声消除。
2.1小波包分解将语音信号进行小波包分解，得到多层的近似系数和细节系数。
2.2频带选择根据噪声和语音信号在不同频带上的能量分布特性，选择合适的频带对语音信号进行噪声消除。
2.3阈值处理对选定的频带进行阈值处理，将噪声成分消除。
2.4逆变换对处理后的系数进行逆变换，得到去噪后的语音信号。
三、小波域滤波小波域滤波是一种基于小波变换的滤波方法，通过选择合适的小波函数和滤波器来实现噪声消除。
小波阈值降噪算法中最优分解层数的自适应确定及仿真
1 引 言
发动机的故障诊断需要测量多种传感器的输出信 号 。实际测试过程中测试信号中含有大量的噪声 , 这些 噪声会影响到信号的分析精度和分析结果并进一步影响 故障诊断的准确程度 。因此 , 进行信号的降噪处理是非 常必要的 。近年来 , 基于小波变换的阈值降噪方法得到 [ 12 2] 了广泛的研究和应用 。 实际应用中 ,通过实验发现不仅阈值和阈值函数的 选取是影响降噪效果的关键 , 小波分解的层数 (即尺度 )
3. 1 小波系数的去相关白化检验
则依数理统计的理论 , 其近似服从 F ( m , m ) 分布 。在原 假设条件下 ,有 2 2 2 ρ 1 +ρ 2 + … +ρ m 2 2 2 - 1 = 0 ρ ′ ′ ′ 1 +ρ 2 + … +ρ m
( 8)
^ ( m , m ) - 1 的取值较大时应 所以 ,当检验统计量 F 拒绝原假设 。这样 ,给定显著水平 α , 查自由度为 F ( m , ^(m , m ) m ) 分布表 ,得到临界值 Fα , 当实际计算结果 F
摘 要 : 小波阈值降噪算法是一种有效的从测试信号中去除噪声的方法 。通过对有用信号和噪声信号在小波空间上传播特性 的不同进行分析 ,提出了一种基于小波去相关白噪声检验的最优分解层数自适应确定算法 。该算法可以根据含噪声信号的特 点和信噪比 ,自适应的选择小波变换的最优分解层数以达到最优的降噪效果 。最后 ,在 MATLAB 环境下进行了仿真实验 ,并进 行了工程应用 。仿真实验和工程应用结果表明 ,该方法可以有效的确定合理分解层数得到最优的信噪比 。 关键词 : 小波降噪 ; 分解层数 ; 去相关 ; 白化检验 中图分类号 : O174. 2 文献标识码 : A 国家标准学科分类代码 : 520. 60
自适应小波阈值去噪原理
自适应小波阈值去噪原理小波变换的出现为信号处理领域带来了新的处理方法，其中的小波阈值去噪技术由于其出色的去噪效果而备受关注。
该技术在如何确定阈值方面存在许多争议，为了解决这个问题，自适应小波阈值去噪技术应运而生。
本文将详细介绍自适应小波阈值去噪技术的原理和实现方式。
小波阈值去噪技术是基于小波变换的信号去噪方法，其基本原理是：将噪声信号通过小波变换转换到小波域，利用小波变换的分解性质将噪声和信号分开，通过加入阈值进行噪声的滤除，然后将小波域上的信号逆变换回时域，得到经过去噪后的信号。
具体来说，对于一个长度为N的信号$x(n)$，它可以进行小波变换得到其小波系数$CJ_k$，即：$$CJ_k = \sum_{n=0}^{N-1}x(n)\psi_{j,k}(n)$$$\psi_{j,k}(n)$为小波基函数，它们可以由小波变换的不同种类选择。
通过多层小波分解，可以得到多个小波系数矩阵$CJ_{nj}$，其中$n$表示小波变换的层数，$j$表示小波系数的关键字，$j=(n,j)$。
在小波域中，噪声和信号的表现方式不同。
通常情况下，信号的小波系数分布在某个范围内，而噪声则分布在零附近。
我们可以通过以零为中心的阈值将小波系数分为两部分：大于阈值的系数表示信号成分，小于阈值的系数表示噪声成分。
然后将小于阈值的小波系数清零，再通过逆变换将小波系数转换回原始信号。
小波阈值去噪技术的核心问题是如何确定阈值。
传统的小波阈值去噪技术采用全局阈值，所有小波系数均采用同一个阈值进行处理。
这种方法可能会使信号丢失部分重要信息，从而影响其质量。
如果在将全部小波系数同时处理时，不同频带的信号成分和噪声带宽差异较大，无法很好地选取合理的阈值。
为了解决这些问题，自适应小波阈值去噪技术应运而生。
该方法采用自适应阈值，在不同频带上分别应用不同的阈值，以便更好地保留信号信息。
自适应小波阈值去噪技术的步骤如下：1. 利用小波变换将噪声信号转换到小波域。
小波门限消噪法应用中分解层数及阈值的确定
KEY WORDS: Wavelet transform; Decomposition order; 3σ rule; Threshold; Verification of white noise
摘要：基于小波变换的门限去噪算法是去除数字信号中白噪 声的有效算法。在实际应用中，这种非线性滤波方法有 2 个 核心问题需要解决。一个是门限阈值的选取；另一个是信号 分解层数的确定。该文通过数字仿真证明了确定合适的分解 层数的重要性。分析了白噪声污染的有用信号的小波变换系 数特点。提出了 1 种分解层数的自适应确定方法，并提出了 1 种基于 3σ 法则原理的各层小波空间中阈值的选取方法。 仿真结果表明，该文方法具有较好的去噪效果，尤其适合于 强噪声背景下弱信号的监测。该文方法明确提出了基于小波 变换的门限去噪算法中分解层数和门限阈值 2 个重要参数 的确定方法，增强了这种去噪算法在工程应用中的实用性。 关键词：小波变换；分解层数；3σ 法则；门限阈值；白化
① 对数据序列进行一步小波分解； ② 对①分解所得到的细节系数即小波系数进 行白化检验，若系数序列为白噪声序列则到下一步；
若系数序列为非白噪声序列，则跳至④；
③ 计算本层的门限阈值，依式(1)对本层的小 波系数进行处理，跳至第①步。
④ 放弃最后一次分解的结果，即假设共分解
120
中国电机工程学报
第 24 卷
知识可知[5]：
p{−3σ < z − μ < 3σ } = 0.9974
(4)
式中 z ~ N (μ ,σ 2 ) ，在本文中，z ~WN (0,σ 2 ) ，即 均值 z=0 零、白噪声的方差为σ 2 。
对通过白化检验的小波系数序列，可以通过计 算系数序列的方差来估计白噪声序列的方差σ 2。得 到σ之后即可取门限阈值为 3σ，小波序列经此门限 值作用之后，白噪声的能量系数基本已全部滤掉， 而有用信号由于小波变换系数较大，将得到保留。 文[6]提出参数 c 在区间[3，4]内选取效果是满意的 结论，笔者认为此结论实际上是 3σ法则的体现。因 为离散白噪声序列的值落在[-4σ，4σ]区间内的概率 几乎是 100%。所以本文也可以直观而简单地得出 文[6]所提出的结论。在第 4 部分的仿真结果表明，
摘要：基于小波变换的门限去噪算法是去除数字信号中白噪 声的有效算法。在实际应用中，这种非线性滤波方法有 2 个 核心问题需要解决。一个是门限阈值的选取；另一个是信号 分解层数的确定。该文通过数字仿真证明了确定合适的分解 层数的重要性。分析了白噪声污染的有用信号的小波变换系 数特点。提出了 1 种分解层数的自适应确定方法，并提出了 1 种基于 3σ 法则原理的各层小波空间中阈值的选取方法。 仿真结果表明，该文方法具有较好的去噪效果，尤其适合于 强噪声背景下弱信号的监测。该文方法明确提出了基于小波 变换的门限去噪算法中分解层数和门限阈值 2 个重要参数 的确定方法，增强了这种去噪算法在工程应用中的实用性。 关键词：小波变换；分解层数；3σ 法则；门限阈值；白化
① 对数据序列进行一步小波分解； ② 对①分解所得到的细节系数即小波系数进 行白化检验，若系数序列为白噪声序列则到下一步；
若系数序列为非白噪声序列，则跳至④；
③ 计算本层的门限阈值，依式(1)对本层的小 波系数进行处理，跳至第①步。
④ 放弃最后一次分解的结果，即假设共分解
120
中国电机工程学报
第 24 卷
知识可知[5]：
p{−3σ < z − μ < 3σ } = 0.9974
(4)
式中 z ~ N (μ ,σ 2 ) ，在本文中，z ~WN (0,σ 2 ) ，即 均值 z=0 零、白噪声的方差为σ 2 。
对通过白化检验的小波系数序列，可以通过计 算系数序列的方差来估计白噪声序列的方差σ 2。得 到σ之后即可取门限阈值为 3σ，小波序列经此门限 值作用之后，白噪声的能量系数基本已全部滤掉， 而有用信号由于小波变换系数较大，将得到保留。 文[6]提出参数 c 在区间[3，4]内选取效果是满意的 结论，笔者认为此结论实际上是 3σ法则的体现。因 为离散白噪声序列的值落在[-4σ，4σ]区间内的概率 几乎是 100%。所以本文也可以直观而简单地得出 文[6]所提出的结论。在第 4 部分的仿真结果表明，
小波去噪的流程图
影响： 1.零件的加工精度 2.表面粗糙度
1.主轴回转误差运动的测量
编码器 主轴
位移传感器X 测试球 位移传感器Y 传感器支架
1.主轴回转误差运动的测量
Y E F
敏感方向
E' D'
θ ΔY(θ) B θ A
D
C
A' X
ΔX(θ)
1.主轴回转误差运动的测量
主轴
光电索引传感器 测试球 电容位移传感器
小波去噪在主轴回转误差运动测量中的应用
报 告 人： 陈野 同组成员：谢胜龙 机械学院 2018年8月3日
1
主轴回转误差运动的测量 拟解决的问题 方法和工具
2
3
4
结论
1.主轴回转误差运动的测量
1.主轴回转误差运动的测量
1.主轴回转误差运动的测量
轴颈的圆度误差 轴承的缺陷和间隙 主轴受力变形挠曲 主轴支承的两端对轴 颈中心线不垂直
3.方法和工具
小波分析去噪的原理：
有用信号通常表现为低频信号或是相对比较平稳。而噪声 信号通常表现为高频信号。利用小波对含噪声的原始信号分解
后，含噪部分主要集中在高频小波系数中，并且，包含有用信
号的小波系数幅值较大，但数目少；而噪声对应的小波系数幅 值小，数目较多。 基于上述特点，可以通过不同的阈值标准的选取来对小波 系数进行处理。常用的阈值标准有硬阈值（即对较小的小波系
3 level
4 level
5 level
6 level
3.方法和工具
不同小波的选取进行对比： （coif1小波）
2 level
3 level
4 level
5 level
3.方法和工具
不同小波的选取进行对比： （ dmey小波）
小波阈值降噪算法中最优分解层数的自适应选择_蔡铁
第2期
蔡 铁等: 小波阈值降噪算法中最优分解层数的自适应选择
219
图 2 不同分解层数下小波系数序列的奇异谱
系数的奇异谱, 可以判断出小波域信号能量压缩和 噪声能量扩散的程度, 从而选择适当的小波分解层
数用于小波阈值降噪.
3. 2 最优分解层数的自适应选择
根 据 3. 1 节中小波系数序列的奇异谱特性, 本 文提出一种自适应选择最优分解层数的小波降噪算
应选择方法, 可有效提高小波阈值降噪算法的性能,
进一步增强算法的实用性.
2 小波阈值降噪算法
基于阈值处理的小波降噪算法是一种直观而
有 效的去噪算法. 设纯净的语音信号为 s, 其长度为
N ; 加入高斯白噪声 d 的带噪语音为 x , 噪声 d 的方
差为 R2. 于是可表示为
x = s + d.
定值, 难以使算法在不同信噪比下都获得最优的降
噪效果.
3. 1 小波系数的奇异谱分析
根 据小波变换理论可知, 当小波分解层数过少
时, 有用信号的能量压缩不明显, 其对应的小波系数
与其他系数在幅值上相差不多, 此时白噪声将在小
波空间占主导地位, 小波系数表现为白噪声特性; 当
小波分解层数达到一定数量时, 有用信号的能量压
Adaptive Selection of Optimal Decomposition Level in Threshold De-noising Algorithm Based on Wavelet
CA I T ie, ZH U J ie
( Depar tment of Electr onic Eng ineering, Shanghai Jiao tong U niv ersit y , Shang hai 200030, China. Co rr espo ndent: CA I T ie, E-mail: ct 1977@ sjtu. edu. cn)
小波去噪阈值的确定和分解层数的确定
代价函数的基本要求：单调性。可加性（次可加性）
代价函数M:
01
常用代价函数：
02
数列中大于给定门限的系数的个数。即预先给定一门限值 ，并计数数列中绝对值大于 的元素的个数。
03
范数。
01
常用代价函数：
02
熵
常用代价函数：
能量对数
“最优树”的搜索方法：
二元树搜索方法：
[thr2,nkeep]=wdcbm(c,l,alpha2);%获得阈值
获取各个高频段的阈值，
阈值选取是根据Birge-Massart准则。
小波去噪阈值的几种方法
[thr,sorh,keepapp]=ddencmp('den','wv',x); xd2=wdencmp('gbl',c,l,wname,level,thr,'h',1);
02
小波包阈值去噪的过程
1 DecompositionFor a given wavelet, compute the wavelet packet decomposition of signal x at level N.（计算信号x在N层小波包分解的系数）2 Computation of the best treeFor a given entropy, compute the optimal wavelet packet tree. Of course, this step is optional. The graphical tools provide a Best Tree button for making this computation quick and easy.（以熵为准则，计算最佳树，当然这一步是可选择的。）3 Thresholding of wavelet packet coefficientsFor each packet (except for the approximation), select a threshold and apply thresholding to coefficients.（对于每一个小波包分解系数，选择阈值并应用于去噪）The graphical tools automatically provide an initial threshold based onbalancing the amount of compression and retained energy. This threshold is.（工具箱会根据压缩量和剩余能量提供一个初始化的阈值，不过仍需要不断测试来选择阈值优化去噪效果）a reasonable first approximation for most cases. However, in general youwill have to refine your threshold by trial and error so as to optimize theresults to fit your particular analysis and design criteria.
代价函数M:
01
常用代价函数：
02
数列中大于给定门限的系数的个数。即预先给定一门限值 ，并计数数列中绝对值大于 的元素的个数。
03
范数。
01
常用代价函数：
02
熵
常用代价函数：
能量对数
“最优树”的搜索方法：
二元树搜索方法：
[thr2,nkeep]=wdcbm(c,l,alpha2);%获得阈值
获取各个高频段的阈值，
阈值选取是根据Birge-Massart准则。
小波去噪阈值的几种方法
[thr,sorh,keepapp]=ddencmp('den','wv',x); xd2=wdencmp('gbl',c,l,wname,level,thr,'h',1);
02
小波包阈值去噪的过程
1 DecompositionFor a given wavelet, compute the wavelet packet decomposition of signal x at level N.（计算信号x在N层小波包分解的系数）2 Computation of the best treeFor a given entropy, compute the optimal wavelet packet tree. Of course, this step is optional. The graphical tools provide a Best Tree button for making this computation quick and easy.（以熵为准则，计算最佳树，当然这一步是可选择的。）3 Thresholding of wavelet packet coefficientsFor each packet (except for the approximation), select a threshold and apply thresholding to coefficients.（对于每一个小波包分解系数，选择阈值并应用于去噪）The graphical tools automatically provide an initial threshold based onbalancing the amount of compression and retained energy. This threshold is.（工具箱会根据压缩量和剩余能量提供一个初始化的阈值，不过仍需要不断测试来选择阈值优化去噪效果）a reasonable first approximation for most cases. However, in general youwill have to refine your threshold by trial and error so as to optimize theresults to fit your particular analysis and design criteria.
小波去噪阈值的确定和分解层数的确定
小波包阈值去噪的过程
4 Reconstruction Compute wavelet packet reconstruction based on the original approximation coefficients at level N and the modified coefficients.（根据计算后的小 波包系数重构原信号。）
1
0.5
0
-0.5
获得单个阈值，对所有的高频小波系数进行处理。
-1
-1.5
0
50
100
150
200
250
300
350
400
450
软阈值去噪 1.5
1
0.5
0
-0.5
-1
-1.5
0
50
100
150
200
250
300
350
400
450
小波去噪阈值的几种方法
1.5 1
小波包分解和重构去噪
[c,l]=wavedec(x,level,wname); ca3=appcoef(c,l,wname,3); cd3=detcoef(c,l,3); cd2=detcoef(c,l,2); cd1=detcoef(c,l,1); xd4=wrcoef('a',c,l,wname,level);
小波包阈值去噪的过程
1 Decomposition For a given wavelet, compute the wavelet packet decomposition of signal x at level N.（计算信号x在N层小波包分解的系数） 2 Computation of the best tree For a given entropy, compute the optimal wavelet packet tree. Of course, this step is optional. The graphical tools provide a Best Tree button for making this computation quick and easy.（以熵为准则，计算最佳树，当然 这一步是可选择的。） 3 Thresholding of wavelet packet coefficients For each packet (except for the approximation), select a threshold and apply thresholding to coefficients.（对于每一个小波包分解系数，选择阈值 并应用于去噪） The graphical tools automatically provide an initial threshold based on balancing the amount of compression and retained energy. This threshold is.（工具箱会根据压缩量和剩余能量提供一个初始化的阈值，不过仍需要不 断测试来选择阈值优化去噪效果） a reasonable first approximation for most cases. However, in general you will have to refine your threshold by trial and error so as to optimize the results to fit your particular analysis and design criteria.
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
➢代价函数的基本要求： 1.单调性。 2.可加性（次可加性）
小波去噪阈值确定和分解 层数确定
常用代价函数：
1、数列中大于给定门限的系数的个数。即预先给
定一门限值 0 ，并计数数列中绝对值大于 的
元素的个数。
2、范数。
M ({xk}) {xk}
1
通常选，{xk } ＝(
xp)p k
k
p0
（范数愈小，能量愈集中。）
“最优树”的搜索方法：
二元树搜索方法： M1
M2
M3
选择准则： 若M1 M 2 M 3,则选M 2＋M 3
否则，选M1
小波去噪阈值确定和分解层数确定
选择步骤：
➢（1）将代表信息代价的数字写在树的结点里。 ➢（2）从最下层开始，为在每个代表结点的框中的代价函数 值都标上*号。
小波去噪阈值确定和分解层数确定
小波去噪阈值确定和分解 层数确定
小波包阈值去噪的过程
4 Reconstruction Compute wavelet packet reconstruction based on the original approximation coefficients at level N and the modified coefficients.（根据计算后的小 波包系数重构原信号。）
小波包阈值去噪的过程小波去噪阈值确定和分解 层数确定
1 Decomposition For a given wavelet, compute the wavelet packet decomposition of signal x at level N.（计算信号x在N层小波包分解的系数） 2 Computation of the best tree For a given entropy, compute the optimal wavelet packet tree. Of course, this step is optional. The graphical tools provide a Best Tree button for making this computation quick and easy.（以熵为准则，计算最佳树，当然这一步是可选择 的。） 3 Thresholding of wavelet packet coefficients For each packet (except for the approximation), select a threshold and apply thresholding to coefficients.（对于每一个小波包分解系数，选择阈值并应用于 去噪） The graphical tools automatically provide an initial threshold based on balancing the amount of compression and retained energy. This threshold is. （工具箱会根据压缩量和剩余能量提供一个初始化的阈值，不过仍需要不断测试 来选择阈值优化去噪效果） a reasonable first approximation for most cases. However, in general you will have to refine your threshold by trial and error so as to optimize the results to fit your particular analysis and design criteria.
常用代价函数：
小波去噪阈值确定和分解 层数确定
3、熵
M ({xk }) | xk |2 log | xk |2 k
(与均方意义下恢复原始信号所需的系数个数成 正比。）
常用代价函数：
4、能量对数
M ({xk }) log | xk |2
k
(表征信号的系数间的相关性。）
小波去噪阈值确定和分解层数确定
➢（3）将最低层的信息代价作为一个初始值，称上层结点为父结点， 下层结点为子结点，若父结点的信息代价比子结点低，那么就标记父 结点，否则不标记，将该值加上括号且把两个子结点的和值写在括号 外，如此上推，直到顶层。 ➢（4）检查所有结点，取最上层所标记的结点，一经选定，其下方各 层的值就不考虑。选出带有*号框的全体组成VN的一组正交基。
小波阈值去噪方法简洁有效，在工程中得到了广泛应用。目前对该方 法的改进主要集中在阈值函数的改进以及阈值选取规则的改进上
小波阈值去噪法的流程如下所示：
小波去噪阈值确定和分 解层数确定
在以上过程中，小波基和分解层数j的选择，阈值λ的选取规则，和阈 值函数的设计，都是影响最终去噪效果的关键因素。
小波基的选择
小波去噪阈值确定和分解 层数确定
最优小波包分解树的选择
➢在对函数或信号进行小波包分解时，由于Wj有不同的分解方式， 我们面临“最优分解树”的选择问题。
代ቤተ መጻሕፍቲ ባይዱ函数M:
小波去噪阈值确定和分解 层数确定
➢定义一个序列的代价函数，、寻找使代价函数最 小的分解树 ，对一个给定向量来说，代价最小 就是最有效的表示，此基便为“最优树”。
小波去噪阈值确定和分解 层数确定
• 小波基的选择
• 对于连续性较差的信号，Haar小波的去噪效果要好 于Sym8小波。
• 对于连续性和光滑性较好的信号，Sym8小波的去 噪效果更好。sym8小波函数具有紧支集，且具有 良好的连续性和对称性，因此其更适合于对连续性 较好的信号进行去噪。
• 由于小波基函数在处理信号时各有特点，且没有任 何一种小波基函数可以对所有类型信号都取得最优 的去噪效果。一般来讲，db小波系和sym小波系在 语音去噪中是经常会被用到的两族小波基。
分解尺度的选择
小波去噪阈值确定和分解 层数确定
不同信号,不同信噪比下都存在一个去噪效果最好或接近最好 的分解层数。分解层数对于消噪效果的影响很大, 通常分解 层数过多, 而且对所有的各层小波空间的系数都进行阈值处 理会造成信号的信息丢失严重, 消噪后的信噪比反而下降, 同 时导致运算量增大, 使处理变慢。分解层数过少则消噪效果 不理想, 信噪比提高不多, 但不会出现信噪比下降的情况。
小波去噪阈值确定和分解 层数确定
常用代价函数：
1、数列中大于给定门限的系数的个数。即预先给
定一门限值 0 ，并计数数列中绝对值大于 的
元素的个数。
2、范数。
M ({xk}) {xk}
1
通常选，{xk } ＝(
xp)p k
k
p0
（范数愈小，能量愈集中。）
“最优树”的搜索方法：
二元树搜索方法： M1
M2
M3
选择准则： 若M1 M 2 M 3,则选M 2＋M 3
否则，选M1
小波去噪阈值确定和分解层数确定
选择步骤：
➢（1）将代表信息代价的数字写在树的结点里。 ➢（2）从最下层开始，为在每个代表结点的框中的代价函数 值都标上*号。
小波去噪阈值确定和分解层数确定
小波去噪阈值确定和分解 层数确定
小波包阈值去噪的过程
4 Reconstruction Compute wavelet packet reconstruction based on the original approximation coefficients at level N and the modified coefficients.（根据计算后的小 波包系数重构原信号。）
小波包阈值去噪的过程小波去噪阈值确定和分解 层数确定
1 Decomposition For a given wavelet, compute the wavelet packet decomposition of signal x at level N.（计算信号x在N层小波包分解的系数） 2 Computation of the best tree For a given entropy, compute the optimal wavelet packet tree. Of course, this step is optional. The graphical tools provide a Best Tree button for making this computation quick and easy.（以熵为准则，计算最佳树，当然这一步是可选择 的。） 3 Thresholding of wavelet packet coefficients For each packet (except for the approximation), select a threshold and apply thresholding to coefficients.（对于每一个小波包分解系数，选择阈值并应用于 去噪） The graphical tools automatically provide an initial threshold based on balancing the amount of compression and retained energy. This threshold is. （工具箱会根据压缩量和剩余能量提供一个初始化的阈值，不过仍需要不断测试 来选择阈值优化去噪效果） a reasonable first approximation for most cases. However, in general you will have to refine your threshold by trial and error so as to optimize the results to fit your particular analysis and design criteria.
常用代价函数：
小波去噪阈值确定和分解 层数确定
3、熵
M ({xk }) | xk |2 log | xk |2 k
(与均方意义下恢复原始信号所需的系数个数成 正比。）
常用代价函数：
4、能量对数
M ({xk }) log | xk |2
k
(表征信号的系数间的相关性。）
小波去噪阈值确定和分解层数确定
➢（3）将最低层的信息代价作为一个初始值，称上层结点为父结点， 下层结点为子结点，若父结点的信息代价比子结点低，那么就标记父 结点，否则不标记，将该值加上括号且把两个子结点的和值写在括号 外，如此上推，直到顶层。 ➢（4）检查所有结点，取最上层所标记的结点，一经选定，其下方各 层的值就不考虑。选出带有*号框的全体组成VN的一组正交基。
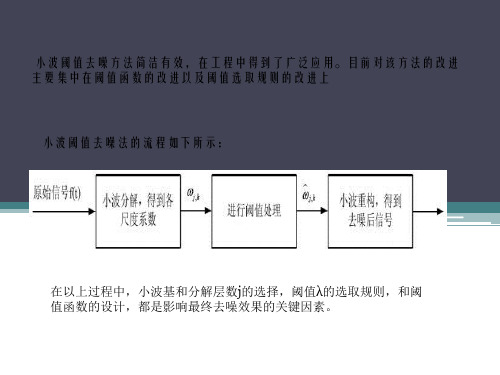
小波阈值去噪方法简洁有效，在工程中得到了广泛应用。目前对该方 法的改进主要集中在阈值函数的改进以及阈值选取规则的改进上
小波阈值去噪法的流程如下所示：
小波去噪阈值确定和分 解层数确定
在以上过程中，小波基和分解层数j的选择，阈值λ的选取规则，和阈 值函数的设计，都是影响最终去噪效果的关键因素。
小波基的选择
小波去噪阈值确定和分解 层数确定
最优小波包分解树的选择
➢在对函数或信号进行小波包分解时，由于Wj有不同的分解方式， 我们面临“最优分解树”的选择问题。
代ቤተ መጻሕፍቲ ባይዱ函数M:
小波去噪阈值确定和分解 层数确定
➢定义一个序列的代价函数，、寻找使代价函数最 小的分解树 ，对一个给定向量来说，代价最小 就是最有效的表示，此基便为“最优树”。
小波去噪阈值确定和分解 层数确定
• 小波基的选择
• 对于连续性较差的信号，Haar小波的去噪效果要好 于Sym8小波。
• 对于连续性和光滑性较好的信号，Sym8小波的去 噪效果更好。sym8小波函数具有紧支集，且具有 良好的连续性和对称性，因此其更适合于对连续性 较好的信号进行去噪。
• 由于小波基函数在处理信号时各有特点，且没有任 何一种小波基函数可以对所有类型信号都取得最优 的去噪效果。一般来讲，db小波系和sym小波系在 语音去噪中是经常会被用到的两族小波基。
分解尺度的选择
小波去噪阈值确定和分解 层数确定
不同信号,不同信噪比下都存在一个去噪效果最好或接近最好 的分解层数。分解层数对于消噪效果的影响很大, 通常分解 层数过多, 而且对所有的各层小波空间的系数都进行阈值处 理会造成信号的信息丢失严重, 消噪后的信噪比反而下降, 同 时导致运算量增大, 使处理变慢。分解层数过少则消噪效果 不理想, 信噪比提高不多, 但不会出现信噪比下降的情况。