混凝土受压力学性能统一计算方法_余志武
常用混凝土收缩模型对高强混凝土的适用性分析

常用混凝土收缩模型对高强混凝土的适用性分析
刘均利;王雷;张晋豪;余学志
【期刊名称】《混凝土》
【年(卷),期】2018(0)11
【摘要】为了研究常用的几种混凝土收缩模型对高强混凝土的适用性,收集了63组收缩试验数据,并与JTG—04、B3、GL2000、ACI 92模型四个常用模型的计算值进行比较.分析了各模型的高(低)估情况,并采用B3变异系数法评估了各模型的预测精度.结果表明:对于高强混凝土的收缩,GL2000模型预测效果最好,B3模型次之,最差的是JTG—04、ACI 92模型,JTG—04模型普遍低估收缩应变,ACI 92模型则在收缩应变较小时低估收缩应变,在收缩应变较大时高估收缩应变.
【总页数】4页(P5-8)
【作者】刘均利;王雷;张晋豪;余学志
【作者单位】广西岩土力学与工程重点实验室, 广西桂林 541004;桂林理工大学土木与建筑工程学院, 广西桂林 541004;桂林理工大学土木与建筑工程学院, 广西桂林 541004;桂林理工大学土木与建筑工程学院, 广西桂林 541004;桂林理工大学土木与建筑工程学院, 广西桂林 541004
【正文语种】中文
【中图分类】TU528.01
【相关文献】
1.岩土力学中常用力学模型的适用性分析 [J], 孙禹成;李松然
2.粉煤灰对高强混凝土收缩徐变的影响试验研究及其修正模型 [J], 汪建群;方志;邓波;马占飞;祝明桥
3.环保企业评估中常用估值模型的适用性分析 [J], 熊悦茗
4.多段压裂水平井产能预测常用解析模型适用性与精度分析 [J], 田刚;兰正凯;陈昂;马明伟
5.CFX4中常用模型在复杂流动中适用性分析 [J], 崔泽艳;陈大宏
因版权原因,仅展示原文概要,查看原文内容请购买。
基于数理统计的混凝土抗压-劈裂抗拉强度关系式的研究

基于数理统计的混凝土抗压-劈裂抗拉强度关系式的研究陈伟;张文博;毛明杰;杨秋宁;逯君【摘要】混凝土结构的抗拉强度大多采用劈裂抗拉试验方法检测,探明混凝土立方体试件的劈裂抗拉强度与抗压强度的关系,对混凝土结构有实际意义.在对国内外关于混凝土抗压和劈裂抗拉强度试验结果统计分析的基础上,通过对大量文献数据的回归分析,提出了适用于C60以下混凝土的抗压-劈裂抗拉强度关系式.结果表明,依据所提出的关系式由抗压强度所计算出的劈裂抗拉强度与试验值吻合度较高.【期刊名称】《宁夏工程技术》【年(卷),期】2016(015)002【总页数】5页(P118-122)【关键词】混凝土;劈裂抗拉强度;抗压强度;关系式【作者】陈伟;张文博;毛明杰;杨秋宁;逯君【作者单位】宁夏大学土木与水利工程学院,宁夏银川 750021;宁夏大学土木与水利工程学院,宁夏银川 750021;宁夏大学土木与水利工程学院,宁夏银川750021;宁夏大学土木与水利工程学院,宁夏银川 750021;宁夏大学新华学院,宁夏银川 750021【正文语种】中文【中图分类】TU528.01混凝土浇筑后的早期龄期内,水化热导致混凝土内部温度积聚过高,内部温度难以在短时间内散发,从而容易引起混凝土表面发生温度裂缝。
随着龄期的增长,混凝土因水化、干燥等原因易导致混凝土结构体积收缩,混凝土与已有结构的黏结抑制其收缩时,混凝土结构内部将产生收缩裂缝。
另外,在混凝土结构正常服役期间,也可能产生外力作用下的结构裂缝。
混凝土结构开裂后将加快其内部钢筋的腐蚀,影响结构的安全性、耐久性及适用性。
混凝土抗拉强度作为混凝土的一项基本力学指标,涉及到混凝土结构的抗剪、抗扭和裂缝宽度计算等。
虽然混凝土轴心抗拉强度较劈裂抗拉强度更能反映混凝土的实际抗拉强度,但混凝土轴心抗拉试验操作较为困难,而劈裂抗拉强度试验的操作相对较简单,且劈裂抗拉强度也较为接近混凝土的实际抗拉强度。
因此,劈裂抗拉强度试验仍是评定混凝土抗拉强度时较为普遍使用的方法。
基于损伤泊松比的混凝土多轴强度准则

据基本假设(1),则在发生破坏耗能时其本构关系可表示为
⎪⎨⎧εε12
⎫ ⎪ ⎬
⎪⎩ε3 ⎪⎭
=
1 Ec
⎡1 ⎢⎢−v ⎢⎣−v
−v 1
−v
−v ⎤
−v
⎥ ⎥
1 ⎥⎦
⎧σ ⎪⎨σ
1 2
⎪⎩σ 3
⎫ ⎪ ⎬ ⎪⎭
+
1− g gEc
⎡1
⎢ ⎢
−r1
⎢⎣−r1
− r2 1 − r2
− −
r3 r3 1
⎤ ⎥ ⎥ ⎥⎦
基于损伤泊松比的混凝土多轴强度准则1
丁发兴*,余志武
(中南大学 土木建筑学院,湖南 长沙 410075)
*E-mail: dinfaxin@
摘 要: 基于两个基本假定并提出损伤泊松比的概念,应用损伤力学理论和最小耗能原理, 根据混凝土单元体的耗能率应受到强度准则的约束,建立了混凝土在多轴应力状态下强度准 则的一般形式并揭示混凝土的破坏机理,指出损伤泊松比是决定混凝土破坏的关键。根据混 凝土破坏包络面的特征和已有试验资料,初步确定了损伤泊松比的表达式,其拉、压子午线 和偏平面特征与已有认识有所差异:在二轴受拉一轴受压和一轴受拉二轴受压应力状态时与 已有认识基本一致,在三轴受拉应力状态时与以往认识略有差别,而在三轴受压应力状态时 与以往认识差别较大。通过与国内外 633 组多轴应力下混凝土强度试验资料的比较,结果表 明该强度准则计算结果与试验结果符合较好。针对二轴应力状态下,新混凝土强度准则可进 一步简化,其形式更简单,且偏于安全。该准则概念清晰,物理意义明确,计算简便,可应 用于 C20~C130 混凝土在二轴受拉一轴受压、一轴受拉二轴受压、三轴受拉和二轴应力状态 下的结构分析和计算。 关键词:混凝土,多轴,破坏准则,子午线,偏平面
钢_混凝土连续组合梁滑移与挠度耦合分析_余志武

COUPLING ANALYSIS OF SLIP AND DEFLECTION OF CONTINUOUS COMPOSITE BEAMS OF STEEL AND CONCRETE
YU Zhi-wu , ZHOU Ling-yu , JIANG Li-zhong
(Civil and architecture college. Central South University, Changsha 410075, China)
j j j j j
连接件间距
负弯矩区配筋 正弯矩区配筋 6Φ 12 6Φ 12 6Φ 12 6Φ 12 6Φ 12 5Φ 10 6Φ 12 9Φ 12 6Φ 12 6Φ 12 5Φ 12
Rp
0.61 0.55 0.72 0.35 0.92 0.58 0.69 1.26 0.69 0.69 0.26
PPR 0.61 0.34 0.78 0.54 0.61 0.73 0.61 0.67 0.61 0.61
1~CCB-11。试件跨度为 2 × 3 .84 m ,试件尺寸如图 1 所示。主要试件参数为负弯矩区综合力比 R p 、部 分预应力比 PPR 和剪力连接度 λ 。
(a) 无板托混凝土叠合板有粘结预应力筋试件截面
(b) 现浇有板托混凝土板无粘结预应力试件截面 图1 试件截面图
Fig.1 Sections of composite beams
从图 2、3 中可以看出滑移规律:(1) 滑移随荷 载的增加而逐步增大;(2) 滑移在集中荷载作用位 置改变方向,且该点相对滑移为零;(3) 滑移曲线
(1) (2)
钢—混凝土连续组合梁滑移与挠度耦合分析
79
为简化分析,忽略掀起对组合梁的影响,假设 混凝土板和钢梁两者竖向变形一致,即 y1 = y 2 = y 如上图所示,分别根据混凝土和钢梁的受力和 平衡条件: ∑ x = 0 、 ∑ y = 0 和 M = 0 ,可得到混 凝土板和钢梁微段内力表达式以及混凝土板和钢 梁内力与位移的关系式为:
C20混凝土在高温条件下的力学性能特征参数变化规律研究
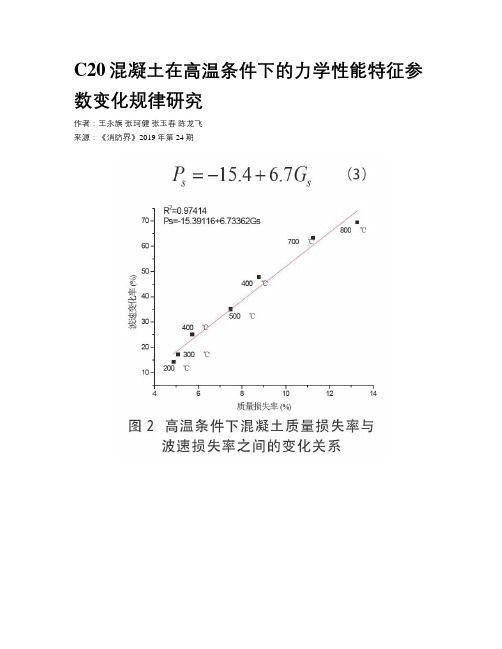
C20混凝土在高温条件下的力学性能特征参数变化规律研究作者:王永旗张珂健张玉春陈龙飞来源:《消防界》2019年第24期摘要:本文研究了C20混凝土在高温条件下的力学性能特征参数变化规律。
试验采用的温度范围为100℃-800℃,对比不同高温条件下C20混凝土的质量损失率、波速损失率与损伤度。
试验结果表明,在不同的高温条件下,C20混凝土的表面颜色及外观有较大差异。
随着温度的升高,C20混凝土的质量损失率、波速损失率及损伤度也随之增大。
同时,C20混凝土的质量损失率与波速损失率之间呈现线性关系。
关键词:C20混凝土;波速;质量损失率;损伤度;波速损失率普通混凝土暴露在火灾或高温条件时,它的性能将发生很大的改变。
近年来,国内外学者对普通混凝土在高温条件下的性能已进行了大量的研究工作。
1980年,Ellondwing、2003年,Kodur、2013年,Kizilkanat等人研究了高温后普通混凝土的物理性质,如密度、比热、热传导率和热膨胀系数等参数在高温下的变化规律和反应过程。
2001年,Shoaib、2005年,余志武、2013年,罗俊礼、2013年,霍静思等人分析了高温后普通混凝土的力学性能,如抗压强度、抗拉强度、弹性模量、收缩性能、钢筋与混凝土之间的粘结强度及残余特性等參数的变化规律。
在火灾或者高温条件下,普通混凝土将会受到不同程度的损伤,而损伤程度的测量与表征是非常重要的。
检测混凝土性质的方法通常分为破损法和非破损法。
相对于破损法来说,非破损法不会对混凝土结构造成破坏,测试仪器简单、操作方便,并且具有可对混凝土结构构件重复测试等优点。
其中,超声波法因超声波对各种材料的穿透力较强、较高的灵敏度、操作方便和检测成本低等优点在工程中得到广泛的应用。
1993年,杨彦克等人较早地通过大量超声试验,以及对火灾混凝土构件的温度分布的研究,发现用超声法来推求火灾混凝土构件温度分布是可行的。
2004年,Prassianakis等人开展了研究证明超声波作为材料的非破坏性测试方法的有效性。
圆钢管混凝土截面轴力-弯矩-曲率关系实用计算方法

圆钢管混凝土截面轴力-弯矩-曲率关系实用计算方法丁发兴;张鹏;余志武;欧进萍【期刊名称】《哈尔滨工业大学学报》【年(卷),期】2009(041)012【摘要】为便于有限元分析,建立圆钢管混凝土压弯构件截面轴力-弯矩-曲率关系实用计算方法,基于合理的钢管混凝土数值本构模型,利用截面分层法对圆钢管混凝土压弯构件截面轴力-弯矩-曲率关系进行全过程分析,根据轴压比、钢管屈服强度、混凝土强度等级和含钢率等各主要因素对轴力-弯矩-曲率关系的影响,通过大量参数分析,分别建立圆钢管混凝土压弯构件截面轴力-弯矩相关方程实用计算公式和轴力-弯矩-曲率关系实用计算方法.通过与圆钢管混凝土压弯构件截面轴力-弯矩相关承载力和轴力-弯矩-曲率关系曲线试验结果的对比,验证该实用计算公式和实用计算方法的正确性.研究结果为圆钢管混凝土结构非线性有限元分析奠定基础.测试结果显示了方法的有效性.【总页数】5页(P133-137)【作者】丁发兴;张鹏;余志武;欧进萍【作者单位】中南大学,土木建筑学院,长沙,410075;哈尔滨工业大学,土木工程学院,哈尔滨,150090;中南大学,土木建筑学院,长沙,410075;中南大学,土木建筑学院,长沙,410075;哈尔滨工业大学,土木工程学院,哈尔滨,150090【正文语种】中文【中图分类】TU398【相关文献】1.圆钢管混凝土桥墩弯矩-曲率关系分析 [J], 臧博;朱东生;冯长友;向中富2.带轴力混凝土截面弯矩-曲率计算解析 [J], 陈旭;章胜平;鲁圣鹏;宋高丽;王春华3.带轴力混凝土截面弯矩-曲率计算解析 [J], 陈旭;章胜平;鲁圣鹏;宋高丽;王春华4.高强矩形螺旋钢筋约束高强混凝土剪力墙截面弯矩-曲率计算方法研究 [J], 赵花静;李青宁;赵珺;李书锋;郑玉5.基于ANSYS二次开发的任意截面轴力弯矩的计算方法研究 [J], 周正凡;肖明;汤福平因版权原因,仅展示原文概要,查看原文内容请购买。
混凝土动态受压力学性能的试验研究
1 . 设备 改进 2
众多材料试验 机上进行 的混凝 土动态压 缩试验往 往得不 到具有下降段 的应力一 应变曲线 , 分析知 由于混凝 土试件是脆性
混凝土动态受压 力学性能 的试验研 究
窦远明,张华伟 ,孙吉书
( 河北工业大学 土木工程学 院,天津 3 0 0) 0 4 1
摘
要 : 混凝土作 为建筑上应用范围最为广泛 的材料 , 动态力学性 能的研究对其充分发挥其抗压性能 、 提高其安全的性 能和降低建筑成
本变得至关重要。 采用改进 的美 国 MT 液压伺候加载系统对 7 m 7 m x 0 mm的标准棱柱体混凝土试件进行单轴加载试验 , S 0 mx 0 i 2 0 n 客观 的完成 了从 l l 4 到 l l■s 个 不同数量级 范围内的混凝 土受压试 验 , x O/ s xO 4 成功得到不同的应变速率下典型的应力一 变全曲线 , 应 从而使 基本受压性能得 到综合 的宏观反应。
c nc eec m p e sv e f r n e S t e o ec t a t mpr v a eya dr d c h ec ns u t nc s. et ei r v dHy r u i i itrl a — o r t o r s i ep ro ma c , Oib c m i c r i l oi o es f t n e u et o t c i r o ot Us h mp o e dal cm n se o d
的松紧度使其相 同; 此时可 以正常加荷 载( 原理如图 2 。 ) 按 照一般经验公式 :
钢-混凝土组合箱梁疲劳性能的有限元分析
图4 组合箱梁截面图Fig.4 Composite box girder cross- sectional view
3.2 计算结果
1)S-N曲线
整理文献[14]中试验的结果如表3,利用一元线性回归分析方法得到等幅循环应力幅与疲劳破坏时循环次数间的关系,即疲劳寿命计算式[17]为
其中:N表示疲劳寿命,单位万次;Δτ表示剪应力幅,单位MPa。
图1 加载路径图Fig.1 Loading path diagram
表1 荷载取值Table 1 Load Value kNTIME 1 2 3 FORCE荷载取值P1 50 P2 125 P3 50
表2 Event组成情况Table 2 Event compositionEvent Loading1 Loading2 partial usage 1 P1 P2 D1 2 P2 P3 D2
表3 组合箱梁疲劳试验数据Table 3 Composite Box Beam fatigue test data编号 荷载/kN上限 下限 幅度 剪应力幅 实测疲劳寿命/万次FSCB -1 250 100 150 86.49 253 FSCB -2 250 100 150 78.64 306 FSCB -3 250 100 150 70.32 348
混凝土单轴受力损伤本构模型
混凝土单轴受力损伤本构模型
混凝土单轴受力损伤本构模型
作者:丁发兴;余志武;欧进萍
作者机构:哈尔滨工业大学,土木工程学院,黑龙江,哈尔滨,150090;中南大学,土木建筑学院,湖南,长沙,410075;中南大学,土木建筑学院,湖南,长沙,410075;哈尔滨工业大学,土木工程学院,黑龙江,哈尔滨,150090 来源:长安大学学报(自然科学版)
ISSN:1671-8879
年:2008
卷:028
期:004
页码:70-73
页数:4
中图分类:TU375
正文语种:chi
关键词:结构工程;混凝土;损伤;演变方程;本构模型
摘要:为了建立一种新的单轴受力下混凝土损伤本构模型,应用损伤力学理论,假设混凝土卸载刚度与初始刚度的比值和混凝土卸载后剩余的弹性应变能与总应变能的比值在数值上是一致的,由此将弹性模量损伤和能量损伤结合为一体,通过数值方法可确定混凝土单轴受力损伤变量的具体数值.在已有不同强度等级混凝土单轴受力的应力一应变全曲线统一计算方法的基础上,通过数值积分和拟合回归,建立了单轴应力状态下混凝土损伤演变方程和损伤本构模型.结果表明:该模型可描述混凝土单轴循环加载受力状态下的力学特性,与混凝土单轴受力试验结果吻合较好;该研究成果可望进一步应用于反复加载下混凝土结构非线性有限元分析中.。
混凝土单轴力学性能统一计算方法
混凝土单轴力学性能统一计算方法1丁发兴*,余志武(中南大学土木建筑学院,湖南长沙 410075)*E-mail: dinfaxin@摘要:目前,国内对普通混凝土(C60以下)、高强混凝土(C60~C100)和超高强混凝土(C100以上)的力学性能指标采用分区描述,导致不同计算公式在分区边界处计算结果误差较大,且适用性较差。
本文通过对国内大量的普通混凝土、高强混凝土和超高强混凝土单轴受力试验研究资料的重分析,发现混凝土强度等级在C10~C140范围时其各力学性能指标均具有连续变化规律。
基于统计分析方法,提出了适用于各种强度等级混凝土的尺寸换算系数、轴心抗压强度、轴心抗拉强度、劈拉强度、弹性模量、轴心受压峰值应变和轴心受拉峰值应变等统一计算公式;比较并优选了应力-应变全曲线上升段数学方程,建议了混凝土轴心受压、受拉应力-应变全曲线方程,并合理确定其中参数的表达式。
关键词:混凝土,力学指标,应力-应变全曲线,单轴受力1.引言迄今为止,国内外学者对混凝土单调荷载下轴心受压、受拉力学性能已进行了大量的试验研究,取得了丰富的研究成果[1~26]。
然而,国内外学者在研究混凝土时,通常将混凝土分为普通混凝土(C10~C60)、高强混凝土(C60~C100)和超高强混凝土(C100以上),并对各种混凝土的基本力学性能指标分区建立不同的计算公式,由此导致混凝土的基本力学性能指标在分区边界处的计算结果误差较大,显然,这不仅引起物理概念的混淆,还给混凝土结构理论分析带来麻烦。
国内外学者在描述单调荷载下混凝土单轴应力-应变特性时提出了不同的数学表达式。
其中有不少物理意义明确、形式简单的数学表达式,需要通过比较,找出其中的最优方程来描述各种强度等级下混凝土的单轴应力-应变特性。
本文通过对国内大量的普通混凝土、高强混凝土和超高强混凝土的基本力学性能试验研究资料的分析,提出适用于各种强度等级混凝土的尺寸换算系数、轴心抗压强度、轴心抗拉强度、劈拉强度、弹性模量、受压峰值应变和受拉峰值应变等力学性能指标的统一计算公式;并建立各种强度等级的混凝土单轴受压、受拉应力-应变全曲线方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
"#$%& ! ’#%()%#*&+ ,#%)&- ./ -01& &//&(* (.&//0(0&2*- ./ (.2(3&*&
!#$ C !#$% &’ 文献 D & E ’+ >: ’+ >: ’+ >: ’+ >: ’+ >: 式 F&G 式 F"G ’+ ><" ’+ >;! ’+ >:: ’+ >!= ’+ >!" ’+ >9; ’+ >9& ’+ >"; ’+ >"" ’+ >&= ’+ >&: ’+ >&" ’+ >’> ’+ >’;
则尚未见到相关的文献。 对于 ?&’’ 以上的混凝土, 本文通过对国内研究资料的重分析,建议尺寸换 算系数的统一计算式 F 图 & G
’K >: ( !#$ J &K &< ! #$% ") &’ M ’K < 表 & 列出了按式 F " G 计算的不同混凝土强度等级
D " E 的计算结 的尺寸换算系数, 显见式 F " G 与文献 D & E 、 果有较好的协调性。
"
45 !
混凝土受压力学指标
尺寸换算系数 根据我国现行规范,混凝土强度等级是用龄期为
而在具体的工程 "= 天边长 &:#I 的立方体试件测定的, 实践中, 经常采用边长 &’#I 的立方体试件进行测定。 由 于混凝土的非匀质脆性特点以及试验机刚度不够大, 存 在着尺寸效应, 边长 &’#I 的立方体试件的强度 !#$% &’ 要 高于边长 &:#I 的立方体试件的强度 !#$, 这种变化随强 度的提高而增大。 对于 ?;’ 以下的混凝土, 文献 D & E 在大 量试验的基础上,建议 !#$ C !#$% &’ 取值为 ’+ >:;对于 文献 D " E 采用如下计算式 ?;’ @ ?&’’ 的混凝土, !#$ !#$% &’ J ’K >& L & !#$% &’ ( &)
@ 中南大学 土木建筑学院, 湖南长沙 !"99BC A
摘要: 目前国内对普通混凝土 @ D>9 以下 A 、 高强混凝土 @ D>9 E D"99 A 和超高强混凝土 @ D"99 以上 A 的力学性能指标采用分 区描述, 导致不同计算公式在分区边界处计算结果误差较大, 且适用性较差。本文通过对国内大量的普通混凝土、 高强混 凝土和超高强混凝土轴心受压试验研究资料的重分析发现混凝土强度等级在 D"9 E D"!9 范围时其各力学性能指标均具 有连续变化规律。本文基于统计分析方法, 提出了适用于各种混凝土强度等级的尺寸换算系数、 轴心抗压强度、 弹性模量、 轴心受压峰值应变和混凝土轴心受压应力 F 应变全曲线等统一计算公式,其计算结果与实测结果吻合较好。本文研究成 果对进一步开展混凝土结构的非线性有限元分析和设计具有参考价值。 关键词:混凝土 G 力学性能 G 应力 F 应变曲线 中图分类号:HI:BC6 94 文献标识码:<
’+ >"< ’+ >"! ’+ >"" ’+ >"& ’+ >"’ ’+ >&> ’+ >&= ’+ >&= ’+ >&< ’+ >&<
注:假设 ?&’’ 以上的混凝土尺寸效应仍服从 ?;’ @ ?&’’ 的混凝土 尺寸效应的规律。
的提高, 裂缝的贯通与峰值应力越来越接近, 裂缝的开 展、 贯通直至破坏越来越快。从破坏面上看, 由粗骨料 胶结面破坏逐步过渡到穿越粗骨料破坏,破坏时常有 混凝土碎片崩出, 并伴有崩裂的声响。 混凝土轴压强度 试验的破坏过程随混凝土强度等级的提高而表现出更 大的脆性。 关于混凝土轴心抗压强度的研究, 国内外已 展开大量的工作 D &% 9% : E 。对 ?;’ 以下混凝土我国现行规 范 NO:’’&’—"’’" D &! E 采用 ( !# J ’+ <; !#$ F AB/ G 9) 文献 D : E 在总结 ?:’ @ ?>’ 混凝土研究成果的基 础上, 提出 ( !# J M &"+ 9& L &+ ’&: !#$ F AB/ G !) 按式 F 9 G 计算时, 按 对 ?;’ 混凝土, !# J !:+ ;AB/; 式 F ! G 计算时, 两者误差达 ;+ ;P , 显然 !# J !=+ :>AB/, 不合理。 通过对图 " 所示国内大量试验资料重分析, 可 得到混凝土轴心抗压强度计算公式统一表达式
图&
混凝土的尺寸换算关系
()*+ & ,-./0)1234)5 6-07--2 !#$% &’ /28 !#$
45 4
轴心抗压强度 图 " 显示了国内大量混凝土轴心抗压强度试验结
图" ()*+ " 混凝土 !# 与 !#$ 关系曲线 ,-./0)1234)5 6-07--2 !# /28 !#$
果。 由图可见, 混凝土轴心抗压强度几乎与其立方体抗 压强度成比例增加。 试验还表明, 随着混凝土强度等级 !"
"
前言
迄今为止, 国内外对混凝土轴心受压的力学性
程完全对应, 适用范围较广泛。然而, 国内外学者在研 究混凝土时,通常将混凝土分为普通混凝土 @ D"9 E 高强混凝土 @ D>9 E D"99 A 和超高强混凝土 @ D"99 D>9 A 、 以上 A , 并对各种混凝土的基本力学性能指标分区建立 不同的计算公式,由此导致混凝土的基本力学性能指 标在分区边界处的计算结果误差较大, 显然, 这不仅引 起物理概念的混淆,还给混凝土结构理论分析带来麻 烦。 本文通过对国内大量的普通混凝土、高强混凝土 和超高强混凝土的基本力学性能试验研究资料的重分 !"
第 4! 卷第 ! 期 499: 年 ; 月 文章编号: "999 = >;>? @ 499: A 9! = 99!" = 9>
建 筑 结 构 学 报 #$%&’() $* +%,)-,’. /0&%10%&23
5$)6 4!7 8$6 ! <%.67 499:
混凝土受压力学性能统一计算方法
余志武 7 丁发兴
,4’ ( 5 123 6 !# 9 (+ ! ! #$ 0) 5!6、 5 0 6 在其适用范围内不同 表 / 显示了式 5 " 6 、
对于 &’( H &)(( 混凝土, 文献 I 0 J 和文献 I / J 分别建议 了下列计算公式
(K ""(! 5 )(! 123 6 "# 9 )K (((/ ! #$ "# 9 5 (K !0) !#$ 8 (K 0 6 5 )(! 123 6
析,提出了适用于各种混凝土强度等级的尺寸换算系 数、 轴心抗压强度、 弹性模量、 抗压峰值应变和混凝土 单轴抗压应力 H 应变全曲线等力学性能指标的统一计 算公式。
!#$% &’ AB/ "’ 9’ !’ :’ ;’ <’ =’ >’ &’’ &&’ &"’ &9’ &!’ &:’
表!
尺寸换算系数计算值的比较
能已进行了大量的试验研究, 取得了丰富的研究成 果 ] "7 :7 C7 B7 ;7 "" E ": ^ ; 尤其是过镇海 ] ; ^ 教授提出的混凝土单 轴受压应力 F 应变全曲线表达式形式简单、物理意义
基金项目: 国家自然科学基金资助项目 @ C99B;99B A 。 作者简介: 余志武 @ "?CC = 收稿日期: 4994 年 ; 月 A, 男, 湖南临湘人, 教授。
轴心抗压强度与立方体抗压强度比值
5,6 ( -)
本文根据国内一些单位的实测数据,提出了轴心 抗压强度的统一计算式
)4" ( 5 123 6 "# 9 .0(( ! #$ .) 表 " 中列出了国内 !00 组混凝土弹性模量实测值
与计算值之比的统计结果。 从图 " 和表 " 中可以看出, 对 &’( 以上的混凝土, 式 5 ’ 6 H 5 - 6 的计算结果与实测结果吻合较差, 式 5’6 5 6 5 6 的计算结果偏小, 而式 , 、 式 - 的计算结果偏大, 本 文建议的计算公式 5 . 6 计算的混凝土弹性模量与实测 值较接近。
I’,*,2- 1()1%)(0,$’ J20K$- $* 1$JL&233,M2 J21K(’,1() L&$L2&0,23 $* 1$’1&202
NI OK,P%7 QR8S T(U,’. @ D,M,) (’- <&1K,0210%&2 D$))2.27 D2’0&() /$%0K I’,M2&3,0V7 DK(’.3K( !"99BC7 DK,’( A !"#$%&’$: W232(&1K2&3 (0 K$J2 ’$P(-(V3 (-$L0 -,M,3,$’() -231&,L0,$’ *$& 0K2 J21K(’,1() ,’-2U23 $* ’$&J() 30&2’.0K 1$’1&202 @ XD>9 A 7 K,.K 30&2’.0K 1$’1&202 @ D>9 E D"99 A (’- 2U0&( K,.K 30&2’.0K 1$’1&202 @ Y D"99 A 7 PK,1K )2(- 0$ 1()1%)(02- &23%)03 2&&$& $* -,**2&2’0 1()1%)(0,$’ *$&J%)(3 (0 -,M,3,$’() Z$&-2&),’2 (’- L$$& (LL),1(Z,),0V6 HK&$%.K &2(’(F )V[,’. ( )(&.2 ’%JZ2&3 $* 0230 &23%)03 $* (U,() 1$JL&233,$’ $* ’$&J() 30&2’.0K 1$’1&2027 K,.K 30&2’.0K 1$’1&202 P,0K 2U0&( K,.K 30&2’.0K 1$’1&202 (0 K$J27 0K,3 L(L2& *,’-3 0K2 &2.%)(&,0V $* 1$’0,’%$%3 M(&,(0,$’ $* J21K(’,1() ,’-2U23 $* 1$’1&202 P,0K 30&2’.0K .&(-2 &(’.,’. *&$J D"9 0$ D"!96 +(32- $’ 30(0,30,1 (’()V3,37 0K,3 L(L2& L&$L$323 0K2 2JL,&,1() 1()1%)(0,$’ *$&J%)(3 PK,1K 1(’ Z2 (LL),2- 0$ M(&,$%3 30&2’.0K $* 1$’1&202 *$& 3,[2 2**210 1$2**,1,2’07 (U,() 1$JL&233,M2 30&2’.0K7 2)(30,1 J$-%)%37 L2(\ 30&(,’ $* (U,() 1$JL&233,$’ (’- 30&233F30&(,’ 1%&M236 < 1$JL(&,3$’ $* 1()1%)(02- &23%)03 P,0K 2UL2&,J2’0() &23%)03 3K$P3 .$$- (.&22J2’06 T,’())V7 &232(&1K (1K,2M2J2’03 $**2&2- ZV 0K,3 L(L2& K(M2 &2*2&2’12 *$& 0K2 *%&0K2& ’$’F),’2(& *,’,02 2)2J2’0 (’()V3,3 (’- -23,.’ $* &2,’*$&12- 1$’1&202 30&%10%&26 ()*+,%-#. 1$’1&202G J21K(’,1() L2&*$&J(’12G 30&233F30&(,’ 1%&M23 明确,其几何特征与混凝土棱柱体受压变形和破坏过
