边界层气象学课件:CH07_稳定边界层
边界层理论PPT课件

第四节 平板绕流摩擦阻力计算
所以,总阻力
S LB yx
y0
1 2
C
f
2
0
LB
0.664 03B2L
另一方面,由边界层积分方程的解,也可以计算 出层流平面绕流摩擦阻力,
即由
和 x
0
3 2
y
1 2
y
3
4.64 x 4.64 x
0
Rex
可得到
x 3 1
yx y0
y y0 2 0
x
y
y
y
Y
1
p y
2 y
x2
2 y
y 2
y方向动量传输方程
注:x
t
x
x
x
y
x
y
z
z
z
X
1
p x
2x
x2
2 x
y 2
2z
z 2
第8页/共48页
第二节 方程)
平面层流边界层微分方程(普朗特边界层微分
考虑不可压缩流体作平面层流(二维流场),此时质
量力对流动产生的影响较小,则有方程组
m l
m x x
m x
d dx
l
dy x
0
x
BC面在边界层之外,流体沿x方向的速度近似等于υ0,故此由BC面流入 的动量在x方向的分量Ml
M l
m l0
0
d dx
l
dy
x
x
0
4)AD面没有质量流入、流出,但有动量通量存在,其值为τ0,故此由
AD面在单位时间内传给流体的粘性动量为τ0Δx。
2! 2 5! 4 8!
8 11!
n1
大气行星边界层第七章ppt课件-PPT文档资料
1 q t
t t/2
t t/2
qdtd
2、平均运动方程求法 大气运动方程
dV Fi dt i
V 是瞬时运动,存在湍流时是不确 定的,只有平均运动才有规律 ——平均运动方程
边界层的特征ห้องสมุดไป่ตู้ 1、几何学特征:D<<L;
2、运动学特征:湍流运动 (受地面粗糙度影响); 3、动力学特征:湍流粘性力重要。
湍流--不规则的、杂乱无章的涡旋 运动。能引起强烈的混合作用。 --物理量输送: 1、存在物理量的梯度
湍流粘性力 动量输送 热 量 水汽、
2、从物理量大值区向小值区输送
3、边界层中物理量的垂直梯度大, 所以,输送主要在垂直方向上。
边界层是热量、水汽源、动量汇
研究边界层目的: 1、边界层本身的特性: 如污染物的扩散,飞机起降、植物 生长等。 2、在整个大气中起重要作用: 如数值预报中的物理过程描述,大气 运动的强迫耗散问题。
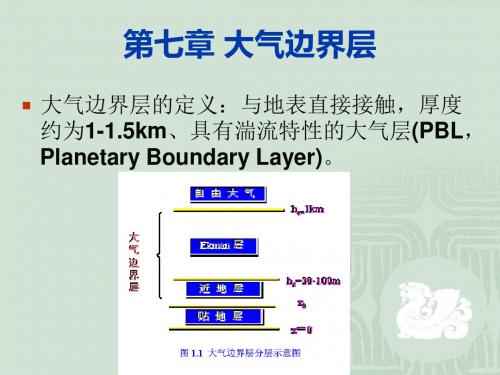
第一节 大气分层
地表既是大气的动力边界,也是大 气的热力边界。 大气边界层,由于受地表(固壁粗糙 不平)影响--湍流边界层。 地表对大气的影响随高度增加而较弱 ——湍流的强度随高度增加而较弱。 ——湍流粘性力随高度增加而减小。 ——湍流粘性力的重要性随高度不同 而不同。
q 1 q 2 q 1 q 2 2q 1 q2 ) q 2 q 1q 2 (q 1q 2 q 1q 2 q 1 q 1q 2 q 1q q 1q 2 q 1q 2 q q x x
二、平均运动方程组
1.平均连续方程:
( V ) 0 瞬时连续方程 t
边界层的基本概念课件

边界层的特征
边界层具有很薄的厚度,其厚 度通常远小于流体中的其他尺 度,如流动的长度和速度。
在边界层内,流体的流动状态 从自由流转变为受壁面限制的 流动,流体的速度和方向发生 急剧变化。
边界层内的流体会产生摩擦阻 力,对流体流动产生重要影响 。
边界层的形成
当流体与固体壁面接触时,由于壁面 的限制作用,流体的速度和方向发生 变化,导致流体的切向应力与法向应 力发生突变,形成边界层。
湍流边界层
在流体流动中,靠近固体表面的 薄层,流速较高,流动方向复杂 ,各层速度梯度较大,流动呈现 湍流状态。
热边界层和流动边界层
热边界层
在传热过程中,靠近固体表面的薄层 ,温度梯度较大,热量传递速率较高 。
流动边界层
在流体流动中,靠近固体表面的薄层 ,流速较高或较低,流动方向或湍或 层,与流体主体存在明显的速度梯度 。
边界层的基本概念课件
目 录
• 边界层定义 • 边界层的重要性 • 边界层的分类 • 边界层方程 • 边界层模拟方法 • 边界层的应用
01
边界层定义
边界层的定义
01
边界层是指流体在运动过程中, 流体的切向应力与法向应力发生 突变的位置,通常出现在流体与 固体壁面接触的地方。
02
在边界层内,流体的流动受到壁 面的限制,流体的速度和方向发 生急剧变化,导致流体的物理性 质发生显著变化。
物理边界层和化学边界层
物理边界层
主要涉及流体的物理特性变化,如温度、压力、速度等。
化学边界层
主要涉及流体的化学特性变化,如浓度、组分、化学反应等 。
04
边界层方程
连续性方程
连续性方程是描述流体运动过程中质 量守恒的方程。
边界层气象学

定义:微气象学就是研究湍流这类小尺度现象的。
微气象学的三种研究途径:1. 随机方法2. 相似理论3. 现象分类虚位温虎位温是研究上升气流普遍采用的一个变最,在同一气压条件下,使干空气密度必须等于湿空气密度的正是此温度。
饱和空气虚位温定义为:2=0(1 + 0.611 —兀)未饱和空气虎位温定义为:0v=6 (l+0.61r-r)粘滞应力定义:当一部分流体运动时,分子间作用力往往会在同一方向拖拽相邻的流体分子使流体产生变形的力叫做粘滞应力。
>当流体中存在剪切运动时便有粘滞应力存在。
运动可以是层流,也可以是湍流。
>粘滞应力可通过除以流体平均密度而成为运动学形式>海面标准人气的运动学粘度>风剪切du/dz=0.5 s1(在大气表面层具有代表性)时,粘滞应力 (注意单位!)>在边界层中,粘滞应力的量值与雷诺应力相比很小,以致在平均风速预报中通常被忽略不计。
然而,湍流涡在局地涡尺度人小地区域中,则具有人的多的剪切,所以在预报湍流时,这个粘性应力不能忽略。
强M流湍流可以由浮力对流过程和机械过程产生,冇时是-•种过程处于支配地位,当机械过程占优势时,边界层被认为处于自由对流状态.片流不稳定导致KH波形成和湍流开另一个值氓指示湍流终I卜•时的临界理査孙数。
・对动力稳定度判据可作如卜说明:-当RivRc时,片流变成湍流:■当Ri>&时,湍流变成片流:・尽管目前Rc和&的精确值还存在某些争议,但采用0=0.2)025, R T M.O似乎还是可以的;・因为班>Rc于足,就出现了滞后作用的问题。
湍流定义:不规则的涡旋运动湍流的特点:(1)随机性:湍流是非规则的、混乱的、不可预测的:(2)非线性:湍流是高度非线性的。
当流动达到某一特定状态,如Re数超过某临界值,流动中的小扰动就会自发地增长,并很快达到一定的扰动幅度;(3)扩散性:湍流会引起热量、动量及流动中的其他物质快速扩散;(4)涡旋性:湍流由无数大小不同的湍涡组成,他们分裂、合并、拉长、旋转:(5)耗散性:湍流的能量是由人湍涡向小湍涡传递,最后通过分子粘性耗散为热能。
边界层气象学:6第五章定常条件下的边界层

中的分布,要解决这个问题,必须求解运动方
程和热流量方程。从最简单情形入手,介绍
Ekman理论。设大气为正压大气,等压线为直
线,忽略风的水平变化,考虑定常、均匀条件
下的大气运动方程:
uw fv 1 p
z
x
vw fu 1 p
z
y
为使方程组闭合,引入K理论
u(z2 ) u*
u(z1 )
Fui
( z2 L*
,)
Fui
(
z1 L*
,)
v(z2 ) u*
v(z1 )
Fv
i
(
z2 L*
,)
Fvi
(
z1 L*
,)
(z2)
T*
(z1 )
Fi
( z2 L*
,)
Fi
( z1 L*
,)
Fui、Fvi 和Fi为普适函数
若取z1=z0,u(z0)=v(z0)=0,则:
Ekman螺线
在地面上,z=0,tgα=0/0,根据罗必达法则: tgα=1,α=45o,在地面,风向与地转风(等压 线)的交角为45o。
随高度增加,α逐渐减小,即风向右偏(北半 球),逐渐趋于等压线(地转风)方向;风 速渐增,逐渐趋于地转风大小。
从定量上说,Ekman解不精确。问题的来源是 假设K为常数。
稳定度参数S代替,可以解决问题。
曲线1、2、3、4、5是 不同研究者在=0理论 值。曲线6a =-100;曲 线6b =-10曲线6c =0; 曲线6d =10;曲线6e =100
u*/Vg随Ro增加而减少, u*/Vg随不稳定增加而增 加。
图5.2.1
曲线1、2是Blackadar 在中性时的实测值;3 是Lettau在中性时的实 测值;4是OpeHKO在 <0时的实测值;5是 >0时的实测值。其它 符号同前。
边界层理论PPT精选文档

5.1、边界层近似及其特征
普朗特重视观察和分析力学现象,养成了非凡的直观洞察能力,善 于抓住物理本质,概括出数学方程。他曾说:“我只是在相信自己对物 理本质已经有深入了解以后,才想到数学方程。方程的用处是说出量的 大小,这是直观得不到的,同时它也证明结论是否正确。” 普朗特 指导过81名博士生,著名学者Blasius、Von Karman是其学生之一。我 国著名的空气动力学专家、北航流体力学教授陆士嘉先生(女,1911– 1986)是普朗特正式接受的唯一中国学生,唯一的女学生。
粘性流体流经任一物体(例如机翼与机身)的问题,归结 为在相应的边界条件下解N—S方程的问题。由于N—S方程太复 杂,在很多实际问题中,不能不作一些近似假设使其简化,以 求问题得以近似地解决。简化时,必须符合物理事实,因此首 先看看空气流过静止物体(例如翼型)的物理图画:
位流区
边界层
流动分为三个区域:1. 边界层:N-S化简为边界层方程 2. 尾迹区:N-S方程 3. 位流区:理想流方程
EXIT
5.1、边界层近似及其特征
2、边界层的特征
(1)边界层定义 严格而言,边界层区与主流区之间无明显界线,通常
以速度达到主流区速度的0.99倍作为边界层的外缘。由边 界层外缘到物面的垂直距离称为边界层名义厚度,用δ表 示。
(2)边界层的有涡性 粘性流体运动总伴随涡量的产生、扩散、衰减。边界
层就是涡层,当流体绕过物面时,无滑移边界条件相当于 使物面成为具有一定强度的连续分布的涡源。
对于曲率不大的弯曲物面,上述边界层方程也近似成立。 只是要将x和y按上述曲线坐标处理即可。当然如果曲率过大, 则沿法向压强保持不变的条件就很难满足了。
EXIT
5.2、平面不可压缩流体层流边界层方程
第5章-边界层理论基础PPT课件

虽然对Re很小的流动,惯性力可以忽略, 但对于Re很大的流动,粘性力却不能忽略, 否则会带来很大的误差,这是何故?
如水和空气,其粘度都很小,在处理其高
速流动时,如果忽略粘性力的影响,就会
导致与实际不符的错误结果。这个矛盾在
普兰德(Plandt)提出边界层学说之后,才获
得令人满意的解答。 -
-
20
卡门边界层方程即适用于层流,也适用 于湍流。
例:流体沿平板壁面流动时层流边界层 的计算,主要目标是边界层厚度和曳力 子数的计算
大量观察和测量得知ux与y的关系与抛 物线近似,因此可假设:
uxabycy2dy3 a,b,c,d 待定
边界条件:
-
21
y 0处ux 0 a 0
dux dy
-
5
随着边界层的厚度逐渐增加,边界层内
部也会发生变化,在边界层厚度较小处,
其内部流动为层流,该区域称为层流边
界层,当其厚度达到其临界厚度δc或临
界距离xc时,其内的流动逐渐经过一过
渡区转变为湍流,此后的边界层称为湍
流边界层,即使在这区域靠近壁面极薄
的一层流体内,仍然维持层流,称为层
流内层。
-
6
临界距离xc的长度与壁面前缘的形状、粗 糙度、流体性质和流速大小有关。壁面愈 粗糙xc愈短。
-
10
但实际中流速ux接近u0到一定程度时,便 可赋予其有应用价值的边界层厚度定义:
(1)
取ux达到u0的99%时的y值,即
ux u0
0 .9 9
处,y的值即为边界层厚度。
(2)可假设一个表示边界层内速度分布的
公式,如抛物线方程,计算当ux达到
u0时的y值,即为边界层厚度。
第八章边界层

动量厚度
0
u U
1
u U
dy
1 g 1 0
g d
无量纲动量厚度
1
0
g
1
g d
壁面切应力
w
du dy
|y0
d Ug d |0
U
无量纲壁面切应力
g'0
代入动量方程
w
U 2
d
湍流光滑区 湍流完全粗糙区
CD f
0.455 ( l g R el )2 . 5 8
( Rel < 109 )
CDf (1 . 8 9 1 . 6 2l g / l)2. 5
[例3] 平板湍流边界层近似计算(2-1)
已知: 一光滑平板长l=0.4m,置于速度为U=3m/s的水流中,水的密度为 ρ=1000kg/m3,运动粘度系数为ν=0.01cm2/s
0U
0
2
2 0
(2) 按动量厚度的定义
u (1- u )dy sin y (1 sin y )dy 2 (sin y sin2 y)d( y)
0U U
0 2
2
0 2
2 2
2
(-cos
y )
2
(1
正弦 曲线
0.137 1.57
4.79
0.655
1.312
精确 解
0.133
5.00
0.664
1.328
[例2] 平板层流边界层近似计算(3-1)
已知: 设无压强梯度平板定常层流边界层内速度分布为正弦曲线:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(s H
t
)Байду номын сангаас
QT
夜间,总通量为负值,一般夜晚,该值总体变化不是很大,假如为 常数,则:
s H QT t
考虑到热交换整体尺度: B HΔ
Δs
得积分厚度:
H (BQT )0.5 t
得地面位温强度: s (QT / B)0.5 t
积分厚度:
H (BQT )0.5 t
地面位温强度: s (QT / B)0.5 t
Stull
(1)稳定边界层的共同特征是有逆温层,此时浮力的 作用不但不能给湍流补充动能,相反,湍流微团在垂直 运动中因反抗重力作功而损失动能,所以湍流能量很弱。 但因为还有切应力的作用,所以湍流不会完全消失,而 是在弱的水平上维持,在大气边界层中仍是一个不可忽 略的因子。这种情况下,湍流热交换过程并不占优势, 而其它的热交换过程例如辐射、平流、气层的抬升及地 形等的影响与湍流热交换过程的影响相当。
热交换整体尺度参数化: B ( f G Zδ )3 2 gQT
Stull
(4)各种特征量在边界层顶没有明显的过渡特征,难于确定层顶 的位置。
总之,由于湍流弱,其他的热力学和动力学因子的作用会表现出来, 并与湍流相互作用而构成稳定边界层的特征。因此随着热力学和动 力学因子大小的变化,稳定边界层就会发生相应的变化,增加了稳 定边界层研究的复杂性和难度。而且,由于湍流及其他各项因子的 量都比较小,使实际观测的精确度受到影响,不易将它们的数值特 征从观测误差中分离。 比较有利的条件只有一点:稳定边界层发展的中、后期,边界层内 的各种过程随时间变化较弱,可以视作为平稳过程。
当热交换总体尺度B大时(较强湍流),位温强度较小,积分厚度较大; 当热交换总体尺度B小时(较弱湍流),位温强度较大,积分厚度较小;
热交换整体尺度参数化: B ( f G Zδ )3 2 gQT
热交换整体尺度B可以用科氏力参数、地转风速、净热通量及宏观 粗糙度(量级约5~10km,不是地表空气动力学粗糙长度)进行参 数化。
位温廓线的理想模式 e:
e,指数:位温随高 度按指数递增,没 有明显的稳定边界 层顶,必须人为假 定。
Δθ(z) Δθsez / HΔθ if Δθ(z) 5%Δθs, h HΔθ ln 0.05 3HΔθ
累积冷却量的预报:
t
uj
x j
θ
2
x
2 j
1
cp
Fj* x j
LE
cp
uj' '
例:晴朗夜晚,f=10-4s-1。Zδ=4km,地转风G=10ms-1, 总冷却量QT=-0.03Kms-1。求6小时后稳定边界层的积 分厚度和位温强度,给出由此产生的对混合模式、线
性模式、指数模式的位温廓线
积分厚度: 地面位温强度:
H (BQT )0.5 t s (QT / B)0.5 t
位温廓线的理想模式 a:
a,稳定混合层模式:
constant, z h
Δ(z)
Δ0, z h
h HΔθ
极端情况,强风及弱地面冷却时,类似于完全 混合层
位温廓线的理想模式 b:
b,线性混合:位温 随高度线性递增, 但稳定边界层顶部 仍保持强逆温跃变。 中等强风和湍流时 易出现。
Δθ(z) (1 z / h) Δθs (z / h) Δθh h 2[Δθs /(Δθs Δθh )] HΔθ
Rf
g
v
w'v '
u' w' u v' w' v
z
z
(3)因湍流很弱,湍涡尺度小,边界层不同层次之间的相互作用 减弱,地面强迫对边界层的响应放缓。下垫表面的强制作用达到边 界层顶所需的时间尺度可长达数个小时,形成分层式湍流,故边界 层往往不能作为整体处理。例如,由地面参量计算的莫宁—奥布霍 夫长度值不能代表边界层中、上层的情况。
0
得到积分冷却量预报:
(s H ) h ...dz
t
0
积分冷却量预报:
(s H )
t
QA QW
QR
QLA
QH
QT
水 垂 垂潜 平 直 直热 平 平 方通 流 流 向量 热 热辐 通 通射 量 量通
量
感总 热热 通通 量量
注意:方程右边热通量均取运动学热通量单位,Kms-1
x j
简化为:
u v w 1 Fz* LE w' '
t
x y z cp z cp z
对边界层厚度积分,代换 θ θ0 θ(z)
h dz h ...dz
0 t
0
h
( 0
(z) )dz
h
...dz
t 0
0
h
(z)dz
h
...dz
t 0
0
h
积分冷却量定义: Δ d z Δs H
CH07.稳定边界层
一、稳定边界层特征 二、稳定边界层模式 三、低空急流
一、稳定边界层特征
如果边界层内位温随着高度增加而升高,就成 为稳定边界层。形成稳定边界层有多种原因,夜间 地表辐射冷却形成的逆位温层结,就是常见的稳定 边界层;另外,若有暖平流流经冷的下垫面,也能 形成稳定边界层。在稳定边界层中,湍流热交换自 上向下输送热量。通常,稳定边界层的厚度大约 100~500m。
e t
g
v
w'v ' u' w'
u z
w' e z
1
w' p' z
(2)理论分析和实验事实均表明,当浮力引起的湍流动能损失 达到切应力产生动能的1/5左右,湍流便会因连续不断地耗散而 衰竭,这相当于通量理查孙数Rf = 0.2。此时湍流结构在空间和时 间上出现不连续,形成所谓的间歇性湍流或波与间歇性湍流共存。
位温廓线的理想模式 c:
c,线性:位温随高 度线性递增,稳定 边界层顶部没有位 温跃变。
Δθ(z) (1 z / h) Δθs, z h h 2HΔθ
位温廓线的理想模式 d:
d,多项式:位温随 高度按多项式递增, 稳定边界层顶部逆 温梯度为零。
Δθ(z) (1 z / h) Δθs , z h, 2,3 h (1 )HΔθ
二、稳定边界层模式
稳定边界层厚度和强度的总体量度
强度:
s 0 s
积分厚度尺度:
h
累积冷却量:Δ d z Δs H
0
HΔθ
1
Δs
h
Δ
0
dz
热交换整体尺度: B HΔ
Δs
稳定边界层的高度:
/ z 0
T / z 0 TKE 0;TKE 0.05TKEs u' w' 0;u' w' 0.05u' w's U max U Ug
