过程设备设计-旋转薄壳理论

若将(3-5)式各项乘

N

N

2
则该式具有简单的物理意义
2 rN sin 2 rr1 ( P sin Pz cos )d 2 C
3-6 区域平衡方程
无力矩理论两个方程
N N Pz r1 r2
3-3
2 rN sin 2 rr1 ( P sin Pz cos )d 2 C
P P PR PD 2 R2 R1 R 2 4
(3-11)
B. 圆柱形容器: R1= R2=R
PD 4 PD 2
(3-12)
2
C. 锥形封头:R1= R2=r/cos =x· tg
中间面
与壳体内外表面等距离的曲面，用中间面来 表示壳体的几何特性
母线
形成中间面的平面 曲线 OAA’
通过回转轴作一纵截 面与壳体曲面相交所 得的交线OBB 通过经线上任意一点 M垂直于中间面的直线， 称为中间面在该点的“法线”
经线
法线
图3-2 任意回转壳体
法线的延长线必与回转轴相交
纬线
作圆锥面与壳体中间面正交，得到的交线
方程两边乘 sin ，并代入
r r2 s i n 得： sin
d ( N r ) rN cos rr1 ( P sin Pz cos ) 0 d d d ( N r sin ) ( N r )sin N r cos 代入上式 d d
(3-3)
Fx 0
N 在经线方向的投影: 周向力
N r1d d cos
经向力
N
在经线方向的投影:
dN dr d N d d r d d ( N r )d d d d d
外载荷在经线方向的投影
P r1d rd
代入 Fx 0 并注意所有分力的方向
据微分法，有：
d ( N r sin ) rr1 ( P sin Pz cos ) 0 将此式积分得： d
N r sin rr1 ( P sin Pz cos )d C
（3-5）
式中C为积分常数，由边界条件决定 所以经向应力和周向应力为：
P z r1d rd Pz r1r2 sin d d
代入 Fz 0 并注意所有分力的方向
N r1 sin d d N r2 sin dd Pz r1r2 sin dd 0
各式同除，
r1r2 sin d d
N N Pz r1 r2
r CB
r r2 sin
dl r1d dl rd
dr dl cos
dr r1 cos d
图3-4
3.2 外力和内力分析 (1) 基本假设 除假设壳体是完全弹性之外，本章还采用以下假设: 小位移或小挠 (nao)度假设：壳体受力后，各点的位移都 远小于壁厚； 直法线假设：壳体在变形前垂直于中面的直线段，在变形 后仍保持为直线，并垂直于变形后的中面，并假设壳体的 厚度不变； 不挤压假设：壳体各层纤维在变形前后均互不挤压。 (2) 外力 容器承受的外力主要是分布面力，如气压、液压等。体积 力如重力、惯性力等可以化为分布力。由于是轴对称问题， 外力不随坐标变化，仅是的函数。
N
g hr1r2 sin cos C
r2 sin 2
(3-19)
r2 N r2 ( Pz ) ghr2 N r1 r1
N
例1 如图，求圆柱壳内的应力
例2 充满液体的球壳，沿对应于 0 的平行 园A-A裙座支承，液体的密度为 ，求壳体 内任一点的应力。
第一曲率半径r1
中间面上任一点M处经线的曲率 半径为该点的“第一曲率半径”
第二曲率半径r2
通过经线上一点M的法线作 垂直于经线的平面与中间面 相割形成的曲线MEF，此曲 线在M点处的曲率半径称为 该点的第二曲率半径
图3-3 任意回转壳体
注意
第二曲率半径的中心K2落在回转轴上，其长度等于法线段MK2
无力矩理论的应用条件
(1) 壳体的厚度、中面曲率与载荷没有突变，构成 同一壳体的材料物理性能(如E、u等)相同 (2) 壳体边界处不横向剪力、弯矩和扭矩的作用 (3)壳体边界处只可有沿经线切线方向的约束,而边 界处转角与挠度不应受到约束 对很多实际问题：无力矩理论求解+有力据理论修正
3.6 回转壳体的不连续分析
d ( N r )d d N r1 cos d d N r ) N r1 cos P r1r 0 d
(3-4)
由(1-4)得： N r2 Pz
r2 N 代入(3-4) r1
r2 d ( N r ) (r2 Pz N )r1 cos P r1r 0 , d r1
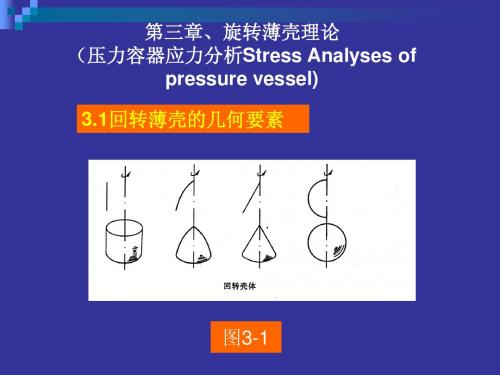
第三章、旋转薄壳理论 （压力容器应力分析Stress Analyses of pressure vessel) 3.1回转薄壳的几何要素
图3-1
回转壳体
有一根对称轴，并由旋转曲面构成的薄壁旋转 壳体(thin shell of revolution)
轴对称问题
薄壁旋转壳体通常属于轴对称问题，即壳 体的几何形状，所受的外部载荷以及约束 条件均对称于旋转轴(axially symmetric shell



一、不连续效应和不连续效应分析的基本方法
连接边缘的变形
二、圆柱壳受边缘力和边缘力矩的弯曲解
1、求解微分方程式 轴对称加载的圆柱壳有力矩理论基本微分方程为
d 4w p 4 4 w ' Nx 4 ' dx D RD
2-16 p38
2-19
p39
由上式写出
求出内力
求应力
三、组合壳体不连续应力的计算举例
圆平板和圆柱壳的连接
2 自限性
不连续应力的危害
例题：一容器如图所示。圆筒中面半径为R，壁厚为t，圆锥和圆筒 的壁厚相等，半锥角为 ，容器内承气体的压力p的作用，且圆筒 中液柱的高度为 H1，圆锥液柱的高度为H2，液体的重度为 ,忽略 壳体的自重。（1）按无力矩理论求A-A, B-B, C-C截面处的经向 和周向应力；（2）若H1>H2, 试求圆锥壳中最大应力作用点的位置 及大小。
（3-7）
pr2 N 2
（3-8）
N r1 ) N (2 r2 ) r1
N r2 ( P
(3-9)
pr2 2 N pr2 r2 (2 ) 2 r1
N
(3-10)
1、受均匀气体内压作用的容器
A. 球形壳体（封头）: r1=R r2=R
(3) 内力
微元体取法 在壳体中任一点沿两个经线截面和两个以第二曲率半 径为木县的旋转法截面取出的微小六面体称单元体。
图3-5
图3-6
图3-5




微元体上的受力有： N : 垂直于纬线截面的经向力，拉为正，压为负； N: 垂直于经线截面的周向力，拉为正，压为负； M：纬线截面内的经向弯矩，使截面向外侧旋转为正， 反之为负； M：经线截面内的周向弯矩，使截面向外侧旋转为正， 反之为负； Q：为横向剪力。
3-6
3.5 无力矩理论在几种常见壳体上的应用
受气压作用
气体压力是垂直作用于壳体表面，且处处相等。有： z P P 常数， P 0 由（3-6）式
2 rN sin 2 rr1 P cos d 2 C
C=0
dr r1 cos d
2 rN sin 2 prdr pr 2
Pr Px sin Px Pr 90 tg 2 sin 2 cos 2 2 cos PR2 Pxtg Px tg 2



(3-13)
D. 椭圆封头
2受液体内压作用的容器
直立壳体,液体压力垂直作用于壳体表面, P 0, Pz h gh
3.4无力矩理论的基本方程
图3-7
（a）
（（b）
（c） 图3-7
a点 建立一空间直角坐标系， x取经线的切向，y取纬线的 切向，z取法向的反向。
Fz 0
N 在法线方向的投影: 周向力
N r1d d sin
N
经向力
N
在法线方向的投影:
N r2 sin d d
外载荷的法线方向分量：
3.3无力矩理论与有力矩理论(membrane
theory and bending theory)
注意
5个内力分量：N、N为法向力，这二个内力是因中面 的拉伸、压缩而产生的，称为薄膜内力(或薄膜力)； Q、为横向剪力；M、M分别为弯矩，这三个内力是 因中面的曲率、扭率改变而产生的，称为弯曲内力。 无力矩理论 壳体很薄，平衡时，就可省略弯 曲内力对平衡的影响，于是得 到无力矩应力状态。省略弯曲 内力（ M、M ， Q ）的壳 体理论，称为或薄膜理论。 有无力矩理论 同时考虑薄膜内力和弯 曲内力，这种理论称为 有力矩理论或弯曲理论
注意
M ( , )
确定曲面上的任一点

周向坐标角，决定经线的位置

经向坐标角，决定纬线的位置
几何关系
r r2 sin
dr r1 cos d
(3-1) (3-2)
(3-2)式的推导： 过B点的平行园的园心C必在旋转 轴OO’上，由图知，经线和纬线的微 长 dl , dl