工程力学弯曲变形(H)详解
合集下载
工程力学11弯曲变形共67页
f ( P 1 P 2 P n ) f 1 ( P 1 ) f 2 ( P 2 ) f n ( P n )
二、结构形式叠加（逐段刚化法）：
14
14
P
q 例3 按叠加原理求A点转角和C点挠
A
B 度。
C
a
a
解、载荷分解如图
P
由梁的简单载荷变形表，
=
A
B
查简单载荷引起的变形。
(0xa) (axL)
最大挠度及最大转角
max(a)
Pa2 2EI
a
P
L
x
fmax f(L)6PE2aI3La
f
13
按叠加原理求梁的挠度与转角
一、载荷叠加：多个载荷同时作用于结构而引起的变形 等于每个载荷单独作用于结构而引起的变形的代数和。
( P 1 P 2 P n ) 1 ( P 1 ) 2 ( P 2 ) n ( P n )
(axL)
L
x
f 写出微分方程的积分并积分
EfI 0 P(ax)
(0xa) (axL)
EIf
1 2
P(a
x)2
C1
D1
11
EIf16P(ax)3 C1xC2 D1xD2
11
梁的挠曲线近似微分方程及其积分
应用位移边界条件求积分常数
EI(f0)1 6P3 aC20
EI(0)1 2P2aC10
a
P
L f
其方程为：
w =f (x)
三、转角与挠曲线的关系：tg d d fx= d d w x小 变形 f
5
(1 )
5
梁的挠曲线近似微分方程及其积分
一、挠曲线近似微分方程
x M>0 f(x)0 f
二、结构形式叠加（逐段刚化法）：
14
14
P
q 例3 按叠加原理求A点转角和C点挠
A
B 度。
C
a
a
解、载荷分解如图
P
由梁的简单载荷变形表，
=
A
B
查简单载荷引起的变形。
(0xa) (axL)
最大挠度及最大转角
max(a)
Pa2 2EI
a
P
L
x
fmax f(L)6PE2aI3La
f
13
按叠加原理求梁的挠度与转角
一、载荷叠加：多个载荷同时作用于结构而引起的变形 等于每个载荷单独作用于结构而引起的变形的代数和。
( P 1 P 2 P n ) 1 ( P 1 ) 2 ( P 2 ) n ( P n )
(axL)
L
x
f 写出微分方程的积分并积分
EfI 0 P(ax)
(0xa) (axL)
EIf
1 2
P(a
x)2
C1
D1
11
EIf16P(ax)3 C1xC2 D1xD2
11
梁的挠曲线近似微分方程及其积分
应用位移边界条件求积分常数
EI(f0)1 6P3 aC20
EI(0)1 2P2aC10
a
P
L f
其方程为：
w =f (x)
三、转角与挠曲线的关系：tg d d fx= d d w x小 变形 f
5
(1 )
5
梁的挠曲线近似微分方程及其积分
一、挠曲线近似微分方程
x M>0 f(x)0 f
工程力学弯曲变形教学课件
复合弯曲
构件在多个方向上的弯曲，如螺 旋弹簧。
特点
弯曲构件应力状态复杂，难以直 观描述。
弯曲变形的应用领域
建筑结构
如板材、梁、柱等结构的设计。
管道工程
例如油气管道的输送、变形与控制。
车辆工程
比如汽车、火车的车体、悬挂、轮轴等的设计。
机械制造
如转子、齿轮的制造及加工工艺的设计。
工程力Байду номын сангаас弯曲变形的研究方法
工程实例分析：高速铁路钢轨的弯曲变形
1 设计要求
2 轨道变形及寿命
3 分析方法
轨道线形和理论分析准确， 轨道表面平整，满足高速 列车的舒适性要求。
铁路轨道在使用过程中会 发生弯曲变形和垂向变形， 会影响轨道寿命和车辆行 驶安全。
载荷计算、应力分析、变 形分析、疲劳寿命分析、 几何形状优化等方法。
弯曲变形未来发展趋势
2 应用
纯弯曲在平面构件及杆件的弯曲变形分析有广泛应用，而复合弯曲则常见于薄壳结构的 变形分析。
工程力学对弯曲变形的判定准则
1
最大应力准则
理想的弯曲构件上，弯曲应力分布处，最大应力是许容应力的一定倍数。
2
最大应变准则
理想的弯曲构件上弯曲应变分布处，最大应变是许容应变的一定倍数。
3
能量方法
包括弯曲形态能、应变能等计算方法。
2 影响
材料弹性模量越大，弯曲变形的刚度越大；模量越小，刚度越小。
不同材料的弯曲特性
铝合金
木材
弯曲特性良好，重量轻，易加工， 耐腐蚀性能好。
弯曲特性较好，在建筑结构、家 具等领域有广泛应用。
钢材
弯曲特性相对较强，适用于制造 各种构件。
基础理论：欧拉梁理论
材料力学第5章弯曲变形ppt课件
qL
4.22kNm
4.22kNm
M
max
32 M
max
76.4MPa
WZ
d 3
例题
20kN m
A
4m
FA
20kN m
A
MA
4m
试求图示梁的支反力
40kN
B
D
2m
2m
B
B1 FB
FB 40kN
B
D
B2
2m
2m
在小变形条件下,B点轴向力较小可忽略不
计,所以为一次超静定.
C
B1 B2
FBBBMF12AA2383qFEqELBqqLI84LI2LLZZ32F35BFF4FEFB83PBPLIEL7Z3L12IZ.218352.k75N5kFkN2PNmEL2IZ2
x
边界条件
A
L2
B
L2
C
y
连续条件
例题 5.5
用积分法求图示各梁挠曲线方程时,试问下列各梁 的挠曲线近似微分方程应分几段;将分别出现几个积 分常数,并写出其确定积分常数的边界条件
全梁仅一个挠曲线方程
C
q
EA
共有两个积分常数 边界条件
L1
A
x
B
EI Z
L
y
例题 5.5
用积分法求图示各梁挠曲线方程时,试问在列各梁 的挠曲线近似微分方程时应分几段;将分别出现几个 积分常数,并写出其确定积分常数的边界条件
q
a
B C LBC
B
2a
FN
B
q2a4
8EIZ
FN 2a3
3EIZ
C
FN
a
D
第14章 弯曲变形
弯矩分段,要分段积分
式中积分常数C、D由边界条件和连续条件确定
要求：（1）约束处满足边界条件 （2）梁中间的点满足连续与光滑条件
边界条件
y A
x =0 , w=0 y ( = 0)
x
x = l , w= 0 =0
2
B
x
x = l , w=0 ( = 0)
光滑连续条件：
wc wc
P
c
c
梁的挠曲线近似微分方程式：
(-) M 0
w 0
EI
d2w dx2
M
(x)
M w或EIw M
EI z
3.积分法求梁的挠曲线
dx2
EI M (x)dx C dx o
xx
EIw [ M (x)dx]dx Cx D 00
左段梁 0 x a
右段梁 a x l
挠曲线近似微分方程
EIw1
M1
x
F
b l
x
EIw2
M2
x
F
b l
x
F
x
a
积分得
EIw1 EIw1
F
b l
x2 2
C1
F
b l
x3 6
C1 x
(1) D1 (2)
EIw2
F
b l
x2 2
EIw2
F
b l
F
x 2
a 2
C2
x3 F x a3
6
6
(1)
弹性变形，以满足特
定的工作需要,例如
车辆上的板弹簧。缓 P / 2
P/2
解车辆受到的冲击
和振动作用。
P
二、弯曲变形的基本概念
工程力学 第10章弯曲变形
dy y ( x) dx
——转角方程
第一节 弯曲变形的概念
5.挠曲线近似微分方程
曲线y＝y（x）上任一点的曲率公式为
d2y 2 1 dx dy ( x) [1 ( ) 2 ]3/ 2 dx
M EI Z
1
d2y M ( x) 2 dx EI Z
y
M ( x) 适用于弹性范围内的小变形情况 EI Z
(2)通常是按强度条件选择截面尺寸，然后用刚度条件校核。
第三节
梁的刚度计算
解：（1）按强度条件选择工字钢截面型号。
M max Pl 10 4 40kNm
（2）刚度校核。梁的最大挠度发生在B截面：
不满足刚度要求。
第三节
梁的刚度计算
（3）按刚度要求重新选择截面型号
由型钢表查得：
f Pl 3 10 103 4 2 1 3 2 . 4 10 l 3EI 3 200 109 11.07，当按强度条件进行计算后，有时还须进 行刚度校核。因为虽然梁满足强度条件时工作应力并没 有超过材料的许用应力，但是由于弯曲变形过大往往也 会使梁不能正常工作，所以要进行刚度校核。 为了满足刚度要求，应该使梁的最大挠度值不超过允许的范围。
(1)梁在使用时有时需同时满足强度条件和刚度条件。
第一节 弯曲变形的概念
利用变形
卡车一轴板簧——减震装置
第一节 弯曲变形的概念
1.挠度 梁轴线上任一点（即横截面形心）在垂直于轴线方向的线位移称 为该点的挠度，用 y 表示。规定向下的挠度为正。单位为（mm）。 2.转角 梁任一横截面在梁变形后相对于原来位置绕中性轴转过一个角度， 称为该截面的转角，通常用θ表示，并以顺时针转向为正。 单位是弧度（rad）。
弯曲变形知识点总结
弯曲变形知识点总结一、弯曲变形的原理1.1 弯曲应力和弯曲应变在外力作用下，梁或梁状结构会发生弯曲变形。
在梁上的任意一点，都会受到弯曲应力的作用。
弯曲应力是指由于梁在受力下产生的内部应力，它的大小和方向取决于梁的截面形状、受力方向和大小等因素。
弯曲应力与梁的截面形状呈二次关系，通常情况下，弯曲应力最大值出现在梁的截面中性轴附近。
随着梁的弯曲，材料内部会产生弯曲应变。
弯曲应变也是和梁的截面形状有关的，并且与弯曲应力呈线性关系。
弯曲应变可以用来描述梁在受力下的变形情况，对于计算梁的弯曲变形非常重要。
1.2 理想弹性梁的弯曲变形对于理想弹性梁而言，其弯曲变形可以通过弯曲方程来描述。
弯曲方程可以根据梁的几何形状和外力作用来得到，通过求解弯曲方程可以得到梁的变形情况。
理想弹性梁的弯曲变形遵循胡克定律，即弯曲应力和弯曲应变成正比。
1.3 破坏弯曲当外力作用到一定程度时，梁会发生破坏弯曲。
在破坏弯曲阶段，梁的抵抗力不足以克服外力作用，导致梁发生不可逆的变形。
在此阶段，梁的弯曲应力和弯曲应变将迅速增大，直至梁失去稳定性。
二、弯曲变形的计算方法2.1 弯曲方程弯曲方程是描述梁弯曲变形的重要工具，可以根据弯曲方程来求解梁的弯曲应力和弯曲应变。
通常情况下，弯曲方程是一种二阶微分方程，需要求解出合适的边界条件，才能得到梁的变形情况。
弯曲方程的求解与梁的截面形状直接相关，对于不同形状的梁，需要采用不同的弯曲方程。
2.2 梁的截面性质对于计算梁的弯曲变形而言，了解梁的截面性质非常重要。
梁的截面性质包括截面面积、截面惯性矩等参数，这些参数会直接影响弯曲方程的求解。
在实际工程中，可以通过截面性质来选择合适的梁截面形状，以满足结构设计的需求。
2.3 数值计算方法为了解决复杂梁的弯曲变形问题，通常需要采用数值计算方法。
数值计算方法可以通过数学模型来描述梁的变形行为，然后通过计算机仿真来得到梁的变形情况。
在工程实践中，有限元方法是一种常用的数值计算方法，可以对复杂结构的弯曲变形问题进行有效求解。
工程力学六 弯曲变形解析
当x1 x2 a时,
w1 w2 (1 2 )
w1 w2
EIw2
Pb l
x2
P( x2
a)
CB段：
EIw2
EI2
Pb l
x22 2
P
( x2
a)2 2
C2
EIw2
Pb l
x23 6
P
( x2
a)3 6
C2 x2
D2
由连续性条件，可求得
C1 C2
D1 D2
由边界条件，可求得
C1
C2
M pa
P PL
2
PL 2
x
P
qa2
2
q
M
qa
x qa 2 2
x
pa
§6.2 挠曲线近似微分方程及其积分
一、挠曲线近似微分方程的导出
力学公式 数学公式
1 M z (x)
EIz
d 2w
1
dx2
[1 ( dw)2 ]3/2
dx
纯弯曲梁变形后中性层的曲率 公式，对于横力弯曲（l>5h） 可近似使用。EIZ称为梁的抗 弯刚度。
最大转角和最大挠度分别为：
得：
ql 3 C ,
D0
24
梁的转角方程和挠曲线方程分别为：
q (6lx2 4x3 l 3 )
24 EI
w qx (2lx2 x3 l3) 24EI
max
A
B
ql 3 24EI
wmax
w
x l 2
5ql 4 384EI
例： 已知梁的抗弯刚度为EI。试求图示悬臂梁在集中力P作用下的转角方
确定积分常数： （1）边界条件
固定端：w = 0,θ = 0
工程力学第12章弯曲变形
AC段 (0 ≤ x ≤ a) 段 BC段 (a ≤ x ≤ L) 段 Fb 2 Fb 2 F EIω1' = EIθ1 = x + C1, EIω2 ' = EIθ2 = x − (x − a)2 + C2 , 2L 2L 2 Fb 3 EIω1 = x + C1x + D , EIω2 = Fb x3 − F (x − a)3 + C2 x + D2 , 1 6L 6L 6 3、确定常数 、 边界条件： 边界条件：
θA 。
X
解：取参考坐标系Axy。 取参考坐标系 。 1、列出梁的弯矩方程 、
d 2ω M(x) 2、 、 2 = dx EIz
(0 ≤ x ≤ L)
1 2 EIω"= − qx 2 积分一次： 积分一次：EIω' = EIθ = − 1 qx3 + C（1） ） 1 46 积分二次： 积分二次： EIω = − qx + Cx + D （2） ） 24
2、积分常数的确定——边界条件和连续条件： 、积分常数的确定 边界条件和连续条件： 边界条件和连续条件 边界条件：梁在其支承处的挠度或转角是已知的，这样的 边界条件：梁在其支承处的挠度或转角是已知的， 已知条件称为边界条件。 已知条件称为边界条件。 连续条件：梁的挠曲线是一条连续、光滑、平坦的曲线。 连续条件：梁的挠曲线是一条连续、光滑、平坦的曲线。因 此，在梁的同一截面上不可能有两个不同的挠度 值或转角值，这样的已知条件称为连续条件。 值或转角值，这样的已知条件称为连续条件。
二、分段列出梁的挠曲线近似微分方程，并对其积分两次 分段列出梁的挠曲线近似微分方程， 1、对挠曲线近似微分方程积分一次，得转角方程： 、对挠曲线近似微分方程积分一次，得转角方程：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第七章 弯曲变形
二、弯曲变形的基本概念
(x)
A x l F
x
l
v( x)
B
描述截面上任一点的位移: 1、形心轴的线位移 —— 挠度 v 2、截面绕形心轴的角位移 ——转角
第七章 弯曲变形
二、弯曲变形的基本概念
(x)
A x l
x
l
v( x)
B
F
F 变弯的形心轴 —— 挠曲线 F 挠度随坐标变化的方程 —— 挠曲线方程
正负号确定——确定坐标系:
v
x
x
M 0, v 0
第七章 弯曲变形
M 0, v 0
§7-3
用积分法求弯曲变形
EIv M ( x )
EIv M ( x) dx C
EIv M ( x)dxdx Cx D
F C、D为积分常数，它由位移边界与连续条件确定。
弯曲变形
解：
ql q 2 M ( x) x x 2 2 ql q 2 EIv x x 2 2
y
q
B
x l x
A ql 2 q 3 EIv x x C 4 6 ql 3 q 4 EIv x x Cx D 12 24
由边界条件：
x 0时，v 0 x l 时，v 0
第七章 弯曲变形
ql 3 B 24 EI
5ql 4 384 EI
x
l 2
例3：已知梁的抗弯刚度为EI。试求图示悬臂梁在集中力 P 作用下的转角方程、挠曲线方程，并确定max 和 vmax。 解： M ( x) P(l x)
y
A
P
x
B
EIv P(l x)
画挠曲线的大致形状
q
C B D
Q
3qa 4
+
qa 2
A
_
qa 4
a
a
a
M
3qa 2 4
+
qa 2 4
qa 2 32
d v M x 2 dx EI
最大转角和最大挠度分别为：
2
x
l
max
vmax
第七章 弯曲变形
Pl 2 B 2 EI
Pl 3 vB 3EI
例4：已知梁的抗弯刚度为EI。试求图示简支梁在集中力 P 作 用下的转角方程、挠曲线方程，并确定max 和 vmax 。
y
A
P
B
x
l 2
C
x
l 2
第七章
弯曲变形
32
挠曲轴微分方程
1 [v( x)]
v( x)
2 32
M x EI
第七章
弯曲变形
方程简化
1 [v( x)]
1
v( x)
2 32
M x EI
小变形时： v2
d 2v M x 2 dx EI
v 向上为正, 逆时针为正.
v
AC段梁的转角方程和挠曲线方程分别为：
P (4 x 2 l 2 ) 16 EI
y
A
P
B
Px v (4 x 2 3l 2 ) 48EI
最大转角和最大挠度分别为：
x
l 2
C
x
l 2
max
vmax
第七章 弯曲变形
Pl 2 A B 16 EI
Pl 3 v l x 48EI 2
左 右 左 右 wC 0, wC 0 C C
左 右 左 右 左 右 wB wB , wE wE E E
可动铰:
vC 0
第七章
弯曲变形
例2：已知梁的抗弯刚度为 EI。试求图示简支梁在均布载荷q
作用下的转角方程、挠曲线方程，并确定 max 和 vmax。
q
A
l
B
第七章
解：AC段:
P M ( x) x 2 P EIv x 2
y
A
P
B
x
l 2
C
x
l 2
P 2 EIv x C 4 P 3 EIv x Cx D 12
由边界条件： 由对称条件：
第七章 弯曲变形
x 0 时，v 0
l x 时， v 0 2
得：
D0
Pl 2 得： C 16
v f ( x)
df(x) F 忽略剪切变形 + 梁的转角一般很小 —— θ tanθ dx
第七章 弯曲变形
§7-2
梁挠曲线的近似微分方程
中性层曲率表示的弯曲变形公式
1 M （纯弯） ρ EI
由高等数学知识
1 M ( x) （推广到非纯弯） ( x) EI
1 v( x) 2 ( x) 1 [v ( x)]
常工作。
第七章
弯曲变形
摇臂钻床的摇臂或车床的主轴变形过大，就会影响零件 的加工精度，甚至会出现废品。
F
F
第七章
弯曲变形
桥式起重机的横梁变形过大,则会使小车行走困难， 出现爬坡现象。
P
P
第七章 弯曲变形
但在另外一些情况下，有时却要求构件具有较大的
弹性变形，以满足特定的工作需要。
例如，车辆上的板弹簧，要求有足够大的变形， 以缓解车辆受到的冲击和振动作用。
x
P 2 EIv x plx C 2 P 3 Pl 2 EIv x x Cx D 6 2
由边界条件： 得：
第七章 弯曲变形
l
x 0 时，v 0,v 0
C D0
梁的转角方程和挠曲线方程分别为：
Px ( x 2l ) 2 EI
y
A
P
x
B
Px v ( x 3l ) 6 EI
第七章 弯曲变形
边界条件：梁截面的已知位移条件
v0
v0
v0
0
连续条件：分段处挠曲轴应满足的连续、光滑条件
FAB源自MDC$ 挠曲线在B、C点连续且光滑 连续:
第七章
v左 v右
光滑:
左 右
弯曲变形
例1：写出梁的挠曲轴方程的边界条件和连续条件
F A E B C D
边界条件： 固定端: v A 0, A 0 自由端：无位移边界条件 连续条件：
第 7章
弯曲变形
※ 工程问题中的弯曲变形 ※ 挠曲线的近似微分方程
※ 用积分法求弯曲变形 ※ 用叠加法求弯曲变形
※ 简单静不定梁
※ 提高弯曲刚度的措施
第七章 弯曲变形
§7-1
概
述
一、工程实践中的弯曲变形问题
在工程实践中，对某些受弯构件，除要求
具有足够的强度外，还要求变形不能过大，即
要求构件有足够的刚度，以保证结构或机器正
得：
第七章
ql 3 C , D0 24
弯曲变形
梁的转角方程和挠曲线方程分别为：
q (6lx 2 4 x 3 l 3 ) 24 EI
y
q
B
x l x
qx v (2lx 2 x 3 l 3 ) 24 EI
最大转角和最大挠度分别为：
A
max A
v max v
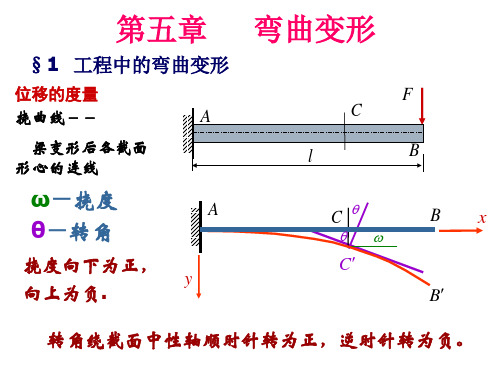
二、弯曲变形的基本概念
(x)
A x l F
x
l
v( x)
B
描述截面上任一点的位移: 1、形心轴的线位移 —— 挠度 v 2、截面绕形心轴的角位移 ——转角
第七章 弯曲变形
二、弯曲变形的基本概念
(x)
A x l
x
l
v( x)
B
F
F 变弯的形心轴 —— 挠曲线 F 挠度随坐标变化的方程 —— 挠曲线方程
正负号确定——确定坐标系:
v
x
x
M 0, v 0
第七章 弯曲变形
M 0, v 0
§7-3
用积分法求弯曲变形
EIv M ( x )
EIv M ( x) dx C
EIv M ( x)dxdx Cx D
F C、D为积分常数，它由位移边界与连续条件确定。
弯曲变形
解：
ql q 2 M ( x) x x 2 2 ql q 2 EIv x x 2 2
y
q
B
x l x
A ql 2 q 3 EIv x x C 4 6 ql 3 q 4 EIv x x Cx D 12 24
由边界条件：
x 0时，v 0 x l 时，v 0
第七章 弯曲变形
ql 3 B 24 EI
5ql 4 384 EI
x
l 2
例3：已知梁的抗弯刚度为EI。试求图示悬臂梁在集中力 P 作用下的转角方程、挠曲线方程，并确定max 和 vmax。 解： M ( x) P(l x)
y
A
P
x
B
EIv P(l x)
画挠曲线的大致形状
q
C B D
Q
3qa 4
+
qa 2
A
_
qa 4
a
a
a
M
3qa 2 4
+
qa 2 4
qa 2 32
d v M x 2 dx EI
最大转角和最大挠度分别为：
2
x
l
max
vmax
第七章 弯曲变形
Pl 2 B 2 EI
Pl 3 vB 3EI
例4：已知梁的抗弯刚度为EI。试求图示简支梁在集中力 P 作 用下的转角方程、挠曲线方程，并确定max 和 vmax 。
y
A
P
B
x
l 2
C
x
l 2
第七章
弯曲变形
32
挠曲轴微分方程
1 [v( x)]
v( x)
2 32
M x EI
第七章
弯曲变形
方程简化
1 [v( x)]
1
v( x)
2 32
M x EI
小变形时： v2
d 2v M x 2 dx EI
v 向上为正, 逆时针为正.
v
AC段梁的转角方程和挠曲线方程分别为：
P (4 x 2 l 2 ) 16 EI
y
A
P
B
Px v (4 x 2 3l 2 ) 48EI
最大转角和最大挠度分别为：
x
l 2
C
x
l 2
max
vmax
第七章 弯曲变形
Pl 2 A B 16 EI
Pl 3 v l x 48EI 2
左 右 左 右 wC 0, wC 0 C C
左 右 左 右 左 右 wB wB , wE wE E E
可动铰:
vC 0
第七章
弯曲变形
例2：已知梁的抗弯刚度为 EI。试求图示简支梁在均布载荷q
作用下的转角方程、挠曲线方程，并确定 max 和 vmax。
q
A
l
B
第七章
解：AC段:
P M ( x) x 2 P EIv x 2
y
A
P
B
x
l 2
C
x
l 2
P 2 EIv x C 4 P 3 EIv x Cx D 12
由边界条件： 由对称条件：
第七章 弯曲变形
x 0 时，v 0
l x 时， v 0 2
得：
D0
Pl 2 得： C 16
v f ( x)
df(x) F 忽略剪切变形 + 梁的转角一般很小 —— θ tanθ dx
第七章 弯曲变形
§7-2
梁挠曲线的近似微分方程
中性层曲率表示的弯曲变形公式
1 M （纯弯） ρ EI
由高等数学知识
1 M ( x) （推广到非纯弯） ( x) EI
1 v( x) 2 ( x) 1 [v ( x)]
常工作。
第七章
弯曲变形
摇臂钻床的摇臂或车床的主轴变形过大，就会影响零件 的加工精度，甚至会出现废品。
F
F
第七章
弯曲变形
桥式起重机的横梁变形过大,则会使小车行走困难， 出现爬坡现象。
P
P
第七章 弯曲变形
但在另外一些情况下，有时却要求构件具有较大的
弹性变形，以满足特定的工作需要。
例如，车辆上的板弹簧，要求有足够大的变形， 以缓解车辆受到的冲击和振动作用。
x
P 2 EIv x plx C 2 P 3 Pl 2 EIv x x Cx D 6 2
由边界条件： 得：
第七章 弯曲变形
l
x 0 时，v 0,v 0
C D0
梁的转角方程和挠曲线方程分别为：
Px ( x 2l ) 2 EI
y
A
P
x
B
Px v ( x 3l ) 6 EI
第七章 弯曲变形
边界条件：梁截面的已知位移条件
v0
v0
v0
0
连续条件：分段处挠曲轴应满足的连续、光滑条件
FAB源自MDC$ 挠曲线在B、C点连续且光滑 连续:
第七章
v左 v右
光滑:
左 右
弯曲变形
例1：写出梁的挠曲轴方程的边界条件和连续条件
F A E B C D
边界条件： 固定端: v A 0, A 0 自由端：无位移边界条件 连续条件：
第 7章
弯曲变形
※ 工程问题中的弯曲变形 ※ 挠曲线的近似微分方程
※ 用积分法求弯曲变形 ※ 用叠加法求弯曲变形
※ 简单静不定梁
※ 提高弯曲刚度的措施
第七章 弯曲变形
§7-1
概
述
一、工程实践中的弯曲变形问题
在工程实践中，对某些受弯构件，除要求
具有足够的强度外，还要求变形不能过大，即
要求构件有足够的刚度，以保证结构或机器正
得：
第七章
ql 3 C , D0 24
弯曲变形
梁的转角方程和挠曲线方程分别为：
q (6lx 2 4 x 3 l 3 ) 24 EI
y
q
B
x l x
qx v (2lx 2 x 3 l 3 ) 24 EI
最大转角和最大挠度分别为：
A
max A
v max v