离散数学一阶逻辑命题符号化共26页
合集下载
离散数学四省公开课一等奖全国示范课微课金奖PPT课件

f : DIn DI , 称 f 为f在I中解释.
(d) 对每一个n元谓词符号FL, 有一个DI上n元谓词常项 ,F 称 F 为F在I中解释. 设公式A, 取个体域DI , 把A中个体常项符号a、函数符
号f、谓词符号F分别替换成它们在I中解释 、a 、f ,F称
所得到公式A为A在I下解释, 或A在I下被解释成A.
比如,x(F(x,y)G(x,z)), x为指导变元,(F(x,y)G(x,z))为 x 辖域,x两次出现均为约束出现,y与 z 均为自由出现
又如, x(F(x,y,z)y(G(x,y)H(x,y,z))), x中x是指导变元, 辖域为(F(x,y,z)y(G(x,y)H(x,y,z))). y中y是指导变元, 辖 域为(G(x,y)H(x,y,z)). x3次出现都是约束出现, y第一次出 现是自由出现, 后2次是约束出现, z2次出现都是自由出现
19
第19页
实例
例7 判断以下公式中,哪些是永真式,哪些是矛盾式? (1) xF(x)(xyG(x,y)xF(x))
重言式 p(qp) 代换实例,故为永真式. (2) (xF(x)yG(y))yG(y)
矛盾式 (pq)q 代换实例,故为永假式. (3) x(F(x)G(x))
解释I1: 个体域N, F(x):x>5, G(x): x>4, 公式为真 解释I2: 个体域N, F(x):x<5, G(x):x<4, 公式为假 结论: 非永真式可满足式
2
第2页
谓词
谓词——表示个体词性质或相互之间关系词 谓词常项 如, F(a):a是人 谓词变项 如, F(x):x含有性质F n(n1)元谓词 一元谓词(n=1)——表示性质 多元谓词(n2)——表示事物之间关系 如, L(x,y):x与 y 相关系 L,L(x,y):xy,… 0元谓词——不含个体变项谓词, 即命题常项 或命题变项
(d) 对每一个n元谓词符号FL, 有一个DI上n元谓词常项 ,F 称 F 为F在I中解释. 设公式A, 取个体域DI , 把A中个体常项符号a、函数符
号f、谓词符号F分别替换成它们在I中解释 、a 、f ,F称
所得到公式A为A在I下解释, 或A在I下被解释成A.
比如,x(F(x,y)G(x,z)), x为指导变元,(F(x,y)G(x,z))为 x 辖域,x两次出现均为约束出现,y与 z 均为自由出现
又如, x(F(x,y,z)y(G(x,y)H(x,y,z))), x中x是指导变元, 辖域为(F(x,y,z)y(G(x,y)H(x,y,z))). y中y是指导变元, 辖 域为(G(x,y)H(x,y,z)). x3次出现都是约束出现, y第一次出 现是自由出现, 后2次是约束出现, z2次出现都是自由出现
19
第19页
实例
例7 判断以下公式中,哪些是永真式,哪些是矛盾式? (1) xF(x)(xyG(x,y)xF(x))
重言式 p(qp) 代换实例,故为永真式. (2) (xF(x)yG(y))yG(y)
矛盾式 (pq)q 代换实例,故为永假式. (3) x(F(x)G(x))
解释I1: 个体域N, F(x):x>5, G(x): x>4, 公式为真 解释I2: 个体域N, F(x):x<5, G(x):x<4, 公式为假 结论: 非永真式可满足式
2
第2页
谓词
谓词——表示个体词性质或相互之间关系词 谓词常项 如, F(a):a是人 谓词变项 如, F(x):x含有性质F n(n1)元谓词 一元谓词(n=1)——表示性质 多元谓词(n2)——表示事物之间关系 如, L(x,y):x与 y 相关系 L,L(x,y):xy,… 0元谓词——不含个体变项谓词, 即命题常项 或命题变项
离散数学-03-一阶逻辑

20
3.1.4 一阶逻辑公式与分类
解释和赋值的直观涵义
例 公式x(F(x)G(x)) 指定1 个体域:全总个体域, F(x): x是人, G(x): x是黄种人 真/假命题? 假命题 指定2 个体域:实数集, F(x): x>10, G(x): x>0 真/假命题? 真命题
21
3.1.4 一阶逻辑公式与分类
离散数学(第3版) 屈婉玲 耿素云 张立昂 编著 清华大学出版社出版
第3章 一阶逻辑
上海大学 谢江
1
第3章 一阶逻辑
• 3.1 一阶逻辑基本概念 • 3.2 一阶逻辑等值演算
2
3.1 一阶逻辑基本概念
• 3.1.1 命题逻辑的局限性 • 3.1.2 个体词、谓词与量词
– 个体常项、个体变项、个体域、全总个体域 – 谓词常项、谓词变项 – 全称量词、存在量词
n元谓词P(x1, x2,…, xn): 含n个个体变项的谓词, 是定义在 个体域上, 值域为{0,1}的n元函数 一元谓词: 表示事物的性质 多元谓词(n2): 表示事物之间的关系 0元谓词: 不含个体变项的谓词,即命题常项或命题变项 0元谓词是命题? 命题均可表示成0元谓词?
8
3.1.2 个体词、谓词与量词
• 3.1.3 一阶逻辑命题符号化
3
3.1 一阶逻辑基本概念(续)
• 3.1.4 一阶逻辑公式与分类
– 一阶语言L (字母表、项、原子公式、合式 公式) – 辖域和指导变元、约束出现和自由出现 – 闭式 – 一阶语言L 的解释 – 永真式、矛盾式、可满足式 – 代换实例
4
3.1.1 命题逻辑的局限性
11
3.1.3 一阶逻辑命题符号化
一阶逻辑命题符号化
3.1.4 一阶逻辑公式与分类
解释和赋值的直观涵义
例 公式x(F(x)G(x)) 指定1 个体域:全总个体域, F(x): x是人, G(x): x是黄种人 真/假命题? 假命题 指定2 个体域:实数集, F(x): x>10, G(x): x>0 真/假命题? 真命题
21
3.1.4 一阶逻辑公式与分类
离散数学(第3版) 屈婉玲 耿素云 张立昂 编著 清华大学出版社出版
第3章 一阶逻辑
上海大学 谢江
1
第3章 一阶逻辑
• 3.1 一阶逻辑基本概念 • 3.2 一阶逻辑等值演算
2
3.1 一阶逻辑基本概念
• 3.1.1 命题逻辑的局限性 • 3.1.2 个体词、谓词与量词
– 个体常项、个体变项、个体域、全总个体域 – 谓词常项、谓词变项 – 全称量词、存在量词
n元谓词P(x1, x2,…, xn): 含n个个体变项的谓词, 是定义在 个体域上, 值域为{0,1}的n元函数 一元谓词: 表示事物的性质 多元谓词(n2): 表示事物之间的关系 0元谓词: 不含个体变项的谓词,即命题常项或命题变项 0元谓词是命题? 命题均可表示成0元谓词?
8
3.1.2 个体词、谓词与量词
• 3.1.3 一阶逻辑命题符号化
3
3.1 一阶逻辑基本概念(续)
• 3.1.4 一阶逻辑公式与分类
– 一阶语言L (字母表、项、原子公式、合式 公式) – 辖域和指导变元、约束出现和自由出现 – 闭式 – 一阶语言L 的解释 – 永真式、矛盾式、可满足式 – 代换实例
4
3.1.1 命题逻辑的局限性
11
3.1.3 一阶逻辑命题符号化
一阶逻辑命题符号化
离散数学 第四章 一阶逻辑基本概念

18
§4.1 一阶逻辑命题符号化
(3)没有人登上过木星。 令H(x):x登上过木星, M(x):x是人。命题符号化为 ┐x(M(x)∧H(x))。 命题真值为真。 (4)在美国留学的学生未必都是亚洲人。 令F(x):x是在美国留学的学生,G(x):x是亚洲人。符号化 ┐x(F(x)→G(x)) 命题真值为真。
个体词、谓词和量词,以期达到表达出个体与总体的内在 联系和数量关系。
4
§4.1 一阶逻辑命题符号化
一阶逻辑命题符号化的三个基本要素
个体词
谓词
量词
5
个体词及相关概念
个体词:指所研究对象中可以独立存在的具体的 或抽象的客体。
举例
命题:电子计算机是科学技术的工具。 个体词:电子计算机。 命题:他是三好学生。 个体词:他。
个体域为全总个体域
令 M(x):x是人 , F(x):x呼吸 , G(x):x用左手写字
能否将”凡人都呼吸”符号化为 (∀x) (M(x)∧F(x) ) ? 不可以。 (∀x) (M(x)∧F(x) )表示宇宙中的万物都是人并 且会呼吸 能否将”有的人用左手写字”符号化为 (x)( M(x)→G(x) ) ? 不可以。(x)( M(x)→G(x) ) 表示在宇宙万物中存在某个 个体x,”如果x是人则x会用左手写字”
6
个体词及相关概念
个体常项:表示具体或特定的客体的个体词,用小写字母 a, b, c,…表示。 个体变项:表示抽象或泛指的客体的个体词,用x, y, z,… 表示。 个体域(或称论域):指个体变项的取值范围。 可以是有穷集合,如{a, b, c}, {1, 2}。 可以是无穷集合,如N,Z,R,…。 全总个体域(universe)——宇宙间一切事物组成 。
《离散数学》一阶逻辑

关于存在量词的:
x(A(x)B)xA(x)B x(A(x)B)xA(x)B
x(A(x)B)xA(x)B
x(BA(x))BxA(x)
注意量词的变化
注意量词的变化
33
证明:设D={a1,a2,…,an}
(1)x(A(x)∨B) (A(a1)∨B) ∧(A(a2)∨B)∧… ∧(A(an)∨B) (A(a1)∧A(a2)∧…∧A(an)) ∨B xA(x)∨B
设D={a1,a2,…,an} xA(x)A(a1)A(a2)…A(an) xA(x)A(a1)A(a2)…A(an)
31
量词否定等值式
❖定理2.1 量词否定等值式
▪ xA(x) xA(x)
▪ xA(x) xA(x)
❖证明:设D={a1,a2,…,an}
▪
xA(x)
A(a(A1)(∨a1)∧AA(a(a2)2∨)∧……∨∧AA(a(na)n))
10
明确个体域
例2.(1) 凡人都要死的。( 2) 有人活百岁以上
❖ 考虑个体域D为人类集合
▪ F(x): x是要死的。 x F(x)
个体域不同,符号化不同
▪ G(x): x活百岁以上。 x G(x)
❖ 考虑个体域为全总个体域
▪ 对于所有个体而言,如果它是人,则它是要死的。引入新谓词 M(x): x是人。
(此点以后再讨论); ❖ 当个体域为有限集时,如果D={a1,a2,…an},由量词的意义可以看出,对于
任意的谓词A(x), 都有:
▪ xA(x) A(a1)∧A (a2) ∧…∧A (an); ▪ xA(x) A (a1)∨A (a2) ∨…∨A (an).
13
嵌套量词
❖多个量词同时出现时,不能随意颠倒他们的顺序。 ❖对任意的x,存在着y,使得 x+y=5.
离散数学课件 4.1一阶逻辑命题符号化

说明: x yG(x, y) 和 x yG(x, y)表示的含义不同!
第 10 页
四、符号化
例2 在一阶逻辑中将下面命题符号化。
(1)人都爱美。
(2)有人用左手写字。
个体域分别为:
(a) D为人类集合 (b) D为全总个体域
解: (a)设F(x):x爱美,G(x):x用左手写字,则
(1) xF(x) (2) xG(x)
, L(x,y): x与y跑得同样快。 (5) ﹁ x y(F(x) G(y) H(x, y)) (6) ﹁ x y(F(x) F(y) L(x, y))
第 16 页
总结和作业
➢ 小结 ◆ 理解个体词、谓词、量词的含义 ◆ 掌握一阶逻辑命题的符号化
➢ 作业(做书上)
课本63-64页 4(1) (3), 5(1) (3),6 (1) (3) (5)
第1 页
第四章 一阶逻辑基本概念
➢ 命题逻辑的局限性
在命题逻辑中,研究的基本单位是简单命题,对简单 命题不再进行分解,并且不考虑命题之间的内在联系和数 量关系。
➢ 一阶逻辑所研究的内容
为了克服命题逻辑的局限性,将简单命题再细分,分 析出个体词、谓词和量词,以期达到表达出个体与总体的 内在联系和数量关系。 ◆ §4.1一阶逻辑命题符号化 ◆ §4.2一阶逻辑公式及解释 ◆ §5.1一阶逻辑等值式与置换规则 ◆ §5.2一阶逻辑前束范式
第四章 一阶逻辑基本概念
➢ 苏格拉底三段论
◆ 所有的人都是要死的。 ◆ 苏格拉底是人。 ◆ 所以,苏格拉底是要死的。 试证明此推理。 解:令p:所有的人都是要死的,q:苏格拉底是人,r:苏格拉底 是要死的,则 前提:p,q 结论:r 推理的形式结构: p Ù q ® r
第 10 页
四、符号化
例2 在一阶逻辑中将下面命题符号化。
(1)人都爱美。
(2)有人用左手写字。
个体域分别为:
(a) D为人类集合 (b) D为全总个体域
解: (a)设F(x):x爱美,G(x):x用左手写字,则
(1) xF(x) (2) xG(x)
, L(x,y): x与y跑得同样快。 (5) ﹁ x y(F(x) G(y) H(x, y)) (6) ﹁ x y(F(x) F(y) L(x, y))
第 16 页
总结和作业
➢ 小结 ◆ 理解个体词、谓词、量词的含义 ◆ 掌握一阶逻辑命题的符号化
➢ 作业(做书上)
课本63-64页 4(1) (3), 5(1) (3),6 (1) (3) (5)
第1 页
第四章 一阶逻辑基本概念
➢ 命题逻辑的局限性
在命题逻辑中,研究的基本单位是简单命题,对简单 命题不再进行分解,并且不考虑命题之间的内在联系和数 量关系。
➢ 一阶逻辑所研究的内容
为了克服命题逻辑的局限性,将简单命题再细分,分 析出个体词、谓词和量词,以期达到表达出个体与总体的 内在联系和数量关系。 ◆ §4.1一阶逻辑命题符号化 ◆ §4.2一阶逻辑公式及解释 ◆ §5.1一阶逻辑等值式与置换规则 ◆ §5.2一阶逻辑前束范式
第四章 一阶逻辑基本概念
➢ 苏格拉底三段论
◆ 所有的人都是要死的。 ◆ 苏格拉底是人。 ◆ 所以,苏格拉底是要死的。 试证明此推理。 解:令p:所有的人都是要死的,q:苏格拉底是人,r:苏格拉底 是要死的,则 前提:p,q 结论:r 推理的形式结构: p Ù q ® r
离散数学命题符号化课件 21页PPT文档

人,卻一毛錢也沒賺到!』算命仙摸著下巴說:「那就奇怪了,不過既然不準,錢就還給你吧 。」
當麥芽糖商人回去後,糕餅商人也怒氣衝天的跑進來。『今天我都沒賺到錢,把我的錢還 給我!』算命仙停頓了一下,問說:「那麼,是否有碰到來自東方的人呢?」糕餅商搔著頭說 :『沒有耶,只碰到來自南方的人。』「那就對啦,我是說你如果碰到從東方來的人就會賺錢 ,可沒說碰到從南方來的人會賺錢啊。」糕餅商聽這話似乎有理,就回去了。
偽值表清楚的顯示只有在 3 的情形之下才會發生。所以,用「如果 p 就 q」的方法幫人家算命,總會有四分之三機率是準確的。因此,即使 承諾「如果算不準就退錢」,算命仙仍然可能賺到錢。因為,算不準 的機準只有四分之一。小心別上當哦! • 大人常對小孩說:「如果你乖乖,我就給你糖吃。」不知道有沒 有小孩了解,即使不乖,還是可能有糖可吃這件事呢?
离散数学 第一章 命题逻辑
4
• 故事中的算命仙就是巧妙地運用了這種條件命題而賺到錢的。讓我們 來研究一下他是如何辦到的。
• 我們考慮“ P= 碰上來自東方的人,Q= 賺到錢 ”有四種情形會發 生:
1. 碰到來自東方的人,而賺到錢。 2. 碰到來自東方的人,但沒有賺到錢。 3. 沒有碰到來自東方的人,而賺到錢。 4. 沒有碰到來自東方的人,也沒賺到錢。 • 然而,算命仙算不準的情形即是「如果 p 就 q」為偽的情形。上面的真
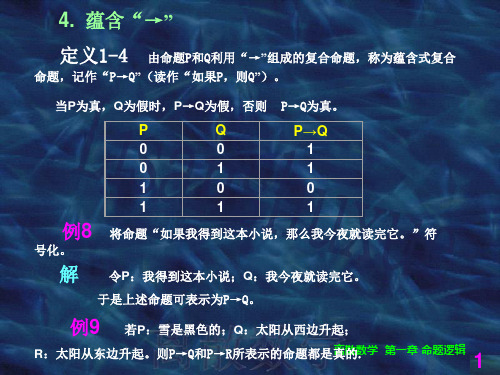
4. 蕴含“→”
定义1-4 由命题P和Q利用“→”组成的复合命题,称为蕴含式复合
命题,记作“P→Q”(读作“如果P,则Q”)。
当P为真,Q为假时,P→Q为假,否则 P→Q为真。
P
Q
P→Q
0
0
1
0
1
1
1
0
0
當麥芽糖商人回去後,糕餅商人也怒氣衝天的跑進來。『今天我都沒賺到錢,把我的錢還 給我!』算命仙停頓了一下,問說:「那麼,是否有碰到來自東方的人呢?」糕餅商搔著頭說 :『沒有耶,只碰到來自南方的人。』「那就對啦,我是說你如果碰到從東方來的人就會賺錢 ,可沒說碰到從南方來的人會賺錢啊。」糕餅商聽這話似乎有理,就回去了。
偽值表清楚的顯示只有在 3 的情形之下才會發生。所以,用「如果 p 就 q」的方法幫人家算命,總會有四分之三機率是準確的。因此,即使 承諾「如果算不準就退錢」,算命仙仍然可能賺到錢。因為,算不準 的機準只有四分之一。小心別上當哦! • 大人常對小孩說:「如果你乖乖,我就給你糖吃。」不知道有沒 有小孩了解,即使不乖,還是可能有糖可吃這件事呢?
离散数学 第一章 命题逻辑
4
• 故事中的算命仙就是巧妙地運用了這種條件命題而賺到錢的。讓我們 來研究一下他是如何辦到的。
• 我們考慮“ P= 碰上來自東方的人,Q= 賺到錢 ”有四種情形會發 生:
1. 碰到來自東方的人,而賺到錢。 2. 碰到來自東方的人,但沒有賺到錢。 3. 沒有碰到來自東方的人,而賺到錢。 4. 沒有碰到來自東方的人,也沒賺到錢。 • 然而,算命仙算不準的情形即是「如果 p 就 q」為偽的情形。上面的真
4. 蕴含“→”
定义1-4 由命题P和Q利用“→”组成的复合命题,称为蕴含式复合
命题,记作“P→Q”(读作“如果P,则Q”)。
当P为真,Q为假时,P→Q为假,否则 P→Q为真。
P
Q
P→Q
0
0
1
0
1
1
1
0
0
离散数学命题符号化课件
当P和Q的真值相同时,P↔Q取真,否则取假。
例10
P
Q
P Q
0
0
1
0
1
0
1
0
0
1
1
1
非本仓库工作人员,一律不得入内。
解
令P:某人是仓库工作人员;
Q:某人可以进入仓库。
则上述命题可表示为P↔Q。
离散数学 第一章 命题逻辑
8
例11 黄山比喜马拉雅山高,当且仅当3是素数
令P:黄山比喜马拉雅山高;Q:3是素数 本例可符号化为PQ
离散数学 第一章 命题逻辑
6
例. P: 月亮下山 Q: 3+3=6
则P→Q: 若月亮下山,则3+3=6 (并没有实质蕴含关系,仍承认)
Q→P: 叫做P→Q的逆命题 ┐P→┐Q : 叫做P→Q的反命题 ┐Q→┐P: 叫做P→Q的逆反命题
离散数学 第一章 命题逻辑
7
5.等值“↔”
定义1-5 由命题P和Q,利用“↔”组成的复合命题,称为等值式 复合命题,记作“P↔Q” (读作“P当且仅当Q”)。
21
2
條件否定¬(P→Q)的真值表:
P
Q
0
0
0
1
1
0
1
1
于是得到:¬(P→Q) 与 P∧¬Q 等价。
P∧¬Q 0 0 1 0
換個角度來看,既然下雨地就會溼;那麼如果地是乾的,就一定是沒有下雨。 下面的真偽值表可以反應這個關係:
P
Q
¬Q → ¬P
0
0
1
0
1
1
1
0
0
1
1
1
「非 Q則非P」為「若 P 則 Q」之逆否命題(contrapositive),和「若 P 則 Q 」 為等價之命題。我們稱 Q 為 P之必要條件。
4.1-一阶逻辑命题符号化newPPT课件

(1)所有的人都呼吸。 所有的个体都呼吸。 (2)有的人用左手写字。有的个体用左手写字。
所以个体域是全总个体域时,命题应转述为: (1)对于任意的个体,如果它是人,则它是要呼吸的。
(2)存在着个体,它是人并且用左手写字。
需要引进一种新的谓词(特性谓词)将人与其它事 物区分开来 令M(x):x是人。
使用特性谓词M(x),所给命题就可以符号化为: (1)x(M(x)→F(x)) (2)x(M(x)∧ G(x))
命题可看成“存在在美国留学的学生不是亚洲 人”。
令F(x):x是在美国留学的学生;
G(x):x是亚洲人 命题符号化为:x(F(x)∧┐G(x)) 或者命题可看成“在美国留学的任意学生都是亚 洲人”的否定。 命题符号化为:┐x(F(x)→G(x))
2021
18
2021
19
例 使用多元谓词将下列命题符号化。 (1)兔子比乌龟跑得快。 (2)有的兔子比所有的乌龟跑得快。 (3)并不是所有的兔子都比乌龟跑的快。 (4)不存在跑的同样快的两只兔子。
解:本题未给出个体域,因而以全总个体域为个体域 令M(x):x为人
(1)令F(x):x长着黑头发
可将命题转述为:对所有个体而言,如果它是人, 那么它就长着黑头发。
命题符号化为:x(M(x)→F(x))
2021
16
(2)有的人登上过月球。 令G(x):x登上过月球 可将命题转述为:存在着个体,它是人并且登上过
不带个体变项的谓词称为0元谓词。 例如:F(a),G(a,b),P(a1,a2,…,an) 都是0元谓词。
2021
8
例 将下面命题用0元谓词符号化。 (1)只有2是素数,4才是素数 (2)如果5大于4,则4大于6
命题的谓词符号化步骤: (a)找出谓词、个体词常项 (b)符号化谓词和个体词常项 (c)使用符号化了的谓词和个体词以及逻辑运算符
所以个体域是全总个体域时,命题应转述为: (1)对于任意的个体,如果它是人,则它是要呼吸的。
(2)存在着个体,它是人并且用左手写字。
需要引进一种新的谓词(特性谓词)将人与其它事 物区分开来 令M(x):x是人。
使用特性谓词M(x),所给命题就可以符号化为: (1)x(M(x)→F(x)) (2)x(M(x)∧ G(x))
命题可看成“存在在美国留学的学生不是亚洲 人”。
令F(x):x是在美国留学的学生;
G(x):x是亚洲人 命题符号化为:x(F(x)∧┐G(x)) 或者命题可看成“在美国留学的任意学生都是亚 洲人”的否定。 命题符号化为:┐x(F(x)→G(x))
2021
18
2021
19
例 使用多元谓词将下列命题符号化。 (1)兔子比乌龟跑得快。 (2)有的兔子比所有的乌龟跑得快。 (3)并不是所有的兔子都比乌龟跑的快。 (4)不存在跑的同样快的两只兔子。
解:本题未给出个体域,因而以全总个体域为个体域 令M(x):x为人
(1)令F(x):x长着黑头发
可将命题转述为:对所有个体而言,如果它是人, 那么它就长着黑头发。
命题符号化为:x(M(x)→F(x))
2021
16
(2)有的人登上过月球。 令G(x):x登上过月球 可将命题转述为:存在着个体,它是人并且登上过
不带个体变项的谓词称为0元谓词。 例如:F(a),G(a,b),P(a1,a2,…,an) 都是0元谓词。
2021
8
例 将下面命题用0元谓词符号化。 (1)只有2是素数,4才是素数 (2)如果5大于4,则4大于6
命题的谓词符号化步骤: (a)找出谓词、个体词常项 (b)符号化谓词和个体词常项 (c)使用符号化了的谓词和个体词以及逻辑运算符
