高中数学——2020新高考数学真题全刷——基础2000题——01第一章 函数
2020年高考全国2卷理科数学带答案解析

2020年普通高等学校招生全国统一考试理科数学本试卷共23题,共150分,共4页。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生先将自己的姓名、准考证号码填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.12i 12i +=-A.43i 55-- B.43i 55-+ C.34i 55-- D.34i 55-+2.已知集合22{(,)|3,,A x y x y x y =+≤∈∈Z Z},则A 中元素的个数为A.9 B.8 C.5 D.43.函数2e e ()x xf x x --=的图象大致为4.已知向量a ,b 满足||1=a ,1⋅=-a b ,则(2)⋅-=a a b A.4B.3C.2D.05.双曲线22221(0,0)x y a b a b -=>>的离心率为3,则其渐近线方程为A.2y x =±B.3y x =±C.22y x =± D.32y x =± 6.在ABC △中,5cos 25C =,1BC =,5AC =,则AB =A.42 B.30 C.29 D.257.为计算11111123499100S =-+-++-,设计了右侧的程序框图,则在空白框中应填入A.1i i =+B.2i i =+ C.3i i =+D.4i i =+8.我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30723=+.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是A.112 B.114 C.115 D.1189.在长方体1111ABCD A B C D -中,1AB BC ==,13AA =,则异面直线1AD 与1DB 所成角的余弦值为A.15B.56 C.55D.2210.若()cos sin f x x x =-在[,]a a -是减函数,则a 的最大值是A.π4 B.π2 C.3π4D.π11.已知()f x 是定义域为(,)-∞+∞的奇函数,满足(1)(1)f x f x -=+.若(1)2f =,则(1)(2)(3)(50)f f f f ++++= A.50- B.0 C.2 D.5012.已知1F ,2F 是椭圆22221(0)x y C a b a b +=>>:的左,右焦点,A 是C 的左顶点,点P 在过A 且斜率为36的直线上,12PF F △为等腰三角形,12120F F P ∠=︒,则C 的离心率为A.23 B.12 C.13D.14二、填空题:本题共4小题,每小题5分,共20分。
压轴题01 函数性质的综合运用(原卷版)-2023年高考数学压轴题专项训练(江苏专用)

压轴题01函数性质的综合运用函数是高中数学的主干,也是高考考查的重点,而函数的性质是函数的灵魂,它对函数概念的理解以及利用函数性质来解决相关函数问题起到十分重要的作用.此外在高考试题的考查中函数的性质也是常见题型.考向一:利用奇偶性、单调性解函数不等式考向二:奇函数+M 模型与奇函数+函数模型考向三:周期运用的综合运用1.单调性技巧(1)证明函数单调性的步骤①取值:设1x ,2x 是()f x 定义域内一个区间上的任意两个量,且12x x ;②变形:作差变形(变形方法:因式分解、配方、有理化等)或作商变形;③定号:判断差的正负或商与1的大小关系;④得出结论.(2)函数单调性的判断方法①定义法:根据增函数、减函数的定义,按照“取值—变形—判断符号—下结论”进行判断.②图象法:就是画出函数的图象,根据图象的上升或下降趋势,判断函数的单调性.③直接法:就是对我们所熟悉的函数,如一次函数、二次函数、反比例函数等,直接写出它们的单调区间.(3)记住几条常用的结论:①若()f x是增函数,则()f x-为减函数;若()f x是减函数,则()f x-为增函数;②若()f x和()g x均为增(或减)函数,则在()f x和()g x的公共定义域上()()f xg x+为增(或减)函数;③若()0f x>且()f x为增函数,1()f x为减函数;④若()0f x>且()f x为减函数,1()f x为增函数.2.奇偶性技巧(1)函数具有奇偶性的必要条件是其定义域关于原点对称.(2)奇偶函数的图象特征.函数()f x是偶函数⇔函数()f x的图象关于y轴对称;函数()f x是奇函数⇔函数()f x的图象关于原点中心对称.(3)若奇函数()y f x=在0x=处有意义,则有(0)0f=;偶函数()y f x=必满足()(||)f x f x=.(4)偶函数在其定义域内关于原点对称的两个区间上单调性相反;奇函数在其定义域内关于原点对称的两个区间上单调性相同.(5)若函数()f x的定义域关于原点对称,则函数()f x能表示成一个偶函数与一个奇函数的和的形式.记1()[()()]2g x f x f x=+-,1()()()]2h x f x f x=--,则()()()f xg xh x=+.(6)运算函数的奇偶性规律:运算函数是指两个(或多个)函数式通过加、减、乘、除四则运算所得的函数,如()(),()(),()(),()()f xg x f x g x f x g x f x g x+-⨯÷.对于运算函数有如下结论:奇±奇=奇;偶±偶=偶;奇±偶=非奇非偶;奇()⨯÷奇=偶;奇()⨯÷偶=奇;偶()⨯÷偶=偶.(7)复合函数[()]y f g x=的奇偶性原来:内偶则偶,两奇为奇.(8)常见奇偶性函数模型奇函数:①函数1()()01x x a f x m x a +=≠-()或函数1()()1x x a f x m a -=+.②函数()()x x f x a a -=±-.③函数2()log log (1)aa x m m f x x m x m +==+--或函数2()log log (1)a a x m m f x x m x m-==-++④函数()log )a f x x =或函数()log )a f x x =.注意:关于①式,可以写成函数2()(0)1xm f x m x a =+≠-或函数2()()1x mf x m m R a =-∈+.偶函数:①函数()()x x f x a a -=±+.②函数()log (1)2mx a mxf x a =+-.③函数(||)f x 类型的一切函数.④常数函数3.周期性技巧()()()()211();()2()()()()2()()4()()2()()()()()2()()()2()()()(x R f x T f x T f x T f x T f x T f x T T f x f x f x T f x T T f x T f x T T f a x f a x b a f b x f b x f a x f a x a f x f a x f a x b a f b x f b x f a ∈+=+=-+=+=-+=-+=--+=-⎧-⎨+=-⎩+=-⎧⎨⎩+=--⎧-⎨+=--⎩函数式满足关系()周期为偶函数)()2()()()4()()()()()4()()()4()x f a x a f x f a x f a x b a f b x f b x f a x f a x a f x f a x f a x af x +=--⎧⎨⎩+=-⎧-⎨+=--⎩+=-⎧⎨⎩+=--⎧⎨⎩为奇函数为奇函数为偶函数4.函数的的对称性与周期性的关系(1)若函数()y f x =有两条对称轴x a =,()x b a b =<,则函数()f x 是周期函数,且2()T b a =-;(2)若函数()y f x =的图象有两个对称中心(,),(,)()a c b c a b <,则函数()y f x =是周期函数,且2()T b a =-;(3)若函数()y f x =有一条对称轴x a =和一个对称中心(,0)()b a b <,则函数()y f x =是周期函数,且4()T b a =-.5.对称性技巧(1)若函数()y f x =关于直线x a =对称,则()()f a x f a x +=-.(2)若函数()y f x =关于点()a b ,对称,则()()2f a x f a x b ++-=.(3)函数()y f a x =+与()y f a x =-关于y 轴对称,函数()y f a x =+与()y f a x =--关于原点对称.1.(2023·河北唐山·开滦第二中学校考一模)已知函数()222e e 287x x f x x x --=++-+则不等式()()232f x f x +>+的解集为()A.1(1)3--,B.1(,1)(,)3-∞--+∞ C.1(1)3-,D.1(,(1,)3-∞-⋃+∞2.(2023·安徽宣城·统考二模)已知函数()f x 及其导函数()f x '的定义域均为R ,记()()g x f x '=.若()3f x +为奇函数,322g x ⎛⎫+ ⎪⎝⎭为偶函数,且()03g =-,()12g =,则()20231i g i ==∑()A.670B.672C.674D.6763.(2023·甘肃定西·统考一模)定义在R 上的函数()f x 满足()()()f x y f x f y +=+,当0x >时,()0f x <,则不等式()()22530f x f x x -+-<的解集为()A.5,3⎛⎫-∞ ⎪⎝⎭B.51,2⎛⎫- ⎪⎝⎭C.()5,1,2⎛⎫-∞-⋃+∞ ⎪⎝⎭D.5,3⎛⎫+∞ ⎪⎝⎭4.(2023·吉林通化·梅河口市第五中学校考一模)已知函数()()lg 122x xf x x -=-++,则不等式()()12f x f x +<的解集为()A.()(),11,-∞-⋃+∞B.()2,1--C.()(),21,-∞-+∞ D.()()1,1,3-∞-⋃+∞5.(2023·内蒙古·模拟预测)已知()f x 是定义在[]4,4-上的增函数,且()f x 的图象关于点()0,1对称,则关于x 的不等式()()23350f x f x x +-+->的解集为()A.(),1-∞B.()1,+∞C.(]1,7D.(]1,26.(2023·广西梧州·统考一模)已知定义在R 上的函数()f x 在(,1]-∞上单调递增,若函数(1)f x +为偶函数,且(3)0f =,则不等式()0xf x >的解集为()A.(1,3)-B.(,1)(3,)-∞-⋃+∞C.(,1)(0,3)-∞-⋃D.(1,0)(3,)-+∞ 7.(2023·河南·开封高中校考模拟预测)已知()f x 是定义域为R 的奇函数,当0x >时,()()2ln 1f x x x =++,则不等式()211ln2f x +>+的解集为()A.{1}∣<x x B.{0}x x <∣C.{1}xx >∣D.{0}xx >∣8.(2023·福建泉州·校考模拟预测)已知函数()f x 是定义在R 上的偶函数,且函数()f x 在[0,)+∞上是减函数,如果()31f =-,则不等式()110f x -+≥的解集为()A.](2-∞,B.[)2,+∞C.[]24-,D.[]14,9.(2023·陕西西安·高三西北工业大学附属中学校考阶段练习)已知函数()(32e log e 1xx f x x =++在[],(0)k k k ->上的最大值与最小值分别为M 和m ,则M m +=()A.2-B.0C.2D.410.(2023·江西南昌·统考一模)已知函数()()35112=-+f x x ,若对于任意的[]2,3x ∈,不等式()()21+-≤f x f a x 恒成立,则实数a 的取值范围是()A.(),2-∞B.(],2-∞C.(),4-∞D.(],4∞-11.(2023·全国·高三专题练习)已知函数()e e 2x xf x x x -=-++在区间[]22-,上的最大值与最小值分别为,M N ,则M N +的值为()A.2-B.0C.2D.412.(2023·全国·高三专题练习)若对x ∀,R y ∈.有()()()4f x y f x f y +=+-,则函数22()()1xg x f x x =++在[2018-,2018]上的最大值和最小值的和为()A.4B.8C.6D.1213.(多选题)(2023·浙江杭州·统考二模)已知函数()f x (x ∈R )是奇函数,()()2f x f x +=-且()12f =,()f x '是()f x 的导函数,则()A.()20232f =B.()f x '的一个周期是4C.()f x '是偶函数D.()11f '=14.(多选题)(2023·安徽滁州·统考二模)已知函数()f x 及其导函数()f x '的定义域均为R ,记()()g x f x '=,若12f x ⎛⎫- ⎪⎝⎭,()1g x +均为奇函数,则()A.()00f =B.()00g =C.()()14f f -=D.()()14g g -=15.(多选题)(2023·吉林·统考三模)设定义在R 上的可导函数()f x 与()g x 导函数分别为()f x '和()g x ',若()()212f x g x x =-+,()1f x +与()g x 均为偶函数,则()A.()11g '=B.()20220323g =-'C.()24f '=-D.991198100i f i =⎛⎫= ⎪⎝'⎭∑16.(多选题)(2023·海南海口·校考模拟预测)已知定义在R 上的函数()f x 在(],2-∞上单调递增,且()2f x +为偶函数,则()A.()f x 的对称中心为()2,0B.()f x 的对称轴为直线2x =C.()()14f f -<D.不等式()()34f x f x +>的解集为()1,1,5⎛⎫-∞+∞ ⎪⎝⎭ 17.(多选题)(2023·广东佛山·佛山一中校考一模)设函数()y f x =的定义域为R ,且满足(1)(1)f x f x +=-,(2)()0f x f x -+-=,当[]1,1x ∈-时,()1f x x =-+,则下列说法正确的是()A.()1y f x =+是偶函数B.()3y f x =+为奇函数C.函数()lg =-y f x x 有8个不同的零点D.()202311k f k ==∑18.(2023·江西吉安·统考一模)已知函数()f x 的定义域为R ,其导函数为()g x ,若函数(22)f x +为偶函数,函数(1)g x -为偶函数,则下列说法正确的序号有___________.①函数()f x 关于2x =轴对称;②函数()f x 关于(1,0)-中心对称;③若(2)1,(5)1f f -==-,则(26)(16)=3g f +-;④若当12x -≤≤时,1()e 1x f x +=-,则当1417x ≤≤时,17()e 1x f x -=-.19.(2023·陕西榆林·统考一模)已知函数()f x 是定义在()2,2-上的增函数,且()f x 的图象关于点()0,2-对称,则关于x 的不等式()()240f x f x +++>的解集为__________.20.(2023·全国·校联考模拟预测)已知定义在R 上的函数()f x 满足:对任意实数a ,b 都有()()()1a a b b f f f +=+-,且当0x >时,()1f x >.若()23f =,则不等式()212f x x --<的解集为______.21.(2023·江西赣州·高三统考阶段练习)已知()f x 是定义在[]4,4-上的增函数,且()f x 的图象关于点()0,1对称,则关于x 的不等式()()23350f x f x x +-+->的解集为______.22.(2023·湖南湘潭·高三湘钢一中校考开学考试)已知()f x 是定义在()5,5-上的增函数,且()f x 的图象关于点()0,1-对称,则关于x 的不等式()()211320f x f x x ++-++>的解集为_________.23.(2023·江苏常州·高三校联考开学考试)已知函数()2e e e ex xx x f x x ---=++,则不等式()()21122f x f x x ++-<+的解集为__________.24.(2023·辽宁·鞍山一中校联考模拟预测)已知函数()f x ,()g x 的定义域均为R ,()1f x +是奇函数,且()()12f x g x -+=,()()32f x g x +-=,则下列结论正确的是______.(只填序号)①()f x 为偶函数;②()g x 为奇函数;③()20140k f k ==∑;④()20140k g k ==∑.25.(2023·陕西西安·西北工业大学附属中学校考模拟预测)已知函数()(32e log e 1xxf x x =++在[](),0k k k ->上的最大值与最小值分别为M 和m ,则函数()()()31g x M m x M m x -=+++-⎡⎤⎣⎦的图象的对称中心是___________.26.(2023·全国·高三专题练习)设函数()())221ln1x xf x x ++=+的最大值为M ,最小值为N ,则M N +的值为________。
2020年高考总复习理科数学题库第一章《集合》RB

2020年高考总复习 理科数学题库第一章 集合学校:__________题号 一 二 三 总分 得分第I 卷(选择题)请点击修改第I 卷的文字说明 评卷人 得分一、选择题1. i 是虚数单位,若集合{}1,0,1S =-,则( ). A .i S ∈ B .2i S ∈ C . 3i S ∈ D .2iS ∈(2011福建理)2.若集合{||21|3}A x x =-<,21{|0}3x B x x +=<-,则A B I 是A .{x |-1<x <12-或2<x <3}B .{x |2<x <3}C .{x |12-<x <2}D .{x |-1<x <12-}(2009安徽理)[解析]集合1{|12},{|3}2A x x B x x x =-<<=<->或,∴1{|1}2A B x x =-<<-I 选3.已知集合{1,1}M =-,11{|24,}2x N x x Z +=<<∈则M N =I ( )BA . {1,1}- B . {1}- C . {0} D . {1,0}-(2007年高考山东理科2).4.设A 、B 、I 均为非空集合,且满足A ⊆B ⊆I ,则下列各式中错误..的是( ) A.(I A )∪B =IB.(I A )∪(I B )=IC.A ∩(I B )=∅D.(I A )∩(I B )=I B (2004全国1理6)解析一:∵A 、B 、I 满足A ⊆B ⊆I ,先画出文氏图,根据文氏图可判断出A 、C 、D 都是正确的.B AI解析二:设非空集合A 、B 、I 分别为A ={1},B ={1,2},I ={1,2,3}且满足A ⊆B ⊆I .根据设出的三个特殊的集合A 、B 、I 可判断出A 、C 、D 都是正确的.5.已知集合A ={1,2,3,4},那么A 的真子集的个数是( ) A .15 B .16C .3D .4(2000广东1)6.已知全集I =N *,集合A ={x |x =2n ,n ∈N *},B ={x |x =4n ,n ∈N },则( ) A .I =A ∪BB .I =(IC A )∪BC .I =A ∪(I C B )D .I =(I C A )∪(I C B )(1996全国理,1)7.已知集合A{x| 2x -3x +2=0,x ∈R } , B={x|0<x <5,x ∈N },则满足条件A ⊆C ⊆B 的集合C 的个数为 A 1 B 2 C 3 D 48.设集合{}08U x x =∈<N ≤,{}1245S =,,,,{}357T =,,,则()U S T =I ð( ) A .{}124,, B .{}123457,,,,, C .{}12, D .{}124568,,,,,(2008天津文) 1.9.设集合A={3123|≤-≤-x x },集合B 为函数)1lg(-=x y 的定义域,则A ⋂B= (A )(1,2) (B )[1,2] (C )[ 1,2) (D )(1,2 ]10.定义集合运算:{},,.A B z z xy x A y B *==∈∈设{}1,2A =,{}0,2B =,则集合A B *的所有元素之和为( )A .0B .2C .3D .6(2008江西理) 2.(文科2)11.已知U =R ,{}|0A x x =>,{}|1B x x =-≤,则()()U UA B B A I U I痧=( )(A )∅ (B ){}|0x x ≤(C ){}|1x x >- (D ){}|01x x x >≤-或(2008浙江理) (2)12.设全集U=N M Y ={1,2,3,4,5},M U N I ð={2,4},则N=( )(A ).{1,2,3} (B ).{1,3,5} (C ).{1,4,5} (D ).{2,3,4}(2011湖南文1)【精讲精析】选 B.Θ M U N I ð={2,4},∴N 中一定没元素2和 4.假设N ∉1,则U 1N,1M 1M N ∈∉∴∉⋃,ð,与已知条件矛盾,所以1是N 中的元素,同理,3和5也是N 中的元素.13.若集合{}1213A x x =-≤+≤,20,x B xx-⎧⎫=≤⎨⎬⎩⎭则A B ⋂=( ) A.{}10x x -≤< B.{}01x x <≤ C. {}02x x ≤≤ D. {}01x x ≤≤(2011江西理2)【精讲精析】选B.由题意得A={}{}x 12x 13x 1x 1,-≤+≤=-≤≤{}x 2B x 0x 0x 2x ⎧-⎫=≤=<≤⎨⎬⎩⎭{}{}{}A B x 1x 1x 0x 2x 0x 1.==⋂-≤≤⋂<≤<≤所以14.第二十九届夏季奥林匹克运动会将于2008年8月8日在北京举行,若集合A ={参加北京奥运会比赛的运动员},集合B ={参加北京奥运会比赛的男运动员}。
2024年高考数学高频考点(新高考通用)柯西不等式(精讲+精练)解析版

【一轮复习讲义】2024年高考数学高频考点题型归纳与方法总结(新高考通用)
素养拓展01柯西不等式(精讲+精练)
1.二维形式的柯西不等式
.),,,,,()())((22222等号成立时当且仅当bc ad R d c b a bd ac d c b a =∈+≥++2.二维形式的柯西不等式的变式
bd ac d c b a +≥+⋅+2222)1( .),,,,,(等号成立时当且仅当bc ad R d c b a =∈bd ac d c b a +≥+⋅+2222)2(
.),,,,,(等号成立时当且仅当bc ad R d c b a =∈.)
,0,,,(())()(3(2等号成立,时当且仅当bc ad d c b a bd ac d c b a =≥+≥++3.
二维形式的柯西不等式的向量形式
.),,,(等号成立时使或存在实数是零向量当且仅当βαβk k =≤注:有条件要用;没有条件,创造条件也要用。
比如,对2
2
2
c b a ++,并不是不等式的形状,但变成
()()
2222221113
1
c b a ++∙++∙就可以用柯西不等式了。
4.扩展:()()233221122322212
2322
21)(n n n n b a b a b a b a b b b b a a a a ++++≥++++++++ ,当且仅当n n b a b a b a :::2211=== 时,等号成立.
【题型训练1-刷真题】
二、题型精讲精练
一、知识点梳理。
天津市2020〖人教版〗高考复习试卷习题资料春季高考数学试卷

天津市2020年〖人教版〗高考复习试卷习题资料春季高考数学试卷创作人:百里公地创作日期:202X.04.01审核人:北堂址重创作单位:博恒中英学校一、填空题(本大题满分36分)本大题共有12题,要求直接填写结果,每题填对得3分,否则一律得0分.1.(3分)函数y=log2(x+2)的定义域是.2.(3分)方程2x=8的解是.3.(3分)抛物线y2=8x的准线方程是.4.(3分)函数y=2sinx的最小正周期是.5.(3分)已知向量,.若,则实数k=.6.(3分)函数y=4sinx+3cosx的最大值是.7.(3分)复数2+3i(i是虚数单位)的模是.8.(3分)在△ABC中,角A,B,C所对边长分别为a,b,c,若a=5,c=8,B=60°,则b=.9.(3分)正方体ABCD﹣A1B1C1D1中,异面直线A1B与B1C所成角的大小为.10.(3分)从4名男同学和6名女同学中随机选取3人参加某社团活动,选出的3人中男女同学都有的概率为(结果用数值表示).11.(3分)若等差数列的前6项和为23,前9项和为57,则数列的前n项和S n=.12.(3分)36的所有正约数之和可按如下方法得到:因为36=22×32,所以36的所有正约数之和为(1+3+32)+(2+2×3+2×32)+(22+22×3+22×32)=(1+2+22)(1+3+32)=91,参照上述方法,可求得2000的所有正约数之和为.二.选择题(本大题满分36分)本大题共有12题,每题都给出四个结论,其中有且只有一个结论是正确的.考生必须把真确结论的代码写在题后的括号内,选对得3分,否则一律得0分.13.(3分)展开式为ad﹣bc的行列式是()A.B.C.D.14.(3分)设f﹣1(x)为函数f(x)=的反函数,下列结论正确的是()A.f﹣1(2)=2 B.f﹣1(2)=4 C.f﹣1(4)=2 D.f﹣1(4)=4 15.(3分)直线2x﹣3y+1=0的一个方向向量是()A.(2,﹣3)B.(2,3)C.(﹣3,2)D.(3,2)16.(3分)函数f(x)=的大致图象是()A.B.C.D.17.(3分)如果a<b<0,那么下列不等式成立的是()A.B.ab<b2C.﹣ab<﹣a2D.18.(3分)若复数z 1,z2满足z1=,则z1,z2在复数平面上对应的点Z1,Z2()A.关于x轴对称B.关于y轴对称C.关于原点对称D.关于直线y=x对称19.(3分)(1+x)10的二项展开式中的一项是()A.45x B.90x2C.120x3D.252x420.(3分)既是偶函数又在区间(0,π)上单调递减的函数是()A.y=sinx B.y=cosx C.y=sin2x D.y=cos2x21.(3分)若两个球的表面积之比为1:4,则这两个球的体积之比为()A.1:2 B.1:4 C.1:8 D.1:1622.(3分)设全集U=R,下列集合运算结果为R的是()A.Z∪∁U N B.N∩∁U N C.∁U(∁u∅) D.∁U{0}23.(3分)已知a,b,c∈R,“b2﹣4ac<0”是“函数f(x)=ax2+bx+c的图象恒在x轴上方”的()A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件24.(3分)已知A,B为平面内两个定点,过该平面内动点m作直线AB的垂线,垂足为N.若=λ•,其中λ为常数,则动点m的轨迹不可能是()A.圆B.椭圆C.双曲线D.抛物线三、解答题(本大题满分78分)本大题共有7题,解答下列各题必须写出必要的步骤.25.(7分)如图,在正三棱柱ABC﹣A1B1C1中,AA1=6,异面直线BC1与AA1所成角的大小为,求该三棱柱的体积.26.(7分)如图,某校有一块形如直角三角形ABC的空地,其中∠B为直角,AB长40米,BC长50米,现欲在此空地上建造一间健身房,其占地形状为矩形,且B为矩形的一个顶点,求该健身房的最大占地面积.27.(8分)已知数列{a n}的前n项和为S,数列{b n}满足b,求.28.(13分)已知椭圆C的两个焦点分别为F1(﹣1,0)、F2(1,0),短轴的两个端点分别为B1,B2(1)若△F1B1B2为等边三角形,求椭圆C的方程;(2)若椭圆C的短轴长为2,过点F2的直线l与椭圆C相交于P,Q两点,且,求直线l的方程.29.(12分)已知抛物线C:y2=4x 的焦点为F.(1)点A,P满足.当点A在抛物线C上运动时,求动点P的轨迹方程;(2)在x轴上是否存在点Q,使得点Q关于直线y=2x的对称点在抛物线C上?如果存在,求所有满足条件的点Q的坐标;如果不存在,请说明理由.30.(13分)在平面直角坐标系xOy中,点A在y轴正半轴上,点P n在x轴上,其横坐标为x n,且{x n}是首项为1、公比为2的等比数列,记∠P n AP n+1=θn,n∈N*.(1)若,求点A的坐标;(2)若点A的坐标为(0,8),求θn的最大值及相应n的值.31.(18分)已知真命题:“函数y=f(x)的图象关于点P(a,b)成中心对称图形”的充要条件为“函数y=f(x+a)﹣b 是奇函数”.(1)将函数g(x)=x3﹣3x2的图象向左平移1个单位,再向上平移2个单位,求此时图象对应的函数解析式,并利用题设中的真命题求函数g(x)图象对称中心的坐标;(2)求函数h(x)=图象对称中心的坐标;(3)已知命题:“函数y=f(x)的图象关于某直线成轴对称图象”的充要条件为“存在实数a和b,使得函数y=f(x+a)﹣b 是偶函数”.判断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).参考答案与试题解析一、填空题(本大题满分36分)本大题共有12题,要求直接填写结果,每题填对得3分,否则一律得0分.1.(3分)函数y=log2(x+2)的定义域是(﹣2,+∞).【分析】要使函数有意义,只需令x+2>0即可.【解答】解:欲使函数有意义,须有x+2>0,解得x>﹣2,所以函数的定义域为(﹣2,+∞).故答案为:(﹣2,+∞).【点评】本题考查函数定义域的求法,属基础题.2.(3分)方程2x=8的解是3.【分析】由已知条件2x=8=23,可得x=3,由此可得此方程的解.【解答】解:由2x=8=23,可得x=3,即此方程的解为3,故答案为 3.【点评】本题主要考查指数方程的解法,属于基础题.3.(3分)抛物线y2=8x的准线方程是x=﹣2.【分析】根据抛物线方程的标准形式,可得抛物线以原点为顶点,开口向右,由2p=8算出=2,即可得到抛物线的准线方程.【解答】解:∵抛物线的方程为y2=8x∴抛物线以原点为顶点,开口向右.由2p=8,可得=2,可得抛物线的焦点为F(2,0),准线方程为x=﹣2故答案为:x=﹣2【点评】本题给出抛物线的标准方程,求抛物线的准线方程,着重考查了抛物线的标准方程与简单几何性质等知识,属于基础题.4.(3分)函数y=2sinx的最小正周期是2π.【分析】根据函数y=2sinωx的最小正周期是,运算可得结果.【解答】解:函数y=2sinx的最小正周期是==2π,故答案为 2π.【点评】本题主要考查三角函数的周期性及求法,属于基础题.5.(3分)已知向量,.若,则实数k=.【分析】根据向量平行的充要条件可得关于k的方程,解出即可.【解答】解:由,得1×(k﹣6)﹣9k=0,解得k=﹣,故答案为:.【点评】本题考查向量共线的充要条件,若,则⇔x1y2﹣x2y1=0.6.(3分)函数y=4sinx+3cosx的最大值是5.【分析】利用辅助角公式把所给的函数解析式化为y=5sin(x+∅),再根据正弦函数的值域,求得它的最大值.【解答】解:∵函数y=4sinx+3cosx=5(sinx+cosx)=5sin(x+∅),(其中,cos∅=,sin∅=)故函数的最大值为5,故答案为5.【点评】本题主要考查辅助角公式的应用,正弦函数的值域,属于中档题.7.(3分)复数2+3i(i是虚数单位)的模是.【分析】利用模长公式|z|=,代入计算即可得出复数2+3i(i是虚数单位)的模.【解答】解:∵复数2+3i,∴2+3i的模=.故答案为:.【点评】本题考查复数的概念及模长计算公式,是一道基础题.8.(3分)在△ABC中,角A,B,C所对边长分别为a,b,c,若a=5,c=8,B=60°,则b=7.【分析】根据余弦定理b2=a2+c2﹣2accosB,代入题中的数据得b2=25+64﹣2×5×8×cos60°=49,解之即可得到b=7.【解答】解:∵在△ABC中,a=5,c=8,B=60°,∴根据余弦定理,得b2=a2+c2﹣2accosB=25+64﹣2×5×8×cos60°=49解之得b=7(舍负)故答案为:7【点评】本题给出△ABC两条边长及其夹角大小,求第三边的长度.着重考查了利用余弦定理解三角形的知识,属于基础题.9.(3分)正方体ABCD﹣A1B1C1D1中,异面直线A1B与B1C所成角的大小为60°.【分析】连接A1D,根据正方体的几何特征及异面直线夹角的定义,我们可得∠BA1D即为异面直线A1B与B1C所成的角,连接BD后,解三角形BA1D即可得到异面直线A1B与B1C所成的角.【解答】解:连接A1D,由正方体的几何特征可得:A1D∥B1C,则∠BA1D即为异面直线A1B与B1C所成的角,连接BD,易得:BD=A1D=A1B故∠BA1D=60°故答案为:60°【点评】本题考查的知识点是异面直线及其所成的角,其中根据正方体的几何特征及异面直线夹角的定义判断出∠BA1D即为异面直线A1B与B1C所成的角,是解答本题的关键.10.(3分)从4名男同学和6名女同学中随机选取3人参加某社团活动,选出的3人中男女同学都有的概率为(结果用数值表示).【分析】先求对立事件“选出的3人中只有男同学或只有女同学”的概率,然后根据对立事件的概率和为1可得答案.【解答】解:从10人中选出的3人中只有男同学或只有女同学的概率为:=,则选出的3人中男女同学都有的概率为:1﹣=.故答案为:.【点评】本题考查古典概型及其概率计算公式,属基础题.11.(3分)若等差数列的前6项和为23,前9项和为57,则数列的前n项和S n=.【分析】设等差数列的前n项和S n=an2+bn,则由题意可得,解得a、b的值,即可求得数列的前n项和S n的解析式.【解答】解:设等差数列的前n项和S n=an2+bn,则由题意可得,解得,故数列的前n项和S n=,故答案为.【点评】本题主要考查等差数列的前n项和公式的结构特征,用待定系数法函数的解析式,属于基础题.12.(3分)36的所有正约数之和可按如下方法得到:因为36=22×32,所以36的所有正约数之和为(1+3+32)+(2+2×3+2×32)+(22+22×3+22×32)=(1+2+22)(1+3+32)=91,参照上述方法,可求得2000的所有正约数之和为4836.【分析】这是一个类比推理的问题,在类比推理中,参照上述方法,2000的所有正约数之和可按如下方法得到:因为2000=24×53,所以2000的所有正约数之和为(1+2+22+23+24)(1+5+52+53),即可得出答案.【解答】解:类比36的所有正约数之和的方法,有:2000的所有正约数之和可按如下方法得到:因为2000=24×53,所以2000的所有正约数之和为(1+2+22+23+24)(1+5+52+53)=4836.可求得2000的所有正约数之和为 4836.故答案为:4836.【点评】类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).二.选择题(本大题满分36分)本大题共有12题,每题都给出四个结论,其中有且只有一个结论是正确的.考生必须把真确结论的代码写在题后的括号内,选对得3分,否则一律得0分.13.(3分)展开式为ad﹣bc的行列式是()A.B.C.D.【分析】根据叫做二阶行列式,它的算法是:ad﹣bc,再根据所给的式子即可得出答案.【解答】解:根据叫做二阶行列式,它的算法是:ad﹣bc,由题意得,=ad﹣bc.故选:B.【点评】本题考查的是二阶行列式与逆矩阵,根据题意二阶行列式的意义得出所求代数式是解答此题的关键.14.(3分)设f﹣1(x)为函数f(x)=的反函数,下列结论正确的是()A.f﹣1(2)=2 B.f﹣1(2)=4 C.f﹣1(4)=2 D.f﹣1(4)=4【分析】本题的关键是求函数f(x)=的反函数,欲求原函数的反函数,即从原函数式f(x)=中反解出x,后再进行x,y互换,即得反函数的解析式.【解答】解:∵f﹣1(x)为函数f(x)=的反函数,∴f﹣1(x)=x2,(x≥0),∴f﹣1(2)=4,f﹣1(4)=16,故选:B.【点评】本题考查反函数的求法及不等关系,属于基础题目,要会求一些简单函数的反函数,掌握互为反函数的函数图象间的关系.15.(3分)直线2x﹣3y+1=0的一个方向向量是()A.(2,﹣3)B.(2,3)C.(﹣3,2)D.(3,2)【分析】题意可得首先求出直线的斜率为:k=,即可得到它的一个方向向量(1,k),再利用平面向量共线(平行)的坐标表示即可得出答案.【解答】解:由题意可得:直线2x﹣3y+1=0的斜率为k=,所以直线2x﹣3y+1=0的一个方向向量=(1,),或(3,2)故选:D.【点评】本题主要考查直线的方向向量,以及平面向量共线(平行)的坐标表示,是基础题.16.(3分)函数f(x)=的大致图象是()A.B.C.D.【分析】筛选法:利用幂函数的性质及函数的定义域进行筛选即可得到答案.【解答】解:因为﹣<0,所以f(x)在(0,+∞)上单调递减,排除选项B、C;又f(x)的定义域为(0,+∞),故排除选项D,故选:A.【点评】本题考查幂函数的图象及性质,属基础题,筛选法是解决选择题的常用技巧,要掌握.17.(3分)如果a<b<0,那么下列不等式成立的是()A.B.ab<b2C.﹣ab<﹣a2D.【分析】由于a<b<0,不妨令a=﹣2,b=﹣1,代入各个选项检验,只有D正确,从而得出结论.【解答】解:由于a<b<0,不妨令a=﹣2,b=﹣1,可得=﹣1,∴,故A不正确.可得ab=2,b2=1,∴ab>b2,故B不正确.可得﹣ab=﹣2,﹣a2=﹣4,∴﹣ab>﹣a2,故C不正确.故选:D.【点评】本题主要考查不等式与不等关系,利用特殊值代入法比较几个式子在限定条件下的大小关系,是一种简单有效的方法,属于基础题.18.(3分)若复数z1,z2满足z1=,则z1,z2在复数平面上对应的点Z1,Z2()A.关于x轴对称B.关于y轴对称C.关于原点对称D.关于直线y=x对称【分析】由题意可得z1,z2的实部相等,虚部互为相反数,故z1,z2在复数平面上对应的点Z1,Z2关于x轴对称.【解答】解:若复数z 1,z2满足z1=,则z1,z2的实部相等,虚部互为相反数,故z1,z2在复数平面上对应的点Z1,Z2关于x轴对称,故选:A.【点评】本题主要考查共轭复数的定义,复数与复平面内对应点间的关系,属于基础题.19.(3分)(1+x)10的二项展开式中的一项是()A.45x B.90x2C.120x3D.252x4【分析】根据(1+x)10的二项展开式的通项公式为T r=•x r,即可得出结+1论.【解答】解:(1+x)10的二项展开式的通项公式为T r=•x r,故当r=3时,+1此项为120x3,故选:C.【点评】本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式中的某一项,属于中档题.20.(3分)既是偶函数又在区间(0,π)上单调递减的函数是()A.y=sinx B.y=cosx C.y=sin2x D.y=cos2x【分析】根据函数的奇偶性排除A、C,再根据函数的单调性排除D,经检验B 中的函数满足条件,从而得出结论.【解答】解:由于函数y=sinx和 y=sin2x都是奇函数,故排除A、C.由于函数y=cosx是偶函数,周期等于2π,且在(0,π)上是减函数,故满足条件.由于函数y=cos2x是偶函数,周期等于π,在(0,)上是减函数,在(,π)上是增函数,故不满足条件.故选:B.【点评】本题主要考查余弦函数的奇偶性和单调性,属于中档题.21.(3分)若两个球的表面积之比为1:4,则这两个球的体积之比为()A.1:2 B.1:4 C.1:8 D.1:16【分析】设两个球的半径分别为r1、r2,根据球的表面积公式算出它们的表面积之比为=,解之得=,由此结合球的体积公式即可算出这两个球的体积之比.【解答】解:设两个球的半径分别为r1、r2,根据球的表面积公式,可得它们的表面积分别为S1=4,S2=4∵两个球的表面积之比为1:4,∴===,解之得=(舍负)因此,这两个球的体积之比为==()3=即两个球的体积之比为1:8故选:C.【点评】本题给出两个球的表面积之比,求它们的体积之比.着重考查了球的表面积公式和体积公式等知识,属于基础题.22.(3分)设全集U=R,下列集合运算结果为R的是()A.Z∪∁U N B.N∩∁U N C.∁U(∁u∅) D.∁U{0}【分析】根据题目中条件“全集U=R”,对各个选项一一进行集合的运算,即可得出答案.【解答】解:∵全集U=R,∴Z∪∁U N=R,N∩∁U N=∅,∁U(∁u∅)=∅,∁U{0}={x∈R|x≠0}.故选:A.【点评】本题主要考查了交、并、补集的混合运算,属于基础题.23.(3分)已知a,b,c∈R,“b2﹣4ac<0”是“函数f(x)=ax2+bx+c的图象恒在x轴上方”的()A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分又非必要条件【分析】根据充要条件的定义可知,只要看“b2﹣4ac<0”与“函数f(x)=ax2+bx+c的图象恒在x轴上方”能否相互推出即可.【解答】解:若a≠0,欲保证函数f(x)=ax2+bx+c的图象恒在x轴上方,则必须保证抛物线开口向上,且与x轴无交点;则a>0且△=b2﹣4ac<0.但是,若a=0时,如果b=0,c>0,则函数f(x)=ax2+bx+c=c的图象恒在x轴上方,不能得到△=b2﹣4ac<0;反之,“b2﹣4ac<0”并不能得到“函数f(x)=ax2+bx+c的图象恒在x轴上方”,如a<0时.从而,“b2﹣4ac<0”是“函数f(x)=ax2+bx+c的图象恒在x轴上方”的既非充分又非必要条件.故选:D.【点评】本题考查的是必要条件、充分条件与充要条件的判断,二次函数的性质,难度一般.学生要熟记二次函数的性质方能得心应手的解题.24.(3分)已知A,B为平面内两个定点,过该平面内动点m作直线AB的垂线,垂足为N.若=λ•,其中λ为常数,则动点m的轨迹不可能是()A.圆B.椭圆C.双曲线D.抛物线【分析】建立直角坐标系,设出A、B坐标,以及M坐标,通过已知条件求出M的方程,然后判断选项.【解答】解:以AB所在直线为x轴,AB中垂线为y轴,建立坐标系,设M(x,y),A(﹣a,0)、B(a,0);因为=λ•,所以y2=λ(x+a)(a﹣x),即λx2+y2=λa2,当λ=1时,轨迹是圆.当λ>0且λ≠1时,是椭圆的轨迹方程;当λ<0时,是双曲线的轨迹方程.当λ=0时,是直线的轨迹方程;综上,方程不表示抛物线的方程.故选:D.【点评】本题考查曲线轨迹方程的求法,轨迹方程与轨迹的对应关系,考查分类讨论思想、分析问题解决问题的能力以及计算能力.三、解答题(本大题满分78分)本大题共有7题,解答下列各题必须写出必要的步骤.25.(7分)如图,在正三棱柱ABC﹣A1B1C1中,AA1=6,异面直线BC1与AA1所成角的大小为,求该三棱柱的体积.【分析】因为CC1∥AA1.根据异面直线所成角的定义得∠BC1C为异面直线BC1与AA1所成的角,从而∠BC1C=.在Rt△BC1C中,求得BC,从而求出S△ABC,最后利用柱体的体积公式即可求出该三棱柱的体积.【解答】解:因为 CC1∥AA1.所以∠BC1C为异面直线BC1与AA1所成的角,即∠BC1C=.在Rt△BC1C中,BC=CC1tan∠BC1C=6×=2,==3,从而S△ABC因此该三棱柱的体积为V=S×AA1=3×6=18.△ABC【点评】本题考查三棱柱体积的计算,考查学生分析解决问题的能力,属于中档题.26.(7分)如图,某校有一块形如直角三角形ABC的空地,其中∠B为直角,AB长40米,BC长50米,现欲在此空地上建造一间健身房,其占地形状为矩形,且B为矩形的一个顶点,求该健身房的最大占地面积.【分析】设出矩形的边FP的边长,利用三角形相似求出矩形的宽,表示出矩形面积,利用二次函数的最值求解即可.【解答】解:如图,设矩形为EBFP,FP长为x米,其中0<x<40,健身房占地面积为y平方米.因为△CFP∽△CBA,以,,求得BF=50﹣,从而y=BF•FP=(50﹣)•x=﹣=﹣≤500.当且仅当x=20时,等号成立.答:该健身房的最大占地面积为500平方米.【点评】本题考查函数的实际应用,表示出函数的表达式是解题的关键,考查分析问题解决问题的能力.27.(8分)已知数列{a n}的前n项和为S,数列{b n}满足b,求.【分析】先由S n求出a n,进而得到b n,由b n的表达式可判断数列{b n}是无穷等比数列,从而可得答案.【解答】解:当n≥2时,=﹣2n+2,且a1=S1=0,所以a n=﹣2n+2.因为=,所以数列{b n}是首项为1、公比为的无穷等比数列.故==.【点评】本题考查数列的极限、等差数列的前n项和,解答本题的关键是根据S n与a n的关系求出a n.28.(13分)已知椭圆C的两个焦点分别为F1(﹣1,0)、F2(1,0),短轴的两个端点分别为B1,B2(1)若△F1B1B2为等边三角形,求椭圆C的方程;(2)若椭圆C的短轴长为2,过点F2的直线l与椭圆C相交于P,Q两点,且,求直线l的方程.【分析】(1)由△F1B1B2为等边三角形可得a=2b,又c=1,集合a2=b2+c2可求a2,b2,则椭圆C的方程可求;(2)由给出的椭圆C的短轴长为2,结合c=1求出椭圆方程,分过点F2的直线l的斜率存在和不存在讨论,当斜率存在时,把直线方程和椭圆方程联立,由根与系数关系写出两个交点的横坐标的和,把转化为数量积等于0,代入坐标后可求直线的斜率,则直线l的方程可求.【解答】解:(1)设椭圆C的方程为.根据题意知,解得,故椭圆C的方程为.(2)由2b=2,得b=1,所以a2=b2+c2=2,得椭圆C的方程为.当直线l的斜率不存在时,其方程为x=1,不符合题意;当直线l的斜率存在时,设直线l的方程为y=k(x﹣1).由,得(2k2+1)x2﹣4k2x+2(k2﹣1)=0.设P(x1,y1),Q(x2,y2),则,因为,所以,即===,解得,即k=.故直线l的方程为或.【点评】本题考查了椭圆的标准方程,考查了数量积的坐标运算,考查了直线和圆锥曲线的关系,考查了分类讨论的数学思想方法和数学转化思想方法,训练了根与系数关系,属有一定难度题目.29.(12分)已知抛物线C:y2=4x 的焦点为F.(1)点A,P满足.当点A在抛物线C上运动时,求动点P的轨迹方程;(2)在x轴上是否存在点Q,使得点Q关于直线y=2x的对称点在抛物线C 上?如果存在,求所有满足条件的点Q的坐标;如果不存在,请说明理由.【分析】(1)设出动点P和A的坐标,求出抛物线焦点F的坐标,由得出P点和A点的关系,由代入法求动点P的轨迹方程;(2)设出点Q的坐标,在设出其关于直线y=2x的对称点Q′的坐标,由斜率关系及中点在y=2x上得到两对称点坐标之间的关系,再由点Q′在抛物线上,把其坐标代入抛物线方程即可求得Q点的坐标.【解答】解:(1)设动点P的坐标为(x,y),点A的坐标为(x A,y A),则,因为F的坐标为(1,0),所以,由,得(x﹣x A,y﹣y A)=﹣2(x A﹣1,y A).即,解得代入y2=4x,得到动点P的轨迹方程为y2=8﹣4x.(2)设点Q的坐标为(t,0).点Q关于直线y=2x的对称点为Q′(x,y),则,解得.若Q′在C上,将Q′的坐标代入y2=4x,得4t2+15t=0,即t=0或.所以存在满足题意的点Q,其坐标为(0,0)和().【点评】本题考查了轨迹方程,考查了直线和圆锥曲线间的关系,考查了代入法求曲线方程,考查了存在性问题的求解方法,属中档题.31.(18分)已知真命题:“函数y=f(x)的图象关于点P(a,b)成中心对称图形”的充要条件为“函数y=f(x+a)﹣b 是奇函数”.(1)将函数g(x)=x3﹣3x2的图象向左平移1个单位,再向上平移2个单位,求此时图象对应的函数解析式,并利用题设中的真命题求函数g(x)图象对称中心的坐标;(2)求函数h(x)=图象对称中心的坐标;(3)已知命题:“函数y=f(x)的图象关于某直线成轴对称图象”的充要条件为“存在实数a和b,使得函数y=f(x+a)﹣b 是偶函数”.判断该命题的真假.如果是真命题,请给予证明;如果是假命题,请说明理由,并类比题设的真命题对它进行修改,使之成为真命题(不必证明).【分析】(1)先写出平移后图象对应的函数解析式为y=(x+1)3﹣3(x+1)2+2,整理得y=x3﹣3x,由于函数y=x3﹣3x是奇函数,利用题设真命题知,函数g(x)图象对称中心.(2)设h(x)=的对称中心为P(a,b),由题设知函数h(x+a)﹣b是奇函数,从而求出a,b的值,即可得出图象对称中心的坐标.(3)此命题是假命题.举反例说明:函数f(x)=x的图象关于直线y=﹣x成轴对称图象,但是对任意实数a和b,函数y=f(x+a)﹣b,即y=x+a﹣b总不是偶函数.修改后的真命题:“函数y=f(x)的图象关于直线x=a成轴对称图象”的充要条件是“函数y=f(x+a)是偶函数”.【解答】解:(1)平移后图象对应的函数解析式为y=(x+1)3﹣3(x+1)2+2,整理得y=x3﹣3x,由于函数y=x3﹣3x是奇函数,由题设真命题知,函数g(x)图象对称中心的坐标是(1,﹣2).(2)设h(x)=的对称中心为P(a,b),由题设知函数h(x+a)﹣b是奇函数.设f(x)=h(x+a)﹣b,则f(x)=﹣b,即f(x)=.由不等式的解集关于原点对称,则﹣a+(4﹣a)=0,得a=2.此时f(x)=﹣b,x∈(﹣2,2).任取x∈(﹣2,2),由f(﹣x)+f(x)=0,得b=1,所以函数h(x)=图象对称中心的坐标是(2,1).(3)此命题是假命题.举反例说明:函数f(x)=x的图象关于直线y=﹣x成轴对称图象,但是对任意实数a和b,函数y=f(x+a)﹣b,即y=x+a﹣b总不是偶函数.修改后的真命题:“函数y=f(x)的图象关于直线x=a成轴对称图象”的充要条件是“函数y=f(x+a)是偶函数”.【点评】本小题主要考查命题的真假判断与应用,考查函数单调性的应用、函数奇偶性的应用、函数的对称性等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.30.(13分)在平面直角坐标系xOy中,点A在y轴正半轴上,点P n在x轴上,其横坐标为x n,且{x n}是首项为1、公比为2的等比数列,记∠P n AP n+1=θn,n∈N*.(1)若,求点A的坐标;(2)若点A的坐标为(0,8),求θn的最大值及相应n的值.【分析】(1)利用{x n}是首项为1、公比为2的等比数列,确定通项,利用差角的正切公式,建立方程,即可求得A的坐标;(2)表示出tanθn=tan(∠OAP n+1﹣∠OAP n),利用基本不等式,结合正切函数的单调性,即可求得结论.【解答】解:(1)设A(0,t)(t>0),根据题意,x n=2n﹣1.由,知,而tanθ3=tan(∠OAP4﹣∠OAP3)==,所以,解得t=4或t=8.故点A的坐标为(0,4)或(0,8).(2)由题意,点P n的坐标为(2n﹣1,0),tan∠OAP n=.∴tanθn=tan(∠OAP n+1﹣∠OAP n)==.因为≥,所以tanθn≤=,当且仅当,即n=4时等号成立.∵0<θn<,y=tanx在(0,)上为增函数,∴当n=4时,θn最大,其最大值为.【点评】本题考查等比数列,考查差角的正切函数,考查基本不等式的运用,正确运用差角的正切公式是关键.创作人:百里公地创作日期:202X.04.01审核人:北堂址重创作单位:博恒中英学校。
2020届高考数学(文)总复习讲义:函数y=Asin(ωx+φ)的图象及应用
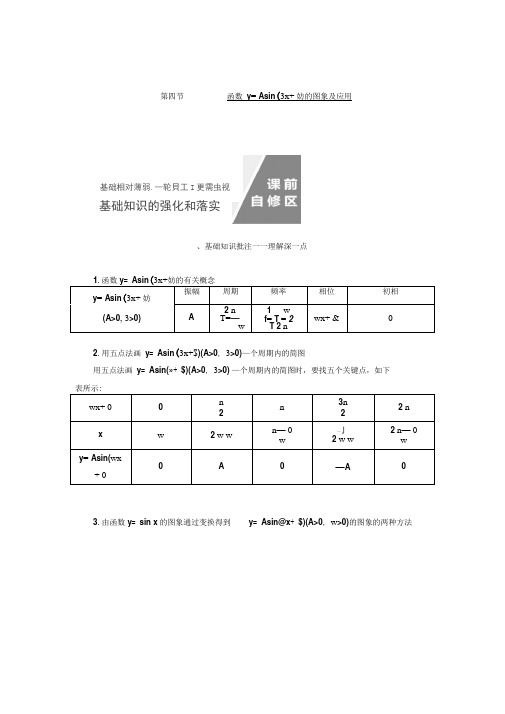
、基础知识批注一一理解深一点y = Asin (3x+ 妨 振幅 周期频率 相位 初相(A>0, 3>0)A2 nT=—w1w f = T = 2 T 2 nwx+ & 02.用五点法画 y = Asin (3x+$)(A>0, 3>0)—个周期内的简图用五点法画 y = Asin(»+ $)(A>0, 3>0) —个周期内的简图时,要找五个关键点,如下 wx+ 0n2 n 3n 22 n x w2 w wn — 0 w—』2 w w2 n — 0wy = Asin(wx+ 00 A—A3.由函数y = sin x 的图象通过变换得到y = Asin@x + $)(A>0, w >0)的图象的两种方法第四节函数 y = Asin (3x+ 妨的图象及应用基础相对薄弱.一轮貝工I 更需虫视基础知识的强化和落实严S"戎平移I I 卜也应咼七f 皿h®斜到严吧G+讪的图象卜_號一>]野到丫=皆価7工购图象- 槽坐标变为原榊M逬T;訣平/虬杠Pj^lipCOJ(jj_ _______ I ____________ t fs11圈到厂血(叭+讪的图竦一驟一I 咼到厂伽(警坤)的图救U*無生荐■更为 应皋的X 惜(1) 两种变换的区别变换)再相位变换,平移的量是 号(3>0)个单位长度.(2) 变换的注意点无论哪种变换,每一个变换总是针对自变量 x 而言的,即图象变换要看 “自变量x ”发生多大变化,而不是看角“3X+矿的变化.、基础小题强化一一功底牢一点一判一判对的打“V”,错的打“X”(1) 函数f(x)= Asin@x + <f ))(A 丰0)的最大值为 A ,最小值为— A.()(2) 函数y = sin (X — :的图象是由y = sin[+訂的图象向右平移 专个单位得到的.()⑶利用图象变换作图时“先平移,后伸缩”与“先伸缩,后平移”中平移的单位长度 一致.()2 % (4) 函数y = Asin (3x+ <的最小正周期为 T =—.()CO1(5) 把函数y = sin x 的图象上各点纵坐标不变,横坐标缩短为原来的 ?,所得图象对应的函数解析式为y = sin^x.()答案:(1)x ⑵V ⑶X ⑷X (5)X(二)选一选1•为了得到函数 y = sin(x + 1)的图象,只需把函数y = sin x 的图象上所有的点()①先相位变换再周期变换 (伸缩变换),平移的量是|训个单位长度;②先周期变换 (伸缩A .向左平移1个单位长度B.向右平移1个单位长度C .向左平移 n 个单位长度D .向右平移n 个单位长度解析:选A 因为由y = sin x 到y = sin(x + 1),只是横坐标由x 变为x + 1,所以要得到 函数y = sin(x + 1)的图象,只需把函数y = sin x 的图象上所有的点向左平移1个单位长度.2.函数y = 2sin 2x +才的振幅、频率和初相分别为 A . 2,C . 2,3.函数 y = cosx|tan x| 0< x <(三)填一填4.用五点法作函数y = sin x — f 在一个周期内的图象时,主要确定的五个点是 ________5.若函数f(x) = sin (3x —妨3>0, |训w 2的部分图象如图所示,贝V0= ________ .解析:由图象可知,函数的周期为4 23— (— 3丿"=4n,所以3=2n= 2,将1丿代 —0 , 得 扌-0=^ + 2k n k € Z ,即 0= — f - 2k n, k € Z ,又 T | 胪亍,二 0=n解析: 选A 由振幅、频率和初相的定义可知,函数 y = 2sin2x + n 的振幅为2,频率解析:选C由题意知y = 0n x , x € 0, n—sin x , x €结合图象知选 C.入 y = sin ^x6.答案:考点一求函数y = Asin@x +妨的解析式[典例] ⑴已知函数 f(x)= Asin (3x+$)(A>0, 3>0, 0< g n)其部分图象如图所示, 则函数f(x)的解析式为()f(x)= 2sin 吳+ 4(i3 nB. f(x)= 2sin ?x + 才(1 3n]C. f(x)= 2sin 4X + 4D . f(x)= 2sin2x +:最高点和它相邻的一个最低点的距离为2 2 ,且过点2, — 2 ,则函数f(x)=[解析]⑴由题图可知A = 2, T = 2X 春5— L 2丿"=4 n,故今=4 n 解得«=殳 所以 f(x)= 2sin *x + $ .把点!— 2),2代入可得2sin ;x —寸卄 丄2, 即 sin $— 4 = 1,所以 $— ;= 2k n+ 寸化€ Z),:(k € Z).又 0< $<n,所以 $= 3n.4若点不宜整合太大,挖掘过深稳取120分就是大胜(2)(20佃皖南八校联考)已知函数n 皆n 的图象上的一个f(x)= sin (3x+ 妨所以 f(x)= 2sin *x + 3j n.数图象过点 2— 1,因此sin( n 妨=一 1,即sin (j )=1,而一疔三皆壬故0=n 所以f(x) I 2 丿 2 2 2 2 6.n , n= sin2x+[答案](1)B (2)sin 器 + fl[解题技法]确定y = Asin (3x+妨+ B(A>0, 3>0)的解析式的步骤M 一 m M + m(1)求A , B ,确定函数的最大值M 和最小值 m ,贝U A =—^, B = —2 n⑵求3,确定函数的周期 T ,贝U 3=〒. (3) 求0 ,常用方法有以下 2种代入法 把图象上的一个已知点代入(此时要注意该点在上升区间上还是在下降区间上把图象的最高点或最低点代入)或五点法确定0值时,往往以寻找“五点法”中的特殊点作为突破口[题组训练]1.函数f(x)= Asin (3x+0 A>0, 3>O , |训<才的部分图象如图B .-子解析:选D 由图象可得 A = ,2,最小正周期T = 4X 気一;=兀则3= 7^7"= 2.由f2sin 亍一1.(2)依题意得寸22+再2 = 2谄,则£= 2,即3=n ,所以f(x)= sin 玄+ 0,由于该函所示,则f步的值为( )一 2 ,|0<寸,得 0= n 则 f(x)= , 2sin 2x +2.(2018 咸阳三模)已知函数 f(x) = Asin(3x+ 0(A>0 ,12^3 \0-2V3=2sinn ,所以fsin确的是()个单位长度,得到曲线 C 2个单位长度,得到曲线 C 23>0, |0V n 的部分图象如图所示,贝y f (x )的解析式为(B .f(x)= 2<3sin 冒 + 扌] f(x)= 2 3sin J+ 3j n冗x n f (x )=2 3sin-4.— Ttx 3 nf(x)= 2 3sin "8 — ~4解析:选D 由图象可得,A = 2 3, T = 2 X [6 — (— 2)] = 16 , 所以3一 3—n所以 3一 T 一 16 一 8. 所以 f(x)— 2 3sin f x + $ .由函数的对称性得 f(2) — — 2 3, 即 f(2) — 2 3sin n2+ $ —— 2 3, 即 sin 4 + $ —— 1,所以 $— 2k n —訴 € Z), 解得 $— 2k n — 3j n(k € Z).因为 I $< n 所以 k — 0, $—— 故函数的解析式为f(x)— 2 3sin 曽-节.考点二 函数y — Asin (3x+ $的图象与变换[典例] (2017全国卷I )已知曲线 G : y — cos x ,y -sin 2x + 23n,则下面结论正A .把C 1上各点的横坐标伸长到原来的 2倍,纵坐标不变,再把得到的曲线向右平移n6B .把C 1上各点的横坐标伸长到原来的 2倍,纵坐标不变,再把得到的曲线向左平移n12C.把C1上各点的横坐标缩短到原来的2倍,纵坐标不变,再把得到的曲线向右平移单位长度,得到曲线 C 2D .把C 1 上各点的横坐标缩短到原来的 *倍,纵坐标不变,再把得到的曲线向左平移谥个单位长度,得到曲线 C *[解析]易知Ci :y = cosx = sin x +扌,把曲线C i 上的各点的横坐标缩短到原来的 *倍, 纵坐标不变,得到函数y = sin 2x +扌的图象,再把所得函数的图象向左平移 磊个单位长度, 可得函数y = sin2[x+ $戶才"=singx +尹」的图象,即曲线 C 2.[答案]D[解题技法]三角函数图象变换中的 3个注意点(1)变换前后,函数的名称要一致,若不一致,应先利用诱导公式转化为同名函数;⑵要弄清变换的方向,即变换的是哪个函数的图象,得到的是哪个函数的图象,切不 可弄错方向; ⑶要弄准变换量的大小,特别是平移变换中,函数 y = Asin x 到y = Asin (x +妨的变换量是|训个单位,而函数 y = Asin到y = Asin (wx+妨时,变换量是 乜 个单位.CO[题组训练]1.将函数y = sin x + n的图象上所有的点向左平移 才个单位长度,再把图象上各点的横 坐标扩大到原来的2倍(纵坐标不变),则所得图象对应的函数解析式为( )A . y = sin 2x + 芯 x n C . y = sin 2- 12解析:选B 将函数y = sin x +f 的图象上所有的点向左平移 才个单位长度,得到函数 y = sin ^x + n + 6 -sin [x +寻丿的图象,再把图象上各点的横坐标扩大到原来的 2倍(纵坐标不变),可得函数 y = sin 2x + 的图象,因此变换后所得图象对应的函数解析式为 y =x 丄5n sin 2+12 .2. (2019潍坊统一考试)函数y = .''3sin 2x -cos 2x 的图象向右平移 $ 0<拆寸个单位长 度后,得到函数 g (x )的图象,若函数 g (x )为偶函数,则 $的值为()7t 7tB.6n nC.4D.3解析:选B由题意知y= 3sin 2x—cos 2x = 2sin 2x—其图象向右平移0个单位长度后,得到函数g(x)= 2sin 2x— 2 $—看的图象,因为g(x)为偶函数,所以2时許扌+ k n, k€ Z ,所以(j)= j6+ ¥,“ Z,又因为[o,才j所以片f.考点三三角函数模型及其应用[典例]据市场调查,某种商品一年内每件出厂价在7千元的基础上,按月呈f(x)= Asin(3x+妨+ B A>0, w>0, |训弓的模型波动(x为月份),已知3月份达到最高价9千元,9月份价格最低为5千元,则7月份的出厂价格为___________ 元.[解析]作出函数f(x)的简图如图所示,三角函数模型为:f(x) = Asin(»+ 0 + B,由题意知:A = 2 000, B= 7 000 , T = 2X (9 —3) = 12,2 n n… 3= =T 6.将(3, 9 000)看成函数图象的第二个特殊点,则有n x 3+ $=n, ••• 0= 0,6 2n *故f(x) = 2 000sin§x+ 7 000(1 < x< 12, x € N ).• f(7) = 2 000X sin^5* 7 000 = 6 000.故7月份的出厂价格为 6 000元.[答案]6 000[解题技法]三角函数模型在实际应用中的 2种类型及解题策略(1)已知函数模型,利用三角函数的有关性质解决问题,其关键是准确理解自变量的意 义及自变量与函数之间的对应法则;⑵把实际问题抽象转化成数学问题,建立三角函数模型,再利用三角函数的有关知识 解决问题,其关键是建模.[题组训练]1.如图,某港口一天 6时到18时的水深变化曲线近似满足函 数y = 3sin f x ++ k ,据此函数可知,这段时间水深 (单位:的最大值为(B . 6D . 10y = 20.5.答案:20.5 [课时跟踪检测]A 级 --- 保大分专练解析:选 C 设水深的最大值为 M ,由题意并结合函数图象可得3+ k = M ,k — 3= 2,解得M2•某城市 年中12个月的平均气温与月份的关系可近似地用函数y = a + Acos 6(x(x = 1,2,3,…,12)来表示,已知6月份的月平均气温最高为 28 C, 12月份的月平均气温最低为18 C,贝U 10月份的平均气温为 __________ C .解析:由题意得了 + A = 28,a — A =18,即严23,A = 5, 所以 y = 23+ 5cos ^x — 6J ,令 x = 10,得n」—2,n上的简图是( 1 .函数y= sin除C ,故选A.2•函数f (x ) = tan 讥3>0)的图象的相邻两支截直线 y = 2所得线段长为 寸,则f 特丿的值 是()A . — 3B 並B.3C . 1D. 3解析:选D由题意可知该函数的周期为 n,•••n =n ,3= 2, f (x )= tan 2x.co 2 • f6 =tan3 = 3■3. (2018天津高考)将函数y = singx + 勺图象向右平移 希个单位长度,所得图象对应的函数()A .在区间单调递增B .在区间 3n , n 上单调递减 C .在区间 亍3n 上 单调递增 D .在区间37,2n 上单调递减解析:选A 将函数y = sin 2x + n 的图象向右平移 诂个单位长度后的解析式为 y =sin 2x - - +; =sin 2x ,则函数y = sin 2x 的一个单调递增区间为 于,J 一个单调递 减区间为怦,T 由此可判断选项 A 正确.解析:选A 令x = 0,得y = sin =排除B 、D.由f —4.(20佃 贵阳检测)已知函数 f(x) = Asin(»+初部分图象如图所示,则 0的值为()nB・3nD.6[1 \1 d \tL-11—3解析:选B 由题意,得T = n—6 =扌,所以T = n,由T = ¥得3= 2,由图可知A = 1,所以 f(x)= sin(2x + 册.又因为 f 扌=sin5.(20佃 武汉调研)函数f(x) = Acos(»+妨(少0)的部分图象如图所示,给出以下结论: ①f(x)的最小正周期为2; ②f(x)图象的一条对称轴为直线x =— 1;③f(x)在2k — 4,2k + 3, k € Z 上是减函数; ④f(x)的最大值为A则正确结论的个数为(B . 2解析:选B 由题图可知,函数f(x)的最小正周期 T = 2X5—4= 2,故①正确;因为函数f(x)的图象过点1 *0和所以函数f(x)图象的对称轴为直线 x =3+ k(k € Z),故直线x = — 丁不是函数f(x)图象的对称轴,故②不正确;由图可知,当1-T+4 4 故③正确; 若 A>0,2.n —<° =0,—扌<0<寸所以°=n3<10)的图象向右平移因为g(x)在[0 , n 合,•一 -;;-+ n= £+ k n k € Z ,解得 w=— 6k , k € 乙又 T 0< o <10 ,•• o = 6.6 3 37t7 .已知函数 f(x)= 2sin 3x + o<n 的图象经过点(0,1),则该函数的振幅为,最小正周期T 为,频率为,初相解析:振幅A = 2,最小正周期 T = 3= 6,频率f = Z 6 因为图象过点(0,1), 所以2sinA 1,所以 sinA2,n n又因为W|<n 所以0=7.2 68.函数 f(x) = Asin (3x+ <f ))(A>0, 3>0,0v 护n 的部分图象如图所示, 贝 U f(x)=解析:由图象可知 A = 2, 3T =n= ^T, T = n • o= 2 , 4 12 64•••当x =n 时,函数f(x)取得最大值,6•2X n+0=★ 2k n k € Z), n•••片丄+ 2k n k € Z),6T 0< 0<n, 0=n ,- f(x) = 2sin 2x +答案:2sin [2x +訂9.已知函数f(x)= sin T — oxo >0)向左平移上的值域为则o 的取值范围是解析:由题意,得g(x)= sin ;—o因为g(x)在[0 , n =sin 一 n — 由 x € [0 , n]得cox —n €3n.一 3, on —3X—. n 'sin ox —3,10 •某地农业监测部门统计发现:该地区近几年的生猪收购价格每四个月会重复出 现•下表是今年前四个月的统计情况:选用一个三角函数模型来近似描述收购价格(元/斤)与相应月份之间的函数关系为解析:设 y = Asin (3x+$)+ B(A>0 , 3>0), 由题意得A = 1, B = 6, T = 4,因为T = 2~n ,所以3=2,所以y = sin 牙x +隔+ 6. 因为当x = 1时,y = 6,所以sin 扌+ 0 = 0, 故才+ 0= 2k n, k € Z ,可取0=—扌,n n 亠 n所以 y = sin 2x — 2 + 6=— cos2x + 6. 答案:y = — cos ^x + 611.设函数f(x)= cos (3x+ 0 3>0,— 2*< 0<0的最小正周期为 n 且f 2(1)求3和的值;(2)在给定坐标系中作出函数f(x)在[0 , n 上的图象.解:(1)因为T = 2^= n,所以3= 2,3又因为f n = cos 2X 才+ 0 =cos ^+ 0 = — sin 0=宁且一n <0<o ,所以 0= —n故3的取值范围是答案:-5 51J6, 3一解得5“ 3."5 51J6, 3J再将y = sin 2x +才的图象上所有点的横坐标变为原来的1 一 、2(纵坐标不变)得g(x)=sin 4x+ 6.I n 1• g(x) = sin 4x + 6 .冗⑵由(1)知 f(x)= cos 2x -n . 列表:12. (2019湖北八校联考)函数f(x) = sin (3x+$) «>0, |训<寸在它的某一个周期内的单 调递减区间是12,青.将y = f(x)的图象先向左平移4个单位长度,再将图象上所有点的横1坐标变为原来的2(纵坐标不变),所得到的图象对应的函数记为(1)求g(x)的解析式;T 11 n 5 nn 2 n 解:⑴ V 2 = 72― 12= 2,^ T = n, 3 = — = 2, 又••• sin 2X 誉 0 = 1, | 训<; •••片-扌,f(x)= sin[2x -将函数f(x)的图象向左平移 j 个单位长度得g(x).⑵求g(x)在区间0, n的最大值和最小y = sin 2 x+4 -3 =sin 2x +n,解析:选C因为将函数f(x)= sin 3x ( 3>0)的图象向右平移哀个单位长度得到函数 y =f(x)在n ,5n 上是减函数 f(x)在in ,严上是增函数解析:选 B 由题图知 A = 2,设 m € [a , b],且 f(0)= f(m),贝U f(0 + m)= f(m) = f(0)=3 , • 2sin 0= 3 , sin 9=于,又:丨耳三f ,• 0=3,+2+ 2k n k € Z ,解得一5n + k x <二+ k n, k € Z ,此时f(x)单调递增.所以选项 B正确.n..2. (2019福州四校联考)函数f(x)= sin «x( «>0)的图象向右平移 石个单位长度得到函数数3的值为( )3 B.3当 4x + n= 二g(x )在为增函数,在为减函数,故函数g(x)在区间0,4上的最大值和最小值分别为1和一 2.B 级一一创高分自选1. (2019惠州调研)函数f(x) = Asin(2x + 痕>0, |q <亩的部分图象如 图所示,且f(a)= f(b) = 0,对不同的X 1, X 2€ [a , b],若f(x“= 快),有 + x2)= 3,则()f(x)在一5n ,1n上是减函数B . f(x)在 L in ,12上是增函数••• f(x)= 2singx + n ;!,令一寸+ 2k nC 2x_ny = g(x)的图象,并且函数g(x)在区间6,「单调递增,在区n3,单调递减,则实所以 g(x)max = g1,1 又因为g(0)=2 2 所以 g(x)min =— 2,⑵设 g(x)= f(x)+ 2cos 4x + 3 ,则 g(x)= 2sin Jx + 冒」+ 2cosgx + 扌 I令 t = sin (2x + 才)t € [ — 1,1],记 h(t) = — 4t 2 + 2t + 2= — 4 t — 1 2 因为 t € [ — 1,1], 所以 h(t)€ .— 4 , 9], 即 g(x)€ — 4, 4\,故 a € — 4, 故a 的取值范围为一4 ’ 9 .1 T 1 3kT < x < 4 + 4 + 灯化€ Z),即 2k — 4< x < 2k + ;(k € Z)时,f(x)是减函数, 则最大值是 A ,若AV0,则最大值是-A ,故④不正确.综上知正确结论的个数为g(x)的图象,所以g(x)= sin「单调递增,在区n5,单调递减,所以g n = sin 33n= 1且警扌,所以{ 3= 8k + 2k € Z ,0<3< 6,所3.(2018南昌模拟)函数f(x) = Asin (3x+妨卜>0, 3>0, |训<寸的部 分图象如图所示.(1)求函数f(x)的解析式,并写出其图象的对称中心;⑵若方程f(x) + 2cos4x + n = a 有实数解,求a 的取值范围.1 2y2ni)匹解:(1)由图可得A = 2, 2 =尹―看=n,所以T = n,所以3= 2.,f(x)= 2,可得 2sin 2 x f + 0 = 2, 因为Wl<T,所以0= £2 6所以函数f(x)的解析式为f(x) = 2sin 2x + f .令 2x + n= k n( Z),得 x = k ^— $(k € Z),所以函数f(x)图象的对称中心为 牙n0 (k € Z). 12'=2sin 2x +才卄 2 1 — 2sin 2?x +9 4’ 3 X —又因为函数g(x)在区间n,_66. (2018 •西大同质量检测)将函数f(x)= tan »+长度后与函数f(x)的图象重合,则3=( )A. 9B. 6C . 4D . 8解析:选B 函数f(x)= tan 3x+n的图象向右平移才个单位长度后所得图象对应的函数解析式为y= tan ojx—才产;=tan [x—嚮+;•平移后的图象与函数f(x)的图象重。
2020年新高考数学复习一条特殊的线--函数的切线专题解析

2020年新高考数学复习一条特殊的线--函数的切线专题解析基础知识回顾:(一)与切线相关的定义1、切线的定义:在曲线的某点A 附近取点B ,并使B 沿曲线不断接近A 。
这样直线AB 的极限位置就是曲线在点A 的切线。
(1)此为切线的确切定义,一方面在图像上可定性的理解为直线刚好与曲线相碰,另一方面也可理解为一个动态的过程,让切点A 附近的点向A 不断接近,当与A 距离非常小时,观察直线AB 是否稳定在一个位置上(2)判断一条直线是否为曲线的切线,不再能用公共点的个数来判定。
例如函数3y x =在()1,1--处的切线,与曲线有两个公共点。
(3)在定义中,点B 不断接近A 包含两个方向,A 点右边的点向左接近,左边的点向右接近,只有无论从哪个方向接近,直线AB 的极限位置唯一时,这个极限位置才能够成为在点A 处的切线。
对于一个函数,并不能保证在每一个点处均有切线。
例如y x =在()0,0处,通过观察图像可知,当0x =左边的点向其无限接近时,割线的极限位置为y x =-,而当0x =右边的点向其无限接近时,割线的极限位置为y x =,两个不同的方向极限位置不相同,故y x =在()0,0处不含切线(4)由于点B 沿函数曲线不断向A 接近,所以若()f x 在A 处有切线,那么必须在A 点及其附近有定义(包括左边与右边)2、切线与导数:设函数()y f x =上点()()00,,A x f x ()f x 在A 附近有定义且附近的点()()00,B x x f x x +∆+∆,则割线AB 斜率为:()()()()()000000ABf x x f x f x x f x k x x x x +∆-+∆-==+∆-∆当B 无限接近A 时,即x ∆接近于零,∴直线AB 到达极限位置时的斜率表示为:()()000lim x f x x f x k x∆→+∆-=∆,即切线斜率,由导数定义可知:()()()'0000limx f x x f x k f x x∆→+∆-==∆。
2022年全国新高考1卷数学真题及答案解析

2022年全国新高考1卷数学真题及答案解析今年的高考数学试卷坚持思想性与科学性的统一,从中华优秀传统文化、社会经济发展、科技发展与进步等方面设置了真实情境。
下面是小编为大家收集的关于2022年全国新高考1卷数学真题及答案解析。
希望可以帮助大家。
2022年全国新高考1卷数学真题2022年全国新高考1卷数学答案解析高考数学备考六大复习建议01 函数与导数近几年高考中,函数类试题一般会出现2道选择题、2道填空题、1道解答题。
其中,选择题和填空题经常考的知识点更偏向反函数,函数的定义域和值域,函数的单调性、奇偶性、周期性,函数的图象、导数的概念和应用等,这些知识点要着重复习。
而在分值颇高的解答题中,通常会考查考生对于函数与导数、不等式运用等考点的掌握运用情况。
掌握题目背后的知识点,建立自己的答题思路是非常重要的。
值得考生们注意的是,函数和导数的考查,经常会与其他类型的题目交叉出现,所以需要重视交叉考点问题的训练。
02 三角函数、平面向量和解三角形三角函数是每年必考题,虽是重点但难度较小。
哪怕是基础一般的同学,经过二轮复习的千锤百炼,都可以掌握这部分内容。
所以,三角函数类题目争取一分都不要丢!从题型来看,会覆盖选择题、填空题、解答题三大类型。
大题会出现在二卷解答题的第一个,也证明此类型题目的难度比较小。
在三角函数的部分,高三考生需要熟练的知识点有不少。
(1)掌握三角变换的所有公式,理解公式的意义、应用场景、考查形式、使用方法等。
(2)熟悉三角变换常用的方法——化弦法、降幂法、角的变换法等。
应用以上方法进行三角函数式的求值、化简、证明。
(3)掌握三角变换公式在三角形中应用的特点,并能结合三角形的公式解决一些实际问题。
(4)熟练掌握正弦函数、余弦函数、正切函数、余切函数的性质,并能用它研究复合函数的性质。
同时,也要掌握这些函数图象的形状、特点。
(5)掌握三角函数不等式口诀:sinα上正下负;cosα右正左负;tanα奇正偶负。
