岩土工程有限元大作业
有限元在土木工程中的应用

土体固结分析
➢二维大变形固结分析
假定材料是线性的; 由于大变形即可导致非线性特性,即孔隙比
对渗透系数影响,有限元方法同样可以解决 此非线性问题。
土体固结分析
➢砂井固结分析
采用三维固结有限元方法,工作量较大,一 般转化为平面应变有限元方法计算。
隧道模型横断面尺寸可根据情况取7~10倍的隧 道直径,对于浅埋隧道,模型顶面可取至物理对 象顶面;纵向长度要考虑空间效应的影响。
顶面取自由面,底面为双向约束,左右边界为水 平约体单元或壳单元, 锚杆可采用杆单元。
岩土开挖分析
地层损失 初始地应力平衡
主要内容
➢有限元方法简介 ➢有限元在岩土工程中的应用 ➢有限元在结构工程中的应用 ➢有限元在土木工程中的应用前景
有限元方法简介
➢有限元方法的基础是变分原理和加权余 量法,其基本求解思想是把计算域划分 为有限个互不重叠的单元,在每个单元 内,选择一些合适的节点作为求解函数 的插值点,将微分方程中的变量改写成 由各变量或其导数的节点值与所选用的 插值函数组成的线性表达式 ,借助于变 分原理或加权余量法,将微分方程离散 求解。
有限元方法可以有效地解决此类问题,获取 与解析解吻合很好的数值解。
土体固结分析
➢非饱和土的一维固结分析
非饱和土的固结问题是土木工程中经常遇到 的问题,对此有限元程序,如ABAQUS, 可以给出较为精确的数值解。
假定忽略土水特征线的滞回效应。
土的固结分析
➢三轴试样固结分析
对于最普遍的土工试验-三轴试样固结,包 括固结不排水试验和固结排水试验,有限元 程序也可以建立分析模型求解。
土的渗流计算
➢土体减饱和过程分析
有限元极限分析法在岩土工程项目中的应用

有限元极限分析法在岩土工程项目中的应用在岩土工程中,有限元极限分析法有着广泛的应用价值,下面是小编搜集整理的一篇探究有限元极限分析法应用的论文范文,欢迎阅读参考。
虽然有限元极限分析法在岩土工程中有着较为突出的应用效果和价值,然而,因为这一分析法在实际的应用中,需要进行假设,然后还要将求解划分在合理的有限的范围内,因此,该分析法在岩土工程中的应用有着一定的局限*。
而随着社会的发展,这种分析法也得到了一定的发展,加上其本身所具有的超强适应*,使得其在一些其他的工程中也得到了应用,但是应用的过程中,也会受到局限*的影响。
本文主要就针对有限元极限分析法在岩土工程中的主要应用情况进行深入的分析。
1有限元极限分析法的发展有限元极限分析法在早期主要是由英国的科学家所提出的,并且在提出之初,就应用到了岩土工程中。
而随着时代的演变,在20世纪80、90年代的时候,有限元极限分析法的应用范围逐渐的得到扩展,但是受到当时技术条件的限制,使得该分析法应用的效果并不理想。
我国开始在岩土工程中应用有限元极限分析法的时间在1990年之后,我国当时应用该方法主要是为了针对土坡进行分析,而在2000年之后,就开始应用该分析法对边坡的稳定*进行分析,并衍生出了有限元强度折减法,同时也衍生出了有限元超载法,这两种方法都包含在有限元极限分析法中,有效的推动了有限元极限分析法的发展和应用。
而在最近几年,我国在有限元极限分析法的应用上有了进一步的突破,然而,就整体的应用效果来分析,我国的有限元极限分析法的应用目前还处于初级发展的阶段,还需要采用不同的方法来对有限元极限分析法进行改进,只有这样才能够更好的发挥出有限元极限分析法在岩土工程中的应用作用。
2有限元极限分析法的原理2.1有限元强度折减法原理在岩土工程中,主要采用莫尔-库仑材料,强度折减安全系数T的计算式为:2.2有限元增量超载法在工程中,岩土的破坏,不是朝夕之事,而是一个循序渐进的过程,由线**状态,逐步过渡到塑*流动,最终达到极限破坏状态。
有限元极限分析法发展及其在岩土工程中的应用研究

有限元极限分析法发展及其在岩土工程中的应用研究【摘要】有限元极限分析法适用于岩土工程的设计与分析。
笔者在本文中,主要介绍了岩土工程安全系数、方法和失稳判据等,以及有限元极限分析法在土坡、土基扩大以及基岩边坡基岩的应用,实现革新设计方法的目标。
【关键词】有限元;极限分析法;岩土工程;应用研究在岩土工程中,极限分析法得到了良好的应用,但是由于这一方法需要做假设,而且求解的范围有限,所以方法的应用受到了很大的限制。
但是有限元数值方法,具有很强的适应性,但是由于无法计算出稳定安全系数F,所以其应用也受到一定的限制。
在本文中,笔者探讨了有限元极限分析法的发展,以及其在岩土工程中的应用。
1 有限元极限分析法的发展20世纪70年代中期,英国科学家Zienkiewicz首先提出了有限元极限分析法,并且在岩土工程极限荷载与安全系数的计算中进行了应用。
在随后的1980年代和90年代,这种方法在边坡及地基稳定性分析中也有了良好的应用。
不过,由于当时的技术条件有限,缺乏可靠、强大的大型有限元程序、强度准则等,致使计算精度不够,在岩土工程中没有得到广泛的应用。
20世纪末,关于有限元极限分析法,国际上又出现了多种相关的研究文章,研究的方向主要集中在有限元强度折减法求解均质土坡安全稳定系数F方面。
但是由于计算结果与之前的研究结果比较相似,所以逐步为主流学术界所接受。
一些学者认为,这标志着有限元强度折减法分析边坡的稳定性,进入了一个崭新的时期。
1999年,美国的D. V. Griffith等人用该方法分析了边坡的稳定性,创新点在孔隙水压力与模拟水位两方面,同时也对库水下降情况下的边坡稳定性做了分析。
而我国有限元极限分析法在20世纪末才开始,主要是在土坡分析中的应用。
21世纪初期,国内的一些学者在边坡稳定性的分析中,采用了有限元强度折减法。
这是国内比较早的研究有限元强度折减法的文章,研究的方向集中在基本理论及计算精度两方面。
随着计算精度的不断提高,逐渐被设计单位和岩土工程部门所重视。
岩土工程极限分析有限元法及其运用

岩土工程极限分析有限元法及其运用张 聪(甘肃煤田地质局一三三队,甘肃 白银 730913)摘 要:基于极限分析方法在岩土工程施工中的应用局限文章提出兼具数值分析方法和经典极限分析方法的有限元分析方法,在介绍有限元分析原理、基本理论、安全系数和发展历程的基础上,从边坡、地基、隧道等方面着重分析岩土工程极限分析有限元法的应用,验证有限元分析方法在岩土工程中应用范围的扩大,旨在能够为岩土工程施工建设发展提供更多有力的支持。
关键词:有限元极限分析方法;岩土工程;岩土滑坡中图分类号:TU195 文献标识码:A 文章编号:1002-5065(2020)14-0233-2Finite element method for limit analysis of geotechnical engineering and its applicationZHANG Cong(No.133 team of Gansu Coalfield Geological Bureau, Baiyin 730913,China)Abstract: Based on the limitation of the application of limit analysis method in geotechnical engineering construction, this paper proposes a finite element analysis method which combines numerical analysis method and classical limit analysis method. On the basis of introducing the principle of finite element analysis, basic theory, safety factor and development process, the application of limit analysis finite element method in geotechnical engineering is emphatically analyzed from the aspects of slope, foundation and tunnel, To verify the expansion of the application scope of finite element analysis method in geotechnical engineering, in order to provide more powerful support for the development of geotechnical engineering construction.Keywords: finite element limit analysis method; geotechnical engineering; geotechnical landslide极限分析法的力学基础是土体处于一种理想的弹性、属性状态,这种状态下,土体会出现一种平衡状态,即为土体滑动面上每个点的剪应力会和土地抗剪强度等同。
有限元大作业试验报告
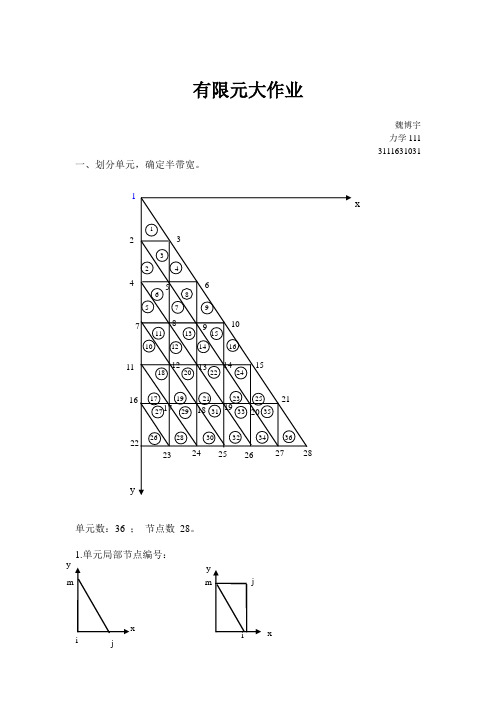
有限元大作业魏博宇力学111 3111631031一、划分单元,确定半带宽。
x13 24 6 85 7 9 11 13 15 10 12 14 1618 20 22 2417 19 21 23 25 27 29 31 33 3526 28 30 32 34 36y单元数:36 ; 节点数 28。
1.单元局部节点编号: y x ijm ijm yx12 3 4 56 7 8 9 10 11121314 1516 17 18 19 20 212223 24 25 26 27 28、单元号 1 2 3 4 5 6 7 8 9 10 11 12i 2 4 5 5 7 8 8 9 9 11 12 12j 3 5 3 6 8 5 9 6 10 12 8 13 m 1 2 2 3 4 4 5 5 6 7 7 8 单元号13 14 15 16 17 18 19 20 21 22 23 24i 13 13 14 14 16 17 17 18 18 19 19 20j 9 14 10 15 17 12 18 13 19 14 20 15 m 8 9 9 10 11 11 12 12 13 13 14 14 单元号25 26 27 28 29 30 31 32 33 34 35 36i 20 22 23 23 24 24 25 25 26 26 27 27j 21 23 17 24 18 25 19 26 20 27 21 28 m 15 16 16 17 17 18 18 19 19 20 20 212.节点坐标结点号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 x 0 0 1 0 1 2 0 1 2 3 0 1 2 3 y 0 1.5 1.5 3 3 3 4.5 4.5 4.5 4.5 6 6 6 6 结点号15 16 17 18 19 20 21 22 23 24 25 26 27 28 x 4 0 1 2 3 4 5 0 1 2 3 4 5 6 y 6 7.5 7.5 7.5 7.5 7.5 7.5 9 9 9 9 9 9 93.带状性1 5 10 15 20 25 28可求半带宽D=(7+1)× 2 = 16二、载荷向节点移置。
有限元分析及应用大作业

有限元分析及应用大作业作业要求:1)个人按上机指南步骤至少选择习题中3个习题独立完成,并将计算结果上交;也可根据自己科研工作给出计算实例。
2)以小组为单位完成有限元分析计算;3)以小组为单位编写计算分析报告;4)计算分析报告应包括以下部分:A、问题描述及数学建模;B、有限元建模(单元选择、结点布置及规模、网格划分方案、载荷及边界条件处理、求解控制)C、计算结果及结果分析(位移分析、应力分析、正确性分析评判)D、多方案计算比较(结点规模增减对精度的影响分析、单元改变对精度的影响分析、不同网格划分方案对结果的影响分析等)题一:图示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:1)分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;(注意ANSYS中用四边形单元退化为三节点三角形单元)2)分别采用不同数量的三节点常应变单元计算;3)当选常应变三角单元时,分别采用不同划分方案计算。
解:1.建模:由于大坝长度>>横截面尺寸,且横截面沿长度方向保持不变,因此可将大坝看作无限长的实体模型,满足平面应变问题的几何条件;对截面进行受力分析,作用于大坝上的载荷平行于横截面且沿纵向方向均匀分布,两端面不受力,满足平面应变问题的载荷条件。
因此该问题属于平面应变问题,大坝所受的载荷为面载荷,分布情况P=98000-9800*Y;建立几何模型,进行求解;假设大坝的材料为钢,则其材料参数:弹性模量E=,泊松比σ=;2:有限元建模过程:进入ANSYS :程序→ANSYS APDL设置计算类型 :ANSYS Main Menu: Preferences →select Structural →OK选择单元类型 :ANSYS Main Menu: Preprocessor →Element Type→Add/Edit/Delete →Add →select Solid Quad 4node 182(三节点常应变单元选择Solid Quad 4node 182,六节点三角形单元选择Solid Quad 8node 183) →OK (back to Element Types window) →Option →select K3: Plane Strain →OK→Close (the Element Type window)定义材料参数:ANSYS Main Menu: Preprocessor →Material Props →Material Models →Structural →Linear →Elastic →Isotropic →input EX:, PRXY: →OK生成几何模型:生成特征点:ANSYS Main Menu: Preprocessor →Modeling →Create →Keypoints →In Active CS →依次输入四个点的坐标:input:1(0,0),2(10,0),3(1,5),4,5) →OK生成坝体截面:ANSYS Main Menu: Preprocessor →Modeling →Create →Areas →Arbitrary →Through KPS →依次连接四个特征点,1(0,0),2(6,0),3(0,10) →OK网格划分:ANSYS Main Menu: Preprocessor →Meshing →Mesh Tool→(Size Controls) lines: Set →依次拾取两条直角边:OK→input NDIV: 15 →Apply→依次拾取斜边:OK →input NDIV: 20 →OK →(back to the mesh tool window)Mesh:Areas, Shape: tri, Mapped →Mesh →Pick All (in Picking Menu) →Close( the Mesh Tool window)模型施加约束:给底边施加x和y方向的约束:ANSYS Main Menu: Solution →Define Loads →Apply →Structural →Displacement →On lines →pick the lines →OK →select Lab2:UX, UY →OK给竖直边施加y方向的分布载荷:ANSYS 命令菜单栏: Parameters →Functions →Define/Edit →1) 在下方的下拉列表框内选择x ,作为设置的变量;2) 在Result窗口中出现{X},写入所施加的载荷函数:98000-9800*{Y}; 3) File>Save(文件扩展名:func) →返回:Parameters →Functions →Read from file:将需要的.func文件打开,参数名取meng,它表示随之将施加的载荷→OK →ANSYS Main Menu: Solution →Define Loads →Apply →Structural →Pressure →On Lines →拾取竖直边;OK →在下拉列表框中,选择:Existing table →OK →选择需要的载荷为meng参数名→OK分析计算:ANSYS Main Menu: Solution →Solve →Current LS →OK(to close the solve Current LoadStep window) →OK结果显示:ANSYS Main Menu: General Postproc →Plot Results →Deformed Shape… → select Def + Undeformed →OK (back to Plot Results window)→Contour Plot →Nodal Solution→select:DOF solution, UX,UY,Def + Undeformed , Stress ,SX,SY,SZ, Def + Undeformed →OK:结果分析:(第一小题)图为采用三节点常应变单元,200个单元,左下图为位移变形图;右下图为应力变形图图为采用六节点三角形单元,200个单元,左下图为位移变形图;右下图为应力变形图根据位移和应力图可得:单元类型Min(位移)Max(位移)Min(应力)Max(应力)常应变三节点05461392364六节点三角形0607043对比分析可得:最大位移都发生在A点,即大坝顶端,最大应力发生在B点附近,即坝底和水的交界处,且整体应力和位移变化分布趋势相似,符合实际情况;结果显示三节点和六节点单元分析出来的最大应力值相差较大根据结果显示,最小三节点和六节点单元分析出来的最小应力值相差极为悬殊,结合理论分析,实际上A点不承受载荷,最小应力接近于零,显然六节点三角形单元分析在这一点上更准确。
岩土工程数值法分析实例 有限元原理

岩土工程数值法班级:63专业:隧道与地下工程姓名:学号:630吉林大学建设工程学院年月日目录一、问题提出 (3)二、围岩离散化 (4)三、数据准备 (5)四、计算过程 (6)五、结果初步分析 (7)六、图形 (7)七、隧道开挖对围岩的影响 (10)八、结语 (12)九、参考文献 (12)随着我国经济快速发展,各种隧道、公路、铁路、房屋以及其它基础设施进入了一个高速建设的阶段,随之而来的是土木工程的跨越式发展。
土木工程的设计和研究手段也有了很大的提高,从以前的基于经验的设计理论逐渐过渡到定量与定性相结合的反分析计算理论。
目前为止,土木工程的研究方法主要有以下五类:类比法;解析法;模型模拟(物理模型方法);现场监控量测;数值法(数值模拟)。
通过岩土工程数值法这门课程,我们系统的学习了数值法中的有限单元法的原理以及它在岩土工程中的应用。
随着计算机的普及和运算速度的提升,为弹性力学的数值解法开辟了广阔的领域,尤其在隧道工程中,采用有限单元法分析都得到了满意的结果。
目前,有限单元法已经是解决不同岩体结构、围岩与支护相互作用、隧道围岩压力、围岩应力和变形、围岩破坏过程与破坏机制的主要方法。
本文将针对一个隧道开挖实例,应用有限单元法进行位移、应力等相关参数的分析。
一、问题提出在岩土体中修建隧道是一件十分复杂的工程。
因为岩土体是地壳内外力长期作用下形成的一种复杂的地质体,具有天然应力、非均质、不连续、各向异性等特点,从而表现在力学性质上具有非线性、剪胀性、蠕变性等。
而有限单元法可以将岩土体复杂多变的力学性质,基本地质因素、复杂和混合的边界条件、岩土体与工程结构物的组合作用等问题统筹考虑,以得到接近实际的数值解答。
目前,隧道施工和设计都是基于“新奥法”,新奥法的核心是充分发挥围岩的承载能力,将围岩视为承载的主体。
随之而来的是如何确定围岩收敛的极限位移,如何确定衬砌的支护时间,如何判定围岩应力的集中程度等问题。
本文基于以下条件进行隧道开挖后的围岩进行分析。
岩土工程有限元大作业

岩土工程有限元大作业题目:平面问题3结点三角形有限元法的Matlab程序实现专业:建筑与土木工程(岩土方向)姓名:学号:_________2014年12 月31 日1.概述对于二维平面问题,运用有限单元法求解时,单元的类型有3结点三角形单元、4结点矩形单元以及高精度的三角形单元(6结点、10结点)等。
三角形单元对复杂边界有较强的适应能力,因此很容易将一个二维域离散成有限个三角形单元,在边界上以若干段直线近似原来的曲线边界,随着单元增多,这种拟合将越精确。
本文即基于相对比较简单且运用广泛的3结点三角形单元的有限元法编制Matlab 程序,解决一个悬臂梁端点承受竖向集中荷载作用时的位移计算问题,并绘出变形前后的图形作对比。
在分析过程中,将此问题简化为平面应力问题,取单位厚度进行分析。
以下一共分为两部分介绍,第一部分是理论部分,介绍三角形有限元法的基本求解过程;第二部分是程序部分,介绍具体的Matlab 程序实现过程。
2.三角形有限元法的基本求解过程 2.1 假设单元的位移函数如图2.1所示为一端部承受竖向集中荷载作用的悬臂梁,将此问题简化为二维平面问题,梁取单位厚度,固定端简化为两个不动铰支座,已知悬臂梁的长度为8米,高度为1米,材料为钢材,它的弹性模量取2.06e11Pa ,泊松比取0.25,右端处作用的竖向荷载为100kN 。
二维域Ω被离散成如图所示的九个三角形单元,后续编程中的结点号和单元号都以此为基础,任取一三角形单元,设其结点编码为m j i ,,,以逆时针编码为正向(见图2.2)。
该三角形单元在x 、y 方向的位移函数表达式为:m m j j i i u N u N u N u ++= (2.1) m m j j i i v N v N v N v ++=(2.2)其中()m j i i N i ,, =称为单元的插值函数或形函数()y c x b a AN i i i i ++=21(2.3)图2.1 任意区域的三角形单元离散 j (x j , y j )xyi (x i , y i )m (x m , y m )图2.2 3结点三角形单元),,(m j i xx c y y b y x y x a m j im j i j m m j i ⎪⎩⎪⎨⎧+-=-=-= (2.4)上式),,(m j i 表示下标轮换,即i m m j j i →→→,,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
岩土工程有限元大作业
题目:平面问题3结点三角形有限元法
的Matlab程序实现
专业:建筑与土木工程(岩土方向)
姓名:
学号:_________
2014年12 月31 日
1.概述
对于二维平面问题,运用有限单元法求解时,单元的类型有3结点三角形单元、4结点矩形单元以及高精度的三角形单元(6结点、10结点)等。
三角形单元对复杂边界有较强的适应能力,因此很容易将一个二维域离散成有限个三角形单元,在边界上以若干段直线近似原来的曲线边界,随着单元增多,这种拟合将越精确。
本文即基于相对比较简单且运用广泛的3结点三角形单元的有限元法编制Matlab 程序,解决一个悬臂梁端点承受竖向集中荷载作用时的位移计算问题,并绘出变形前后的图形作对比。
在分析过程中,将此问题简化为平面应力问题,取单位厚度进行分析。
以下一共分为两部分介绍,第一部分是理论部分,介绍三角形有限元法的基本求解过程;第二部分是程序部分,介绍具体的Matlab 程序实现过程。
2.三角形有限元法的基本求解过程 2.1 假设单元的位移函数
如图2.1所示为一端部承受竖向集中荷载作用的悬臂梁,将此问题简化为二维平面问题,梁取单位厚度,固定端简化为两个不动铰支座,已知悬臂梁的长度为8米,高度为1米,材料为钢材,它的弹性模量取2.06e11Pa ,泊松比取0.25,右端处作用的竖向荷载为100kN 。
二维域Ω被离散成如图所示的九个三角形单元,后续编程中的结点号和单元号都以此为基础,任取一三角形单元,设其结点编码为m j i ,,,以逆时针编码为正向(见图2.2)。
该三角形单元在x 、y 方向的位移函数表达式为:
m m j j i i u N u N u N u ++= (2.1) m m j j i i v N v N v N v ++=
(2.2)
其中()m j i i N i ,, =称为单元的插值函数或形函数
()y c x b a A
N i i i i ++=
21
(2.3)
图2.1 任意区域的三角形单元离散 j (x j , y j )
x
y
i (x i , y i )
m (x m , y m )
图2.2 3结点三角形单元
),,(m j i x
x c y y b y x y x a m j i
m j i j m m j i ⎪⎩⎪
⎨⎧+-=-=-= (2.4)
上式),,(m j i 表示下标轮换,即i m m j j i →→→,,。
(2.1)和(2.2)式简记为
()∑==i
i i m j i i N ,, u u
(2.5)
(2.5)式的矩阵形式是
[
]
e m j i m j
i
v u Na a a a N N N u =⎪⎭
⎪
⎬⎫⎪⎩⎪⎨⎧=⎭
⎬⎫
⎩⎨⎧=
(2.6)
其中⎥⎦⎤⎢
⎣⎡=i i
i N N 00N ,⎭
⎬⎫⎩⎨⎧=i i i v u a 。
2.2 单元应变矩阵和弹性矩阵
将位移函数(2.6)式代入平面问题的几何方程得到单元的应变表达式
[
]
e e m j i
Ba a B B B ε==
(2.7)
其中B 称为应变矩阵,
⎥⎥⎥⎥⎥
⎥⎥⎦
⎤⎢⎢⎢⎢⎢
⎢⎢⎣⎡∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂∂=x N y
N y N x N x N y
N y
N x
N x N y
N y
N x N m m m m j j j
j i i i
i i 0000
B (2.8)
将(2.3)式代入上式得
⎥⎥⎥⎦
⎤⎢⎢
⎢⎣
⎡=m m
m m j j
j j i i i i
b c c b b c c b b c c b A 00000
021B (2.9)
对于平面应力问题,单元的弹性矩阵如下:
⎥⎥⎥⎥⎥⎦
⎤⎢⎢⎢
⎢⎢⎣
⎡
-=2100001
1ννν
D B (2.10)
其中2
1ν-=
E
D 。
2.3 整体平衡方程
根据最小势能原理或变分原理,对总势能取驻值,即0=δπ得
()()∑∑=e
e
e
e
e
F a K
(2.11)
其中,单元刚度矩阵
tdxdy e
e B D B K ⎰Ω
=T
(2.12)
单元载荷列阵
⎰⎰⎰ΩΩ++-=e e
e
s e tds tdxdy tdxdy σ
T N f N σB F T T 0T
(2.13)
本文分析的问题只是在悬臂梁右端某一结点处作用一竖向荷载,荷载列阵相对比较简单,如果涉及到分布荷载,需要局部坐标到整体坐标的转换,形成整体荷载列阵。
2.4 组集单元矩阵到整体方程
按对号入座的原则对单元平衡方程进行组集得到整体求解的结构控制方程
F Ka = (2.14)
2.5 引入边界条件
边界条件包括外力边界条件和位移边界条件,对于本文分析的问题,外力边界条件主要是在右端点处有一个y 方向的集中荷载。
位移边界条件主要是左端的两个结点处在x 、y 两个方向位移为零。
2.6 求解整体离散方程
在求出单元刚度矩阵组集而成的整体刚度矩阵和单元等效荷载列阵以后,求解整体离散方程就变成求解线性方程组的问题了。
经过组集单元矩阵到整体矩阵形成2.14式中的整体刚度矩阵K 以及整体荷载列阵F ,求解位移矩阵就只需要用到Matlab 中的左除符号“\”即可。
3.Matlab程序实现过程
Matlab的求解程序应该包括一个主程序和若干个子程序,若干个子程序分别实现输入数据、计算单元弹性矩阵、应变矩阵、刚度矩阵以及单元刚度矩阵的组集、边界条件的处理、绘图等功能。
另外在主程序中定义全局变量,当在各个子程序中需要使用全局变量时,只需在各子程序中用命令global声明即可。
以下是程序中使用的全局变量的说明(首字母g代表global,表示全局变量Global Variables)
gMP------材料属性(Material Properties)
gNC------结点坐标(Node Coordinates)
gENN------单元结点编号(Element Node Number)
gBC------边界条件(Boundary Conditions)
gKA-------整体刚度矩阵
gFA-------整体荷载列阵
gND------计算得到的结点位移值(Nodal Displacement)
3.1求解主程序
3.2输入数据
3.3计算单元弹性矩阵子程序
3.5计算单元刚度矩阵子程序
3.7计算整体刚度矩阵子程序
3.8处理边界条件子程序3.8.1位移边界条件
3.8.2外力边界条件
3.9绘制变形前后的对比图子程序
说明:trisurf(Tri,x,y,z,c)三角表面图函数,用于生成三角形表面图。
Tri矩阵的每一行表示一个三角形的三个结点的结点编号,x,y,z表示三个结点的结点坐标。
C用来控制颜色。
3.10程序运行结果
3.10.1位移计算结果
3.10.1变形前后对比图(变形放大了1000倍)
4.结论
有限单元法在工程分析中应用广泛,它的基本思想是设法将实际上是无穷多自由度的连续介质问题近似的简化为由有限个“结点”构成的有限个自由度问题,并以这些结点的“自由度”为未知量,设法将控制方程近似的化为一组线性代数方程,然后用计算机求解。
本文通过平面问题三结点三角形有限单元法编制Maltab程序,实现悬臂梁承受集中荷载时的变形计算。
通过编制程序,认识到了有限元求解问题的一般流程,加深了对课程内容的理解与掌握。
在编程的过程中也遇到很多问题,比如这个程序中的核心部分——单元刚度的组集问题,各个单元刚度矩阵按照对号入座的原则组集成整体刚度矩阵,这里要使用两个循环语句才能实现。
另外结点固定的位移边界条件如何处理也不太清楚,在查阅相关有限元书籍后,知道了有划零置一法和乘大数法等,本文中采用的是划零置一法,即在整体矩阵中将与零节点位移相对应的行列中,将主对角元素改为以1,其他元素改为0,在荷载列阵中将与零节点位移相对应的元素改为0。
这种方法引入强制边界条件比较简单,不改变原来方程的阶数和未知量的顺序编号。
最后需要说明的是本文的荷载边界条件是点荷载,编程比较容易处理,进一步的研究中可以考虑均匀分布荷载以及变化的荷载作用下,程序如何编写。
10。
